1. Introduction
Recently, with the development of consumer-grade scanner devices (e.g., Microsoft Kinect, Xtion Pro, Google Project Tango, and Intel RealSense), triangulated meshes can be easily acquired from the real world. The scanned meshes can be further used in a variety of application domains, such as geometry processing, computer vision, virtual reality, cultural heritage preservation, and terrain modeling. However, these scanned meshes are inevitably contaminated by different kinds of noise, introduced by the scanning process and the reconstruction algorithm. The noise can not only degrade the quality of meshes, but also cause errors in downstream geometry applications [
1]. Thus, the task of removing noise from scanned meshes becomes increasingly important. The main challenge is to remove noise while preserving both sharp features (including edges and corners) and fine details as well as preventing introducing undesired staircase effects in smooth regions. This problem becomes more difficult when meshes are polluted by different kinds of noise including Gaussian, impulsive, and mixed noise.
Mesh denoising is a fundamental problem in geometry processing, which has been studied for years. Early, filtering methods are wildly applied in mesh denoising. The filtering methods can be divided into two categories: isotropic and anisotropic methods. The isotropic methods [
2,
3] are classical for their simplicity. Although these methods can remove noise, they often cause significant shape distortion. The reason is that these methods do not consider geometric features during the denoising. Later on, for preserving geometric features, many anisotropic methods were proposed [
4,
5,
6,
7,
8,
9]. When the level of noise is low, the anisotropic methods work well. However, when the noise level increases, these methods tend to blur sharp features. Recently, bilateral filtering methods have been studied in mesh denoising [
10,
11]. Since these methods also belong to anisotropic methods, they still blur sharp features. In order to preserve sharp features, some works [
12,
13,
14] applied the bilateral filtering in the face normal field. Unfortunately, when the noise level is high, the bilateral normal filtering proposed by Zheng et al. [
12] still cannot recover sharp features well. Zhang et al. [
13] proposed a normal filtering method based on a well-designed guided normal field. Although their method can preserve sharp features, it lacks robustness to the mesh topology. The robust normal filtering method [
14] can also preserve sharp features, but it usually blurs fine details.
Recently, variational methods based on sparsity have been proved successful in image restoration [
15,
16,
17] for the edge-preserving property of them. These methods are inspired by the emerging theories of sparse signal reconstruction and compressive sampling [
18,
19]. Inspired by these, sparse optimization methods are introduced in mesh denoising [
20,
21,
22,
23,
24]. He and Schaefer [
20] extended
minimization from images to surfaces, which induces sparsity on an edge-based operator. However, the
minimization is NP-hard. The works [
21,
22] extended total variation (TV) minimization for preserving sharp features of the mesh. To handle irregular sampling meshes corrupted by different kinds of noise, Lu et al. [
24] presented an
-norm normal filtering method. Although the above sparsity-based methods [
20,
21,
22,
23,
24] can remove noise while preserving sharp features, they inevitably suffer undesired staircase effects in smoothly curved regions. This problem is even worse for the
minimization [
20] for its high sparsity requirement. In order to overcome the staircase effects introduced by these first order methods [
20,
21,
22,
23,
24], Liu et al. [
1] proposed a high order normal filtering method, which can preserve sharp features and simultaneously prevent introducing staircase effects in smooth regions. Unfortunately, when the noise level increases, the high order method [
1] sometimes smoothes sharp features.
More recently, researchers proposed some methods based on geometric priors. Assuming the additive noise of the noisy mesh is Gaussian noise, a method based on compressed sensing was proposed to decouple features and the noise [
25]. However, if the noise level is high, it is difficult for this method to distinguish features from the noise. With the assumption of geometric features are not seriously corrupted by the noise, Lu et al. [
23] first detected geometric features from a pre-filtered mesh, and then they reconstructed the denoised result by the detected features. On the contrary, without any assumptions about the underlying surface, a data-driven method has been employed for mesh denoising [
26]. The method first learns non-linear regression functions mapping filtered face normal descriptors to face normals of the clean mesh, and then employs the learned functions for computing the filtered face normals. This method can effectively remove noise and preserve geometric features. Yet, it is very dependent on the completeness of the training data set.
As we can see, the above mentioned mesh denoising methods have their own limitations. In summary, except the method [
1], filtering methods and sparse optimization methods are either preserve fine details or sharp features well. Moreover, without considering the noise type, these methods are difficult to handle different kinds of noise, which often exist in the real data acquired by consumer-grade scanners. To a certain extent, these problems will degrade the quality of denoising results. To overcome the above limitations, we present a two-stage mesh denoising method. At the first stage, we propose a variational normal filtering model based on a triple sparsity prior. After that, we evolve the mesh to match the filtered face normals at the second stage. Taking a noisy mesh as the input, our method can robustly handle various kinds of noise while preserving geometric features.
Specifically, the contributions of the paper are listed as follows:
We present a novel normal filtering model with three sparsity terms. The model can recover both sharp features and fine details and simultaneously prevent introducing unnatural effects in smooth regions. Besides, the model is robust against different kinds of noise.
We develop an efficient algorithm based on variable-splitting and augmented Lagrangian method for solving the problem.
We demonstrate the performance of our denoising method on synthetic meshes and a variety of scanned data produced by the laser scanner, Kinect v1, Kinect v2, and Kinect-fusion. Our method outperforms compared methods for both synthetic meshes and real scanned data.
The rest of the paper is organized as follows. In
Section 2, we first propose a variational normal filtering model based on a triple sparsity prior. Then, an iterative algorithm using augmented Lagrange method and variable-splitting technique is presented to solve the problem. Finally, according to the filtered face normals, the vertex positions are updated by a robust vertex updating scheme. The comparisons about our mesh denoising method and state-of-the-art methods are demonstrated in
Section 3.
Section 4 concludes the paper.
2. Robust Mesh Denoising
Similarly to some previous mesh denoising methods [
9,
12,
13,
14,
21], our method belongs to two-stage methods, i.e., face normal filtering followed by updating vertices.
2.1. Normal Filtering
In this subsection, we first briefly give some necessary notations, and then introduce our normal filtering method. A mesh of arbitrary topology with no degenerate triangles in is represented as M. The set of vertices, edges, and triangle faces of M are denoted as , , and , respectively. Here, , , and are the numbers of vertices, edges, and faces of M. Furthermore, we denote the 1-disk of vertex as , which is the set of triangles containing .
To filter the face normals of the noisy input, we propose a normal filtering model containing three sparsity terms. It consists of a double sparsity prior on first order and second order variations of the face normal field to recover sharp features, fine details, and smooth regions and a third sparsity prior for handling different kinds of noise. Besides, we also present an iterative algorithm to solve the proposed normal filtering model.
2.1.1. Normal Filtering Model
Given a noisy mesh
, we represent its face normals as
. To filter the noise of
, we treat the face normals
as a variable and propose the following normal filtering model:
where
,
, and
are positive parameters used to balance the four terms including one
-norm term and three
-norm terms. The first two terms are used to control the degree of denoising, while the last two terms are used to regularize the noisy mesh for noise removal and feature preserving. In the following, we will introduce the effects of these four terms with
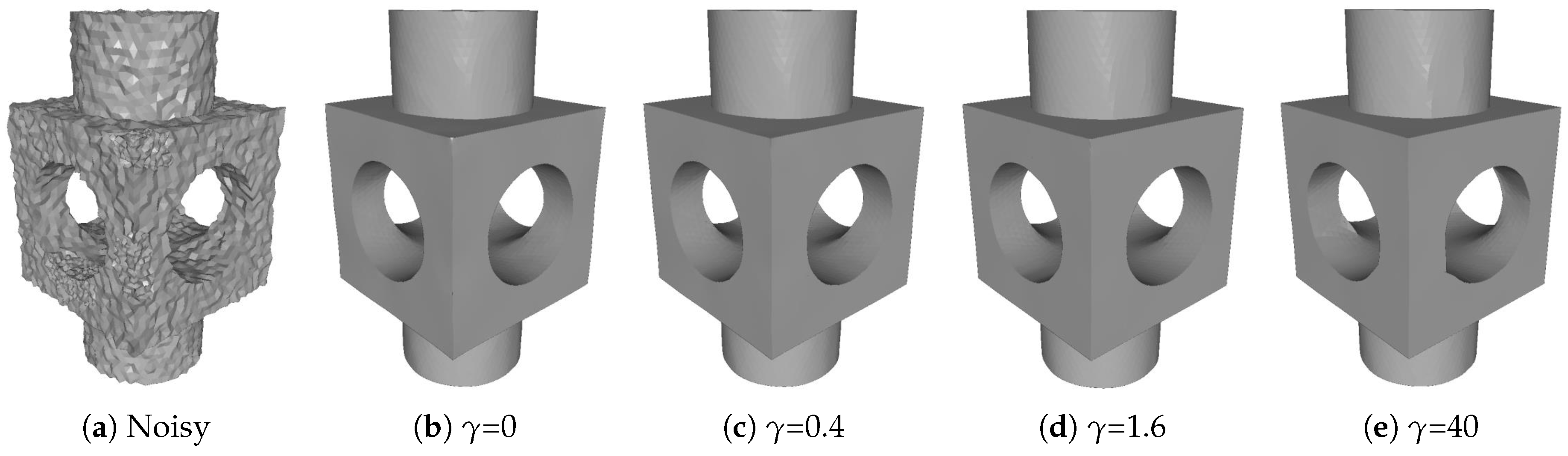
Figure 1.
-norm fidelity term :where
is the area of triangle
. The
-norm fidelity term is used to make the solution to harmonise well with the input face normals. It is well known that this least square fidelity term is used for additive Gaussian noise. As we can see in the first pair of magnified views of
Figure 1, within the patch corrupted by Gaussian noise, this least square fidelity term can keep the solution of the face normals (see the magnified view on the right) close to the input face normals (see the magnified view on the left).
-norm fidelity term : Similarly to the
-norm fidelity term, the
-norm fidelity term also encourages the solution to be close to the input face normals. This
-norm fidelity term is less well known. It can be used to avoid the influence of outliers for impulsive noise. As we can see in the second pair of magnified views of
Figure 1, this
-norm fidelity term encourages replacing the outliers with less dependence on their exact value. In other words, this fidelity term make the regularization be robust against outliers for impulsive noise.
TV regularization term :where
is the length of edge
e, and ∇ is a discrete gradient operator defined over triangulated meshes. This first order operator (gradient operator) is defined on each edge of the mesh, and its computation can refer to Ref. [
21].
The TV regularization has been proven very successful in image processing for its excellent edge-preserving property [
21]. We extend it to mesh denoising for preserving sharp features (including edges and corners) while removing noise. As can be seen in
Figure 1, the TV regularization term can remove undesired geometric oscillations at the edges and corners of the mesh (see the third pair of magnified views). Thus, this TV regularization term enables sharp features preserving while removing noise. However, the TV regularization tends to optimize the face normal field to be a piecewise constant field, which introduces undesired staircase effects in smooth regions [
1]. These undesired staircase effects will degrade the quality of denoising results.
Anisotropic high order regularization term :where
is the length of line
l connecting the barycenter with one vertex of triangle
. The anisotropic second order operator
is defined on each line of the mesh, which reads as follows
where
and
are two edges sharing the common vertex of
l,
is the triangle sharing
with
, and
is the triangle sharing
. For more details about these descriptions, we refer readers to [
1].
and
are positive weights defined as
where
and
are the normals of two faces sharing the common edge
e. We should point out that, we discretize the second order operator
in an anisotropic manner. In contrast, the discretization of the second order operator in Ref. [
1] is isotropic. Compared to the discretization in Ref. [
1], our discretization has better feature-preserving property.
As mentioned before, the TV regularization term will introduce undesired staircase effects in smooth regions. In order to overcome this problem, we use the anisotropic high order regularization (
4) to recover the smooth regions while preventing introducing the staircase effects; see the fourth pair of magnified views of
Figure 1 for example. Moreover, the anisotropic high order regularization will not blur sharp features during the smoothing process.
2.1.2. Augmented Lagrangian Method for Solving the Normal Filtering Model
Because of the nondifferentiability and nonlinear constraints of the model (
1), it is difficult to directly solve it. Recently, variable-splitting and augmented Lagrangian method (ALM) have achieved great success in
related optimization problems [
1,
21,
22]. Here, we introduce three auxiliary variables and employ ALM to solve the problem. Furthermore, since the weights (
5) are estimated from the noisy input, we dynamically update them at each iteration to improve the quality of denoising results.
We first introduce three auxiliary variables
, and
, and then reformulate the problem (
1) as
where
,
, and
To solve the above constrained optimization problem, we define the following augmented Lagrangian function
where
,
, and
are three Lagrange multipliers, and
,
, and
are the positive penalty coefficients. Note that
is the number of lines connecting the barycenter and one vertex of triangle
. We solve the problem (
6) by iteratively solving four subproblems: the
-subproblem,
-subproblem,
-subproblem, and
-subproblem. In the following, we discuss solutions to these four subproblems.
(1)
-subproblem: the sub-minimization problem of
can be written as
which is a quadratic optimization with the unit normal constraints
. We first fix the variables (
, and
), and then use an approximate strategy to solve this problem. Specifically, we ignore the term
and solve the problem
Then, we project the solution of the problem (
7) to a unit sphere. Generally, the solution of the quadratic optimization problem (
7) can be easily achieved by sparse linear system, which can be solved by using various numerical packages, such as Eigen, Taucs, and Math Kernel Library (MKL).
(2)
-subproblem: the sub-minimization problem of
is given as
This problem is easy to solve due to the energy function (
8) can be spatially decomposed, where the minimization problem w.r.t. each face is performed individually. Thus, for each
, we only need to solve the following problem
which has a closed form solution as
where the Shrink operator is defined as Shrink
.
(3)
-subproblem: the sub-minimization problem of
is given as
The sub-problem of
is separable and can be formulated as edge-by-edge problems. So, for each
, we have the following simplified problem
which has a closed form solution as
(4)
-subproblem: the sub-minimization problem of
can be formulated as
Since the energy function (
12) w.r.t. each line is individually performed, the subproblem (
12) can be solved independently. For each
, we solve the following problem
which has a closed form solution
The entire procedure for solving the problem (
6) is outlined in Algorithm 1. The algorithm iteratively solves the above four subproblems and updates the Lagrange multipliers and weights (
5). Since the weights (
5) estimated from noisy face normals are not accurate, we dynamically update them in each iteration for preserving geometric features better.
| Algorithm 1: ALM for Solving Normal Filtering Model (1) |
![Sensors 19 01001 i001]() |
2.2. Robust Vertex Updating
After optimizing the face normals by the normal filtering model (
1), the vertex positions of the mesh should be updated to match the filtered face normals. To this end, we use a vertex updating scheme presented by Liu et al. [
1], which can robustly reconstruct the mesh without foldovers. The method updates the vertex positions by minimizing the following problem
where
are vertices of
with counterclockwise order,
is the vertex positions of the noisy mesh and
is a small positive parameter.
We can reformulate the partial derivatives of (
14) with respect to
as follows:
where
is the updating normal of
according to the updated
v (the derivation process of formula (
15) can refer to Ref. [
1]). With gradient information calculated from (
15) and the initial vertex positions, we adopt Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm [
27] to solve the model (
14). In each iteration, BFGS algorithm uses the energy and gradient evaluated at the current and previous iterations.