Energy/Area-Efficient Scalar Multiplication with Binary Edwards Curves for the IoT
Abstract
:1. Introduction
- The detailed implementation and assessment of energy-reducing techniques are presented. The techniques employed are often used in the literature, but the actual effectiveness of each one is seldom explored. In this paper we aim at filling this gap by providing detailed implementation results. With this study, researchers aiming at producing new low-energy designs can have a precedent for choosing the strategies best suited to their projects.
- Our architectures improve the state of the art in regards to area/energy efficiency. This is in part thanks to the carefully designed cryptosystem, and to the followed design methodology.
- We have created and described a novel evaluation metric for assessing the efficiency of the proposed architectures in terms of energy reduction and area increments. This metric can account for variations in the measurement units, the operational frequency, and the underlying finite field. Thanks to these points we were able to employ the novel metric for benchmarking our architectures and the entirety of the state of the art for low-power/low-energy scalar multiplication realizations.
2. Preliminaries
2.1. Elliptic Curve Cryptography
2.2. Power and Energy
2.3. Percentile Differences
2.4. Evaluation Environment
3. Energy Reduction in the Literature
4. Methods
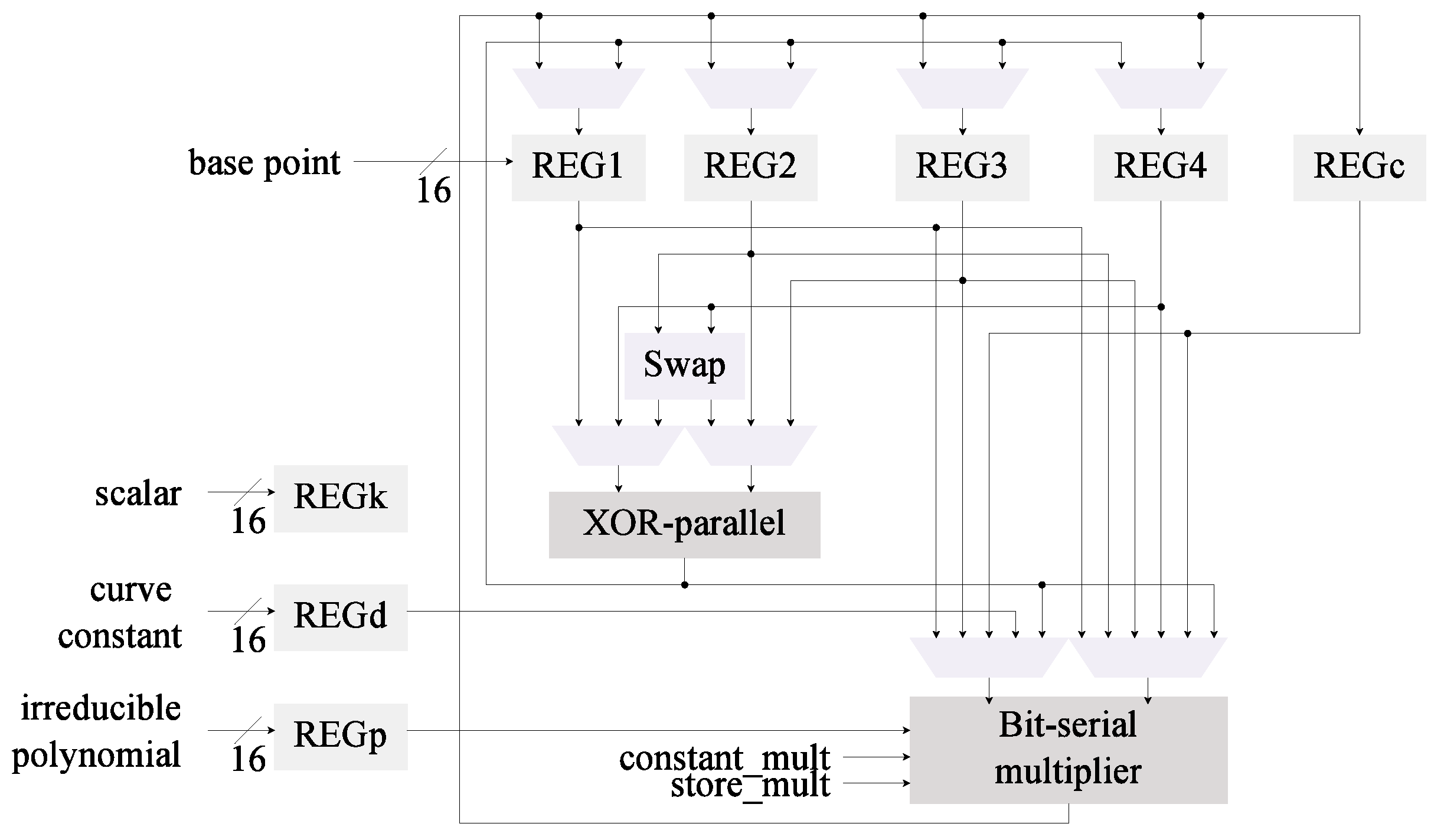
4.1. Starting Point: Low-Area kP Architecture
4.2. Modification 1: Inversion Algorithm
4.2.1. Fermat’s Little Theorem
4.2.2. Divisions on Finite Fields
4.2.3. Wang Inversion
| Algorithm 1 Wang Inversion Method. |
| Input:, the irreducible polynomial of Output: for to do end for return |
4.2.4. Itoh-Tsujii Inversion Algorithms
| Algorithm 2 Itoh-Tsujii Inversion for Where . |
| Input: with , the irreducible polynomial of Output: for to do for to do end for end for return |
| Algorithm 3 Itoh-Tsujii Inversion for Generic Binary Fields Where Extra Storage is Used. |
| Input:, the binary representation of m, the irreducible polynomial of Output: for to do for to do end for end for for to 1 do if then for to do end for end if end for return |
| Algorithm 4 Itoh-Tsujii Inversion for Generic Binary Fields Where Additional Cycles are Required. |
| Input:, the binary representation of m, the irreducible polynomial of Output: for to do for to do end for end for for to 1 do if then for to do end for for to i do for to do end for end for end if end for return |
4.2.5. Comparison of the Inversion Methods Reviewed
4.2.6. Implementation of the Itoh-Tsujii Inversion
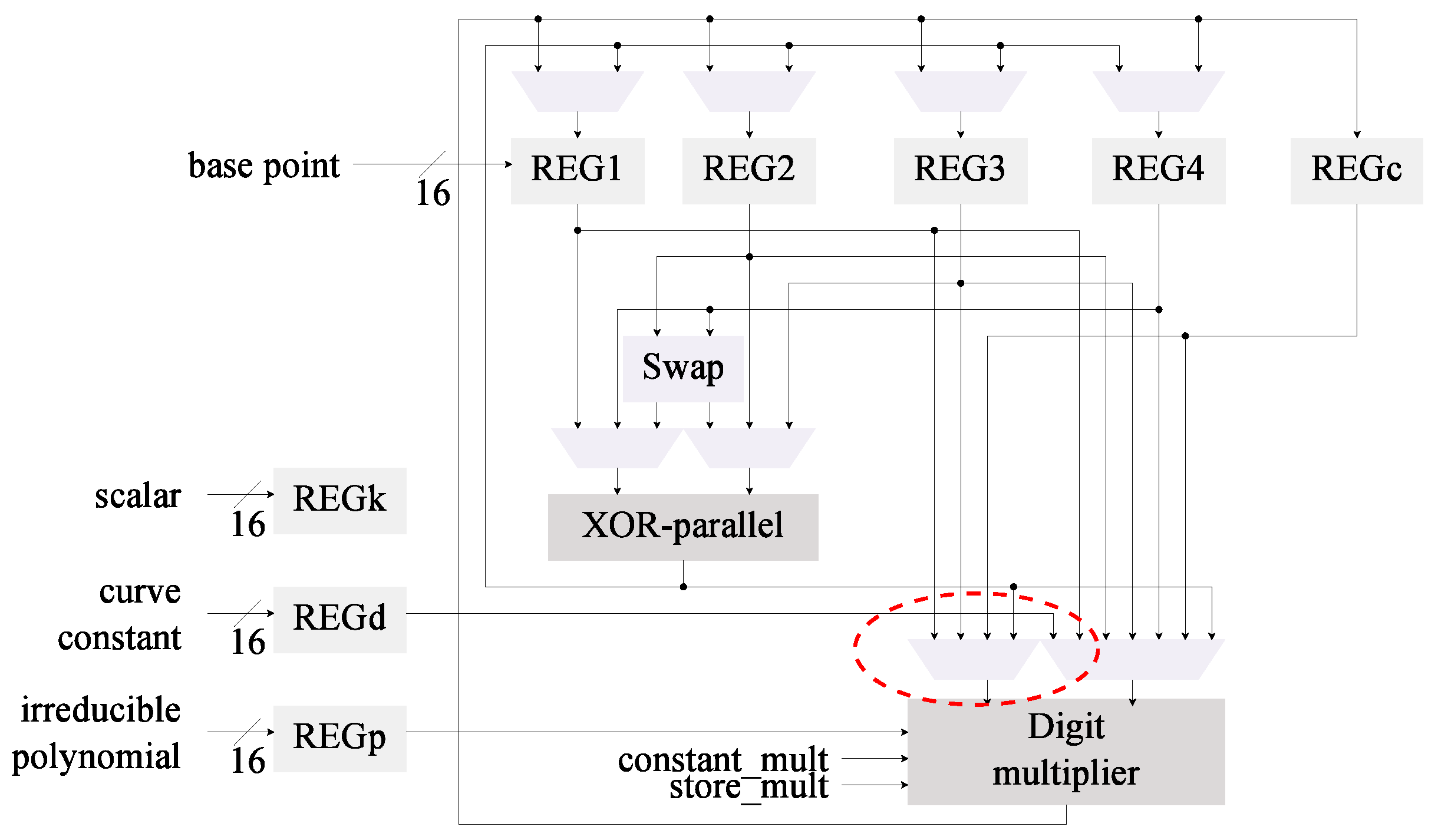
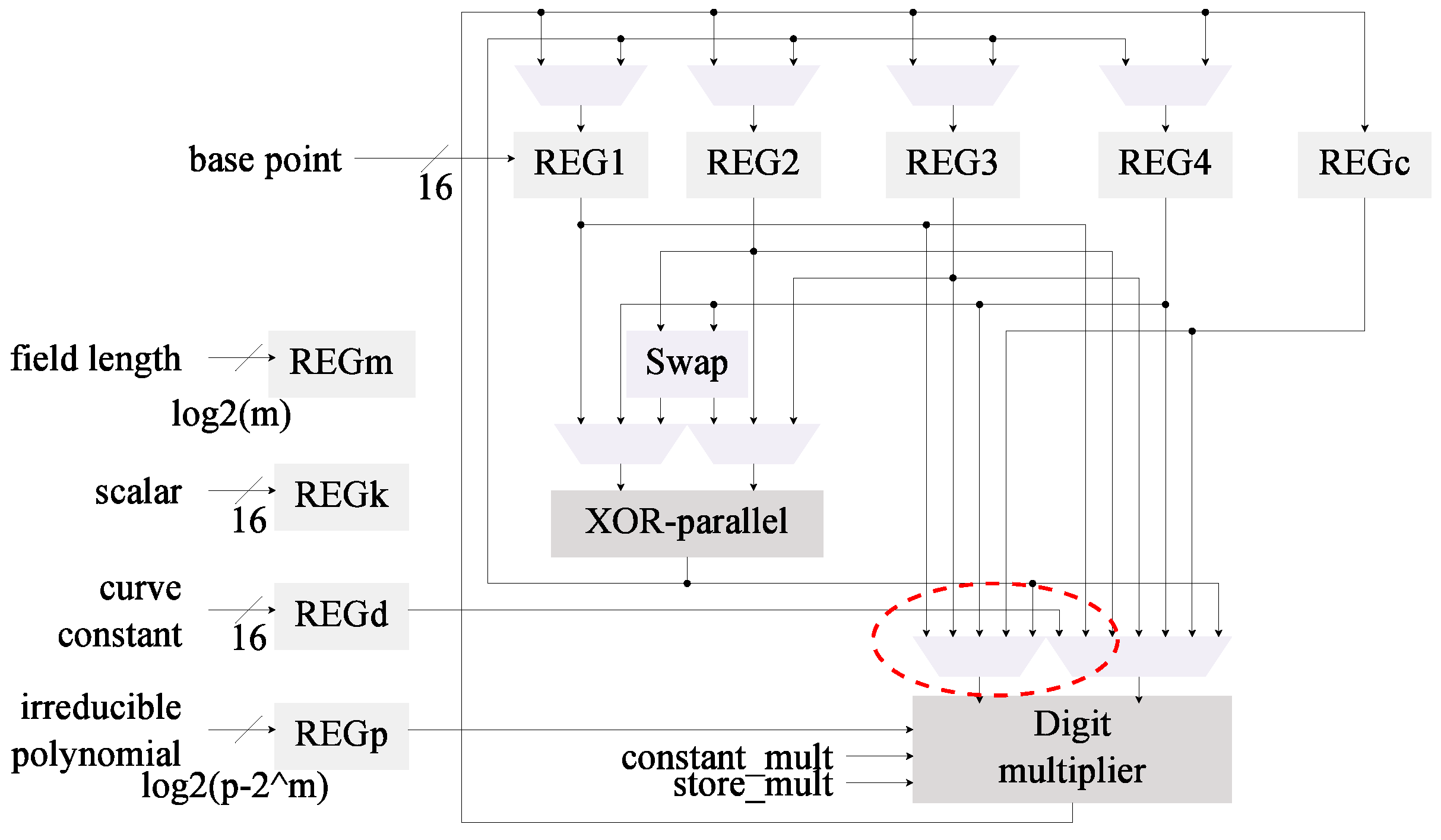
4.3. Modification 2: Field Multiplier
4.3.1. Digit-Based Multiplier
| Algorithm 5 Digit Multiplication in Where d is the Digit Size [55]. |
| Input:, the irreducible polynomial of Output: for to 0 do end for return |
4.3.2. Implementation of the Digit Multiplier
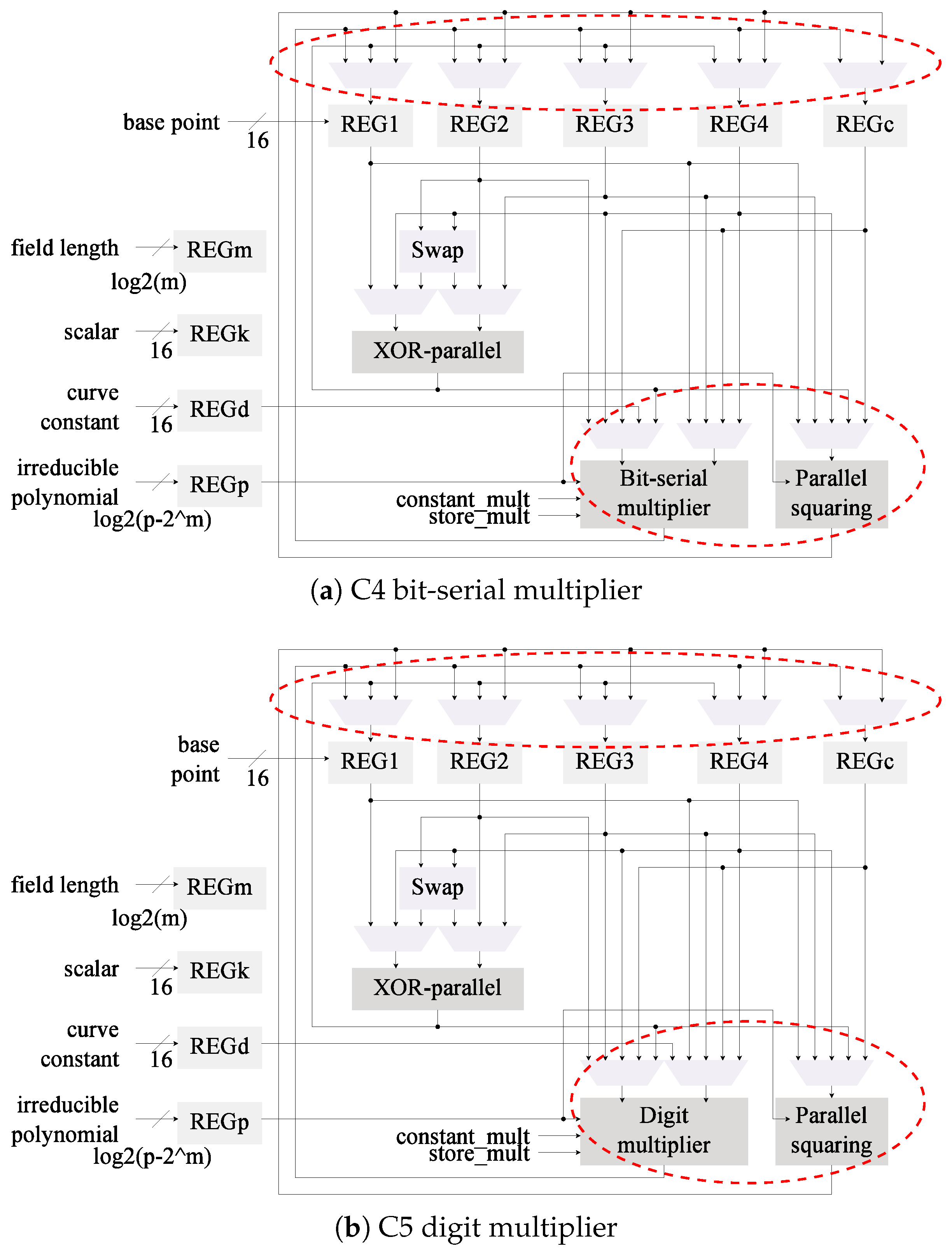
4.4. Modification 3: Squaring Module
4.4.1. Field Squarings
4.4.2. Implementation of the Squaring Module
4.5. Other Strategies
4.6. Summary
5. Energy Savings in Relation to Area Costs
5.1. Novel Metric for Efficiency of Energy Oriented Optimizations in Regards to Area Costs
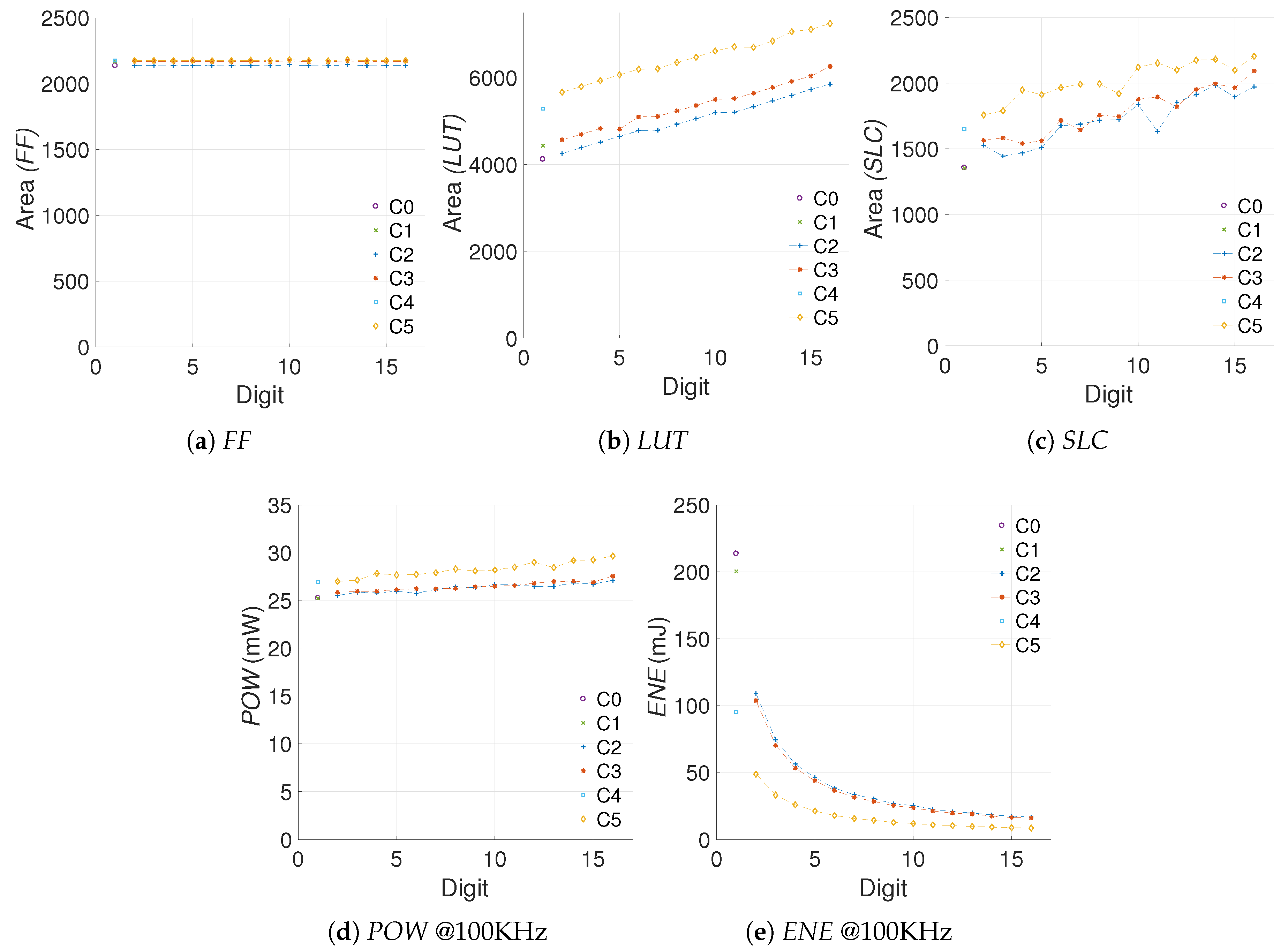
5.1.1. Selecting the Data
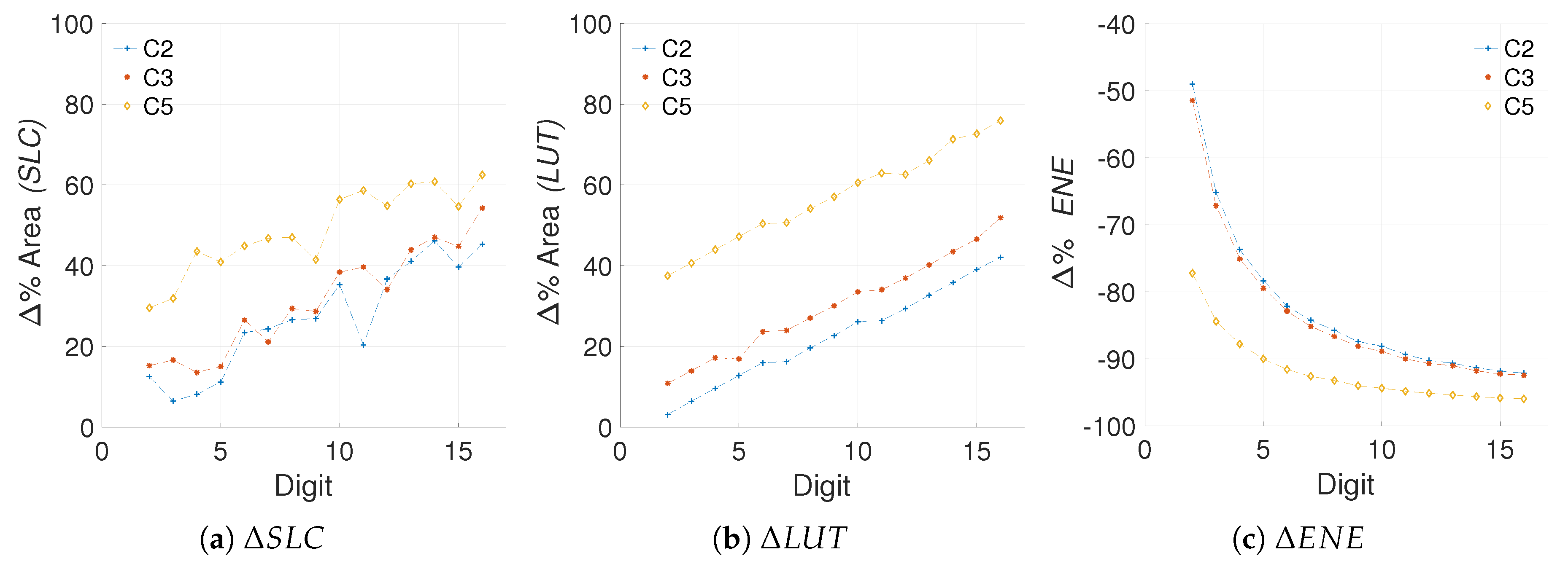
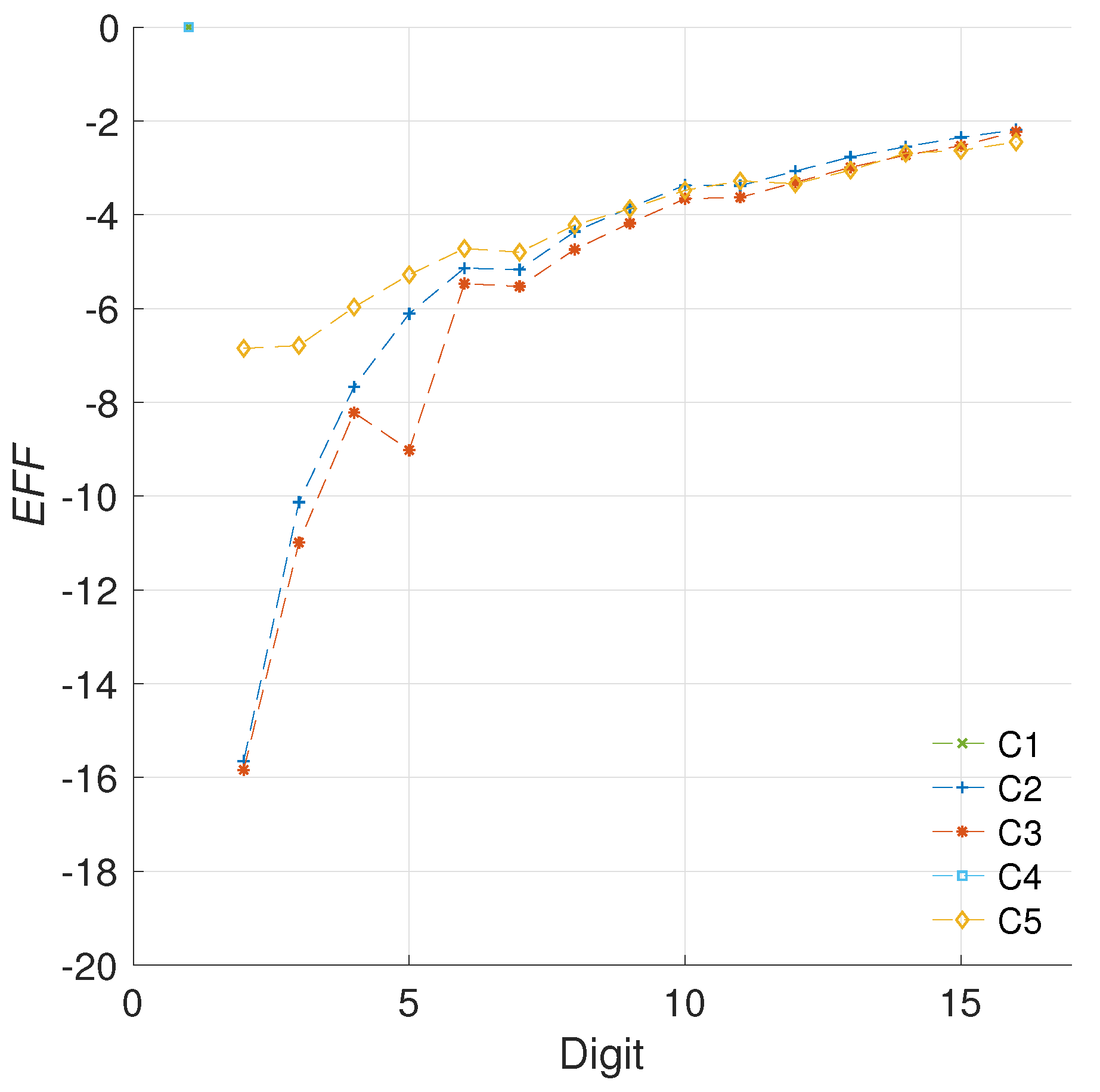
5.1.2. Efficiency Metric
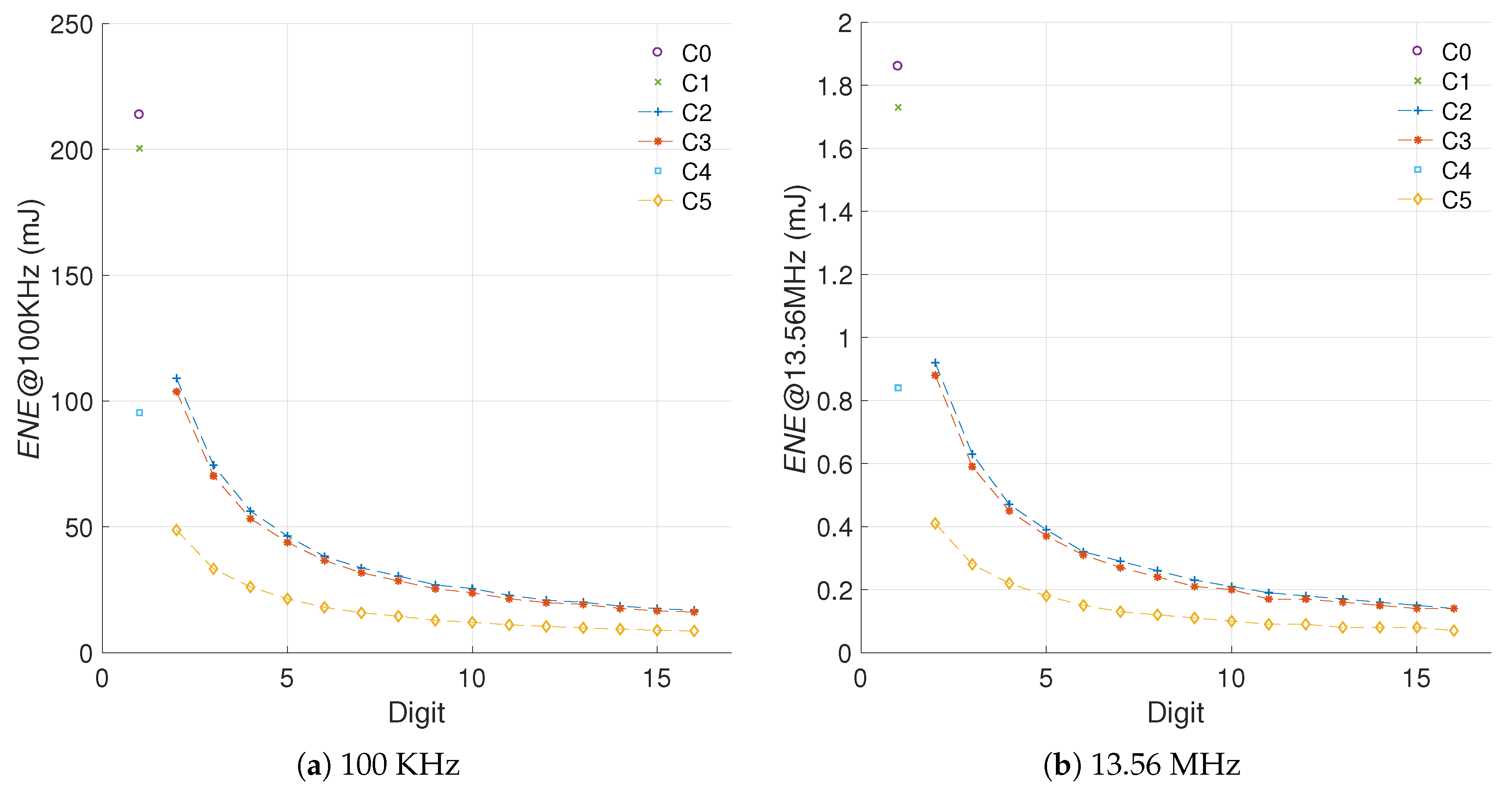
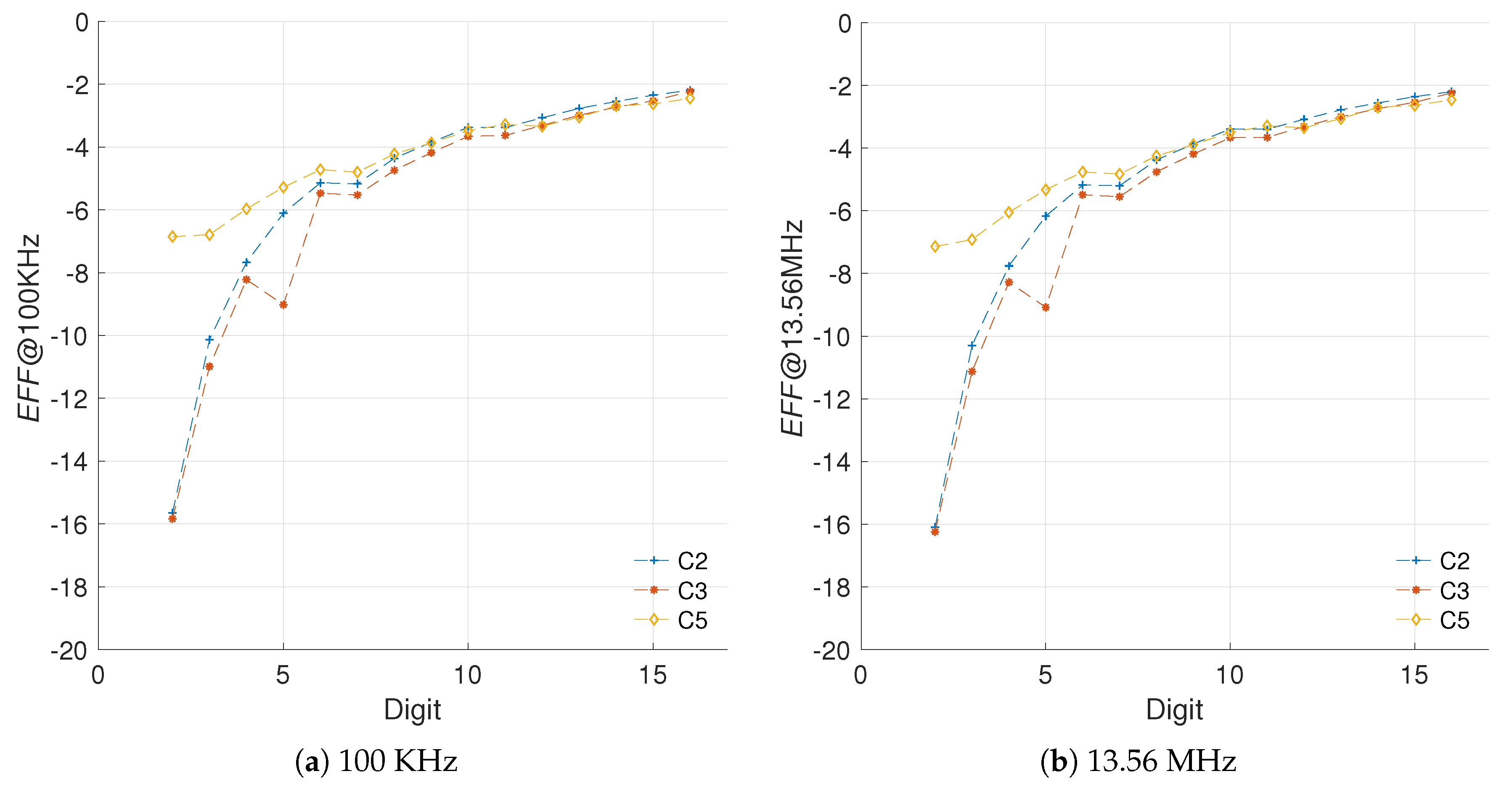
5.1.3. Sensitivity to Frequency Variations
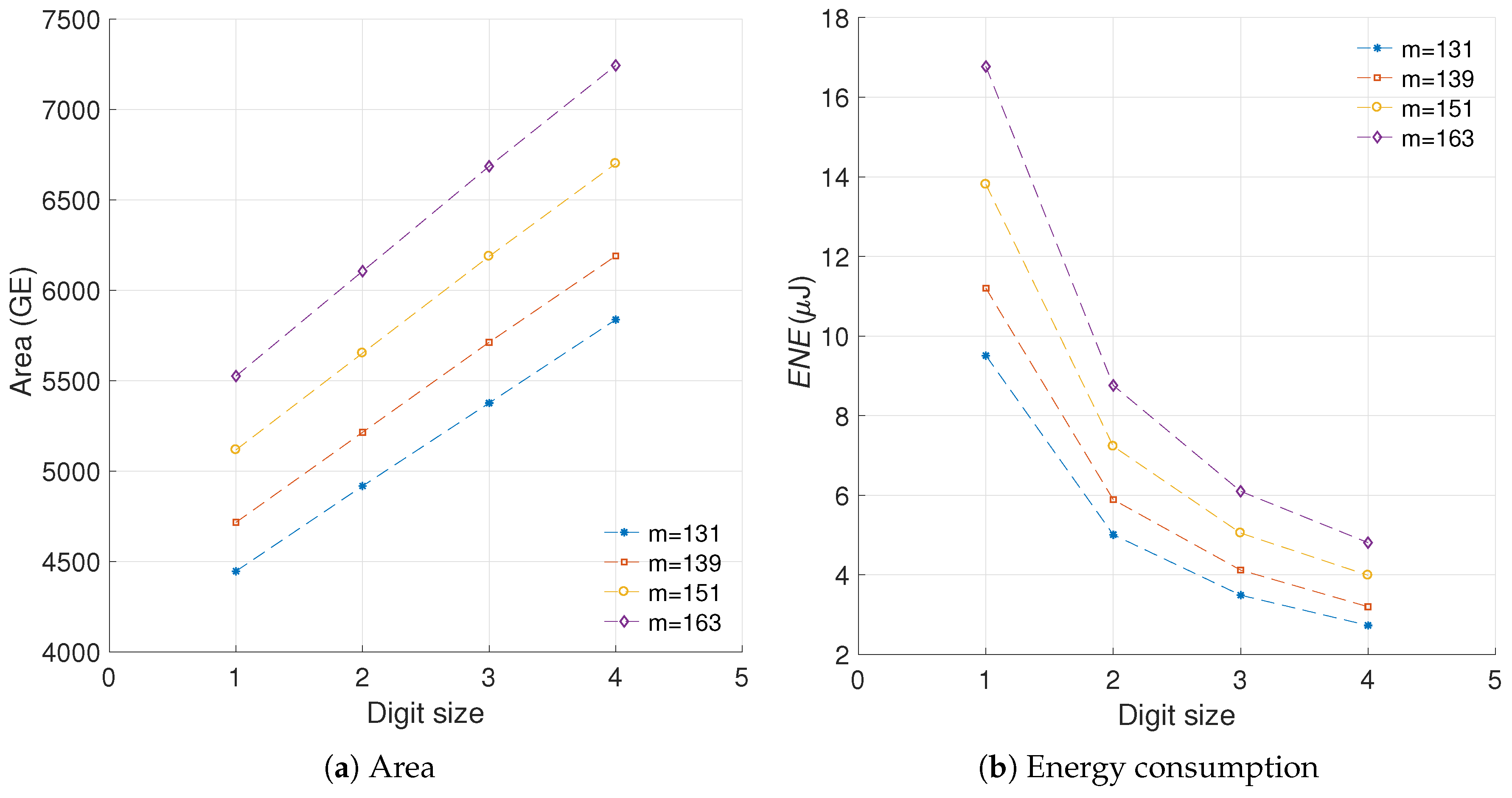
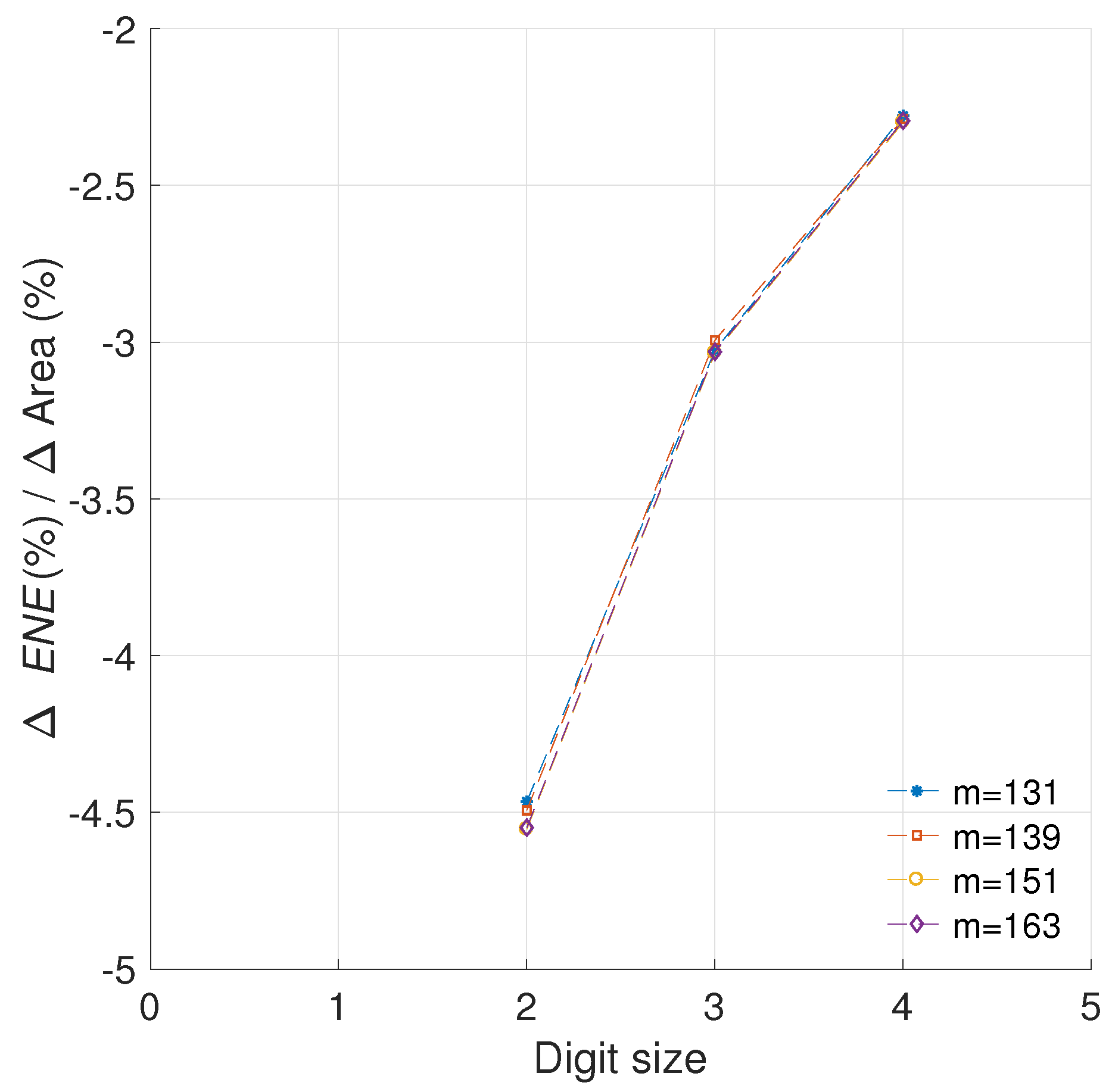
5.1.4. Sensitivity to Different Curve Sizes
5.1.5. Sensitivity to the Implementation Technology
5.2. Applying the Proposed Metric for Comparing Our Work with the State of the Art
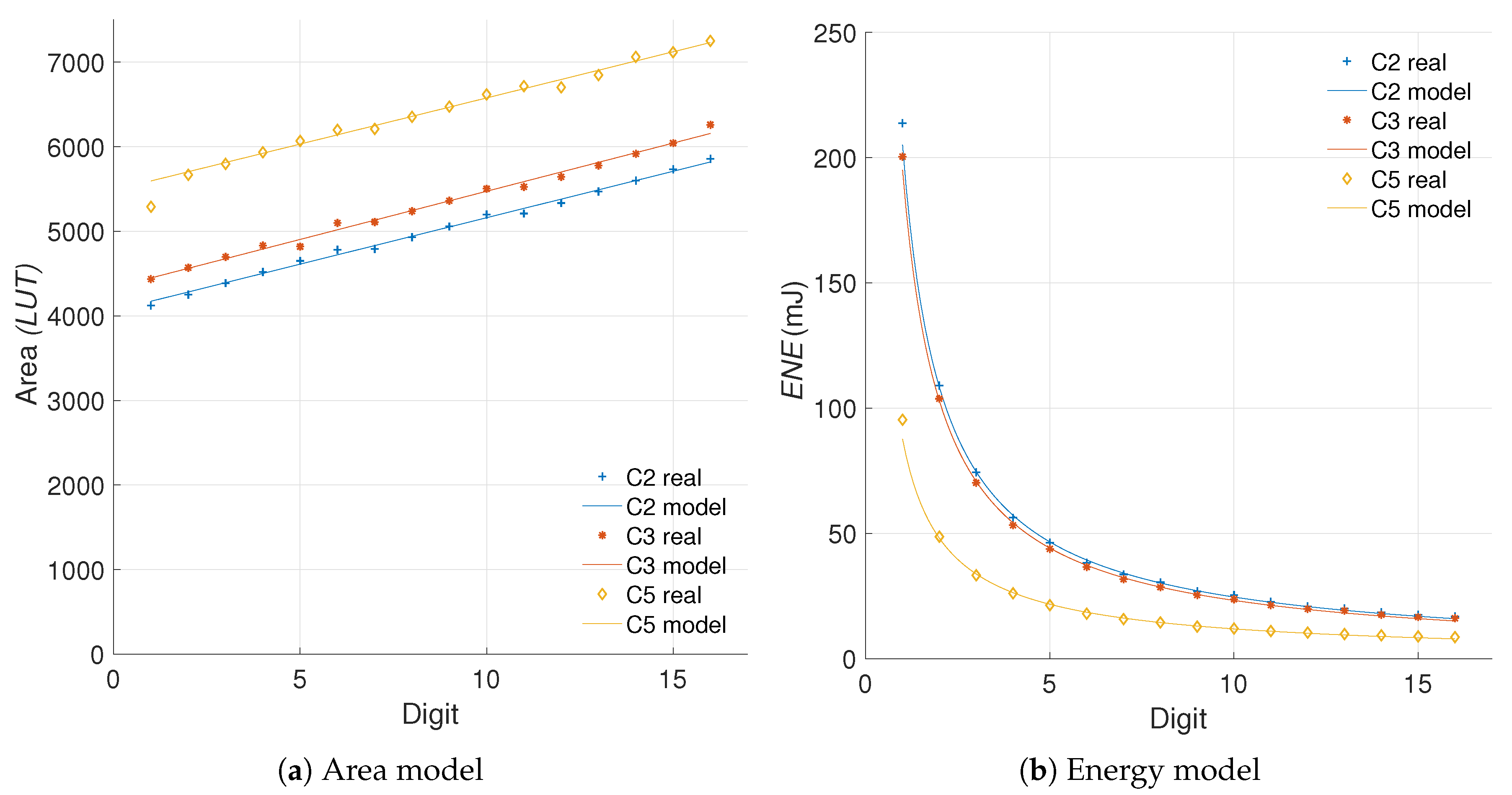
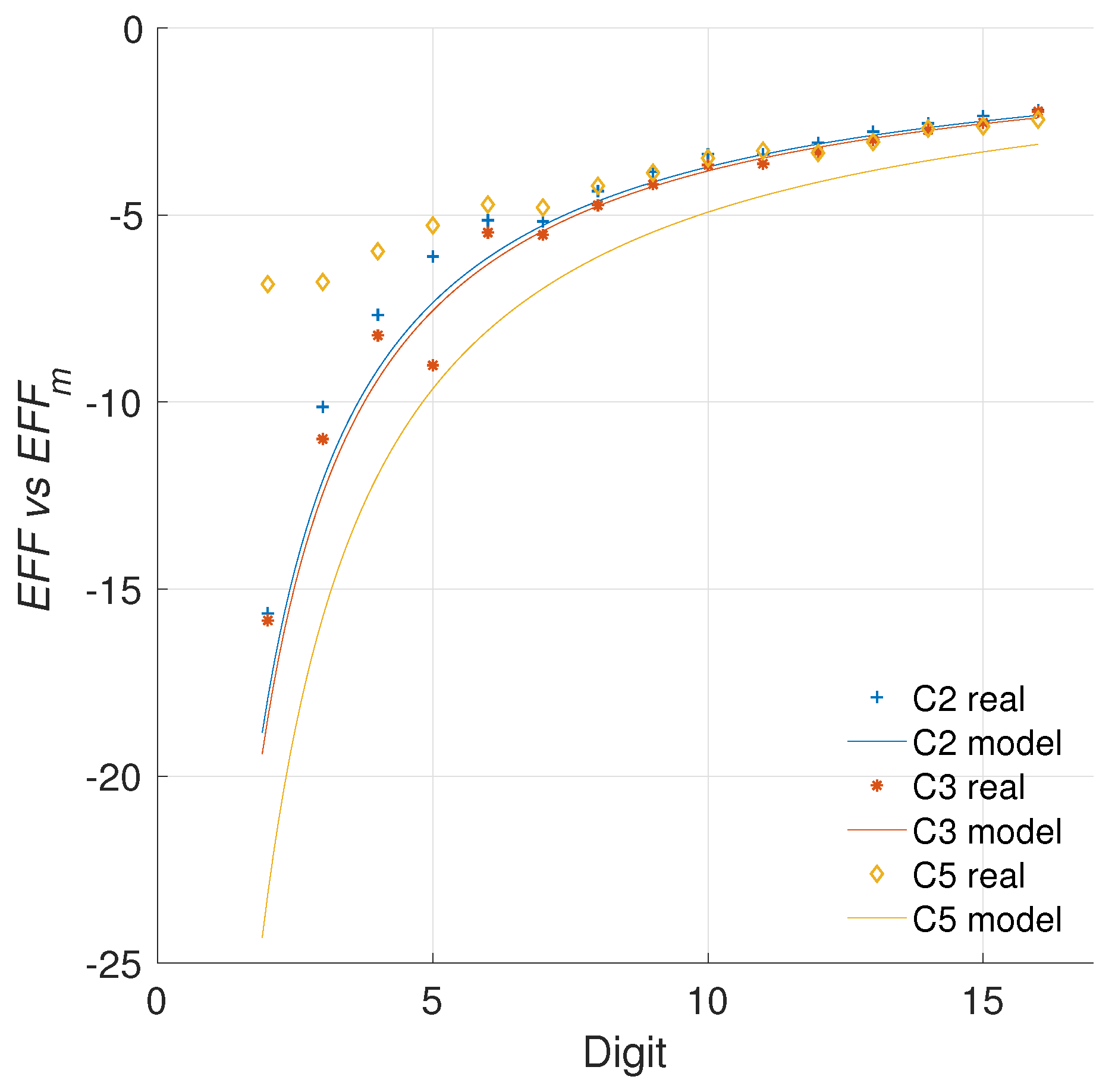
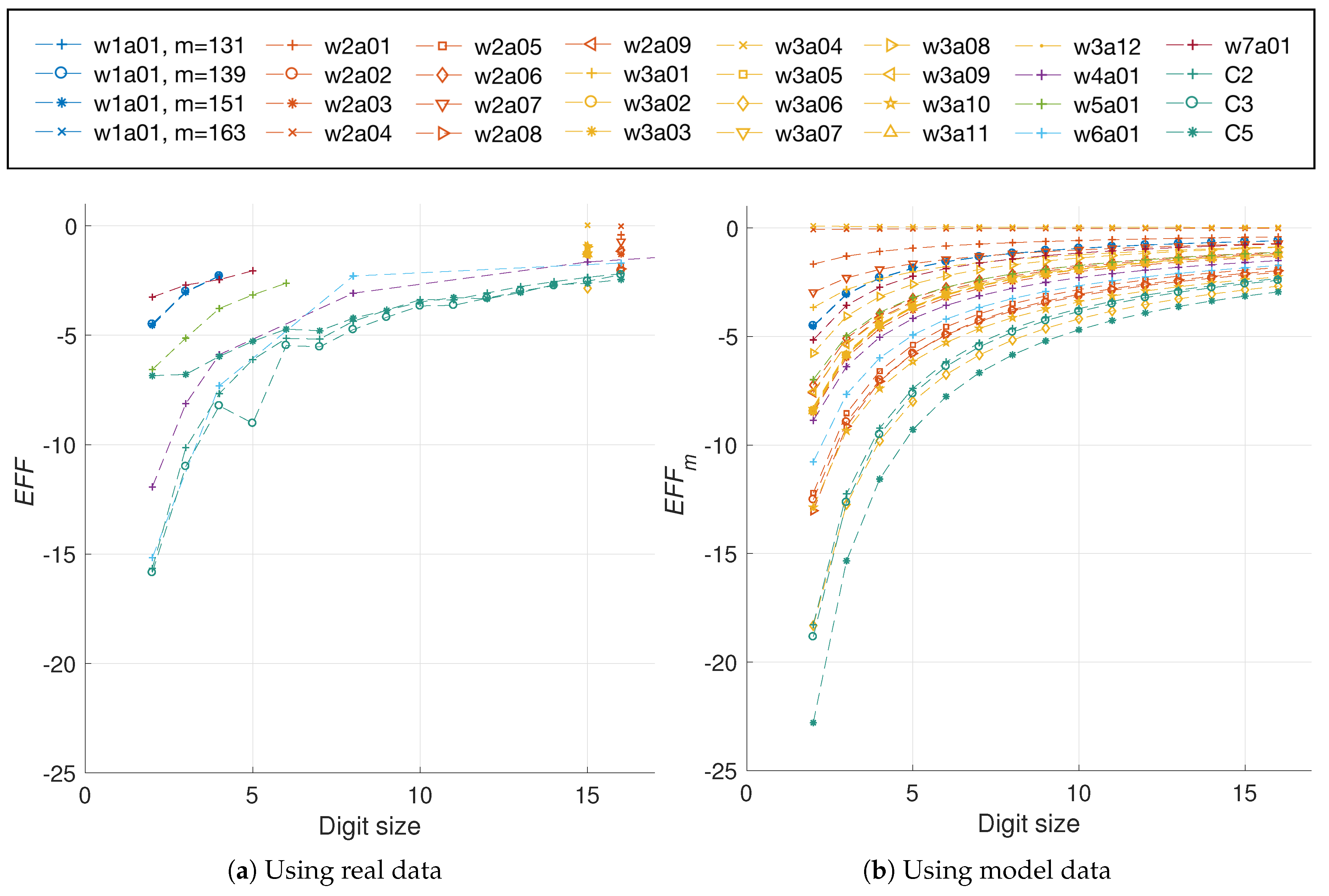
5.2.1. Modeling the Data
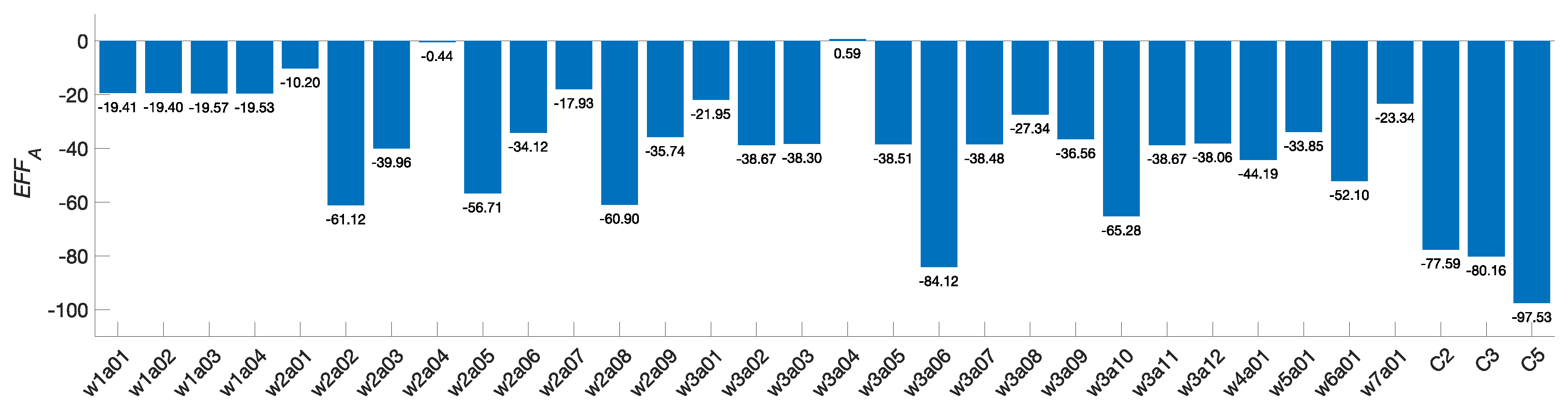
5.2.2. Quantifying the Efficiency
5.2.3. Comparison with the Literature
5.3. Limitations of the Proposed Method
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mangia, M.; Pareschi, F.; Rovatti, R.; Setti, G. Low-Cost Security of IoT Sensor Nodes With Rakeness-Based Compressed Sensing: Statistical and Known-Plaintext Attacks. IEEE Trans. Inf. Forensics Secur. 2018, 13, 327–340. [Google Scholar] [CrossRef]
- Kumar, P.; Lee, H.J. Security Issues in Healthcare Applications Using Wireless Medical Sensor Networks: A Survey. Sensors 2012, 12, 55–91. [Google Scholar] [CrossRef] [PubMed]
- Perez-Torres, R.; Torres-Huitzil, C.; Galeana-Zapien, H. An On-Device Cognitive Dynamic Systems Inspired Sensing Framework for the IoT. IEEE Commun. Mag. 2018, 56, 154–161. [Google Scholar] [CrossRef]
- Khan, M.K.; Alghathbar, K. Cryptanalysis and Security Improvements of ‘Two-Factor User Authentication in Wireless Sensor Networks’. Sensors 2010, 10, 2450–2459. [Google Scholar] [CrossRef] [PubMed]
- Buratti, C.; Conti, A.; Dardari, D.; Verdone, R. An Overview on Wireless Sensor Networks Technology and Evolution. Sensors 2009, 9, 6869–6896. [Google Scholar] [CrossRef] [PubMed]
- Ghiasi, S.; Srivastava, A.; Yang, X.; Sarrafzadeh, M. Optimal Energy Aware Clustering in Sensor Networks. Sensors 2002, 2, 258–269. [Google Scholar] [CrossRef]
- Liu, M.; Cao, J.; Chen, G.; Wang, X. An Energy-Aware Routing Protocol in Wireless Sensor Networks. Sensors 2009, 9, 445–462. [Google Scholar] [CrossRef]
- Liu, Z.; Seo, H. IoT-NUMS: Evaluating NUMS Elliptic Curve Cryptography for IoT Platforms. IEEE Trans. Inf. Forensics Secur. 2019, 14, 720–729. [Google Scholar] [CrossRef]
- Yeh, H.L.; Chen, T.H.; Liu, P.C.; Kim, T.H.; Wei, H.W. A Secured Authentication Protocol for Wireless Sensor Networks Using Elliptic Curves Cryptography. Sensors 2011, 11, 4767–4779. [Google Scholar] [CrossRef]
- Piedra, A.d.l.; Braeken, A.; Touhafi, A. Extending the IEEE 802.15.4 Security Suite with a Compact Implementation of the NIST P-192/B-163 Elliptic Curves. Sensors 2013, 13, 9704–9728. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, D.; Zou, X.; Lin, H.; Cheng, J. Design of an Elliptic Curve Cryptography Processor for RFID Tag Chips. Sensors 2014, 14, 17883–17904. [Google Scholar] [CrossRef] [PubMed]
- Choi, Y.; Lee, D.; Kim, J.; Jung, J.; Nam, J.; Won, D. Security Enhanced User Authentication Protocol for Wireless Sensor Networks Using Elliptic Curves Cryptography. Sensors 2014, 14, 10081–10106. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Seo, H.; Großschädl, J.; Kim, H. Efficient Implementation of NIST-Compliant Elliptic Curve Cryptography for 8-bit AVR-Based Sensor Nodes. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1385–1397. [Google Scholar] [CrossRef]
- Barker, E. NIST Special Publication 800-57. Part 1. Revision 4. Recommendation for Key Management. 2016. Available online: http://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-57pt1r4.pdf (accessed on 15 October 2018).
- Lara-Nino, C.A.; Diaz-Perez, A.; Morales-Sandoval, M. Elliptic Curve Lightweight Cryptography: A Survey. IEEE Access 2018, 6, 72514–72550. [Google Scholar] [CrossRef]
- Schroeppel, R.; Beaver, C.; Gonzales, R.; Miller, R.; Draelos, T. A Low-Power Design for an Elliptic Curve Digital Signature Chip. In Cryptographic Hardware and Embedded Systems, Proceedings of the CHES 2002, 4th International Workshop, Redwood Shores, CA, USA, 13–15 August 2002; Revised Papers; Kaliski, B.S., Koç, ç.K., Paar, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 366–380. [Google Scholar]
- Keller, M.; Byrne, A.; Marnane, W.P. Elliptic Curve Cryptography on FPGA for Low-Power Applications. ACM Trans. Reconfigurable Technol. Syst. 2009, 2, 2. [Google Scholar] [CrossRef]
- Keller, M.; Marnane, W. Energy Efficient Elliptic Curve Processor. In Integrated Circuit and System Design. Power and Timing Modeling, Optimization and Simulation, Proceedings of the 18th International Workshop, PATMOS 2008, Lisbon, Portugal, 10–12 September; Revised Selected Papers; Svensson, L., Monteiro, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 287–296. [Google Scholar]
- Tamura, M.; Ikeda, M. 1.68uJ/signature-generation 256-bit ECDSA over GF(p) signature generator for IoT devices. In Proceedings of the 2016 IEEE Asian Solid-State Circuits Conference (A-SSCC), Toyama, Japan, 7–9 November 2016; pp. 341–344. [Google Scholar]
- Asif, S.; Andersson, O.; Rodrigues, J.; Kong, Y. 65-nm CMOS low-energy RNS modular multiplier for elliptic-curve cryptography. IET Comput. Digit. Tech. 2018, 12, 62–67. [Google Scholar] [CrossRef]
- Öztürk, E.; Sunar, B.; Savaş, E. Low-Power Elliptic Curve Cryptography Using Scaled Modular Arithmetic. In Cryptographic Hardware and Embedded Systems, Proceedings of the CHES 2004, 6th International Workshop, Cambridge, MA, USA, 11–13 August 2004; Joye, M., Quisquater, J.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 92–106. [Google Scholar]
- Batina, L.; Mentens, N.; Sakiyama, K.; Preneel, B.; Verbauwhede, I. Low-Cost Elliptic Curve Cryptography for Wireless Sensor Networks. In Security and Privacy in Ad-Hoc and Sensor Networks, Proceedings of the Third European Workshop, ESAS 2006, Hamburg, Germany, 20–21 September 2006; Revised Selected Papers; Buttyán, L., Gligor, V.D., Westhoff, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 6–17. [Google Scholar]
- Bernstein, D.J.; Lange, T.; Rezaeian Farashahi, R. Binary Edwards Curves. In Cryptographic Hardware and Embedded Systems, Proceedings of the CHES 2008, 10th International Workshop, Washington, DC, USA, 10–13 August 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 244–265. [Google Scholar]
- Koziel, B.; Azarderakhsh, R.; Mozaffari-Kermani, M. Low-Resource and Fast Binary Edwards Curves Cryptography. In Progress in Cryptology, Proceedings of the INDOCRYPT 2015: 16th International Conference on Cryptology in India, Bangalore, India, 6–9 December 2015; Springer International Publishing: Cham, Switzerland, 2015; pp. 347–369. [Google Scholar]
- Keller, M.; Marnane, W. Low Power Elliptic Curve Cryptography. In Integrated Circuit and System Design. Power and Timing Modeling, Optimization and Simulation, Proceedings of the 17th International Workshop, PATMOS 2007, Gothenburg, Sweden, 3–5 September 2007; Azémard, N., Svensson, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 310–319. [Google Scholar]
- Kocabas, U.; Fan, J.; Verbauwhede, I. Implementation of Binary Edwards Curves for very-constrained devices. In Proceedings of the ASAP 2010, Rennes, France, 7–9 July 2010; pp. 185–191. [Google Scholar]
- Dan, Y.P.; He, H.L. Tradeoff Design of Low-Cost and Low-Energy Elliptic Curve Crypto-Processor for Wireless Sensor Networks. In Proceedings of the 2012 8th International Conference on Wireless Communications, Networking and Mobile Computing, Shanghai, China, 21–23 September 2012; pp. 1–5. [Google Scholar]
- Knežević, M.; Nikov, V.; Rombouts, P. Low-Latency Encryption—Is “Lightweight = Light + Wait”? In Proceedings of the Cryptographic Hardware and Embedded Systems, CHES 2012, Leuven, Belgium, 9–12 September 2012; Prouff, E., Schaumont, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 426–446. [Google Scholar]
- Purnaprajna, M.; Puttmann, C.; Porrmann, M. Power Aware Reconfigurable Multiprocessor for Elliptic Curve Cryptography. In Proceedings of the 2008 Design, Automation and Test in Europe, Munich, Germany, 10–14 March 2008; pp. 1462–1467. [Google Scholar]
- Ahmadi, H.R.; Afzali-Kusha, A. A low-power and low-energy flexible GF(p) elliptic-curve cryptography processor. J. Zhejiang Univ. Sci. C 2010, 11, 724–736. [Google Scholar] [CrossRef]
- Iwasaki, A.; Shibata, Y.; Oguri, K.; Harasawa, R. An energy-efficient FPGA-based soft-core processor with a configurable word size ECC arithmetic accelerator. In Proceedings of the 2015 IEEE Symposium in Low-Power and High-Speed Chips (COOL CHIPS XVIII), Yokohama, Japan, 13–15 April 2015; pp. 1–3. [Google Scholar]
- Rožić, V.; Reparaz, O.; Verbauwhede, I. A 5.1 uJ per point-multiplication elliptic curve cryptographic processor. Int. J. Circuit Theory Appl. 2017, 45, 170–187. [Google Scholar] [CrossRef]
- Liu, Z.; Weng, J.; Hu, Z.; Seo, H. Efficient Elliptic Curve Cryptography for Embedded Devices. ACM Trans. Embed. Comput. Syst. 2016, 16, 53. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, X.; Hu, Z.; Khan, M.K.; Seo, H.; Zhou, L. On Emerging Family of Elliptic Curves to Secure Internet of Things: ECC Comes of Age. IEEE Trans. Dependable Secur. Comput. 2016, 14, 237–248. [Google Scholar]
- Chandrakasan, A.P.; Potkonjak, M.; Mehra, R.; Rabaey, J.; Brodersen, R.W. Optimizing Power Using Transformations. Trans. Comp.-Aided Des. Integr. Cir. Syst. 2006, 14, 12–31. [Google Scholar] [CrossRef]
- Kim, H.; Kim, Y.; Yoo, H.J. A 6.3nJ/op low energy 160-bit modulo-multiplier for elliptic curve cryptography processor. In Proceedings of the 2008 IEEE International Symposium on Circuits and Systems, Seattle, WA, USA, 18–21 May 2008; pp. 3310–3313. [Google Scholar]
- Gaubatz, G.; Kaps, J.P.; Ozturk, E.; Sunar, B. State of the art in ultra-low power public key cryptography for wireless sensor networks. In Proceedings of the Third IEEE International Conference on Pervasive Computing and Communications Workshops, Kauai Island, HI, USA, 8–12 March 2005; pp. 146–150. [Google Scholar]
- Fan, J.; Reparaz, O.; Rožić, V.; Verbauwhede, I. Low-energy encryption for medical devices: Security adds an extra design dimension. In Proceedings of the 2013 50th ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 29 May–7 June 2013; pp. 1–6. [Google Scholar]
- Maidhili, R.; Karthik, G. Energy Efficient and Secure Multi-User Broadcast Authentication Scheme in Wireless Sensor Networks. In Proceedings of the 2018 International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 4–6 January 2018; pp. 1–6. [Google Scholar]
- Kreiser, D.; Dyka, Z.; Kabin, I.; Langendoerfer, P. Low-energy key exchange for automation systems. In Proceedings of the 2018 13th International Conference on Design Technology of Integrated Systems In Nanoscale Era (DTIS), Taormina, Italy, 9–12 April 2018; pp. 1–5. [Google Scholar]
- Hein, D.; Wolkerstorfer, J.; Felber, N. ECC Is Ready for RFID—A Proof in Silicon. In Selected Areas in Cryptography, Proceedings of the 15th International Workshop, SAC 2008, Sackville, NB, Canada, 14–15 August 2009; Revised Selected Papers; Avanzi, R.M., Keliher, L., Sica, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 401–413. [Google Scholar]
- Kodali, R.K.; Patel, K.H.; Sarma, N. Energy efficient elliptic curve point multiplication for WSN applications. In Proceedings of the 2013 National Conference on Communications (NCC), New Delhi, India, 15–17 February 2013; pp. 1–5. [Google Scholar]
- Ting, P.; Tsai, J.; Wu, T. Signcryption Method Suitable for Low-Power IoT Devices in a Wireless Sensor Network. IEEE Syst. J. 2018, 12, 2385–2394. [Google Scholar] [CrossRef]
- De Clercq, R.; Uhsadel, L.; Van Herrewege, A.; Verbauwhede, I. Ultra Low-Power Implementation of ECC on the ARM Cortex-M0+. In Proceedings of the 51st Annual Design Automation Conference, DAC ’14, San Francisco, CA, USA, 1–5 June 2014; ACM: New York, NY, USA, 2014; pp. 112:1–112:6. [Google Scholar]
- Zeidler, S.; Goderbauer, M.; Krstić, M. Design of a low-power asynchronous elliptic curve cryptography coprocessor. In Proceedings of the 2013 IEEE 20th International Conference on Electronics, Circuits, and Systems (ICECS), Abu Dhabi, UAE, 8–11 December 2013; pp. 569–572. [Google Scholar]
- Targhetta, A.D.; Owen, D.E.; Israel, F.L.; Gratz, P.V. Energy-efficient Implementations of GF (P) and GF(2M) Elliptic Curve Cryptography. In Proceedings of the 2015 33rd IEEE International Conference on Computer Design (ICCD), ICCD ’15, New York, NY, USA, 18–21 October 2015; IEEE Computer Society: Washington, DC, USA, 2015; pp. 704–711. [Google Scholar]
- Tan, X.; Dong, M.; Wu, C.; Ota, K.; Wang, J.; Engels, D.W. An Energy-Efficient ECC Processor of UHF RFID Tag for Banknote Anti-Counterfeiting. IEEE Access 2017, 5, 3044–3054. [Google Scholar] [CrossRef]
- Dao, V.L.; Nguyen, V.T.; Hoang, V.P. Low Power ECC Implementation on ASIC. In Advances in Information and Communication Technology, Proceedings of the International Conference, ICTA 2016, Thai Nguyen, Vietnam, 12–12 December 2016; Akagi, M., Nguyen, T.T., Vu, D.T., Phung, T.N., Huynh, V.N., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 332–339. [Google Scholar]
- Rabaey, J. Low Power Design Essentials, 1st ed.; Springer Publishing Company: Berlin/Heidelberg, Germany, 2009; Incorporated. [Google Scholar]
- Liu, D.; Liu, Z.; Yong, Z.; Zou, X.; Cheng, J. Design and Implementation of an ECC-Based Digital Baseband Controller for RFID Tag Chip. IEEE Trans. Ind. Electron. 2015, 62, 4365–4373. [Google Scholar] [CrossRef]
- Itoh, T.; Tsujii, S. A Fast Algorithm for Computing Multiplicative Inverses in GF(2M) Using Normal Bases. Inf. Comput. 1988, 78, 171–177. [Google Scholar] [CrossRef]
- Daepp, U.; Gorkin, P. Fermat’s Little Theorem. In Reading, Writing, and Proving: A Closer Look at Mathematics; Springer: New York, NY, USA, 2011; pp. 315–323. [Google Scholar]
- Liskov, M. Fermat’s Little Theorem. In Encyclopedia of Cryptography and Security; van Tilborg, H.C.A., Jajodia, S., Eds.; Springer: Boston, MA, USA, 2011; p. 456. [Google Scholar]
- Guajardo, J. Itoh–Tsujii Inversion Algorithm. In Encyclopedia of Cryptography and Security; van Tilborg, H.C.A., Ed.; Springer: Boston, MA, USA, 2005; p. 313. [Google Scholar]
- Rodríguez-Henríquez, F.; Saqib, N.A.; Díaz-Pérez, A.; Koc, C.K. Cryptographic Algorithms on Reconfigurable Hardware (Signals and Communication Technology); Springer-Verlag New York, Inc.: Secaucus, NJ, USA, 2006. [Google Scholar]

| Inv. | Field | Multiplications | Squarings | Storage Bits |
|---|---|---|---|---|
| Algorithm 1 | ||||
| Algorithm 2 | ||||
| Algorithm 3 | ||||
| Algorithm 4 |
| Inv. | m | M | S | MEM | LAT (Cycles) a | Improvement a | LAT (Cycles) b | Improvement b | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (bits) | Inv. | kP | Inv. | Inv. % | kP | kP% | Inv. | kP | Inv. | Inv. % | kP | kP% | ||||
| Algorithm 1 | 251 | 249 | 250 | 502 | 125,249 | 832,818 | - | - | - | - | 62,749 | 456,818 | - | - | - | - |
| 257 | 255 | 256 | 514 | 131,327 | 872,772 | - | - | - | - | 65,791 | 478,532 | - | - | - | - | |
| Algorithm 2 | 257 | 8 | 256 | 514 | 67,848 | 745,814 | −63,479 | −48 | −126,958 | −15 | 2312 | 351,574 | −60,437 | −92 | −126,958 | −27 |
| Algorithm 3 | 251 | 12 | 250 | 1757 | 65,762 | 713,844 | −59,487 | −47 | −118,974 | −14 | 3262 | 337,844 | −59,487 | −95 | −118,974 | −26 |
| 257 | 8 | 256 | 1799 | 67,848 | 745,814 | −63,479 | −48 | −126,958 | −15 | 2312 | 351,574 | −63,479 | −96 | −126,958 | −27 | |
| Algorithm 4 | 251 | 31 | 367 | 753 | 99,898 | 782,116 | −25,351 | −20 | −50,702 | −6 | 8148 | 347,616 | −54,601 | −87 | −109,202 | −24 |
| 257 | 8 | 256 | 771 | 67,848 | 745,814 | −63,479 | −48 | −126,958 | −15 | 2312 | 351,574 | −63,479 | −96 | −126,958 | −27 | |
| Arch. | m | FF | LUT | SLC | Fmax (MHz) | LAT | t (ms) | POW (mW) | ENE (mJ) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | % | (Cycles) | % | % | % | |||||||||||
| C0 | 127 | 1140 | 2220 | 633 | - | 122 | 223,024 | - | 2230.24 | 16.45 | 23.59 | 26.89 | 52.61 | - | 0.44 | - |
| 163 | 1432 | 2755 | 868 | - | 119 | 362,530 | - | 3625.30 | 26.74 | 24.08 | 27.43 | 87.30 | - | 0.73 | - | |
| 233 | 1994 | 3877 | 1224 | - | 102 | 730,248 | - | 7302.48 | 53.85 | 25.38 | 29.87 | 185.34 | - | 1.61 | - | |
| 251 | 2138 | 4122 | 1357 | - | 109 | 845,395 | - | 8453.95 | 62.34 | 25.28 | 29.83 | 213.72 | - | 1.86 | - | |
| C1 | 127 | 1168 | 2370 | 716 | 13 | 83 | 212,096 | −5 | 2120.96 | 15.64 | 23.66 | 27.04 | 50.18 | −5 | 0.42 | −4 |
| 163 | 1462 | 2981 | 945 | 9 | 99 | 324,596 | −10 | 3245.96 | 23.94 | 24.13 | 27.50 | 78.33 | −10 | 0.66 | −10 | |
| 233 | 2024 | 4173 | 1311 | 7 | 97 | 680,096 | −7 | 6800.96 | 50.15 | 25.15 | 29.65 | 171.04 | −8 | 1.49 | −8 | |
| 251 | 2168 | 4435 | 1352 | 0 | 99 | 793,978 | −6 | 7939.78 | 58.55 | 25.24 | 29.61 | 200.40 | −6 | 1.73 | −7 | |
| Digit | FF | LUT | LAT (Cycles) |
|---|---|---|---|
| 2 | 510 | 786 | 129 |
| 4 | 507 | 1052 | 66 |
| 8 | 506 | 1643 | 35 |
| 16 | 497 | 2662 | 19 |
| Arch. | Digit | FF | LUT | SLC | Fmax (MHz) | LAT | t (ms) | POW (mW) | ENE (mJ) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | % | (Cycles) | % | % | % | |||||||||||
| C2 | 2 | 2138 | 4251 | 1527 | 13 | 88 | 426,980 | −49 | 4269.80 | 31.49 | 25.54 | 29.30 | 109.05 | −49 | 0.92 | −51 |
| 3 | 2138 | 4387 | 1445 | 6 | 98 | 287,843 | −66 | 2878.43 | 21.23 | 25.87 | 29.57 | 74.46 | −65 | 0.63 | −66 | |
| 4 | 2137 | 4518 | 1468 | 8 | 93 | 218,149 | −74 | 2181.49 | 16.09 | 25.80 | 29.37 | 56.28 | −74 | 0.47 | −75 | |
| 5 | 2140 | 4650 | 1509 | 11 | 88 | 178,288 | −79 | 1782.88 | 13.15 | 25.98 | 29.59 | 46.32 | −78 | 0.39 | −79 | |
| 6 | 2137 | 4780 | 1675 | 23 | 63 | 148,455 | −82 | 1484.55 | 10.95 | 25.76 | 29.32 | 38.24 | −82 | 0.32 | −83 | |
| 7 | 2137 | 4793 | 1688 | 24 | 91 | 128,650 | −85 | 1286.50 | 9.49 | 26.18 | 30.06 | 33.68 | −84 | 0.29 | −84 | |
| 8 | 2140 | 4932 | 1718 | 27 | 88 | 115,363 | −86 | 1153.63 | 8.51 | 26.44 | 30.28 | 30.5 | −86 | 0.26 | −86 | |
| 9 | 2136 | 5057 | 1722 | 27 | 85 | 102,076 | −88 | 1020.76 | 7.53 | 26.35 | 30.25 | 26.9 | −87 | 0.23 | −88 | |
| 10 | 2144 | 5198 | 1836 | 35 | 86 | 95,307 | −89 | 953.07 | 7.03 | 26.70 | 30.50 | 25.45 | −88 | 0.21 | −89 | |
| 11 | 2137 | 5210 | 1634 | 20 | 90 | 85,530 | −90 | 855.30 | 6.31 | 26.63 | 30.45 | 22.78 | −89 | 0.19 | −90 | |
| 12 | 2136 | 5334 | 1855 | 37 | 81 | 78,761 | −91 | 787.61 | 5.81 | 26.50 | 30.33 | 20.87 | −90 | 0.18 | −90 | |
| 13 | 2144 | 5469 | 1914 | 41 | 80 | 75,502 | −91 | 755.02 | 5.57 | 26.49 | 30.36 | 20 | −91 | 0.17 | −91 | |
| 14 | 2136 | 5598 | 1983 | 46 | 78 | 68,984 | −92 | 689.84 | 5.09 | 26.85 | 30.75 | 18.52 | −91 | 0.16 | −91 | |
| 15 | 2139 | 5731 | 1896 | 40 | 79 | 65,474 | −92 | 654.74 | 4.83 | 26.72 | 30.40 | 17.49 | −92 | 0.15 | −92 | |
| 16 | 2139 | 5856 | 1972 | 45 | 76 | 62,215 | −93 | 622.15 | 4.59 | 27.11 | 30.93 | 16.87 | −92 | 0.14 | −92 | |
| C3 | 2 | 2168 | 4570 | 1564 | 15 | 84 | 401,075 | −53 | 4010.75 | 29.58 | 25.87 | 29.64 | 103.76 | −51 | 0.88 | −53 |
| 3 | 2168 | 4697 | 1583 | 17 | 77 | 270,464 | −68 | 2704.64 | 19.95 | 25.97 | 29.75 | 70.24 | −67 | 0.59 | −68 | |
| 4 | 2167 | 4831 | 1541 | 14 | 82 | 205,033 | −76 | 2050.33 | 15.12 | 25.98 | 29.86 | 53.27 | −75 | 0.45 | −76 | |
| 5 | 2170 | 4819 | 1561 | 15 | 88 | 167,608 | −80 | 1676.08 | 12.36 | 26.16 | 29.98 | 43.85 | −79 | 0.37 | −80 | |
| 6 | 2167 | 5098 | 1717 | 27 | 81 | 139,602 | −83 | 1396.02 | 10.30 | 26.24 | 30.11 | 36.63 | −83 | 0.31 | −83 | |
| 7 | 2167 | 5110 | 1644 | 21 | 79 | 121,015 | −86 | 1210.15 | 8.92 | 26.23 | 30.04 | 31.74 | −85 | 0.27 | −85 | |
| 8 | 2170 | 5237 | 1756 | 29 | 78 | 108,540 | −87 | 1085.40 | 8.00 | 26.29 | 29.99 | 28.54 | −87 | 0.24 | −87 | |
| 9 | 2166 | 5362 | 1746 | 29 | 74 | 96,065 | −89 | 960.65 | 7.08 | 26.44 | 30.17 | 25.4 | −88 | 0.21 | −89 | |
| 10 | 2174 | 5503 | 1878 | 38 | 72 | 89,702 | −89 | 897.02 | 6.62 | 26.51 | 30.23 | 23.78 | −89 | 0.2 | −89 | |
| 11 | 2167 | 5526 | 1895 | 40 | 73 | 80,534 | −90 | 805.34 | 5.94 | 26.57 | 29.19 | 21.4 | −90 | 0.17 | −91 | |
| 12 | 2166 | 5643 | 1820 | 34 | 69 | 74,171 | −91 | 741.71 | 5.47 | 26.82 | 30.78 | 19.89 | −91 | 0.17 | −91 | |
| 13 | 2174 | 5778 | 1953 | 44 | 72 | 71,115 | −92 | 711.15 | 5.24 | 26.99 | 30.75 | 19.19 | −91 | 0.16 | −91 | |
| 14 | 2166 | 5915 | 1995 | 47 | 71 | 65,003 | −92 | 650.03 | 4.79 | 27.03 | 30.75 | 17.57 | −92 | 0.15 | −92 | |
| 15 | 2169 | 6042 | 1965 | 45 | 71 | 61,696 | −93 | 616.96 | 4.55 | 26.92 | 30.72 | 16.61 | −92 | 0.14 | −92 | |
| 16 | 2169 | 6260 | 2093 | 54 | 68 | 58,640 | −93 | 586.40 | 4.32 | 27.56 | 31.36 | 16.16 | −92 | 0.14 | −92 | |
| Arch. | Digit | FF | LUT | SLC | Fmax (MHz) | LAT | t (ms) | POW (mW) | ENE (mJ) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | % | (Cycles) | % | % | % | |||||||||||
| C4 | 1 | 2176 | 5290 | 1651 | 22 | 88 | 354,264 | −55 | 3542.64 | 26.13 | 26.92 | 32.11 | 95.37 | −52 | 0.84 | −52 |
| C5 | 2 | 2176 | 5668 | 1758 | 30 | 85 | 180,349 | −79 | 1803.49 | 13.30 | 27.01 | 30.88 | 48.71 | −77 | 0.41 | −78 |
| 3 | 2176 | 5797 | 1790 | 32 | 84 | 122,734 | −85 | 1227.34 | 9.05 | 27.14 | 31.22 | 33.31 | −84 | 0.28 | −85 | |
| 4 | 2175 | 5934 | 1948 | 44 | 84 | 93,801 | −89 | 938.01 | 6.92 | 27.84 | 31.99 | 26.11 | −88 | 0.22 | −88 | |
| 5 | 2178 | 6068 | 1912 | 41 | 82 | 77,232 | −91 | 772.32 | 5.70 | 27.68 | 31.83 | 21.38 | −90 | 0.18 | −90 | |
| 6 | 2175 | 6199 | 1966 | 45 | 85 | 64,868 | −92 | 648.68 | 4.78 | 27.74 | 31.80 | 17.99 | −92 | 0.15 | −92 | |
| 7 | 2175 | 6210 | 1992 | 47 | 88 | 56,709 | −93 | 567.09 | 4.18 | 27.92 | 32.02 | 15.83 | −93 | 0.13 | −93 | |
| 8 | 2178 | 6353 | 1995 | 47 | 89 | 51,186 | −94 | 511.86 | 3.77 | 28.31 | 32.29 | 14.49 | −93 | 0.12 | −94 | |
| 9 | 2174 | 6474 | 1920 | 41 | 82 | 45,663 | −95 | 456.63 | 3.37 | 28.10 | 32.12 | 12.83 | −94 | 0.11 | −94 | |
| 10 | 2182 | 6618 | 2122 | 56 | 77 | 42,776 | −95 | 427.76 | 3.15 | 28.20 | 32.33 | 12.06 | −94 | 0.10 | −95 | |
| 11 | 2175 | 6716 | 2153 | 59 | 75 | 38,822 | −95 | 388.22 | 2.86 | 28.50 | 32.96 | 11.06 | −95 | 0.09 | −95 | |
| 12 | 2174 | 6702 | 2101 | 55 | 75 | 35,935 | −96 | 359.35 | 2.65 | 29.02 | 33.37 | 10.43 | −95 | 0.09 | −95 | |
| 13 | 2182 | 6847 | 2175 | 60 | 72 | 34,617 | −96 | 346.17 | 2.55 | 28.46 | 32.61 | 9.85 | −95 | 0.08 | −96 | |
| 14 | 2174 | 7062 | 2182 | 61 | 73 | 31,981 | −96 | 319.81 | 2.36 | 29.20 | 33.87 | 9.34 | −96 | 0.08 | −96 | |
| 15 | 2177 | 7117 | 2099 | 55 | 70 | 30,412 | −96 | 304.12 | 2.24 | 29.27 | 33.45 | 8.90 | −96 | 0.08 | −96 | |
| 16 | 2177 | 7251 | 2205 | 62 | 69 | 29,094 | −97 | 290.94 | 2.15 | 29.67 | 33.96 | 8.63 | −96 | 0.07 | −96 | |
| Conf. | Multiplication | Inversion | Addition | Squaring |
|---|---|---|---|---|
| C0 | Bit-serial | Wang | Combinatorial | Not supported |
| C1 | Bit-serial | Itoh-Tsujii | Combinatorial | Not supported |
| C2 | Digit-serial | Wang | Combinatorial | Not supported |
| C3 | Digit-serial | Itoh-Tsujii | Combinatorial | Not supported |
| C4 | Bit-serial | Itoh-Tsujii | Combinatorial | Combinatorial |
| C5 | Digit-serial | Itoh-Tsujii | Combinatorial | Combinatorial |
| Year | Ref. | m | Curve | Platform | Label | Digit | FF | LUT | SLC | GE | Storage | LAT (Cycles) | Freq. (MHz) | t (ms) | POW (W) | ENE (J) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2006 | [22] | 131 | B131 | 0.13 m | w1a01 | 1 | x | x | x | 4446 | bits | 226,330 | 0.50 | 452.66 | 21.00 | 9.51 |
| 2 | x | x | x | 4917 | bits | 116,480 | 0.50 | 232.96 | 21.50 | 5.01 | ||||||
| 3 | x | x | x | 5376 | bits | 79,300 | 0.50 | 158.60 | 22.00 | 3.49 | ||||||
| 4 | x | x | x | 5837 | bits | 60,710 | 0.50 | 121.42 | 22.50 | 2.73 | ||||||
| 139 | B139 | 1 | x | x | x | 4716 | bits | 254,610 | 0.50 | 509.22 | 22.00 | 11.20 | ||||
| 2 | x | x | x | 5214 | bits | 130,824 | 0.50 | 261.65 | 22.50 | 5.89 | ||||||
| 3 | x | x | x | 5712 | bits | 89,562 | 0.50 | 179.12 | 23.00 | 4.12 | ||||||
| 4 | x | x | x | 6189 | bits | 68,034 | 0.50 | 136.07 | 23.50 | 3.20 | ||||||
| 151 | B151 | 1 | x | x | x | 5117 | bits | 300,150 | 0.50 | 600.30 | 23.00 | 13.81 | ||||
| 2 | x | x | x | 5652 | bits | 153,900 | 0.50 | 307.80 | 23.50 | 7.23 | ||||||
| 3 | x | x | x | 6187 | bits | 105,150 | 0.50 | 210.30 | 24.00 | 5.05 | ||||||
| 4 | x | x | x | 6700 | bits | 79,800 | 0.50 | 159.60 | 25.00 | 3.99 | ||||||
| 163 | B163 | 1 | x | x | x | 5525 | bits | 349,434 | 0.50 | 698.87 | 24.00 | 16.77 | ||||
| 2 | x | x | x | 6105 | bits | 178,848 | 0.50 | 357.70 | 24.50 | 8.76 | ||||||
| 3 | x | x | x | 6685 | bits | 121,986 | 0.50 | 243.97 | 25.00 | 6.10 | ||||||
| 4 | x | x | x | 7243 | bits | 92,502 | 0.50 | 185.00 | 26.00 | 4.81 | ||||||
| 2007 | [25] | 163 | B163 | xc3s1000l | w2a01 | 1 | - | - | 2541 | x | RAM/ROM/Pro | 130,141 | 80.00 | 1.63 | 207,328.39 | 339.62 |
| 16 | - | - | 3721 | x | RAM/ROM/Pro | 92,958 | 80.00 | 1.16 | 236,085.34 | 274.87 | ||||||
| w2a02 | 1 | - | - | 2692 | x | RAM/ROM/Pro | 287,324 | 80.00 | 3.59 | 171,614.10 | 610.82 | |||||
| 16 | - | - | 3728 | x | RAM/ROM/Pro | 40,564 | 80.00 | 0.51 | 252,319.11 | 129.49 | ||||||
| w2a03 | 1 | - | - | 1551 | x | RAM/ROM/Pro | 287,324 | 80.00 | 3.59 | 155,380.33 | 549.74 | |||||
| 16 | - | - | 2556 | x | RAM/ROM/Pro | 40,564 | 80.00 | 0.51 | 173,933.21 | 87.96 | ||||||
| w2a04 | 1 | - | - | 2541 | x | RAM/ROM/Pro | 112,677 | 80.00 | 1.41 | 208,719.85 | 287.09 | |||||
| 16 | - | - | 3728 | x | RAM/ROM/Pro | 112,677 | 80.00 | 1.41 | 205,009.28 | 284.64 | ||||||
| w2a05 | 1 | - | - | 2541 | x | RAM/ROM/Pro | 174,648 | 80.00 | 2.18 | 217,996.29 | 472.77 | |||||
| 16 | - | - | 3728 | x | RAM/ROM/Pro | 25,353 | 80.00 | 0.32 | 224,953.62 | 69.63 | ||||||
| w2a06 | 1 | - | - | 1543 | x | RAM/ROM/Pro | 17,4648 | 80.00 | 2.18 | 153,525.05 | 333.51 | |||||
| 16 | - | - | 2707 | x | RAM/ROM/Pro | 25,353 | 80.00 | 0.32 | 179,035.25 | 54.97 | ||||||
| w2a07 | 1 | - | - | 3033 | x | RAM/ROM/Pro | 116,057 | 80.00 | 1.45 | 222,634.51 | 322.51 | |||||
| 16 | - | - | 4061 | x | RAM/ROM/Pro | 82,817 | 80.00 | 1.04 | 233,766.23 | 244.33 | ||||||
| w2a08 | 1 | - | - | 2624 | x | RAM/ROM/Pro | 238,874 | 80.00 | 2.99 | 212,430.43 | 631.59 | |||||
| 16 | - | - | 3751 | x | RAM/ROM/Pro | 33,803 | 80.00 | 0.42 | 226,345.08 | 97.73 | ||||||
| w2a09 | 1 | - | - | 1641 | x | RAM/ROM/Pro | 238,874 | 80.00 | 2.99 | 157,235.62 | 471.55 | |||||
| 16 | - | - | 2821 | x | RAM/ROM/Pro | 33,803 | 80.00 | 0.42 | 175,324.68 | 76.96 | ||||||
| 2009 | [17] | 163 | B163 | xc3s500e | w3a01 | 1 | 3323 | 3249 | 2873 | x | 7 BRAM | 126,836 | 10.00 | 12.68 | 76,730.00 | 973.18 |
| 15 | 3337 | 5238 | 3738 | x | 7 BRAM | 89,976 | 10.00 | 9.00 | 78,500.00 | 706.26 | ||||||
| w3a02 | 1 | 2005 | 1768 | 1551 | x | 8 BRAM | 281,024 | 10.00 | 28.10 | 73,680.00 | 2070.63 | |||||
| 15 | 2019 | 3748 | 2575 | x | 8 BRAM | 33,720 | 10.00 | 3.37 | 84,650.00 | 285.45 | ||||||
| w3a03 | 1 | 2005 | 1768 | 1551 | x | 8 BRAM | 226,110 | 10.00 | 22.61 | 73,710.00 | 1666.58 | |||||
| 15 | 2019 | 3748 | 2575 | x | 8 BRAM | 28,054 | 10.00 | 2.81 | 84,920.00 | 238.23 | ||||||
| w3a04 | 1 | 3323 | 3249 | 2873 | x | 7 BRAM | 111,188 | 10.00 | 11.12 | 77,230.00 | 858.70 | |||||
| 15 | 3337 | 5238 | 3783 | x | 7 BRAM | 110,884 | 10.00 | 11.09 | 78,080.00 | 865.82 | ||||||
| w3a05 | 1 | 2005 | 1768 | 1551 | x | 8 BRAM | 171,796 | 10.00 | 17.18 | 73,810.00 | 1267.93 | |||||
| 15 | 2019 | 3748 | 2575 | x | 8 BRAM | 21,164 | 10.00 | 2.12 | 83,940.00 | 177.65 | ||||||
| w3a06 | 1 | 3323 | 3249 | 2873 | x | 7 BRAM | 170,214 | 10.00 | 17.02 | 75,700.00 | 1288.45 | |||||
| 15 | 3337 | 5238 | 3738 | x | 7 BRAM | 21,181 | 10.00 | 2.12 | 85,890.00 | 181.93 | ||||||
| w3a07 | 1 | 2005 | 1768 | 1551 | x | 8 BRAM | 172,124 | 10.00 | 17.21 | 73,640.00 | 1267.59 | |||||
| 15 | 2019 | 3748 | 2575 | x | 8 BRAM | 21,492 | 10.00 | 2.15 | 82,850.00 | 178.05 | ||||||
| w3a08 | 1 | 2834 | 2612 | 2384 | x | 8 BRAM | 88,991 | 10.00 | 8.90 | 77,290.00 | 687.84 | |||||
| 15 | 2864 | 6573 | 4447 | x | 8 BRAM | 12,991 | 10.00 | 1.30 | 95,010.00 | 123.43 | ||||||
| w3a09 | 1 | 3658 | 3122 | 2888 | x | 8 BRAM | 61,769 | 10.00 | 6.18 | 80,210.00 | 495.47 | |||||
| 15 | 3688 | 7200 | 4654 | x | 8 BRAM | 10,545 | 10.00 | 1.05 | 98,620.00 | 104.00 | ||||||
| w3a10 | 1 | 3323 | 3249 | 2873 | x | 7 BRAM | 113,098 | 10.00 | 11.31 | 77,480.00 | 876.23 | |||||
| 15 | 3337 | 5238 | 3738 | x | 7 BRAM | 80,216 | 10.00 | 8.02 | 78,980.00 | 633.56 | ||||||
| w3a11 | 1 | 2005 | 1768 | 1551 | x | 8 BRAM | 235,001 | 10.00 | 23.50 | 73,900.00 | 1736.63 | |||||
| 15 | 2019 | 3748 | 2575 | x | 8 BRAM | 28,230 | 10.00 | 2.82 | 84,820.00 | 239.45 | ||||||
| w3a12 | 1 | 2005 | 1768 | 1551 | x | 8 BRAM | 189,372 | 10.00 | 18.94 | 73,860.00 | 1398.72 | |||||
| 15 | 2019 | 3748 | 2575 | x | 8 BRAM | 23,742 | 10.00 | 2.37 | 86,260.00 | 204.79 | ||||||
| 2009 | [18] | 163 | B163 | 0.13 m | w4a01 | 1 | x | x | x | 16,837 | 0 | 169,769 | 0.50 | 339.54 | 16.01 | 5.44 |
| 2 | x | x | x | 17,444 | 0 | 89,417 | 0.50 | 178.83 | 17.33 | 3.10 | ||||||
| 3 | x | x | x | 17,957 | 0 | 62,633 | 0.50 | 125.27 | 19.98 | 2.50 | ||||||
| 4 | x | x | x | 18,567 | 0 | 48,745 | 0.50 | 97.49 | 22.05 | 2.15 | ||||||
| 8 | x | x | x | 20,678 | 0 | 28,905 | 0.50 | 57.81 | 28.03 | 1.62 | ||||||
| 15 | x | x | x | 24,561 | 0 | 18,985 | 0.50 | 37.97 | 34.63 | 1.32 | ||||||
| 19 | x | x | x | 26,777 | 0 | 17,001 | 0.50 | 34.00 | 41.51 | 1.41 | ||||||
| 55 | x | x | x | 47,247 | 0 | 11,049 | 0.50 | 22.10 | 68.23 | 1.51 | ||||||
| 2010 | [26] | 163 | BE163 | 0.13 m | w5a01 | 1 | x | x | x | 11720 | 84 bytes | 219,148 | 0.40 | 547.87 | 7.27* | 3.98 |
| 2 | x | x | x | 12,348 | 84 bytes | 113,428 | 0.40 | 283.57 | 9.10* | 2.58 | ||||||
| 3 | x | x | x | 12,862 | 84 bytes | 78,112 | 0.40 | 195.28 | 10.19* | 1.99 | ||||||
| 4 | x | x | x | 13,427 | 84 bytes | 59,800 | 0.40 | 149.50 | 12.00* | 1.79 | ||||||
| 5 | x | x | x | 13,970 | 84 bytes | 49,336 | 0.40 | 123.34 | 12.69* | 1.57 | ||||||
| 6 | x | x | x | 14,530 | 84 bytes | 42,796 | 0.40 | 106.99 | 13.80* | 1.48 | ||||||
| 2012 | [27] | 163 | B163 | 0.25 m | w6a01 | 1 | x | x | x | 24140 | 0 | 165000 | 10.00 | 16.50 | 5940.00 | 98.01 |
| 2 | x | x | x | 24,742 | 0 | 84,900 | 10.00 | 8.49 | 7180.00 | 60.96 | ||||||
| 4 | x | x | x | 26,156 | 0 | 44,200 | 10.00 | 4.42 | 8640.00 | 38.19 | ||||||
| 8 | x | x | x | 31,333 | 0 | 23,500 | 10.00 | 2.35 | 13,200.00 | 31.02 | ||||||
| 16 | x | x | x | 34,956 | 0 | 13,500 | 10.00 | 1.35 | 17,400.00 | 23.49 | ||||||
| 2016 | [32] | 163 | K163 | 0.13 m | w7a01 | 1 | x | x | x | 10,106 | RAM/ROM | - | 1.13 | - | 36.63 | 9.16 |
| 2 | x | x | x | 11,383 | RAM/ROM | - | 0.59 | - | 21.55 | 5.39 | ||||||
| 3 | x | x | x | 12,236 | RAM/ROM | - | 0.41 | - | 15.75 | 3.94 | ||||||
| 4 | x | x | x | 12,863 | RAM/ROM | - | 0.32 | - | 12.08 | 3.02 | ||||||
| 5 | x | x | x | 13,497 | RAM/ROM | - | 0.27 | - | 11.41 | 2.85 |
| Year | Ref. | m | Curve | Platform | Conf. | R-square | R-square | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2006 | [22] | 131 | B131 | 0.13 m | w1a01 | 463.2000 | 3986.0000 | 99.99% | 9.4985 | −0.9107 | 99.99% |
| 139 | B139 | 491.7000 | 4228.5000 | 99.98% | 11.1861 | −0.9118 | 99.99% | ||||
| 151 | B151 | 528.4000 | 4593.0000 | 99.98% | 13.7842 | −0.9122 | 99.97% | ||||
| 163 | B163 | 573.4000 | 4956.0000 | 99.99% | 16.7408 | −0.9169 | 99.97% | ||||
| 2007 | [25] | 163 | B163 | xc3s1000l | w2a01 | 78.6667 | 2462.3333 | 100% | 339.6200 | −0.0763 | 100% |
| w2a02 | 69.0667 | 2622.9333 | 100% | 610.8200 | −0.5595 | 100% | |||||
| w2a03 | 67.0000 | 1484.0000 | 100% | 549.7400 | −0.6610 | 100% | |||||
| w2a04 | 79.1333 | 2461.8666 | 100% | 287.0900 | −0.0031 | 100% | |||||
| w2a05 | 79.1333 | 2461.8666 | 100% | 472.7700 | −0.6908 | 100% | |||||
| w2a06 | 77.6000 | 1465.4000 | 100% | 333.5100 | −0.6503 | 100% | |||||
| w2a07 | 68.5333 | 2964.4666 | 100% | 322.5100 | −0.1001 | 100% | |||||
| w2a08 | 75.1333 | 2548.8666 | 100% | 631.5900 | −0.6730 | 100% | |||||
| w2a09 | 78.6667 | 1562.3333 | 100% | 471.5500 | −0.6538 | 100% | |||||
| 2009 | [17] | 163 | B163 | xc3s500e | w3a01 | 61.7857 | 2811.2142 | 100% | 973.1800 | −0.1184 | 100% |
| w3a02 | 73.1429 | 1477.8571 | 100% | 2070.6300 | −0.7317 | 100% | |||||
| w3a03 | 73.1429 | 1477.8571 | 100% | 1666.5800 | −0.7183 | 100% | |||||
| w3a04 | 65.0000 | 2808.0000 | 100% | 858.7000 | 0.0030 | 100% | |||||
| w3a05 | 73.1429 | 1477.8571 | 100% | 1267.9300 | −0.7257 | 100% | |||||
| w3a06 | 61.7857 | 2811.2142 | 100% | 1288.4500 | −0.7229 | 100% | |||||
| w3a07 | 73.1429 | 1477.8571 | 100% | 1267.5900 | −0.7248 | 100% | |||||
| w3a08 | 147.3571 | 2236.6428 | 100% | 687.8400 | −0.6344 | 100% | |||||
| w3a09 | 126.1429 | 2761.8571 | 100% | 495.4700 | −0.5765 | 100% | |||||
| w3a10 | 61.7857 | 2811.2141 | 100% | 876.2300 | −0.4678 | 100% | |||||
| w3a11 | 73.1429 | 1477.8571 | 100% | 1736.6300 | −0.7317 | 100% | |||||
| w3a12 | 73.1429 | 1477.8571 | 100% | 1398.7200 | −0.7095 | 100% | |||||
| 2009 | [18] | 163 | B163 | 0.13 m | w4a01 | 562.4282 | 16,236.0223 | 99.99% | 4.9753 | −0.5094 | 89.25% |
| 2010 | [26] | 163 | BE163 | 0.13 m | w5a01 | 556.6000 | 11,194.0000 | 99.95% | 3.9404 | −0.5794 | 99.50% |
| 2012 | [27] | 163 | B163 | 0.25 m | w6a01 | 752.5578 | 23,599.5416 | 95.70% | 95.7553 | −0.5840 | 98.33% |
| 2016 | [32] | 163 | K163 | 0.13 m | w7a01 | 826.2000 | 9538.3999 | 97.40% | 9.1506 | −0.7636 | 99.80% |
| C2 | 110.8941 | 4050.2750 | 99.54% | 1846.3496 | −0.9634 | 99.92% | |||||
| 2019 | This work. | 251 | BE251 | xc6slx16 | C3 | 114.1824 | 4331.0750 | 99.17% | 1725.1535 | −0.9542 | 99.95% |
| C5 | 115.8118 | 5409.7250 | 97.91% | 827.4241 | −0.9371 | 99.76% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lara-Nino, C.A.; Diaz-Perez, A.; Morales-Sandoval, M. Energy/Area-Efficient Scalar Multiplication with Binary Edwards Curves for the IoT. Sensors 2019, 19, 720. https://doi.org/10.3390/s19030720
Lara-Nino CA, Diaz-Perez A, Morales-Sandoval M. Energy/Area-Efficient Scalar Multiplication with Binary Edwards Curves for the IoT. Sensors. 2019; 19(3):720. https://doi.org/10.3390/s19030720
Chicago/Turabian StyleLara-Nino, Carlos Andres, Arturo Diaz-Perez, and Miguel Morales-Sandoval. 2019. "Energy/Area-Efficient Scalar Multiplication with Binary Edwards Curves for the IoT" Sensors 19, no. 3: 720. https://doi.org/10.3390/s19030720
APA StyleLara-Nino, C. A., Diaz-Perez, A., & Morales-Sandoval, M. (2019). Energy/Area-Efficient Scalar Multiplication with Binary Edwards Curves for the IoT. Sensors, 19(3), 720. https://doi.org/10.3390/s19030720





