Understanding Eye Movement Signal Characteristics Based on Their Dynamical and Fractal Features
Abstract
1. Introduction
1.1. Eye Movement Basics
1.2. The State of The Art
1.3. Paper’s Contribution
- introduction of a new set of intervals for analyzing eye movement time series representing one fixation,
- assessment of chaotic eye movement behavior in the defined scopes, taking different filtering methods into account,
- fractal analysis aimed at ascertaining long-range correlation existence in an eye movement signal corresponding to one fixation.
2. Material and Methods
2.1. The Embedding and Fractal Theory
2.2. Dataset Description
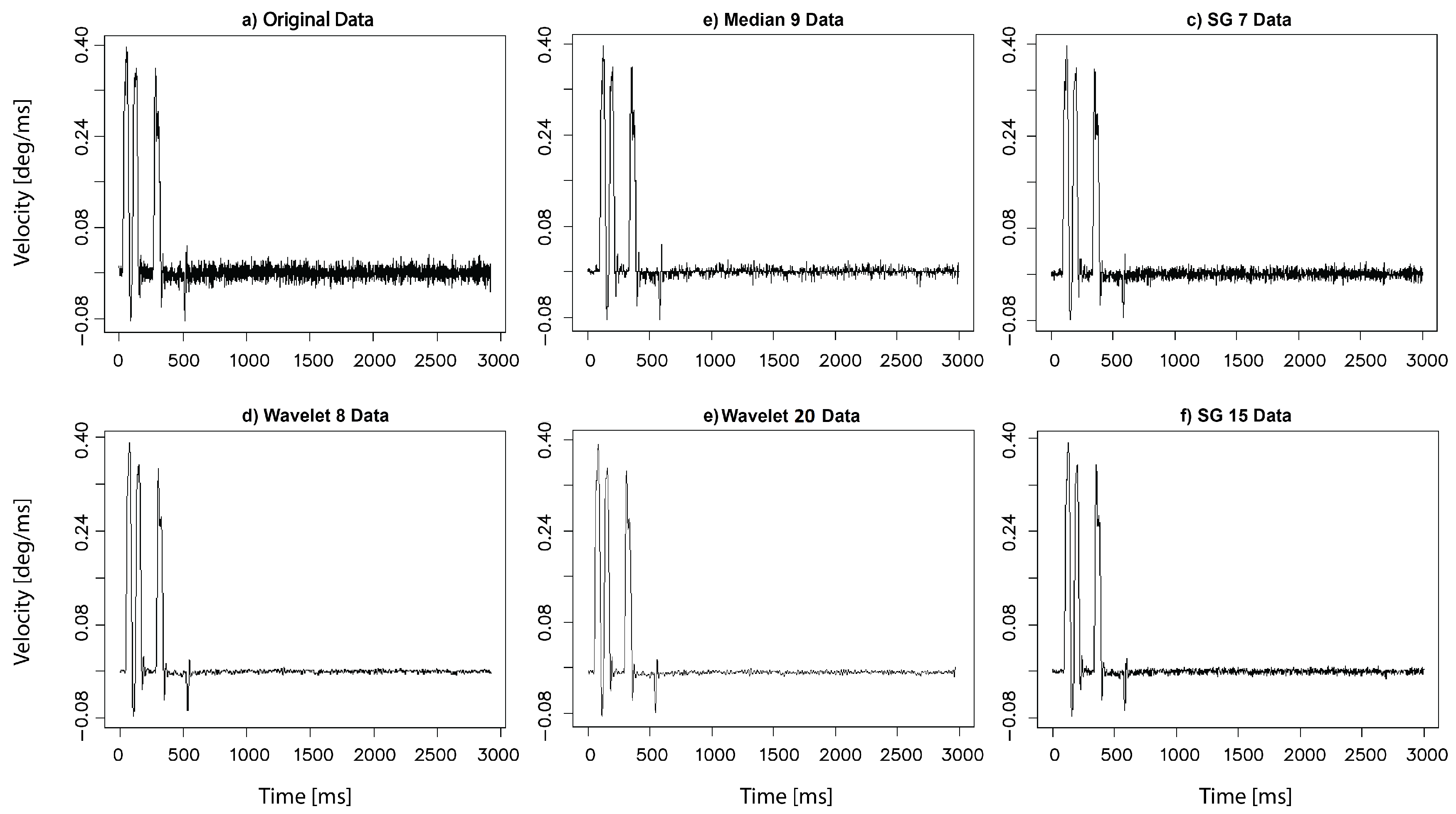
2.3. The Methods Applied
- the Running Median (RM); method replacing the middle element of the defined window—which moves by one element along the axis of the independent variable—with the middle value of the ordered list of window elements. Three window sizes were used: 5, 9, and 15—the resulting filtered observations are denoted by M5, M9, M15.
- the third degree Savitzky-Golay (SG) filter [31] with two window lengths: 7 and 15. The underlying signal within the moving window is approximated by a polynomial of the given order. A least-squares fit of consecutive data points (defined by window size) to a polynomial is performed. The calculated central point of the fitted polynomial curve is the new smoothed data point. Data sets after processing by this method are denoted in the subsequent analysis by SG7, SG15.
- the Daubechies’ wavelets (Db) [32]—a method denoising a signal by means of wavelet transform. It enables presentation of the signal in the form of a linear combination of two types of coefficients representing elements of low and high frequency. By setting the latter coefficients to zero the denoised signal is obtained. Two filter lengths: 8 and 20, three levels in the wavelet decomposition and hard thresholding were used. The smoothed data sets are further referred to as W8, W20;
3. Results
3.1. The Phase Space Reconstruction
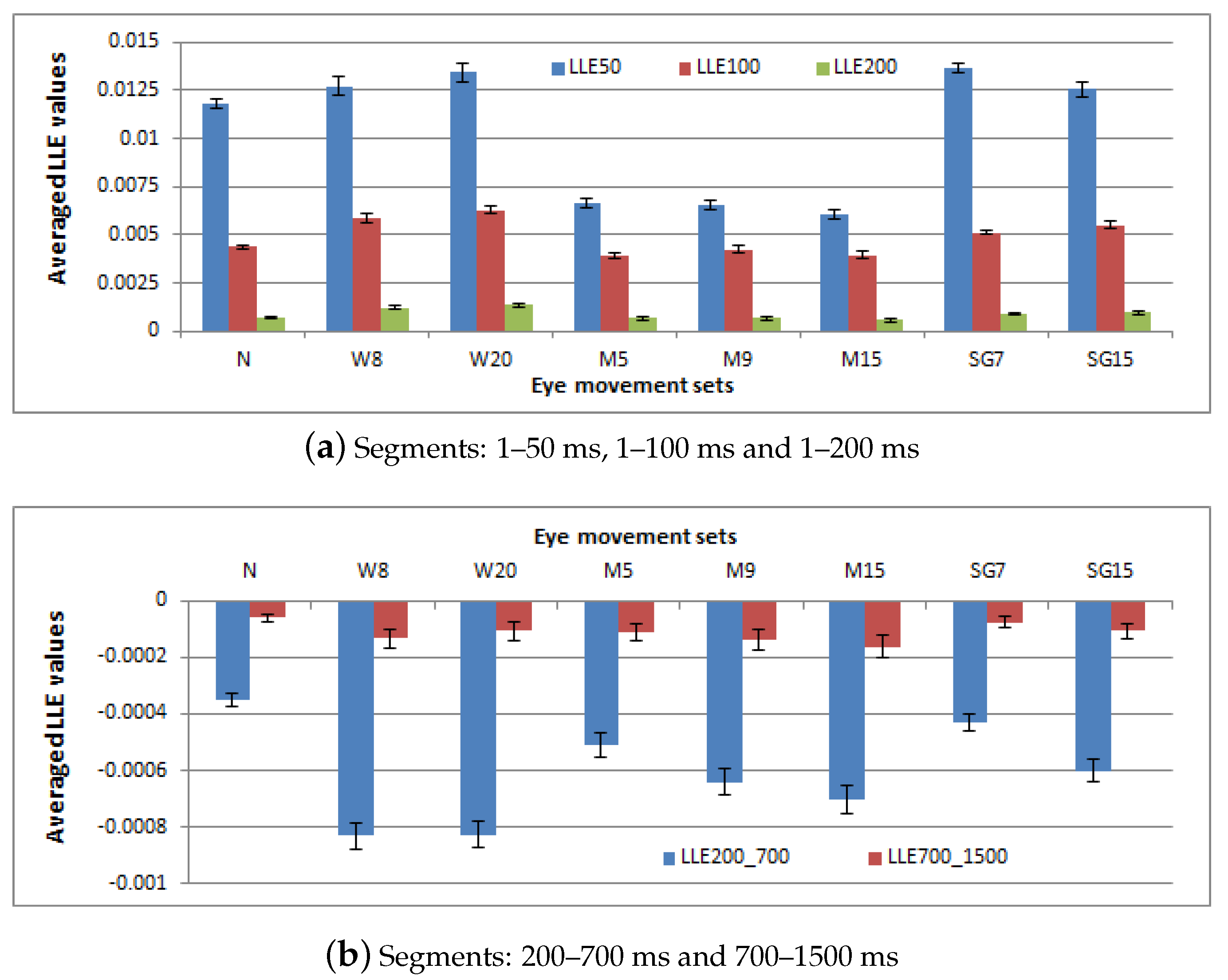
3.2. Signal Characteristics Exploration
- three segments for the first period: 0–50 ms, 0–100 ms and 0–200 ms,
- two for the second one: 200–700 ms and 700–1500 ms.
- the LLE values for the particular time series were indeed higher; the distance between neighbor points was smaller than the initial one, yet did not change with the same rate as in the previous time scope,
- a return to chaotic behavior was observed in the case of a group of time series and, consequently, the occurrence of some positive LLE values influencing the global mean.
3.3. The Phase Space Visualization
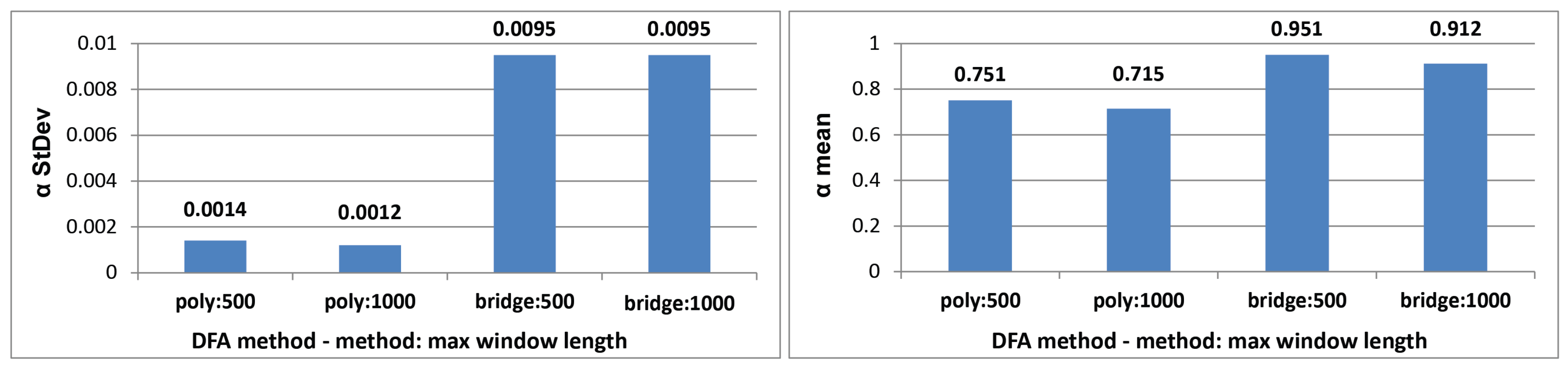
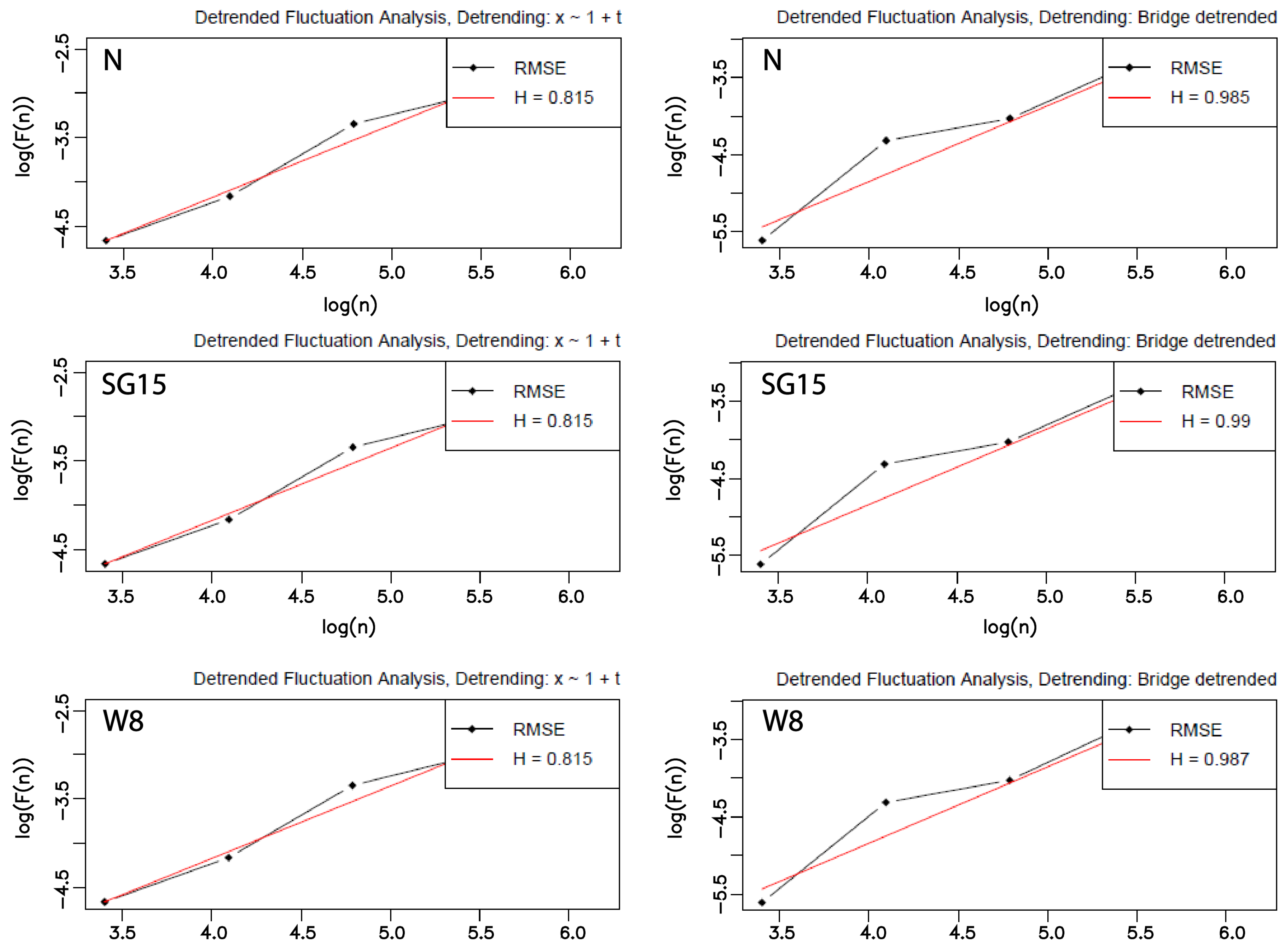
3.4. Detrended Fluctuation Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yuan, Y.; Li, Y.; Mandic, D.P. A comparison analysis of embedding dimensions between normal and epileptic EEG time series. J. Physiol. Sci. 2008, 58, 239–247. [Google Scholar] [CrossRef]
- Majumdar, K.; Myers, M.H. Amplitude suppression and chaos control in epileptic EEG signals. Comput. Math. Methods Med. 2006, 7, 53–66. [Google Scholar] [CrossRef]
- Perc, M. Nonlinear time series analysis of the human electrocardiogram. Eur. J. Phys. 2005, 26, 757. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Human ECG: Nonlinear deterministic versus stochastic aspects. IEE Proc. Sci. Meas. Technol. 1998, 145, 279–284. [Google Scholar] [CrossRef]
- Dingwell, J.B.; Cusumano, J.P. Nonlinear time series analysis of normal and pathological human walking. Chaos 2000, 10, 848–863. [Google Scholar] [CrossRef]
- Terrier, P.; Deriaz, O. Nonlinear dynamics of human locomotion: Effects of rhythmic auditory cueing on local dynamic stability. Front. Physiol. 2013, 4, 230. [Google Scholar] [CrossRef]
- Holmqvist, K.; Nyström, M.; Mulvey, F. Eye tracker data quality: What it is and how to measure it. In Proceedings of the Symposium on Eye Tracking Research and Applications, Santa Barbara, CA, USA, 28–30 March 2012; ACM: New York, NY, USA, 2012; pp. 45–52. [Google Scholar]
- Martinez-Conde, S.; Macknik, S.L.; Hubel, D.H. The role of fixational eye movements in visual perception. Nat. Neurosci. 2004, 5, 229–240. [Google Scholar] [CrossRef]
- Otero-Millan, J.; Troncoso, X.G.; Macknik, S.L.; Serrano-Pedraza, I.; Martinez-Conde, S. Saccades and microsaccades during visual fixation, exploration, and search: Foundations for a common saccadic generator. J. Vis. 2008, 8, 21. [Google Scholar] [CrossRef]
- Martinez-Conde, S.; Otero-Millan, J.; Macknik, S.L. The impact of microsaccades on vision: Towards a unified theory of saccadic function. Nat. Rev. Neurosci. 2013, 14, 83–96. [Google Scholar] [CrossRef]
- Hampson, K.M.; Cufflin, M.P.; Mallen, E.A.H. Sensitivity of chaos measures in detecting stress in the focusing control mechanism of the Short-Sighted Eye. Bull. Math. Biol. 2017, 79, 1870–1887. [Google Scholar] [CrossRef]
- Astefanoaei, C.; Creanga, D.; Pretegiani, E.; Optican, L.; Rufa, A. Dynamical complexity analysis of saccadic eye movements in two different psychological conditions. Rom. Rep. Phys. 2014, 66, 1038–1055. [Google Scholar]
- Murata, A.; Matsuura, T. Nonlinear dynamical analysis of eye movement characteristics using attractor plot and First Lyapunov Exponent. In Human-Computer Interaction: Interaction Technologies; Kurosu, M., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 78–85. [Google Scholar]
- Harezlak, K. Eye movement dynamics during imposed fixations. Inf. Sci. 2017, 384, 249–262. [Google Scholar] [CrossRef]
- Harezlak, K.; Kasprowski, P. Chaotic nature of eye movement signal. In Proceedings of the Intelligent Decision Technologies 2017, Algarve, Portugal, 21–23 June 2017; Czarnowski, I., Howlett, R.J., Jain, L.C., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 120–129. [Google Scholar]
- Harezlak, K.; Kasprowski, P. Searching for chaos evidence in eye movement signals. Entropy 2018, 20, 32. [Google Scholar] [CrossRef]
- Juhola, M. Effects of digital filtering on the parameters of sinusoidal tracking eye movements. Comput. Biomed. Res. 1995, 28, 283–290. [Google Scholar] [CrossRef]
- Špakov, O. Comparison of eye movement filters used in HCI. In Proceedings of the Symposium on Eye Tracking Research and Applications, Santa Barbara, CA, USA, 28–30 March 2012; ACM: New York, NY, USA, 2012; pp. 281–284. [Google Scholar]
- Komogortsev, O.V.; Khan, J.I. Kalman filtering in the design of eye-gaze-guided computer interfaces. In Proceedings of the 12th International Conference on Human-computer Interaction: Intelligent Multimodal Interaction Environments, Beijing, China, 22–27 July 2007; Springer: Berlin, Heidelberg, 2007; pp. 679–689. [Google Scholar]
- Chartier, S.; Renaud, P. An online noise filter for eye-tracker data recorded in a virtual environment. In Proceedings of the 2008 Symposium on Eye Tracking Research & Applications, Savannah, GA, USA, 26–28 March 2008; ACM: New York, NY, USA, 2008; pp. 153–156. [Google Scholar]
- Warman, R.A.; Wibirama, S.; Bejo, A. Performance comparison of signal processing filters on smooth pursuit eye movements. In Proceedings of the 2017 2nd International conferences on Information Technology, Information Systems and Electrical Engineering (ICITISEE), Yogyakarta, Indonesia, 1–2 November 2017; pp. 111–115. [Google Scholar]
- Kasprowski, P.; Harezlak, K. ETCAL—A versatile and extendable library for eye tracker calibration. Digit. Signal Process. 2017, 77, 222–232. [Google Scholar] [CrossRef]
- Abarbanel, H.D.I. Analysis of Observed Chaotic Data; Institute for Nonlinear Science; Springer: New York, NY, USA, 1996. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating Largest Lyapunov Exponents from small data sets. Phys. D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Stadnytska, T.; Braun, S.; Werner, J. Analyzing fractal dynamics employing R. Nonlinear Dyn. Psychol. Life Sci. 2010, 14, 117. [Google Scholar]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1994, 49, 1685–1689. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Koscielny-Bunde, E.; Rego, H.H.; Havlin, S.; Bunde, A. Detecting long-range correlations with detrended fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2001, 295, 441–454. [Google Scholar] [CrossRef]
- Jazz Novo. Ober Consulting. 2018. Available online: http://www.ober-consulting.com/9/lang/1/ (accessed on 10 January 2019).
- Schafer, R.W. What Is a Savitzky-Golay Filter? [Lecture Notes]. IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Juhola, M. Median filtering is appropriate to signals of saccadic eye movements. Comput. Biol. Med. 1991, 21, 43–49. [Google Scholar] [CrossRef]
- Kasprowski, P.; Harężlak, K.; Stasch, M. Guidelines for the eye tracker calibration using points of regard. In Information Technologies in Biomedicine; Piętka, E., Kawa, J., Wieclawek, W., Eds.; Springer International Publishing: Cham, Switzerland, 2014; Volume 4, pp. 225–236. [Google Scholar]
- Nyström, M.; Holmqvist, K. An adaptive algorithm for fixation, saccade, and glissade detection in eyetracking data. Behav. Res. Methods 2010, 42, 188–204. [Google Scholar] [CrossRef]
- Azami, H.; Mohammadi, K.; Bozorgtabar, B. An improved signal segmentation using moving average and Savitzky-Golay filter. J. Signal Inf. Process. 2012, 3, 39. [Google Scholar] [CrossRef]
- Hargittai, S. Savitzky-Golay least-squares polynomial filters in ECG signal processing. Comput. Cardiol. 2005, 2005, 763–766. [Google Scholar]
- Awal, M.A.; Mostafa, S.S.; Ahmad, M. Performance analysis of Savitzky-Golay smoothing filter using ECG signal. Int. J. Comput. Inf. Technol. 2011, 1, 110126. [Google Scholar]
- Bulling, A.; Ward, J.A.; Gellersen, H.; Troster, G. Eye movement analysis for activity recognition using Electrooculography. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 741–753. [Google Scholar] [CrossRef]
- Geetha, G.; Geethalakshmi, S.N. Removing EEG artifacts using spatially constrained Independent Component Analysis and Daubechies wavelet based denoising with Otsu’ thresholding technique. In Perception and Machine Intelligence; Kundu, M.K., Mitra, S., Mazumdar, D., Pal, S.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 346–357. [Google Scholar]
- Dautov, Ç.P.; Özerdem, M.S. Introduction to wavelets and their applications in signal denoising. Bitlis Eren Univ. J. Sci. Technol. 2018, 8, 1–10. [Google Scholar]
- Running Medians—Robust Scatter Plot Smoothing. Available online: https://stat.ethz.ch/R-manual/R-devel/library/stats/html/runmed.html (accessed on 17 August 2018).
- Package ‘rwt’. Available online: https://cran.r-project.org/web/packages/rwt/rwt.pdf (accessed on 17 August 2018).
- Package ‘Signal’. Available online: https://cran.r-project.org/web/packages/signal/signal.pdf (accessed on 17 August 2018).
- Package ‘tseriesChaos’. Available online: https://cran.r-project.org/web/packages/tseriesChaos/tseriesChaos.pdf (accessed on 17 August 2018).
- Package ‘Fractal’. Available online: https://cran.r-project.org/web/packages/fractal/fractal.pdf (accessed on 17 August 2018).
- Scott, D.W. On optimal and data-based histograms. Biometrika 1979, 66, 605–610. [Google Scholar] [CrossRef]
- Student’s t-Test. Available online: https://stat.ethz.ch/R-manual/R-devel/library/stats/html/t.test.html (accessed on 17 August 2018).
- Fit an Analysis of Variance Model. Available online: https://stat.ethz.ch/R-manual/R-devel/library/stats/html/aov.html (accessed on 17 August 2018).
- Compute Tukey Honest Significant Differences. Available online: https://stat.ethz.ch/R-manual/R-patched/library/stats/html/TukeyHSD.html (accessed on 17 August 2018).
- Kruskal-Wallis Rank Sum Test. Available online: https://stat.ethz.ch/R-manual/R-devel/library/stats/html/kruskal.test.html (accessed on 17 August 2018).
- Shapiro-Wilk Normality Test. Available online: https://stat.ethz.ch/R-manual/R-devel/library/stats/html/shapiro.test.html (accessed on 17 August 2018).
- Darrien, J.H.; Herd, K.; Starling, L.J.; Rosenberg, J.R.; Morrison, J.D. An analysis of the dependence of saccadic latency on target position and target characteristics in human subjects. BMC Neurosci. 2001, 2, 1–8. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. Lect. Notes Math. 1981, 898, 366. [Google Scholar]
- Delignières, D. Correlation properties of (discrete) fractional Gaussian noise and fractional Brownian motion. Math. Probl. Eng. 2015, 2015, 485623. [Google Scholar] [CrossRef]
- Lo, M.; Tsai, P.; Lin, P.; Lin, C.; Hsin, Y.L. The nonlinear and nonstationary properties in EEG signals: Probing the complex fluctuations by Hilbert-Huang Transform. Adv. Adapt. Data Anal. 2009, 1, 461–482. [Google Scholar] [CrossRef]
- Gomolka, R.S.; Kampusch, S.; Kaniusas, E.; Thürk, F.; Széles, J.C.; Klonowski, W. Higuchi fractal dimension of heart rate variability during percutaneous auricular vagus nerve stimulation in healthy and diabetic subjects. Front. Physiol. 2018, 9, 1162. [Google Scholar] [CrossRef] [PubMed]




| Filters | Time Delay | EmDim |
|---|---|---|
| N | 9.483 (10.988) | 4.143 (2.638) |
| W8 | 21.149 (12.693) | 6.388 (6.222) |
| W20 | 19.333 (10.922) | 6.247 (6.156) |
| M5 | 13.164 (7.940) | 6.698 (4.544) |
| M9 | 14.560 (6.800) | 7.591 (5.185) |
| M15 | 15.765 (6.529) | 8.324 (5.727) |
| SG7 | 9.500 (9.952) | 3.994 (3.118) |
| SG15 | 15.945 (10.817) | 7.143 (7.884) |
| Segment | ||
|---|---|---|
| 0_50 | 0_100 | 0_200 |
| M5:M9 | M5:M15 | M5:M15 |
| W8:SG15 | N:M9 | M9:M15 |
| W20:SG7 | N:M15 | |
| SG7:SG15 | ||
| Segment | |
|---|---|
| N:SG7 | N:W8 |
| M9:M15 | N:M9 |
| SG7:M15 | N:M15 |
| SG15:M9 | SG7:M15 |
| Filter | Time Delay | emDim | LLE_0_100 | LLE_200_700 | LLE_700_1500 |
|---|---|---|---|---|---|
| N | 10 | 3 | 0.00830 | −0.00082 | −0.00002 |
| M9 | 10 | 5 | 0.00960 | −0.00151 | −0.00009 |
| SG7 | 10 | 3 | 0.00964 | −0.00096 | −0.00002 |
| SG15 | 8 | 3 | 0.01189 | −0.00138 | 0.00000 |
| W8 | 17 | 3 | 0.01349 | −0.00178 | −0.00004 |
| W20 | 19 | 4 | 0.01031 | −0.00187 | −0.00001 |
| Param Set | N | SG7 | SG15 | W8 | W20 | M5 | M9 | M15 |
|---|---|---|---|---|---|---|---|---|
| poly:500 | 0.74962 | 0.75063 | 0.75201 | 0.75102 | 0.75022 | 0.75127 | 0.75194 | 0.75299 |
| (0.0853) | (0.0841) | (0.0831) | (0.0841) | (0.0839) | (0.0837) | (0.0833) | (0.0829) | |
| poly:1000 | 0.71396 | 0.71476 | 0.71589 | 0.71510 | 0.71444 | 0.71528 | 0.71528 | 0.71675 |
| (0.0692) | (0.0682) | (0.0672) | (0.0681) | (0.0679) | (0.0678) | (0.0678) | 0.0670) | |
| bridge:500 | 0.94499 | 0.94812 | 0.95531 | 0.95194 | 0.93809 | 0.95116 | 0.95428 | 0.95859 |
| (0.1690) | (0.1652) | (0.1628) | (0.1628) | (0.1533) | (0.1643) | (0.1640) | (0.1636) | |
| bridge:1000 | 0.90989 | 0.91238 | 0.91814 | 0.91077 | 0.89468 | 0.91479 | 0.91734 | 0.92089 |
| (0.1362) | (0.1331) | (0.1309) | (0.1312) | (0.1236) | (0.1323) | (0.1320) | (0.1315) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harezlak, K.; Kasprowski, P. Understanding Eye Movement Signal Characteristics Based on Their Dynamical and Fractal Features. Sensors 2019, 19, 626. https://doi.org/10.3390/s19030626
Harezlak K, Kasprowski P. Understanding Eye Movement Signal Characteristics Based on Their Dynamical and Fractal Features. Sensors. 2019; 19(3):626. https://doi.org/10.3390/s19030626
Chicago/Turabian StyleHarezlak, Katarzyna, and Pawel Kasprowski. 2019. "Understanding Eye Movement Signal Characteristics Based on Their Dynamical and Fractal Features" Sensors 19, no. 3: 626. https://doi.org/10.3390/s19030626
APA StyleHarezlak, K., & Kasprowski, P. (2019). Understanding Eye Movement Signal Characteristics Based on Their Dynamical and Fractal Features. Sensors, 19(3), 626. https://doi.org/10.3390/s19030626





