Low-Frequency Vibration Sensor with a Sub-nm Sensitivity Using a Bidomain Lithium Niobate Crystal
Abstract
1. Introduction
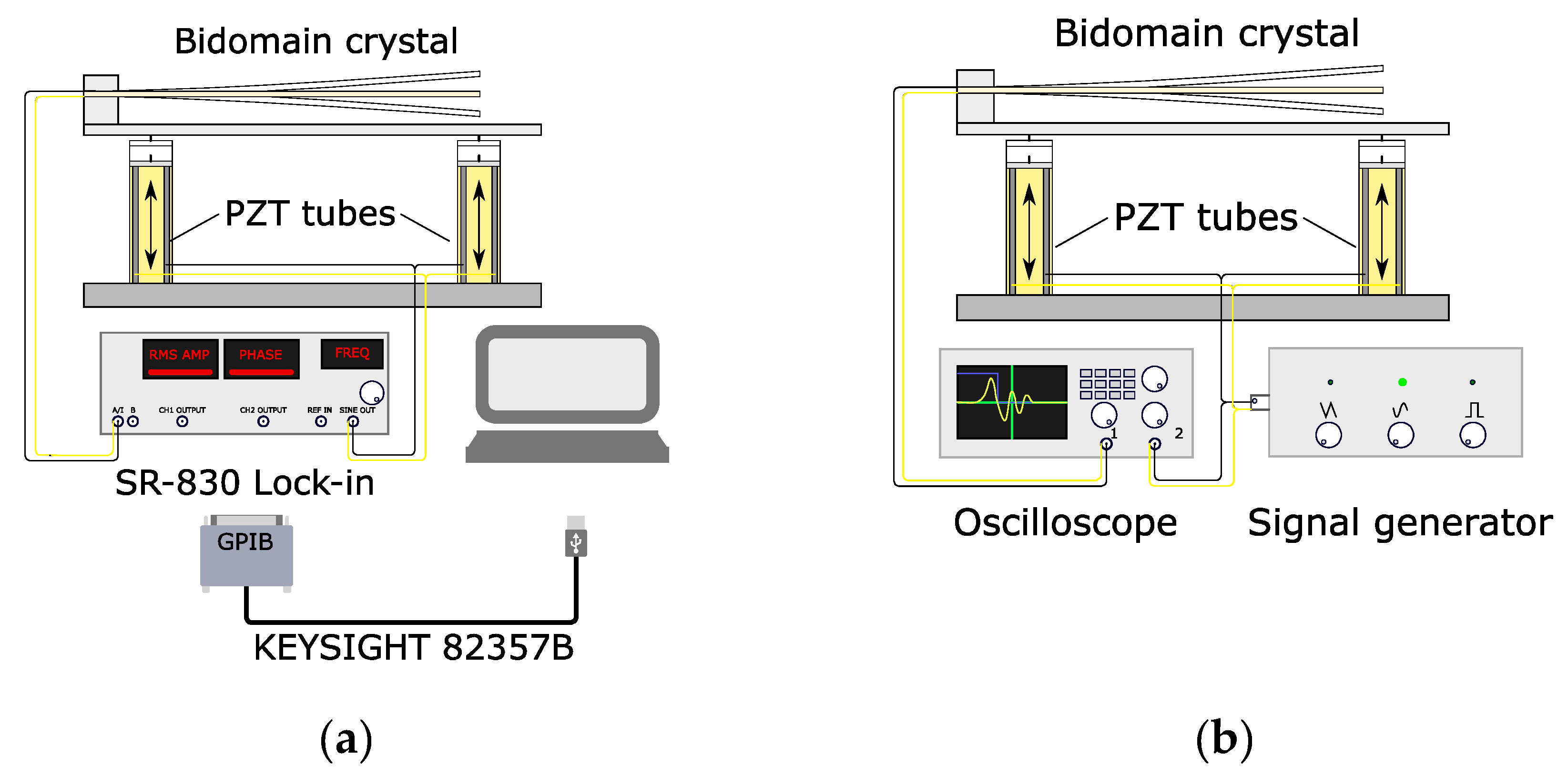
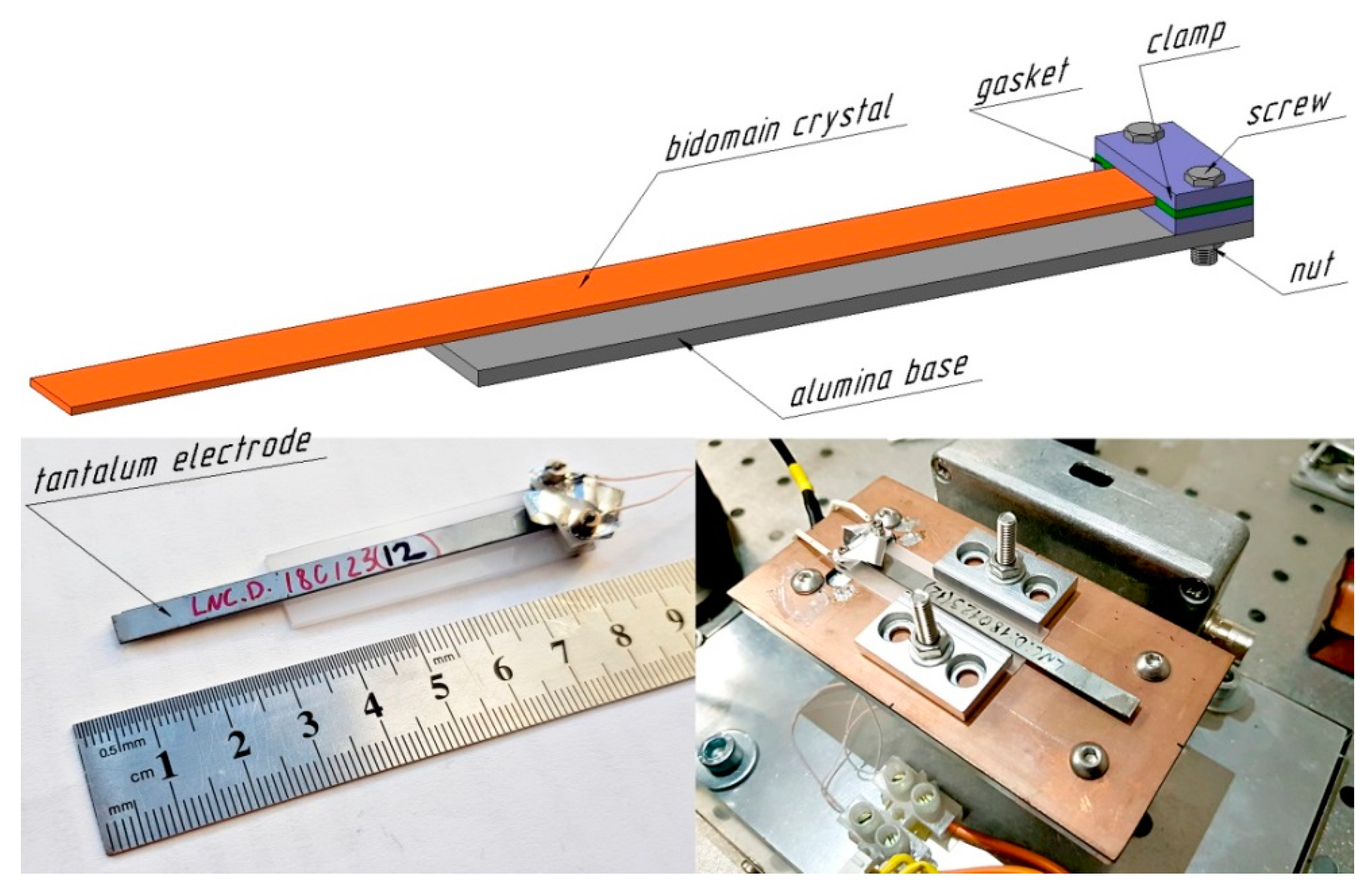
2. Materials and Methods
- (i)
- Lock-in detection of the voltage amplitude by a SR-830 amplifier (Stanford Research Systems Inc., Sunnyvale, CA, USA);
- (ii)
- Registration of oscillograms by a DSO-X 3032A oscilloscope (Agilent Technologies Inc., Santa Clara, CA, USA) with post-processing by the Fourier analysis.
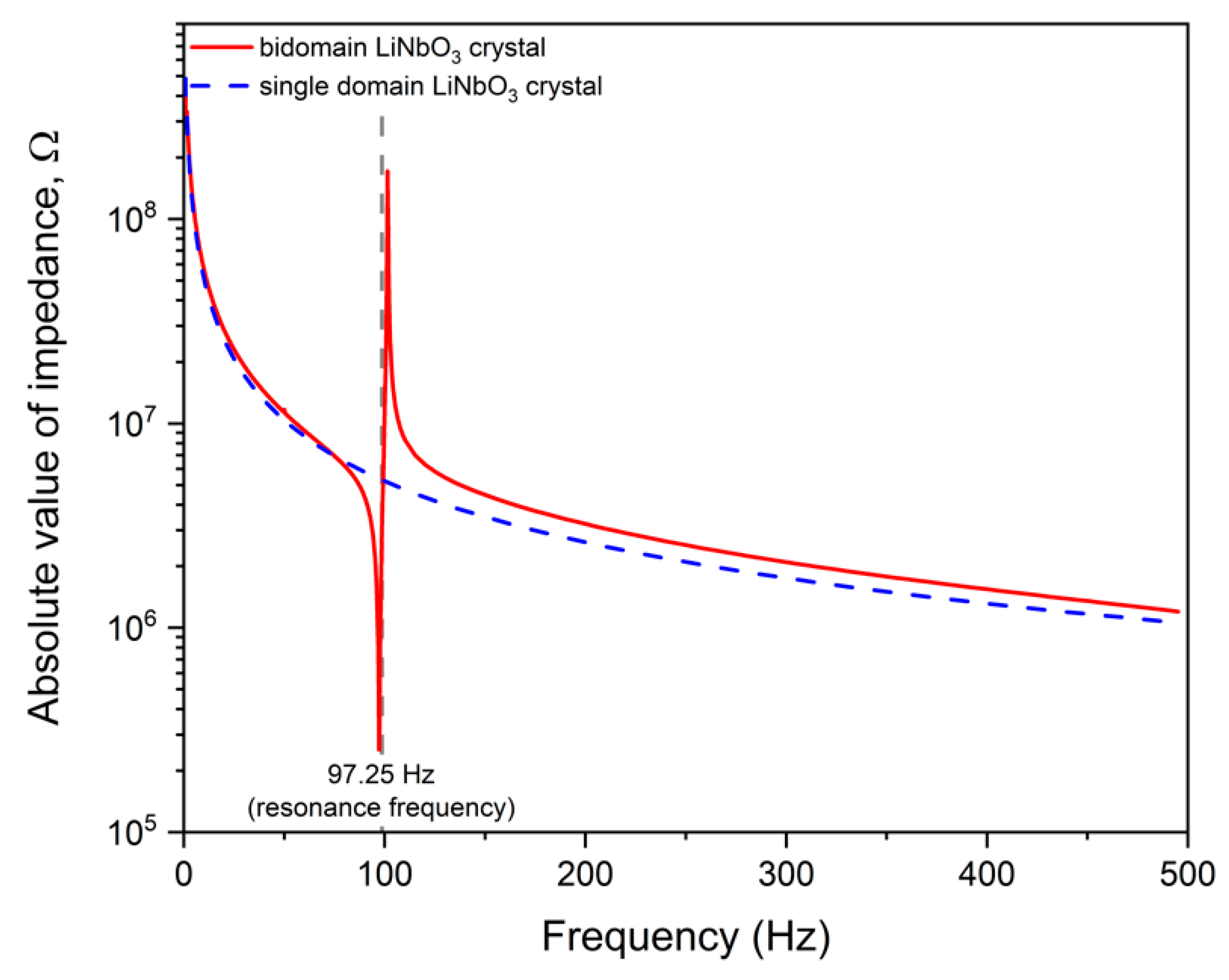
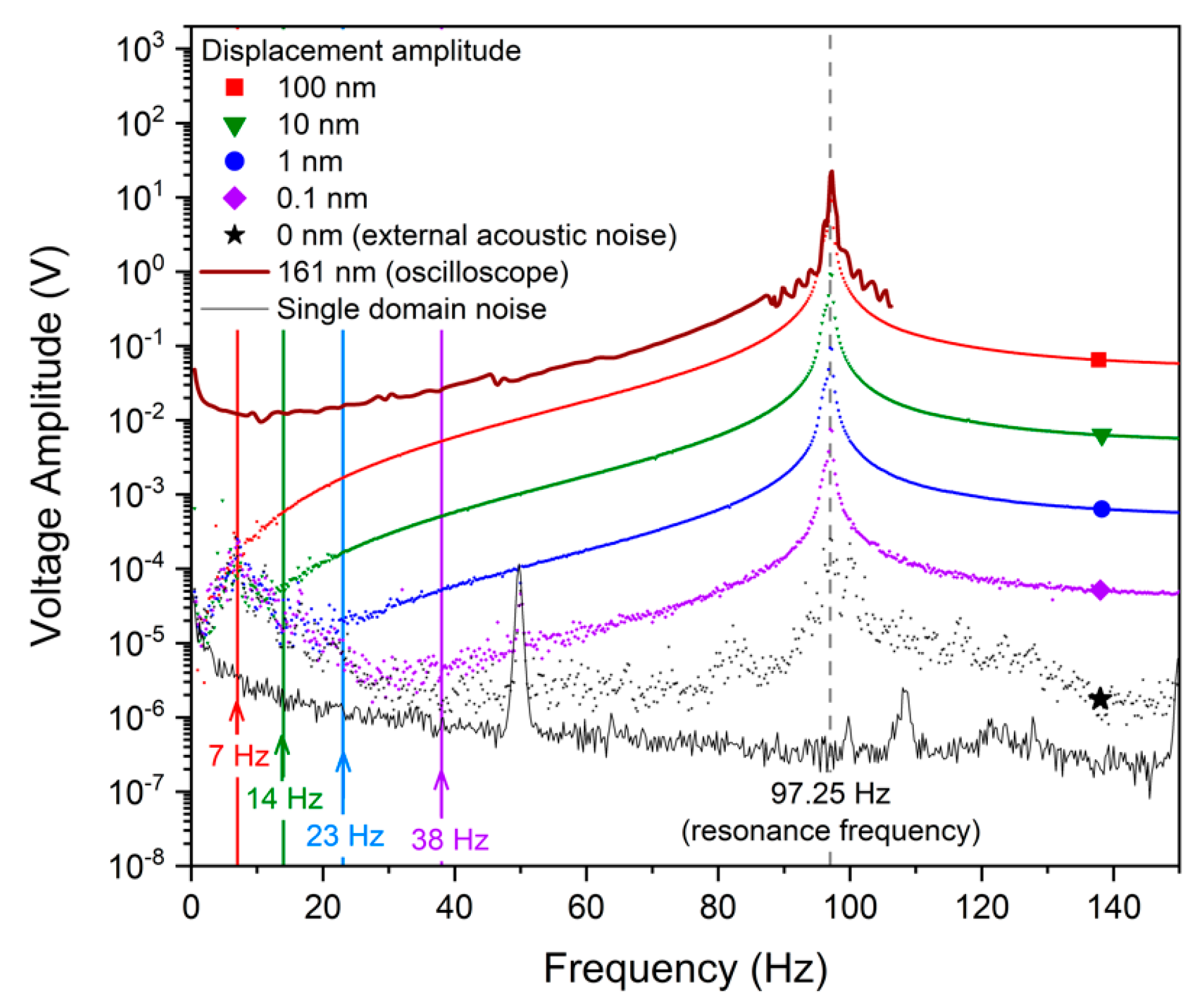
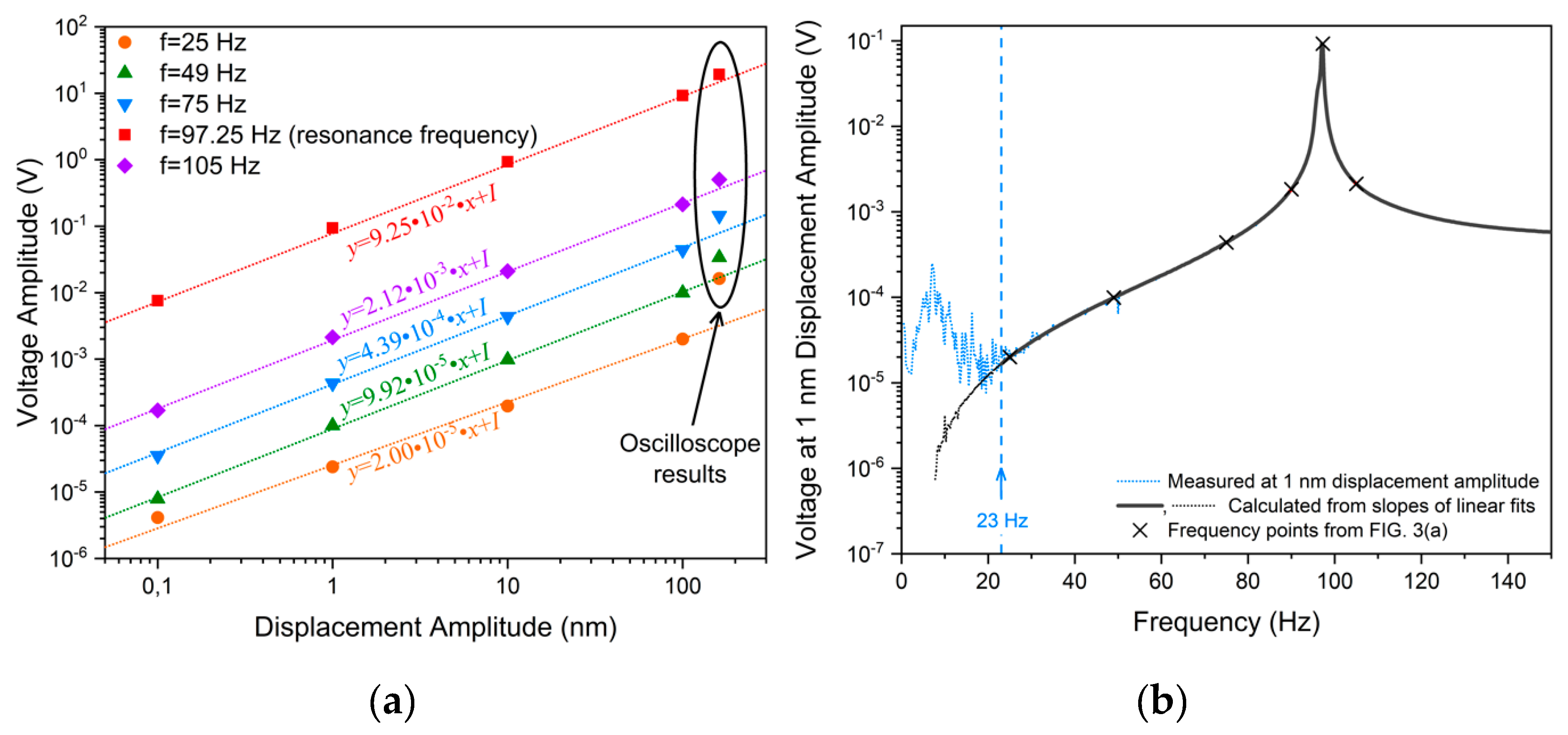
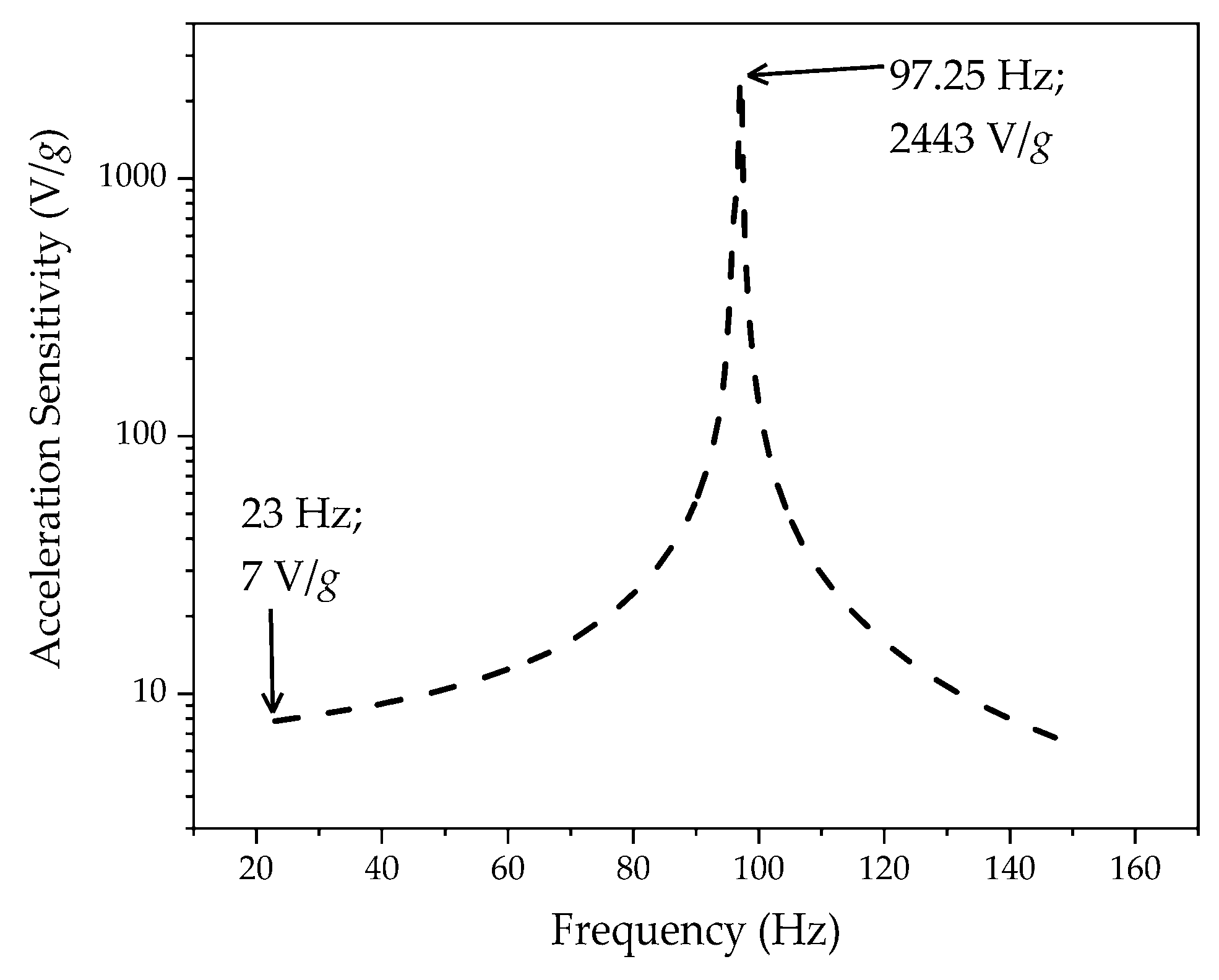
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

Appendix B
- (i)
- Lock-in detection of the voltage amplitude by a SR-830 amplifier (Stanford Research Systems Inc., Sunnyvale, CA, USA);
- (ii)
- Registration of oscillograms by a DSO-X 3032A oscilloscope, with post-processing by the Fourier analysis (Agilent Technologies Inc., Santa Clara, CA, USA).
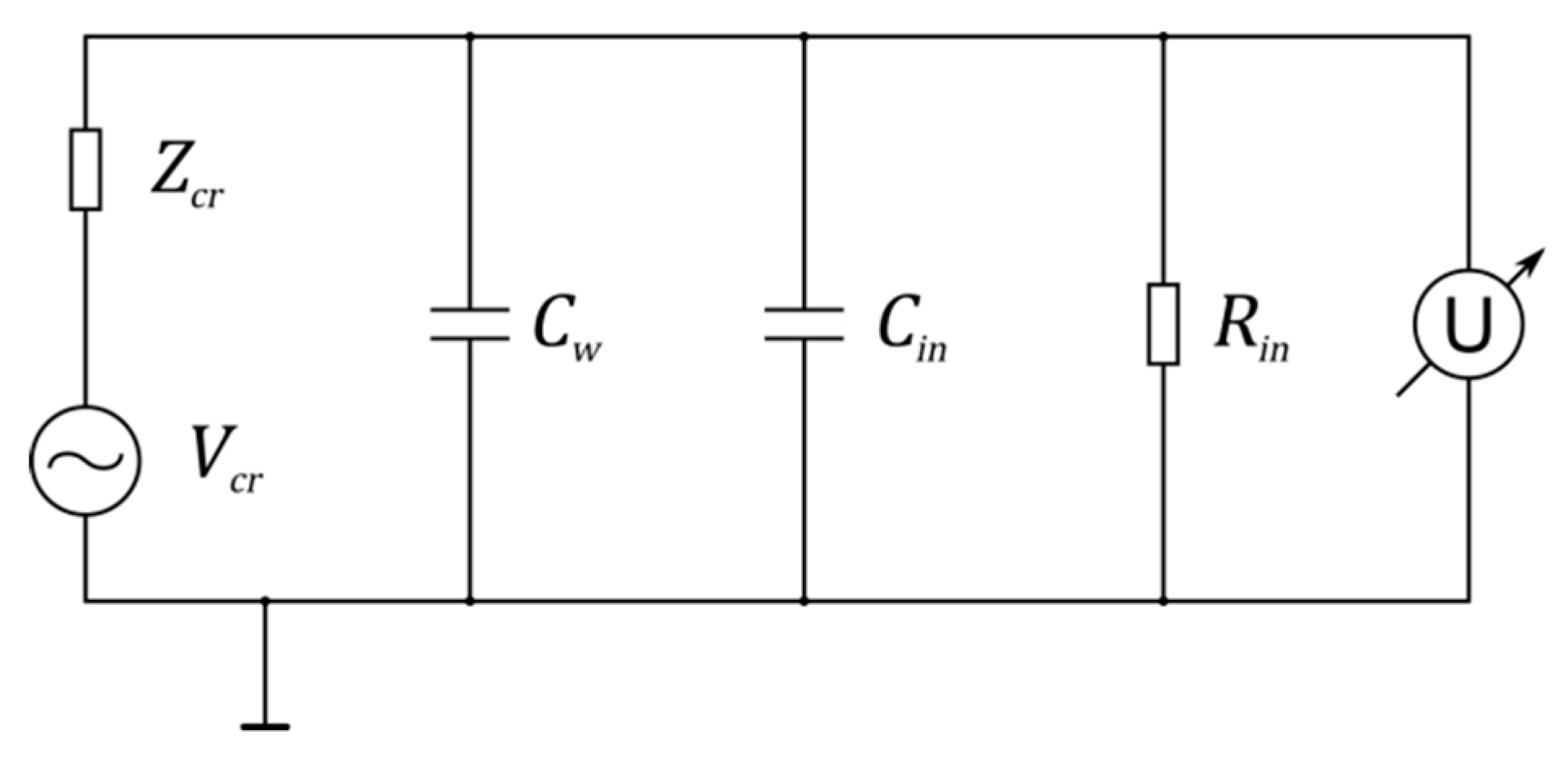
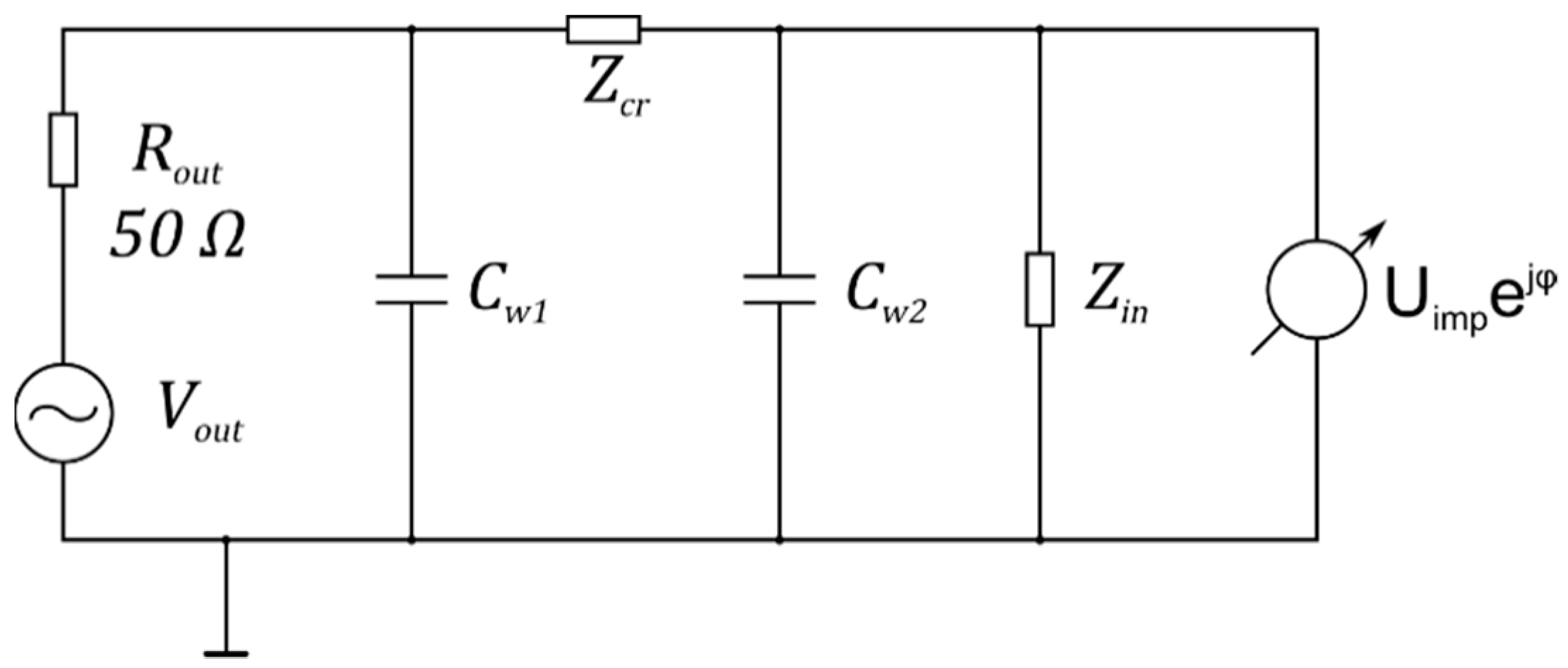
Appendix C
| Sensor Type | Resonance Frequency, Hz | Sensitivity to Displacement | Sensitivity to Acceleration | Reference | ||
|---|---|---|---|---|---|---|
| At a Frequency of 25 Hz, V/nm | At the Resonance Frequency, V/nm | At a Frequency of 25 Hz, V/g | At the Resonance Frequency, V/g | |||
| PZT cantilever with a seismic mass | 50 | – | – | 0.5 | 3.8 | [18] |
| PZT thin film | 9610 | – | 3.5 × 10−5 | – | – | [11] |
| PZT cantilever | 53.6 | – | – | 10 | 170 | [19] |
| Polyvinylidene difluoride (PVDF) thin film | – | - | – | 2.35 × 10−1 | – | [56] |
| PZT fiber composite | 48 | 1 × 10−5 | 2 × 10−3 | – | – | [21] |
| Cantilever based on ZnO nanowires | 44.1 | – | 13 × 10−8 | – | – | [14] |
| PZT cantilever | 275 | – | – | 1 × 10−3 | 4.5 | [20] |
| Bidomain lithium niobate cantilever | 97.25 | 2 × 10−5 | 3.5 × 10−2 | 7 | 2443 | This work |
References
- Lynch, J.P. A Summary Review of Wireless Sensors and Sensor Networks for Structural Health Monitoring. Shock Vib. Dig. 2006, 38, 91–128. [Google Scholar] [CrossRef]
- Zhao, X.; Gao, H.; Zhang, G.; Ayhan, B.; Yan, F.; Kwan, C.; Rose, J.L. Active health monitoring of an aircraft wing with embedded piezoelectric sensor/actuator network: I. Defect detection, localization and growth monitoring. Smart Mater. Struct. 2007, 16, 1208–1217. [Google Scholar] [CrossRef]
- Ubertini, F.; Comanducci, G.; Cavalagli, N. Vibration-based structural health monitoring of a historic bell-tower using output-only measurements and multivariate statistical analysis. Struct. Health Monit. 2016, 15, 438–457. [Google Scholar] [CrossRef]
- He, Q.; Li, K.; Han, R.; Wang, J.; Li, X. Sub-g weak-vibration-triggered high-efficiency energy harvesting for event identification. J. Micromech. Microeng. 2018, 28, 075018. [Google Scholar] [CrossRef]
- Wang, S.Y.; Quek, S.T.; Ang, K.K. Vibration control of smart piezoelectric composite plates. Smart Mater. Struct. 2001, 10, 637–644. [Google Scholar] [CrossRef]
- Sharma, A.; Kumar, R.; Vaish, R.; Chauhan, V.S. Active vibration control of space antenna reflector over wide temperature range. Compos. Struct. 2015, 128, 291–304. [Google Scholar] [CrossRef]
- Aridogan, U.; Basdogan, I. A review of active vibration and noise suppression of plate-like structures with piezoelectric transducers. J. Intell. Mater. Syst. Struct. 2015, 26, 1455–1476. [Google Scholar] [CrossRef]
- Jiang, X.; Kim, K.; Zhang, S.; Johnson, J.; Salazar, G. High-Temperature Piezoelectric Sensing. Sensors 2013, 14, 144–169. [Google Scholar] [CrossRef]
- Wang, W.; Xue, X.; Huang, Y.; Liu, X. A Novel Wireless and Temperature-Compensated SAW Vibration Sensor. Sensors 2014, 14, 20702–20712. [Google Scholar] [CrossRef]
- Akiyama, M.; Kamohara, T.; Nishikubo, K.; Ueno, N.; Nagai, H.; Okutani, T. Ultrahigh temperature vibration sensors using aluminum nitride thin films and W/Ru multilayer electrodes. Appl. Phys. Lett. 2005, 86, 022106. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Q.-M. Transient response of piezoelectric thin-film vibration sensor under pulse excitation. J. Appl. Phys. 2006, 99, 014107. [Google Scholar] [CrossRef]
- Castille, C.; Dufour, I.; Lucat, C. Longitudinal vibration mode of piezoelectric thick-film cantilever-based sensors in liquid media. Appl. Phys. Lett. 2010, 96, 154102. [Google Scholar] [CrossRef]
- Tang, Q.C.; He, Q.S.; Li, M.Y.; Dong, C.; Xu, D.C.; Li, X. A self-powered wireless sensing node for event-driven alerting based on a bi-stable vibration energy harvester. In Proceedings of the 2015 Transducers—2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, AK, USA, 21–25 June 2015; pp. 1215–1218. [Google Scholar] [CrossRef]
- Yu, A.; Jiang, P.; Wang, Z.L. Nanogenerator as self-powered vibration sensor. Nano Energy 2012, 1, 418–423. [Google Scholar] [CrossRef]
- Egusa, S.; Iwasawa, N. Piezoelectric paints: Preparation and application as built-in vibration sensors of structural materials. J. Mater. Sci. 1993, 28, 1667–1672. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhang, X.; Wu, H.; Zhang, H. Optimal placement and active vibration control for piezoelectric smart flexible cantilever plate. J. Sound Vib. 2007, 301, 521–543. [Google Scholar] [CrossRef]
- Tressler, J.F.; Alkoy, S.; Newnham, R.E. Piezoelectric Sensors and Sensor Materials. J. Electroceram. 1998, 2, 257–272. [Google Scholar] [CrossRef]
- Ou, Q.; Chen, X.; Gutschmidt, S.; Wood, A.; Leigh, N.; Arrieta, A.F. An experimentally validated double-mass piezoelectric cantilever model for broadband vibration–based energy harvesting. J. Intell. Mater. Syst. Struct. 2012, 23, 117–126. [Google Scholar] [CrossRef]
- Hu, Y.; Tu, H.; Xu, Y. Low-frequency vibration sensors based on a cascaded gapped cantilever. Smart Mater. Struct. 2016, 25, 095007. [Google Scholar] [CrossRef]
- Bong, Y.J.; Kok, S.L. Characterization on Piezoelectric Cantilever for its Linear Response at Low Frequency for Measuring Acceleration Level of Vibration. Appl. Mech. Mater. 2015, 761, 579–583. [Google Scholar] [CrossRef]
- Chen, Q.; Sun, Y.; Wang, Q.M.; Qin, L.; Xue, H.; Xiong, Z. Piezoelectric PZT fiber composite as a low frequency vibration sensor. In Proceedings of the 2013 Joint IEEE International Symposium on Applications of Ferroelectric and Workshop on Piezoresponse Force Microscopy (ISAF/PFM), Prague, Czech Republic, 21–25 July 2013; pp. 302–305. [Google Scholar] [CrossRef]
- Mecea, V.M. Loaded vibrating quartz sensors. Sens. Actuators A Phys. 1994, 40, 1–27. [Google Scholar] [CrossRef]
- Ansorge, E.; Schimpf, S.; Hirsch, S.; Sauerwald, J.; Fritze, H.; Schmidt, B. Evaluation of langasite (La3Ga5SiO14) as a material for high temperature microsystems. Sens. Actuators A Phys. 2006, 130–131, 393–396. [Google Scholar] [CrossRef]
- Turner, R.C.; Fuierer, P.A.; Newnham, R.E.; Shrout, T.R. Materials for high temperature acoustic and vibration sensors: A review. Appl. Acoust. 1994, 41, 299–324. [Google Scholar] [CrossRef]
- Kim, K.; Zhang, S.; Salazar, G.; Jiang, X. Design, fabrication and characterization of high temperature piezoelectric vibration sensor using YCOB crystals. Sens. Actuators A Phys. 2012, 178, 40–48. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, F. Piezoelectric Materials for High Temperature Sensors. J. Am. Ceram. Soc. 2011, 94, 3153–3170. [Google Scholar] [CrossRef]
- Yuan, Y.; Shyong Chow, K.; Du, H.; Wang, P.; Zhang, M.; Yu, S.; Liu, B. A ZnO thin-film driven microcantilever for nanoscale actuation and sensing. Int. J. Smart Nano Mater. 2013, 4, 128–141. [Google Scholar] [CrossRef]
- Kawamata, A.; Hosaka, H.; Morita, T. Non-hysteresis and perfect linear piezoelectric performance of a multilayered lithium niobate actuator. Sens. Actuators A Phys. 2007, 135, 782–786. [Google Scholar] [CrossRef]
- Kim, H.S.; Kim, J.-H.; Kim, J. A review of piezoelectric energy harvesting based on vibration. Int. J. Precis. Eng. Manuf. 2011, 12, 1129–1141. [Google Scholar] [CrossRef]
- Karami, M.A.; Bilgen, O.; Inman, D.J.; Friswell, M.I. Experimental and analytical parametric study of single-crystal unimorph beams for vibration energy harvesting. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1508–1520. [Google Scholar] [CrossRef] [PubMed]
- Wlodkowski, P.A.; Deng, K.; Kahn, M. The development of high-sensitivity, low-noise accelerometers utilizing single crystal piezoelectric materials. Sens. Actuators A Phys. 2001, 90, 125–131. [Google Scholar] [CrossRef]
- Ohnishi, N. An Etching Study on a Heat-Induced Layer at the Positive-Domain Surface of LiNbO3. Jpn. J. Appl. Phys. 1977, 16, 1069–1070. [Google Scholar] [CrossRef]
- Nakamura, K.; Ando, H.; Shimizu, H. Partial Domain Inversion in LiNbO3 Plates and its Applications to Piezoelectric Devices. In Proceedings of the IEEE 1986 Ultrasonics Symposium, Williamsburg, VA, USA, 17–19 November 1986; pp. 719–722. [Google Scholar] [CrossRef]
- Nakamura, K.; Ando, H.; Shimizu, H. Ferroelectric domain inversion caused in LiNbO3 plates by heat treatment. Appl. Phys. Lett. 1987, 50, 1413–1414. [Google Scholar] [CrossRef]
- Kubasov, I.V.; Kislyuk, A.M.; Bykov, A.S.; Malinkovich, M.D.; Zhukov, R.N.; Kiselev, D.A.; Ksenich, S.V.; Temirov, A.A.; Timushkin, N.G.; Parkhomenko, Y.N. Bidomain structures formed in lithium niobate and lithium tantalate single crystals by light annealing. Crystallogr. Rep. 2016, 61, 258–262. [Google Scholar] [CrossRef]
- Blagov, A.E.; Bykov, A.S.; Kubasov, I.V.; Malinkovich, M.D.; Pisarevskii, Y.V.; Targonskii, A.V.; Eliovich, I.A.; Kovalchuk, M.V. An electromechanical X-ray optical element based on a hysteresis-free monolithic bimorph crystal. Instrum. Exp. Tech. 2016, 59, 728–732. [Google Scholar] [CrossRef]
- Bykov, A.S.; Malinkovich, M.D.; Kubasov, I.V.; Kislyuk, A.M.; Kiselev, D.A.; Ksenich, S.V.; Zhukov, R.N.; Temirov, A.A.; Chichkov, M.V.; Polisan, A.A.; et al. Application of Radioactive Isotopes for Beta-Voltaic Generators. Russ. Microelectron. 2017, 46. [Google Scholar] [CrossRef]
- Kubasov, I.V.; Popov, A.V.; Bykov, A.S.; Temirov, A.A.; Kislyuk, A.M.; Zhukov, R.N.; Kiselev, D.A.; Chichkov, M.V.; Malinkovich, M.D.; Parkhomenko, Y.N. Deformation Anisotropy of Y + 128°-Cut Single Crystalline Bidomain Wafers of Lithium Niobate. Russ. Microelectron. 2017, 46, 557–563. [Google Scholar] [CrossRef]
- Nakamura, K.; Ando, H.; Shimizu, H. Bending Vibrator Consisting of a LiNbO3 Plate with a Ferroelectric Inversion Layer. Jpn. J. Appl. Phys. 1987, 26, 198. [Google Scholar] [CrossRef]
- Nakamura, K.; Shimizu, H. Hysteresis-free piezoelectric actuators using LiNbO3 plates with a ferroelectric inversion layer. Ferroelectrics 1989, 93, 211–216. [Google Scholar] [CrossRef]
- Nakamura, K.; Nakamura, T.; Yamada, K. Torsional Actuators Using LiNbO3 Plates with an Inversion Layer. Jpn. J. Appl. Phys. 1993, 32, 2415–2417. [Google Scholar] [CrossRef]
- Kugel, V.D.; Rosenman, G. Domain inversion in heat-treated LiNbO3 crystals. Appl. Phys. Lett. 1993, 62, 2902–2904. [Google Scholar] [CrossRef]
- Rosenman, G.; Kugel, V.D.; Shur, D. Diffusion-induced domain inversion in ferroelectrics. Ferroelectrics 1995, 172, 7–18. [Google Scholar] [CrossRef]
- Antipov, V.V.; Bykov, A.S.; Malinkovich, M.D.; Parkhomenko, Y.N. Formation of bidomain structure in lithium niobate single crystals by electrothermal method. Ferroelectrics 2008, 374, 65–72. [Google Scholar] [CrossRef]
- Bykov, A.S.; Grigoryan, S.G.; Zhukov, R.N.; Kiselev, D.A.; Ksenich, S.V.; Kubasov, I.V.; Malinkovich, M.D.; Parkhomenko, Y.N. Formation of bidomain structure in lithium niobate plates by the stationary external heating method. Russ. Microelectron. 2014, 43, 536–542. [Google Scholar] [CrossRef]
- Kubasov, I.V.; Timshina, M.S.; Kiselev, D.A.; Malinkovich, M.D.; Bykov, A.S.; Parkhomenko, Y.N. Interdomain region in single-crystal lithium niobate bimorph actuators produced by light annealing. Crystallogr. Rep. 2015, 60, 700–705. [Google Scholar] [CrossRef]
- Funasaka, T.; Furuhata, M.; Hashimoto, Y.; Nakamura, K. Piezoelectric generator using a LiNbO3 plate with an inverted domain. In Proceedings of the 1998 IEEE Ultrasonics Symposium (Cat. No. 98CH36102), Sendai, Japan, 5–8 October 1998; Volume 1, pp. 959–962. [Google Scholar] [CrossRef]
- Kubasov, I.V.; Kislyuk, A.; Malinkovich, M.; Temirov, A.A.; Ksenich, S.V.; Kiselev, D.A.; Bykov, A.S.; Parkhomenko, Y.N. Vibrational Power Harvester Based on Lithium Niobate Bidomain Plate. Acta Phys. Pol. A 2018, 134, 90–92. [Google Scholar] [CrossRef]
- Vidal, J.V.; Turutin, A.V.; Kubasov, I.V.; Malinkovich, M.D.; Parkhomenko, Y.N.; Kobeleva, S.P.; Kholkin, A.L.; Sobolev, N.A. Equivalent Magnetic Noise in Magnetoelectric Laminates Comprising Bidomain LiNbO3 Crystals. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 1102–1119. [Google Scholar] [CrossRef] [PubMed]
- Turutin, A.V.; Vidal, J.V.; Kubasov, I.V.; Kislyuk, A.M.; Malinkovich, M.D.; Parkhomenko, N.; Kobeleva, S.P.; Kholkin, A.L.; Sobolev, N.A. Low-frequency magnetic sensing by magnetoelectric metglas/bidomain LiNbO3 long bars. J. Phys. D Appl. Phys. 2018, 51, 214001. [Google Scholar] [CrossRef]
- Turutin, A.V.; Vidal, J.V.; Kubasov, I.V.; Kislyuk, A.M.; Malinkovich, M.D.; Parkhomenko, Y.N.; Kobeleva, S.P.; Pakhomov, O.V.; Kholkin, A.L.; Sobolev, N.A. Magnetoelectric metglas/bidomain y + 140°-cut lithium niobate composite for sensing fT magnetic fields. Appl. Phys. Lett. 2018, 112, 262906. [Google Scholar] [CrossRef]
- Kubasov, I.V.; Kislyuk, A.M.; Malinkovich, M.D.; Temirov, A.A.; Ksenich, S.V.; Kiselev, D.A.; Bykov, A.S.; Parkhomenko, Y.N. A Novel Vibration Sensor Based on Bidomain Lithium Niobate Crystal. Acta Phys. Pol. A 2018, 134, 106–108. [Google Scholar] [CrossRef]
- Yamada, T.; Niizeki, N.; Toyoda, H. Piezoelectric and Elastic Properties of Lithium Niobate Single Crystals. Jpn. J. Appl. Phys. 1967, 6, 151–155. [Google Scholar] [CrossRef]
- Smith, R.T.; Welsh, F.S. Temperature Dependence of the Elastic, Piezoelectric, and Dielectric Constants of Lithium Tantalate and Lithium Niobate ARTICLES YOU MAY BE INTERESTED IN Determination of Elastic and Piezoelectric Constants for Crystals in Class (3 m). J. Appl. Phys. 1971, 42, 2219. [Google Scholar] [CrossRef]
- Chen, F.; Kong, L.; Song, W.; Jiang, C.; Tian, S.; Yu, F.; Qin, L.; Wang, C.; Zhao, X. The electromechanical features of LiNbO3 crystal for potential high temperature piezoelectric applications. J. Mater. 2018. [Google Scholar] [CrossRef]
- Wan, Z.; Ji, T.; Shang, Y.Y. PVDF Piezoelectric Film Accelerometer for Low Frequency and Ultra-Low Frequency. Appl. Mech. Mater. 2011, 63–64, 465–469. [Google Scholar] [CrossRef]
- Nassau, K.; Levinstein, H.J.; Loiacono, G.M. The domain structure and etching of ferroelectric lithium niobate. Appl. Phys. Lett. 1965, 6, 228–229. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubasov, I.V.; Kislyuk, A.M.; Turutin, A.V.; Bykov, A.S.; Kiselev, D.A.; Temirov, A.A.; Zhukov, R.N.; Sobolev, N.A.; Malinkovich, M.D.; Parkhomenko, Y.N. Low-Frequency Vibration Sensor with a Sub-nm Sensitivity Using a Bidomain Lithium Niobate Crystal. Sensors 2019, 19, 614. https://doi.org/10.3390/s19030614
Kubasov IV, Kislyuk AM, Turutin AV, Bykov AS, Kiselev DA, Temirov AA, Zhukov RN, Sobolev NA, Malinkovich MD, Parkhomenko YN. Low-Frequency Vibration Sensor with a Sub-nm Sensitivity Using a Bidomain Lithium Niobate Crystal. Sensors. 2019; 19(3):614. https://doi.org/10.3390/s19030614
Chicago/Turabian StyleKubasov, Ilya V., Aleksandr M. Kislyuk, Andrei V. Turutin, Alexander S. Bykov, Dmitry A. Kiselev, Aleksandr A. Temirov, Roman N. Zhukov, Nikolai A. Sobolev, Mikhail D. Malinkovich, and Yuriy N. Parkhomenko. 2019. "Low-Frequency Vibration Sensor with a Sub-nm Sensitivity Using a Bidomain Lithium Niobate Crystal" Sensors 19, no. 3: 614. https://doi.org/10.3390/s19030614
APA StyleKubasov, I. V., Kislyuk, A. M., Turutin, A. V., Bykov, A. S., Kiselev, D. A., Temirov, A. A., Zhukov, R. N., Sobolev, N. A., Malinkovich, M. D., & Parkhomenko, Y. N. (2019). Low-Frequency Vibration Sensor with a Sub-nm Sensitivity Using a Bidomain Lithium Niobate Crystal. Sensors, 19(3), 614. https://doi.org/10.3390/s19030614










