Contactless In Situ Electrical Characterization Method of Printed Electronic Devices with Terahertz Spectroscopy
Abstract
1. Introduction
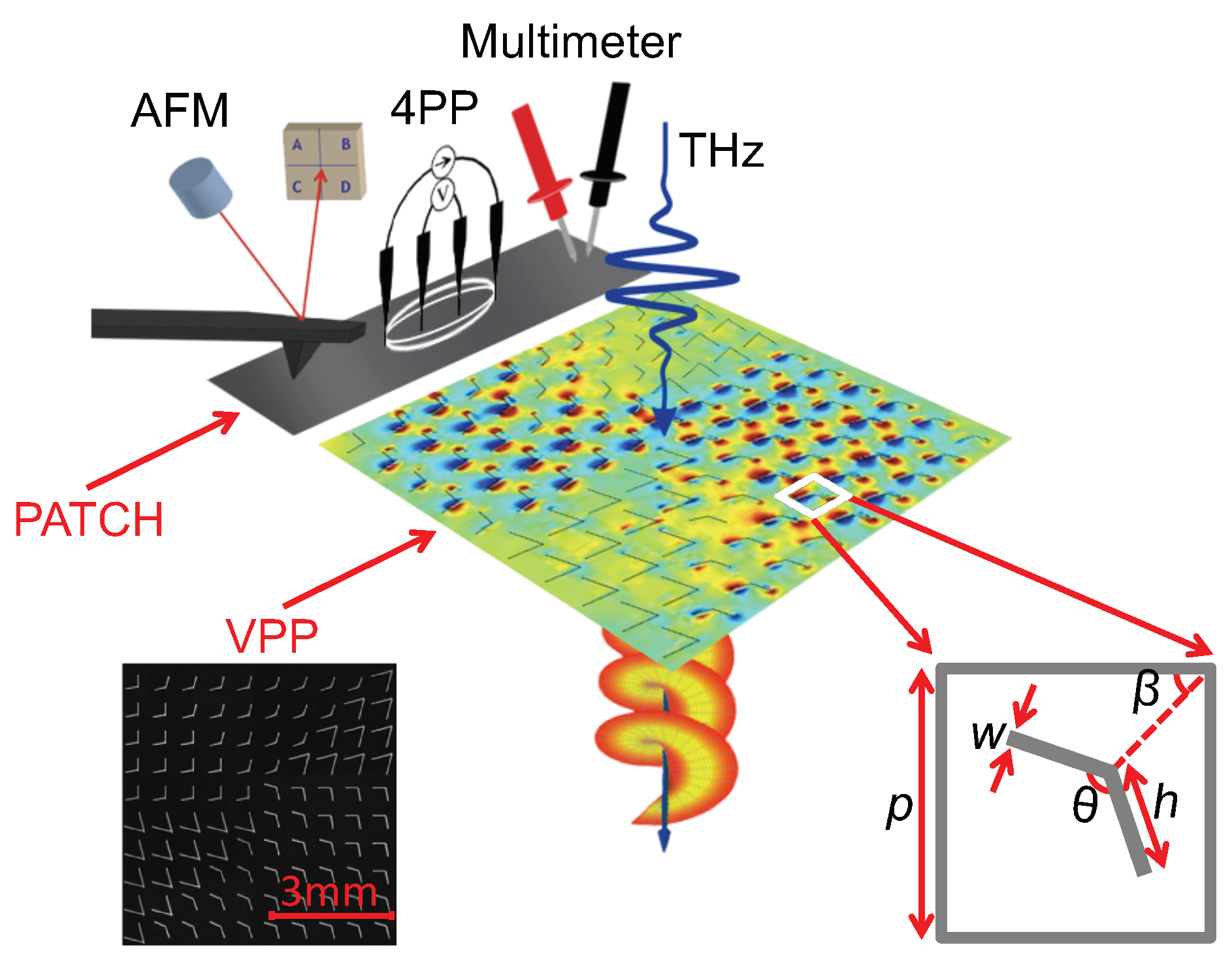
2. Materials and Methods
2.1. Sample Fabrication
2.2. THz Time-Domain Spectroscopy (THz-TDS)
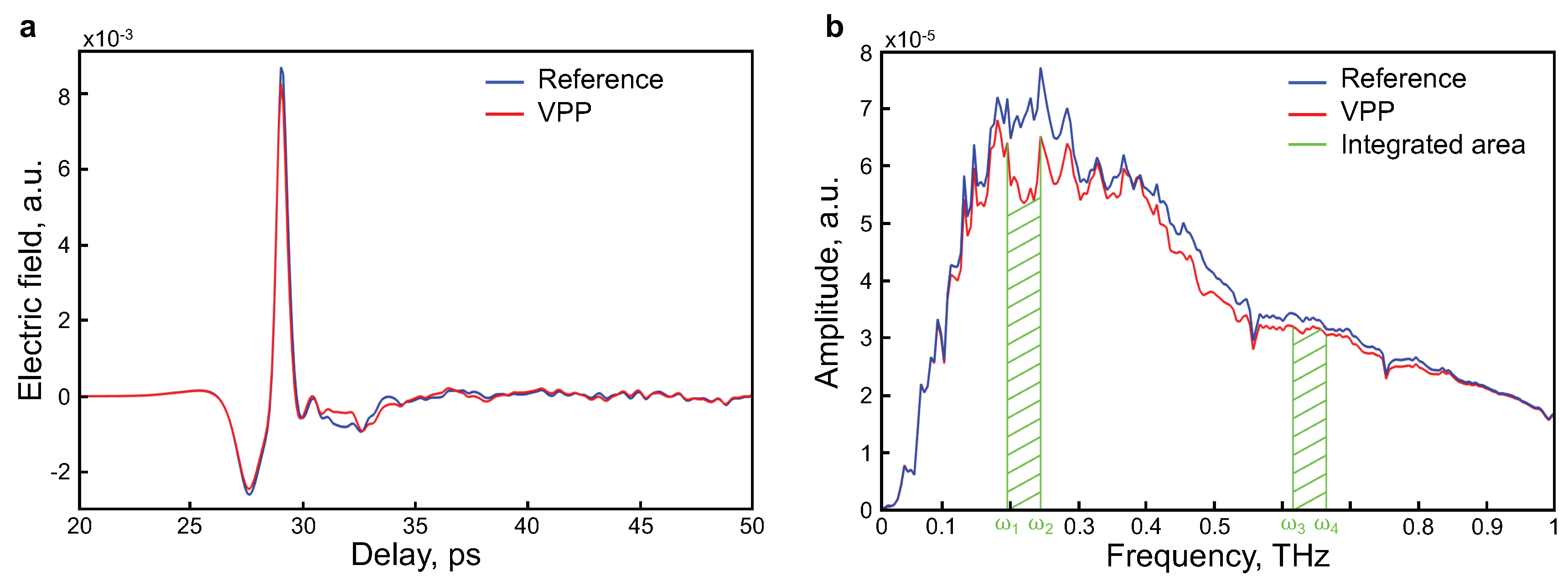
2.3. Dual-Wavelength THz Spectroscopy (DWTS)
2.4. Comparison with Conventional Techniques
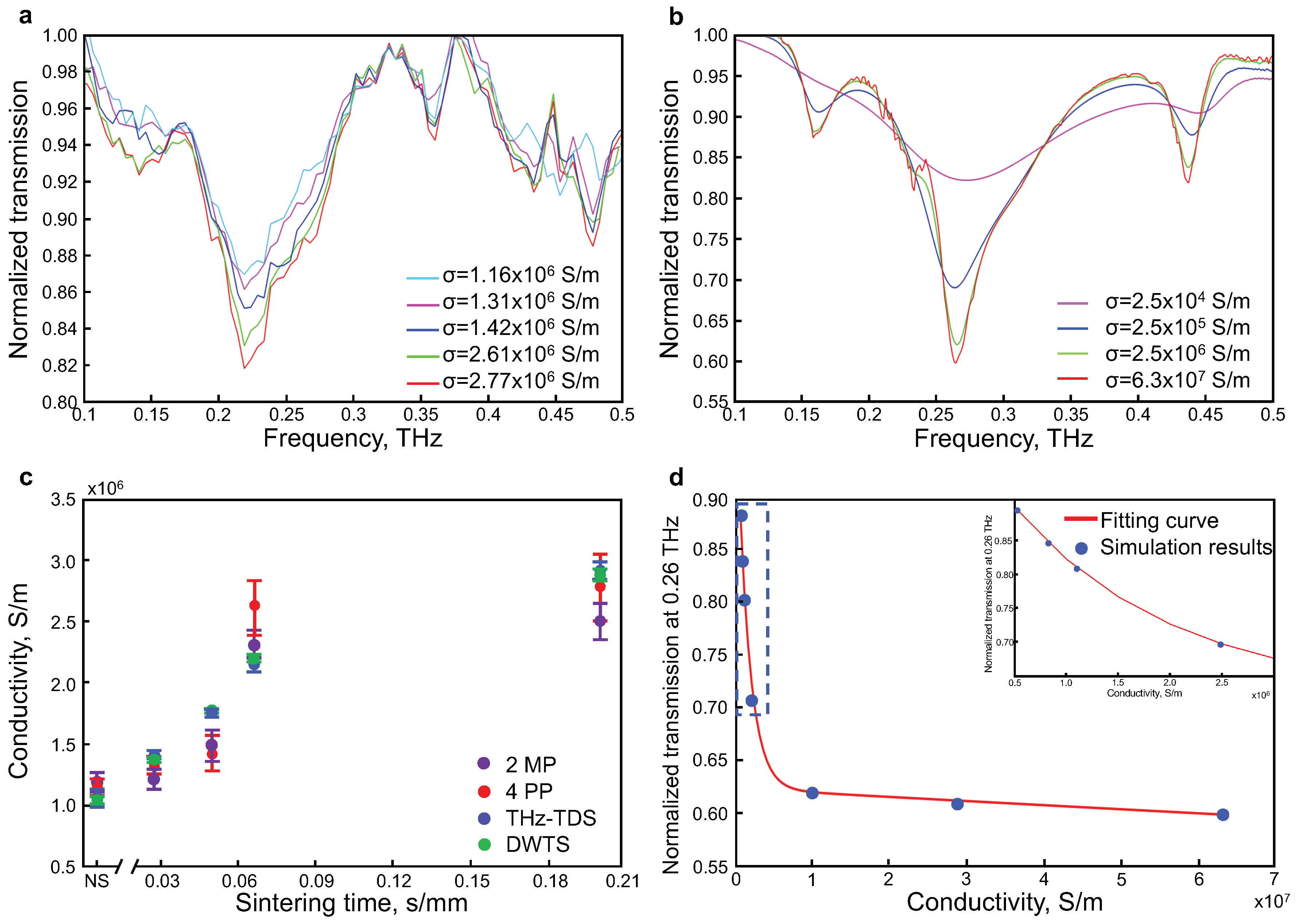
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jenkins, G.; Wang, Y.; Xie, Y.L.; Wu, Q.; Huang, W.; Wang, L.; Yang, X. Printed electronics integrated with paper-based microfluidics: New methodologies for next-generation health care. Microfluid. Nanofluid. 2015, 19, 251–261. [Google Scholar] [CrossRef]
- Liu, Y.; Pharr, M.; Salvatore, G.A. Lab-on-skin: A review of flexible and stretchable electronics for wearable health monitoring. ACS Nano 2017, 11, 9614–9635. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Haverinen, H.M.; Dhagat, P.; Jabbour, G.E. Inkjet printing—Process and its applications. Adv. Mater. 2010, 22, 673–685. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liu, J. Recent advancements in liquid metal flexible printed electronics: Properties, technologies, and applications. Micromachines 2016, 7, 206. [Google Scholar] [CrossRef]
- Perelaer, J.; Smith, P.J.; Mager, D.; Soltman, D.; Volkman, S.K.; Subramanian, V.; Korvink, J.G.; Schubert, U.S. Printed electronics: The challenges involved in printing devices, interconnects, and contacts based on inorganic materials. J. Mater. Chem. 2010, 20, 8446–8453. [Google Scholar] [CrossRef]
- Khan, S.; Lorenzelli, L.; Dahiya, R. Technologies for printing sensors and electronics over large flexible substrates: A review. IEEE Sens. J. 2014, 15, 3164–3185. [Google Scholar] [CrossRef]
- Trudeau, C.; Bolduc, M.; Beaupré, P.; Topart, P.; Alain, C.; Cloutier, S. Inkjet-printed flexible active multilayered structures. MRS Adv. 2017, 2, 1015–1020. [Google Scholar] [CrossRef]
- Ko, S.H.; Pan, H.; Grigoropoulos, C.P.; Luscombe, C.K.; Fréchet, J.M.J.; Poulikakos, D. All-inkjet-printed flexible electronics fabrication on a polymer substrate by low-temperature high-resolution selective laser sintering of metal nanoparticles. Nanotechnology 2007, 18, 345202. [Google Scholar] [CrossRef]
- Kamyshny, A.; Magdassi, S. Conductive nanomaterials for printed electronics. Small 2014, 10, 3515–3535. [Google Scholar] [CrossRef]
- Matsuhisa, N.; Kaltenbrunner, M.; Yokota, T.; Jinno, H.; Kuribara, K.; Sekitani, T.; Someya, T. Printable elastic conductors with a high conductivity for electronic textile applications. Nat. Commun. 2015, 6, ncomms8461. [Google Scholar] [CrossRef]
- Tavakoli, M.; Malakooti, M.H.; Paisana, H.; Ohm, Y.; Marques, D.G.; Alhais Lopes, P.; Piedade, A.P.; de Almeida, A.T.; Majidi, C. EGaIn-Assisted Room-Temperature Sintering of Silver Nanoparticles for Stretchable, Inkjet-Printed, Thin-Film Electronics. Adv. Mater. 2018, 30, 1801852. [Google Scholar] [CrossRef] [PubMed]
- Ermak, O.; Zenou, M.; Toker, G.B.; Ankri, J.; Shacham-Diamand, Y.; Kotler, Z. Rapid laser sintering of metal nano-particles inks. Nanotechnology 2016, 27, 385201. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.S.; Kim, H.S.; Ryu, J.; Hahn, H.T.; Jang, S.; Joung, J.W. Inkjet printed electronics using copper nanoparticle ink. J. Mater. Sci. Mater. Electron. 2010, 21, 1213–1220. [Google Scholar] [CrossRef]
- Chen, W.; Nikiforov, M.P.; Darling, S.B. Morphology characterization in organic and hybrid solar cells. Energy Environ. Sci. 2012, 5, 8045–8074. [Google Scholar] [CrossRef]
- Rossander, L.H.; Zawacka, N.K.; Dam, H.F.; Krebs, F.C.; Andreasen, J.W. In situ monitoring of structure formation in the active layer of polymer solar cells during roll-to-roll coating. AIP Adv. 2014, 4, 87105. [Google Scholar] [CrossRef]
- Hedström, S.; Henriksson, P.; Wang, E.; Andersson, M.R.; Persson, P. Temperature-Dependent Optical Properties of Flexible Donor-Acceptor Polymers. J. Phys. Chem. C 2015, 119, 6453–6463. [Google Scholar] [CrossRef]
- Pastorelli, F.; Accanto, N.; Jørgensen, M.; Hulst, N.F.; Krebs, F.C. In situ electrical and thermal monitoring of printed electronics by two-photon mapping. Sci. Rep. 2017, 7, 3787. [Google Scholar] [CrossRef] [PubMed]
- Rösch, R.; Krebs, F.C.; Tanenbaum, D.M.; Hoppe, H. Quality control of roll-to-roll processed polymer solar modules by complementary imaging methods. Sol. Energy Mater. Sol. Cells 2012, 97, 176–180. [Google Scholar] [CrossRef]
- Pipes, A. Prepress. In Production for Graphic Designers, 4th ed.; Webb, N., Ed.; Laurence King Publishing: London, UK, 2005; pp. 166–167. [Google Scholar]
- Ferguson, B.; Zhang, X.C. Materials for terahertz science and technology. Nat. Mater. 2002, 1, 26. [Google Scholar] [CrossRef]
- Mittleman, D. Terahertz imaging. In Sensing with Terahertz Radiation; Mittleman, D., Ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003; pp. 117–153. [Google Scholar]
- Zeng, Y.; Edwards, M.; Stevens, R.; Bowen, J.W.; Donnan, R.S.; Yang, B. Terahertz characterisation of UV offset lithographically printed electronic-ink. Org. Electron. 2017, 48, 382–388. [Google Scholar] [CrossRef]
- Yen, T.J.; Padilla, W.; Fang, N.; Vier, D.; Smith, D.; Pendry, J.; Basov, D.; Zhang, X. Terahertz magnetic response from artificial materials. Science 2004, 303, 1494–1496. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Azad, A.K.; O’Hara, J.F.; Taylor, A.J.; Zhang, W. Effect of metal permittivity on resonant properties of terahertz metamaterials. Opt. Lett. 2008, 33, 1506–1508. [Google Scholar] [CrossRef]
- Hokari, R.; Kurihara, K.; Takada, N.; Hiroshima, H. Printed optical metamaterials composed of embedded silver nanoparticles for flexible applications. Opt. Express 2018, 26, 10326–10338. [Google Scholar] [CrossRef] [PubMed]
- Walther, M.; Ortner, A.; Meier, H.; Löffelmann, U.; Smith, P.J.; Korvink, J.G. Terahertz metamaterials fabricated by inkjet printing. Appl. Phys. Lett. 2009, 95, 251107. [Google Scholar] [CrossRef]
- Lee, D.; Sung, H.K.; Lim, S. Flexible subterahertz metamaterial absorber fabrication using inkjet printing technology. Appl. Phys. B 2016, 122, 206. [Google Scholar] [CrossRef]
- Lee, S.H.; Gee, S.Y.; Kang, C.; Kee, C.S. Terahertz wave transmission properties of metallic periodic structures printed on a photo-paper. J. Opt. Soc. Korea 2010, 14, 282–285. [Google Scholar] [CrossRef]
- Sushko, O.; Pigeon, M.; Donnan, R.S.; Kreouzis, T.; Parini, C.G.; Dubrovka, R. Comparative study of sub-THz FSS filters fabricated by inkjet printing, microprecision material printing, and photolithography. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 184–190. [Google Scholar] [CrossRef]
- Jahn, D.; Eckstein, R.; Schneider, L.M.; Born, N.; Hernandez-Sosa, G.; Balzer, J.C.; Al-Naib, I.; Lemmer, U.; Koch, M. Digital Aerosol Jet Printing for the Fabrication of Terahertz Metamaterials. Adva. Mater. Technol. 2018, 3, 1700236. [Google Scholar] [CrossRef]
- Kim, H.; Melinger, J.S.; Khachatrian, A.; Charipar, N.A.; Auyeung, R.C.; Piqué, A. Fabrication of terahertz metamaterials by laser printing. Opt. Lett. 2010, 35, 4039–4041. [Google Scholar] [CrossRef]
- Tenggara, A.P.; Park, S.; Yudistira, H.T.; Ahn, Y.; Byun, D. Fabrication of terahertz metamaterials using electrohydrodynamic jet printing for sensitive detection of yeast. J. Micromech. Microeng. 2017, 27, 035009. [Google Scholar] [CrossRef]
- Teguh Yudistira, H.; Pradhipta Tenggara, A.; Dat Nguyen, V.; Teun Kim, T.; Dian Prasetyo, F.; Choi, C.G.; Choi, M.; Byun, D. Fabrication of terahertz metamaterial with high refractive index using high-resolution electrohydrodynamic jet printing. Appl. Phys. Lett. 2013, 103, 211106. [Google Scholar] [CrossRef]
- Paulsen, A.; Nahata, A. K-space design of terahertz plasmonic filters. Optica 2015, 2, 214–220. [Google Scholar] [CrossRef]
- Sengupta, K.; Hajimiri, A. A 0.28 THz power-generation and beam-steering array in CMOS based on distributed active radiators. IEEE J. Solid-State Circuits 2012, 47, 3013–3031. [Google Scholar] [CrossRef]
- Wu, X.; Sengupta, K. Dynamic waveform shaping with picosecond time widths. IEEE J. Solid-State Circuits 2017, 52, 389–405. [Google Scholar] [CrossRef]
- He, J.; Wang, X.; Hu, D.; Ye, J.; Feng, S.; Kan, Q.; Zhang, Y. Generation and evolution of the terahertz vortex beam. Opt. Express 2013, 21, 20230–20239. [Google Scholar] [CrossRef] [PubMed]
- Fan, K.; Padilla, W.J. Dynamic electromagnetic metamaterials. Mater. Today 2015, 18, 39–50. [Google Scholar] [CrossRef]
- Bolduc, M.; Trudeau, C.; Beaupré, P.; Cloutier, S.; Galarneau, P. Thermal dynamics effects using pulse-shaping laser sintering of printed silver inks. Sci. Rep. 2018, 8, 1418. [Google Scholar] [CrossRef]
- Jepsen, P.U.; Cooke, D.G.; Koch, M. Terahertz spectroscopy and imaging–Modern techniques and applications. Laser Photonics Rev. 2011, 5, 124–166. [Google Scholar] [CrossRef]
- Porfirev, A.P.; Khonina, S.N. Simple method for efficient reconfigurable optical vortex beam splitting. Opt. Express 2017, 25, 18722–18735. [Google Scholar] [CrossRef]
- Owen, T. Fundamentals of UV-Visible Spectroscopy: A Primer; Hewlett-Packard: Berlin, Germany, 1996. [Google Scholar]
- Abdelwahab, N.S.; El-Zeiny, B.A.; Tohamy, S.I. Two spectrophotometric methods for simultaneous determination of some antihyperlipidemic drugs. J. Pharm. Anal. 2012, 2, 279–284. [Google Scholar] [CrossRef]
- Pötter, W.; Karst, U. Identification of chemical interferences in aldehyde and ketone determination using dual-wavelength detection. Anal. Chem. 1996, 68, 3354–3358. [Google Scholar] [CrossRef] [PubMed]
- El Haddad, J.; Canioni, L.; Bousquet, B. Good practices in LIBS analysis: Review and advices. Spectrochim. Acta Part B At. Spectrosc. 2014, 101, 171–182. [Google Scholar] [CrossRef]
- Yilmaz, S. The geometric resistivity correction factor for several geometrical samples. J. Semicond. 2015, 36, 082001. [Google Scholar] [CrossRef]
| Sintering Time | Not Sintered | 0.03 s/mm | 0.05 s/mm | 0.07 s/mm | 0.2 s/mm | ||
|---|---|---|---|---|---|---|---|
| Conductivity, S/m | Obtained by | 4 PP | 1.15 ± 4.70% | 1.31 ± 4.47% | 1.42 ± 10.3% | 2.61 ± 8.67% | 2.77 ± 9.82% |
| MM | 1.10 ± 21.1% | 1.19 ± 12.1% | 1.48 ± 17.9% | 2.15 ± 22.2% | 3.01 ± 36.7% | ||
| 2MP | 1.23 ± 6.59% | 1.28 ± 8.44% | 1.49 ± 8.73% | 2.29 ± 6.83% | 2.51 ± 7.58% | ||
| THz-TDS | 1.08 ± 6.14% | 1.38 ± 3.06% | 1.75 ± 1.55% | 2.14 ± 2.52% | 2.91 ± 2.77% | ||
| DWTS | 1.06 ± 3.44% | 1.37 ± 1.28% | 1.78 ± 1.21% | 2.18 ± 1.44% | 2.89 ± 1.80% | ||
| AFM |  |  |  |  |  | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuldybina, M.; Ropagnol, X.; Trudeau, C.; Bolduc, M.; Zednik, R.J.; Blanchard, F. Contactless In Situ Electrical Characterization Method of Printed Electronic Devices with Terahertz Spectroscopy. Sensors 2019, 19, 444. https://doi.org/10.3390/s19030444
Zhuldybina M, Ropagnol X, Trudeau C, Bolduc M, Zednik RJ, Blanchard F. Contactless In Situ Electrical Characterization Method of Printed Electronic Devices with Terahertz Spectroscopy. Sensors. 2019; 19(3):444. https://doi.org/10.3390/s19030444
Chicago/Turabian StyleZhuldybina, Mariia, Xavier Ropagnol, Charles Trudeau, Martin Bolduc, Ricardo J. Zednik, and François Blanchard. 2019. "Contactless In Situ Electrical Characterization Method of Printed Electronic Devices with Terahertz Spectroscopy" Sensors 19, no. 3: 444. https://doi.org/10.3390/s19030444
APA StyleZhuldybina, M., Ropagnol, X., Trudeau, C., Bolduc, M., Zednik, R. J., & Blanchard, F. (2019). Contactless In Situ Electrical Characterization Method of Printed Electronic Devices with Terahertz Spectroscopy. Sensors, 19(3), 444. https://doi.org/10.3390/s19030444





