Most Relevant Spectral Bands Identification for Brain Cancer Detection Using Hyperspectral Imaging
Abstract
1. Introduction
2. Materials
2.1. Intraoperative Hyperspectral (HS) Acqusition System
2.2. In Vivo Human Brain Cancer Database
3. Methodology
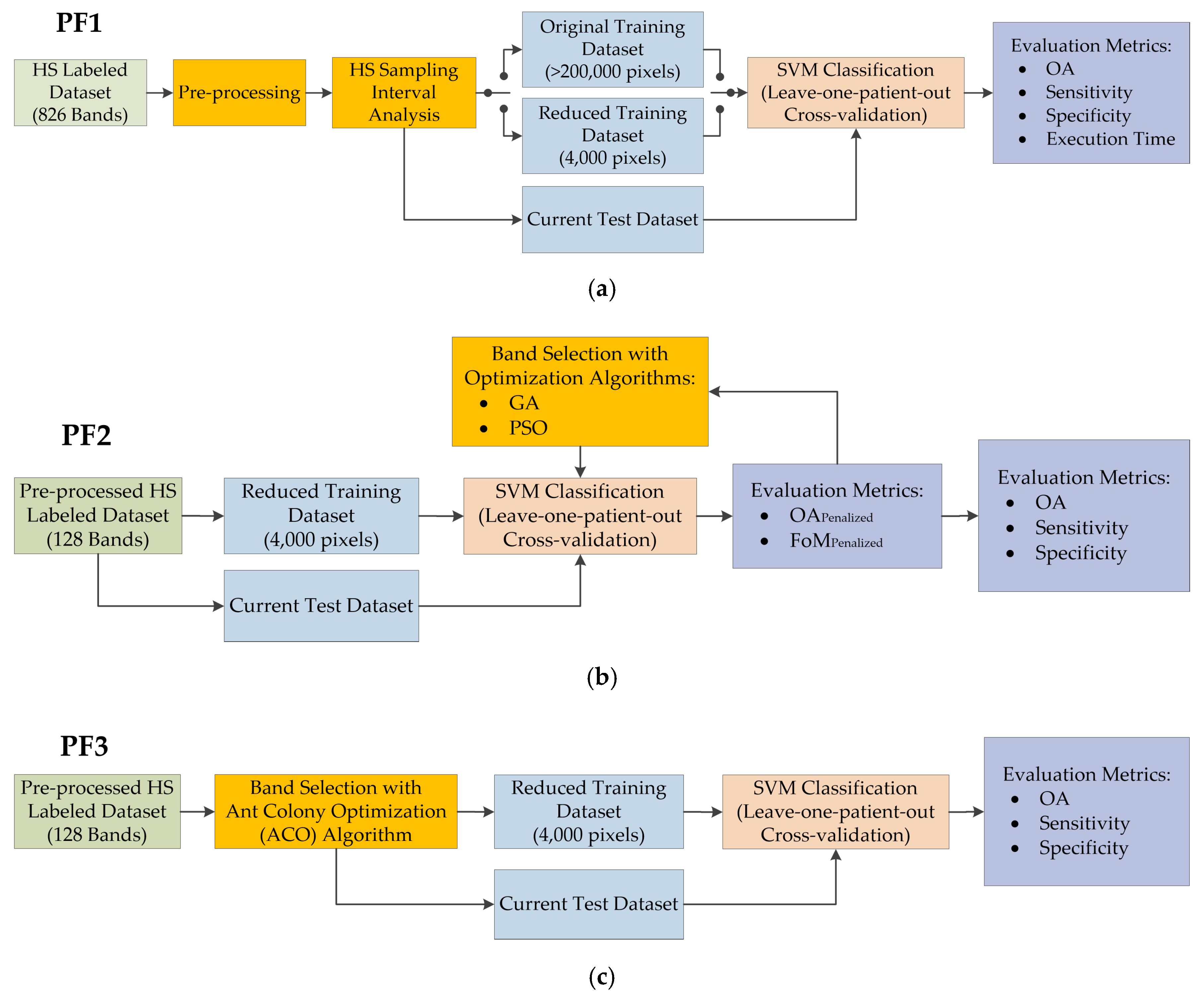
3.1. Processing Framework 1 (PF1): Sampling Interval Analysis and Training Dataset Reduction
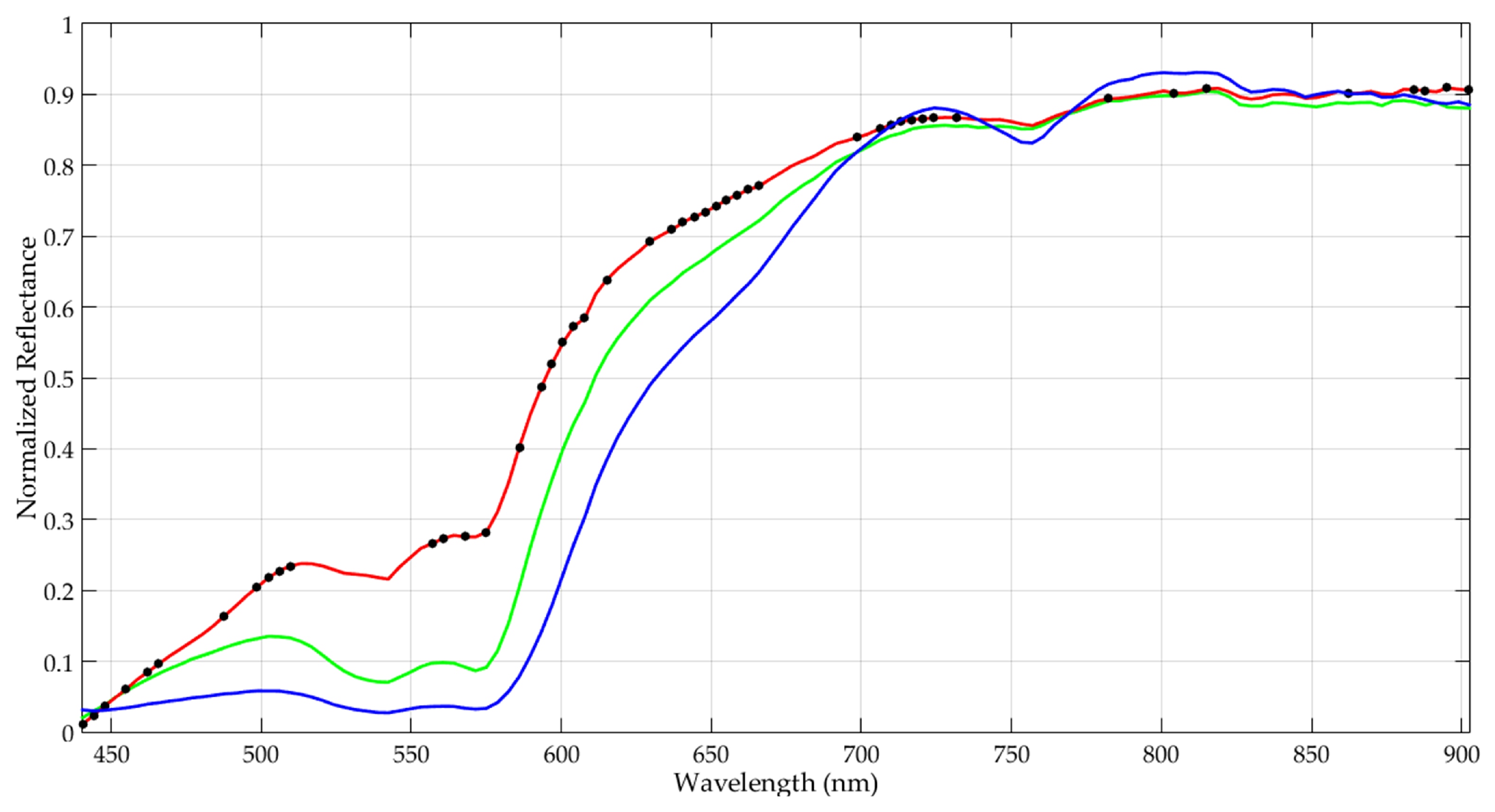
3.1.1. Data Pre-Processing
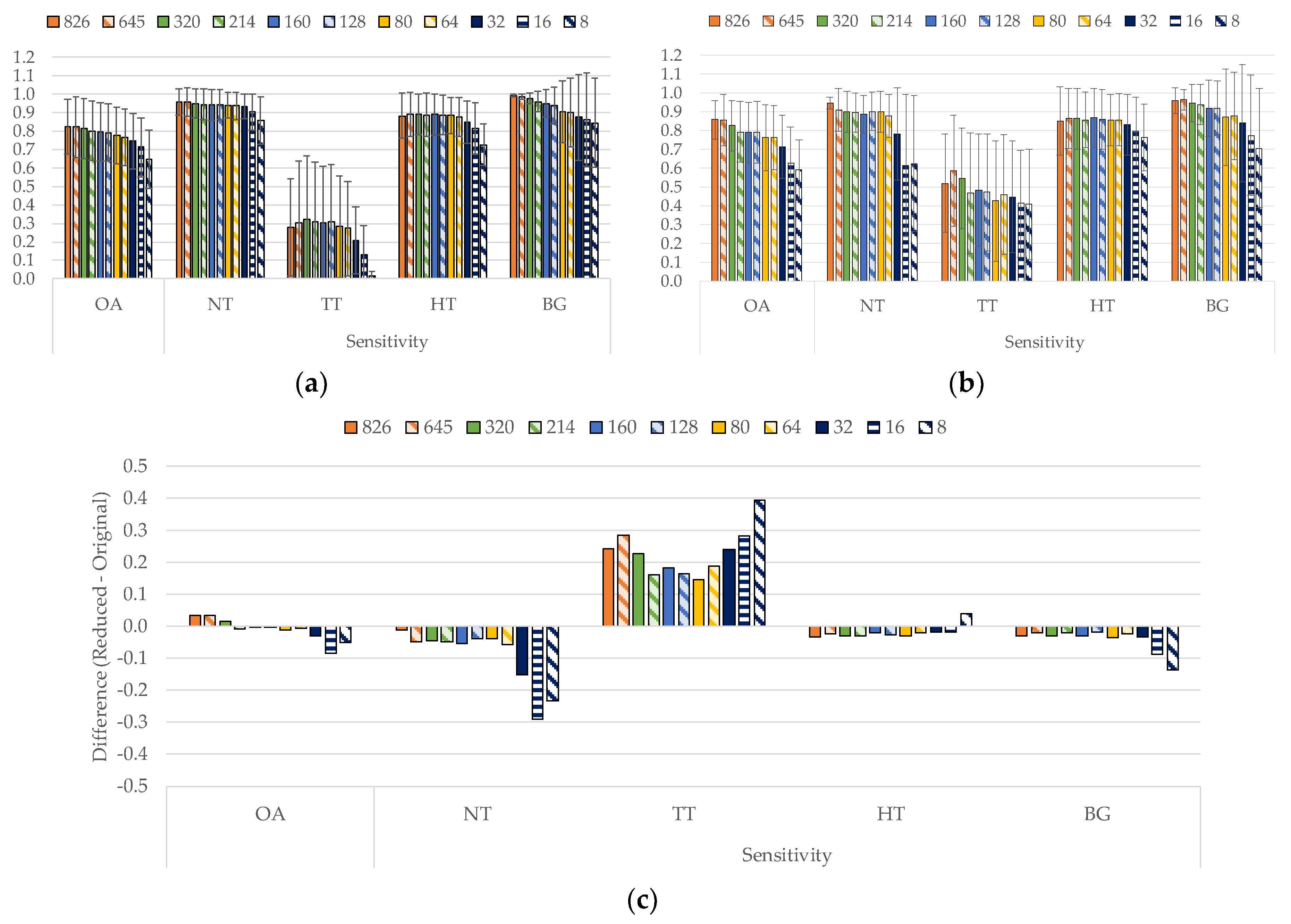
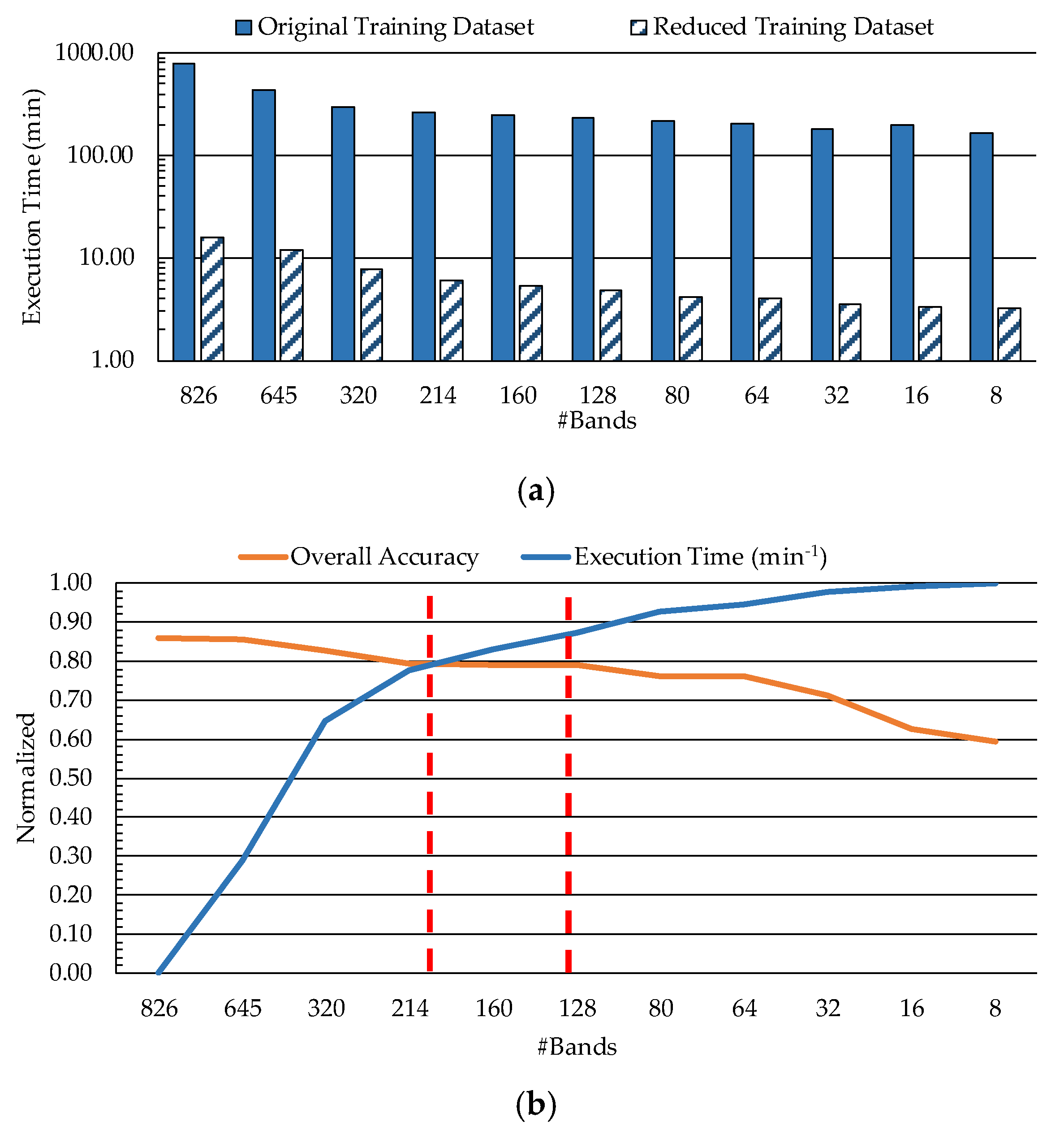
3.1.2. Sampling Interval Analysis
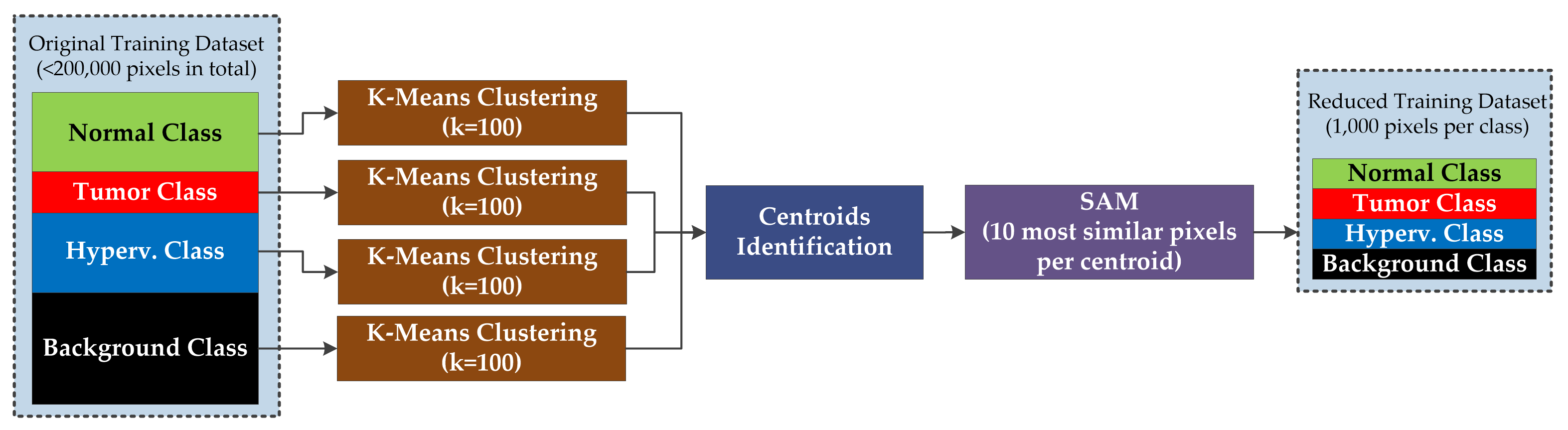
3.1.3. Training Dataset Reduction
3.2. PF2: Band Selection Using Genetic Algorithm (GA) and Particle Swarm Optimization (PSO)
3.2.1. Genetic Algorithm (GA)
- (1)
- Initialization: In this step, the selection of the population is performed in a random way.
- (2)
- Evaluation: The goal is to study the results obtained from the initial population (parents) and each of the descendant generations (children).
- (3)
- Selection: This point is responsible for keeping the best result obtained during the evaluation process.
- (4)
- Recombination: In this step, the combination of the different initial contributions (parents) for the creation of better solutions (children) is performed. This crossing is performed by dividing the populations in two (or more) parts and exchanging part of those populations with each other.
- (5)
- Mutation: This technique is performed in the same way as in the recombination step. However, instead of exchanging parts of the populations among themselves, a single value of each of the populations is modified.
- (6)
- Replacement: After performing the recombination and mutation steps, these generations (children) replace the initial populations (parents).
3.2.2. Particle Swarm Optimization (PSO) Algorithm
- (1)
- Initialization: This step initializes a random population with different positions and velocities.
- (2)
- Selection: In this step, each particle evaluates the best location found and the best position found by the rest of the swarm.
- (3)
- Evaluation: Here, a comparison of all the results and selection of the pbest is performed. The same process is applied to find the best gbest.
- (4)
- Replacement: In this last step, the new results replace the initial population and the process is repeated up to a maximum number of generations established by the user or until the solution converges.
3.3. PF3: Band Selection Using Ant Colony Optimization (ACO)
Ant Colony Optimization (ACO) Algorithm
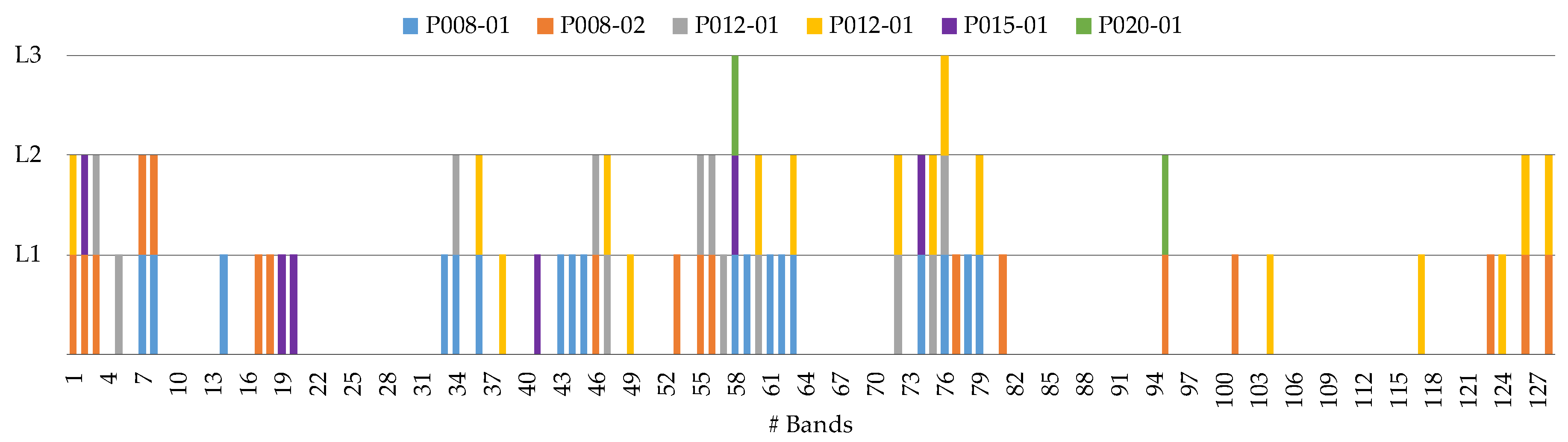
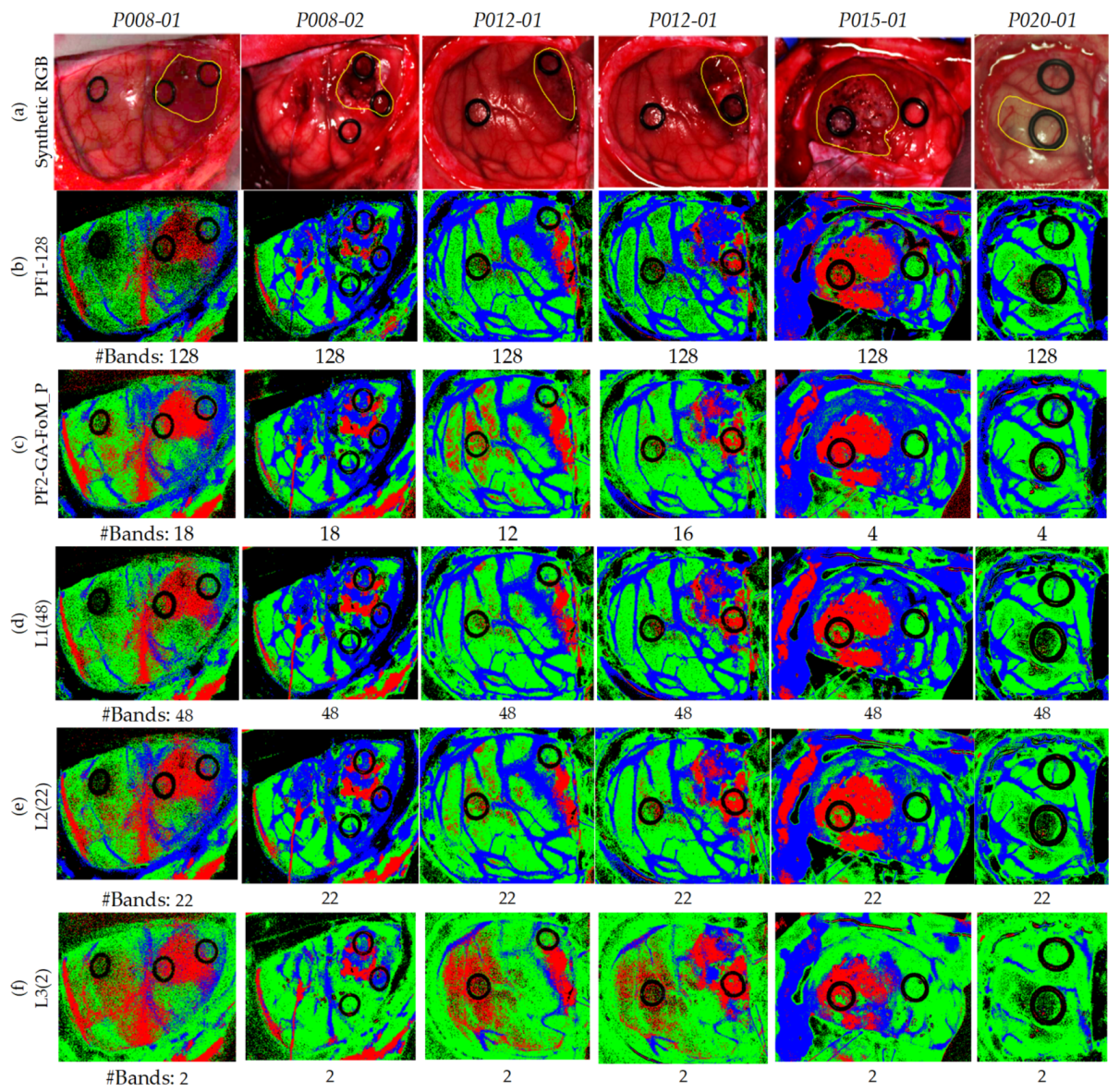
3.4. Coincident Bands Evaluation Methodology
- First level (L1): the coincident and non-coincident bands from all the test images were used to generate and evaluate the results.
- Second level (L2): the coincident bands repeated in at least two test images were used to generate and evaluate the results.
- Third level (L3): the coincident bands repeated in at least three test images were used to generate and evaluate the results.
3.5. Evaluation Metrics
4. Experimental Results and Discussion
4.1. Sampling Interval Analysis (PF1)
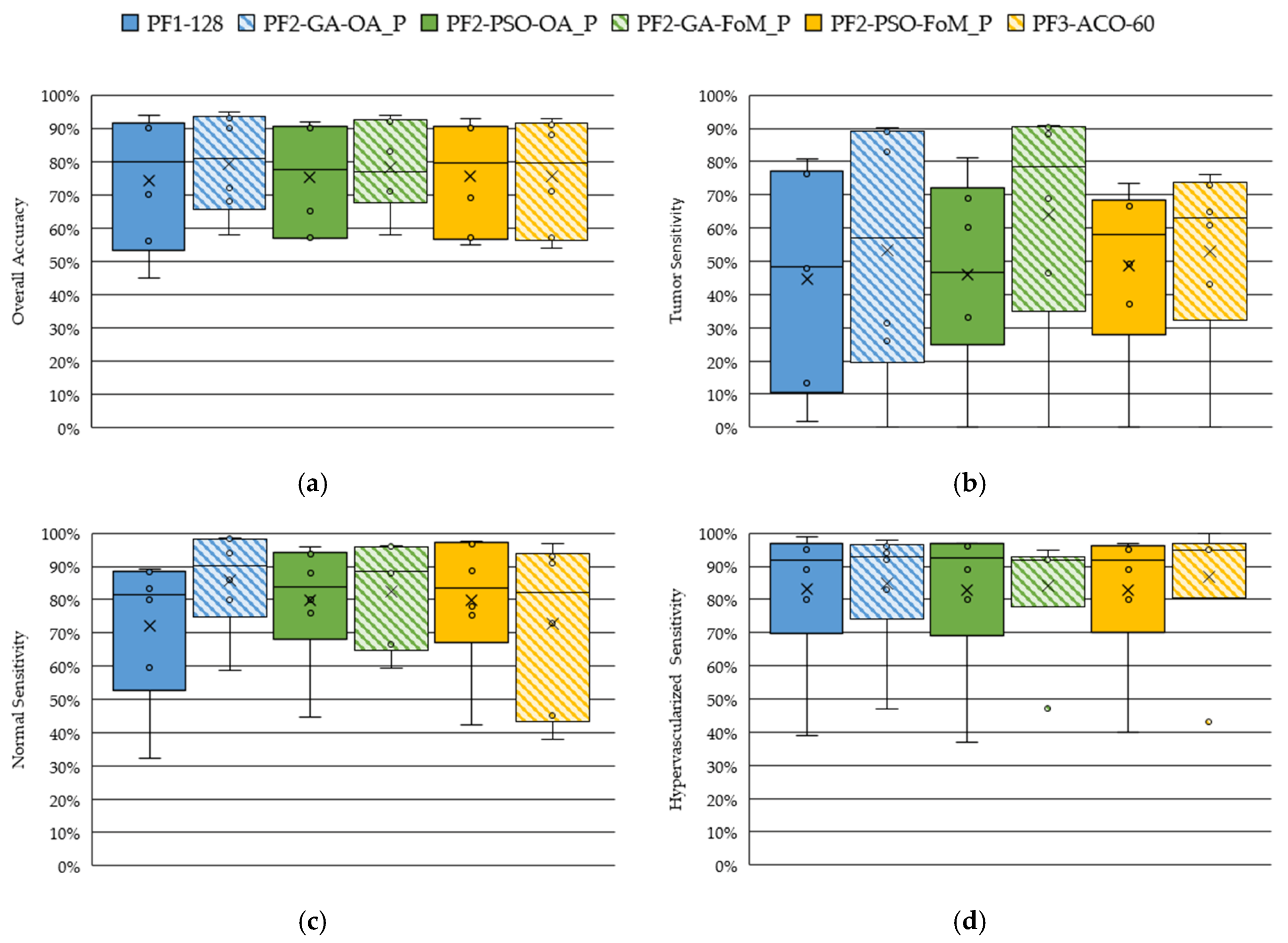
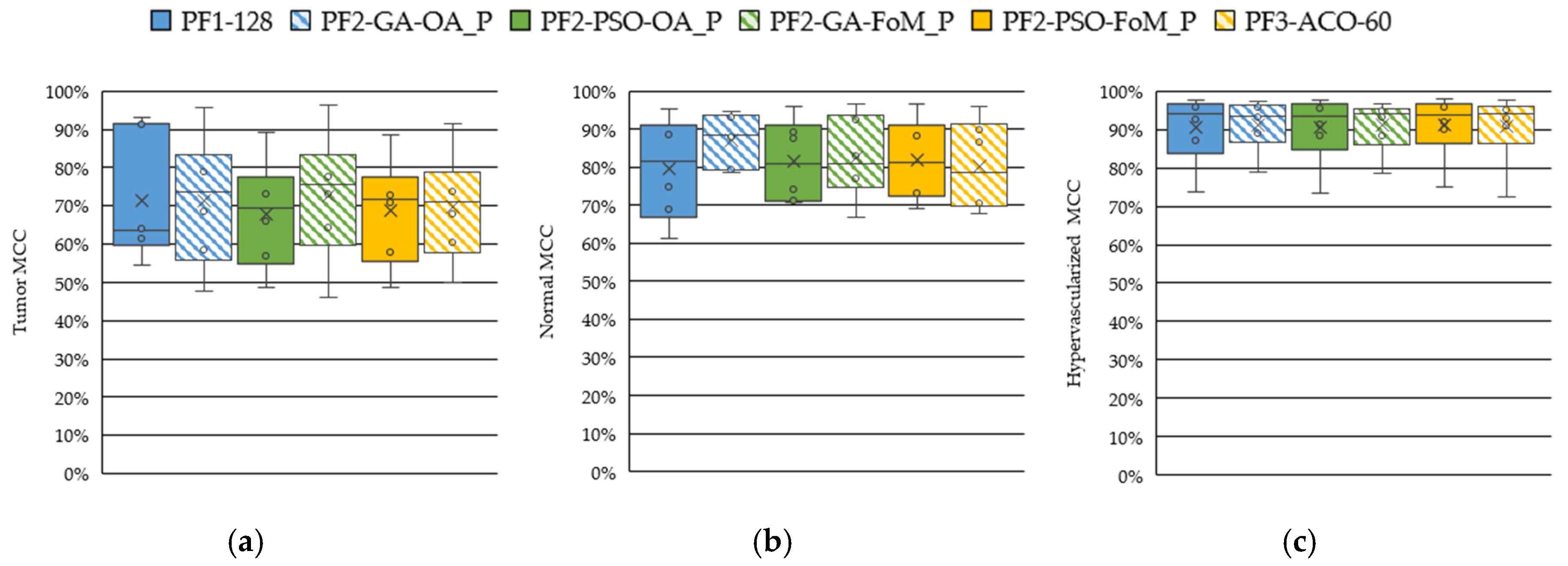
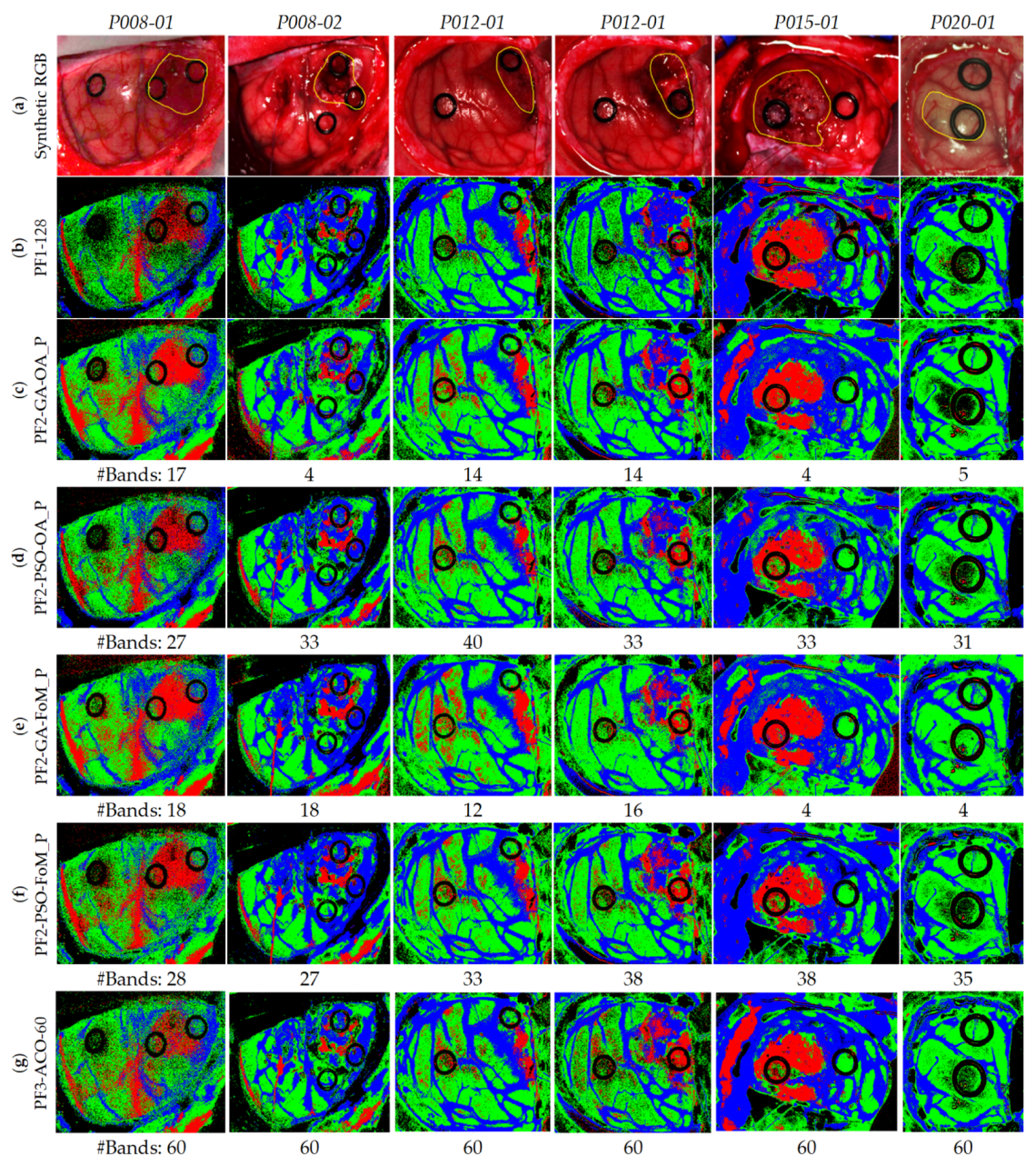
4.2. Band Selection Using Optimization Algorithms (PF2 and PF3)
4.3. Coincident Bands Evaluation of the GA Algorithm with Figure of Merit (FoMPenalized)
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
| PF1-128 | Processing Framework 1 using 128 bands |
| PF2-GA-OA_P | Processing Framework 2 using Genetic Algorithm and the Overall Accuracy Penalized evaluation metric |
| PF2-GA-FoM_P | Processing Framework 2 using Genetic Algorithm and the Figure of Merit Penalized evaluation metric |
| PF2-PSO-OA_P | Processing Framework 2 using Particle Swarm Optimization algorithm and the Overall Accuracy Penalized evaluation metric |
| PF2-PSO-FoM_P | Processing Framework 2 using Particle Swarm Optimization algorithm and the Figure of Merit Penalized evaluation metric |
| PF3-ACO-60 | Processing Framework 3 using Ant Colony Optimization algorithm taking into account 60 bands |
References
- Hammill, K.; Stewart, C.G.; Kosic, N.; Bellamy, L.; Irvine, H.; Hutley, D.; Arblaster, K. Exploring the impact of brain cancer on people and their participation. Br. J. Occup. Ther. 2019, 82, 162–169. [Google Scholar] [CrossRef]
- Joshi, D.M.; Rana, N.K.; Misra, V.M. Classification of Brain Cancer using Artificial Neural Network. In Proceedings of the 2010 2nd International Conference on Electronic Computer Technology, Kuala Lumpur, Malaysia, 7–10 May 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 112–116. [Google Scholar]
- Perkins, A.; Liu, G. Primary Brain Tumors in Adults: Diagnosis and Treatment—American Family Physician. Am. Fam. Physician 2016, 93, 211–218. [Google Scholar] [PubMed]
- Halicek, M.; Fabelo, H.; Ortega, S.; Callico, G.M.; Fei, B. In-Vivo and Ex-Vivo Tissue Analysis through Hyperspectral Imaging Techniques: Revealing the Invisible Features of Cancer. Cancers 2019, 11, 756. [Google Scholar] [CrossRef] [PubMed]
- Kamruzzaman, M.; Sun, D.W. Introduction to Hyperspectral Imaging Technology. Comput. Vis. Technol. Food Qual. Eval. 2016, 111–139. [Google Scholar] [CrossRef]
- Mordant, D.J.; Al-Abboud, I.; Muyo, G.; Gorman, A.; Sallam, A.; Ritchie, P.; Harvey, A.R.; McNaught, A.I. Spectral imaging of the retina. Eye 2011, 25, 309–320. [Google Scholar] [CrossRef]
- Johnson, W.R.; Wilson, D.W.; Fink, W.; Humayun, M.; Bearman, G. Snapshot hyperspectral imaging in ophthalmology. J. Biomed. Opt. 2007. [Google Scholar] [CrossRef]
- Gao, L.; Smith, R.T.; Tkaczyk, T.S. Snapshot hyperspectral retinal camera with the Image Mapping Spectrometer (IMS). Biomed. Opt. Express 2012, 3, 48–54. [Google Scholar] [CrossRef]
- Akbari, H.; Kosugi, Y.; Kojima, K.; Tanaka, N. Detection and Analysis of the Intestinal Ischemia Using Visible and Invisible Hyperspectral Imaging. IEEE Trans. Biomed. Eng. 2010, 57, 2011–2017. [Google Scholar] [CrossRef]
- Ortega, S.; Fabelo, H.; Camacho, R.; Plaza, M.L.; Callicó, G.M.; Sarmiento, R. Detecting brain tumor in pathological slides using hyperspectral imaging. Biomed. Opt. Express 2018, 9, 818–831. [Google Scholar] [CrossRef]
- Zhu, S.; Su, K.; Liu, Y.; Yin, H.; Li, Z.; Huang, F.; Chen, Z.; Chen, W.; Zhang, G.; Chen, Y. Identification of cancerous gastric cells based on common features extracted from hyperspectral microscopic images. Biomed. Opt. Express 2015, 6, 1135–1145. [Google Scholar] [CrossRef]
- Lu, C.; Mandal, M. Toward automatic mitotic cell detection and segmentation in multispectral histopathological images. IEEE J. Biomed. Health Inform. 2014, 18, 594–605. [Google Scholar] [CrossRef] [PubMed]
- Khouj, Y.; Dawson, J.; Coad, J.; Vona-Davis, L. Hyperspectral Imaging and K-Means Classification for Histologic Evaluation of Ductal Carcinoma In Situ. Front. Oncol. 2018, 8, 17. [Google Scholar] [CrossRef] [PubMed]
- Bjorgan, A.; Denstedt, M.; Milanič, M.; Paluchowski, L.A.; Randeberg, L.L. Vessel contrast enhancement in hyperspectral images. In Optical Biopsy XIII: Toward Real-Time Spectroscopic Imaging and Diagnosis; Alfano, R.R., Demos, S.G., Eds.; SPIE—International Society For Optics and Photonics: Bellingham, WA, USA, 2015. [Google Scholar]
- Akbari, H.; Kosugi, Y.; Kojima, K.; Tanaka, N. Blood vessel detection and artery-vein differentiation using hyperspectral imaging. In Proceedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society: Engineering the Future of Biomedicine, EMBC 2009, Minneapolis, MN, USA, 3–6 September 2009; pp. 1461–1464. [Google Scholar]
- Milanic, M.; Bjorgan, A.; Larsson, M.; Strömberg, T.; Randeberg, L.L. Detection of hypercholesterolemia using hyperspectral imaging of human skin. In Proceedings of the SPIE—European Conference on Biomedical Optics, Munich, German, 21–25 June 2015; Brown, J.Q., Deckert, V., Eds.; SPIE—The International Society for Optical Engineering: Bellingham, WA, USA, 2015; p. 95370C. [Google Scholar]
- Zhi, L.; Zhang, D.; Yan, J.; Li, Q.L.; Tang, Q. Classification of hyperspectral medical tongue images for tongue diagnosis. Comput. Med. Imaging Graph. 2007, 31, 672–678. [Google Scholar] [CrossRef] [PubMed]
- Yudovsky, D.; Nouvong, A.; Pilon, L. Hyperspectral Imaging in Diabetic Foot Wound Care. J. Diabetes Sci. Technol. 2010, 4, 1099–1113. [Google Scholar] [CrossRef] [PubMed]
- Lu, G.; Fei, B. Medical hyperspectral imaging: A review. J. Biomed. Opt. 2014, 19, 10901. [Google Scholar] [CrossRef] [PubMed]
- Calin, M.A.; Parasca, S.V.; Savastru, D.; Manea, D. Hyperspectral imaging in the medical field: Present and future. Appl. Spectrosc. Rev. 2014, 49, 435–447. [Google Scholar] [CrossRef]
- Ortega, S.; Fabelo, H.; Iakovidis, D.; Koulaouzidis, A.; Callico, G.; Ortega, S.; Fabelo, H.; Iakovidis, D.K.; Koulaouzidis, A.; Callico, G.M. Use of Hyperspectral/Multispectral Imaging in Gastroenterology. Shedding Some–Different–Light into the Dark. J. Clin. Med. 2019, 8, 36. [Google Scholar] [CrossRef]
- Akbari, H.; Uto, K.; Kosugi, Y.; Kojima, K.; Tanaka, N. Cancer detection using infrared hyperspectral imaging. Cancer Sci. 2011, 102, 852–857. [Google Scholar] [CrossRef]
- Kiyotoki, S.; Nishikawa, J.; Okamoto, T.; Hamabe, K.; Saito, M.; Goto, A.; Fujita, Y.; Hamamoto, Y.; Takeuchi, Y.; Satori, S.; et al. New method for detection of gastric cancer by hyperspectral imaging: A pilot study. J. Biomed. Opt. 2013, 18, 026010. [Google Scholar] [CrossRef]
- Baltussen, E.J.M.; Kok, E.N.D.; Brouwer de Koning, S.G.; Sanders, J.; Aalbers, A.G.J.; Kok, N.F.M.; Beets, G.L.; Flohil, C.C.; Bruin, S.C.; Kuhlmann, K.F.D.; et al. Hyperspectral imaging for tissue classification, a way toward smart laparoscopic colorectal surgery. J. Biomed. Opt. 2019, 24, 016002. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, A.; Wang, X.; Sun, Z.; Wang, M.D.; Xie, T. In vivo use of hyperspectral imaging to develop a noncontact endoscopic diagnosis support system for malignant colorectal tumors. J. Biomed. Opt. 2016, 21, 016001. [Google Scholar] [CrossRef] [PubMed]
- Panasyuk, S.V.; Yang, S.; Faller, D.V.; Ngo, D.; Lew, R.A.; Freeman, J.E.; Rogers, A.E. Medical hyperspectral imaging to facilitate residual tumor identification during surgery. Cancer Biol. Ther. 2007, 6, 439–446. [Google Scholar] [CrossRef] [PubMed]
- Pourreza-Shahri, R.; Saki, F.; Kehtarnavaz, N.; Leboulluec, P.; Liu, H. Classification of ex-vivo breast cancer positive margins measured by hyperspectral imaging. In Proceedings of the 2013 IEEE International Conference on Image Processing, ICIP 2013, Melbourne, Australia, 15–18 September 2013; pp. 1408–1412. [Google Scholar]
- Lu, G.; Halig, L.; Wang, D.; Chen, Z.G.; Fei, B. Hyperspectral imaging for cancer surgical margin delineation: Registration of hyperspectral and histological images. In SPIE Medical Imaging 2014: Image-Guided Procedures, Robotic Interventions, and Modeling; Yaniv, Z.R., Holmes, D.R., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2014; Volume 9036, p. 90360S. [Google Scholar]
- Pike, R.; Lu, G.; Wang, D.; Chen, Z.G.; Fei, B. A Minimum Spanning Forest-Based Method for Noninvasive Cancer Detection With Hyperspectral Imaging. IEEE Trans. Biomed. Eng. 2016, 63, 653–663. [Google Scholar] [CrossRef] [PubMed]
- Fei, B.; Lu, G.; Wang, X.; Zhang, H.; Little, J.V.; Patel, M.R.; Griffith, C.C.; El-Diery, M.W.; Chen, A.Y. Label-free reflectance hyperspectral imaging for tumor margin assessment: A pilot study on surgical specimens of cancer patients. J. Biomed. Opt. 2017, 22, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Halicek, M.; Little, J.V.; Wang, X.; Chen, A.Y.; Fei, B. Optical biopsy of head and neck cancer using hyperspectral imaging and convolutional neural networks. J. Biomed. Opt. 2019, 24, 1–9. [Google Scholar] [CrossRef]
- Regeling, B.; Thies, B.; Gerstner, A.O.H.; Westermann, S.; Müller, N.A.; Bendix, J.; Laffers, W. Hyperspectral Imaging Using Flexible Endoscopy for Laryngeal Cancer Detection. Sensors 2016, 16, 1288. [Google Scholar] [CrossRef]
- Halicek, M.; Dormer, J.D.; Little, J.V.; Chen, A.Y.; Myers, L.; Sumer, B.D.; Fei, B. Hyperspectral Imaging of Head and Neck Squamous Cell Carcinoma for Cancer Margin Detection in Surgical Specimens from 102 Patients Using Deep Learning. Cancers 2019, 11, 1367. [Google Scholar] [CrossRef]
- Fabelo, H.; Ortega, S.; Ravi, D.; Kiran, B.R.; Sosa, C.; Bulters, D.; Callicó, G.M.; Bulstrode, H.; Szolna, A.; Piñeiro, J.F.; et al. Spatio-spectral classification of hyperspectral images for brain cancer detection during surgical operations. PLoS ONE 2018, 13, e0193721. [Google Scholar] [CrossRef]
- Fabelo, H.; Ortega, S.; Lazcano, R.; Madroñal, D.; M Callicó, G.; Juárez, E.; Salvador, R.; Bulters, D.; Bulstrode, H.; Szolna, A.; et al. An Intraoperative Visualization System Using Hyperspectral Imaging to Aid in Brain Tumor Delineation. Sensors 2018, 18, 430. [Google Scholar] [CrossRef]
- Fabelo, H.; Halicek, M.; Ortega, S.; Shahedi, M.; Szolna, A.; Piñeiro, J.F.; Sosa, C.; O’Shanahan, A.J.; Bisshopp, S.; Espino, C.; et al. Deep Learning-Based Framework for In Vivo Identification of Glioblastoma Tumor using Hyperspectral Images of Human Brain. Sensors 2019, 19, 920. [Google Scholar] [CrossRef]
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, A.J. Advanced Spectral Classifiers for Hyperspectral Images: A review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef]
- Van Der Maaten, L.J.P.; Postma, E.O.; Van Den Herik, H.J. Dimensionality Reduction: A Comparative Review. J. Mach. Learn. Res. 2009, 10, 1–41. [Google Scholar] [CrossRef]
- Lunga, D.; Prasad, S.; Crawford, M.M.; Ersoy, O. Manifold-Learning-Based Feature Extraction for Classification of Hyperspectral Data: A Review of Advances in Manifold Learning. IEEE Signal Process. Mag. 2014, 31, 55–66. [Google Scholar] [CrossRef]
- Dai, Q.; Cheng, J.H.; Sun, D.W.; Zeng, X.A. Advances in Feature Selection Methods for Hyperspectral Image Processing in Food Industry Applications: A Review. Crit. Rev. Food Sci. Nutr. 2015, 55, 1368–1382. [Google Scholar] [CrossRef]
- Sastry, K.; Goldberg, D.E.; Kendall, G. Genetic Algorithms. In Search Methodologies; Springer: Boston, MA, USA, 2014; pp. 93–117. [Google Scholar]
- Perez, R.E.; Behdinan, K. Particle Swarm Optimization in Structural Design. Swarm Intell. Focus Ant Part. Swarm Optim. 2012, 1–24. [Google Scholar] [CrossRef]
- Sharma, S.; Buddhiraju, K.M. Spatial-spectral ant colony optimization for hyperspectral image classification. Int. J. Remote Sens. 2018, 39, 2702–2717. [Google Scholar] [CrossRef]
- Rashmi, S.; Addamani, S.; Ravikiran, A. Spectral Angle Mapper algorithm for remote sensing image classification. IJISET Int. J. Innov. Sci. Eng. Technol. 2014, 1, 201–205. [Google Scholar] [CrossRef]
- Halicek, M.; Fabelo, H.; Ortega, S.; Little, J.V.; Wang, X.; Chen, A.Y.; Callicó, G.M.; Myers, L.; Sumer, B.; Fei, B. Cancer detection using hyperspectral imaging and evaluation of the superficial tumor margin variance with depth. In Medical Imaging 2019: Image-Guided Procedures, Robotic Interventions, and Modeling; Fei, B., Linte, C.A., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 10951, p. 45. [Google Scholar]
- Lu, G.; Qin, X.; Wang, D.; Chen, Z.G.; Fei, B. Quantitative wavelength analysis and image classification for intraoperative cancer diagnosis with hyperspectral imaging. In Proceedings of the Progress in Biomedical Optics and Imaging—Proceedings of SPIE, Orlando, FL, USA, 21–26 February 2015; Volume 9415. [Google Scholar]
- Fabelo, H.; Ortega, S.; Szolna, A.; Bulters, D.; Pineiro, J.F.; Kabwama, S.; J-O’Shanahan, A.; Bulstrode, H.; Bisshopp, S.; Kiran, B.R.; et al. In-Vivo Hyperspectral Human Brain Image Database for Brain Cancer Detection. IEEE Access 2019, 7, 39098–39116. [Google Scholar] [CrossRef]
- Chen, P.C.; Lin, W.C. Spectral-profile-based algorithm for hemoglobin oxygen saturation determination from diffuse reflectance spectra. Biomed. Opt. Express 2011, 2, 1082–1096. [Google Scholar] [CrossRef]
- Eaton, W.A.; Hanson, L.K.; Stephens, P.J.; Sutherland, J.C.; Dunn, J.B.R. Optical spectra of oxy- and deoxyhemoglobin. J. Am. Chem. Soc. 1978, 100, 4991–5003. [Google Scholar] [CrossRef]
- Sekar, S.K.V.; Bargigia, I.; Mora, A.D.; Taroni, P.; Ruggeri, A.; Tosi, A.; Pifferi, A.; Farina, A. Diffuse optical characterization of collagen absorption from 500 to 1700 nm. J. Biomed. Opt. 2017, 22, 015006. [Google Scholar] [CrossRef] [PubMed]
- Camps-Valls, G.; Bruzzone, L.; Electr, E.; Escola, T.; Val, U. De Kernel-based methods for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1351–1362. [Google Scholar] [CrossRef]
- Fabelo, H.; Halicek, M.; Ortega, S.; Szolna, A.; Morera, J.; Sarmiento, R.; Callicó, G.M.; Fei, B. Surgical aid visualization system for glioblastoma tumor identification based on deep learning and in-vivo hyperspectral images of human patients. In Medical Imaging 2019: Image-Guided Procedures, Robotic Interventions, and Modeling; SPIE: Bellingham, WA, USA, 2019; Volume 10951, p. 35. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Moore, A. K-means and Hierarchical Clustering. Available online: http://www.cs.cmu.edu/afs/cs/user/awm/web/tutorials/kmeans11.pdf (accessed on 24 November 2019).
- Akhter, N.; Dabhade, S.; Bansod, N.; Kale, K. Feature Selection for Heart Rate Variability Based Biometric Recognition Using Genetic Algorithm. In Intelligent Systems Technologies and Applications; Springer: Cham, Switzerland, 2016; pp. 91–101. [Google Scholar]
- Haupt, S.E.; Haupt, R.L. Genetic algorithms and their applications in environmental sciences. In Advanced Methods for Decision Making and Risk Management in Sustainability Science; Nova Science Publishers: Hauppauge, NY, USA, 2007; pp. 183–196. [Google Scholar]
- Zortea, M.; Plaza, A. Spatial Preprocessing for Endmember Extraction. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2679–2693. [Google Scholar] [CrossRef]
- Boughorbel, S.; Jarray, F.; El-Anbari, M. Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric. PLoS ONE 2017, 12, e0177678. [Google Scholar] [CrossRef] [PubMed]
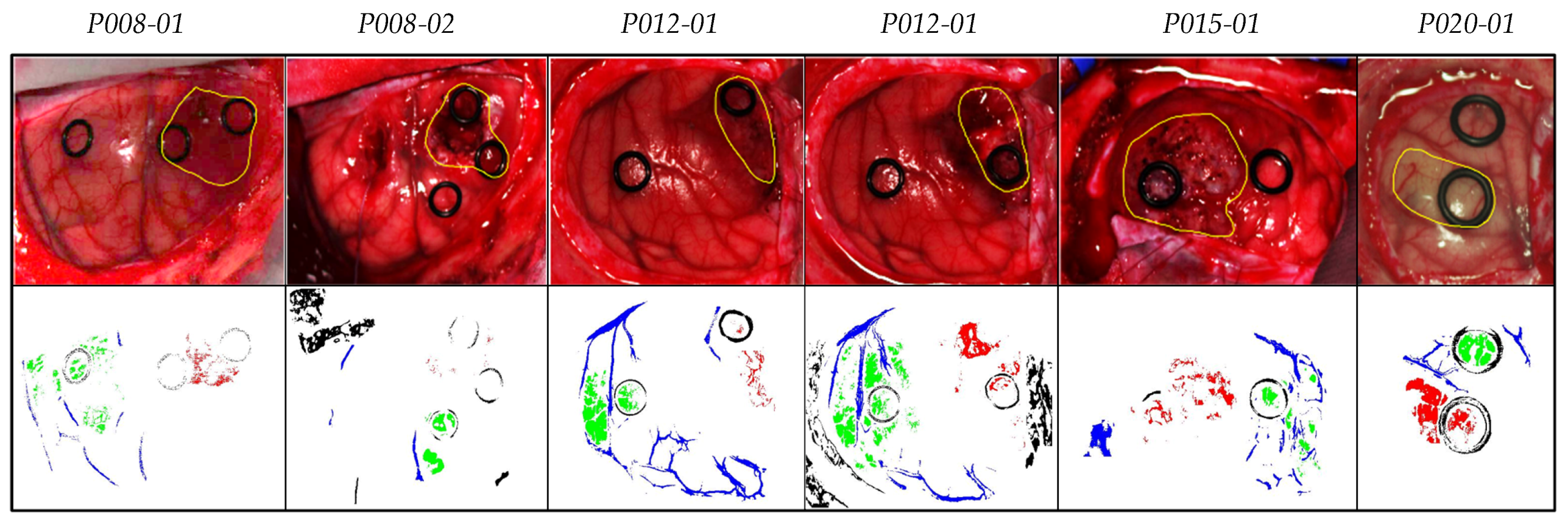
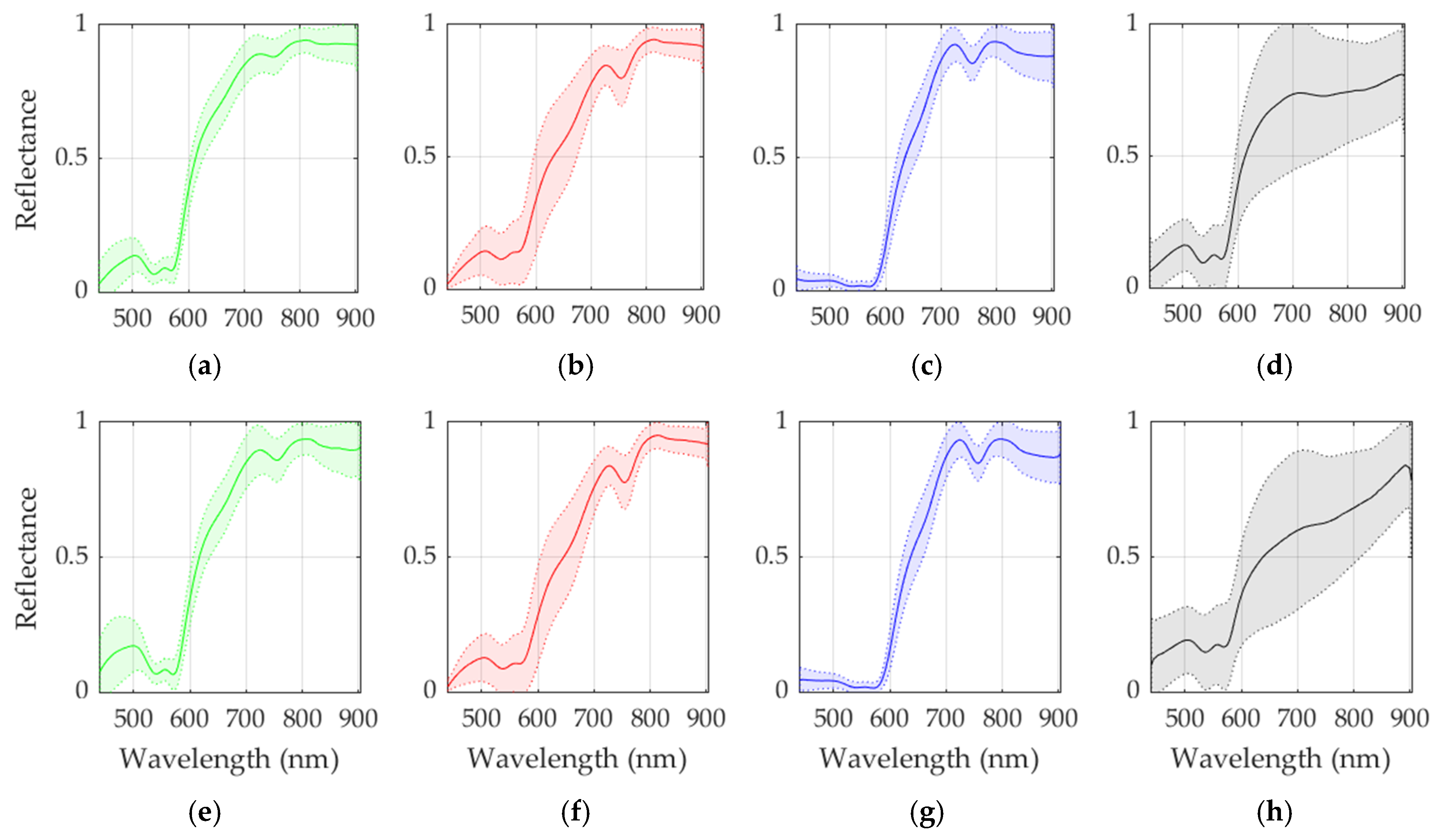
| Class | #Labeled Pixels | #Images | #Patients |
|---|---|---|---|
| Normal Tissue | 101,706 | 26 | 16 |
| Tumor Tissue (Glioblastoma-GBM) | 11,054 | 6 | 4 |
| Hypervascularized Tissue | 38,784 | 25 | 16 |
| Background | 118,132 | 24 | 15 |
| Total | 269,676 | 26 | 16 |
| #Spectral Bands | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 826 | 645 | 320 | 214 | 160 | 128 | 80 | 64 | 32 | 16 | 8 | |
| λmin (nm) | 400 | 440 | 440 | 440 | 440 | 440 | 440 | 440 | 440 | 440 | 440 |
| λmax (nm) | 1000 | 902 | 902 | 902 | 902 | 902 | 902 | 902 | 902 | 902 | 902 |
| Sampling Interval (nm) | 0.73 | 0.73 | 1.44 | 2.16 | 2.89 | 3.61 | 5.78 | 7.22 | 14.44 | 28.88 | 57.75 |
| Size (MB) | 1328.3 | 1037.3 | 514.6 | 344.1 | 257.3 | 205.8 | 128.6 | 102.9 | 51.4 | 25.7 | 12.8 |
| Level (#bands) | OA (%) (STD) | MCC (%) (STD) | Sensitivity (%) - (STD) | Specificity (%) - (STD) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| NT | TT | HT | BG | NT | TT | HT | BG | |||
| L1 (48) | 77.9 (17.0) | 83.6 (9.1) | 85.1 (17.6) | 52.7 (29.8) | 83.5 (20.9) | 92.5 (14.2) | 87.3 (12.2) | 94.6 (8.3) | 96.7 (5.1) | 85.3 (18.0) |
| L2 (22) | 77.0 (16.8) | 83.3 (8.6) | 83.7 (19.9) | 57.0 (32.6) | 81.9 (23.0) | 90.1 (20.1) | 85.2 (13.4) | 91.2 (14.4) | 97.1 (4.9) | 87.7 (17.6) |
| L3 (2) | 53.8 (21.2) | 68.9 (11.4) | 52.8 (42.6) | 57.6 (36.5) | 48.8 (26.4) | 84.8 (27.1) | 72.9 (13.2) | 70.3 (30.8) | 93.1 (8.0) | 80.0 (21.1) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez, B.; Leon, R.; Fabelo, H.; Ortega, S.; Piñeiro, J.F.; Szolna, A.; Hernandez, M.; Espino, C.; J. O’Shanahan, A.; Carrera, D.; et al. Most Relevant Spectral Bands Identification for Brain Cancer Detection Using Hyperspectral Imaging. Sensors 2019, 19, 5481. https://doi.org/10.3390/s19245481
Martinez B, Leon R, Fabelo H, Ortega S, Piñeiro JF, Szolna A, Hernandez M, Espino C, J. O’Shanahan A, Carrera D, et al. Most Relevant Spectral Bands Identification for Brain Cancer Detection Using Hyperspectral Imaging. Sensors. 2019; 19(24):5481. https://doi.org/10.3390/s19245481
Chicago/Turabian StyleMartinez, Beatriz, Raquel Leon, Himar Fabelo, Samuel Ortega, Juan F. Piñeiro, Adam Szolna, Maria Hernandez, Carlos Espino, Aruma J. O’Shanahan, David Carrera, and et al. 2019. "Most Relevant Spectral Bands Identification for Brain Cancer Detection Using Hyperspectral Imaging" Sensors 19, no. 24: 5481. https://doi.org/10.3390/s19245481
APA StyleMartinez, B., Leon, R., Fabelo, H., Ortega, S., Piñeiro, J. F., Szolna, A., Hernandez, M., Espino, C., J. O’Shanahan, A., Carrera, D., Bisshopp, S., Sosa, C., Marquez, M., Camacho, R., Plaza, M. d. l. L., Morera, J., & M. Callico, G. (2019). Most Relevant Spectral Bands Identification for Brain Cancer Detection Using Hyperspectral Imaging. Sensors, 19(24), 5481. https://doi.org/10.3390/s19245481









