Environmental Cross-Validation of NLOS Machine Learning Classification/Mitigation with Low-Cost UWB Positioning Systems
Abstract
1. Introduction
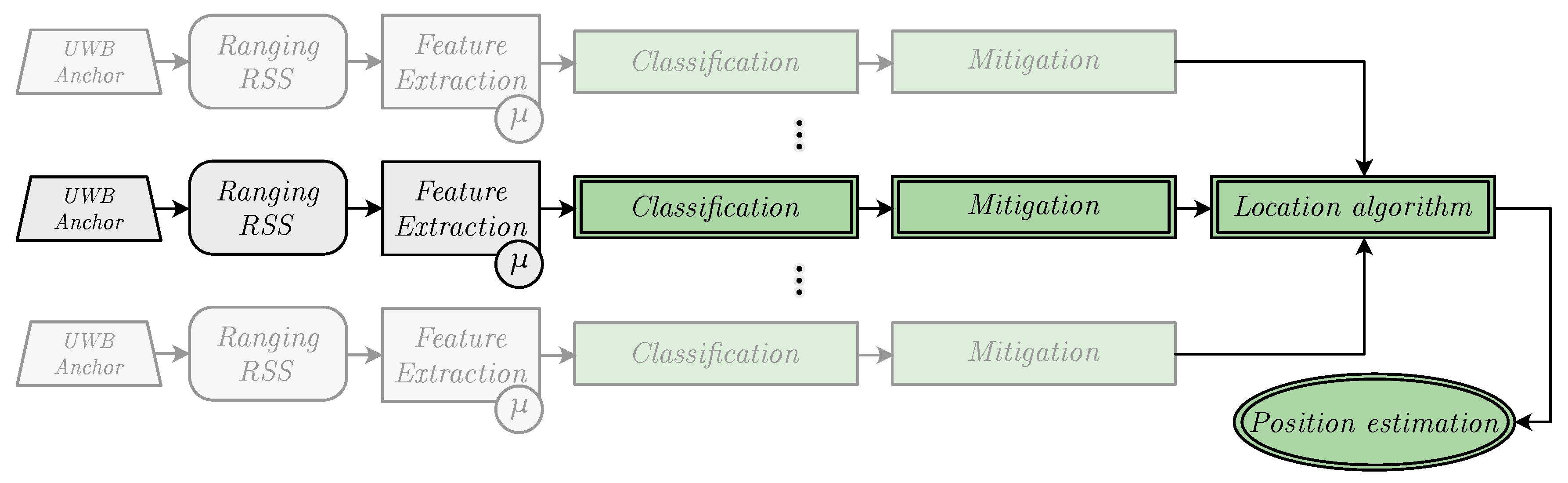
- Measurement campaigns in two different scenarios. Two different measurement campaigns were carried out in two distinct scenarios: The first one—referred to as the ML model-generation scenario—captured the measurements used to train, validate, and test the classification and mitigation algorithms, whereas the second one—called the evaluation scenario—compiled another different set of measurements to evaluate the performance of the previous ML algorithms over the position estimates. Both campaigns are detailed in Section 2.
- Model generation. Considering the RSS and ranging measurements recorded in the ML model-generation scenario, several ML algorithms—including multilayer Perceptrons (MLPs)—were used to train different classification and mitigation models. Section 3 details the considered algorithms, the features selected for the training, and the chosen hyper-parameters.
- Positioning estimation. The previously generated models were applied directly to the measurements obtained in the evaluation scenario. Once classified and mitigated, the resulting data were used to feed positioning algorithms—described in Section 4—to generate position estimates.
- Analysis of the results. Finally, the obtained position estimates were analyzed to assess the performance of the proposed approach. The results are shown in Section 5 together with the descriptions of the different considered configurations.
Main Contributions
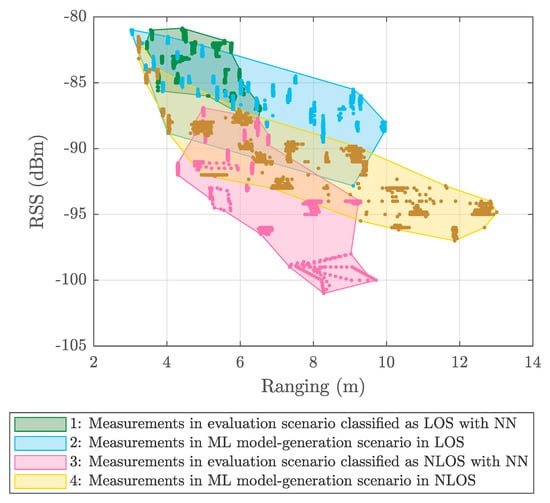
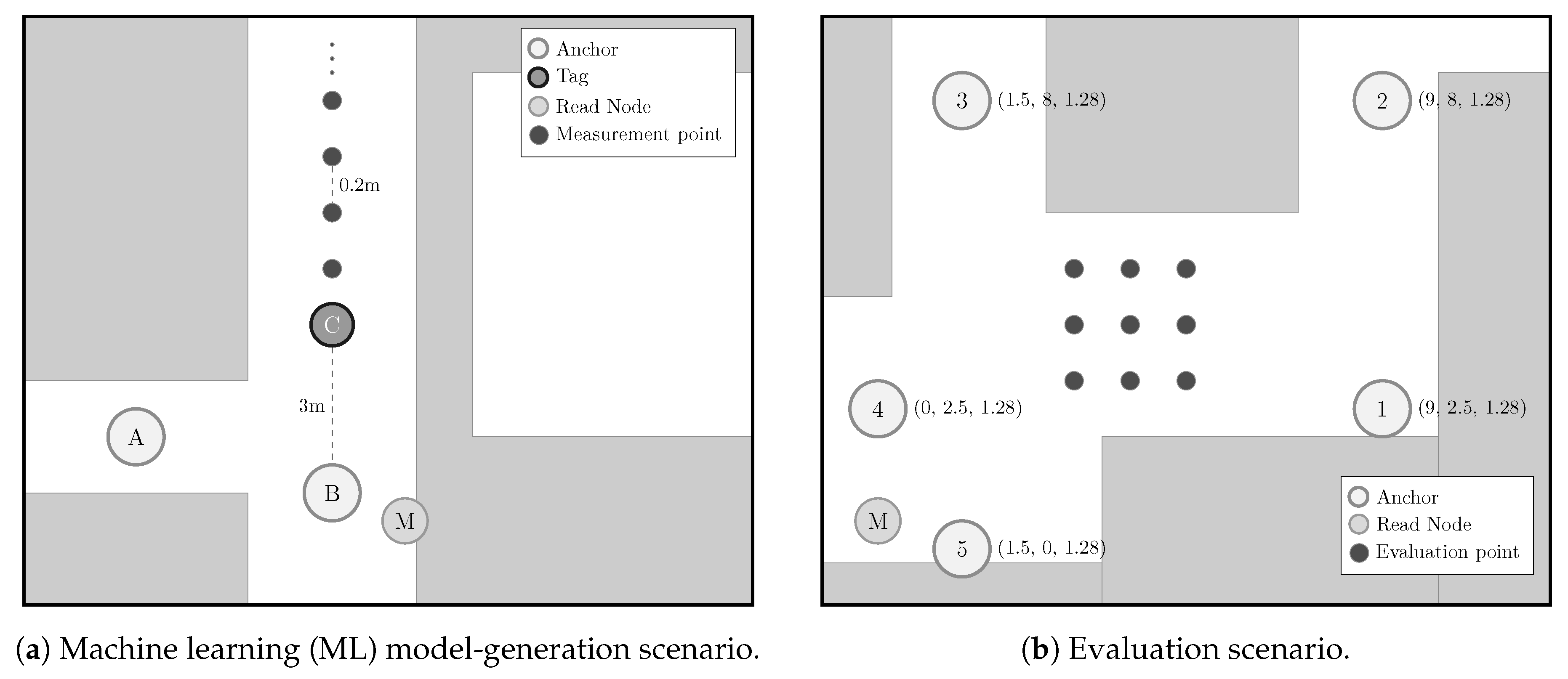
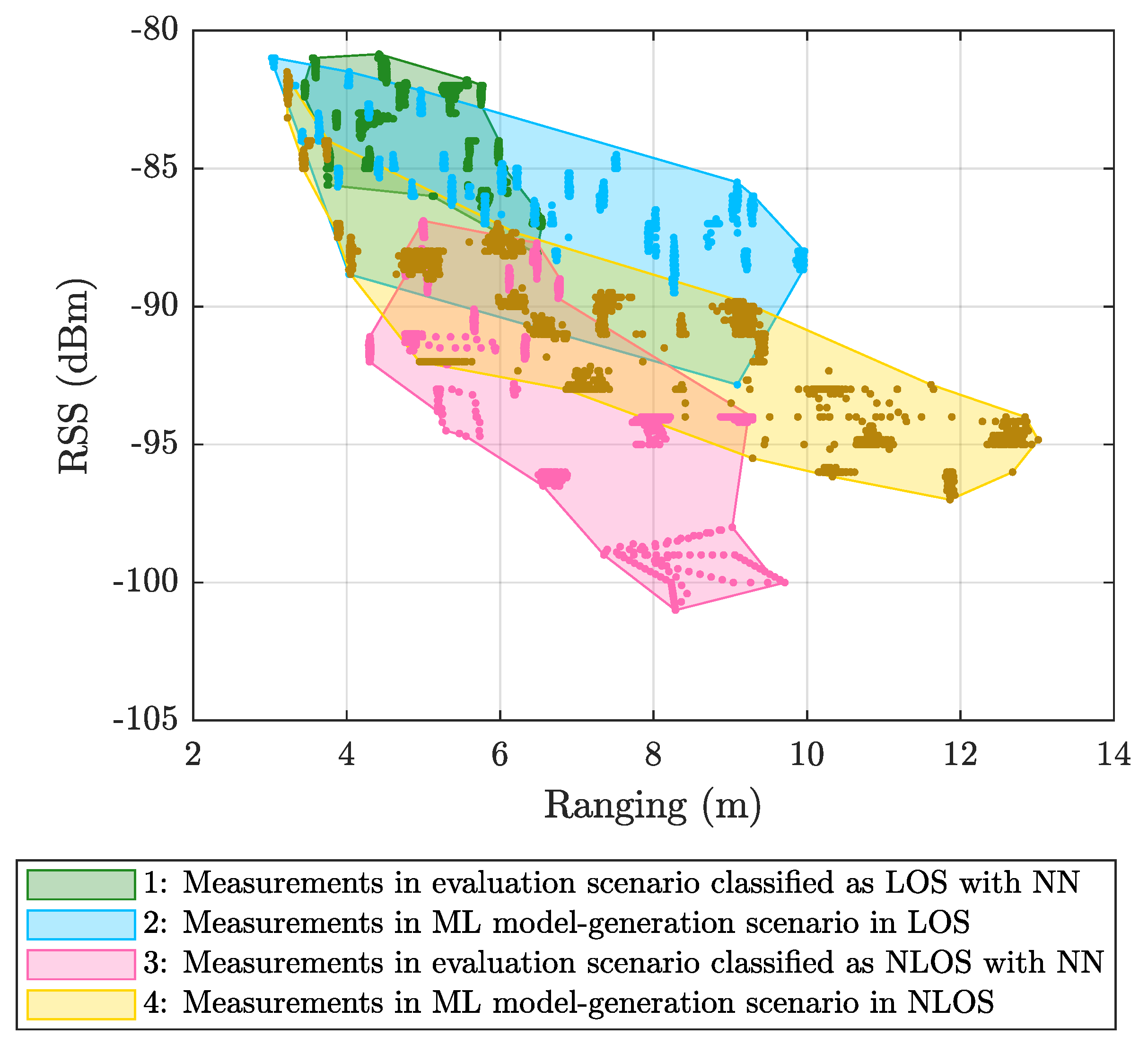
- NLOS detection and mitigation algorithms based on ML techniques were trained considering ranging and RSS values from a UWB measurement campaign carried out in the ML model-generation scenario (see Figure 2a), whereas those models were applied to data from another UWB measurement campaign carried out in a different scenario: The evaluation scenario (see Figure 2b).
- Apart from some of the ML algorithms considered by the authors in previous works [5], this time another different method of this type was included in the experiments: The MLP. Thus, two different MLPs (see Section 3.1.2) were trained, validated, and tested for NLOS detection and mitigation, employing the data measured in the ML model-generation scenario.
- Two different location algorithms—nonlinear least squares (NLS) with a Gauss–Newton iterative procedure and an implementation of the iterative extended Kalman filter (IEKF)—were employed to fully evaluate the positioning performance of the proposed approach from the ranging data measured in the evaluation scenario (Figure 2b) after being processed with different NLOS detection and mitigation configurations (see Section 5).
- A comparison was made of the performance of the localization in the evaluation scenario with respect to the same scenario with an ideal situation where UWB measurements taken from the ML model-generation scenario were considered. This was possible thanks to the realistic UWB simulator that the authors developed in [8]. The results of this comparison can be seen in Section 5.2.
2. Measurements
2.1. Hardware
2.2. Scenarios
3. Machine Learning Techniques
3.1. k-Nearest Neighbors
3.1.1. Gaussian Process Regression Model
3.1.2. Multilayer Perceptron
4. Location Algorithms
4.1. Nonlinear Least Squares with Gauss–Newton
4.2. Iterative Extended Kalman Filter
5. Experiments and Results
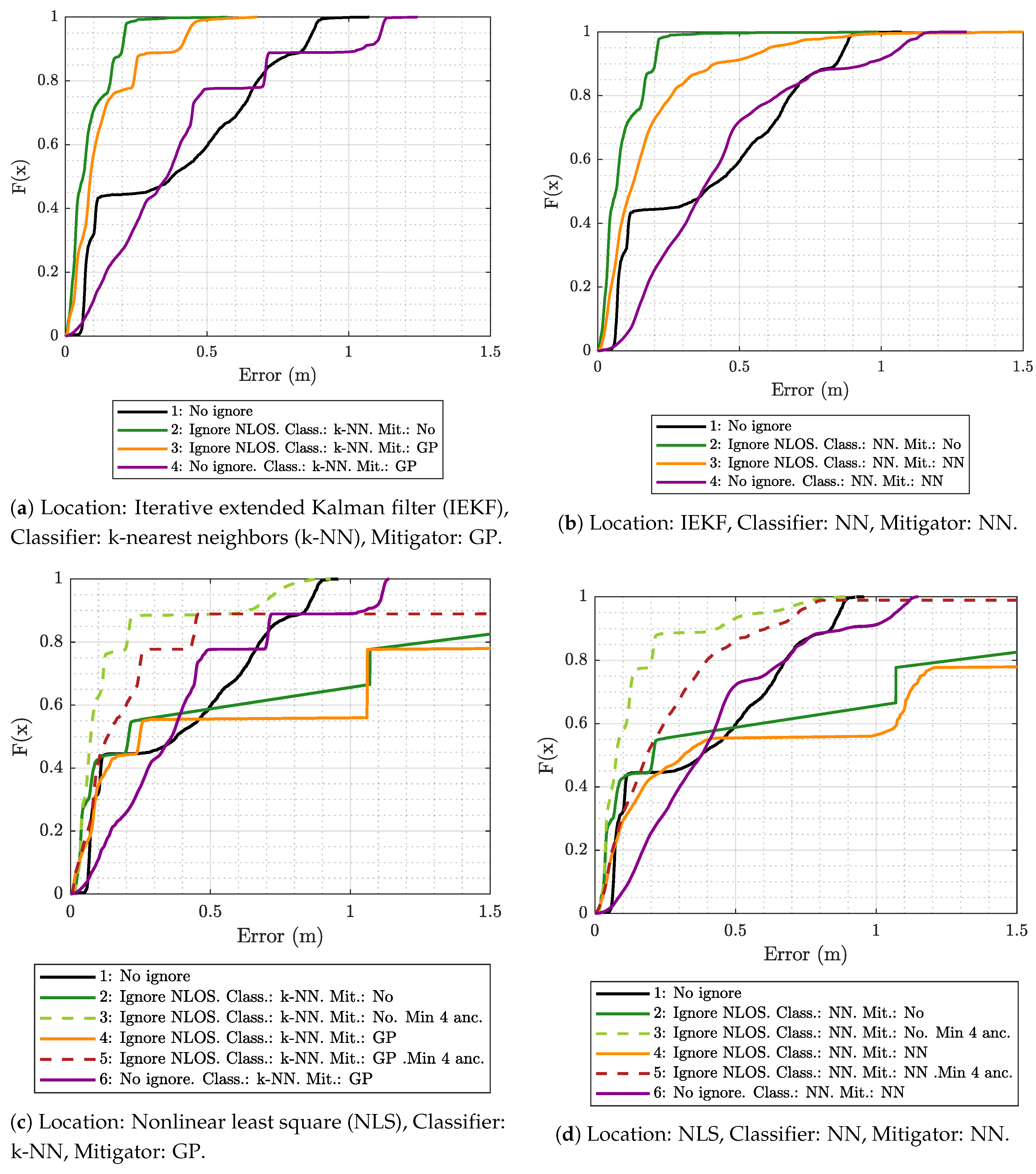
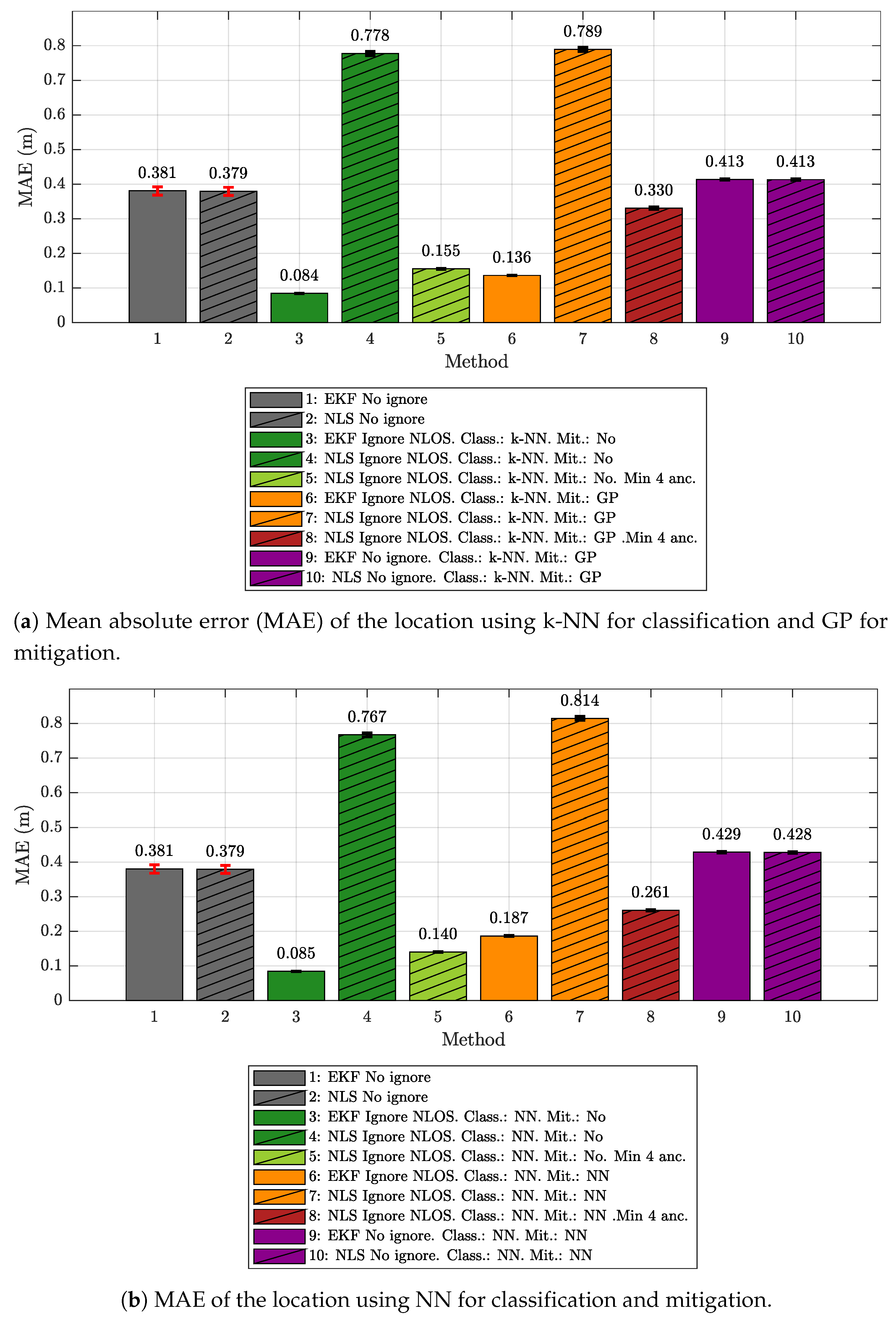
5.1. Results Obtained Considering Different Scenarios for Generating and Evaluating the Models
- The k-NN algorithm as the classifier and the GP regression model as the mitigator.
- The NN as both classifier and mitigator.
- The IEKF as the positioning algorithm.
- The NLS with Gauss as the positioning algorithm.
- No ignore. This is the configuration that serves as the reference for the location error. In this case, the positioning algorithms employ all raw measurement data recorded in the scenario, without any previous classification or mitigation processes. That is to say, the measurement data are the direct input to the positioning algorithms.
- Ignore NLOS and no mitigation. Either k-NN or NN is used to classify each measured value as LOS or NLOS. Subsequently, the positioning algorithms will only be fed with the measurement data in the LOS category, without any mitigation, and ignoring data classified as NLOS.
- Ignore NLOS with at least four anchors and no mitigation. NLOS data are classified and ignored as in configuration 2, but while ensuring at least four ranging values for the positioning algorithms, enabling algorithms such as the NLS, which otherwise could not provide an estimate in the three dimensions. When less than four values are classified as LOS in one iteration, then the necessary values classified as NLOS are included. More specifically, the ranging values classified as NLOS with the lowest score, i.e., those which are less likely to belong to the NLOS category, are selected to replace the missing LOS values. Again, no mitigation mechanism is applied to the ranging data. This configuration was not tested with the IEKF, as this algorithm does not need to have at least four values to estimate a position.
- Ignore NLOS with mitigation. NLOS ranging values are classified and removed from the positioning process. The errors in the remaining ranging values (classified as LOS) are mitigated with one of the algorithms before being sent to the positioning algorithms to finally produce position estimates.
- Ignore NLOS with at least four anchors and mitigation. This is a combination of configurations 3 and 4: NLOS ranging values are ignored, but the ones more likely to be classified as LOS are considered to ensure four ranging values in each iteration. Before running the positioning algorithm, each measurement value is passed through an LOS mitigator. Again, this configuration was not tested with the IEKF, as this algorithm does not need to have at least four values to estimate a position.
- No ignore with mitigation. The same as configuration 1, but each measurement is passed through a mitigator—modeled according to the category determined by the classifier (i.e., LOS or NLOS)—before being processed by the positioning algorithms.
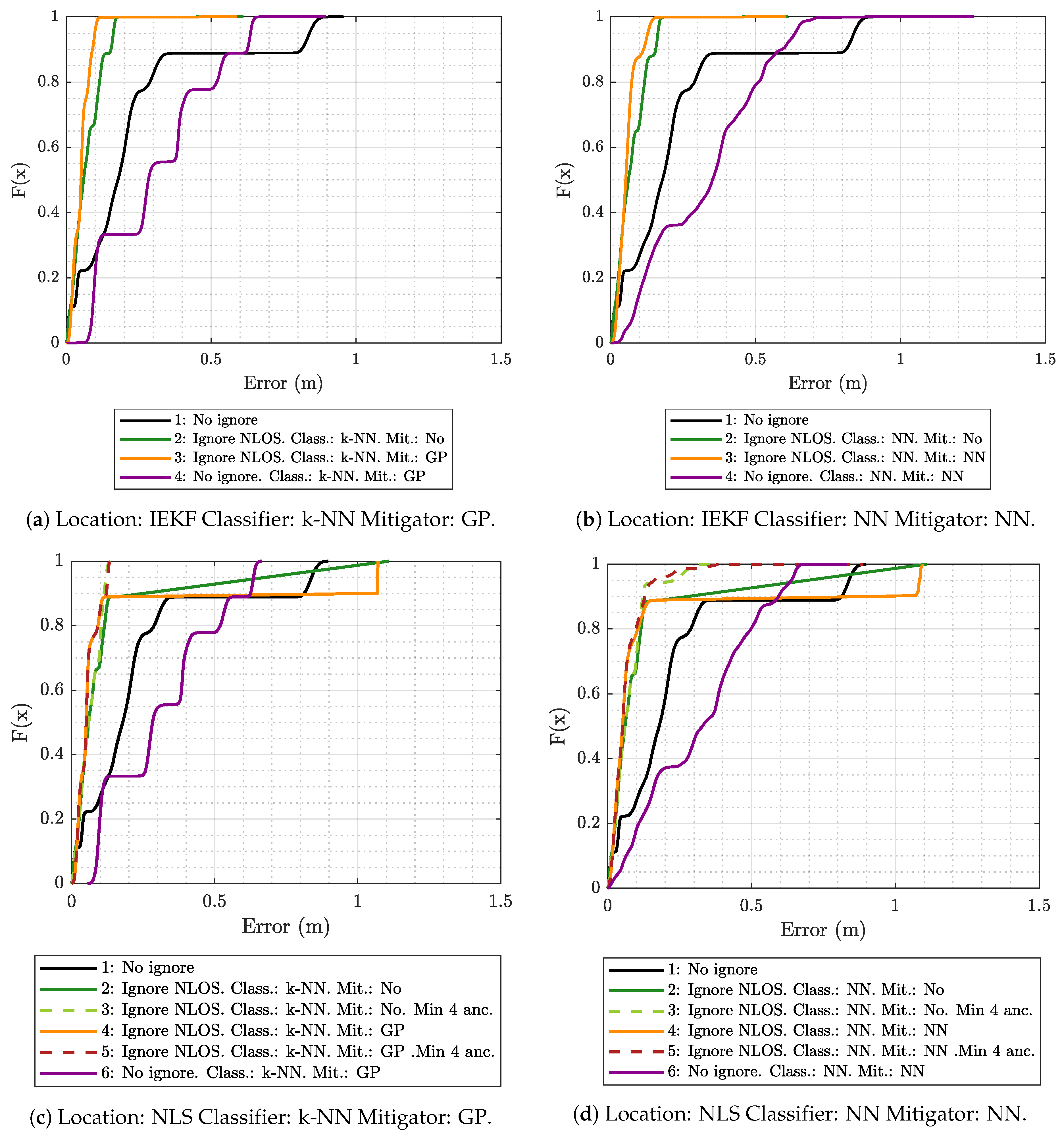
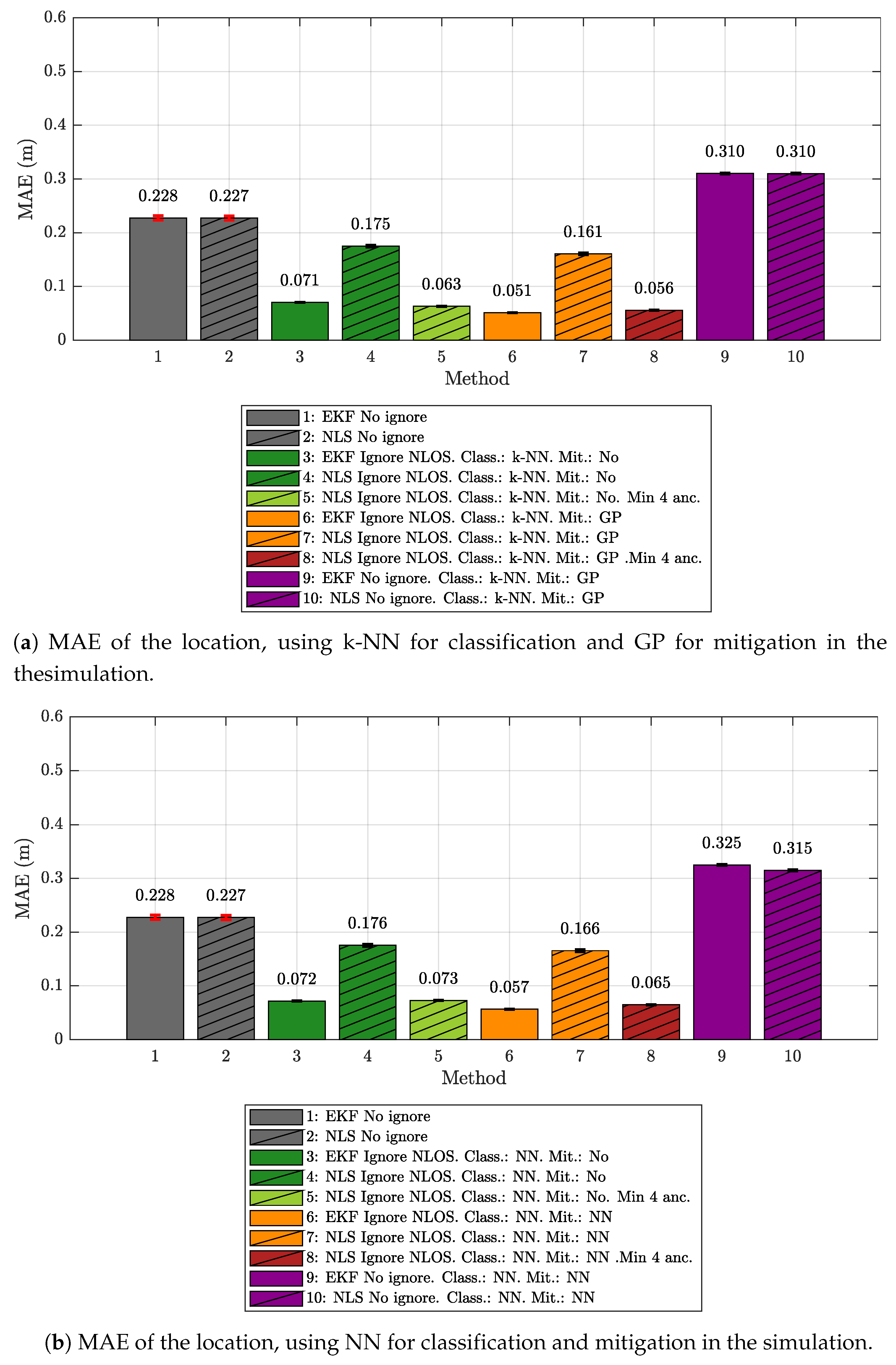
5.2. Results Obtained for Model Generation and Evaluation Based on the Same Scenario
- A measurement campaign was carried out in the same real-world ML model-generation scenario considered in this work (see Figure 2a).
- These measurements were used to train, validate, and test a series of ML models capable of providing estimates of ranging, ranging variance, RSS, and RSS variance from two input values: The distance between the tag and the simulated anchor, and the propagation conditions between them: LOS, NLOS-Soft, or NLOS-Hard.
- Finally, a 3D ray-tracing model was developed to estimate the type of scenario between the tag and the anchors. More specifically, the simulator assigns the LOS type when the signal propagates from the tag to the anchor without touching any obstacles. It assigns NLOS-Soft when the signal encounters an obstacle between them, but is able to cross it (according to some configuration parameters of the simulator). Finally, the simulator assigns the NLOS-Hard type in the case of finding a big obstacle between the tag and the anchors, but it is capable of tracing a connection between both after bouncing off of a wall or the floor of the simulated scenario. Notice that, for the sake of simplicity, rebounds on the ceiling are not considered in the current version of the simulator.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Acronyms
| ARD | automatic relevance determination |
| AWGN | additive white Gaussian noise |
| CIR | channel impulse response |
| ECDF | empirical cumulative distribution function |
| GP | Gaussian process |
| IEKF | iterative extended Kalman filter |
| k-NN | k-nearest neighbors |
| LED | leading edge detection |
| LOS | line-of-sight |
| MAE | mean absolute error |
| ML | machine learning |
| MLP | multilayer Perceptron |
| NLOS | non-line-of-sight |
| NLS | nonlinear least squares |
| NN | neural network |
| RSS | received signal strength |
| TDOA | time difference of arrival |
| TOA | time of arrival |
| TOF | time of flight |
| TWR | two-way ranging |
| UWB | ultra-wideband |
References
- Dardari, D.; Conti, A.; Ferner, U.; Giorgetti, A.; Win, M.Z. Ranging with ultrawide bandwidth signals in multipath environments. Proc. IEEE 2009, 97, 404–426. [Google Scholar] [CrossRef]
- Maali, A.; Mimoun, H.; Baudoin, G.; Ouldali, A. A new low complexity NLOS identification approach based on UWB energy detection. In Proceedings of the IEEE Radio and Wireless Symposium, San Diego, CA, USA, 18–22 January 2009; pp. 675–678. [Google Scholar] [CrossRef]
- Al-Jazzar, S.; Caffery, J., Jr. New algorithms for NLOS identification. In Proceedings of the 14th IST Mobile and Wireless Communications Summit, Dresden, Germany, 19–23 June 2005. [Google Scholar]
- Güvenç, İ.; Chong, C.C.; Watanabe, F.; Inamura, H. NLOS identification and weighted least-squares localization for UWB systems using multipath channel statistics. EURASIP J. Adv. Signal Proc. 2007, 2008, 271984. [Google Scholar] [CrossRef]
- Barral, V.; Escudero, C.J.; García-Naya, J.A.; Maneiro-Catoira, R. NLOS identification and mitigation using low-cost UWB devices. Sensors 2019, 19, 3464. [Google Scholar] [CrossRef] [PubMed]
- Marano, S.; Gifford, W.M.; Wymeersch, H.; Win, M.Z. NLOS identification and mitigation for localization based on UWB experimental data. IEEE J. Sel. Areas Commun. 2010, 28, 1026–1035. [Google Scholar] [CrossRef]
- Li, W.; Zhang, T.; Zhang, Q. Experimental researches on an UWB NLOS identification method based on machine learning. In Proceedings of the 2013 15th IEEE International Conference on Communication Technology, Guilin, China, 17–19 November 2013; pp. 473–477. [Google Scholar]
- Barral, V.; Suárez-Casal, P.; Escudero, C.J.; García-Naya, J.A. Multi-sensor accurate forklift location and tracking simulation in industrial indoor environments. Electronics 2019, 8, 1152. [Google Scholar] [CrossRef]
- Barral, V.; Escudero, C.J.; García-Naya, J.A. NLOS Classification Based on RSS and Ranging Statistics Obtained from Low-Cost UWB Devices: Dataset. Available online: https://ieee-dataport.org/documents/nlos-identification-and-mitigation-using-low-cost-uwb-devices (accessed on 10 December 2019).
- Barral, V.; Escudero, C.J.; García-Naya, J.A. Environment Cross Validation of NLOS Machine Learning Classification/Mitigation in Low-Cost UWB Positioning Systems: Dataset. Available online: https://ieee-dataport.org/open-access/environment-cross-validation-nlos-machine-learning-classificationmitigation-low-cost-uwb (accessed on 10 December 2019).
- UDC. Area Científica. Available online: https://goo.gl/maps/59pCfNgZ75Siy6gf7 (accessed on 3 June 2019).
- Pozyx. Pozyx Site. Available online: http://www.pozyx.com/ (accessed on 22 May 2019).
- DecaWave. Decawave Site. Available online: http://www.decawave.com/ (accessed on 22 May 2019).
- Decuir, J. Two Way Time Transfer Based Ranging; IEEE 802.15-04a Documents 15-04-0573-00-004a; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar]
- Dashti, M.; Ghoraishi, M.; Haneda, K.; Takada, J.i. High-precision time-of-arrival estimation for UWB localizers in indoor multipath channels. In Novel Applications of the UWB Technologies; IntechOpen: London, UK, 2011. [Google Scholar]
- Barral, V.; Suárez-Casal, P.; Escudero, C.; García-Naya, J.A. Assessment of UWB ranging bias in multipath environments. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN), Madrid, Spain, 4–7 October 2016. [Google Scholar]
- Pozyx. Pozyx Documentation. Available online: https://ardupozyx.readthedocs.io/en/latest/api/pozyx_class.html (accessed on 23 August 2019).
- Barral, V.; Escudero, C.J.; García-Naya, J.A. NLOS classification based on RSS and ranging statistics obtained from low-cost UWB devices. In Proceedings of the 27th European Signal Processing Conference, EUSIPCO, A Coruña, Spain, 2–6 September 2019. [Google Scholar]
- Mullin, M.D.; Sukthankar, R. Complete cross-validation for nearest neighbor classifiers. In Proceedings of the Seventeenth International Conference on Machine Learning (ICML ’00), Stanford, CA, USA, 29 June–2 July 2000; pp. 639–646. [Google Scholar]
- Betrò, B. Bayesian methods in global optimization. J. Global Optim. 1991, 1, 1–14. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian Processes in Machine Learning; Summer School on Machine Learning; Springer: Berlin, Germany, 2003; pp. 63–71. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. In Proceedings of the 25th International Conference on Neural Information Processing Systems (NIPS’12)—Volume 2, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2951–2959. [Google Scholar]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Norrdine, A. An algebraic solution to the multilateration problem. In Proceedings of the 15th International Conference on Indoor Positioning and Indoor Navigation, Sydney, Australia, 13–15 November 2012; Volume 1315. [Google Scholar]
- Wang, Y. Linear least squares localization in sensor networks. Eurasip J. Wirel. Commun. Netw. 2015, 2015, 51. [Google Scholar] [CrossRef]
- Murphy, W.S. Determination of a Position Using Approximate Distances and Trilateration; Colorado School of Mines: Golden, CO, USA, 2007. [Google Scholar]
- Ravindra, S.; Jagadeesha, S. Time of arrival based localization in wireless sensor networks: A non-linear approach. Signal Image Proc. 2015, 6, 45. [Google Scholar]
- Hartley, H.O. The modified Gauss-Newton method for the fitting of non-linear regression functions by least squares. Technometrics 1961, 3, 269–280. [Google Scholar] [CrossRef]
- Gelb, A. Applied Optimal Estimation; MIT Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. Signal processing, sensor fusion, and target recognition VI. Int. Soc. Opt. Photonics 1997, 3068, 182–194. [Google Scholar]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics (Intelligent Robotics and Autonomous Agents); The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Gazebo. Gazebo Simulator. 2019. Available online: http://gazebosim.org (accessed on 9 December 2019).

| Mitigation Class | Kernel | |
|---|---|---|
| LOS | ARD Exponential | 40.43 |
| NLOS | Exponential | 49.82 |
| NN | # Hidden Layers | # Neurons | Act. Fun. Hidden Layers | Act. Fun. Last Layer |
|---|---|---|---|---|
| Classification | 3 | Hyperbolic tangent sigmoid | Soft max | |
| Mitigation LOS | 2 | Hyperbolic tangent sigmoid | Linear | |
| Mitigation NLOS | 2 | Hyperbolic tangent sigmoid | Linear |
| Parameter | Value |
|---|---|
| Maximum Epochs | 1000 |
| Maximum Training Time | ∞ |
| Performance Goal | 0 |
| Minimum Gradient | 1 × 10−6 |
| Maximum Validation Checks | 6 |
| 5 × 10−5 | |
| 5 × 10−7 |
| IEKF | Measured | Simulated | Difference |
|---|---|---|---|
| No Ignore | |||
| Ignore NLOS. Class.: k-NN. Mit.: No. | |||
| Ignore NLOS. Class.: k-NN. Mit.: GP. | |||
| No Ignore. Class.: k-NN. Mit.: GP. | |||
| Ignore NLOS. Class.: NN. Mit.: No. | |||
| Ignore NLOS. Class.: NN. Mit.: NN. | |||
| No Ignore. Class.: NN. Mit.: NN. |
| NLS | Measured | Simulated | Difference |
|---|---|---|---|
| No Ignore | |||
| Ignore NLOS. Class.: k-NN Mit.: No. | |||
| Ignore NLOS. Class.: k-NN Mit.: No. Min 4. | |||
| Ignore NLOS. Class.: k-NN Mit.: GP. | |||
| Ignore NLOS. Class.: k-NN Mit.: GP. Min 4. | |||
| Ignore NLOS. Class.: NN Mit.: No. | |||
| Ignore NLOS. Class.: NN Mit.: No. Min 4. | |||
| Ignore NLOS. Class.: NN Mit.: NN. | |||
| Ignore NLOS. Class.: NN Mit.: NN. Min 4. | |||
| No Ignore. Class.: NN Mit.: NN. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barral, V.; Escudero, C.J.; García-Naya, J.A.; Suárez-Casal, P. Environmental Cross-Validation of NLOS Machine Learning Classification/Mitigation with Low-Cost UWB Positioning Systems. Sensors 2019, 19, 5438. https://doi.org/10.3390/s19245438
Barral V, Escudero CJ, García-Naya JA, Suárez-Casal P. Environmental Cross-Validation of NLOS Machine Learning Classification/Mitigation with Low-Cost UWB Positioning Systems. Sensors. 2019; 19(24):5438. https://doi.org/10.3390/s19245438
Chicago/Turabian StyleBarral, Valentín, Carlos J. Escudero, José A. García-Naya, and Pedro Suárez-Casal. 2019. "Environmental Cross-Validation of NLOS Machine Learning Classification/Mitigation with Low-Cost UWB Positioning Systems" Sensors 19, no. 24: 5438. https://doi.org/10.3390/s19245438
APA StyleBarral, V., Escudero, C. J., García-Naya, J. A., & Suárez-Casal, P. (2019). Environmental Cross-Validation of NLOS Machine Learning Classification/Mitigation with Low-Cost UWB Positioning Systems. Sensors, 19(24), 5438. https://doi.org/10.3390/s19245438