The star sensor model analyzed in this work is an ideal spherical star sensor, capable of measuring the direction and energy of every photon incident on its surface. This ideal star sensor is able to observe stars from any direction, that is, it has a field of view of
. The knowledge on the incoming direction of photons in this model is limited only by diffraction at the star sensor aperture, assumed to be circular with the same radius of the star sensor itself. In other words, it is assumed that the star sensor aperture is given by the projection of the star sensor body on a plane perpendicular to the direction of incoming photons.
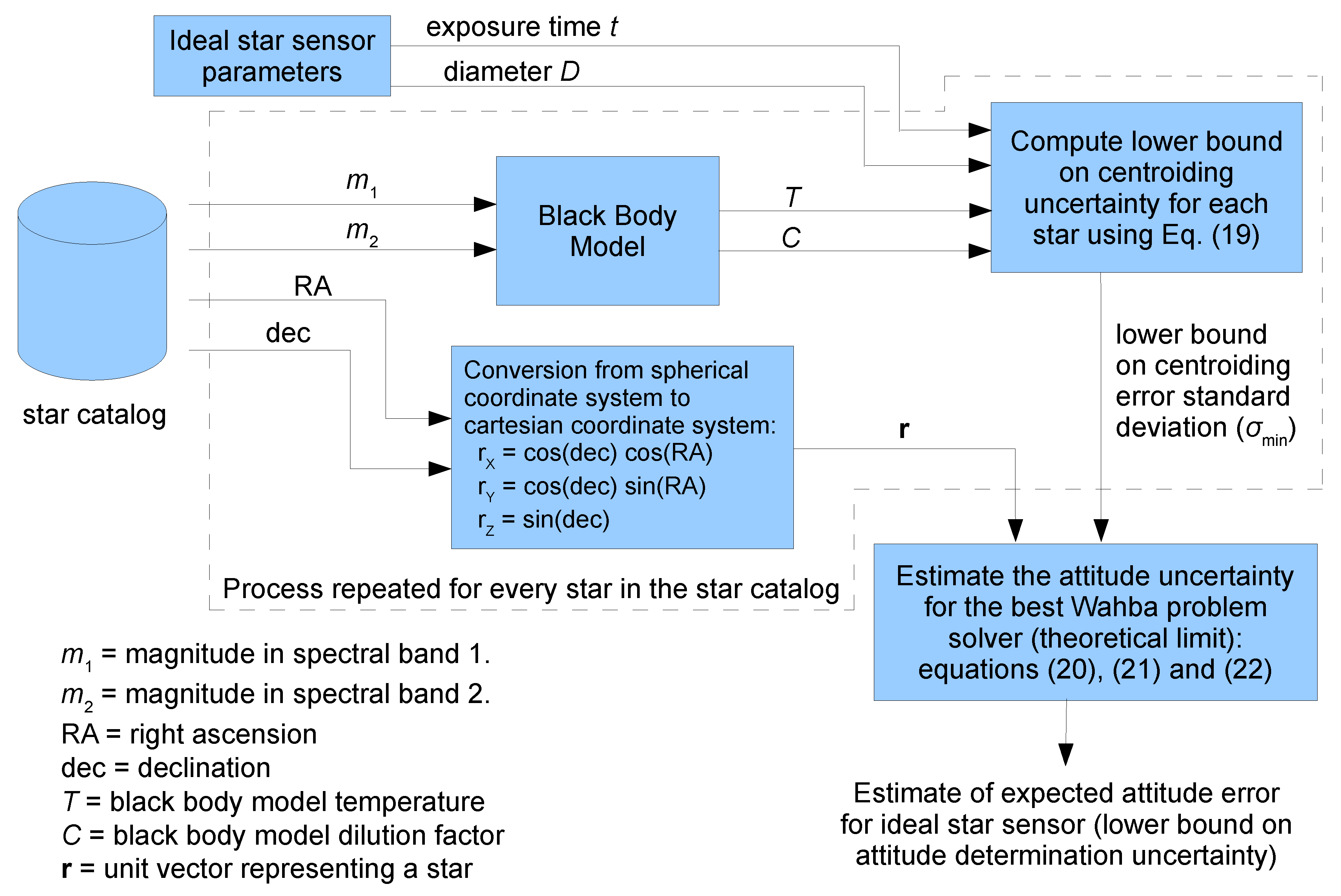
Figure 1 provides a sketch of the star sensor model adopted in this work. In this model, the accuracy of the centroids of each star is limited only by diffraction and shot noise. These effects depend only on the star sensor aperture, stellar spectra, and integration time (exposure time). This ideal star sensor is completely black, as it absorbs every photon impinging on it.
Section 2.1 and
Section 2.2 provide more details on the assumptions adopted in this model.
2.1. Basic Assumptions
The following basic assumptions were made:
Assumption 1. The star sensor has a spherical shape with a diameter D.
Assumption 2. It is able to detect every photon of stellar origin impinging on its surface.
Assumption 3. It is capable of registering the incoming direction and energy of every detected photon with an accuracy limited only by Heisenberg’s Uncertainty Principle.
Assumption 4. Only photons detected during a period of length t—the exposure or integration time—are considered for attitude determination.
Assumption 5. It is at absolute zero temperature.
Assumption 6. The coordinates of the stars in an inertial reference frame with origin in the star sensor are known with absolute precision.
Assumption 7. An unbiased optimal estimator is used to determine the star sensor attitude, and computations are performed with infinite precision.
Assumption 8. Measurements obtained with this ideal star sensor are not merged with external measurements.
Assumption 2 implies that the star sensor field of view is , in other words, it is capable of observing the whole celestial sphere simultaneously, a fact that coupled to its spherical shape, implies that the accuracy of this ideal star sensor does not depend on its attitude.
Assumption 3 and the fact that every photon is detected implies that the optics are ideal: transmission, with no defocusing and blurring, except for the blurring dictated by diffraction.
Assumption 5 means there is no noise of thermal origin within the star sensor.
Assumptions 4 and 8 limit the number of photons that will be observed by the ideal star sensor. If exposure time were not constrained, it would be possible to get attitude measurement uncertainty as low as desired, just by increasing the exposure time. In addition, this model does not consider the possibility of combining current observations with previous observations to improve accuracy. Assumption 4 also implies that the star sensor is able to measure just photons and no other particles. The basis for this assumption is the fact that the only other particle known to science that could, perhaps, convey better the positions of stars are neutrinos emitted at their core. However, these particles interact so weakly with ordinary matter that their detection in star sensors is currently impossible and may never become a reality [
15].
Assumption 6 implies that the star catalog is perfect and that all corrections needed to bring the coordinates, brightness and colors from the star catalog reference frame origin to the star sensor location (corrections for stellar aberration, parallax, and redshift/blueshift) are performed with no errors.
Assumption 8 expresses the goal of obtaining a lower bound on attitude error for a single star sensor used in isolation. If measurements from multiple sensors were permitted to be merged, a significant improvement in attitude measurement accuracy would become possible. For example, by interferometrically combining measurements from a small number of star sensors mounted in a rigid structure and separated by a distance much greater than their diameters, it would be possible to improve attitude determination by many orders of magnitude in comparison to the theoretical estimate presented in this work, with attitude uncertainty being roughly inversely proportional to the distance between them [
16,
17].
2.2. Simplifying Assumptions
In addition to the previous assumptions, to make this study feasible, the following additional assumptions were also made:
Assumption 9. The whole Universe is assumed to be composed only by stars.
Assumption 10. Stars are considered as polychromatic point sources of light.
Assumption 11. Stellar spectra are approximated by the spectra of black bodies that best match the cataloged star intensity given by star catalogs adopted here.
Assumption 12. All Solar System bodies (including the Sun) are disregarded.
Assumption 13. Stellar proper motion is disregarded.
Assumption 14. The star sensor is not rotating.
Assumption 15. It is assumed that each detected photon can be univocally associated with the star from where it originated.
Assumption 16. Stars are considered to be at an infinite distance.
Assumption 17. There is no obstruction from spacecraft structures or nearby bodies.
Simplifying Assumption 9 means that we are not considering as additional sources of attitude information extended bodies, such as interstellar clouds, given that these sources are difficult to precisely model and would hardly significantly increase our attitude knowledge. However, it does not necessarily mean that all non-stellar pointlike sources will be excluded from analysis. This means simply that any non-stellar pointlike source present in star catalogs, such as some quasars and some distant galaxies, will be treated as if they were stars.
Regarding simplifying Assumption 11, ideally, the actual spectra of stars should be used, at least for the brightest stars, something to be attempted in future works.
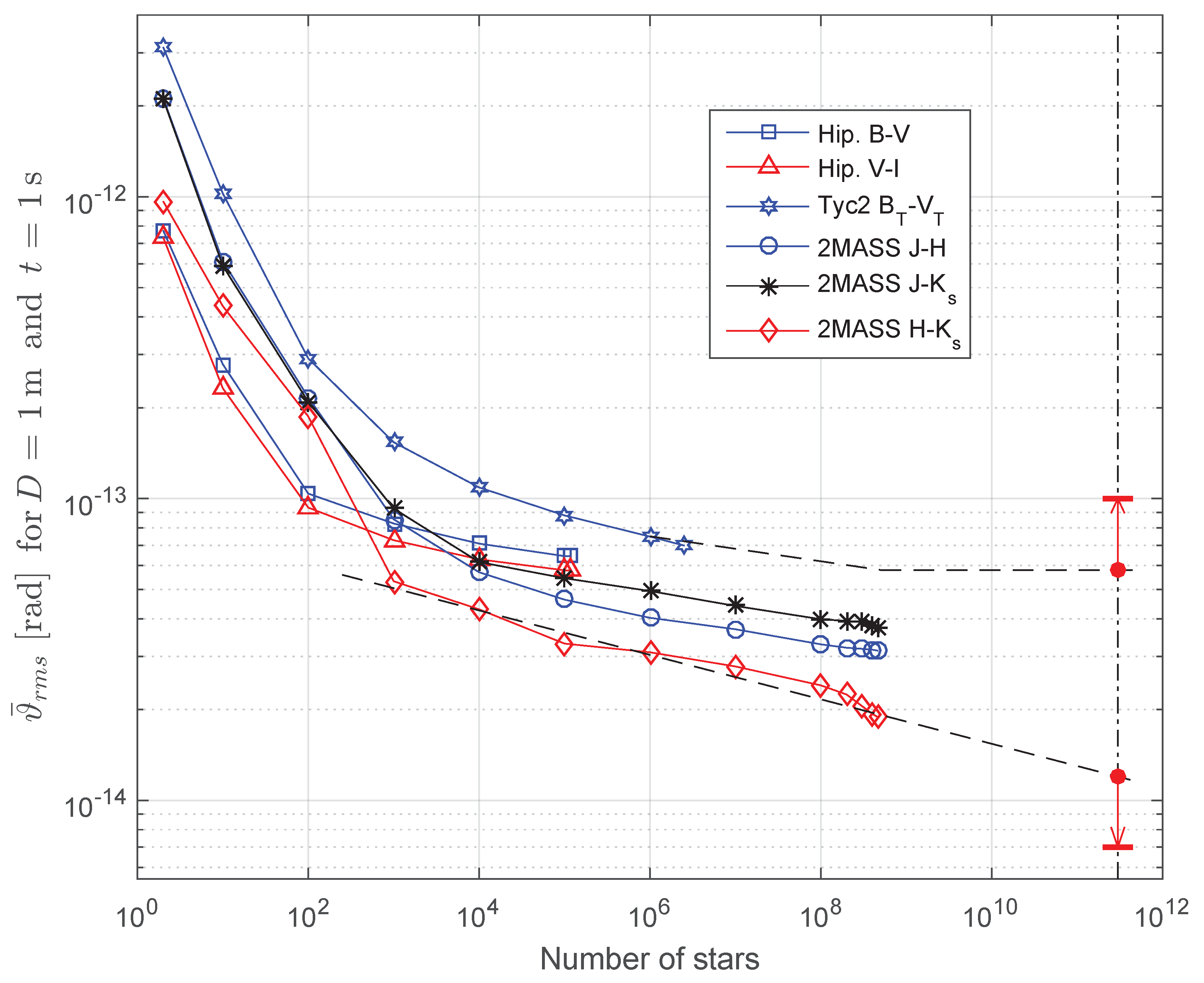
Section 3.2 discusses the adequacy of this approximation.
About simplifying Assumption 14, had the star sensor been rotating, but with knowledge of the precise instant each photon was detected and a very accurate knowledge of its own angular velocity vector, it would be possible to compute the incoming direction of every photon in a non-rotating reference frame attached to the star sensor, thus reducing the problem of attitude determination of a spinning star sensor to the problem of attitude determination of a non-rotating star sensor.
Regarding simplifying Assumption 17, had there been any obstruction in the field of view of the ideal star sensor (such as obstruction from nearby bodies or obstruction by spacecraft structures), its accuracy would necessarily be worse, since the obstructed stars would no longer contribute to the attitude information gathered by the star sensor. Therefore, we assume that it has an unrestricted view of the whole celestial sphere. In
Section 3.4 we investigate the effects of reductions in the field of view.
Our computations disregard the Sun and other Solar System objects as additional references for attitude determination, since these sources are difficult to model accurately. Also, the Sun being many orders of magnitude closer and brighter than the other stars, from our vantage point in the Universe, it is too bright to be directly observed by most, if not all, star sensors. However, an attitude sensor in a distant future which is able to use and model very accurately the Sun and a neighboring planetary body as additional attitude references, could, perhaps, overcome the estimates on the lower bound of attitude uncertainty computed in this work. This is a topic to be better investigated in the future.
2.4. Black Body Model for Stars
In the model adopted in this work, the spectrum of each star is considered to be the spectrum of an equivalent spherical black body, diluted by a non-dimensional geometric factor
C arising from its distance to the star sensor. Given that the spectral exitance of a black body is uniquely determined by its temperature, only two parameters are needed in this model to determine the spectral distribution and intensity of the electromagnetic radiation received by the star sensor from each star, the temperature
T and the dilution factor
C. Mathematically:
where:
is the spectral irradiance received from star i by a surface located at the same place of the star sensor and perpendicular to incoming rays, evaluated at wavelength ;
is the geometric dilution factor for star i;
is the temperature of the black body that represents star i;
is the spectral exitance of the surface of the equivalent black body, at wavelength .
In this equation, both and are given in unit of power per unit of area and per unit of wavelength (e.g., W/m/nm).
To uniquely determine these two parameters (
T and
C) for each star, at least two samples of their flux taken at different wavelengths or at different spectral bands are needed. The following sections describe how
T and
C are derived for each star from Hipparcos catalog data [
18], using the cataloged
magnitudes and
color indexes. A similar procedure is performed with data from Hipparcos using the
color indexes and data from other star catalogs.
2.5. Black Body Temperatures from Color Indexes
Taking as an example data from the Hipparcos catalog, the spectra of stars is taken as the spectra of black bodies with intensities adjusted so that the integrated spectra over the Johnson’s
B and
V bands [
19,
20] match simultaneously the flux at these bands derived from catalog data. To determine equivalent black bodies temperatures for stars in the Hipparcos catalog, an empirical relation is established in this section, linking the
color indexes given in the Hipparcos catalog with black body temperatures.
The spectral exitance at wavelength
of a black body at a temperature
T can be computed as follows [
21]:
where
h is the Planck’s constant,
c is the speed of light in vacuum and
k is the Boltzmann constant. The spectral exitance will have units of power per unit area per unit wavelength (
in SI units). Numerical values of
h,
c and
k used in computations were those adopted in the 2019 redefinition of the SI base units [
22].
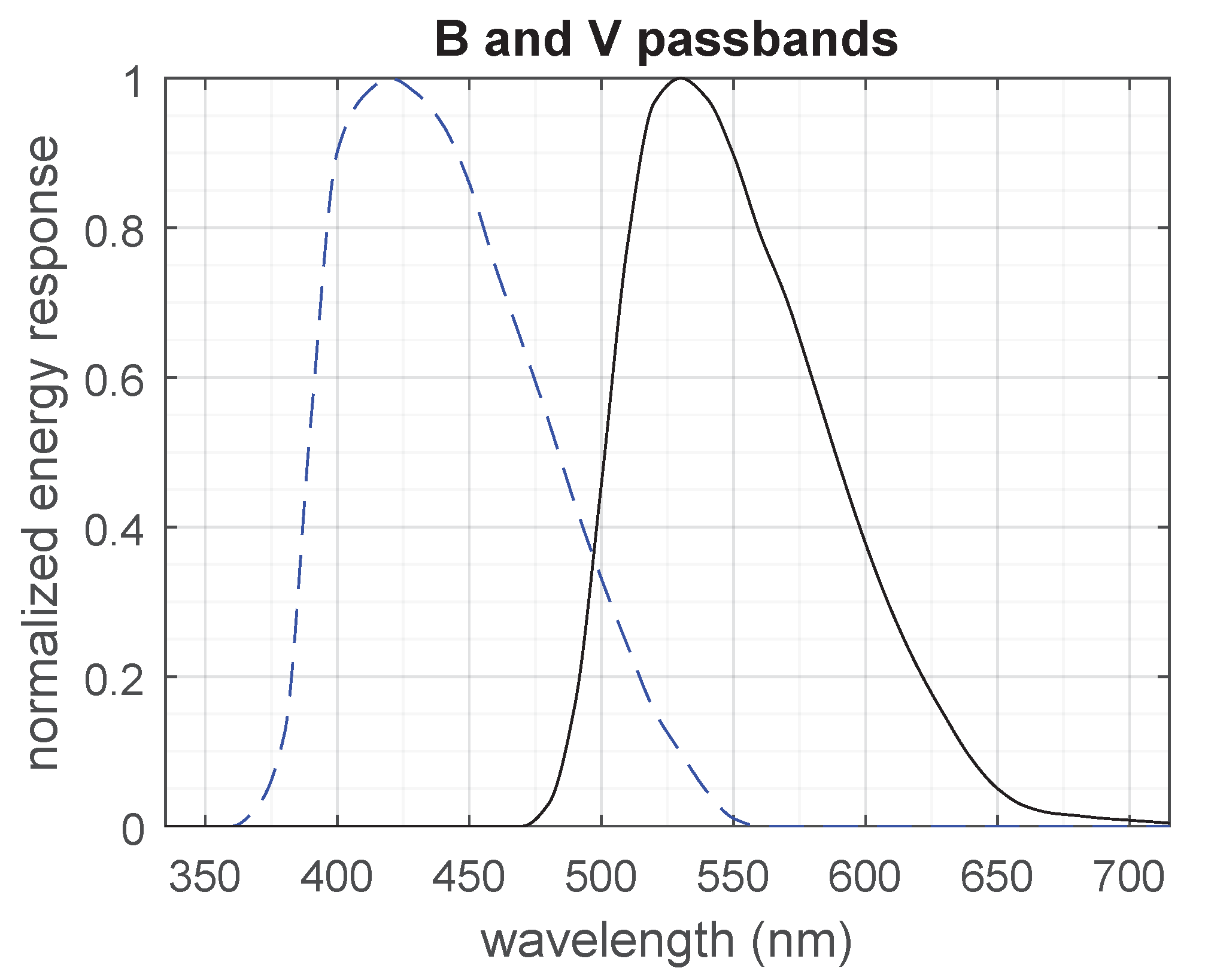
By integrating the product of the spectral exitance of a black body with the Johnson’s
B and
V bands energy responses it is possible to obtain the black-body fluxes in the
B and
V bands at its surface. This procedure is described in detail by Bessell in Reference [
19], Section 1.6—Synthetic Photometry:
where
= flux at the surface of a black body at temperature
T in the Johnson’s
B band and
= spectral energy response function of the Johnson’s
B band. Analogously,
and
are quantities related to the Johnson’s
V band.
The
and
response functions were obtained by converting the tabulated values recommended by Bessell (Table 1 on page 146 of Reference [
20]) from normalized photonic responses to normalized energy responses and interpolating the resulting values. The energy response functions adopted in this work are shown in
Figure 3.
The conversion from normalized photonic response to normalized energy response was done by multiplying the photonic response by the wavelength and renormalizing the results (Equation (A9) in Reference [
20]). The explanation for this procedure is given in Section A2 in the appendix of Reference [
20], on page 153. The method of interpolation used was a “shape-preserving piecewise cubic interpolation”, provided by the MATLAB/GNU Octave function
interp1 with method “pchip”. Computations were performed in MATLAB R2015b with the script
plot_BV_BB_script.m from the .zip archive which supplements this work (see “
Supplementary Materials” on page 20).
From the fluxes in the
B and
V bands, the magnitudes in these bands can be computed:
These equations give the apparent magnitudes in the
B and
V spectral bands of a spherical black body for an observer situated just above its surface looking down towards its center.
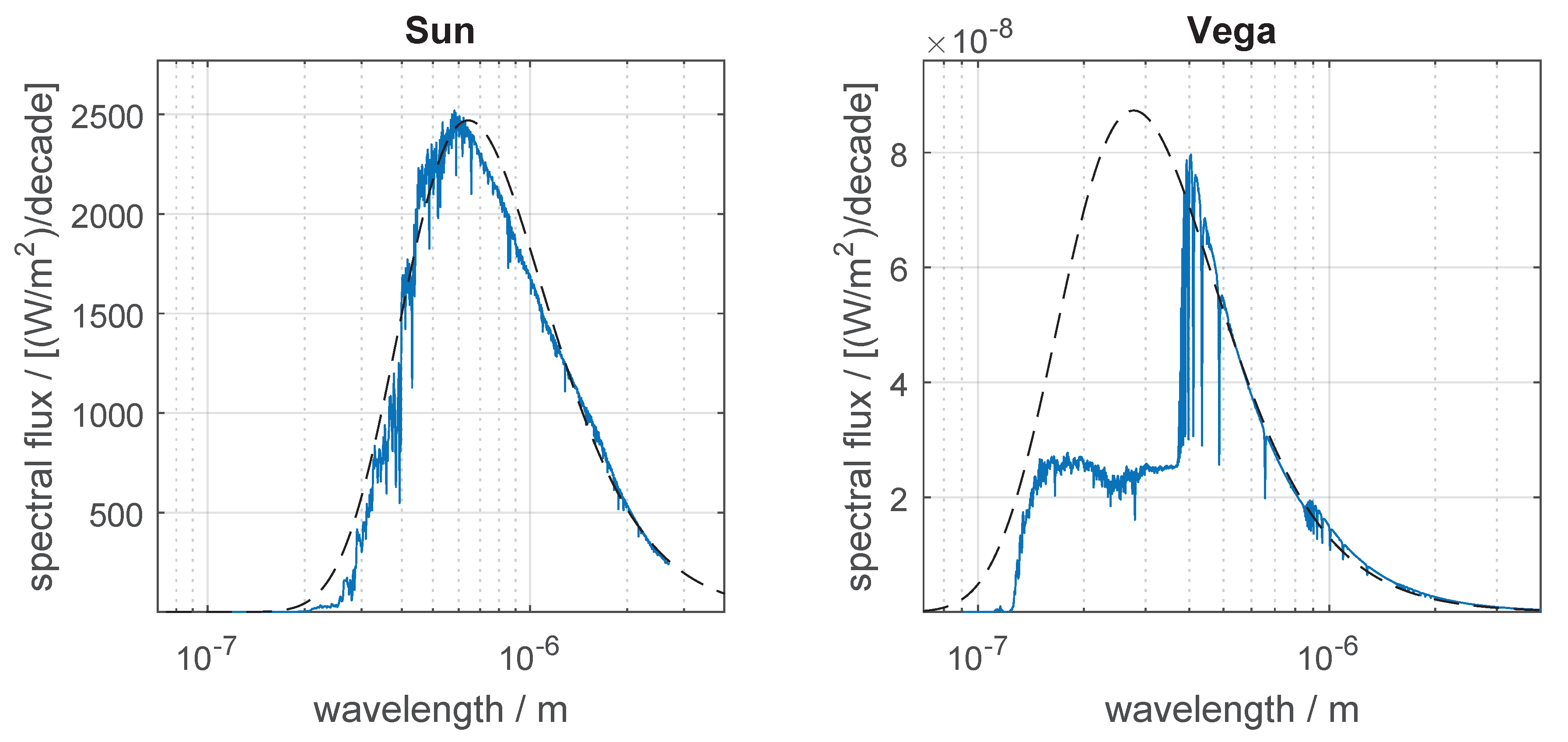
and
are the reference fluxes that define the zero points of the magnitude scales in these bands, having being obtained by numerically integrating the spectrum of Vega (
-Lyr) multiplied by the band responses, and adjusting their values such that the computed
B and
V magnitudes of Vega matches those in the star catalog (
and
in Hipparcos). Mathematically:
where
is the spectral irradiance from Vega measured at the top of Earth’s atmosphere. The spectrum of Vega used in Equations (
7) and (
8) was obtained from file
alpha_lyr_stis_008.fits from the CALSPEC database [
23], which at the time of this writing was available at
http://www.stsci.edu/hst/instrumentation/reference-data-for-calibration-and-tools/astronomical-catalogs/calspec.
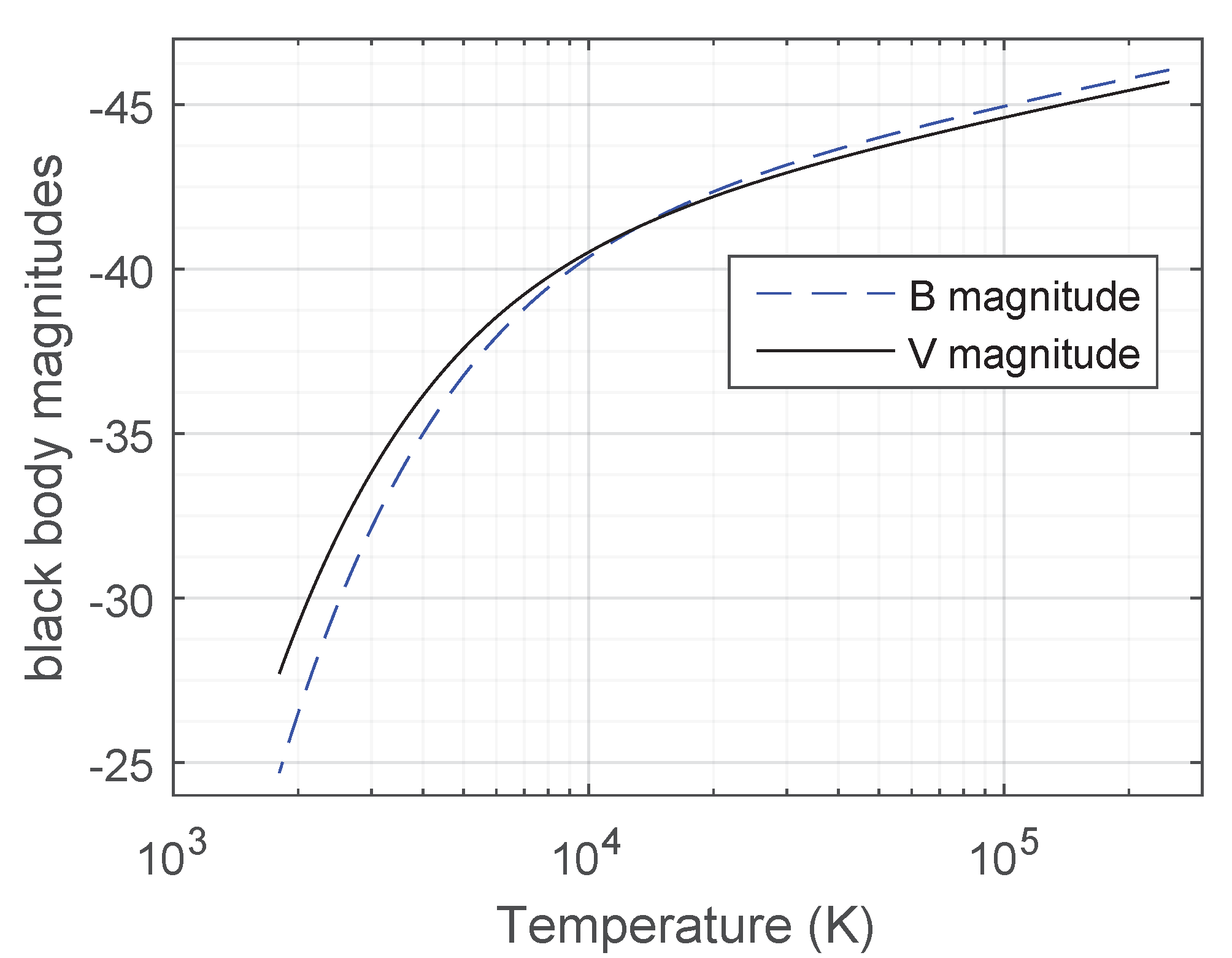
Figure 4 shows the apparent magnitudes of black bodies versus temperature in the Johnson’s
B and
V bands for an observer located at their surface. In this plot, brighter sources (more negative magnitudes) are at the top. Note that the magnitude scale used in astronomy is reversed, with smaller magnitudes meaning brighter sources. The magnitudes are said to be apparent because they depend on the observer location, contrasting to stellar absolute magnitudes which are magnitudes of a star as seen from a standardized distance [
24].
The difference between the
B and
V magnitudes of a celestial body is its
color index.
Figure 5 presents the relation between the
color index and temperature for black-bodies. The plot to the right relates the
color index with the multiplicative inverse of its temperature. Note that this curve is much more linear than the direct relation between temperature and
color index. Therefore, to get equivalent black-body temperatures for stars in the catalog, we use the 1/
T versus
curve for interpolation. To avoid temperature estimates with large errors from appearing, the
color indexes in the Hipparcos catalog are clamped into the interval
before conversion. These limits correspond to black-body temperatures of
K and 2000 K, respectively. Most stars have effective temperatures in that range.
It should be noted that for many stars, the temperature T used in our model will not be equal to the effective temperature of the star but will usually be smaller. This is caused by interstellar reddening—selective absorption by dust in the intervening light path from that star to the star sensor. Likewise, the constant C will also have a different value.
2.7. Number of Photons Detected Per Unit Wavelength
This section derives equations for the number of photons that will be detected, per wavelength, by the idealized star sensor used in this model, for a given exposure time
t and a given star sensor diameter
D, also assumed to be equal to its aperture diameter. The energy of each photon is related to its frequency
by the following equation:
Dividing the spectral irradiance at the location of the star sensor due to the black-body equivalent of star
i (Equations (
1) and (
2)) by the energy of a photon of wavelength
, the following expression for the spectral photon flux density received by the star sensor from the equivalent of star
i is obtained:
This flux density has units of photons per unit of time per unit of area per unit of wavelength. Multiplying this by the star sensor’s cross section area
and by the integration time
t we obtain:
which is the number of photons from star
i black body equivalent being collected by the star sensor, per unit wavelength.
2.8. Diffraction and Photon Noise
Diffraction and optics blurring set the format of the point spread function (PSF) of stellar image. In an ideal star sensor, there is no optical blurring, except for that set by diffraction. Therefore, for the star sensor model adopted in this work, the PSF function will be the diffraction pattern given by a circular aperture of diameter
D contained in a plane perpendicular to the incoming direction of photons. This is the well known Airy pattern, consisting of a center disk with a series of concentric rings [
25].
If the description of Nature given by Classical Mechanics were correct, it would be possible, at least in theory, to measure the intensity of the electromagnetic fields at the detector plane of an ideal equivalent system composed by ideal lens and ideal detector with no error, from where the true, error free direction of the incoming light rays would be obtained. However, the fact that light is discretized in photons limits the amount of information that can be obtained, regardless of the system considered. Instead of precisely defining the intensity of the electromagnetic fields at each point in the detector (as thought by 19th century physicists), the PSF defines the probability density function that a photon coming from a point source at infinity will be detected in a particular location on the detector. Given that the number of photons detected is finite and these arrive at random positions following the PSF, the centroid estimate for each observed star will be noisy, even for an ideal system. The lower bound for the resulting uncertainty in centroiding can be obtained by many different methods [
26,
27,
28]. Section 4.1.1 in Reference [
26] provides a detailed explanation, targeted at telescopes and interferometers. In the next section we show how this derivation can be extended for polychromatic sources (black-bodies).
2.9. Lower Bound on Centroiding Error for Single Stars
Heisenberg’s uncertainty principle sets a fundamental limit for centroiding, and this limit assumes the following form for monochromatic light of wavelength
[
26,
27,
28]:
where:
= angular centroiding uncertainty along an axis x perpendicular to the direction of incoming photons, in radians;
is the root mean square extension of the star sensor aperture (entrance pupil) along the x axis, being the position in x of the aperture geometric center; and
N = number of photons detected.
For circular apertures of diameter
D,
. Substituting this into Equation (
13) the following expression for the reciprocal of the lower bound of variance of centroiding error (the Fisher information
F) over a circular aperture of diameter
D, for monochromatic sources of light, is obtained:
Since stars are incoherent sources of light, the detection of a given photon is not correlated with the detection of another photon from the same star. This means that the number of detected photons from a given star will follow a Poisson distribution with parameter
, being
the expected number of detected photons (we are using the Greek letter
instead of the more common
for the Poisson distribution parameter to avoid confusion with
used for wavelength). This parameter can be obtained by integrating Equation (
12). For large values of
, the Poisson distribution narrows down in comparison to the value of
. This means that when the expected number of detected photons is significantly large, the true value of the lower bound of centroiding accuracy will be very close to the value predicted by Equation (
14) if we substitute
N by
. Numerical tests have shown, assuming that the centroiding error for exactly
N detected photons follows a Gaussian distribution with a standard deviation given by Equation (
13), that the error between the actual centroiding error and the value estimated by Equation (
14) using
in place of
N will be smaller than
for
,
for
and
for
. It is true that the actual probability density function for centroiding error along one axis will not be exactly Gaussian, especially for a low number of detected photons, but a Gaussian distribution provides a good approximation even when only one photon is detected.
Another consequence of the fact that the detection of a given photon is not correlated with the detection of another photon from the same star is that the centroiding error of a centroid computed using photons in the wavelength interval is independent on the centroiding error using photons in the wavelength interval when these intervals do not overlap ( or ). Therefore, we can consider each wavelength interval individually and then merge the centroid estimates for each wavelength.
For the discrete case of having
n independent unbiased estimates of the same physical variable (e.g., the
x coordinate of a star centroid), each having a variance
, the best estimate for that variable is obtained by summing these estimates using the reciprocal of their variances as weights [
27,
29]. In that case, the variance of this optimal estimate will be given by:
where
= total variance in the estimate of a scalar physical variable obtained by merging
n independent measurements and
= variance of each individual measurement
i. Since the spectra of black bodies is continuous, the following adaptation of Equation (
15) is used to compute centroid estimates for black bodies:
The contribution from each wavelength to the knowledge of the centroid position can be obtained from Equation (
14) by replacing
N with
, where
is the derivative with wavelength of the number of photons from star
i entering the star sensor aperture within an integration time of
t, as given by Equation (
12) from
Section 2.7. Hence, for each star
i, the wavelength derivative of the maximum knowledge physically attainable of its centroid position (derivative of its centroiding Fisher information) is given by:
Here we have dropped the subscript
i to simplify notation. Plugging Equation (
12) into Equation (
17) yields:
Integrating this equation for
to
∞ gives
, the Fisher information for stellar centroid
i and its reciprocal
, the minimum variance for the centroid position error in
x direction, being
x an axis perpendicular to the incoming light rays:
where
is the Riemann zeta function evaluated at 5. Since the aperture is symmetrical, Equation (
19) gives the minimum centroiding variance for star
i (
) along any axis perpendicular to the direction of incoming light rays. From this equation, it can be noted that the lower bound of the standard deviation on centroiding error along any axis perpendicular to the true direction of the star is proportional to
and
, when the number of detected photons is sufficiently large. This means that the star sensor diameter has a much larger effect in the ultimate centroid accuracy and precision than the exposure time.
2.10. Estimating the Lower Bound of Attitude Error from Many Stars
This section follows the formulation given by Markley and Crassidis in Reference [
30], Section 5.5. This formulation is valid when measurement errors are small, uncorrelated and axially symmetric around the true direction of stars, conditions fulfilled by our model, except for ideal star sensors with microscopic dimensions.
According to Equations (5.113) and (5.114) in Reference [
30], the covariance matrix (
) of the rotation vector error (
) for an optimal attitude estimator is the inverse of the Fisher information matrix
:
with:
for the ideal star sensor model adopted in this work. In this equation,
is a
identity matrix and
is the true direction of star
i, represented by a unit vector expressed as a
column matrix.
is given in an inertial reference frame and
N is the number of identified stars used in attitude computation.
2.11. A Compact Metric for the Attitude Error
Even though the covariance matrix
provides detailed information about the attitude uncertainty, as it has six independent parameters it has the disadvantage of being hard to visualize. Therefore, to perform comparisons, we use a more compact metric derived from it:
The trace of the covariance matrix gives the variance of the overall attitude error, that is, the sum of the variances of the attitude error around the three defining axes of the reference frame. It is also equal to the square of the limiting value of the root mean square (rms) of the angle theta () of the Euler axis/angle parameterization of the attitude error when the number of attitude determinations tends to infinity.
When the star sensor diameter and exposure time are large enough so that most stars contributing to the Fisher information matrix
F have many detected photons, the lower bound of the expected rms value of theta (
) can be computed by Equations (
19)–(
22). These equations can also be rearranged in the following manner, which makes more explicit the dependence of
with
D and
t:
with
G is a constant that depends only on stellar distribution around the star sensor, stellar brightness and on attenuation of stellar light by the intervening medium.