1. Introduction
As estimated, lung cancer has been responsible for close to 1 in 5 deaths in 2018, which remains the leading cause of cancer death [
1]. According to the latest TNM 8 edition, the five-year average survival rate of stage IVA patients is 10%, and that of stage IVB patients is as low as 0% [
2]. Despite the high mortality rate, early diagnosis can increase the chance of efficient treatment [
3] and survival rate for lung cancer patients [
4]. Radiological detection, such as computed tomography or positron-emission tomography, has enabled the lungs to be imaged for diagnosis of cancer [
5]. However, these conventional detection methods are expensive and occasionally miss tumors (low sensitivity), and therefore cannot be used as widespread screening tools [
6]. Moreover, radiation from medical imaging may cause adverse health effect on the human body [
7]. Therefore, it is crucial to develop an effective diagnosis method for lung cancer, which is also feasible for wide screening with high sensitivity, especially for high risk patients [
8].
Human volatilome analysis is a new and promising area in disease detection [
9]. As a non-invasive tool for lung cancer detection [
10,
11], breath analysis becomes a fast-growing research field [
12,
13]. More than 3000 volatile organic compounds (VOCs) are found in human exhaled breath, which are directly or indirectly related to internal biochemical processes in the human body [
14]. Breath print, interpreted as VOCs inside exhaled breath [
15], can be analyzed by different instruments such as gas chromatography in combination with mass spectrometry (GC-MS), proton-transfer-reaction mass spectrometry, ion mobility spectrometry, and electronic nose (e-nose) [
16]. E-noses are sensor arrays that consist of non-selective chemical sensors and each sensor is sensitive to a large number of VOCs with different sensitivity [
17]. E-noses have been widely used in food analysis [
18], environment control [
19], and disease diagnosis [
20]. As a promising non-invasive detection device, e-noses can identify different diseases such as lung cancer [
21], prostate cancer [
22], urinary tract infections [
23], urinary pathogens [
24], and gut bacterial populations [
25]. Different from those expensive, time-consuming and complicated analysis methods by compounds identification, e-nose is popular as a simple, inexpensive, and portable sensing technology in lung cancer detection, but it relies heavily on computer analysis [
26].
Although new computer-assisted diagnosis (CAD) methods emerge continuously and rapidly, effective algorithms of analyzing e-nose data for lung cancer remain far from perfection. Since e-nose cannot directly distinguish between specific VOCs [
26], in addition to effective sample acquisition, another key procedure is the follow-up signal processing by using computer methods. In e-nose detection, feature extraction and classification are two basic and essential steps. Feature extraction methods are applied for analyzing high-dimensional signal data, which is the prerequisite for subsequent detection. Classification models aim to study the difference of the sensor features under different physiological conditions to achieve final diagnosis. There are many pattern recognition frameworks in diagnosing diseases by e-nose, as shown in
Table 1. It can be concluded that data processing is a pivotal step to develop effective e-nose diagnosis system, which requires further improvement.
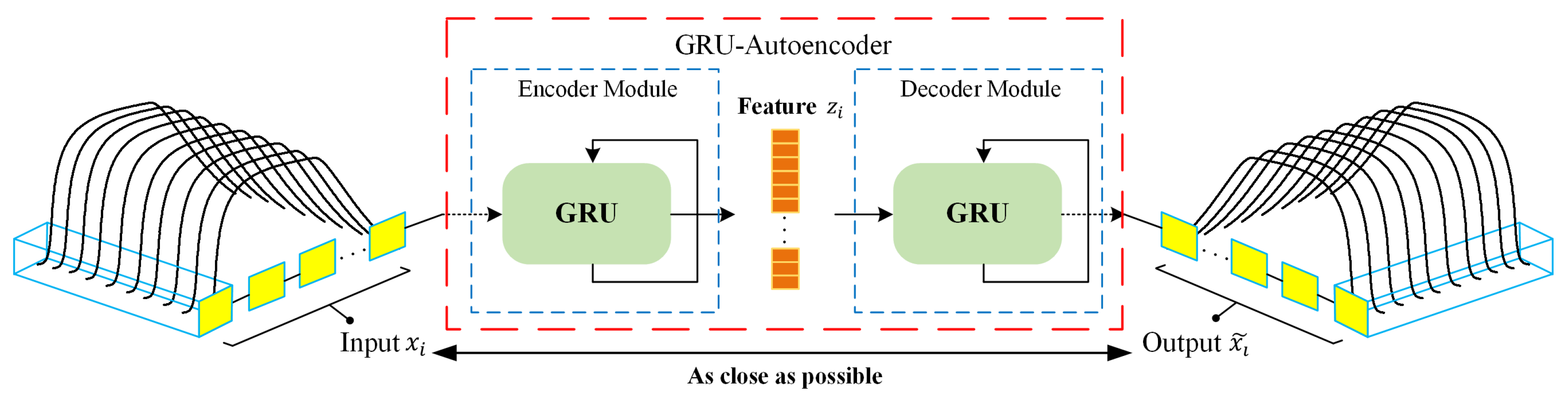
As an unsupervised learning method, autoencoder demonstrated strength in extracting relevant information from high-dimensional signal data [
35]. Meanwhile, gated recurrent unit (GRU) [
36] has been shown to be one of the state-of-the-art architectures in extracting temporal features. Compared with long short-term memory (LSTM) [
37], GRU has no cell state and directly employs hidden state for the transmission of signal information, thus possessing rapid training time. Thus far, deep learning algorithms have only been sparsely applied for feature extraction on e-nose data. Gated recurrent unit based autoencoder (GRU-AE) integrates GRU with the autoencoder, which leverages GRU cells to discover the dependency and temporality among multi-dimensional time series signal [
38]. By introducing GRU-AE into the field of e-nose analysis for lung cancer detection, the effort to manually engineer complex features is minimized, which tremendously simplifies data processing procedures for e-noses.
As for classification models, ensemble learning has been a popular and desirable learning paradigm for the analysis of e-nose data [
39]. The basic idea of ensemble learning is to build multiple component learners whose predictions are aggregated with the aim of outperforming the constituent members [
40]. Typically, ensemble learning algorithms consist of two stages: the production of diverse base learners and their combination [
41]. High precision and diversity are two key requirements for individual learners to guarantee the performance of the final ensemble [
42]. However, combining all the individual learners requires massive storage and computing resources. Even worse, the larger size of the ensemble model cannot constantly guarantee the better performance [
43]. For these reasons, ensemble pruning has arisen as an intermediate stage prior to combination, which is also termed as ensemble thinning, selective ensemble, or ensemble selection [
41]. Ensemble pruning searches a good subset of base learners to form the sub-ensemble that can reduce the ensemble size and resource consumption while maintaining or even enhancing the performance of the complete ensemble. However, the complexity of finding the best sub-ensemble is an NP-complete problem [
44], and therefore the optimal solution by global search is infeasible for large or even medium ensemble size [
45]. Alternatively, it is more appropriate to use approximation techniques that guarantee the near-optimal sub-ensembles.
Many ensemble pruning strategies have been proposed to obtain the optimal or near-optimal sub-ensembles, which can be mainly categorized into ordering-based techniques [
46,
47], clustering-based techniques [
48], and optimization-based techniques [
43,
49]. Ordering-based techniques attempt to rank individual classifiers based on the evaluation measures, and only the first few classifiers are selected in the pruned ensemble. Since the ranking mechanism tends to consume less time and storage resources, ordering-based ensemble pruning is the simplest and fastest one among all the ensemble pruning techniques, which is widely applied as CAD models with high accuracy [
50].
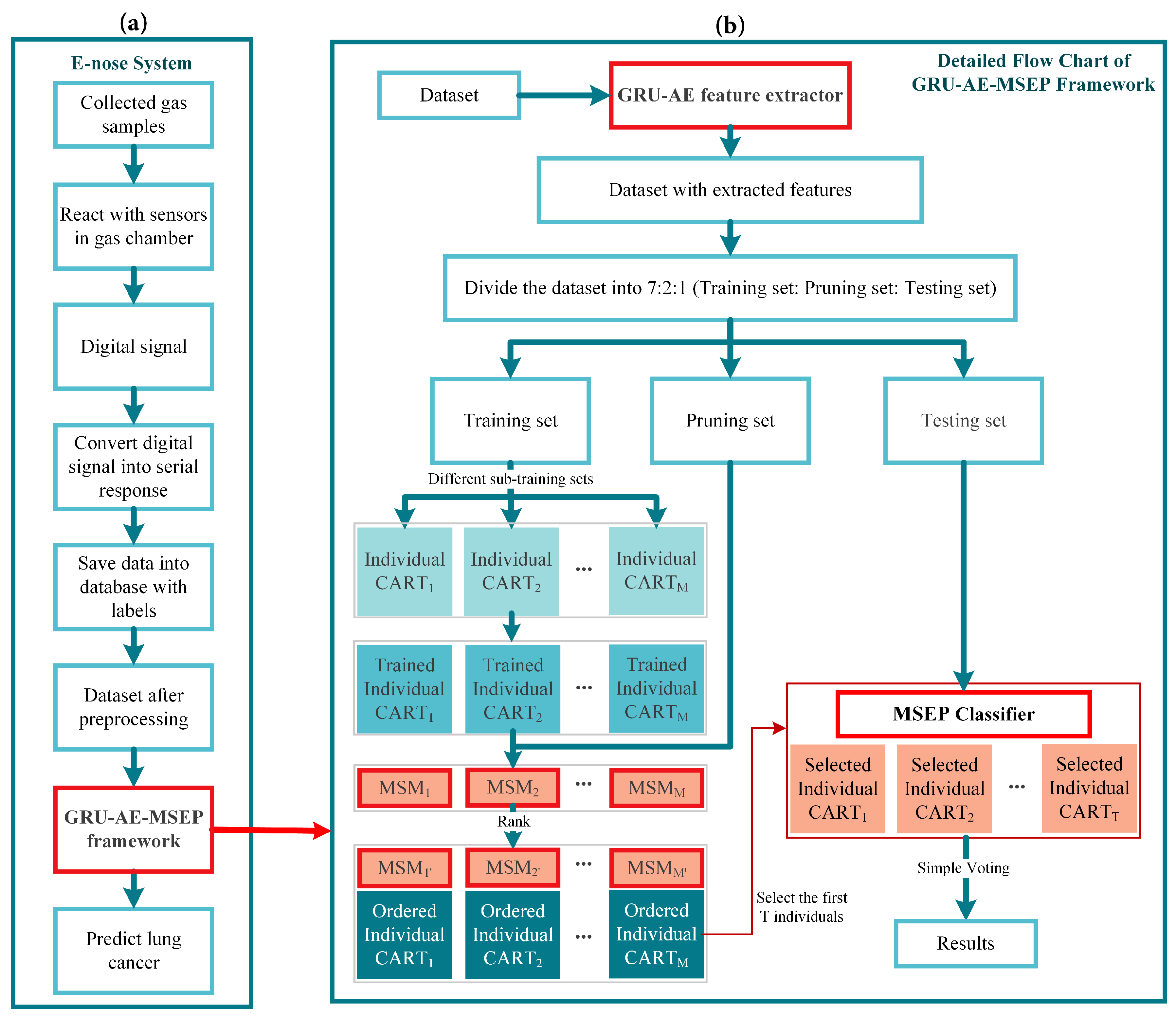
Therefore, in this paper, a novel gated recurrent unit based autoencoder combined with margin and sensitivity based ordering ensemble pruning (GRU-AE-MSEP) framework is proposed. This framework consists of three major steps. (1) The GRU-AE is adopted to extract principal features from high-dimensional and complex signal data. (2) The compressed features are used to train classification and regression trees (CARTs). (3) MSEP is employed to order and select well-trained CARTs to form final sub-ensemble for lung cancer classification. Correspondingly, the main contributions of this study are listed as follows:
For the first time in the field of lung cancer screening, GRU-AE is introduced into the feature extraction of e-nose signal data. As far as we know, this fills the gap of applying deep learning methods to automatically extract principal features from temporal and high-dimensional data in the e-nose system.
Based on the gained insight through theoretical analysis of three other ensemble pruning measures, we design and propose a heuristic margin and sensitivity based measure (MSM) for explicitly evaluating the contribution of each component classifier, which considers both instance importance and classification sensitivity. Previous studies only focused on improving the recognition accuracy of the model. To our knowledge, this is the first time that sensitivity is introduced into ensemble pruning to meet the needs of medical fields.
A novel MSEP is established for lung cancer detection. The proposed ensemble pruning model contributes to increasing the survival rate by decreasing missed diagnosis of lung cancer patients while guaranteeing overall performance.
Compared with other state-of-the-art frameworks, we demonstrate the feasibility and effectiveness of the proposed framework on collected breath samples by e-nose and three open source datasets. Therefore, the proposed intelligent framework provides a new insight into machine learning algorithms and lung cancer detection.
The remainder of this paper is organized as follows. In
Section 2, the acquisition process and pre-processing of the collected data are explained and summarized.
Section 3 proposes the feature extraction method of GRU-AE and classification models based on ensemble pruning techniques. In
Section 4, the performance of the proposed framework is tested and further validated by comparison with other algorithms. Discussion is shown in
Section 5. Finally,
Section 6 draws some conclusions of this study.
5. Discussion
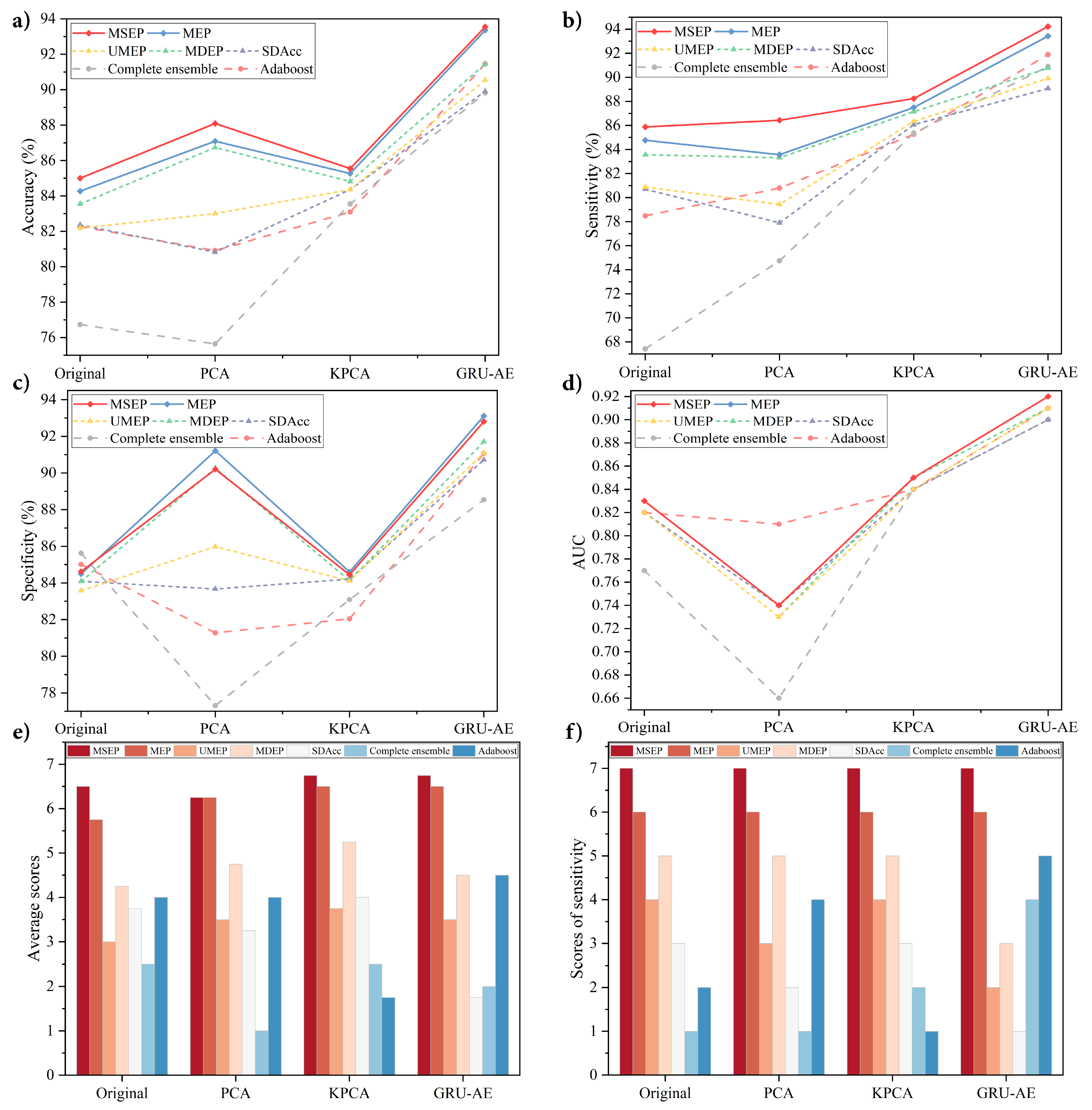
This paper presents a novel and reliable GRU-AE-MSEP framework for non-invasive lung cancer detection by the e-nose system. The proposed framework especially contributes to enhancing sensitivity and reducing missed diagnosis rate. The proposed framework was compared with the widely adopted feature extraction methods and existing ordering ensemble pruning techniques. Meanwhile, elaborate ablation experiments based on MSEP and MEP were carried out, which aimed to explore the role of the bonus term in improving sensitivity. To confirm the effectiveness of the proposed framework, all methods were examined under a set of standard metrics, i.e., Acc, Sen, Spe, and AUC. Moreover, all listed methods were experimented on the same dataset collected from patients with different kinds of lung cancer and diverse healthy controls. To further verify the portability of the proposed framework to other signal data, three open source datasets were tested based on the above metrics. In the experiments presented in
Section 4.3.1, GRU-AE-MSEP performed best by comparing different feature extractors and classifiers on the collected lung cancer dataset, and the sensitivity achieved by the proposed framework was high and stable. Additionally, the proposed framework had effective classification performance on distinguishing between clinical stages, lung diseases and smoking status. In the experiments presented in
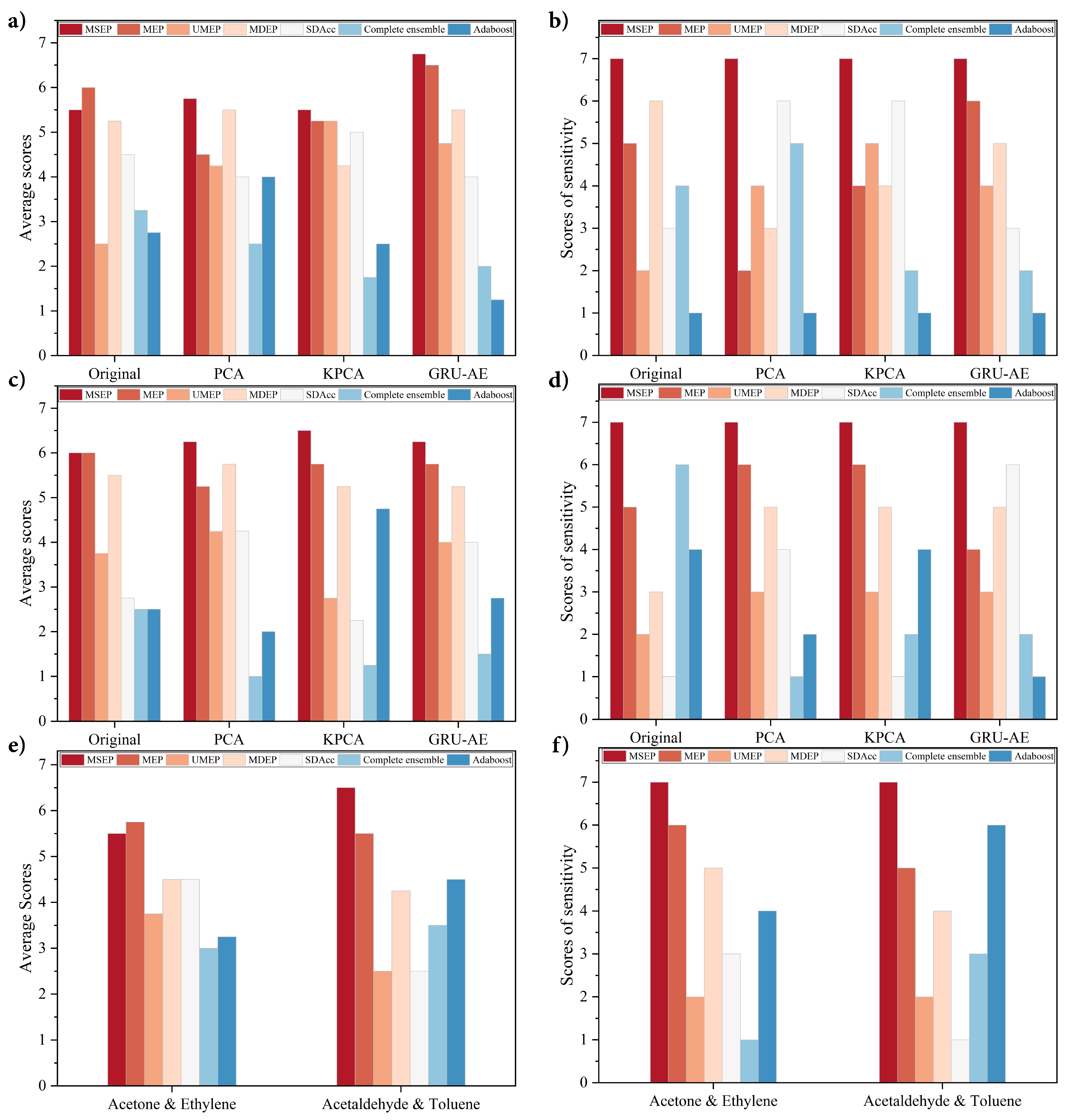
Section 4.4, GRU-AE-MSEP was further validated on three open source datasets to test its portability and it outperformed other methods as well.
Dimensionality reduction methods are essential in the analysis of sensor signals, and the extracted principal features perform as a prerequisite for subsequent classification. From the experimental results, metrics of classifiers varied unstably based on PCA and KPCA, while the application of GRU-AE generally improved the performance of classifiers. Since PCA only extracts linear features and cannot deal with nonlinear information, PCA-based frameworks were inferior to those based on original data in several situations. Compared with the original data, the features extracted by KPCA improved the performance of classifiers slightly but were far less effective than the features extracted by GRU-AE. Since conventional feature extraction methods are hand-crafted and require heavy computation as well as domain knowledge, it is hard to judge the impact of the feature extraction process on the final classification results. Moreover, the signal data from e-nose were rather complex, which consisted of linear, nonlinear, and redundant information. As a method based on deep learning training, GRU-AE can process high-dimensional nonlinear data by virtue of automatic feature extraction, especially to process temporal data, which was further verified in
Section 4.4.
Ensemble learning is popular in enhancing performance, while ensemble pruning models are developed as efficient improvement techniques by reducing redundant costs in the complete ensemble. Among 56 situations in four datasets, complete ensemble only achieved two highest values in total, i.e., the highest specificity in original lung cancer dataset and in Acetaldehyde and Toluene dataset. It indicated that there existed classifiers with little or negative contribution to the complete ensemble. UMEP, MDEP, and SDAcc are three existing ensemble pruning methods and have been proved to be effective in their original papers. Compared with the complete ensemble and adaboost, experimental results indicate that pruning models were better in the evaluation of overall performance and sensitivity. Therefore, it is reasonable to aggregate classifiers with better performance, and pruning techniques are deemed to be effective for lung cancer non-invasive detection as the results verified.
However, sensitivity and specificity formed a trade-off dilemma when the accuracy was stable and high enough. The aim of calculating average scores was to ensure that the overall performance was not sacrificed as the sensitivity improved. Among seven classification models, the proposed MSEP exhibited more robust performance, which was consistent with the theoretical analysis in
Section 3.2.3. By giving up hard samples, UMEP and MDEP were capable of increasing accuracy, but the development space was also limited by hard samples, thus leading to their mediocre performance. The vague and overlapped marking mechanism of SDAcc resulted in fluctuating and unstable ranks in both average scores and sensitivity scores. By adjusting the threshold term, i.e.,
, MSEP can determine what proportion of hard samples to be retained. Instead of abandoning all difficult samples in UMEP and MDEP, the proposed method achieved superb results by taking them into account. Since frameworks based on MSEP achieved the highest average scores and sensitivity scores in every group in lung cancer dataset, MSEP not only improved the sensitivity but also the three other metrics. Therefore, the proposed MSEP can achieve as high sensitivity as possible while ensuring excellent overall performance. In most situations, MEP ranked only second to MSEP in average scores but had unstable ranks in sensitivity in Diabetes and GSHAM datasets, which illustrated the capability of proposed margin-based method in improving classification performance and the effectiveness of bonus term in sensitivity enhancement.
To make the experiments more exhaustive, we investigated as many categories as possible in the experiments presented in
Section 4.3.2. For the detection of different clinical stages, stage II had the highest accuracy and sensitivity, which could suggest the valuable prospect of the proposed system for early lung cancer diagnosis. By identifying the COPD and lung cancer, the results were competitive and may provide a further application area. Never versus long-term smokers were distinguished from lung cancer with high accuracy and sensitivity. It may indicate that smoking is a high influence factor for VOC alteration in human breath.
When evaluating on three open source datasets, the performance of the proposed GRU-AE-MSEP framework achieved enormous success as well. MSEP ranked first in every group in terms of sensitivity, and the proposed GRU-AE-MSEP framework obtained the highest accuracy and sensitivity in every dataset, which proved the portability and robustness of the framework. Classification is one of the most popular topics in bioinformatics and disease detection. It is reasonable that one classifier cannot always achieve both highest sensitivity and specificity under certain accuracy, but sensitivity is what we valued and paid attention to. Our practical and transplantable framework demonstrated the ability to promote classification sensitivity in various scenarios.
In the literature, many studies have focused on the detection of lung cancer based on e-nose system, as illustrated in
Table 7. The feasibility and effectiveness of the machine learning classifiers were demonstrated on small datasets [
66,
67,
68]. With the development of deep learning methods, the neural network was used by van de Goor [
69] and Chang [
11]. By contrast, this study provides a new perspective for the non-destructive screening of lung cancer, aiming to design an algorithm to improve the detection sensitivity. In addition to the innovation of feature extraction and classification methods, compared with other studies, the proposed GRU-AE-MSEP framework based on a larger sample size demonstrated superior overall performance and higher sensitivity.
Although the proposed GRU-AE-MSEP framework performed optimally, there is still room for improvement. Primarily, the quantity of the dataset was still limited. To achieve expert-level diagnostic detection, the framework requires more sufficient and diverse data. Secondly, the study of clinical stages, lung diseases, and smoking status is worth delving into in the future. In future research, these limitations in automatic detection of lung cancer could be overcome by using multi-class classification training on gargantuan dataset collected from different types of machine.