Super-Resolution for Improving EEG Spatial Resolution using Deep Convolutional Neural Network—Feasibility Study
Abstract
1. Introduction
2. Materials and Methods
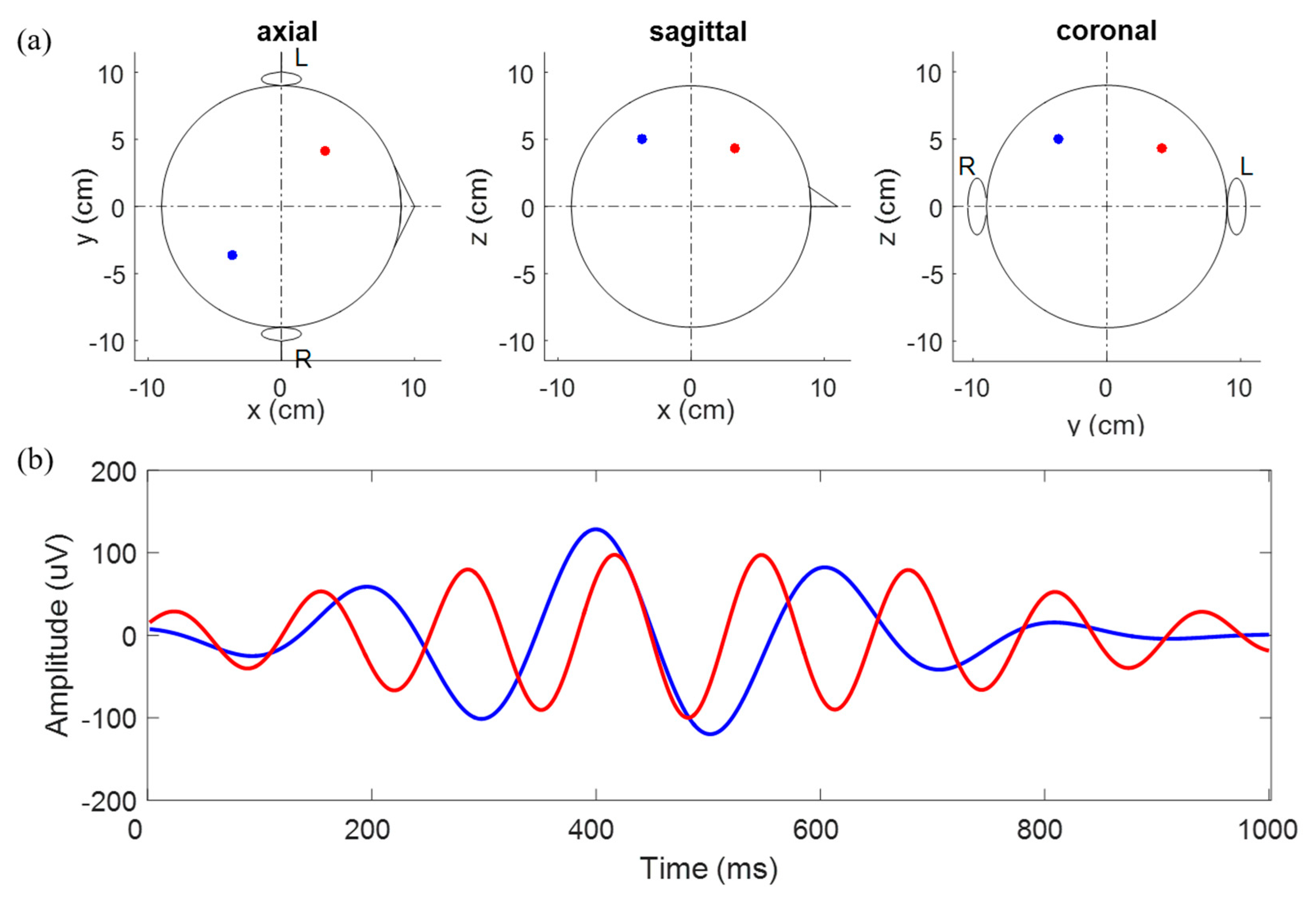
2.1. Simulated Data
2.2. Experimental Data
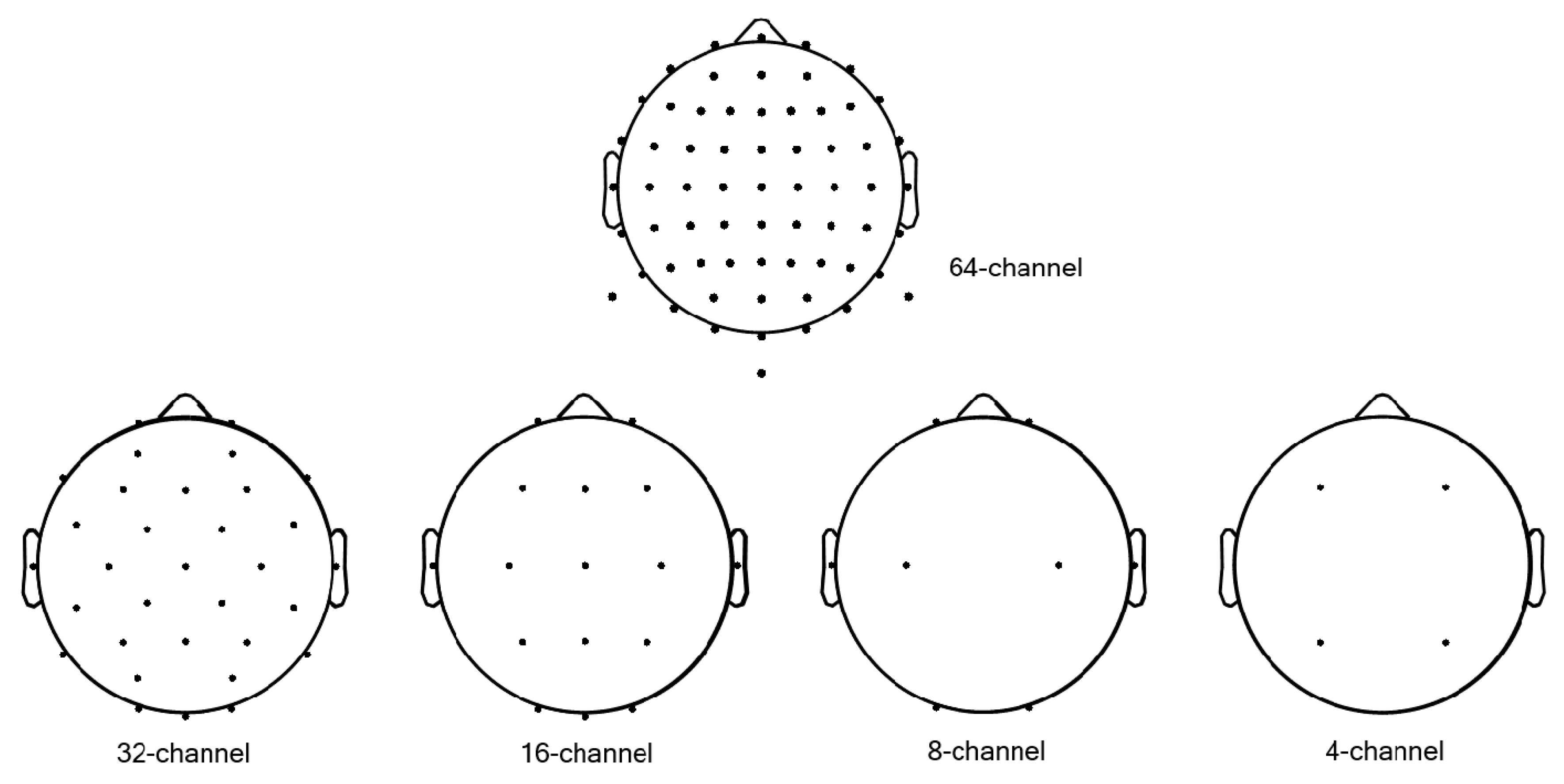
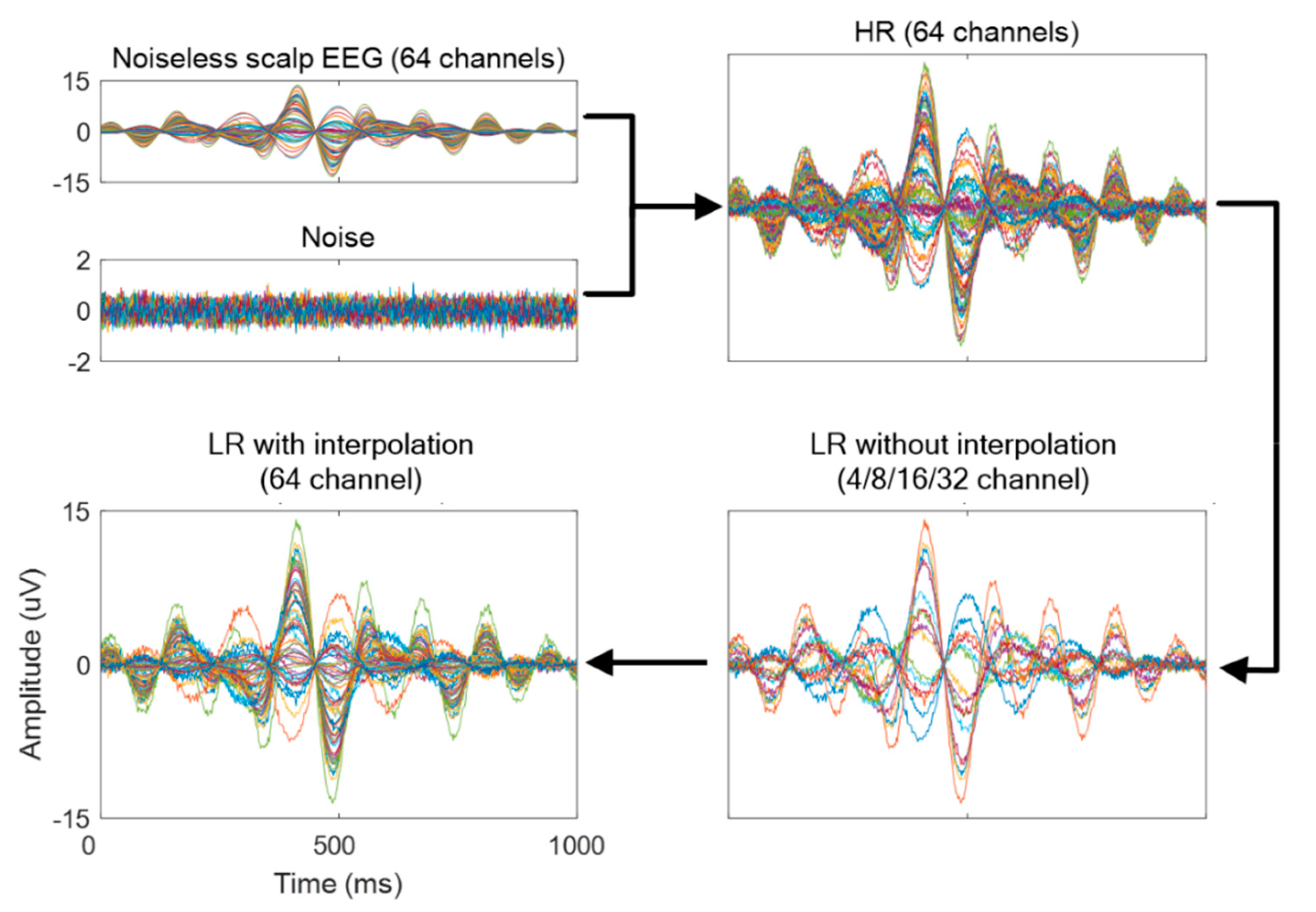
2.3. Generating Low Spatial Resolution Data
- Conventional interpolation approach (LR): Data for missing channels were estimated from known nearby channels by simple linear interpolation (Figure 3). We note that this simple transformation of data with fewer channels (4-, 8-, 16-, or 32-channel data) to interpolated LR data (64-channel data) is a fundamentally ill-posed problem; Dong et al., up-scaled their input LR images to the size desired using bicubic interpolation to achieve good beginning initialization [1].
2.4. Deep CNN for Super-Resolution
2.5. Evaluation
2.5.1. Simulated Data
- Sensor Level Metrics
- ▪
- Mean Squared Error (MSE):
- ▪
- Pearson Correlation Coefficient:
- Source Level (localization) MetricsThe evaluation metrics were calculated using correct source detection trials at the source level.
- ▪
- Amplitude Error:
- ▪
- Localization Error:
- ▪
- Focality of Localization:
2.5.2. Experimental Data
- Sensor Level Metrics
- ▪
- Amplitude Error:
- ▪
- Latency Error:
- ▪
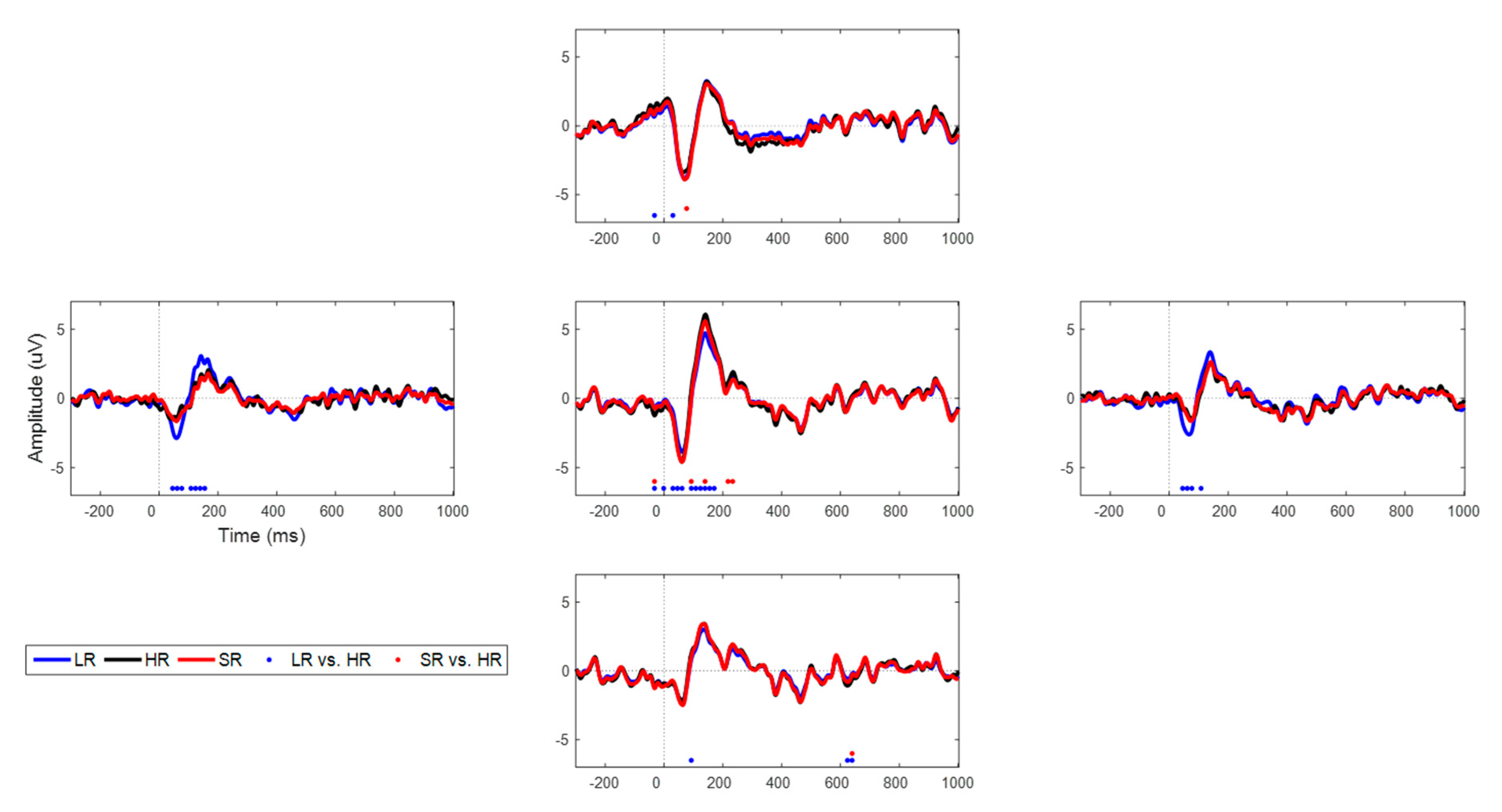
- Statistical test: We conducted a statistical analysis (at time point) between LR and HR, and SR and HR for the experimental data. Test data were down-sampled temporally by 8 for simplicity, after which a paired Student’s t-test was performed for each time sample. Statistical results at AFz, CPz, TP7, TP8, and POz channels were compared. The statistically different time points (uncorrected, p < 0.01) indicated that LR and SR data failed to follow the HR data.
- Source Level (localization) MetricsDetected sources were quite focal in several regions and were activated strongly or weakly depending on conditions, while small activation values were observed in other regions (largely, activation < 0.1). From this observation, we set 0.1 as a power threshold empirically because of its visibility in the AEP data.
- ▪
- Amplitude Error:
- ▪
- The number of error sources: When HR data detect the source at a specific voxel, but LR or SR data did not detect sources at the voxels, then the sources count as an error source. The opposite case also includes error sources.
3. Results
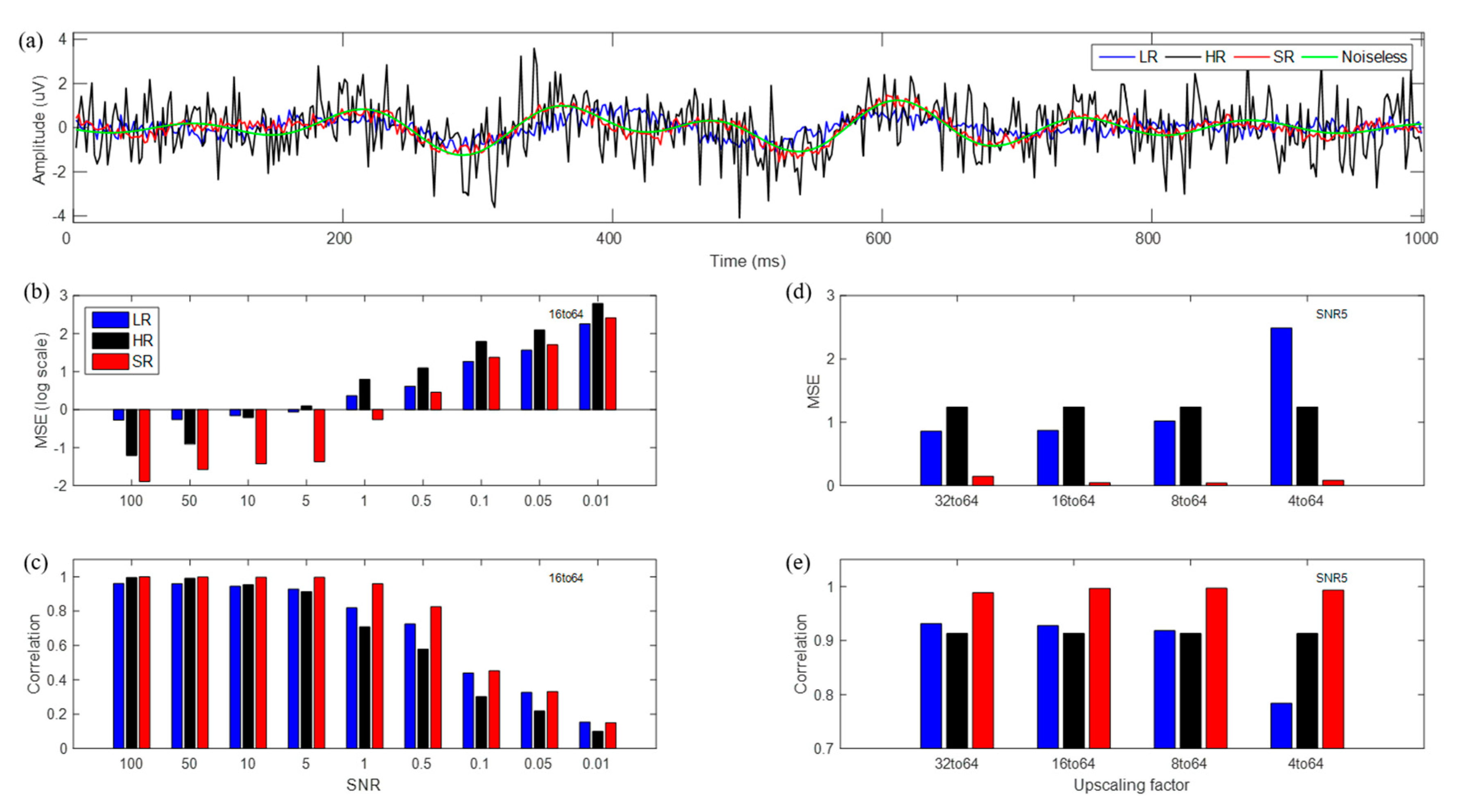
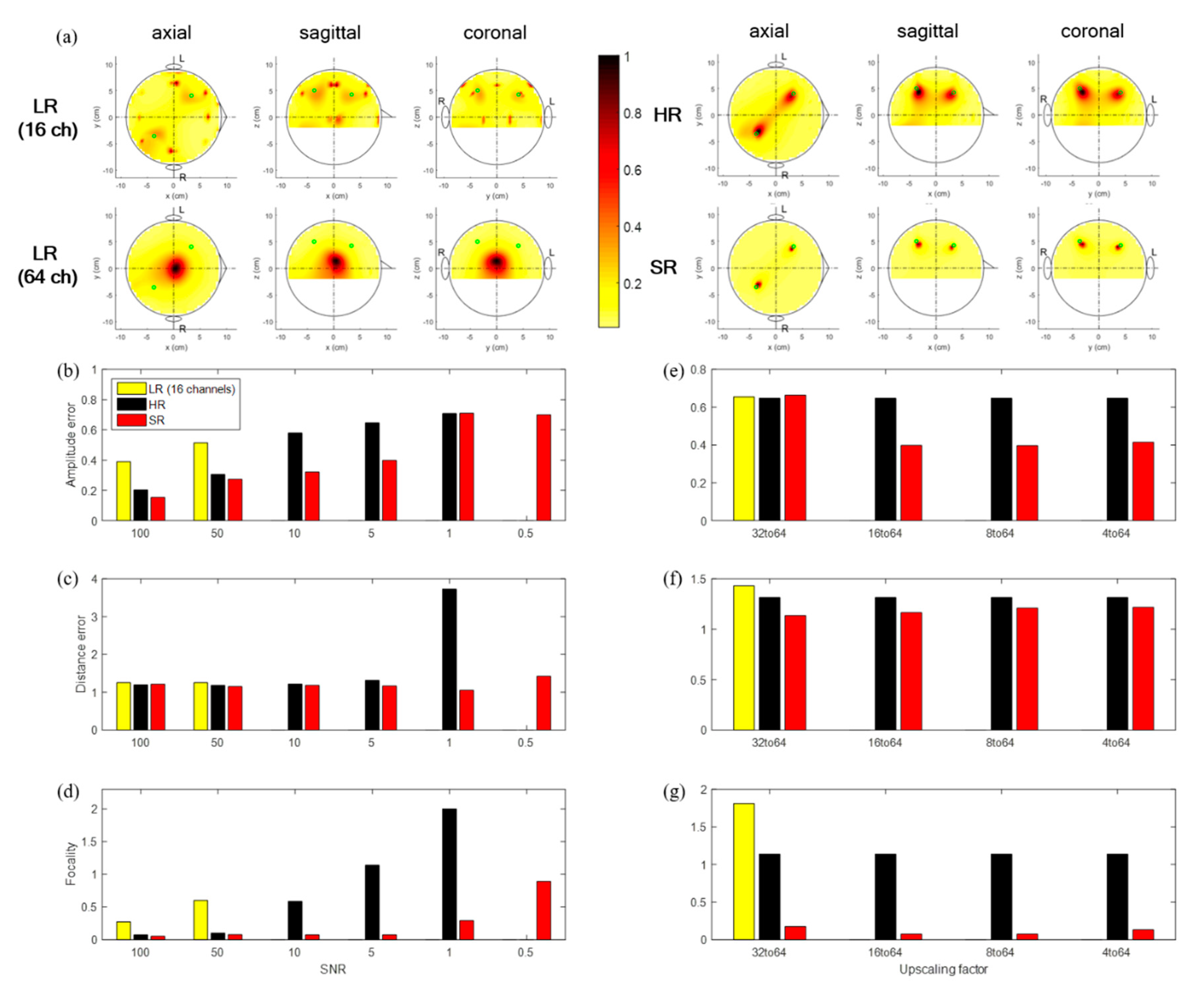
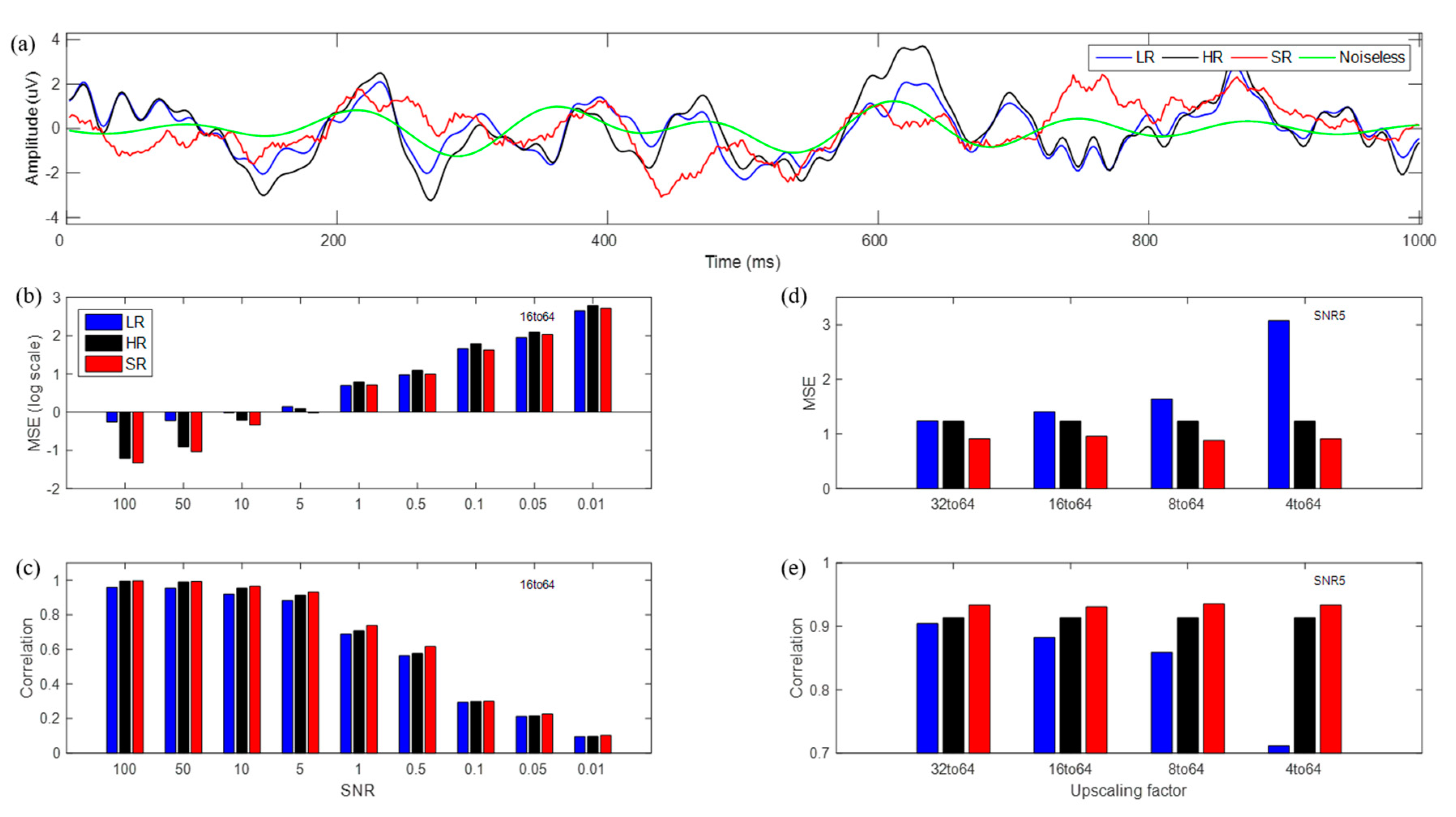
3.1. SR Results for Simulated Data (White Gaussian Noise)
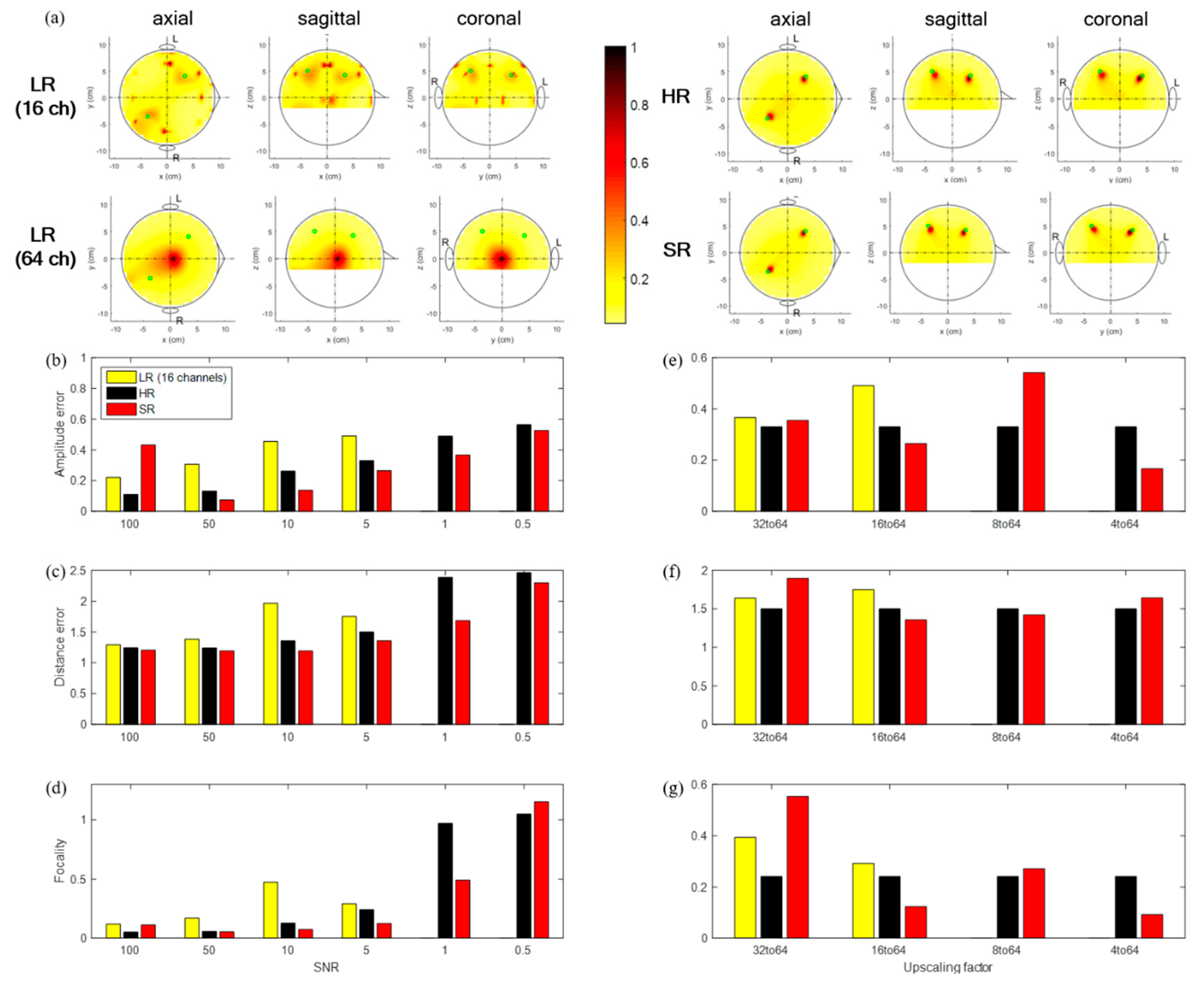
3.2. SR Results for Simulated Data (Real Brain Noise)
3.3. SR Results for Experimental AEP Data
4. Discussion
4.1. Interpretation of SR Approaches at Sensor and Source Levels
4.2. Validation of Simulated and Experimental Data
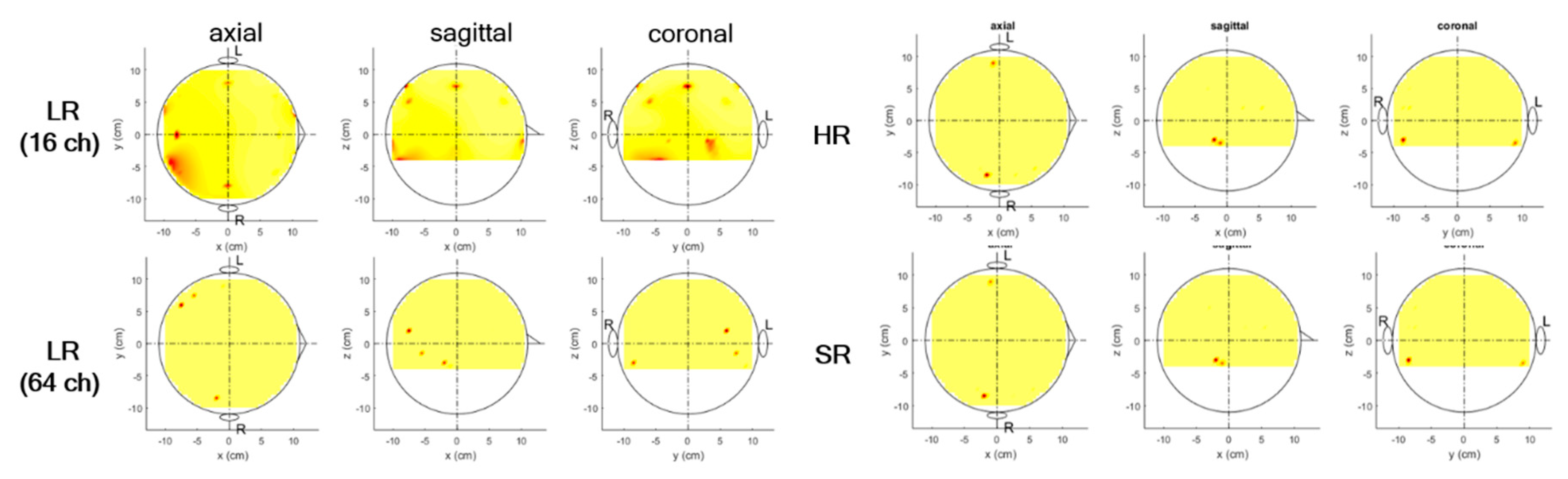
4.3. Source Localization Results for Experimental AEP Data
4.4. Enhancing EEG Spatial Resolution Methods
4.5. Activation Functions
4.6. Study Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dong, C.; Loy, C.C.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, M. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.K.; Lee, L.M. Deeply-recursive convolutional network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1637–1645. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Huszar, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar] [CrossRef]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual dense network for image super-resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2472–2481. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Weinberger, K.Q.; Maaten, L. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar] [CrossRef]
- Kuleshov, V.; Enam, S.Z.; Ermon, S. Audio super-resolution using neural nets. arXiv 2017, arXiv:1708.00853. [Google Scholar]
- Song, J.; Davey, C.; Poulsen, C.; Luu, P.; Turovets, S.; Anderson, E.; Li, K.; Tucker, D. EEG source localization: Sensor density and head surface coverage. J. Neurosci. Methods 2015, 256, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Lantza, G.; Peraltaa, R.G.; Spinellia, L.; Seeckc, M.; Michela, C.M. Epileptic source localization with high density EEG: How many electrodes are needed? Clin. Neurophysiol. 2003, 114, 63–69. [Google Scholar] [CrossRef]
- Srinivasan, R.; Tucker, D.M. Estimating the spatial Nyquist of the human EEG. Behav. Res. Methods Instrum. Comput. 1998, 31, 8–19. [Google Scholar] [CrossRef]
- Tucker, D.M. Spatial sampling of head electrical fields: The geodesic sensor net. Electroencephalogr. Clin. Neurophysiol. 1993, 87, 154–163. [Google Scholar] [CrossRef]
- Gwin, J.T.; Gramann, K.; Makeig, S.; Ferris, D.P. Removal of movement artifact from high-density EEG recorded during walking and running. J. Neurophysiol. 2010, 103, 3526–3534. [Google Scholar] [CrossRef]
- Hjorth, B. An on-line transformation of EEG scalp potentials into orthogonal source derivations. Electroencephalogr. Clin. Neurophysiol. 1975, 39, 526–530. [Google Scholar] [CrossRef]
- MacKay, D.M. On-line source-density computation with a minimum of electrodes. Electroencephalogr. Clin. Neurophysiol. 1983, 56, 696–708. [Google Scholar] [CrossRef]
- Babiloni, F.; Cincotti, F.; Carducci, F.; Rossini, P.M.; Babiloni, C. Spatial enhancement of EEG data by surface Laplacian estimation: The use of magnetic resonance imaging-based head models. Clin. Neurophysiol. 2001, 112, 724–727. [Google Scholar] [CrossRef]
- Perrin, F.; Pernier, J.; Bertrand, O.; Giard, M.H.; Echallier, J.F. Mapping of scalp potentials by surface spline interpolation. Electroencephalogr. Clin. Neurophysiol. 1987, 66, 75–81. [Google Scholar] [CrossRef]
- Nunez, P.L. Neocortical Dynamics and Human EEG Rhythms; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Srinivasan, R.; Nunez, P.L.; Tucker, D.M.; Silberstein, R.B.; Cadusch, P.J. Spatial sampling and filtering of EEG with spline Laplacians to estimate cortical potentials. Brain Topogr. 1996, 8, 355–366. [Google Scholar] [CrossRef] [PubMed]
- Ferree, T.C.; Srinivasan, R. Theory and Calculation of the Scalp Surface Laplacian; Electrical Geodesics, Inc.: Eugene, OR, USA, 2000. [Google Scholar]
- Nunez, P.L. Electric Fields of the Brain; Oxford University Press: New York, NY, USA, 1981. [Google Scholar]
- Gevins, A.; Brickett, P.; Costales, B.; Le, J.; Reutter, B. Beyond topographic mapping: Towards functional-anatomical imaging with 124-channel EEGs and 3-D MRIs. Brain Topogr. 1990, 3, 53–64. [Google Scholar] [CrossRef]
- Tenke, C.E.; Kayser, J. Generator localization by current source density (CSD): Implications of volume conduction and field closure at intracranial and scalp resolutions. Clin. Neurophysiol. 2012, 123, 2328–2345. [Google Scholar] [CrossRef] [PubMed]
- Kayser, J.; Tenke, C.E. Principal components analysis of Laplacian waveforms as a generic method for identifying ERP generator patterns: I. Evaluation with auditory oddball tasks. Clin. Neurophysiol. 2006, 117, 348–368. [Google Scholar] [CrossRef]
- Nunez, P.L.; Silberstein, R.B.; Cadusch, P.J.; Wijesinghe, R. Comparison of high resolution EEG methods having different theoretical bases. Brain Topogr. 1993, 5, 361–364. [Google Scholar] [CrossRef]
- Burle, B.; Spieser, L.; Roger, C.; Casini, L.; Hasbroucq, T.; Vidal, F. Spatial and temporal resolutions of EEG: Is it really black and white? A scalp current density view. Int. J. Psychophysiol. 2015, 97, 210–220. [Google Scholar] [CrossRef]
- Aviyente, S. Compressed Sensing Framework for EEG Compression. In Proceedings of the IEEE/SP 14th Workshop on Statistical Signal Processing, Madison, WI, USA, 26–29 August 2007; pp. 181–184. [Google Scholar] [CrossRef]
- Zhang, Z.; Jung, T.-P.; Makeig, S.; Rao, B.D. Compressed sensing of EEG for wireless telemonitoring with low energy consumption and inexpensive hardware. IEEE Trans. Biomed. Eng. 2013, 64, 221–224. [Google Scholar] [CrossRef]
- Morabito, F.C.; Labate, D.; Morabito, G.; Palamara, I.; Szu, H. Monitoring and diagnosis of Alzheimer’s disease using noninvasive compressive sensing EEG. Proc. SPIE 2013, 8750, Y1–Y10. [Google Scholar] [CrossRef]
- Morabito, F.C.; Labate, D.; Bramanti, A.; Foresta, F.L.; Morabito, G.; Palamara, I.; Szu, H. Enhanced compressibility of EEG signal in Alzheimer’s disease patients. IEEE Sens. J. 2013, 13, 3255–3262. [Google Scholar] [CrossRef]
- Corley, I.A.; Huang, Y. Deep EEG super-resolution: Upsampling EEG spatial resolution with generative adversarial networks. In Proceedings of the IEEE EMBS International Conference on Biomedical & Health Information, Las Vegas, NV, USA, 4–7 March 2018; pp. 100–103. [Google Scholar] [CrossRef]
- Han, S.; Kwon, M.; Lee, S.; Jun, S.C. Feasibility study of EEG super-resolution using deep convolutional networks. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Miyazaki, Japan, 7–10 October 2018. [Google Scholar] [CrossRef]
- Zhang, Z. A fast method to comput surface potentials generated by dipoles within multilayer anisotropic spheres. Phys. Med. Biol. 1995, 40, 335–349. [Google Scholar] [CrossRef] [PubMed]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked denoising autoencoders: Learning useful representaitons in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- Odena, A.; Dumoulin, V.; Olah, C. Deconvolution and checkerboard artifacts. Distill 2016, 10, 23915. [Google Scholar] [CrossRef]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A compact convolutional neural network for EEG-based brain-computer interface. J. Neural Eng. 2018, 15, 1–17. [Google Scholar] [CrossRef]
- Schirrmeister, R.T.; Springenberg, J.T.; Fieder, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef]
- Cecotti, H.; Graser, A. Convolutional neural networks for P300 detection with application to brain–computer interfaces. IEEE Trans. Pattern Anal. 2011, 33, 433–445. [Google Scholar] [CrossRef]
- Gupta, K.; Majumdar, A. Sparsely connected autoencder. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; pp. 1940–1947. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. In Proceedings of the IEEE Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar] [CrossRef]
- Kingma, P.; Ba, J. ADAM: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Sekihara, K.; Nagarajan, S.S. Adaptive Spatial Filters for Electromagnetic Brain Imaging; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Stropahl, M.; Bauer, A.K.R.; Debener, S.; Bleichner, M.G. Source-modeling auditory processes of EEG data using EEGLAB and Brainstorm. Front. Neurosci. 2018, 12. [Google Scholar] [CrossRef]
- Goodin, D.S.; Squires, K.C.; Henderson, B.H.; Starr, A. Age-related variations in evoked potentials to auditory stimuli in normal human subjects. Electroencephalogr. Clin. Neurophysiol. 1978, 44, 447–458. [Google Scholar] [CrossRef]
- Cirelli, L.K.; Bosnyak, D.; Manning, F.C.; Spinelli, C.; Marie, C.; Fujioka, T.; Ghahremani, A.; Trainor, L.J. Beat-induced fluctuations in auditory cortical beta-band activity: Using EEG to measure age-related changes. Front. Psychol. 2014, 5, 724. [Google Scholar] [CrossRef]
- Wen, Z.; Xu, R.; Du, J. A novel convolutional neural networks for emotion recognition based on EEG signal. In Proceedings of the International Conference on Security, Pattern Analysis, and Cybernetics, Shenzhen, China, 15–17 December 2017; pp. 672–677. [Google Scholar]
- Looney, D.; Park, C.; Kidmose, P.; Rank, M.L.; Ungstrup, M.; Rosenkranz, K.; Mandic, D.P. An in-the-ear platform for recording electroencephalogram. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 6882–6885. [Google Scholar] [CrossRef]
- Mikkelsen, K.B.; Kappel, S.L.; Mandic, D.P.; Kidmose, P. EEG recorded from the Ear: Characterizing the Ear-EEG method. Front. Neurosci. 2015, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Mikkelsen, K.B.; Villadsen, D.B.; Otto, M.; Kidmose, P. Automatic sleep staging using ear-EEG. Biomed. Eng. Online 2017, 16, 111. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, T.; Alqurashi, Y.D.; Morrell, M.J.; Mandic, D.P. Automatic detection of drowsiness using in-ear EEG. In Proceedings of the International Joint Conference on Neural Networks, Rio de Janeiro, Brazil, 8–13 July 2018; pp. 5569–5574. [Google Scholar] [CrossRef]
- Sałabun, W. Processing and spectral analysis of the raw EEG signal from the MindWave. Prz. Elektrotechniczny 2014, 90, 169–174. [Google Scholar] [CrossRef]
- Krigolson, O.E.; Williams, C.C.; Norton, A.; Hassall, C.D.; Colino, F.L. Choosing MUSE: Validation of a low-cost, portable EEG system for ERP research. Front. Neurosci. 2017, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]



| N1 Component | CPz | AFz | TP7 | TP8 | POz | ||||||
| Amplitude (uV) | Latency (ms) | Amplitude (uV) | Latency (ms) | Amplitude (uV) | Latency (ms) | Amplitude (uV) | Latency (ms) | Amplitude (uV) | Latency (ms) | ||
| 32to64 | LR | 4.4 ± 0.3 | 67.0 ± 2.6 | 4.3 ± 0.6 | 70.8 ± 2.3 | 2.9 ± 0.6 | 68.8 ± 3.0 | 2.9 ± 0.3 | 72.0 ± 4.0 | 2.6 ± 0.3 | 68.2 ± 3.9 |
| HR | 5.0 ± 0.3 | 65.8 ± 3.5 | 4.2 ± 0.7 | 68.8 ± 4.6 | 1.6 ± 0.4 | 61.8 ± 21.7 | 1.9 ± 0.4 | 72.8 ± 3.0 | 2.4 ± 0.3 | 68.8 ± 3.3 | |
| SR | 5.0 ± 0.4 | 66.6 ± 3.0 | 4.5 ± 0.6 | 71.6 ± 1.7 | 1.8 ± 0.5 | 68.2 ± 7.6 | 1.9 ± 0.3 | 71.6 ± 3.6 | 2.8 ± 0.3 | 67.4 ± 3.0 | |
| 16to64 | LR | 4.5 ± 0.4 | 68.0 ± 2.8 | 4.4 ± 0.6 | 70.4 ± 3.0 | 3.3 ± 0.4 | 68.2 ± 4.3 | 3.1 ± 0.4 | 69.6 ± 3.3 | 2.5 ± 0.2 | 67.8 ± 3.5 |
| HR | 5.0 ± 0.3 | 65.8 ± 3.5 | 4.2 ± 0.7 | 68.8 ± 4.6 | 1.6 ± 0.4 | 61.8 ± 21.7 | 1.9 ± 0.4 | 72.8 ± 3.0 | 2.4 ± 0.3 | 68.8 ± 3.3 | |
| SR | 5.0 ± 0.3 | 67.0 ± 3.3 | 4.4 ± 0.5 | 71.6 ± 2.2 | 1.8 ± 0.4 | 69.8 ± 5.1 | 2.0 ± 0.3 | 73.2 ± 3.0 | 2.7 ± 0.4 | 68.0 ± 2.4 | |
| 8to64 | LR | 5.2 ± 0.7 | 68.4 ± 2.2 | 3.5 ± 0.5 | 71.6 ± 3.6 | 3.2 ± 0.4 | 68.2 ± 4.3 | 3.0 ± 0.4 | 70.8 ± 3.0 | 1.5 ± 0.3 | 67.4 ± 4.9 |
| HR | 5.0 ± 0.3 | 65.8 ± 3.5 | 4.2 ± 0.7 | 68.8 ± 4.6 | 1.6 ± 0.4 | 61.8 ± 21.7 | 1.9 ± 0.4 | 72.8 ± 3.0 | 2.4 ± 0.3 | 68.8 ± 3.3 | |
| SR | 5.5 ± 0.7 | 68.2 ± 4.3 | 4.6 ± 0.6 | 73.2 ± 3.0 | 2.0 ± 0.4 | 68.2 ± 6.6 | 2.1 ± 0.4 | 73.2 ± 4.1 | 3.1 ± 0.2 | 68.2 ± 3.3 | |
| 4to64 | LR | 2.2 ± 0.3 | 68.6 ± 5.0 | 2.9 ± 0.4 | 73.6 ± 4.3 | 2.1 ± 0.2 | 68.2 ± 6.5 | 2.0 ± 0.3 | 68.4 ± 4.1 | 2.2 ± 0.3 | 68.6 ± 5.0 |
| HR | 5.0 ± 0.3 | 65.8 ± 3.5 | 4.2 ± 0.7 | 68.8 ± 4.6 | 1.6 ± 0.4 | 61.8 ± 21.7 | 1.9 ± 0.4 | 72.8 ± 3.0 | 2.4 ± 0.3 | 68.8 ± 3.3 | |
| SR | 4.0 ± 0.4 | 70.8 ± 2.7 | 4.2 ± 0.5 | 72.0 ± 1.4 | 1.8 ± 0.4 | 60.2 ± 10.6 | 2.3 ± 0.2 | 73.6 ± 5.9 | 2.8 ± 0.3 | 69.6 ± 3.3 | |
| P2 Component | CPz | AFz | TP7 | TP8 | POz | ||||||
| Amplitude (uV) | Latency (ms) | Amplitude (uV) | Latency (ms) | Amplitude (uV) | Latency (ms) | Amplitude (uV) | Latency (ms) | Amplitude (uV) | Latency (ms) | ||
| 32to64 | LR | 5.0 ± 0.5 | 139.4 ± 4.8 | 2.9 ± 0.6 | 150.4 ± 8.8 | 2.6 ± 0.3 | 147.6 ± 10.9 | 2.6 ± 0.4 | 146.4 ± 12.1 | 3.3 ± 0.5 | 137.4 ± 3.8 |
| HR | 6.1 ± 0.6 | 139.4 ± 4.8 | 2.9 ± 0.6 | 150.8 ± 8.7 | 2.0 ± 0.3 | 150.6 ± 11.2 | 2.3 ± 0.3 | 149.0 ± 12.9 | 3.5 ± 0.6 | 133.8 ± 5.4 | |
| SR | 5.5 ± 0.5 | 138.6 ± 5.5 | 2.9 ± 0.7 | 150.6 ± 8.7 | 1.7 ± 0.2 | 151.8 ± 12.0 | 2.4 ± 0.3 | 147.2 ± 10.3 | 3.7 ± 0.6 | 133.0 ± 6.3 | |
| 16to64 | LR | 4.8 ± 0.5 | 140.2 ± 5.2 | 3.0 ± 0.6 | 149.6 ± 8.1 | 3.2 ± 0.4 | 143.0 ± 3.5 | 3.3 ± 0.4 | 137.4 ± 7.9 | 3.2 ± 0.5 | 137.8 ± 4.4 |
| HR | 6.1 ± 0.6 | 139.4 ± 4.8 | 2.9 ± 0.6 | 150.8 ± 8.7 | 2.0 ± 0.3 | 150.6 ± 11.2 | 2.3 ± 0.3 | 149.0 ± 12.9 | 3.5 ± 0.6 | 133.8 ± 5.4 | |
| SR | 5.6 ± 0.6 | 139.4 ± 4.8 | 2.9 ± 0.7 | 151.2 ± 9.4 | 1.6 ± 0.2 | 152.2 ± 11.3 | 2.3 ± 0.3 | 144.2 ± 10.8 | 3.6 ± 0.5 | 132.6 ± 5.5 | |
| 8to64 | LR | 4.7 ± 0.5 | 141.4 ± 4.8 | 2.2 ± 0.5 | 153.8 ± 12.2 | 2.9 ± 0.4 | 143.2 ± 2.7 | 2.9 ± 0.4 | 137.8 ± 8.3 | 2.2 ± 0.7 | 131.0 ± 7.6 |
| HR | 6.1 ± 0.6 | 139.4 ± 4.8 | 2.9 ± 0.6 | 150.8 ± 8.7 | 2.0 ± 0.3 | 150.6 ± 11.2 | 2.3 ± 0.3 | 149.0 ± 12.9 | 3.5 ± 0.6 | 133.8 ± 5.4 | |
| SR | 5.0 ± 0.6 | 137.8 ± 6.1 | 3.2 ± 0.7 | 156.0 ± 12.0 | 1.8 ± 0.4 | 153.6 ± 11.4 | 2.3 ± 0.4 | 144.0 ± 13.9 | 3.4 ± 0.7 | 130.6 ± 6.2 | |
| 4to64 | LR | 2.0 ± 0.3 | 143.8 ± 5.1 | 2.1 ± 0.4 | 153.6 ± 11.4 | 2.0 ± 0.3 | 143.4 ± 4.2 | 2.0 ± 0.4 | 136.6 ± 7.5 | 2.0 ± 0.3 | 143.8 ± 5.1 |
| HR | 6.1 ± 0.6 | 139.4 ± 4.8 | 2.9 ± 0.6 | 150.8 ± 8.7 | 2.0 ± 0.3 | 150.6 ± 11.2 | 2.3 ± 0.3 | 149.0 ± 12.9 | 3.5 ± 0.6 | 133.8 ± 5.4 | |
| SR | 3.6 ± 0.8 | 137.4 ± 4.8 | 2.8 ± 0.6 | 149.0 ± 6.2 | 1.8 ± 0.3 | 150.2 ± 9.9 | 1.8 ± 0.3 | 145.4 ± 6.3 | 3.0 ± 0.7 | 132.6 ± 5.2 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, M.; Han, S.; Kim, K.; Jun, S.C. Super-Resolution for Improving EEG Spatial Resolution using Deep Convolutional Neural Network—Feasibility Study. Sensors 2019, 19, 5317. https://doi.org/10.3390/s19235317
Kwon M, Han S, Kim K, Jun SC. Super-Resolution for Improving EEG Spatial Resolution using Deep Convolutional Neural Network—Feasibility Study. Sensors. 2019; 19(23):5317. https://doi.org/10.3390/s19235317
Chicago/Turabian StyleKwon, Moonyoung, Sangjun Han, Kiwoong Kim, and Sung Chan Jun. 2019. "Super-Resolution for Improving EEG Spatial Resolution using Deep Convolutional Neural Network—Feasibility Study" Sensors 19, no. 23: 5317. https://doi.org/10.3390/s19235317
APA StyleKwon, M., Han, S., Kim, K., & Jun, S. C. (2019). Super-Resolution for Improving EEG Spatial Resolution using Deep Convolutional Neural Network—Feasibility Study. Sensors, 19(23), 5317. https://doi.org/10.3390/s19235317






