Thermal Shock Response of Yeast Cells Characterised by Dielectrophoresis Force Measurement
Abstract
1. Introduction
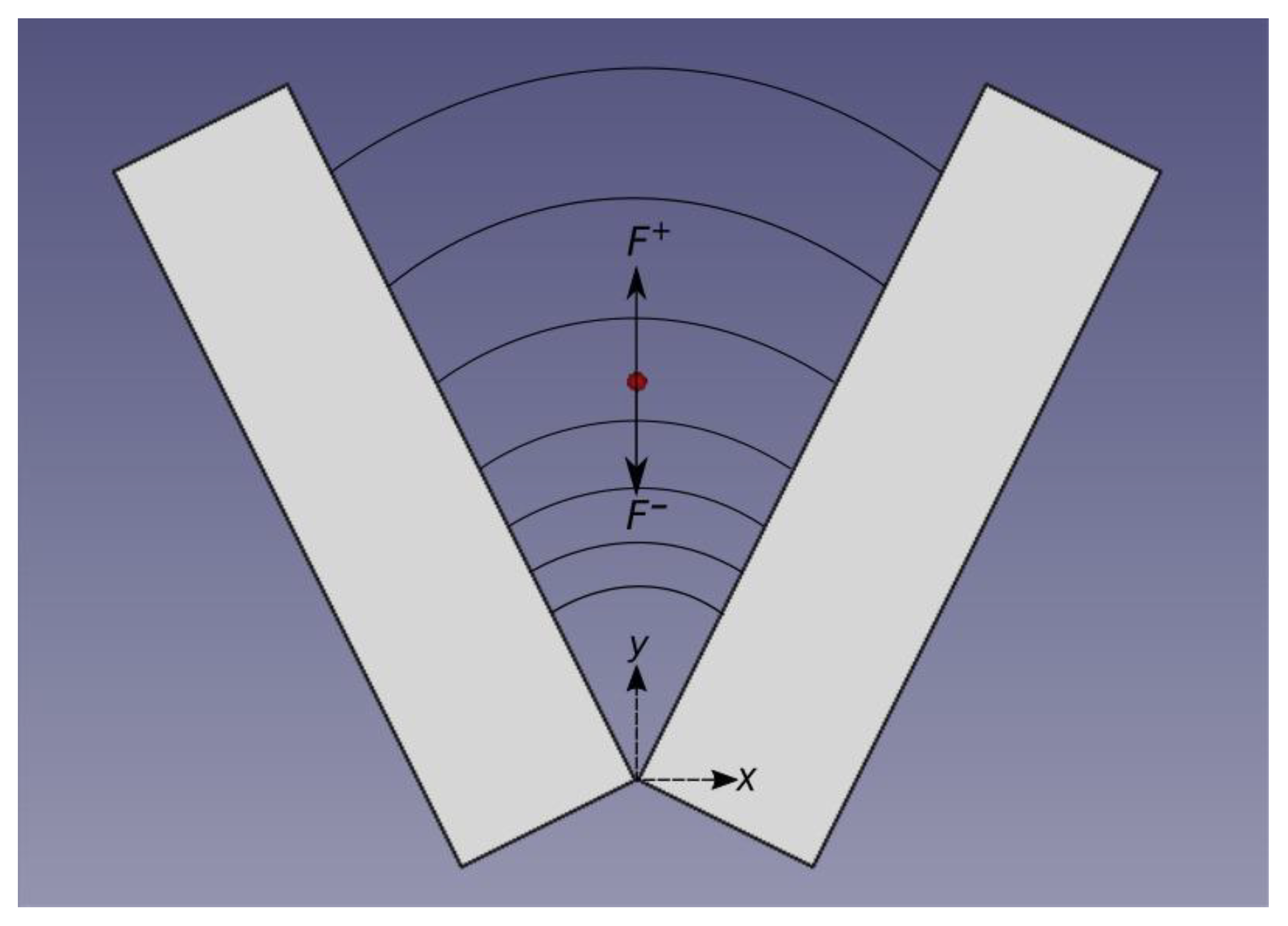
2. Theoretical Model
3. Materials and Methods
3.1. Electron Microscopy
3.2. Measurement of Cell Viability
3.3. Dielectrophoretic Device
- The experiment’s execution: different days, different solutions, etc.
- All cells in a culture are different (e.g., size, different microenvironments...).
- Real cells differ from the theoretical model. For example, the number of cells at the electrodes (distorting the field perception), different speed at the time of measurement.
3.4. Cellular Suspension
3.5. Experimental Procedure
4. Results
4.1. Electron Microscopy
4.2. Cell Viability
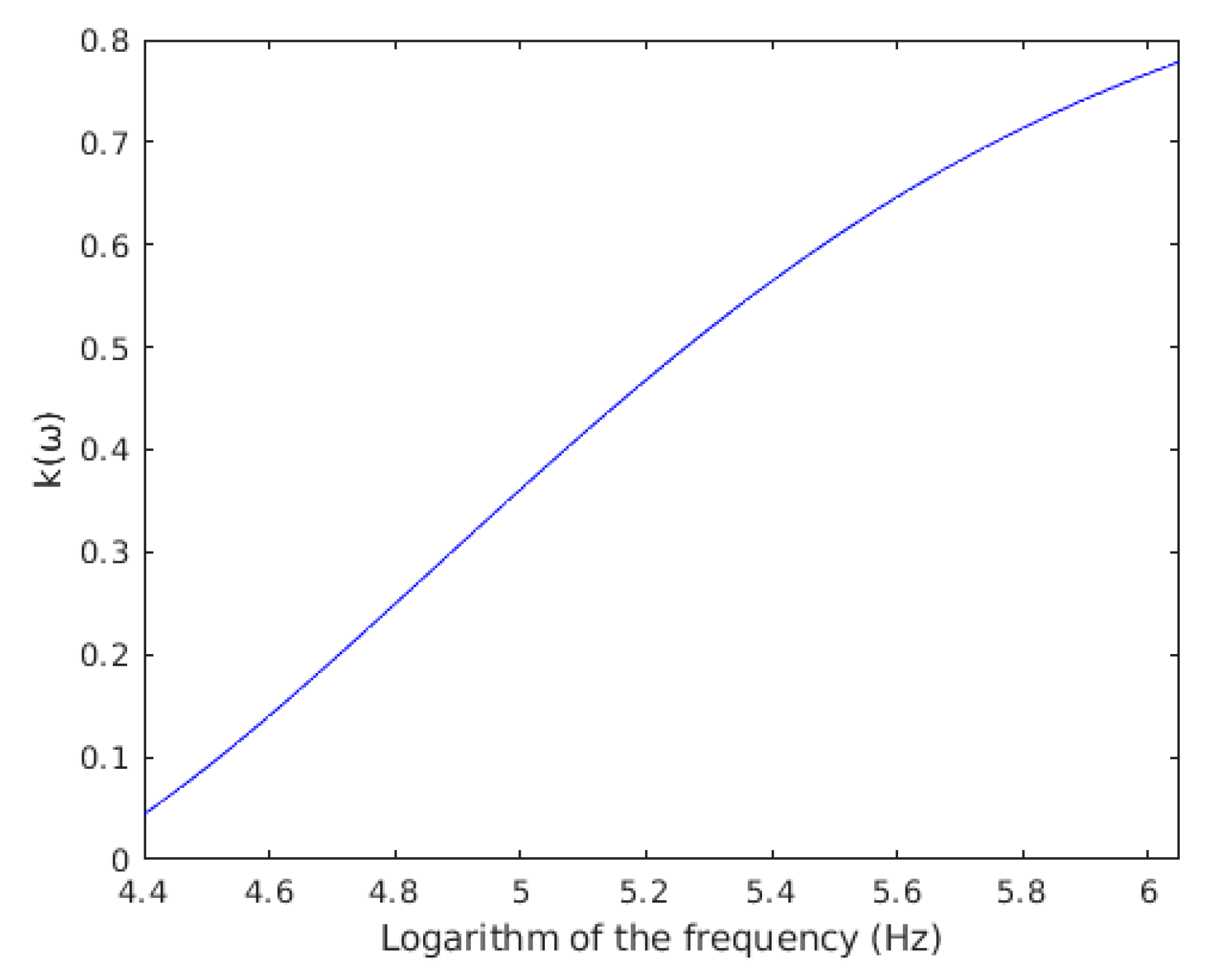
4.3. Measurement of the Electrical Properties of the Dielectrophoretic Chamber
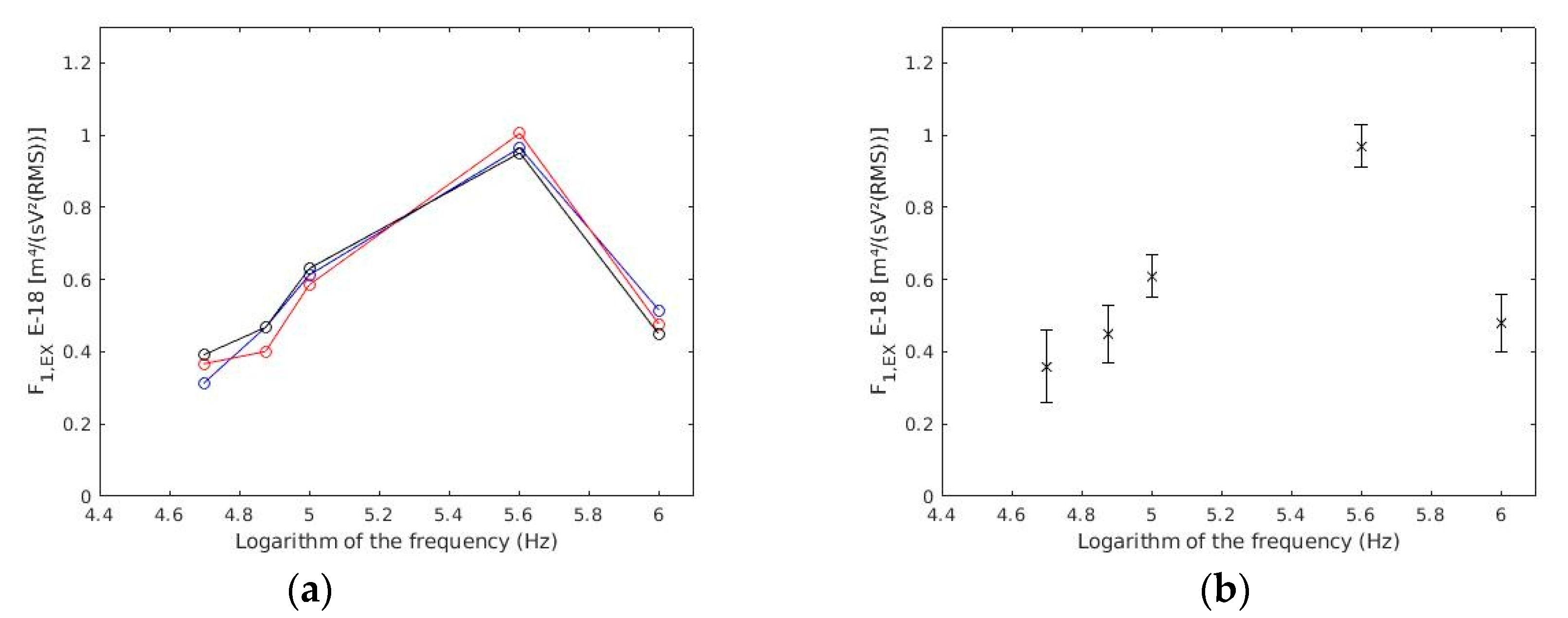
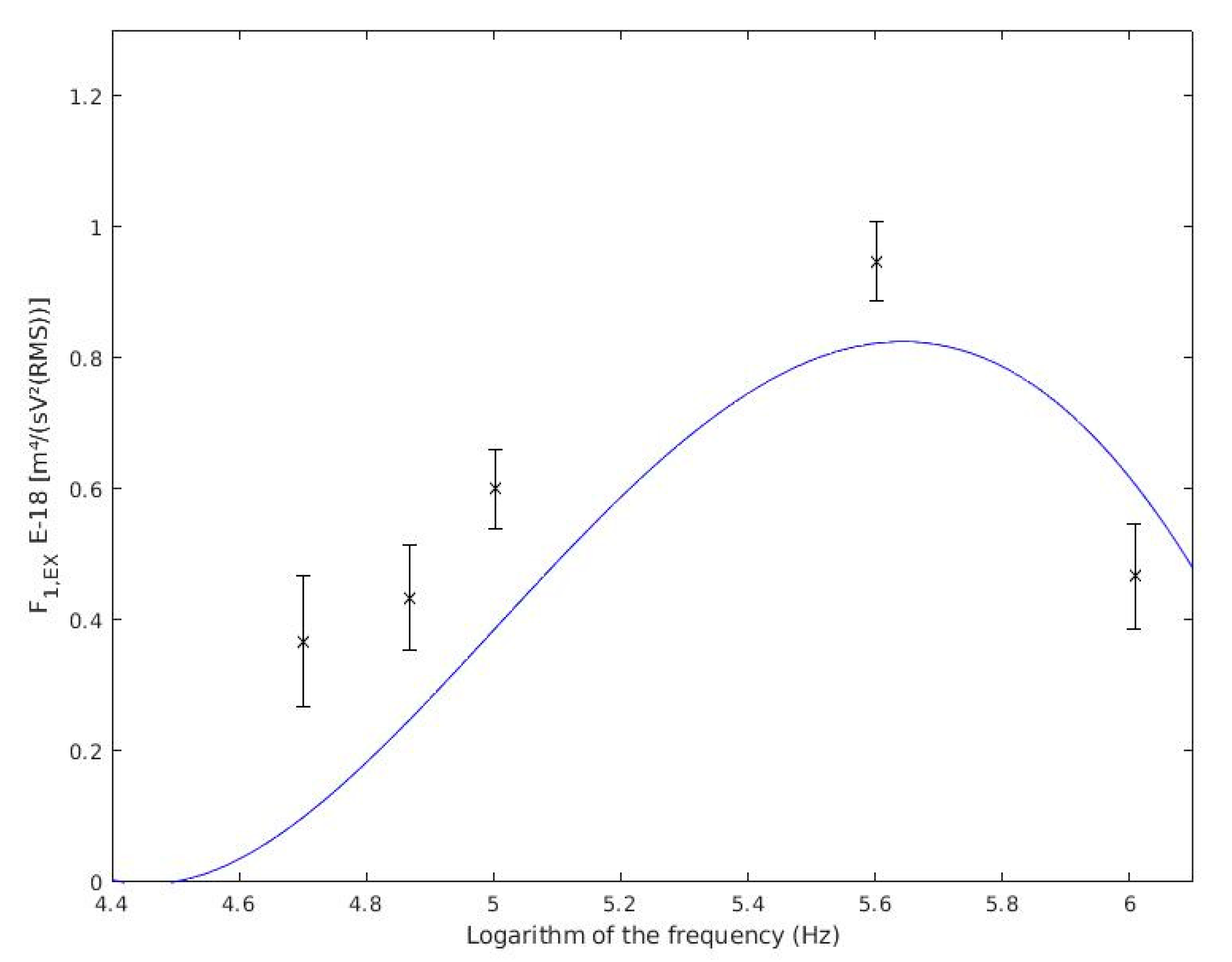
4.4. Cell DEP Measurements
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pethig, R. Review—Where Is Dielectrophoresis (DEP) Going? J. Electrochem. Soc. 2017, 164, 3049–3055. [Google Scholar] [CrossRef]
- Burgarella, S.; Merlo, S.; Dell’Anna, B.; Zarola, G.; Bianchessi, M. A modular micro-fluidic platform for cells handling by dielectrophoresis. Microelectron. Eng. 2010, 87, 2124–2133. [Google Scholar] [CrossRef]
- Burgarella, S.; Bari, M.D. A portable and integrated instrument for cell manipulation by dielectrophoresis: Microfluidics and Miniaturization. Electrophoresis 2015, 36, 1466–1470. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.V.; DeMichele, A.F.; Kemp, L.; Hayes, M.A. Differentiation of Escherichia coli serotypes using DC gradient insulator dielectrophoresis. Anal. Bioanal. Chem. 2013, 406, 183–192. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Rosano, J.; Wang, Y.; Garson, C.J.; Prabhakarpandian, B.; Pant, K.; Klarmann, G.J.; Perantoni, A.; Alvarez, L.M.; Lai, E. Continuous-flow sorting of stem cells and differentiation products based on dielectrophoresis. Lab. Chip 2015, 15, 1320–1328. [Google Scholar] [CrossRef] [PubMed]
- Hyun, C.; Kaur, H.; McNabb, D.S.; Li, J. Dielectrophoretic stretching of DNA tethered to a fiber tip. Nanotechnology 2015, 26, 125501. [Google Scholar] [CrossRef]
- Kumemura, M.; Collard, D.; Sakaki, N.; Yamahata, C.; Hosogi, M.; Hashiguchi, G.; Fujita, H. Single-DNA-molecule trapping with silicon nanotweezers using pulsed dielectrophoresis. J. Micromech. Microeng. 2011, 21, 054020. [Google Scholar] [CrossRef]
- Manouchehri, S.; Ibsen, S.; Wright, J.; Rassenti, L.; Ghia, E.M.; Widhopf, G.F.; Kipps, T.J.; Heller, M.J. Dielectrophoretic recovery of DNA from plasma for the identification of chronic lymphocytic leukemia point mutations. Int. J. Hematol. Oncol. 2016, 5, 27–35. [Google Scholar] [CrossRef]
- Sonnenberg, A.; Marciniak, J.Y.; McCanna, J.; Krishnan, R.; Rassenti, L.; Kipps, T.J.; Heller, M.J. Dielectrophoretic isolation and detection of cfc-DNA nanoparticulate biomarkers and virus from blood: Nucleic Acids. Electrophoresis 2013, 34, 1076–1084. [Google Scholar] [CrossRef]
- Ding, J.; Lawrence, R.M.; Jones, P.V.; Hogue, B.G.; Hayes, M.A. Concentration of Sindbis virus with optimized gradient insulator-based dielectrophoresis. Analyst 2016, 141, 1997–2008. [Google Scholar] [CrossRef]
- Morimoto, A.; Mogami, T.; Watanabe, M.; Lijima, K.; Akiyama, Y.; Katayama, K.; Futami, T.; Yamamoto, N.; Sawada, T.; Koizumi, F.; et al. High-Density Dielectrophoretic Microwell Array for Detection, Capture, and Single-Cell Analysis of Rare Tumor Cells in Peripheral Blood. PLoS ONE 2015, 10, e0130418. [Google Scholar] [CrossRef] [PubMed]
- Alshareef, M.; Metrakos, N.; Juarez Perez, E.; Azer, F.; Yang, F.; Yang, X.; Wang, G. Separation of tumor cells with dielectrophoresis-based microfluidic chip. Biomicrofluidics 2013, 7, 011803. [Google Scholar] [CrossRef] [PubMed]
- Mathew, B.; Alazzam, A.; Khashan, S.; Abutayeh, M. Lab-on-chip for liquid biopsy (LoC-LB) based on dielectrophoresis. Talanta 2017, 64, 608–611. [Google Scholar] [CrossRef] [PubMed]
- Kong, T.F.; Shen, X.; Yang, M.; Yang, C. Lab-on-chip microfluidic impedance measurement for laminar flow ratio sensing and differential conductivity difference detection. Appl. Phys. Lett. 2017, 110, 233501. [Google Scholar] [CrossRef]
- Nakano, M.; Obara, R.; Ding, Z.; Suehiro, J. Detection of norovirus and rotavirus by dielectrophoretic impedance measurement. In Proceedings of the Seventh International Conference on Sensing Technology (ICST), Wellington, New Zealand, 3–5 December 2013; pp. 374–378. [Google Scholar]
- Nakano, M.; Ding, Z.; Suehiro, J. Dielectrophoresis and dielectrophoretic impedance detection of adenovirus and rotavirus. Jpn. J. Appl. Phys. 2016, 55, 017001. [Google Scholar] [CrossRef]
- Heller, M.J.; Krishnan, R.; Sonnenberg, A. Rapid detection of cancer related DNA nanoparticulate biomarkers and nanoparticles in whole blood. In Proceedings of the SPIE NanoScience + Engineering, San Diego, CA, USA, 1–5 August 2010; p. 77590P. [Google Scholar]
- Sonnenberg, A.; Marciniak, J.Y.; Skowronski, E.A.; Manouchehri, S.; Rassenti, L.; Ghia, E.M.; Widhopf, G.F.; Kipps, T.J.; Heller, M.J. Dielectrophoretic isolation and detection of cancer-related circulating cell-free DNA biomarkers from blood and plasma: Nucleic acids. Electrophoresis 2014, 35, 1828–1836. [Google Scholar] [CrossRef]
- Henslee, E.A.; Sano, M.B.; Rojas, A.D.; Schmelz, E.M.; Davalos, R.V. Selective concentration of human cancer cells using contactless dielectrophoresis. Electrophoresis 2011, 32, 2523–2529. [Google Scholar] [CrossRef]
- Park, S.; Zhang, Y.; Wang, T.-H.; Yang, S. Continuous dielectrophoretic bacterial separation and concentration from physiological media of high conductivity. Lab. Chip 2011, 11, 2893. [Google Scholar] [CrossRef]
- Cherukulappurath, S.; Lee, S.H.; Campos, A.; Haynes, C.L.; Oh, S.-H. Rapid and Sensitive in Situ SERS Detection Using Dielectrophoresis. Chem. Mater. 2014, 26, 2445–2452. [Google Scholar] [CrossRef]
- Huh, D.; Gu, W.; Kamotani, Y.; Grotberg, J.B.; Takayama, S. Microfluidics for flow cytometric analysis of cells and particles. Physiol. Meas. 2005, 26, R73–R98. [Google Scholar] [CrossRef]
- Yafouz, B.; Kadri, N.A.; Rothan, H.A.; Yusof, R.; Ibrahim, F. Discriminating dengue-infected hepatic cells (WRL-68) using dielectrophoresis: Microfluidics and Miniaturization. Electrophoresis 2016, 37, 511–518. [Google Scholar] [CrossRef] [PubMed]
- Abd Rahman, N.; Ibrahim, F.; Yafouz, B. Dielectrophoresis for Biomedical Sciences Applications: A Review. Sensors 2017, 17, 449. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Graham, K.A.; Johannessen, A.C.; Costea, D.E.; Labeed, F.H. Human oral cancer cells with increasing tumorigenic abilities exhibit higher effective membrane capacitance. Integr. Biol. 2014, 6, 545–554. [Google Scholar] [CrossRef] [PubMed]
- Ismail, A.; Hughes, M.; Mulhall, H.; Oreffo, R.; Labeed, F. Characterization of human skeletal stem and bone cell populations using dielectrophoresis: Dielectrophoretic properties of skeletal populations. J. Tissue Eng. Regen. Med. 2015, 9, 162–168. [Google Scholar] [CrossRef] [PubMed]
- Shafiee, H.; Jahangir, M.; Inci, F.; Wang, S.; Willenbrecht, R.B.M.; Giguel, F.F.; Tsibris, A.M.N.; Kuritzkes, D.R.; Demirci, U. Acute On-Chip HIV Detection Through Label-Free Electrical Sensing of Viral Nano-Lysate. Small 2013, 9, 2553–2563. [Google Scholar] [CrossRef]
- Manczak, R.; Saada, S.; Provent, T.; Dalmay, C.; Bessette, B.; Begaud, G.; Battu, S.; Blondy, P.; Jauberteau, M.O.; Baristiran Kaynak, C.; et al. UHF-Dielectrophoresis Crossover Frequency as a New Marker for Discrimination of Glioblastoma Undifferentiated Cells. IEEE J. Electromagn. RF Microw. Med. Biol. 2019, 3, 191–198. [Google Scholar] [CrossRef]
- Flanagan, L.A.; Lu, J.; Wang, L.; Marchenko, S.A.; Jeon, N.L.; Lee, A.P.; Monuki, E.S. Unique Dielectric Properties Distinguish Stem Cells and Their Differentiated Progeny. Stem Cells 2008, 26, 656–665. [Google Scholar] [CrossRef]
- Mishra, P.; Mishra, K.P.; Singh, D.; Ganju, L.; Kumar, B.; Singh, S.B. Advances in Rapid Detection and Antimicrobial Susceptibility Tests: A Review. Def. Life Sci. J. 2018, 4, 12–20. [Google Scholar] [CrossRef]
- Cruz, J.M.; Garcia-Diego, F.-J. Dielectrophoretic force measurements in yeast cells by the Stokes method. In Proceedings of the IAS’97. Conference Record of the 1997 IEEE Industry Applications Conference Thirty-Second IAS Annual Meeting, New Orleans, LA, USA, 5–9 October 1997; pp. 2012–2018. [Google Scholar]
- Cruz, J.M.; García-Diego, F.-J. Dielectrophoretic motion of oblate spheroidal particles. Measurements of motion of red blood cells using the Stokes method. J. Phys. Appl. Phys. 1998, 31, 1745–1751. [Google Scholar] [CrossRef]
- García-Diego, F.-J.; Rubio-Chavarría, M.; Beltrán, P.; Espinós, F.J. Characterization of Simple and Double Yeast Cells Using Dielectrophoretic Force Measurement. Sensors 2019, 19, 3813. [Google Scholar]
- Md Ali, M.A.; Kayani, A.B.A.; Yeo, L.Y.; Chrimes, A.F.; Ahmad, M.Z.; Ostrikov, K.K.; Majlis, B.Y. Microfluidic dielectrophoretic cell manipulation towards stable cell contact assemblies. Biomed. Microdevices 2018, 20, 95. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Chu, H.K.; Lu, B.; Lai, J.; Cheng, L. Automated Cell Patterning System with a Microchip using Dielectrophoresis. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 634–639. [Google Scholar]
- Tixier-Mita, A.; Ihida, S.; Shinohara, M.; Eiler, A.C.; Cathcart, G.A.; Faure, P.M.; Kohno, T.; Sakai, Y.; Lévi, T.; Toshiyoshi, H. 2D Dielectrophoresis using an active matrix array made by thin-film-transistor technology. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 1280–1288. [Google Scholar] [CrossRef]
- Wu, Y.; Ren, Y.; Tao, Y.; Hou, L.; Jiang, H. High-Throughput Separation, Trapping, and Manipulation of Single Cells and Particy Combined Dielectrophoresis at a Bipolar Electrode Array. Anal. Chem. 2018, 90, 11461–11469. [Google Scholar] [CrossRef] [PubMed]
- Lewpiriyawong, N.; Xu, G.; Yang, C. Enhanced cell trapping throughput using DC-biased AC electric field in a dielectrophoresis-based fluidic device with densely packed silica beads. Electrophoresis 2018, 39, 878–886. [Google Scholar] [CrossRef]
- Zhao, K.; Duncker, L.B.P.; Li, D. Continuous Cell Characterization and Separation by Microfluidic Alternating Current Dielectrophoresis. Anal. Chem. 2019, 91, 6304–6314. [Google Scholar] [CrossRef]
- Luu, Y.; Macreadie, I. Development of Convenient System for Detecting Yeast Cell Stress, Including That of Amyloid Beta. Int. J. Mol. Sci. 2018, 19, 2136. [Google Scholar] [CrossRef]
- Li, H.; Multari, C.; Palego, C.; Ma, X.; Du, X.; Ning, Y.; Buceta, J.; Hwang, J.C.M.; Cheng, X. Differentiation of live and heat-killed E. coli by microwave impedance spectroscopy. Sensors Actuators B Chem. 2018, 255, 1614–1622. [Google Scholar] [CrossRef]
- Duarte, C.; Gudiña, E.J.; Lima, C.F.; Rodrigues, L.R. Effects of biosurfactants on the viability and proliferation of human breast cancer cells. AMB Express 2014, 4, 40. [Google Scholar] [CrossRef]
- Verghese, J.; Abrams, J.; Wang, Y.; Morano, K.A. Biology of the Heat Shock Response and Protein Chaperones: Budding Yeast (Saccharomyces cerevisiae) as a Model System. Microbiol. Mol. Biol. Rev. 2012, 76, 115–158. [Google Scholar] [CrossRef]
- Guerrero, S.; Lopez-Malo, A.; Alzamora, S.M. Effect of ultrasound on the survival of Saccharomyces cere¨visiae: influence of temperature, pH and amplitude. Innov. Food Sci. Emerg. Technol. 2001, 2, 31–39. [Google Scholar] [CrossRef]
- Lentacker, I.; De Cock, I.; Deckers, R.; De Smedt, S.C.; Moonen, C.T.W. Understanding ultrasound induced sonoporation: Definitions and underlying mechanisms. Adv. Drug Deliv. Rev. 2014, 72, 49–64. [Google Scholar] [CrossRef] [PubMed]
- Hölzel, R.; Lamprecht, I. Dielectric properties of yeast cells as determined by electrorotation. Biochim. Biophys. Acta 1992, 1104, 195–200. [Google Scholar] [CrossRef]
- Pohl, H.A. Dielectrophoresis: The Behavior of Neutral Matter in Nonuniform Electric Fields; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1978. [Google Scholar]
- Jones, T.B. Electromechanics of Particles; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Pierce, J.S. For the Analysis Committee. Institute of brewing analysis committee: Measurement of yeast viability. J. Inst. Brew. 1970, 76, 442–443. [Google Scholar] [CrossRef]
- Bonneu, M.; Crouzet, M.; Urdaci, M.; Aigle, M. Direct detection of yeast mutants with reduced viability on plates by erythrosine B staining. Anal. Biochem. 1991, 193, 225–230. [Google Scholar] [CrossRef]
- Talary, M.S.; Pethig, R. Optical technique for measuring the positive and negative dielectrophoretic behaviour of cells and colloidal suspensions. IEE Proc. Sci. Meas. Technol. 1994, 141, 395–399. [Google Scholar] [CrossRef]
- Asami, K.; Yonezawa, T. Dielectric Behavior of Wild-Type Yeast and Vacuole-Deficient Mutant Over a Frequency Range of 10 kHz to 10 GHz. Biophys. J. 1996, 71, 2192–2200. [Google Scholar] [CrossRef]
- Pavlin, M.; Miklavčič, D. Effective Conductivity of a Suspension of Permeabilized Cells: A Theoretical Analysis. Biophys. J. 2003, 85, 719–729. [Google Scholar] [CrossRef]
- Hibino, M.; Shigemori, M.; Itoh, H.; Nagayama, K.; Kinosita, K., Jr. Membrane conductance of an electroporated cell analyzed by submicrosecond imaging of transmembrane potential. Biophys. J. 1991, 59, 209–220. [Google Scholar] [CrossRef]
- Huang, Y.; Hölzel, R.; Pethig, R.; Wang, X.-B. Differences in the AC electrodynamics of viable and non-viable yeast cells determined through combined dielectrophoresis and electrorotation studies. Phys. Med. Biol. 1992, 37, 1499. [Google Scholar] [CrossRef]
- Afshar, S.; Fazelkhah, A.; Salimi, E.; Butler, M.; Thomson, D.J.; Bridges, G.E. Dielectric properties of single cells subjected to heat shock using DEP cytometry. TMTT 2018, 66, 1817–1830. [Google Scholar] [CrossRef]
- Bonincontro, A.; Mariutti, G. Influence of hyperthermia, pH and culturing conditions on the electrical parameters of Chinese hamster V79 cells. Phys. Med. Biol. 1988, 33, 557–568. [Google Scholar] [CrossRef] [PubMed]

| Parallel resistance (Ω) | |
| Parallel capacitance (F) |
| Frequency (log(Hz)) | Standard Error | Selected Cells | Measured Cells | |
|---|---|---|---|---|
| 4.699 | 0.36 | 0.05 | 12 | 21 |
| 4.875 | 0.45 | 0.04 | 16 | 72 |
| 5.000 | 0.61 | 0.03 | 29 | 69 |
| 5.602 | 0.97 | 0.03 | 31 | 64 |
| 6.000 | 0.48 | 0.04 | 14 | 53 |
| Conductivities (S/m) | |
| Medium | 4 × 10−3 |
| Cell wall | 1.1 × 10−2 |
| Cell membrane | 0 |
| Cytoplasm | 0.008 |
| Relative permittivity | |
| Medium (εm) | 77 |
| Cell wall | 60 |
| Cell membrane | 5.2 |
| Cytoplasm | 58 |
| Geometric parameters (m) | |
| Cell radius (R) | 3.25 × 10−6 |
| Cell wall thickness | 0.25 × 10−6 |
| Cell membrane thickness | 7 × 10−9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernando-Juan, G.-D.; Rubio-Chavarría, M.; Beltrán, P.; Espinós, F.J. Thermal Shock Response of Yeast Cells Characterised by Dielectrophoresis Force Measurement. Sensors 2019, 19, 5304. https://doi.org/10.3390/s19235304
Fernando-Juan G-D, Rubio-Chavarría M, Beltrán P, Espinós FJ. Thermal Shock Response of Yeast Cells Characterised by Dielectrophoresis Force Measurement. Sensors. 2019; 19(23):5304. https://doi.org/10.3390/s19235304
Chicago/Turabian StyleFernando-Juan, García-Diego, Mario Rubio-Chavarría, Pedro Beltrán, and Francisco J. Espinós. 2019. "Thermal Shock Response of Yeast Cells Characterised by Dielectrophoresis Force Measurement" Sensors 19, no. 23: 5304. https://doi.org/10.3390/s19235304
APA StyleFernando-Juan, G.-D., Rubio-Chavarría, M., Beltrán, P., & Espinós, F. J. (2019). Thermal Shock Response of Yeast Cells Characterised by Dielectrophoresis Force Measurement. Sensors, 19(23), 5304. https://doi.org/10.3390/s19235304





