Nondestructive Determination of Nitrogen, Phosphorus and Potassium Contents in Greenhouse Tomato Plants Based on Multispectral Three-Dimensional Imaging
Abstract
1. Introduction
- (i)
- Monocular vision imaging: the plants images are captured by a color camera [7,8,9] or scanner [10,11], the determination of plant nutrients based on monocular vision imaging mainly uses the characteristic parameters or combinations of two-dimensional (2D) images (such as [2G − (R + B)]/(R + G + B), R + G − B, etc) in RGB, HSV, YUV, and Lab color space models to establish models for determining the plant nutrients. This method very simple, but it has high requirements for the illumination environment during image collection, and the model has relatively low applicability. Plant nutrient measurements based on a scanner require that plant samples are collected for scanning, which is relatively inefficient, and the types of nutrients that can be measured are very limited [10,11].
- (ii)
- Multispectral imaging: several characteristic bands are selected according to the sensitive characteristics of plant nutrients, such as one or more characteristic special bands in visible and near-infrared bands respectively [12,13,14]. According to the images or reflectance values of multiple characteristic bands of plants, the plant canopy nutrient prediction models are established. Most of the imaging areas are plant canopy images or band reflectance values. Generally, only one plant nutrient content can be measured at one time. The imaging area of this method is very limited, and the stability of the measurement models are greatly affected by the imaging area and the natural light environment.
- (iii)
- Hyperspectral imaging: hyperspectral imaging is mainly used for the selection of the characteristic wavelengths of the plant nutrients [15,16,17]. The characteristic wavelengths that reflect the physicochemical properties of the materials are extracted. Multispectral imaging can be applied for the practical determination of plant nutrients [2]. Characteristic wavelengths are mainly extracted using the artificial neural network (ANN) [2], random frog (RF) algorithm [18], correlation coefficient (r) [18,19,20,21,22,23,24], principal component analysis (PCA) [25,26,27], successive projections algorithm (SPA) [26,27,28], uninformative variable elimination (UVE) [28], segmented principal components analysis (SPCA) [29], and competitive adaptive reweighted sampling (CARS) [28,30], etc. For the plant nutrient models established according to the characteristic band spectral reflectance or vegetation indices, the modeling methods are mainly divided into linear and nonlinear types. The linear correction methods include linear regression (LR) [31], multiple linear regression (MLR) [20,24], stepwise regression (SWR) [23], and partial least squares (PLS) [18,20,21,28,30,32], etc. The nonlinear correction methods include ANN [19,20,27,28,32], the support vector machine (SVM) [19,21], and RF [32]. Among them, PLS and ANN are the most widely applied algorithms.
- (iv)
- Fluorescence imaging: fluorescence imaging system, according to the fluorescence induction curve of plant chlorophyll, collects the fluorescence images of plant leaves or canopy by controlling the intensity of laser source (such as measuring light, actinic light, saturation light), and extracts the fluorescence parameters of plant leaves, such as minimum fluorescence under dark adaptation F0, maximum fluorescence under dark adaptation Fm, etc. Based on fluorescence imaging, models for determining a plant’s physiological information, such as nutrients, diseases, and stress, are established mainly from the plant’s fluorescence properties [33,34]. This technology has high requirements for the imaging environment, excitation light source, and imaging equipment. In addition, it has high operational requirements, uses very expensive equipment, and cannot be widely applied at a large scale.
- (v)
- Proximal optical sensors: mainly includes chlorophyll meter, reflectance sensor and fluorescence-based flavonols meters. The representative chlorophyll meters mainly include SPAD-502 (Konica Minolta, Tokyo, Japan), DUALEX (Force-A, Orsay, France), MC-100 Chlorophyll Concentration Meter (Apogee Instruments Inc., Logan, UT, USA), etc. The representative reflectance sensor mainly include Crop Circle ACS 430 (Holland Scientific, Lincoln, NE, USA), MSR5/87/16R (CropScan Inc., Rochester, MN, USA), and GreenSeeker (Trimble Inc., Sunnyvale, CA, USA), etc. The fluorescence-based flavonols meters mainly include DUALEX and MULTIPLEX (Force-A), etc. These sensors are mainly used to measure the N content of plant leaves or canopy, which usually only measures the chlorophyll or NDVI value of a small region of the plant canopy at a time, and the plant nutrient distribution is uneven, particularly in the absence of nutrient elements [1,35,36].
- (vi)
- Plant’s electrical signals: there are also methods for measuring plant K and P contents based on the plant’s electrical signals [37,38]. Plant electrical signals are weak and prone to interference from the measuring environment. This measurement method requires the insertion of probes into plant leaves or stems and is thus destructive. Therefore, it is difficult to use this method to measure plant nutrients at a large scale and periodically during actual production.
2. Materials and Methods
2.1. Sample Cultivation
2.2. Instrument and Spectral Data Collection
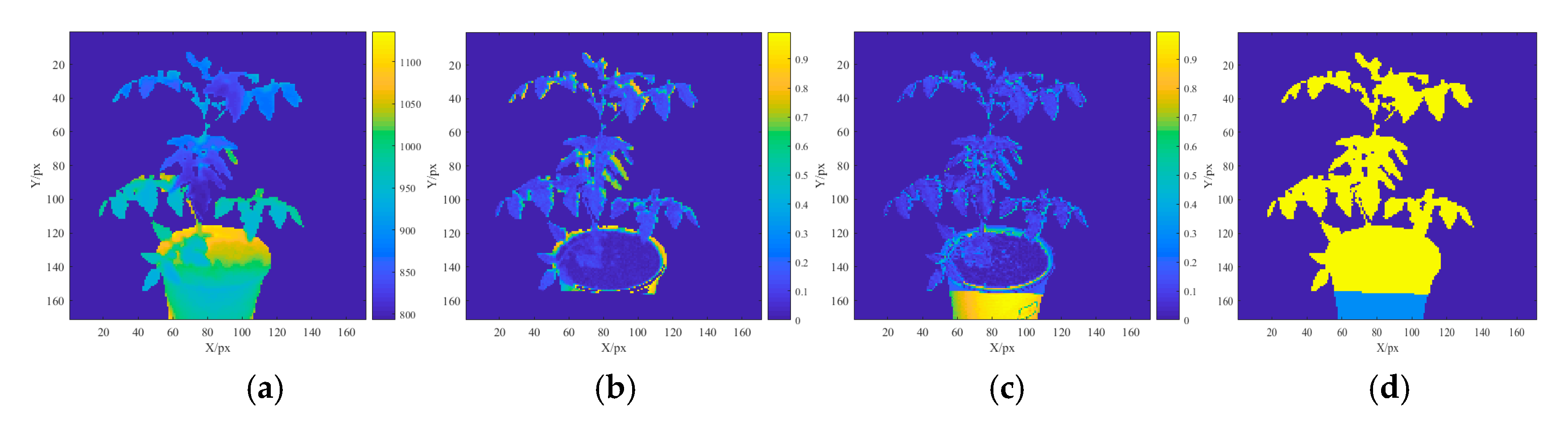
2.3. Multispectral 3D Point Cloud Modeling
2.4. Determination of the Chemical Values of the NPK Nutrients
2.5. Data Processing and Analysis
2.5.1. Optimal Wavelength Selection
2.5.2. Evaluation of the Accuracy of Multispectral 3D Point Cloud Reconstruction
2.5.3. NPK Model Construction and Evaluation
3. Results and Discussion
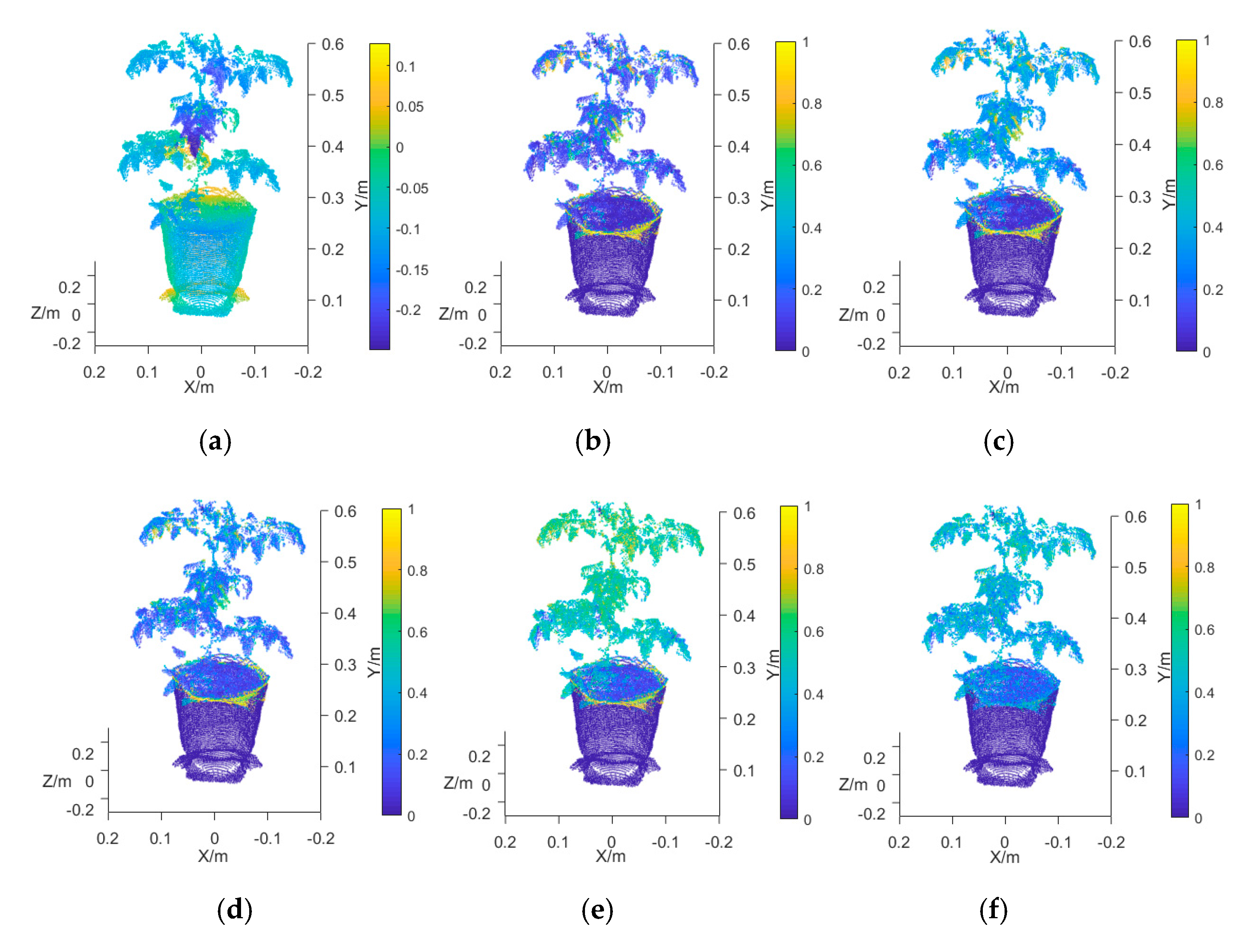
3.1. Multispectral 3D Point Cloud Modeling
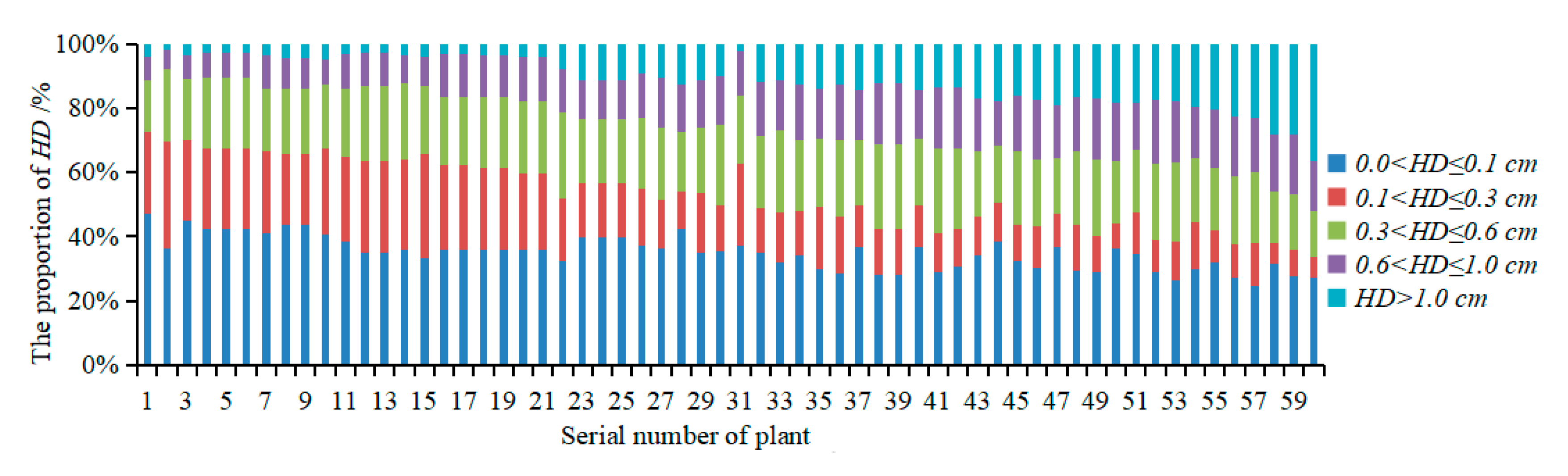
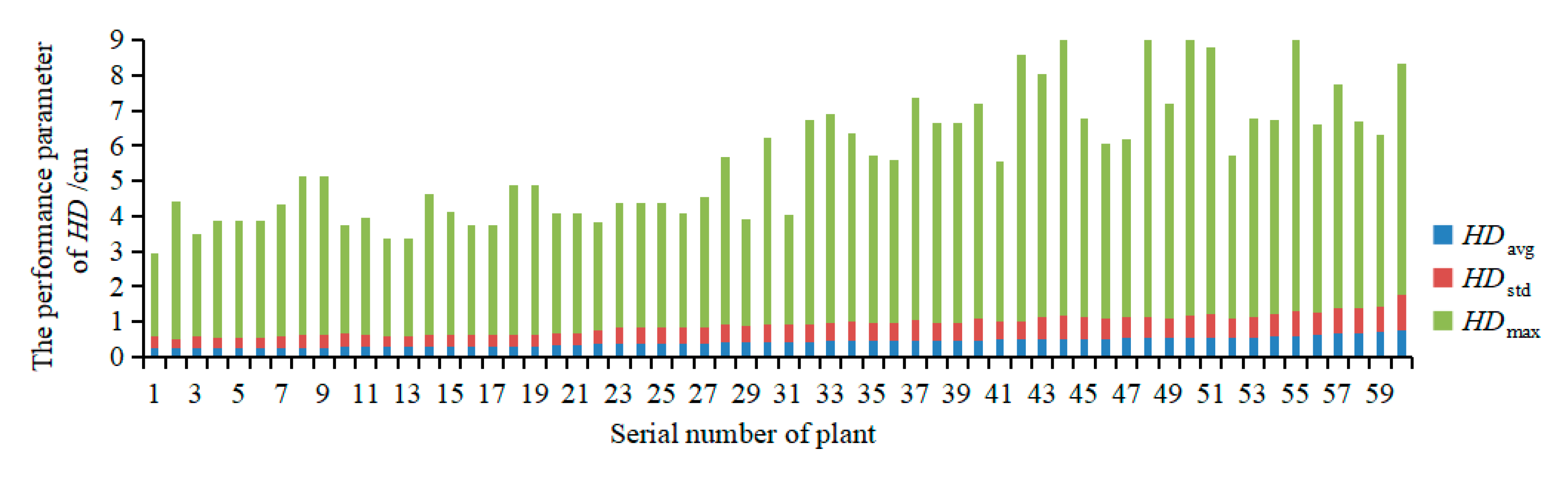
3.2. Analysis of the Accuracy of the Multispectral 3D Point Cloud Reconstruction of Tomato Plants
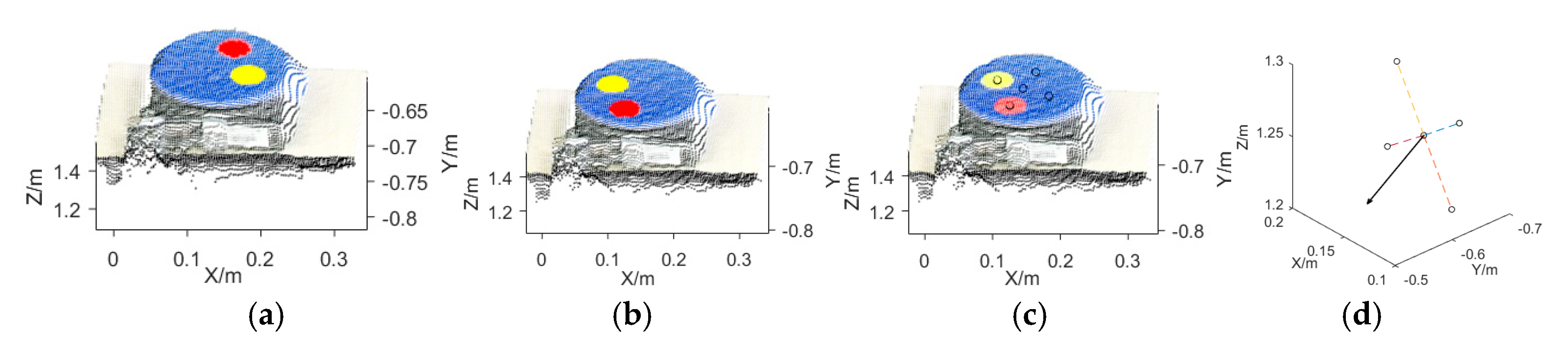
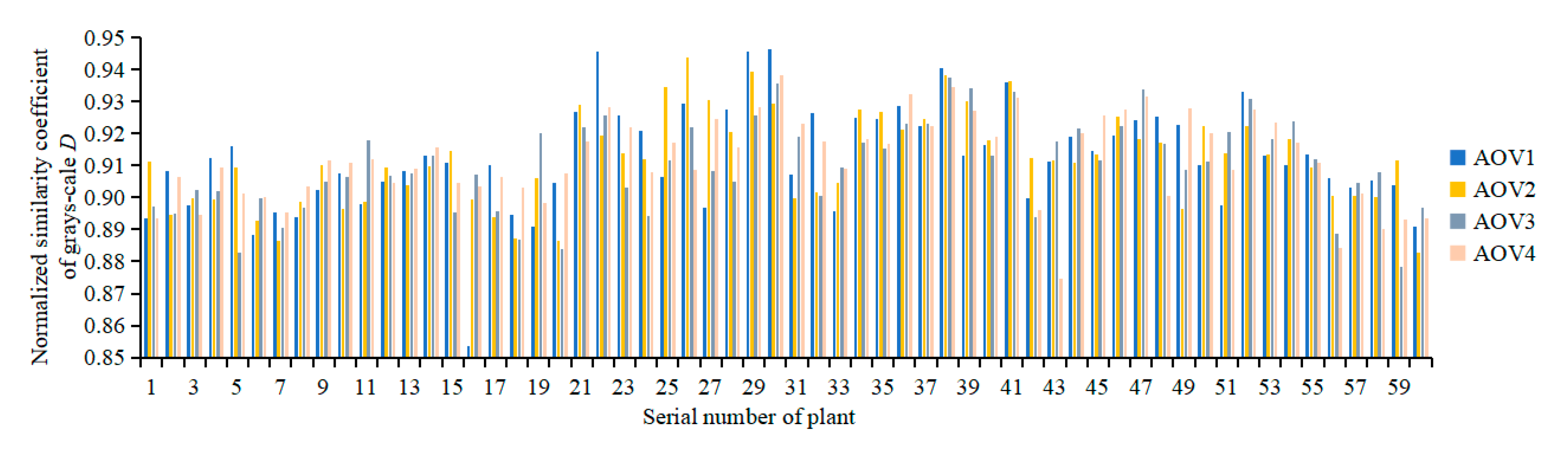
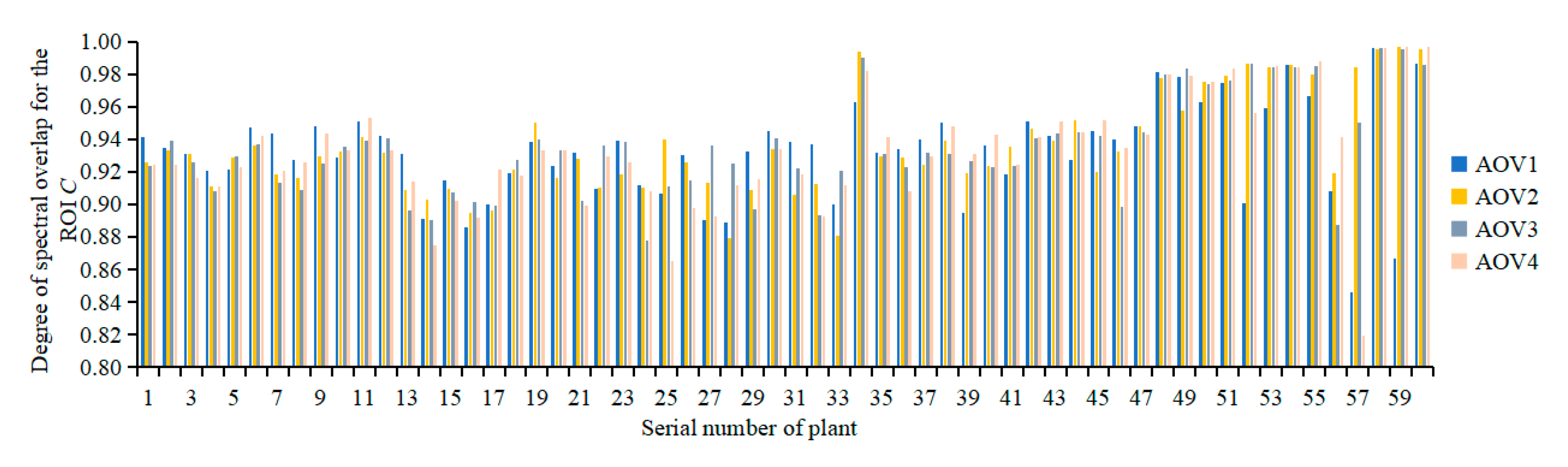
3.2.1. Evaluation of the Registration Quality of Spectral Reflectance
3.2.2. Evaluation of the Accuracy of Multispectral 3D Point Cloud Reconstruction
3.3. Construction of NPK Prediction Models
3.4. Model Verification and Analysis
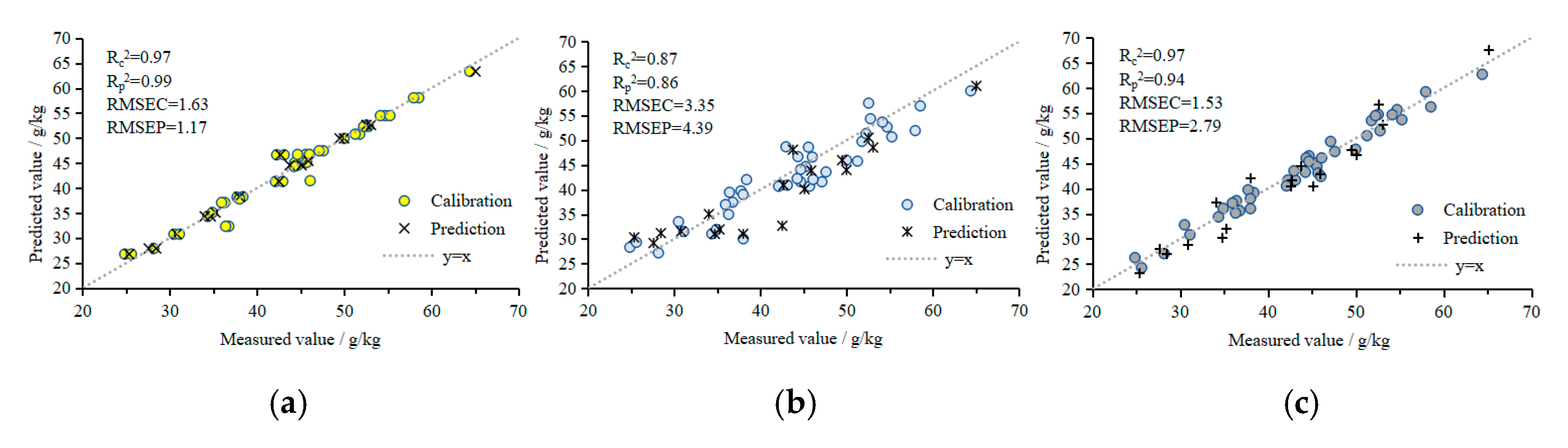
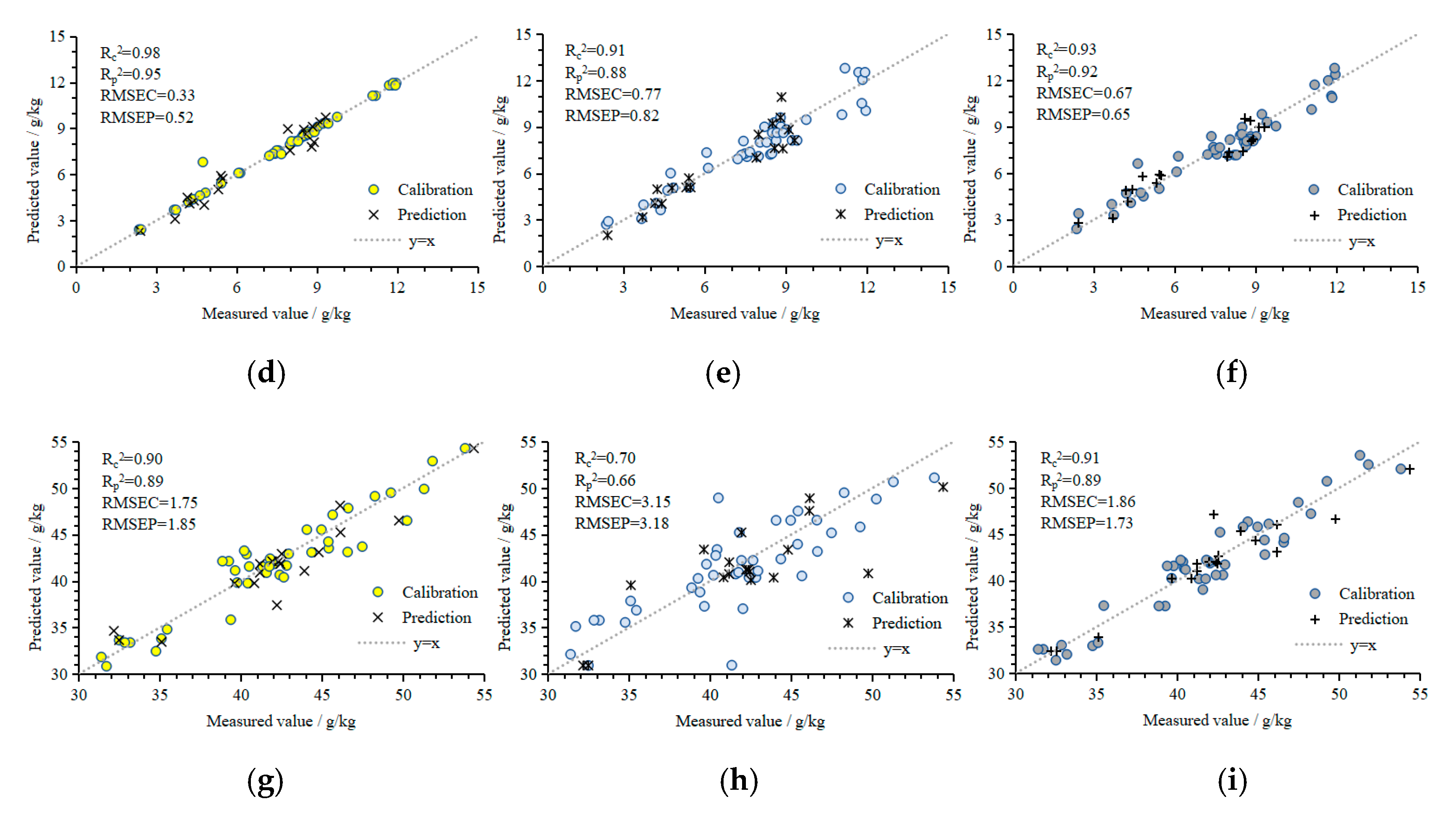
- (i)
- N models: 3DROI multispectral reflectance values were used as the input values for the N prediction models using BPANN, SVMR, and GPR. The Rc2, Rp2, RMSEC, and RMSEP of the BPANN prediction model were 0.97, 0.99, 1.63 mg/g, and 1.17 mg/g, respectively, and the RE was 2.27%. The Rc2, Rp2, RMSEC, and RMSEP of the SVMR prediction model were 0.87, 0.86, 3.35 mg/g, and 4.39 mg/g, respectively, and the RE was 7.46%. The Rc2, Rp2, RMSEC, and RMSEP of the GPR prediction model were 0.97, 0.94, 1.53 mg/g, and 2.79 mg/g, respectively, and the RE was 4.03%. The BPANN, SVMR, and GPR prediction models of the plant N contents all had good predictive performances. The performances of the BPANN and GPR models were similar, and were better than that of the SVMR model.
- (ii)
- P models: 3DROI multispectral reflectance values were used as the input values for the P prediction models using BPANN, SVMR, and GPR. The Rc2, Rp2, RMSEC, and RMSEP of the BPANN prediction model were 0.98, 0.95, 0.33 mg/g, and 0.52 mg/g, respectively, and the RE was 3.32%. The Rc2, Rp2, RMSEC, and RMSEP of the SVMR prediction model were 0.91, 0.88, 0.77 mg/g, and 0.82 mg/g, respectively, and the RE was 8.92%. The Rc2, Rp2, RMSEC, and RMSEP of the GPR prediction model were 0.93, 0.92, 0.67 mg/g, and 0.62 mg/g, respectively, and the RE was 8.41%. The performance of the BPANN model was the best, followed by that of the GPR and SVMR models.
- (iii)
- K models: 3DROI multispectral reflectance values were used as the input values for the K prediction models using BPANN, SVMR, and GPR. The Rc2, Rp2, RMSEC, and RMSEP of the BPANN prediction model were 0.90, 0.89, 1.75 mg/g, and 1.85 mg/g, respectively, and the RE was 3.27%. The Rc2, Rp2, RMSEC, and RMSEP of the SVMR prediction model were 0.70, 0.66, 3.15 mg/g, and 3.18 mg/g, respectively, and the RE was 5.73%. The Rc2, Rp2, RMSEC, and RMSEP of the GPR prediction model were 0.91, 0.89, 1.86 mg/g, and 1.73 mg/g, respectively, and the RE was 3.32%. The performance of the GPR model was the best, followed by that of the BPANN and SVMR models.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Padilla, F.M.; Gallardo, M.; Pena-Fleitas, M.T.; de Souza, R.; Thompson, R.B. Proximal optical sensors for nitrogen management of vegetable crops: A review. Sensors 2018, 18, 2083. [Google Scholar] [CrossRef]
- He, Y.; Peng, J.; Liu, F.; Zhang, C.; Kong, W. Critical review of fast detection of crop nutrient and physiological information with spectral and imaging technology. Trans. Chin. Soc. Agric. Eng. 2015, 31, 174–189. [Google Scholar] [CrossRef]
- Liu, H.; Mao, H.; Zhu, W.; Zhang, X.; Gao, H. Rapid diagnosis of tomato N-P-K nutrition level based on hyperspectral technology. Trans. Chin. Soc. Agric. Eng. 2015, 31, 212–220. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q.; Huang, D. A review of imaging techniques for plant phenotyping. Sensors 2014, 14, 20078–20111. [Google Scholar] [CrossRef] [PubMed]
- Mishra, P.; Asaari, M.S.M.; Herrero-Langreo, A.; Lohumi, S.; Diezma, B.; Scheunders, P. Close range hyperspectral imaging of plants: A review. Biosyst. Eng. 2017, 164, 49–67. [Google Scholar] [CrossRef]
- Barbedo, J.G.A. Detection of nutrition deficiencies in plants using proximal images and machine learning: A review. Comput. Electron. Agric. 2019, 162, 482–492. [Google Scholar] [CrossRef]
- Baresel, J.P.; Rischbeck, P.; Hu, Y.; Kipp, S.; Hu, Y.; Barmeier, G.; Mistele, B.; Schmidhalter, U. Use of a digital camera as alternative method for non-destructive detection of the leaf chlorophyll content and the nitrogen nutrition status in wheat. Comput. Electron. Agric. 2017, 140, 25–33. [Google Scholar] [CrossRef]
- Tavakoli, H.; Gebbers, R. Assessing nitrogen and water status of winter wheat using a digital camera. Comput. Electron. Agric. 2019, 157, 558–567. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.; Shi, P.; Omasa, K. Estimating rice chlorophyll content and leaf nitrogen concentration with a digital still color camera under natural light. Plant Methods 2014, 10, 36. [Google Scholar] [CrossRef]
- Romualdo, L.M.; Luz, P.H.C.; Devechio, F.F.S.; Marin, M.A.; Zúñiga, A.M.G.; Bruno, O.M.; Herling, V.R. Use of artificial vision techniques for diagnostic of nitrogen nutritional status in maize plants. Comput. Electron. Agric. 2014, 104, 63–70. [Google Scholar] [CrossRef]
- Agarwal, A.; Gupta, S.D. Assessment of spinach seedling health status and chlorophyll content by multivariate data analysis and multiple linear regression of leaf image features. Comput. Electron. Agric. 2018, 152, 281–289. [Google Scholar] [CrossRef]
- Ni, J.; Zhang, J.; Wu, R.; Pang, F.; Zhu, Y. Development of an apparatus for crop-growth monitoring and diagnosis. Sensors 2018, 18, 3129. [Google Scholar] [CrossRef] [PubMed]
- Neto, A.J.S.; Lopes, D.C.; Pinto, F.A.C.; Zolnier, S. Vis/NIR spectroscopy and chemometrics for non-destructive estimation of water and chlorophyll status in sunflower leaves. Biosyst. Eng. 2017, 155, 124–133. [Google Scholar] [CrossRef]
- Ulissi, V.; Antonucci, F.; Benincasa, P.; Farneselli, M.; Tosti, G.; Guiducci, M.; Tei, F.; Costa, C.; Pallottino, F.; Pari, L.; et al. Nitrogen concentration estimation in tomato leaves by VIS-NIR non-destructive spectroscopy. Sensors 2011, 11, 6411–6424. [Google Scholar] [CrossRef] [PubMed]
- ElMasry, G.; Mandour, N.; Al-Rejaie, S.; Belin, E.; Rousseau, D. Recent applications of multispectral imaging in seed phenotyping and quality monitoring-an overview. Sensors 2019, 19, 1090. [Google Scholar] [CrossRef] [PubMed]
- Ge, Y.; Bai, G.; Stoerger, V.; Schnable, J.C. Temporal dynamics of maize plant growth, water use, and leaf water content using automated high throughput RGB and hyperspectral imaging. Comput. Electron. Agric. 2016, 127, 625–632. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, F.; He, Y.; Gong, X. Detecting macronutrients content and distribution in oilseed rape leaves based on hyperspectral imaging. Biosyst. Eng. 2013, 115, 56–65. [Google Scholar] [CrossRef]
- Sun, H.; Zheng, T.; Liu, N.; Cheng, M.; Li, M.; Zhang, Q. Vertical distribution of chlorophyll in potato plants based on hyperspectral imaging. Trans. Chin. Soc. Agric. Eng. 2018, 34, 149–156. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, Y.; Qin, K.; Zhao, N.; Yang, Y. Influence of spectral transformation methods on nutrient content inversion accuracy by hyperspectral remote sensing in black soil. Trans. Chin. Soc. Agric. Eng. 2018, 34, 141–147. [Google Scholar] [CrossRef]
- Guo, P.; Su, Y.; Cha, Z.; Lin, Q.; Luo, W.; Lin, Z. Prediction of leaf phosphorus contents for rubber seedlings based on hyperspectral sensitive bands and back propagation artificial neural network. Trans. Chin. Soc. Agric. Eng. 2016, 32, 177–183. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, T.; Zhu, Y.; Zhou, Y.; Xia, T.; Nie, Y. Determination of soybean leaf SPAD value using characteristic wavelength variables preferably selected by IRIV algorithm. Trans. Chin. Soc. Agric. Eng. 2018, 34, 148–154. [Google Scholar] [CrossRef]
- Li, L.; Wang, S.; Ren, T.; Ma, Y.; Wei, Q.; Gao, W.; Lu, J. Evaluating models of leaf phosphorus content of winter oilseed rape based on hyperspectral data. Trans. Chin. Soc. Agric. Eng. 2016, 32, 209–218. [Google Scholar] [CrossRef]
- Zhang, A.; Yan, W.; Guo, C. Inversion model of pasture crude protein content based on hyperspectral image. Trans. Chin. Soc. Agric. Eng. 2018, 34, 188–194. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, F.; Zhang, H.; Li, Z.; Hai, Q.; Chen, L. Optimization of soil salt inversion model based on spectral transformation from hyperspectral index. Trans. Chin. Soc. Agric. Eng. 2018, 34, 110–117. [Google Scholar] [CrossRef]
- Kong, W.; Zhang, C.; Huang, W.; Liu, F.; He, Y. Application of hyperspectral imaging to detect Sclerotinia sclerotiorum on oilseed rape stems. Sensors 2018, 18, 123. [Google Scholar] [CrossRef]
- Yao, Z.; Lei, Y.; He, D. Early visual detection of wheat stripe rust using visible/near-infrared hyperspectral imaging. Sensors 2019, 19, 952. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, T.; Qiu, Z.; Peng, J.; Zhang, C.; He, Y. Fast detection of striped stem-borer (Chilo suppressalis walker) infested rice seedling based on visible/near-infrared hyperspectral imaging system. Sensors 2017, 17, 2470. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Q.; Shi, X.; Gao, X. Hyperspectral nondestructive detection model of chlorogenic acid content during storage of honeysuckle. Trans. Chin. Soc. Agric. Eng. 2019, 35, 291–299. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Y.; Wang, L.; Wang, R.; Song, Y.; Zhang, C.; Su, Z. Prediction for nitrogen content of rice leaves in cold region based on hyperspectrum. Trans. Chin. Soc. Agric. Eng. 2016, 32, 187–194. [Google Scholar] [CrossRef]
- Zhang, Z.; Shang, H.; Wang, H.; Zhang, Q.; Yu, S.; Wu, Q.; Tian, J. Hyperspectral imaging for the nondestructive quality assessment of the firmness of nanguo pears under different freezing/thawing conditions. Sensors 2019, 19, 3124. [Google Scholar] [CrossRef]
- Kong, W.; Huang, W.; Casa, R.; Zhou, X.; Ye, H.; Dong, Y. Off-nadir hyperspectral sensing for estimation of vertical profile of leaf chlorophyll content within wheat canopies. Sensors 2017, 17, 2711. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Fang, Z.; Chen, Z.; Zhou, L.; Yue, X.; Wang, Z.; Wang, C.; Miao, Y. Nitrogen nutrition diagnosis of winter wheat based on ASD Field Spec3. Trans. Chin. Soc. Agric. Eng. 2018, 34, 162–169. [Google Scholar] [CrossRef]
- Kuckenberg, J.; Tartachnyk, I.; Noga, G. Detection and differentiation of nitrogen-deficiency, powdery mildew and leaf rust at wheat leaf and canopy level by laser-induced chlorophyll fluorescence. Biosyst. Eng. 2009, 103, 121–128. [Google Scholar] [CrossRef]
- Mahlein, A.K.; Alisaac, E.; Al Masri, A.; Behmann, J.; Dehne, H.W.; Oerke, E.C. Comparison and combination of thermal, fluorescence, and hyperspectral imaging for monitoring fusarium head blight of wheat on spikelet scale. Sensors 2019, 19, 2281. [Google Scholar] [CrossRef] [PubMed]
- de Souza, R.; Peña-Fleitas, M.T.; Thompson, R.B.; Gallardo, M.; Grasso, R.; Padilla, F.M. The use of chlorophyll meters to assess crop N status and derivation of sufficiency values for sweet pepper. Sensors 2019, 19, 2949. [Google Scholar] [CrossRef] [PubMed]
- Cui, D.; Li, M.; Zhang, Q. Development of an optical sensor for crop leaf chlorophyll content detection. Comput. Electron. Agric. 2009, 69, 171–176. [Google Scholar] [CrossRef]
- Li, J.; Li, M.; Mao, H.; Zhu, W. Diagnosis of potassium nutrition level in Solanum lycopersicum based on electrical impedance. Biosyst. Eng. 2016, 147, 130–138. [Google Scholar] [CrossRef]
- Li, M.; Li, J.; Mao, H.; Wu, Y. Diagnosis and detection of phosphorus nutrition level for Solanum lycopersicum based on electrical impedance spectroscopy. Biosyst. Eng. 2016, 143, 108–118. [Google Scholar] [CrossRef]
- Cheng, M.; Cai, Z.; Ning, W.; Yuan, H. System design for peanut canopy height information acquisition based on LiDAR. Trans. Chin. Soc. Agric. Eng. 2019, 35, 180–187. [Google Scholar] [CrossRef]
- Thapa, S.; Zhu, F.; Walia, H.; Yu, H.; Ge, Y. A novel LiDAR-based instrument for high-throughput, 3D measurement of morphological traits in Maize and Sorghum. Sensors 2018, 18, 1187. [Google Scholar] [CrossRef]
- Sun, G.; Wang, X. Three-dimensional point cloud reconstruction and morphology measurement method for greenhouse plants based on the kinect sensor self-calibration. Agronomy 2019, 9, 596. [Google Scholar] [CrossRef]
- Andujar, D.; Calle, M.; Fernandez-Quintanilla, C.; Ribeiro, A.; Dorado, J. Three-dimensional modeling of weed plants using low-cost photogrammetry. Sensors 2018, 18, 1077. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Teng, P.; Shimizu, Y.; Hosoi, F.; Omasa, K. Estimating 3D leaf and stem shape of nursery paprika plants by a novel multi-camera photography system. Sensors 2016, 16, 874. [Google Scholar] [CrossRef] [PubMed]
- Itakura, K.; Kamakura, I.; Hosoi, F. Three-dimensional monitoring of plant structural parameters and chlorophyll distribution. Sensors 2019, 19, 413. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Xie, J.; Li, Z.N. Research on optimal near-infrared band selection of chlorophyll (SPAD) 3D distribution about rice PLANT. Spectrosc. Spectr. Anal. 2017, 37, 3749–3757. [Google Scholar] [CrossRef]
- Sun, G.; Wang, X.; Sun, Y.; Ding, Y.; Lu, W. Measurement method based on multispectral three-dimensional imaging for the chlorophyll contents of greenhouse tomato plants. Sensors 2019, 19, 3345. [Google Scholar] [CrossRef]
- Vázquez-Arellano, M.; Reiser, D.; Paraforos, D.S.; Garrido-Izard, M.; Burce, M.E.C.; Griepentrog, H.W. 3-D reconstruction of maize plants using a time-of-flight camera. Comput. Electron. Agric. 2018, 145, 235–247. [Google Scholar] [CrossRef]
- Henke, M.; Junker, A.; Neumann, K.; Altmann, T.; Gladilin, E. Automated alignment of multi-modal plant images using integrative phase correlation approach. Front. Plant Sci. 2018, 9, 1519. [Google Scholar] [CrossRef]
- Hu, P.; Guo, Y.; Li, B.; Zhu, J.; Ma, Y. Three-dimensional reconstruction and its precision evaluation of plant architecture based on multiple view stereo method. Trans. Chin. Soc. Agric. Eng. 2015, 31, 209–214. [Google Scholar] [CrossRef]

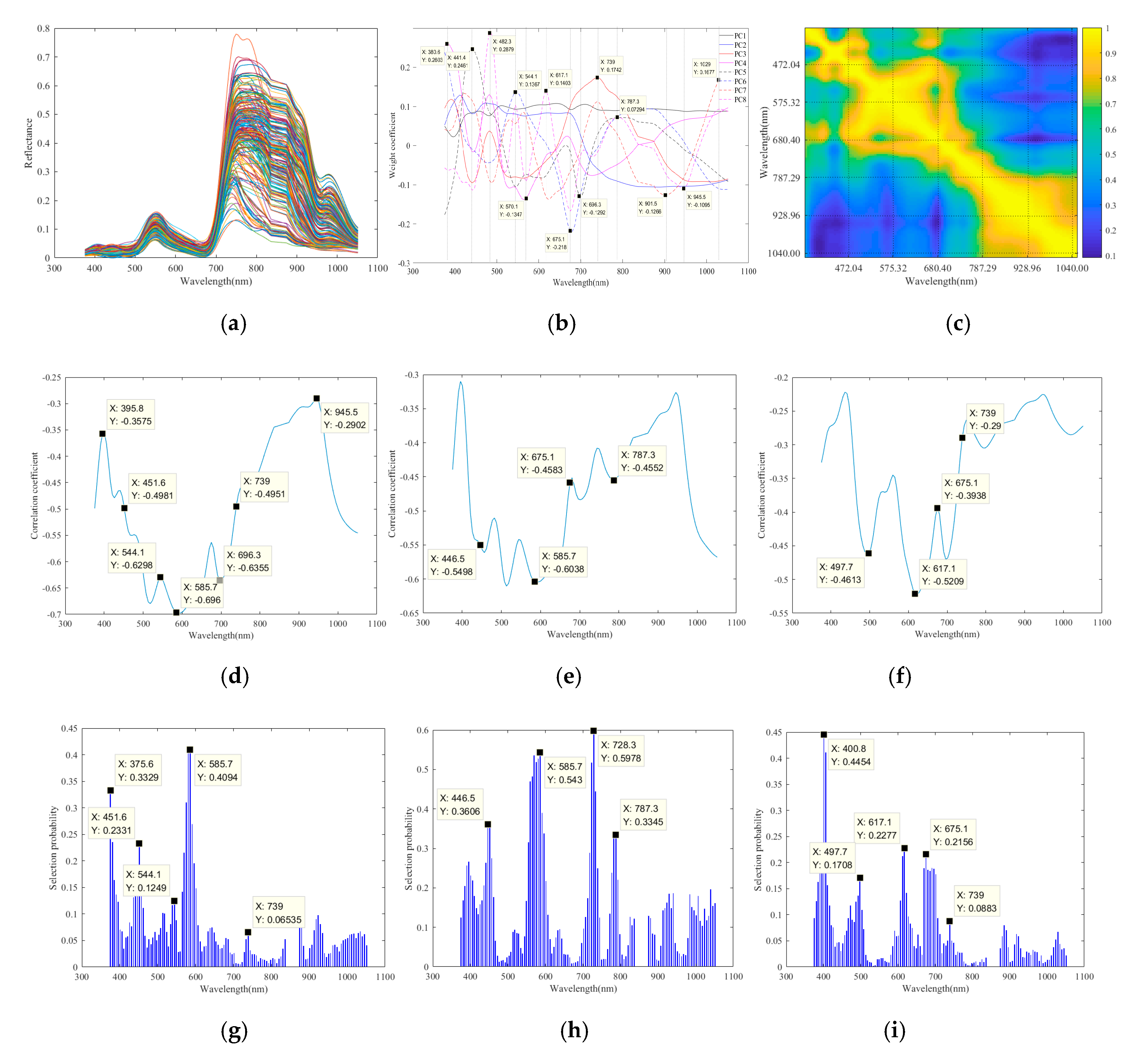
| Nutrients | Method | Number | Characteristic Wavelength/nm |
|---|---|---|---|
| N | PCA-CC-RF | 5 | 451.6, 544.1, 585.7, 696.3 *, 739.0 |
| P | PCA-CC-RF | 5 | 446.5, 585.7, 675.1 *, 728.3, 787.3 |
| K | PCA-CC-RF | 5 | 497.7, 585.7 *, 617.1, 675.1, 739.0 |
| Model | BPANN | SVMR | GPR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Input | Rc2 | RMSEC | Rp2 | RMSEP | Rc2 | RMSEC | Rp2 | RMSEP | Rc2 | RMSEC | Rp2 | RMSEP | |
| N | AOV1 | 0.95 | 2.14 | 0.90 | 3.72 | 0.93 | 2.52 | 0.90 | 3.71 | 0.94 | 2.18 | 0.95 | 2.64 |
| AOV2 | 0.98 | 1.26 | 0.94 | 2.67 | 0.90 | 2.86 | 0.85 | 4.17 | 0.95 | 2.10 | 0.92 | 3.14 | |
| AOV3 | 0.90 | 2.88 | 0.84 | 4.25 | 0.73 | 4.87 | 0.77 | 4.93 | 0.96 | 1.94 | 0.95 | 2.65 | |
| AOV4 | 0.92 | 2.56 | 0.93 | 2.77 | 0.83 | 3.84 | 0.81 | 4.68 | 0.98 | 1.32 | 0.94 | 3.04 | |
| 3DROI | 0.97 | 1.63 | 0.99 | 1.17 | 0.87 | 3.35 | 0.86 | 4.39 | 0.97 | 1.53 | 0.94 | 2.79 | |
| P | AOV1 | 0.94 | 0.69 | 0.92 | 0.85 | 0.90 | 0.86 | 0.87 | 0.82 | 0.93 | 0.67 | 0.93 | 0.62 |
| AOV2 | 0.98 | 0.37 | 0.95 | 0.55 | 0.91 | 0.81 | 0.90 | 0.72 | 0.94 | 0.65 | 0.92 | 0.65 | |
| AOV3 | 0.98 | 0.41 | 0.93 | 0.61 | 0.89 | 0.84 | 0.84 | 0.95 | 0.93 | 0.68 | 0.90 | 0.71 | |
| AOV4 | 0.97 | 0.57 | 0.92 | 1.00 | 0.89 | 0.90 | 0.90 | 0.98 | 0.94 | 0.97 | 0.90 | 1.10 | |
| 3DROI | 0.98 | 0.33 | 0.95 | 0.52 | 0.91 | 0.77 | 0.88 | 0.82 | 0.93 | 0.67 | 0.92 | 0.65 | |
| K | AOV1 | 0.87 | 1.98 | 0.89 | 1.88 | 0.69 | 3.12 | 0.60 | 3.51 | 0.90 | 1.77 | 0.89 | 1.79 |
| AOV2 | 0.88 | 1.96 | 0.84 | 2.52 | 0.75 | 2.82 | 0.71 | 3.12 | 0.94 | 1.47 | 0.90 | 1.93 | |
| AOV3 | 0.86 | 2.14 | 0.87 | 2.02 | 0.58 | 3.56 | 0.52 | 4.84 | 0.93 | 1.61 | 0.88 | 1.87 | |
| AOV4 | 0.93 | 1.44 | 0.88 | 1.94 | 0.66 | 3.38 | 0.64 | 3.52 | 0.92 | 1.62 | 0.91 | 1.62 | |
| 3DROI | 0.90 | 1.75 | 0.89 | 1.85 | 0.70 | 3.15 | 0.66 | 3.18 | 0.91 | 1.86 | 0.89 | 1.73 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, G.; Ding, Y.; Wang, X.; Lu, W.; Sun, Y.; Yu, H. Nondestructive Determination of Nitrogen, Phosphorus and Potassium Contents in Greenhouse Tomato Plants Based on Multispectral Three-Dimensional Imaging. Sensors 2019, 19, 5295. https://doi.org/10.3390/s19235295
Sun G, Ding Y, Wang X, Lu W, Sun Y, Yu H. Nondestructive Determination of Nitrogen, Phosphorus and Potassium Contents in Greenhouse Tomato Plants Based on Multispectral Three-Dimensional Imaging. Sensors. 2019; 19(23):5295. https://doi.org/10.3390/s19235295
Chicago/Turabian StyleSun, Guoxiang, Yongqian Ding, Xiaochan Wang, Wei Lu, Ye Sun, and Hongfeng Yu. 2019. "Nondestructive Determination of Nitrogen, Phosphorus and Potassium Contents in Greenhouse Tomato Plants Based on Multispectral Three-Dimensional Imaging" Sensors 19, no. 23: 5295. https://doi.org/10.3390/s19235295
APA StyleSun, G., Ding, Y., Wang, X., Lu, W., Sun, Y., & Yu, H. (2019). Nondestructive Determination of Nitrogen, Phosphorus and Potassium Contents in Greenhouse Tomato Plants Based on Multispectral Three-Dimensional Imaging. Sensors, 19(23), 5295. https://doi.org/10.3390/s19235295





