A New Multiple Hypothesis Tracker Integrated with Detection Processing
Abstract
1. Introduction
2. Integration of Detection with Target Tracking
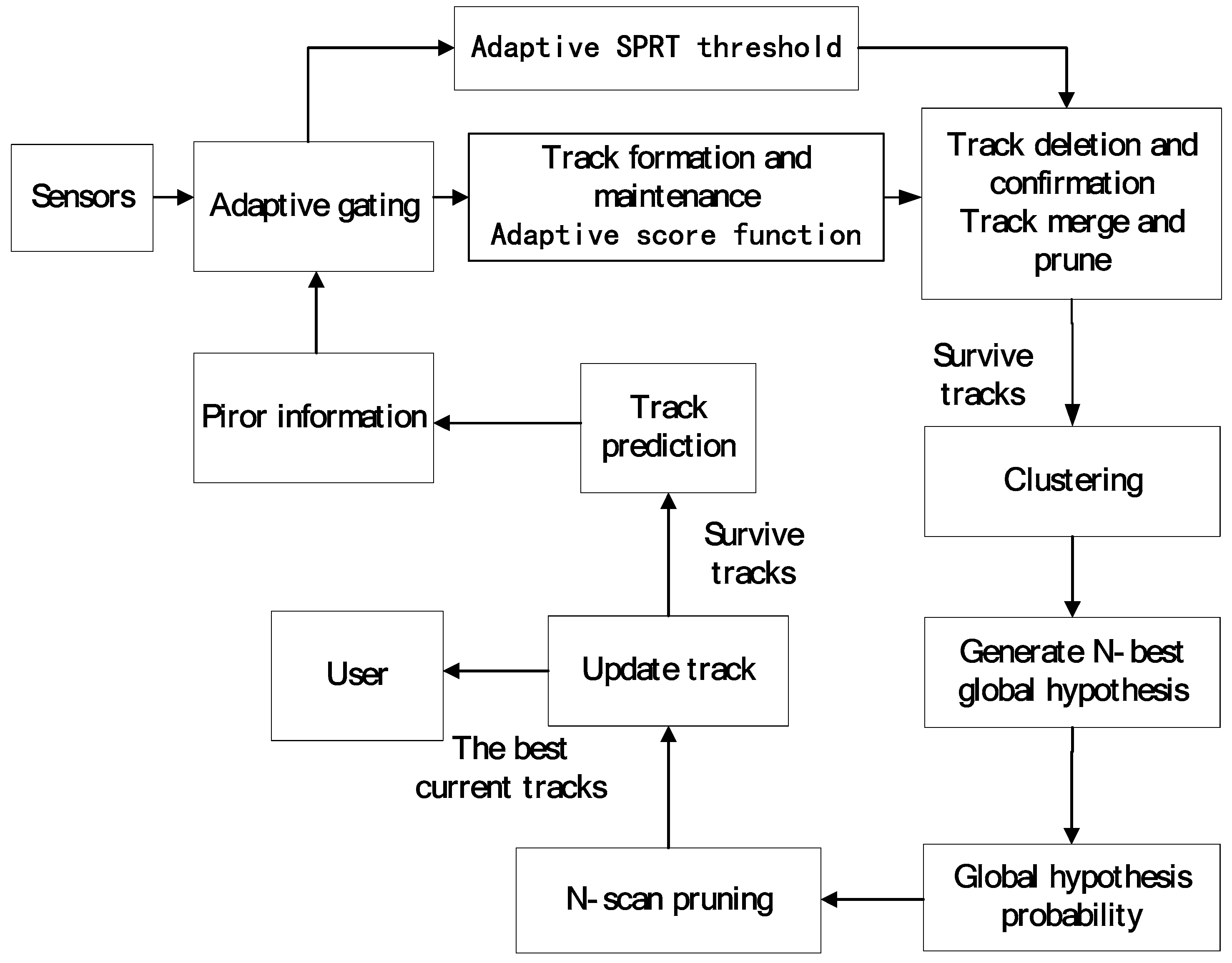
3. The MHT-IDP Algorithm
3.1. Adaptive Detection Module
3.1.1. Detection Probability
3.1.2. Clutter Density
3.2. Adaptive Score Function
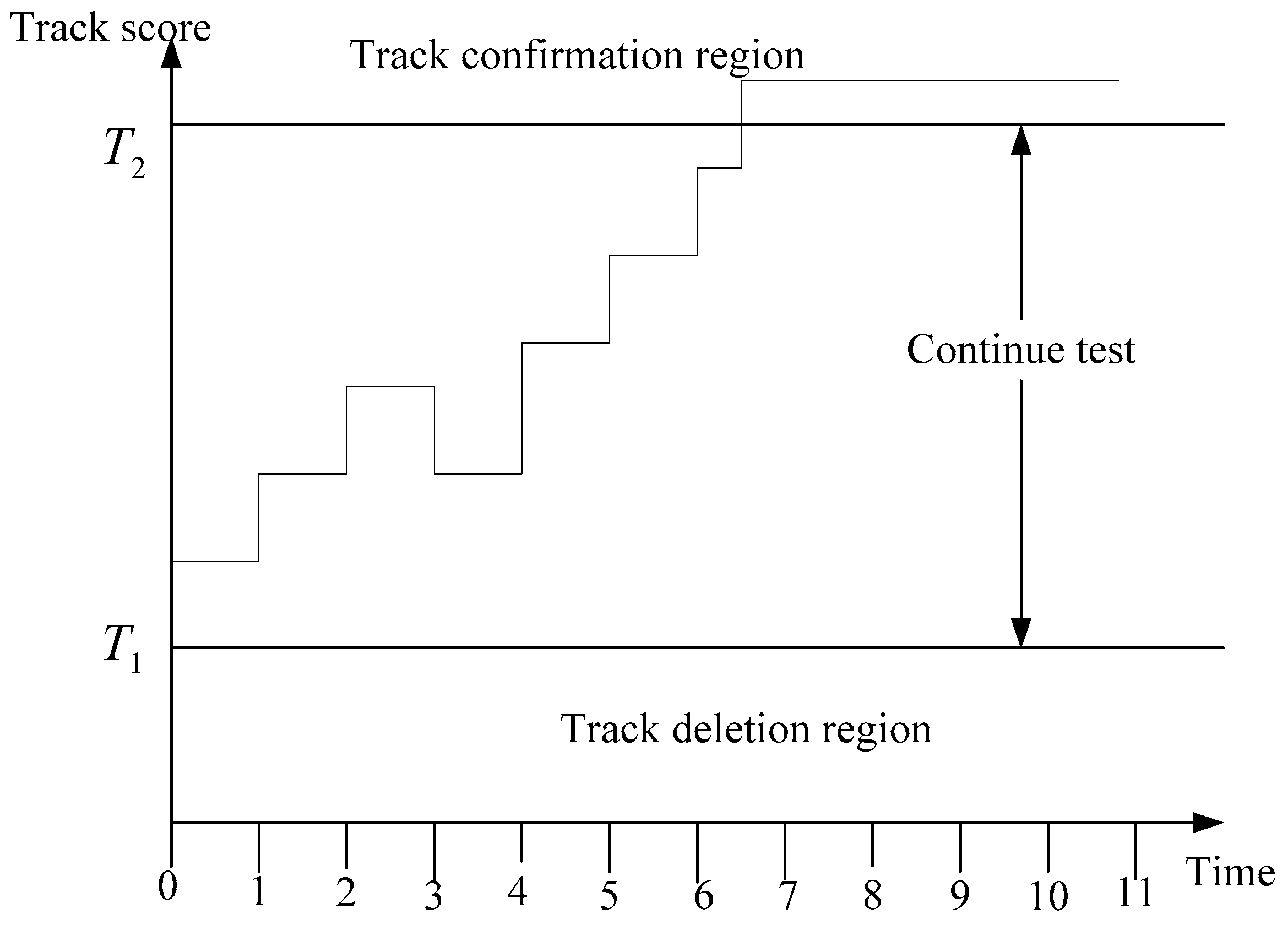
3.3. Adaptive SPRT Threshold
| Algorithm 1 Pseudo-code of the MHT-IDP algorithm. |
| Input: the measurement data z(k). Output: the best tracks 1: Set k=1. 2: for i=1→length (z(k)) 3: calculate the adaptive threshold τi(k) with (14) 4: if amplitude ai(k) > τi(k) 5: calculate the adaptive detection probability with (19) and calculate the clutter density and with (22). 6: calculate the adaptive score function with (26) and acquire the changing alarm number with (29). 7: end if 8: end for 9: calculate the track score Lt(k), t = 1,2,...,N. with (24). 10: calculate the adaptive SPRT threshold with (31)and (32) 11: for t = 1→N 12: if Lt(k) > T1(k), confirm the track, end if 13: else if T2(k) ≤ Lt(k) ≤ T1(k), continue to test track, end if 14: else if Lt(k) < T2(k), delete the track, end if 15: end for 16: cluster the tracks, form the global hypothesizes and N-best pruning the tracks. |
| 17: Set k = k+1, return the predicted data to step 2. |
4. Experimental Results
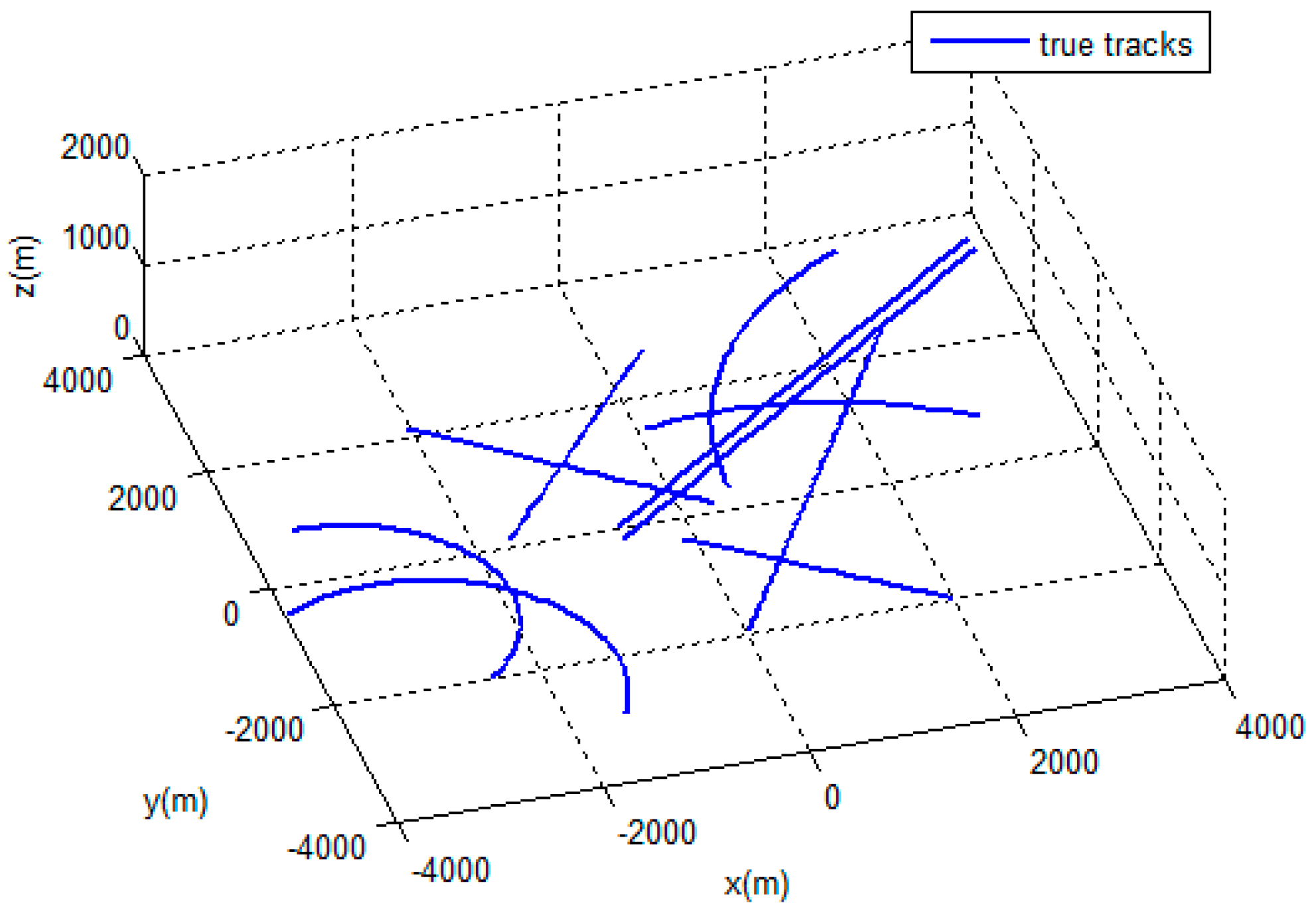
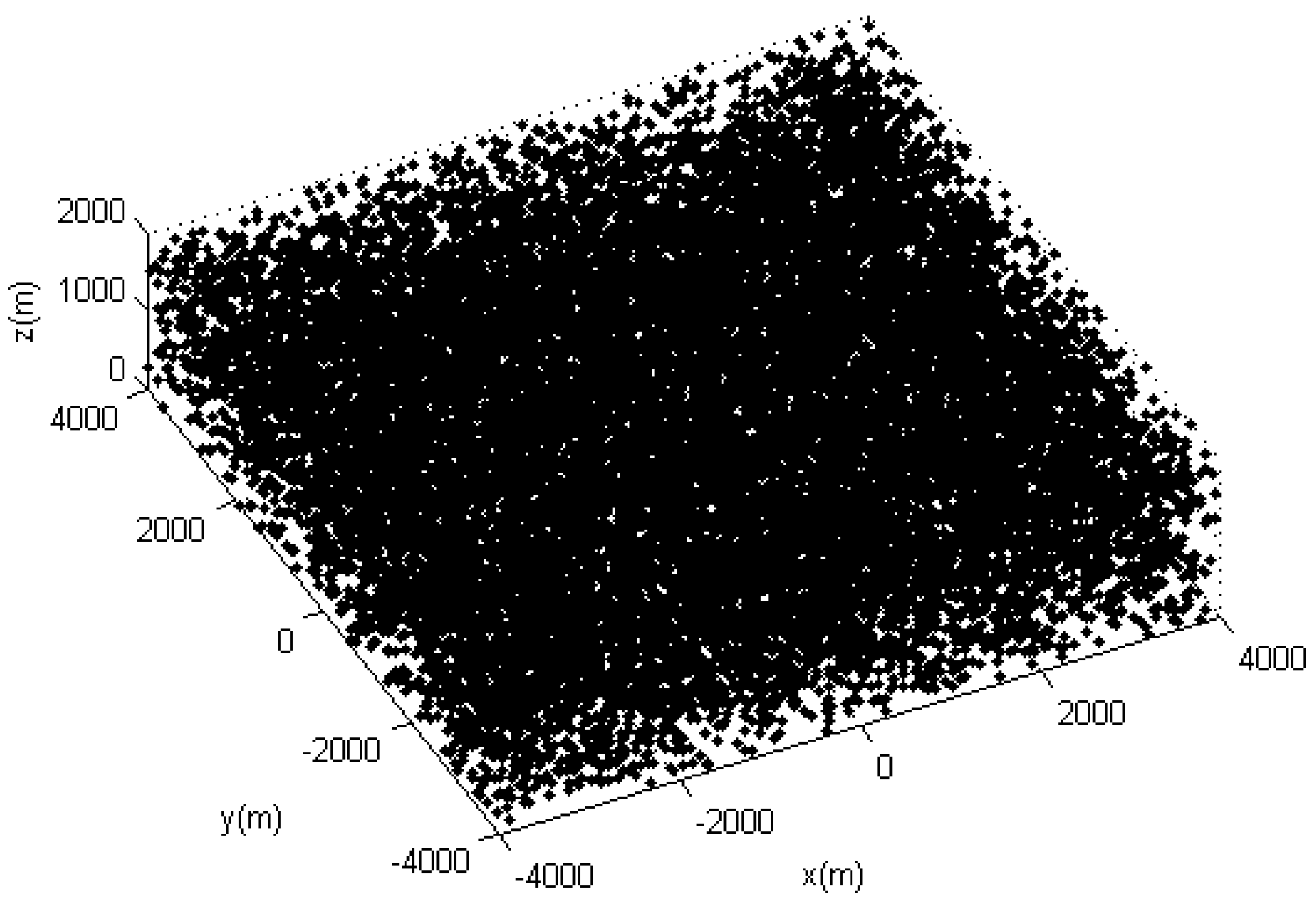
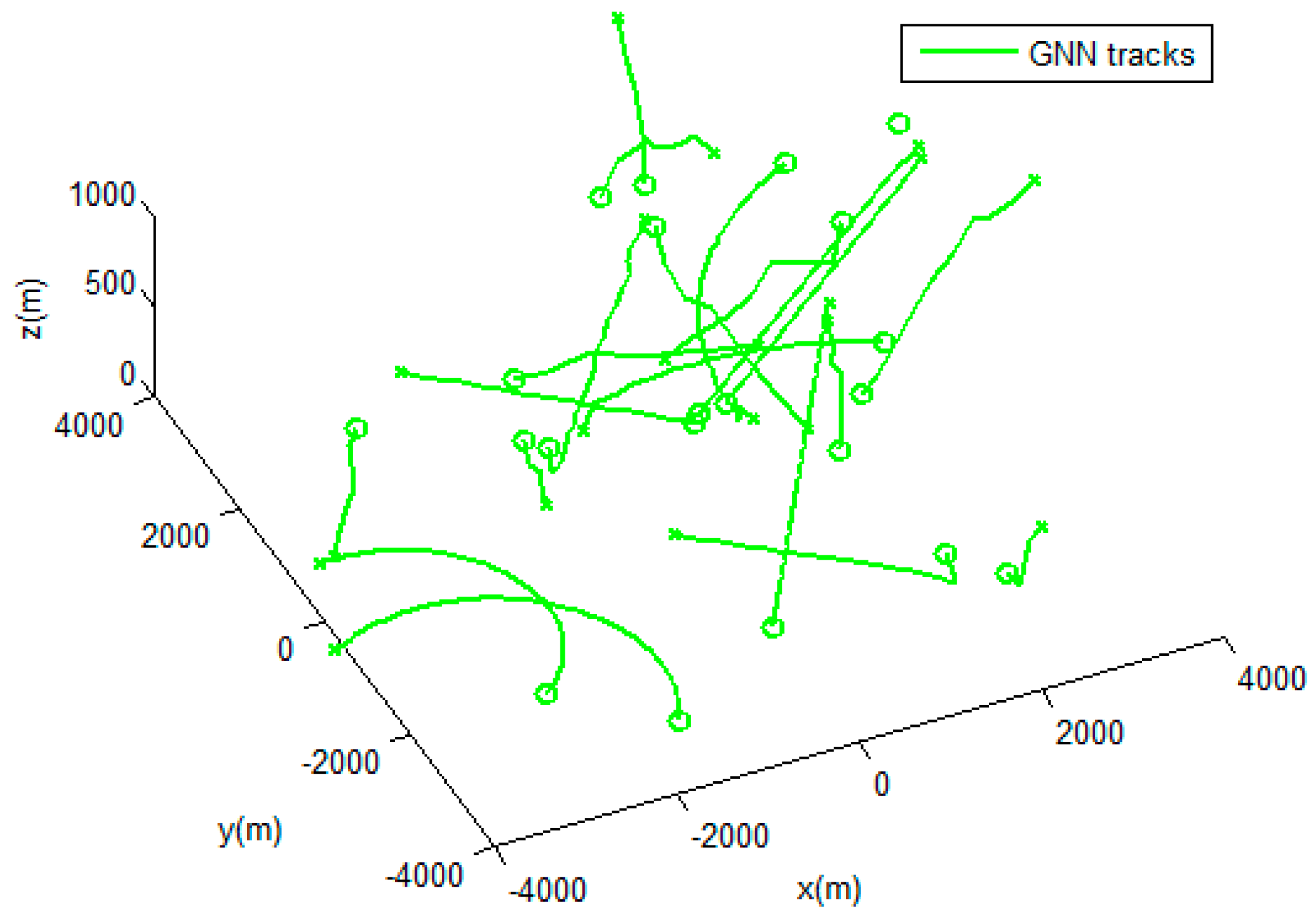
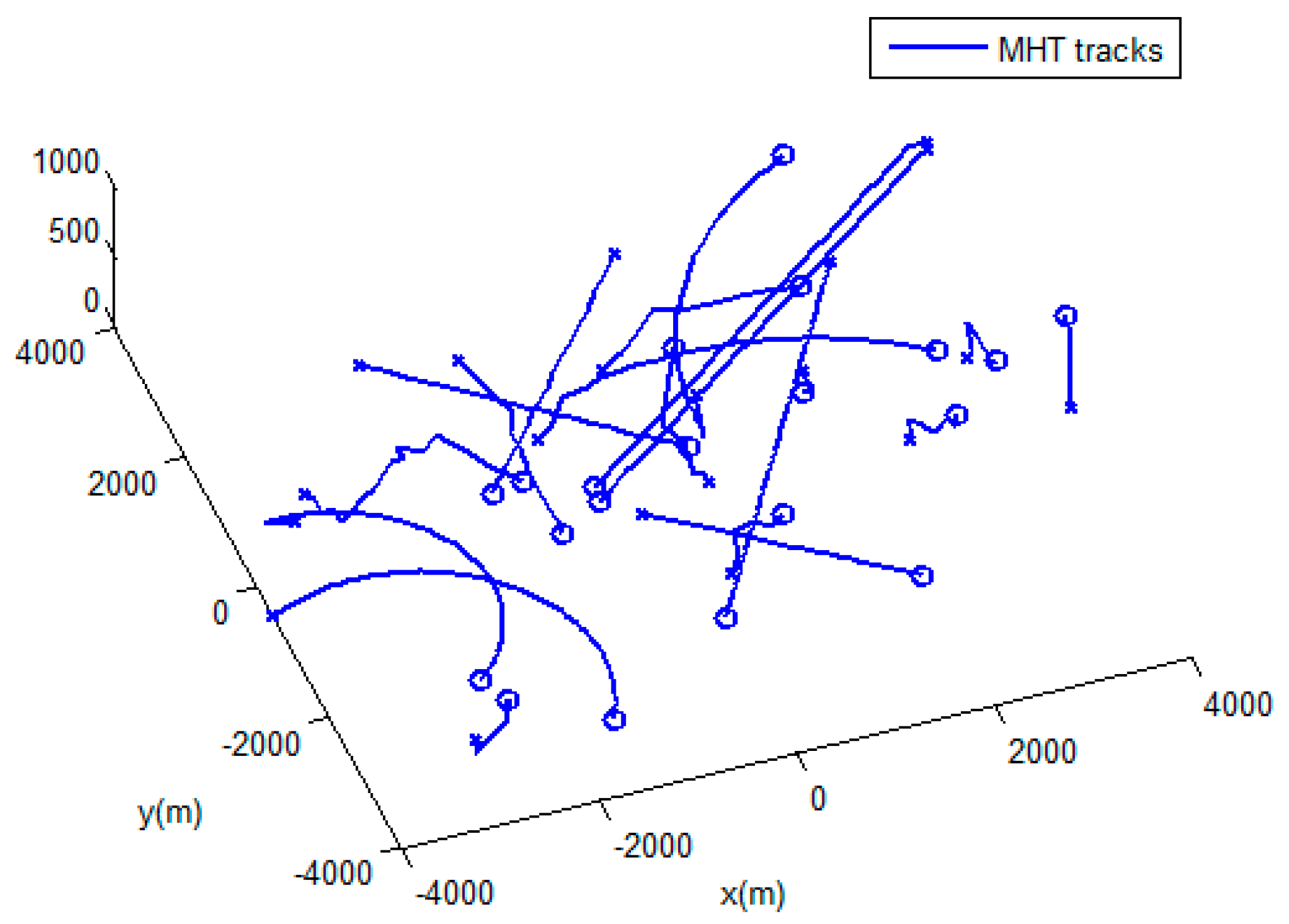
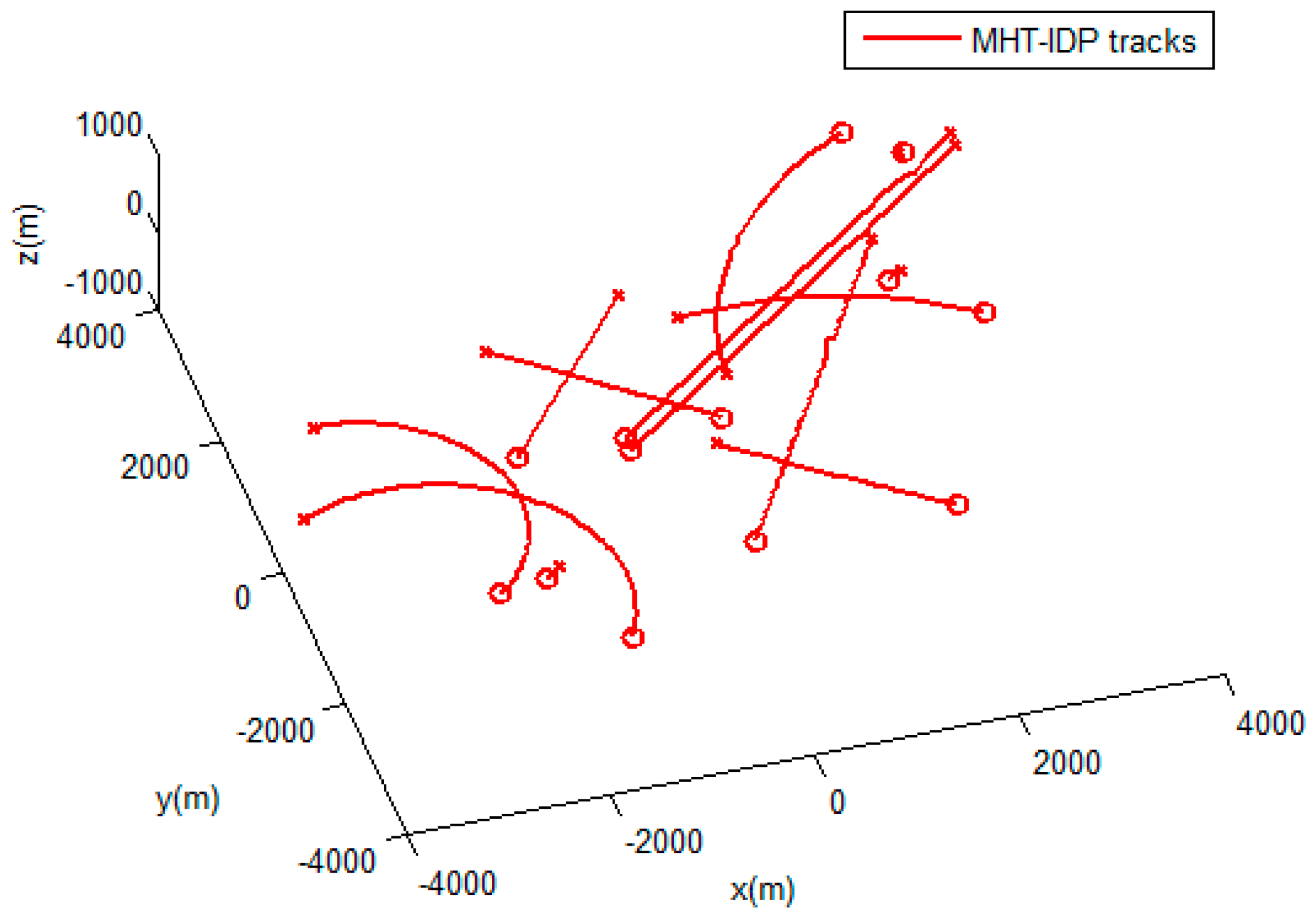
4.1. Simulation Scenairo.
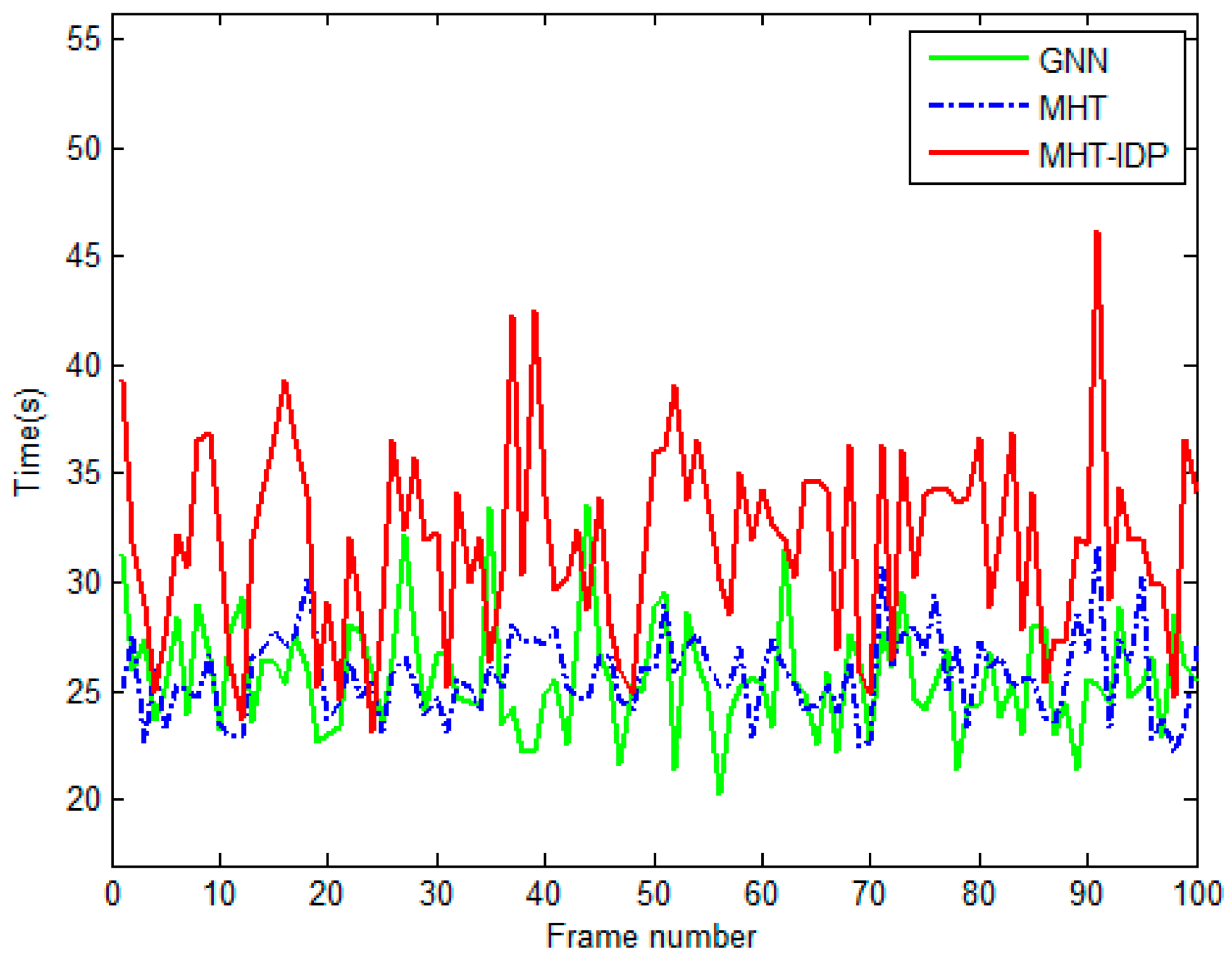
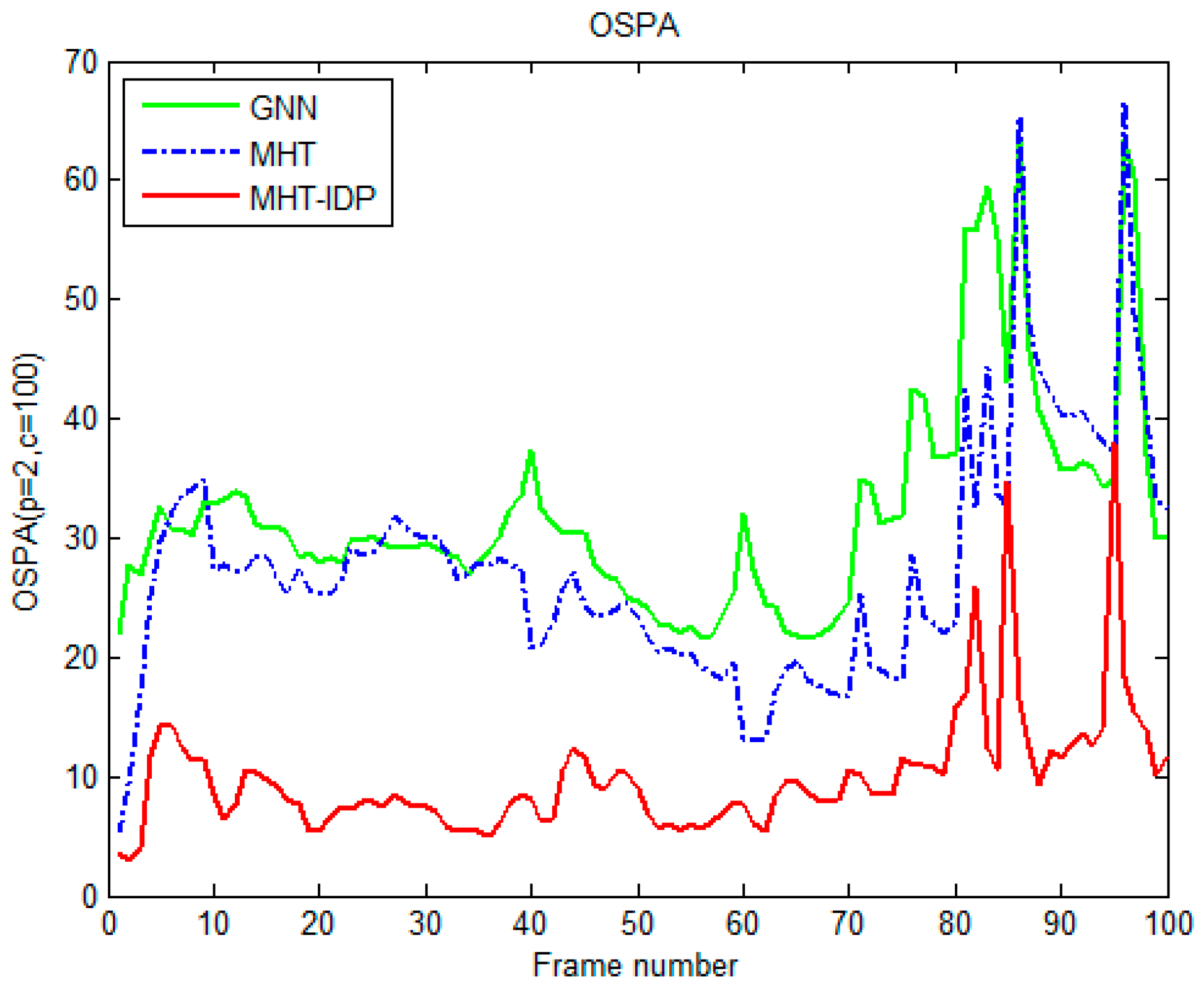
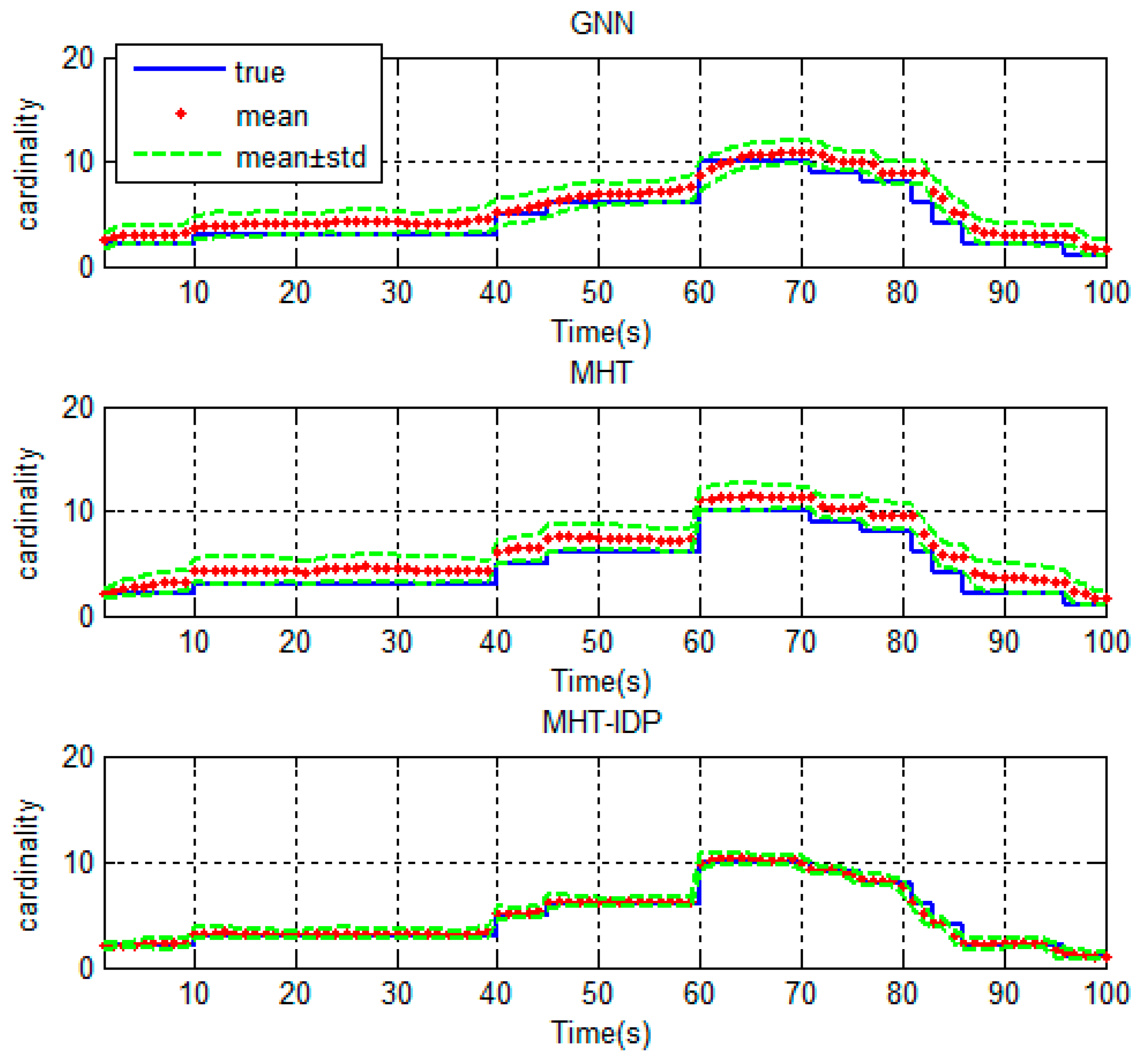
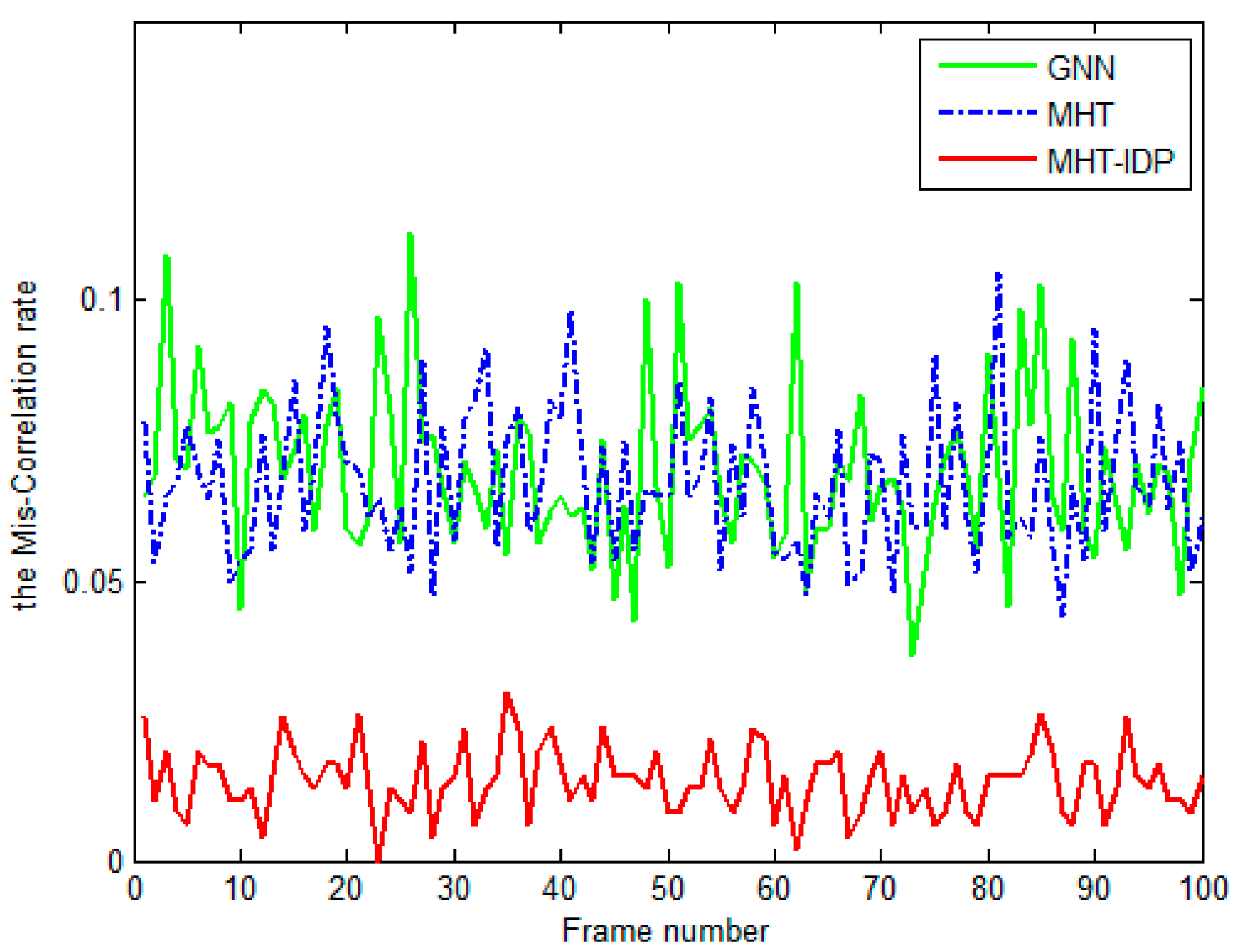
4.2. Results and Evaluation.
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bar-Shalom, Y.; Thomas, E.F.; Peter, G.C. Tracking and data association. J. Acoust. Soc. 1990, 87, 918–919. [Google Scholar] [CrossRef]
- Blackman, S.; Popolo, R. Design and Analysis of Modem Tracking System; Artech House: Boston, MA, USA, 1999. [Google Scholar]
- Raguraman, P.; Ramasundaram, M.; Balakrishnan, V. Localization in Wireless Sensor Networks: A Dimension based pruning approach in 3D environments. Appl. Soft Comput. 2018, 68, 219–232. [Google Scholar] [CrossRef]
- Strumberger, I.; Minovic, M.; Tuba, M.; Bacanin, N. Performance of Elephant Herding Optimization and Tree Growth Algorithm Adapted for Node Localization in Wireless Sensor Networks. Sensors 2019, 19, 2515. [Google Scholar] [CrossRef] [PubMed]
- Blackman, S. Multiple hypothesis tracking for multiple target tracking. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 5–18. [Google Scholar] [CrossRef]
- Willett, P.; Niu, R.; Bar-Shalom, Y. Integration of Bayes detection with target tracking. IEEE Trans. Signal Process. 2001, 49, 17–29. [Google Scholar] [CrossRef]
- Fortmann, T.; Bar-Shalom, Y.; Scheffe, M.; Gelfand, S. Detection thresholds for tracking in clutter—A connection between estimation and signal processing. IEEE Trans. Autom. Control 1985, 30, 221–229. [Google Scholar] [CrossRef]
- Boers, Y.; Driessen, H. Modified Riccati equation and its application to target tracking. IEE Proc. Radar Sonar Navig. 2006, 153, 7–12. [Google Scholar] [CrossRef]
- Aslan, M.S.; Saranli, A. Threshold optimization for tracking a nonmaneuvering target. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2844–2859. [Google Scholar] [CrossRef]
- Zeng, T.; Zheng, L.; Li, Y.; Chen, X.; Long, T. Offline Performance Prediction of PDAF with Bayesian Detection for Tracking in Clutter. IEEE Trans. Signal Process. 2012, 61, 770–781. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Kong, L.J.; YI, W.; Yang, X.B. Integration of Detection with JPDAF for Multi-Target Tracking. Radar Sci. Technol. 2014, 12, 143–148. [Google Scholar]
- Reid, D. An algorithm for tracking multiple targets. IEEE Trans. Autom. Control. 1979, 24, 843–854. [Google Scholar] [CrossRef]
- Demos, G.C. Applications of MHT to dim moving targets. In Proceedings of the Signal and Data Processing of Small Targets, Orlando, FL, USA, 1 October 1990; pp. 297–309. [Google Scholar]
- Werthmann, J.R. Step-by-step description of a computationally efficient version of multiple hypothesis tracking. In Proceedings of the Signal and Data Processing of Small Targets, Orlando, FL, USA, 25 August 1992; pp. 288–300. [Google Scholar]
- Frank, A.; Smyth, P.; Ihler, A. Beyond MAP estimation with the track-oriented multiple hypothesis tracker. IEEE Trans. Signal Process. 2014, 62, 2413–2423. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, B.; Chen, Y. Multiple hypothesis tracking with adaptive association depth. Syst. Eng. Electron. 2016, 38, 2000–2007. [Google Scholar]
- Zhang, Z.; Fu, K.; Sun, X.; Ren, W. Multiple target tracking based on multiple hypotheses tracking and modified ensemble Kalman filter in multi-sensor fusion. Sensors 2019, 19, 3118. [Google Scholar] [CrossRef] [PubMed]
- Klemm, R. Applications of Space-Time Adaptive Processing; IET: London, UK, 2004. [Google Scholar]
- Wald, A. Sequential tests of statistical hypotheses. Ann. Math. Stat. 1945, 16, 117–186. [Google Scholar] [CrossRef]
- Fu, J.; Sun, J.; Lu, S.; Zhang, Y. Multiple hypothesis tracking based on the shiryayev sequential probability ratio test. Sci. China Inf. Sci. 2016, 59, 1–11. [Google Scholar] [CrossRef][Green Version]
- Liu, Y.; Li, X.R. Sequential multiple-model detection of target maneuver termination. In Proceedings of the International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011. [Google Scholar]
- Sun, J.; Li, Q.; Zhang, X.; Sun, W. An Efficient Implementation of Track-Oriented Multiple Hypothesis Tracker Using Graphical Model Approaches. Math. Probl. Eng. 2017, 10, 1–11. [Google Scholar] [CrossRef]
- Leung, H.; Hu, Z.; Blanchette, M. Evaluation of multiple radar target trackers in stressful environments. IEEE Trans. Aerosp. Electron. Syst. 2002, 35, 663–674. [Google Scholar] [CrossRef]
- Hoffman, J.R.; Mahler, P.S. Multitarget miss distance via optimal assignment. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2004, 34, 327–336. [Google Scholar] [CrossRef]
- Yan, J.; Liu, H.; Jiu, B.; Liu, Z.; Bao, Z. Joint Detection and Tracking Processing Algorithm for Target Tracking in Multiple Radar System. IEEE Sens. J. 2015, 15, 6534–6541. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Li, Y.; Yu, J.; Li, X. A novel probabilistic data association for target tracking in a cluttered environment. Sensors 2016, 16, 2180. [Google Scholar] [CrossRef] [PubMed]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]
- He, S.; Shin, H.S.; Tsourdos, A. Joint Probabilistic Data Association Filter with Unknown Detection Probability and Clutter Rate. Sensors 2018, 18, 269. [Google Scholar]
| Algorithm | |||
|---|---|---|---|
| GNN | 0.901 | 10 | 0.283s |
| MHT | 0.924 | 11 | 0.309s |
| MHT-IDP | 0.982 | 3 | 0.486s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Sun, J.; Li, Q.; Ding, G. A New Multiple Hypothesis Tracker Integrated with Detection Processing. Sensors 2019, 19, 5278. https://doi.org/10.3390/s19235278
Wang Z, Sun J, Li Q, Ding G. A New Multiple Hypothesis Tracker Integrated with Detection Processing. Sensors. 2019; 19(23):5278. https://doi.org/10.3390/s19235278
Chicago/Turabian StyleWang, Ziwei, Jinping Sun, Qing Li, and Guanhua Ding. 2019. "A New Multiple Hypothesis Tracker Integrated with Detection Processing" Sensors 19, no. 23: 5278. https://doi.org/10.3390/s19235278
APA StyleWang, Z., Sun, J., Li, Q., & Ding, G. (2019). A New Multiple Hypothesis Tracker Integrated with Detection Processing. Sensors, 19(23), 5278. https://doi.org/10.3390/s19235278





