Exploring the Laplace Prior in Radio Tomographic Imaging with Sparse Bayesian Learning towards the Robustness to Multipath Fading
Abstract
:1. Introduction
- The image quality and localization accuracy are improved by enhancing the robustness to multipath fading.
- The computational cost in localization becomes reduced as well, this is owning to the adoption of the fast algorithm.
2. Preliminaries and Problem Statement
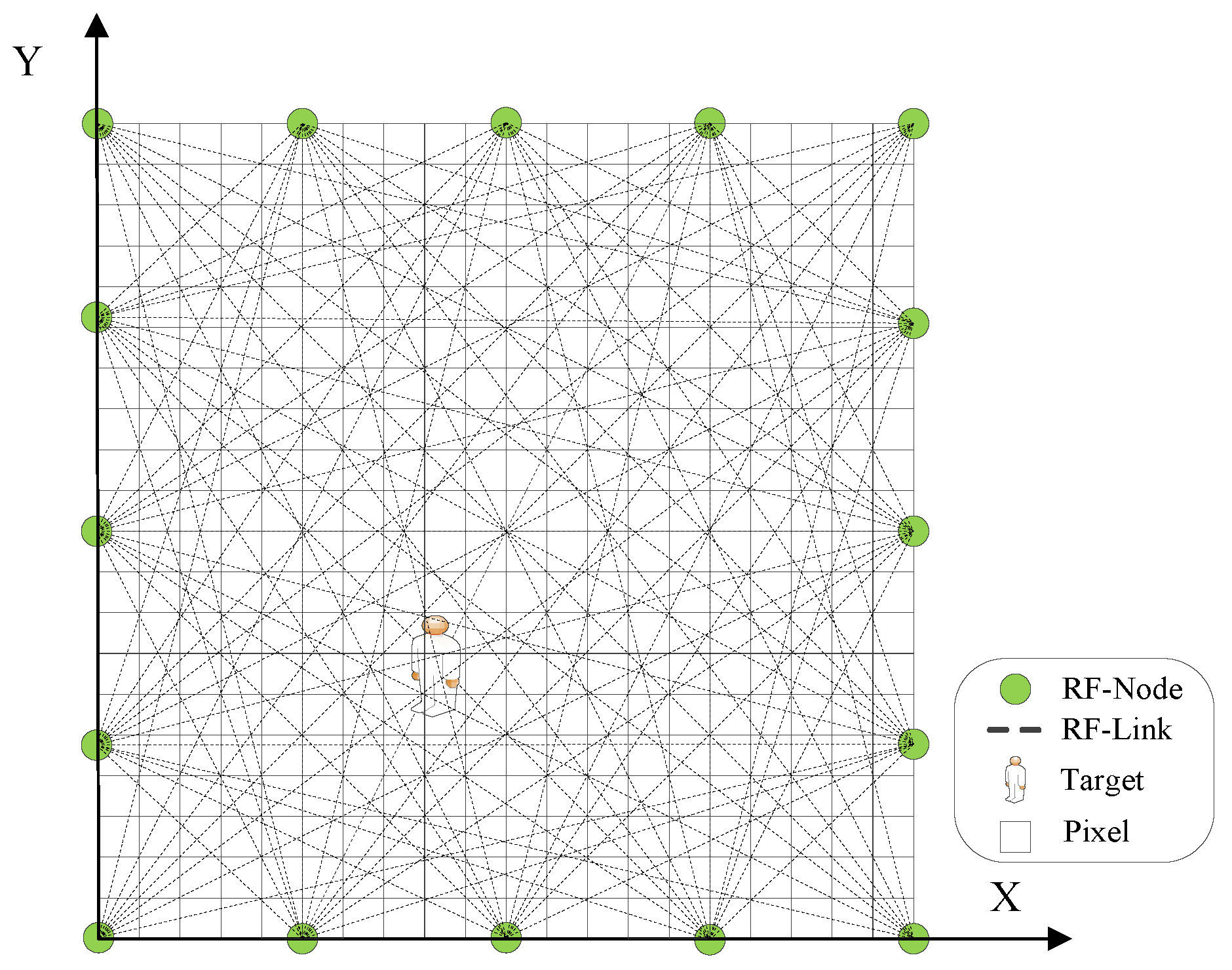
2.1. Radio Tomographic Imaging
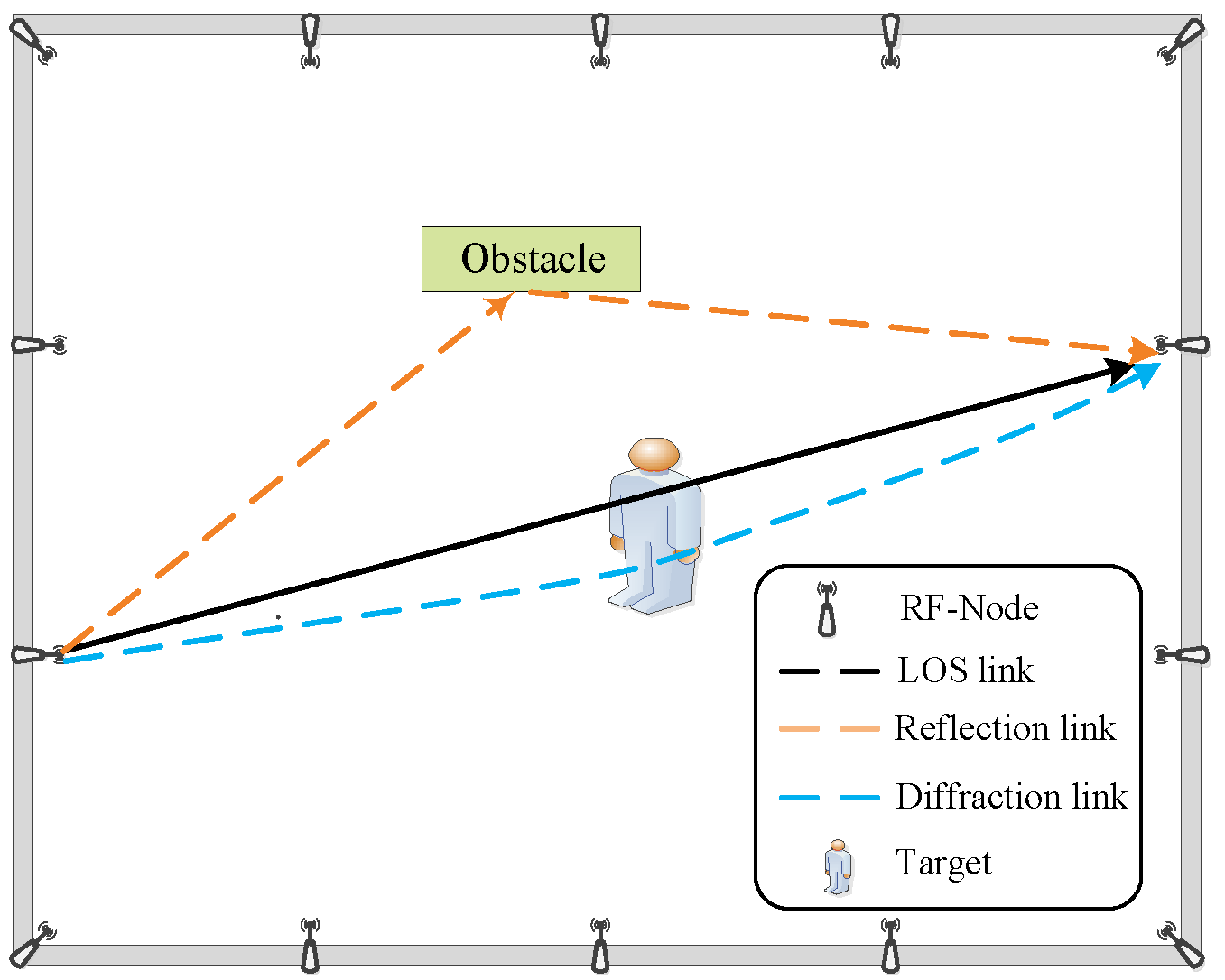
2.2. Problem Statement
3. RTI using SBL with Laplace Prior
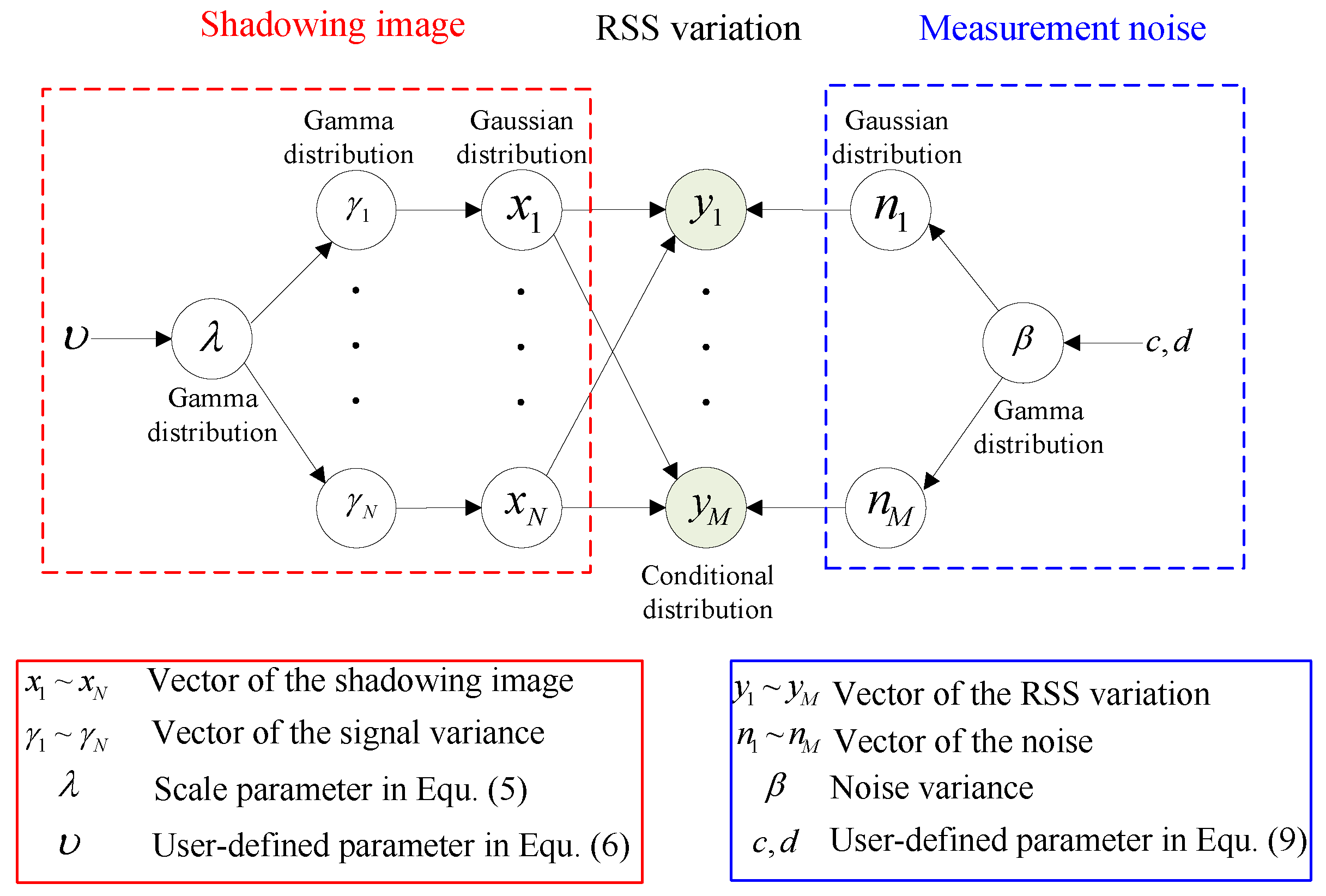
3.1. Laplace Prior used to Characterize the Shadowing Image
3.2. Bayesian Inference to Obtain the Sparse Maximum-a-Posterior Solution
| Algorithm 1: Fast algorithm of RTI using SBL with Laplace prior |
 |
4. Experiments and Results
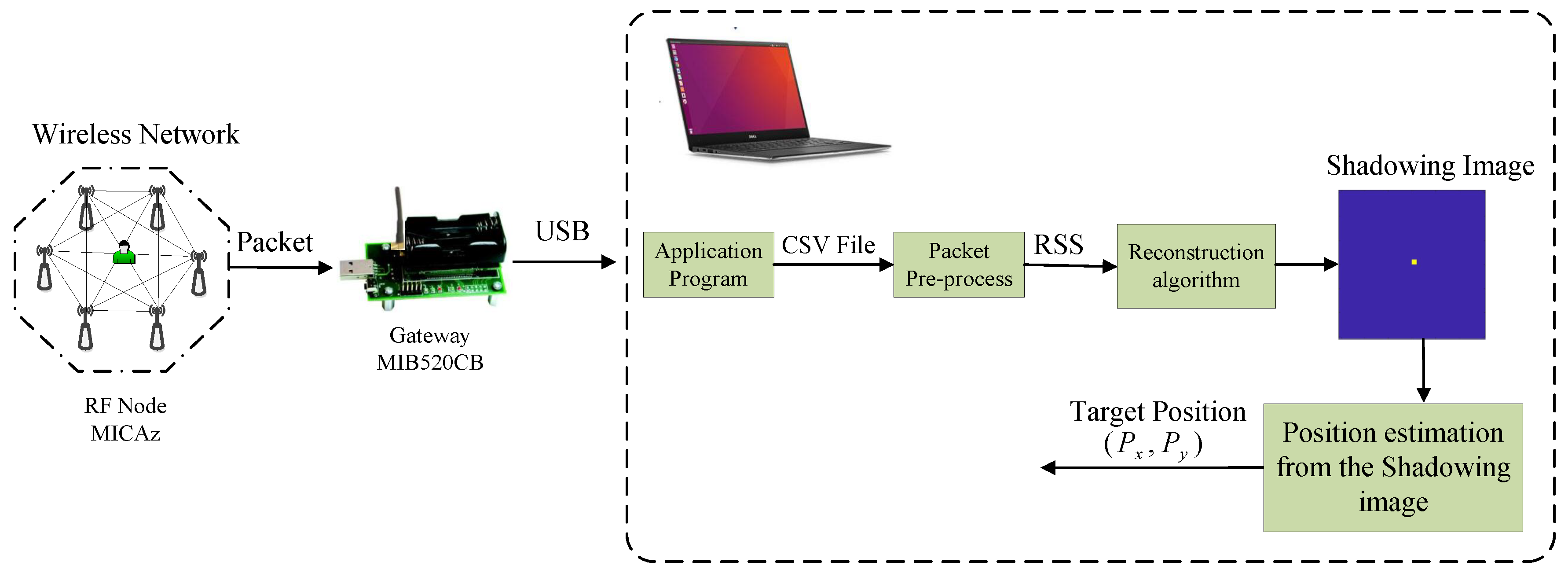
4.1. Experimental Setup
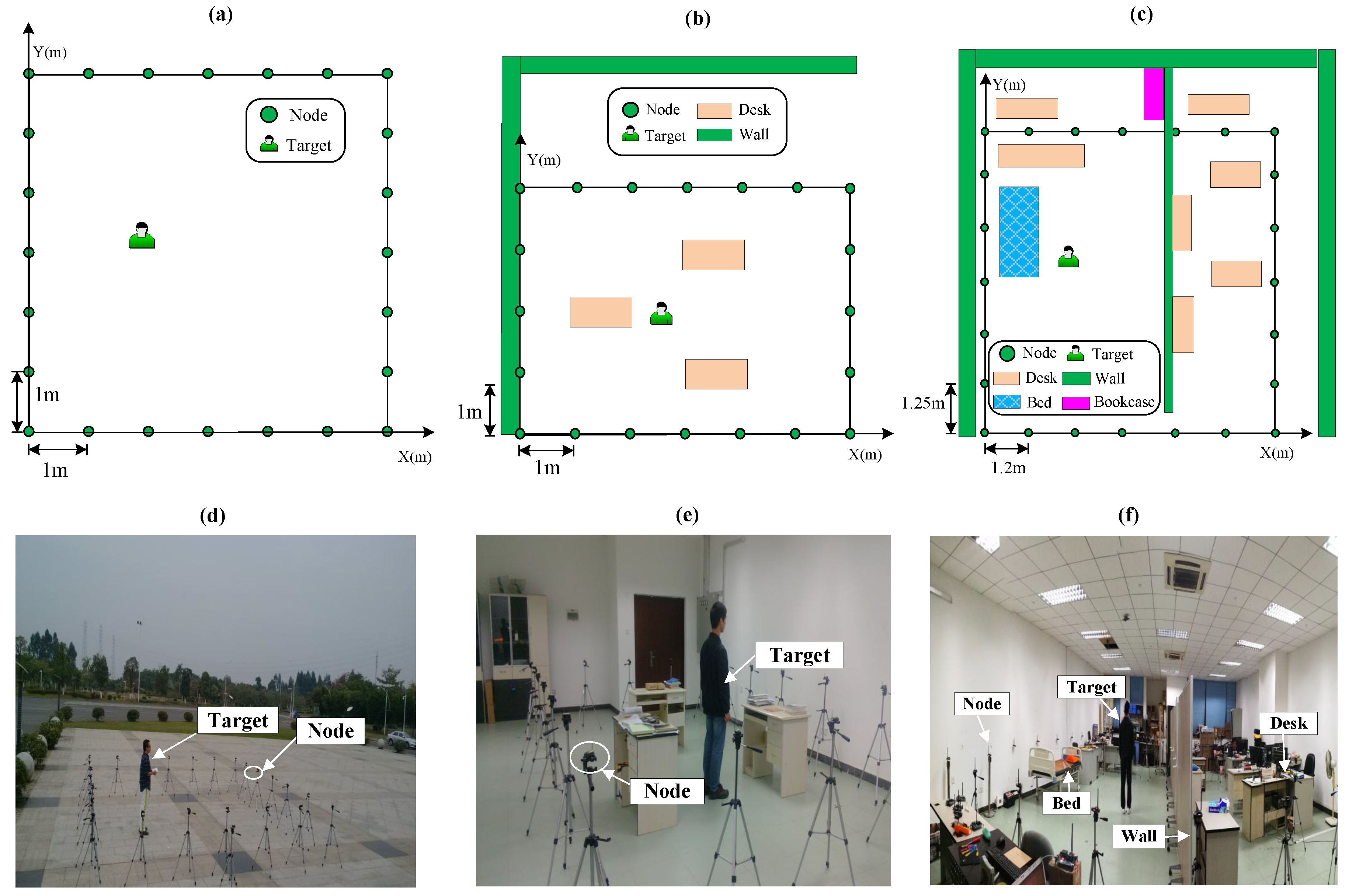
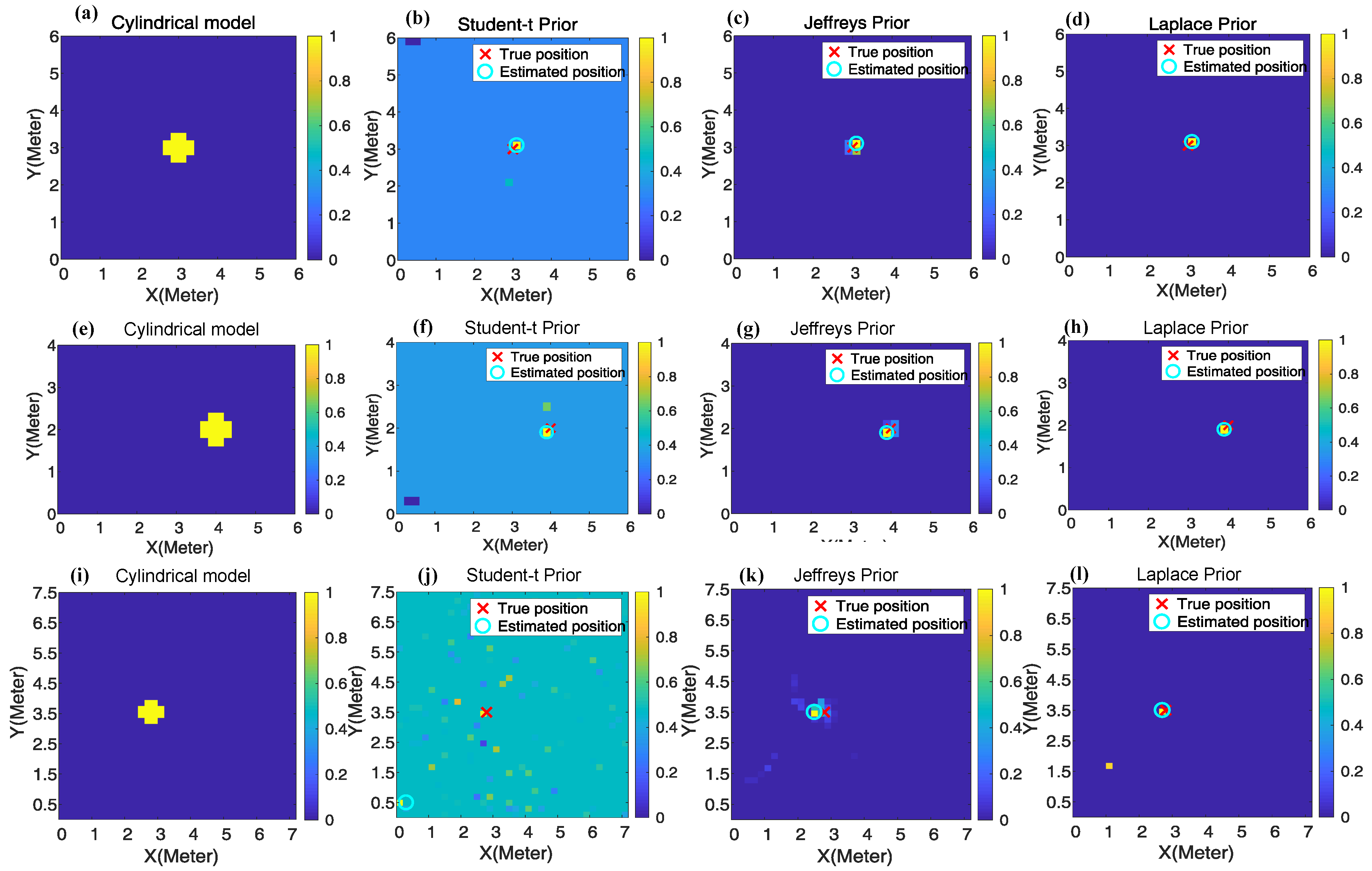
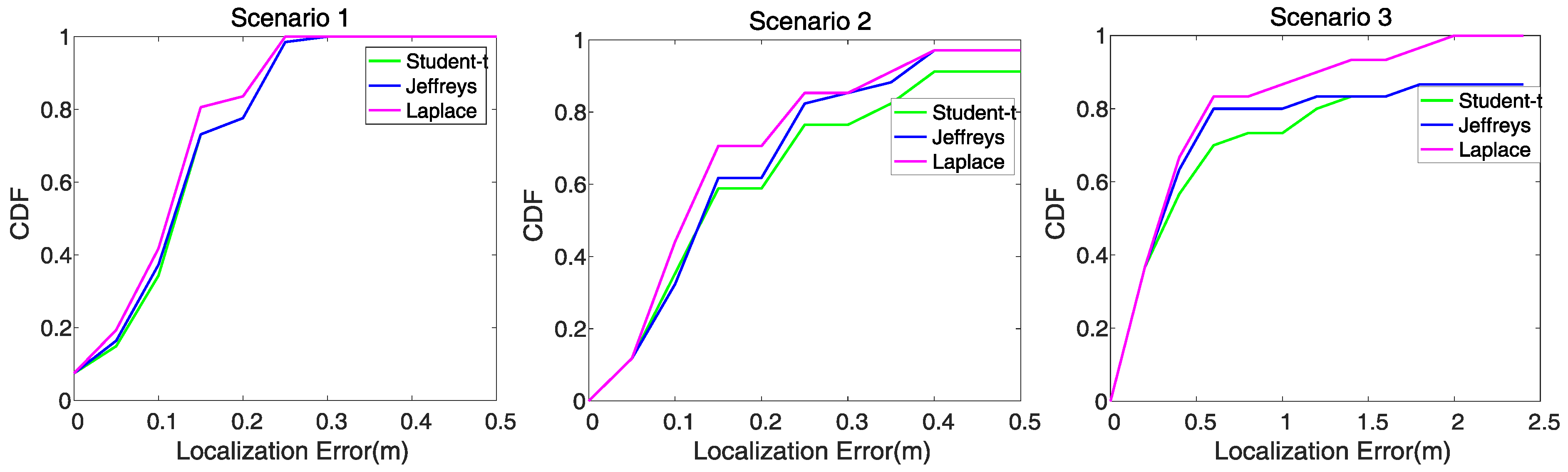
- Scenario 1: 24 RF-sensing nodes are deployed to cover an outdoor 6 m × 6 m area with each node 1 meter apart from the ground. The layout and photograph are presented in Figure 4a,d.
- Scenario 2: A sensing area of 6 m × 4 m is surrounded by 20 nodes in an indoor obstructed laboratory, as shown in Figure 4b,e. Three desks and some books are inside the sensing area.
- Scenario 3: The monitored 7.2 m × 7.5 m area is covered by 24 RF-sensing nodes in an indoor through-wall environment. As shown in Figure 4c,f, plenty of furniture, such as bed, desks, bookcase and computers obstruct the LOS of many RF links.
4.2. Imaging Experiment
4.3. Device-free Localization Experiment
4.4. Experiment in Localization Time
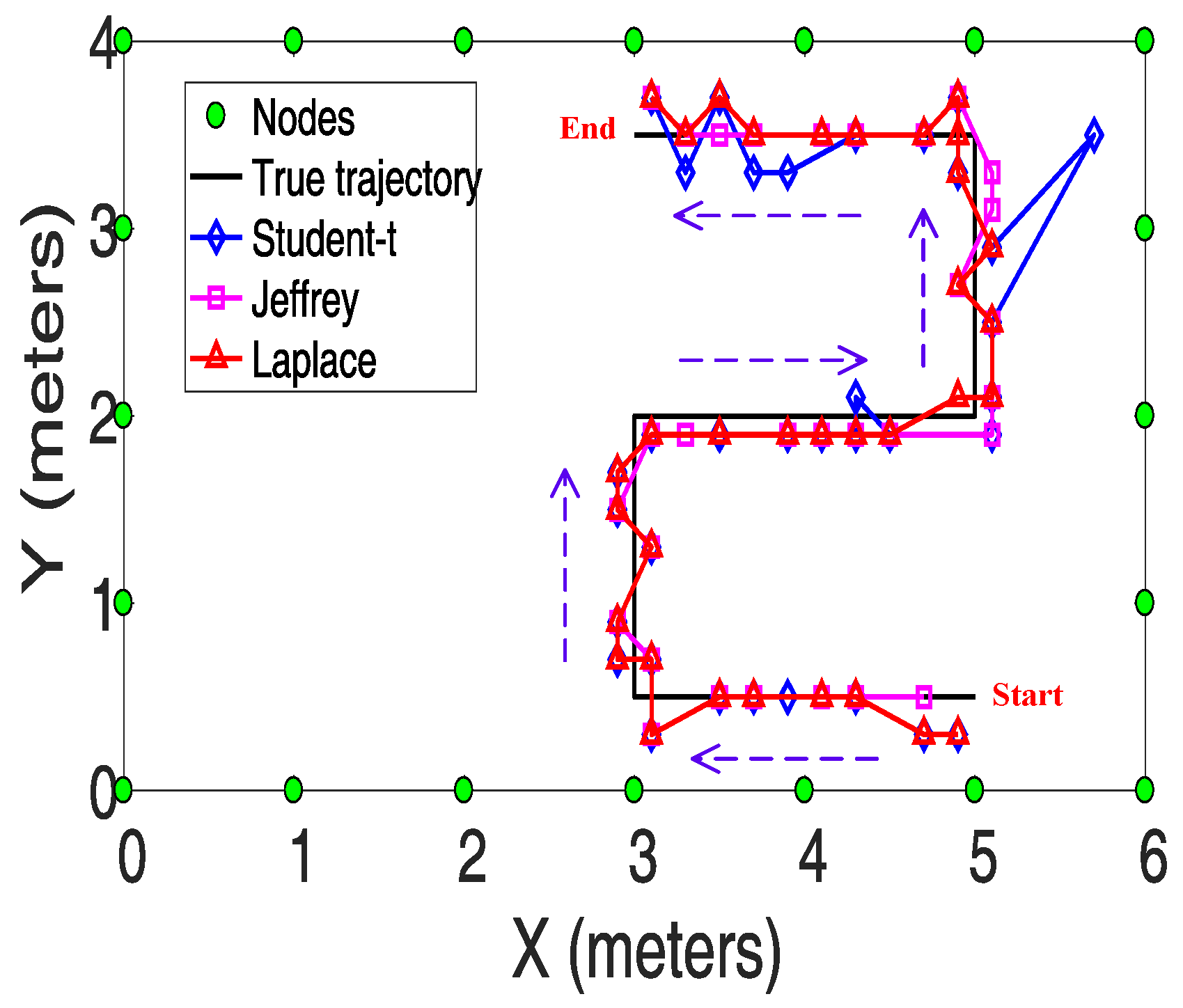
4.5. Device-free Tracking Experiment
5. Conclusions and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| RTI | Radio Tomographic Imaging |
| RF | Radio Frequency |
| RSS | Received Signal Strength |
| LOS | Line of Sight |
| NLOS | Non Line of Sight |
| SBL | Sparse Bayesian Learning |
| MAP | maximum-a-posterior |
| PIR | pyroelectric infrared |
| UWB | ultra-wide band |
| CSI | Channel State Information |
| SVD | Singular Value Decomposition |
| HBCS | heterogeneous Bayesian compressive sensing |
| MSE | Mean Square Error |
| CDF | Cumulative Distribution Function |
| Variable List | |
| Variable | Explanation |
| RSS variation | |
| Vector of the shadowing image | |
| Measurement noise | |
| Measurement matrix | |
| Distance between the transmitter and the receiver | |
| Distance between the target and the transmitter | |
| Distance between the target and the receiver | |
| Scale parameter of the Laplace distribution | |
| Vector of the signal variance | |
| Inverse of the noise variance | |
| Posterior mean | |
| Posterior covariance | |
| ‘Sparsity factor’ variable | |
| ‘Quality factor’ variable | |
| Vector of the estimated shadowing image | |
| Vector of the reference shadowing image | |
| Mean square error of the shadowing image | |
| Estimated position of the target | |
| True position of the target | |
| Localization error | |
| Mean tracking error |
References
- Joey, W.; Neal, P. Radio tomographic imaging with wireless networks. IEEE Trans. Mob. Comput. 2010, 9, 621–632. [Google Scholar]
- Dustin, M.; Joey, W.; Neal, P. Toward a rapidly deployable radio tomographic imaging system for tactical operations. In Proceedings of the 38th Annual IEEE Conference on Local Computer Networks, Sydney, NSW, Australia, 21–24 October 2013; pp. 203–210. [Google Scholar]
- Cesare, A.; Maurizio, B.; Giacomo, B.; Neal, P.; Manuel, R. RTI goes wild: Radio tomographic imaging for outdoor people detection and localization. IEEE Trans. Mob. Comput. 2016, 15, 2585–2598. [Google Scholar]
- Christopher, A.; Martin, R.; Owens, W.; Ryan, T. Radio tomography for roadside surveillance. IEEE J. Sel. Top. Signal Process. 2014, 8, 66–79. [Google Scholar]
- Ossi, K.; Maurizio, B.; Neal, P. Follow@ grandma: Long-term device-free localization for residential monitoring. In Proceedings of the 37th Annual IEEE Conference on Local Computer Networks, Clearwater, FL, USA, 22–25 October 2012; pp. 991–998. [Google Scholar]
- Nathavuth, K.; Hirozumi, Y.; Teruo, H. EasyTrack: Zero-Calibration Smart-Home Tracking System. J. Inf. Process. Syst. 2019, 27, 445–455. [Google Scholar]
- Maurizio, B.; Ossi, K.; Neal, P. Radio Tomographic Imaging for Ambient Assisted Living. Evaluating AAL Systems Through Competitive Benchmarking; Springer: Berlin/Heidelberg, Germany, 2013; pp. 108–130. [Google Scholar]
- Goncalo, M.; Rui, P. An Indoor Monitoring System for Ambient Assisted Living Based on Internet of Things Architecture. Int. J. Environ. Res. Public Health 2016, 13, 1152. [Google Scholar]
- Millar, G.; Aghdasi, F.; Lei, W. Tracking Moving Objects using a Camera Network. U.S. Patent 9615064, 2017. [Google Scholar]
- Jong-Wan, Y.; Taejoon, P. Maximizing Localization Accuracy via Self-Configurable Ultrasonic Sensor Grouping Using Genetic Approach. IEEE Trans. Instrum. Meas. 2016, 65, 1518–1529. [Google Scholar]
- Zhang, S.; Liu, K.H.; Ma, Y.T.; Huang, X.D.; Gong, X.L.; Zhang, Y.L. An Accurate Geometrical Multi-Target Device-Free Localization Method Using Light Sensors. IEEE Sens. J. 2018, 18, 7619–7632. [Google Scholar] [CrossRef]
- Jurgen, K.; Daniel, H. Passive infrared localization with a Probability Hypothesis Density filter. In Proceedings of the 7th Workshop on Positioning, Navigation and Communication, Dresden, Germany, 11–12 March 2010; pp. 68–76. [Google Scholar]
- Sujay, N.; Sujay, N.; Vijay, S.R.; Prabhakar, T.V.; Sripad, S.K.; Madhuri, S.I. PIR sensors: Characterization and novel localization technique. In IPSN ’15 Proceedings of the 14th International Conference on Information Processing in Sensor Networks; ACM Digital Library: Seattle, WA, USA, 2015; pp. 142–153. [Google Scholar]
- Wilson, J.; Patwari, N. See-through walls: Motion tracking using variance-based radio tomography networks. IEEE Trans. Mob. Comput. 2011, 10, 612–621. [Google Scholar] [CrossRef]
- Wang, X.Y.; Gao, L.J.; Mao, S.W.; Santosh, P. CSI-based fingerprinting for indoor localization: A deep learning approach. IEEE Trans. Veh. Technol. 2017, 66, 763–776. [Google Scholar] [CrossRef]
- Wu, K.; Xiao, J.; Yi, Y.; Chen, D.; Luo, X.; Ni, L. CSI-based indoor localization. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 1300–1309. [Google Scholar] [CrossRef]
- Neal, P.; Joey, W. RF Sensor Networks for Device-Free Localization: Measurements, Models, and Algorithms. Proc. IEEE 2010, 98, 1961–1973. [Google Scholar]
- Henri, N.; Anssi, R.; Simo, A.L.; Robert, P. Particle filter and smoother for indoor localization. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Montbeliard-Belfort, France, 28–31 October 2014; pp. 1–10. [Google Scholar]
- Min, P.J.; Ki, A.C.; Yuriy, S.S.; Peng, S.; Taeg, L.M. Accurate and reliable human localization using composite particle/FIR filtering. IEEE Trans. Hum.-Mach. Syst. 2017, 47, 332–342. [Google Scholar]
- Li, Z.; Liu, J.B.; Yang, F.; Niu, X.G.; Li, L.L.; Wang, Z.M.; Chen, R.Z. A Bayesian Density Model Based Radio Signal Fingerprinting Positioning Method for Enhanced Usability. Sensors 2018, 18, 4063. [Google Scholar] [CrossRef] [PubMed]
- Erick, S.; Misbahuddin, A.M.; David, A. A Performance Study of a Fast-Rate WLAN Fingerprint Measurement Collection Method. IEEE Trans. Instrum. Meas. 2018, 67, 2273–2281. [Google Scholar]
- Talampas, M.C.R.; Low, K.S. A geometric filter algorithm for robust device-free localization in wireless networks. IEEE Trans. Ind. Inf. 2016, 12, 1670–1678. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, W.D.; Zhang, S.; Huang, S.D. Device-Free Localization via an Extreme Learning Machine with Parameterized Geometrical Feature Extraction. Sensors 2017, 17, 879. [Google Scholar] [CrossRef]
- Kaltiokallio, O.; Jäntti, R.; Patwari, N. ARTI: An Adaptive Radio Tomographic Imaging System. IEEE Trans. Veh. Technol. 2017, 66, 7302–7316. [Google Scholar] [CrossRef]
- Huseyin, Y.; Riku, J.; Ossi, K.; Neal, P. Detector Based Radio Tomographic Imaging. IEEE Trans. Mob. Comput. 2017, 17, 58–71. [Google Scholar]
- Wang, Z.; Su, H.; Guo, X.M.; Wang, G.L. Radio Tomographic Imaging with Feedback-Based Sparse Bayesian Learning. In Proceedings of the 2018 Eighth International Conference on Information Science and Technology (ICIST), Cordoba, Spain, 30 June–6 July 2018; pp. 50–56. [Google Scholar]
- Daniel, R.; Donghoon, L.; Georgios, B.G. Blind Radio Tomography. IEEE Trans. Signal Process. 2018, 66, 2055–2069. [Google Scholar]
- Yigitler, H. Narrowband Radio Frequency Inference: Physical Modeling and Measurement Processing. Ph.D. Thesis, Aalto University, Otakaari, Finland, 2018. [Google Scholar]
- Yigitler, H.; Ossi, K.; Riku, J. Received Signal Strength Models for Narrowband Radios; IGI Global: Hershey, PA, USA, 2018; Chapter 2. [Google Scholar]
- Jakub, N.; Zdenek, T.; Vlastimil, B.; Ladislav, P.; Ondrej, K.; Libor, B.; Jiri, S.; Tomas, K. Study of the performance of RSSI based Bluetooth Smart indoor positioning. In Proceedings of the 2016 26th International Conference Radioelektronika (RADIOELEKTRONIKA), Kosice, Slovakia, 19–20 April 2016; pp. 121–125. [Google Scholar]
- Bo, W.; Ambuj, V.; Neal, P.; Wen, H.; Thiemo, V.; Chou, C.T. dRTI: Directional radio tomographic imaging. In Proceedings of the 14th International Conference on Information Processing in Sensor Networks, Seattle, WA, USA, 13–16 April 2015; pp. 166–177. [Google Scholar]
- Cheng, Q.; Peter, H.; Amal, A.H.; Neal, P.; Gregory, D.D. On-Wall, Wide Bandwidth E-Shaped Patch Antenna for Improved Whole-Home Radio Tomography. IEEE J. Radio Freq. Identif. (RFID) 2017, 1, 22–31. [Google Scholar]
- Xu, S.X.; Liu, H.; Gao, F.; Wang, Z.H. Compressive Sensing Based Radio Tomographic Imaging with Spatial Diversity. Sensors 2019, 19, 439. [Google Scholar] [CrossRef] [PubMed]
- Kaltiokallio, O.; Bocca, M.; Patwari, N. Enhancing the accuracy of radio tomographic imaging using channel diversity. In Proceedings of the 2012 IEEE 9th International Conference on Mobile Ad-Hoc and Sensor Systems (MASS 2012), Las Vegas, NV, USA, 8–11 October 2012; pp. 254–262. [Google Scholar]
- Stijn, D.; Rafael, B.; Glenn, E.; Maarten, W. Multi-frequency sub-1 GHz radio tomographic imaging in a complex indoor environment. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 1–8. [Google Scholar]
- Jin, J.; Ke, W.; Lu, J.; Wang, Y.L.; Zoran, S. Multi-channel RTI fusion based on improved joint sparse model. In Proceedings of the 2018 Ubiquitous Positioning, Indoor Navigation and Location-Based Services (UPINLBS), Wuhan, China, 22–23 March 2018; pp. 1–6. [Google Scholar]
- Wang, J.; Gao, Q.; Wang, H.; Cheng, P.; Xin, K. Device-free localization with multidimensional wireless link information. IEEE Trans. Veh. Technol. 2015, 64, 356–366. [Google Scholar] [CrossRef]
- Wilson, J.; Patwari, N. A fade-level skew-laplace signal strength model for device-free localization with wireless networks. IEEE Trans. Mob. Comput. 2012, 11, 947–958. [Google Scholar] [CrossRef]
- Yang, L.W.; Huang, K.D.; Wang, G.L.; Guo, X.M. An enhanced multi-scale model for shadow fading in radio tomographic imaging. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 5925–5930. [Google Scholar]
- Tan, J.J.; Zhao, X.; Yang, L.W.; Guo, X.M.; Wang, G.L. Backprojection and Integration for the Multi-Scale Spatial Model in Radio Tomographic Imaging. In Proceedings of the 2018 IEEE 8th Annual International Conference on CYBER Technology in Autoumation, Control, and Intelligent System (CYBER), Tianjin, China, 19–23 July 2018; pp. 522–527. [Google Scholar]
- Tan, J.J.; Zhao, Q.Q.; Guo, X.M.; Zhao, X.; Wang, G.L. Radio Tomographic Imaging Based on Low-Rank and Sparse Decomposition. IEEE Access 2019, 7, 50223–50231. [Google Scholar] [CrossRef]
- Huang, K.D.; Guo, Y.; Guo, X.M.; Wang, G.L. Heterogeneous Bayesian compressive sensing for sparse signal recovery. IET Signal Process. 2014, 8, 1009–1017. [Google Scholar] [CrossRef]
- Huang, K.D.; Tan, S.B.; Luo, Y.B.; Guo, X.M.; Wang, G.L. Enhanced radio tomographic imaging with heterogeneous Bayesian compressive sensing. Pervasive Mob. Comput. 2017, 40, 450–463. [Google Scholar] [CrossRef]
- Andrea, E.; Michael, R. Background Subtraction for Online Calibration of Baseline RSS in RF Sensing Networks. IEEE Trans. Mob. Comput. 2013, 12, 2386–2398. [Google Scholar]
- Viani, F.; Rocca, P.; Oliveri, G.; Trinchero, D.; Massa, A. Localization, tracking, and imaging of targets in wireless sensor networks: An invited review. Radio Sci. 2011, 46, 1–12. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian learning and the relevance vector machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Wang, Z.; Qin, L.; Guo, X.M.; Wang, G.L. Dual radio tomographic imaging with shadowing-measurement awareness. IEEE Trans. Instrum. Meas. 2019. [Google Scholar] [CrossRef]
- Derin, B.S.; Rafael, M.; Aggelos, K.K. Bayesian Compressive Sensing Using Laplace Priors. IEEE Trans. Image Process. 2010, 19, 53–63. [Google Scholar]
- Michael, E.T.; Anita, F. Fast Marginal Likelihood Maximisation for Sparse Bayesian Models. In Proceedings of the Ninth International Workshop on Artificial Intelligence and Statistics (AISTATS), Cambridge, UK, 26 June 2003; pp. 1–8. [Google Scholar]
- Ji, S.H.; Xue, Y.; Lawrence, C. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Figueiredo, M. Adaptive sparseness using Jeffreys prior. In Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic, Vancouver, BC, Canada, 3–8 December 2001; pp. 697–704. [Google Scholar]
- Kun, M. Jeffreys Prior: Philosophy, Information Geometry and Empirical Bayesian Methods. Available online: https://www.researchgate.net/publication/323736141_Jeffreys_Prior_Philosophy_Information_Geometry_and_Empirical_Bayesian_Methods (accessed on 17 November 2019).

| Symbol | Appearance | Value | Explanation |
|---|---|---|---|
| Section 2.1 | 0.2 m | Pixel size | |
| Equation (2) | 0.02 m | Ellipse width | |
| Equation (6) | 2 | Shape and scale parameters for | |
| c | Equation (9) | 1 | Shape parameter for |
| d | Equation (9) | 0 | Scale parameter for |
| Algorithm 1 | 0.01 | Initial noise variance | |
| Algorithm 1 | 1000 | Maximum iteration number | |
| Algorithm 1 | 0.01 | Precision during the iteration | |
| R | Equation (22) | 0.4 m | Radius of the cylindrical model |
| Setup | Student-t Prior | Jeffrey’s Prior | Laplace Prior |
|---|---|---|---|
| Scenario-1 | 1.5 | 0.3 | 0.2 |
| Scenario-2 | 2.2 | 1.2 | 0.3 |
| Scenario-3 | 90.8 | 79.5 | 1.1 |
| Setup | Student-t Prior | Jeffrey’s Prior | Laplace Prior |
|---|---|---|---|
| Scenario-1 | 0.0232 | 0.0024 | 0.0023 |
| Scenario-2 | 0.1041 | 0.0182 | 0.0085 |
| Scenario-3 | 0.1916 | 0.0042 | 0.0018 |
| Setup | Student-t Prior | Jeffrey’s Prior | Laplace Prior |
|---|---|---|---|
| Scenario-1 | 0.13 | 0.12 | 0.11 |
| Scenario-2 | 0.33 | 0.19 | 0.18 |
| Scenario-3 | 0.88 | 0.70 | 0.43 |
| Setup | Student-t Prior | Jeffrey’s Prior | Laplace Prior |
|---|---|---|---|
| Scenario-1 | 30.3 | 749.9 | 27.2 |
| Scenario-2 | 21.3 | 449.1 | 15.1 |
| Scenario-3 | 39.8 | 2802.5 | 30.2 |
| Prior | Tracking Error |
|---|---|
| Student-t | 0.26 |
| Jeffrey’s | 0.23 |
| Laplace | 0.21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Guo, X.; Wang, G. Exploring the Laplace Prior in Radio Tomographic Imaging with Sparse Bayesian Learning towards the Robustness to Multipath Fading. Sensors 2019, 19, 5126. https://doi.org/10.3390/s19235126
Wang Z, Guo X, Wang G. Exploring the Laplace Prior in Radio Tomographic Imaging with Sparse Bayesian Learning towards the Robustness to Multipath Fading. Sensors. 2019; 19(23):5126. https://doi.org/10.3390/s19235126
Chicago/Turabian StyleWang, Zhen, Xuemei Guo, and Guoli Wang. 2019. "Exploring the Laplace Prior in Radio Tomographic Imaging with Sparse Bayesian Learning towards the Robustness to Multipath Fading" Sensors 19, no. 23: 5126. https://doi.org/10.3390/s19235126
APA StyleWang, Z., Guo, X., & Wang, G. (2019). Exploring the Laplace Prior in Radio Tomographic Imaging with Sparse Bayesian Learning towards the Robustness to Multipath Fading. Sensors, 19(23), 5126. https://doi.org/10.3390/s19235126





