A Sensor for Spirometric Feedback in Ventilation Maneuvers during Cardiopulmonary Resuscitation Training
Abstract
1. Introduction
2. Mathematical Modeling of Propeller Type Flow Sensors
3. Materials and Methods
3.1. YF-S201 Flow Sensor
3.2. Calibration
3.3. Spirometric Tests
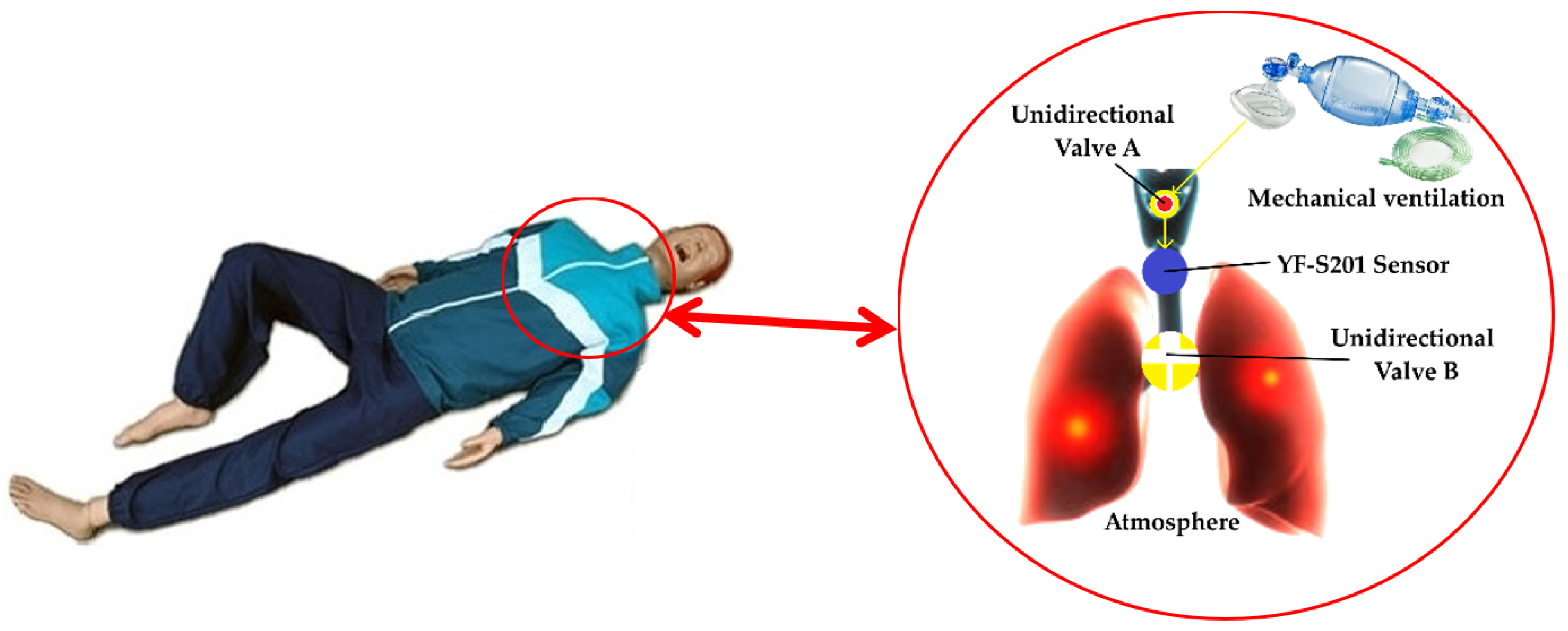
3.4. Spirometric Feedback in Ventilation Maneuvers during Cardiopulmonary Resuscitation Training
4. Results and Discussion
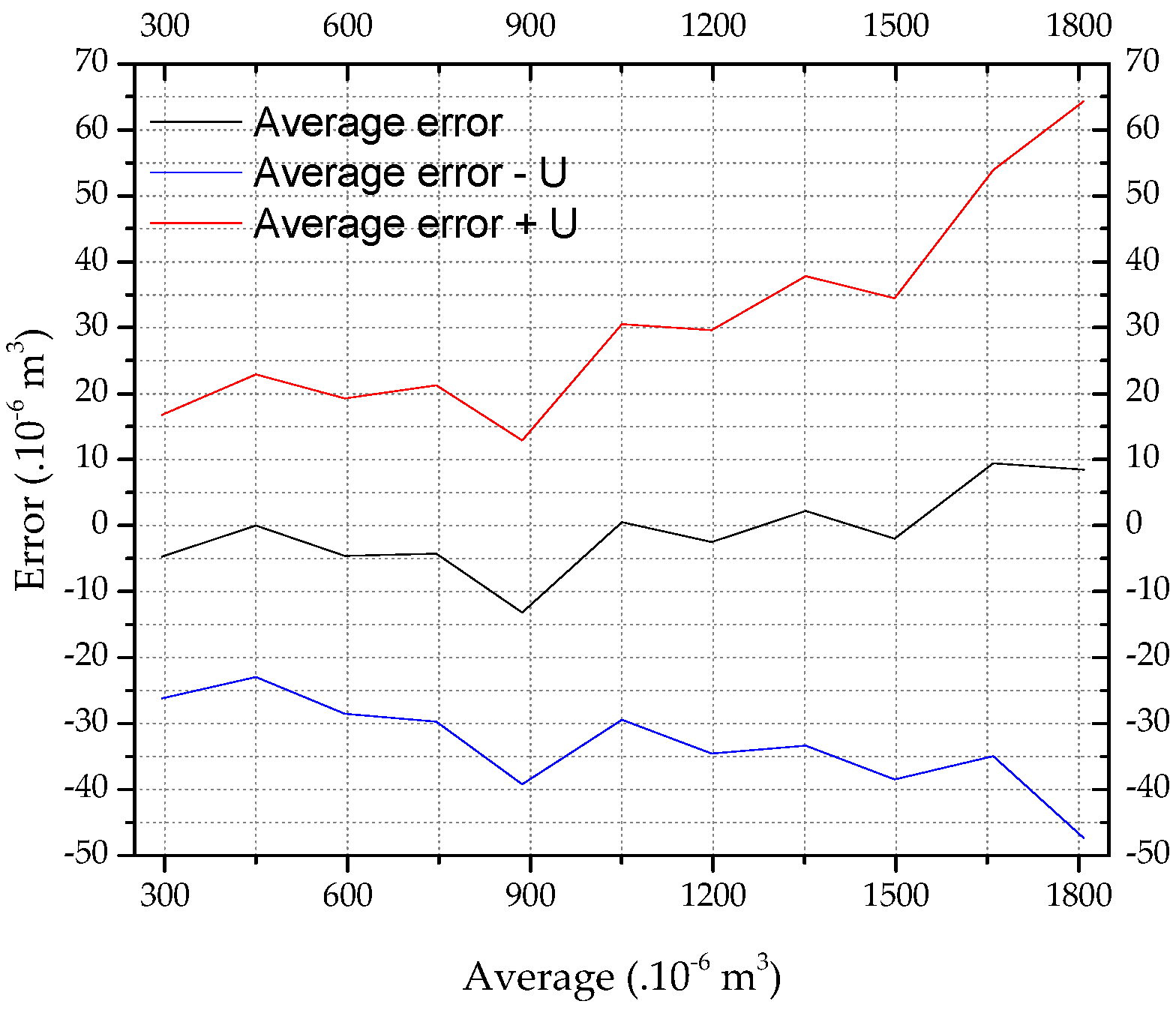
4.1. Calibration and Validation
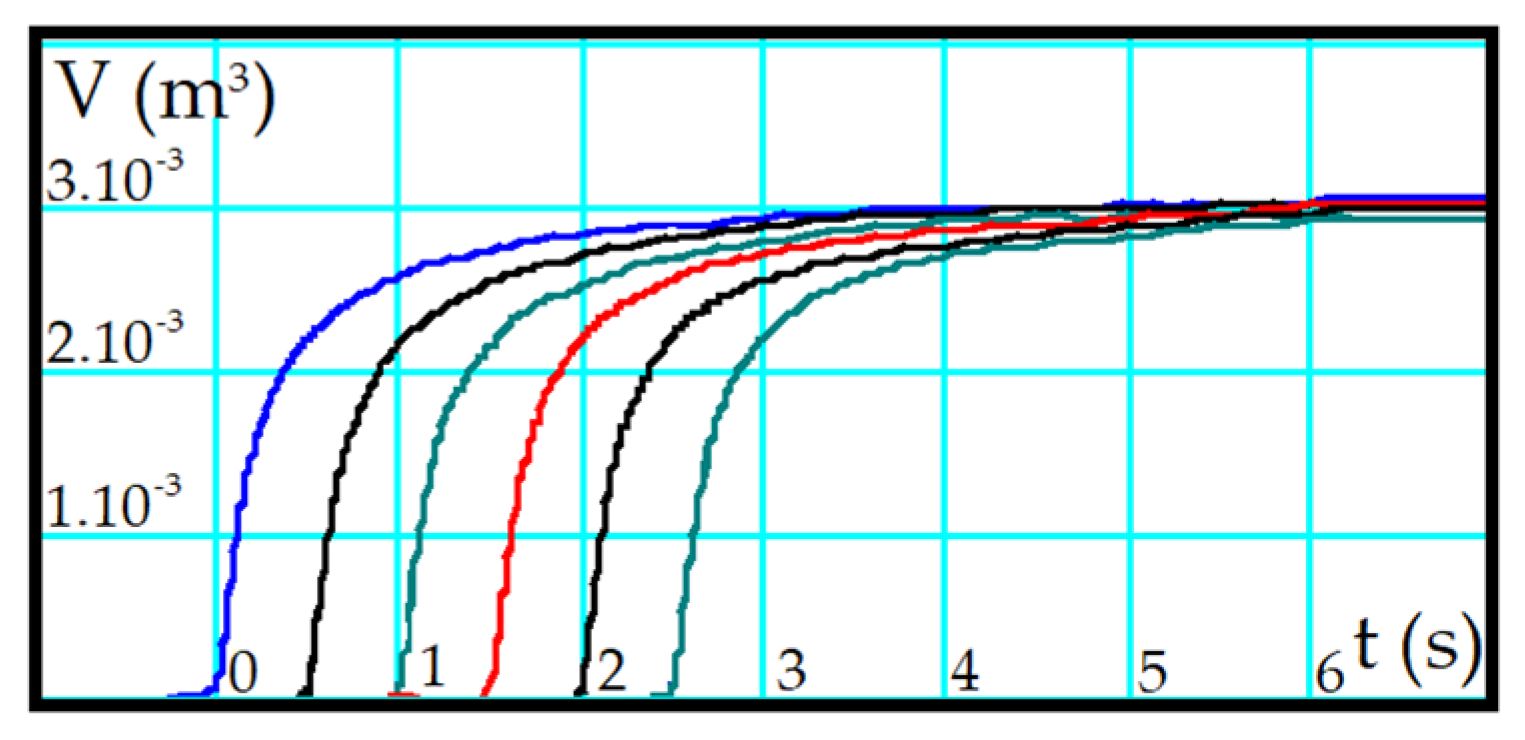
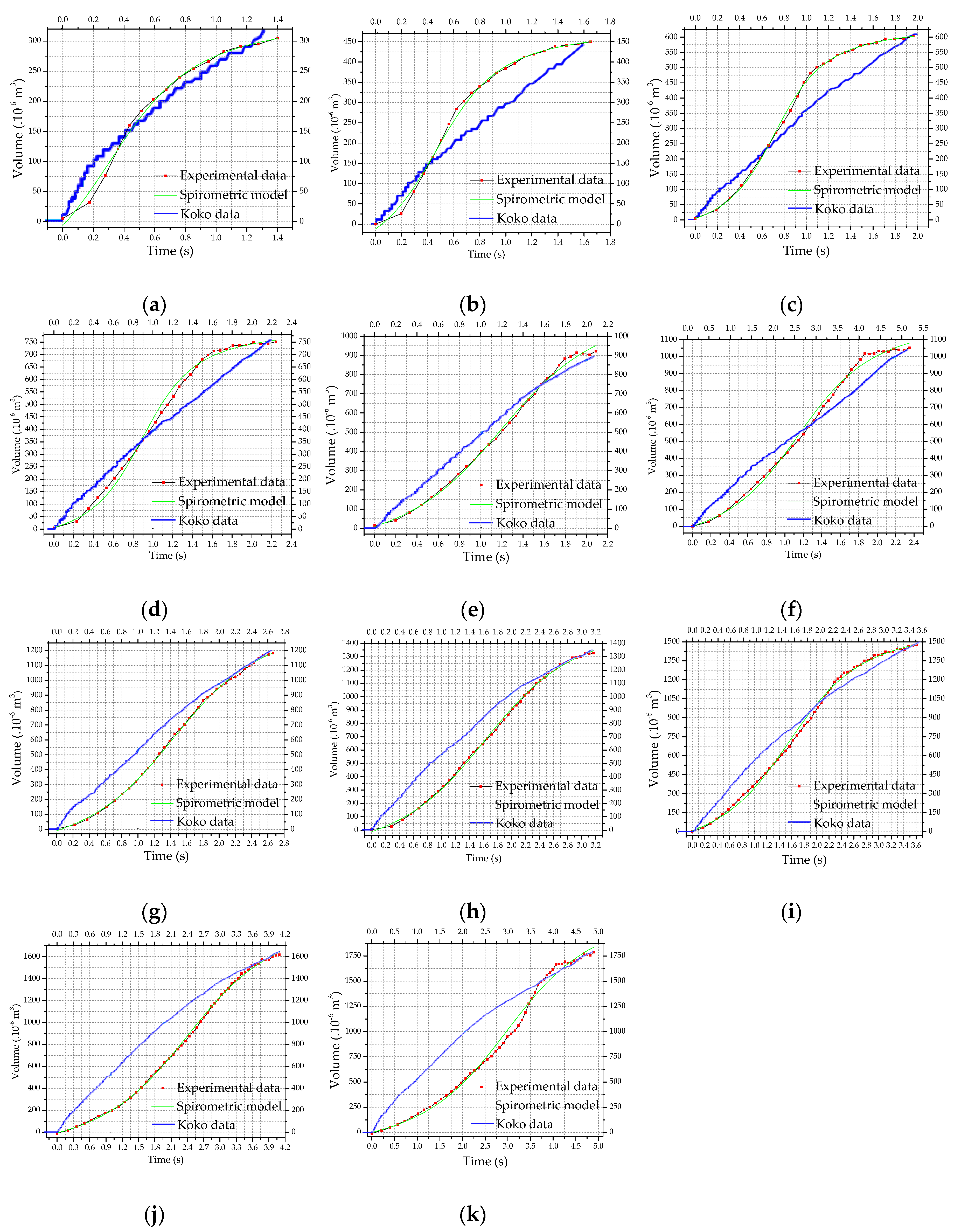
4.2. Spirometric Tests
4.3. Spirometric Feedback in Ventilation Maneuvers during Cardiopulmonary Resuscitation Training
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gu, S.; Leader, J.; Zheng, B.; Chen, Q.; Sciurba, F.; Kminski, N.; Gur, D.; Pu, J. Direct assessment of lung function in COPD using CT densitometric measures Direct assessment of lung function in COPD using CT densitometric measures. Physiol. Meas. 2014, 35, 833–845. [Google Scholar] [CrossRef] [PubMed]
- Kongstad, T.; Buchvald, F.F.; Green, K.; Lindblad, A.; Robinson, T.E.; Nielsen, K.G. Improved air trapping evaluation in chest computed tomography in children with cystic fi brosis using real-time spirometric monitoring and biofeedback. J. Cyst. Fibros. 2013, 12, 559–566. [Google Scholar] [CrossRef] [PubMed]
- Monfraix, S.; Bayat, S.; Porra, L.; Berruyer, G. Physics in Medicine & Biology Quantitative measurement of regional lung gas volume by synchrotron radiation computed tomography Quantitative measurement of regional lung gas volume by synchrotron radiation computed tomography. Phys. Med. Biol. 2005, 50, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Karimi, R.; Tornling, G.; Forsslund, H.; Mikko, M.; Wheelock, A.M.; Nyrén, S.; Sköld, C.M. Differences in regional air trapping in current smokers with normal spirometry. Eur. Respir. J. 2017, 49, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Chun, E.; Suh, S.; Yang, J.; Shim, S. Evaluation of postoperative change in lung volume in adolescent idiopathic scoliosis Measured by computed tomography. Indian J. Orthop. 2014, 48, 360–365. [Google Scholar] [PubMed]
- Nyeng, T.B.; Kallehauge, J.F.; Høyer, M.; Petersen, J.B.B.; Poulsen, P.R.; Muren, L.P. Clinical validation of a 4D-CT based method for lung ventilation measurement in phantoms and patients. Acta Oncol. 2011, 50, 897–907. [Google Scholar] [CrossRef]
- Nebuya, S.; Mills, G.H.; Milnes, P.; Brown, B.H. Indirect measurement of lung density and air volume from electrical impedance tomography (EIT) data. Physiol. Meas. 2011, 32, 1953–1967. [Google Scholar] [CrossRef]
- Riera, J.; Corte’s, J.; Masclans, J.R.; Rello, J. Effect of High-Flow Nasal Cannula and Body Position on End-Expiratory Lung Volume: A Cohort Study Using Electrical Impedance Tomography. Respir. Care 2013, 58, 589–596. [Google Scholar] [CrossRef]
- Kyriazis, A.; De Alejo, R.P.; Rodriguez, I.; Olsson, L.E.; Ruiz-cabello, J. A MRI and Polarized Gases Compatible Respirator and Gas Administrator for the Study of the Small Animal Lung: Volume Measurement and Control. IEEE Trans. Biomed. Eng. 2010, 57, 1745–1749. [Google Scholar] [CrossRef]
- Sonigo, P.; Mahieu-Caputo, D.; Dommergues, M.; Fournet, J.C.; Thalabard, J.C.; Abarca, C.; Benachi, A.; Brunelle, F.; Dumez, Y. Fetal lung volume measurement by magnetic resonance imaging in congenital diaphragmatic hernia. Br. J. Obstet. Gynaecol. 2001, 108, 863–868, PII: S0306-5456(00)00184-4. [Google Scholar]
- Li, W.; Davlouros, P.A.; Kilner, P.J.; Pennell, D.J.; Gibson, D.; Henein, M.Y.; Gatzoulis, M.A. Doppler-echocardiographic assessment of pulmonary regurgitation in adults with repaired tetralogy of Fallot: Comparison with cardiovascular magnetic resonance imaging. Am. Heart J. 2004, 147, 165–172. [Google Scholar] [CrossRef]
- Kitchen, M.J.; Lewis, R.A.; Morgan, M.J.; Wallace, M.J.; Siew, M.L.; Siu, K.K.W.; Habib, A.; Fouras, A.; Yagi, N.; Uesugi, K.; et al. Dynamic measures of regional lung air volume using phase contrast x-ray imaging. Phys. Med. Biol. 2008, 53, 6065–6077. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Jiang, H.; Chen, J.; Huang, M. Ultrasound Imaging System. IEEE Sens. J. 2016, 16, 9014–9020. [Google Scholar] [CrossRef]
- Prina, E.; Torres, A.; Roberto, C.; Carvalho, R. Lung ultrasound in the evaluation of pleural effusion. J. Bras. Pneumol. 2014, 40, 1–5. [Google Scholar] [CrossRef]
- Lynnworth, L.C.; Korba, J.M.; Wallace, D.R. Fast Response Ultrasonic Flowmeter Measures Breathing Dynamics. IEEE Trans. Biomed. Eng. 1985, BME-32, 530–535. [Google Scholar] [CrossRef]
- Buess, C.; Pietsch, P.; Guggenbuhl, W.; Koller, E.A. Design and Construction of a Pulsed Ultrasonic Air Flowmeter. IEEE Trans. Biomed. Eng. 1986, BME-33, 768–774. [Google Scholar] [CrossRef]
- Hitomi, J.; Murai, Y.; Park, H.J.I.N.; Tasaka, Y. Ultrasound Flow-Monitoring and Flow-Metering of Air – Oil – Water Three-Layer Pipe Flows. IEEE Acess 2017, 5, 15021–15029. [Google Scholar] [CrossRef]
- Rundell, K.W.; Evans, T.M.; Baumann, J.M.; Kertesz, M.F. Lung function measured by impulse oscillometry and spirometry following eucapnic voluntary hyperventilation. Can. Respir. J. 2005, 12, 257–264. [Google Scholar] [CrossRef][Green Version]
- Marotta, A.; Klinnert, M.D.; Price, M.R.; Larsen, G.L.; Liu, A.H. Impulse oscillometry provides an effective measure of lung dysfunction in 4-year-old children at risk for persistent asthma. J. Allergy Clin. Immunol. 2003, 112, 4–9. [Google Scholar] [CrossRef]
- Gajewski, J.B. Electrostatic Nonintrusive Method for Measuring the Electric Charge, Mass Flow Rate, and Velocity of Particulates in the Two-Phase Gas—Solid Pipe Flows—Its Only or as Many as 50 Years of Historical Evolution. IEEE Trans. Ind. Appl. 2008, 44, 1418–1430. [Google Scholar] [CrossRef]
- Schwartz, J.G.; Fox, W.W.; Shaffer, T.H. A Method for Measuring Functional Residual Capacity in Neonates with Endotracheal Tubes. IEEE Trans. Biomed. Eng. 1978, BME-25, 304–307. [Google Scholar] [CrossRef] [PubMed]
- Cohen, K.P.; Ladd, W.M.; Beams, D.M.; Sheers, W.S.; Radwin, R.G.; Tompkins, W.J.; Webster, J.G. Comparison of Impedance and Inductance Ventilation Sensors on Adults During Breathing, Motion, and Simulated Airway Obstruction. IEEE Trans. Biomed. Eng. 1997, 44, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Seppa, V.; Viik, J.; Hyttinen, J. Assessment of Pulmonary Flow Using Impedance Pneumography. IEEE Trans. Biomed. Eng. 2010, 57, 2277–2285. [Google Scholar] [CrossRef] [PubMed]
- Incalzi, R.A.; Pennazza, G.; Scarlata, S.; Santonico, M.; Petriaggi, M.; Chiurco, D.; Pedone, C.; D’Amico, A. Reproducibility and Respiratory Function Correlates of Exhaled Breath Fingerprint in Chronic Obstructive Pulmonary Disease. PLoS ONE 2012, 7, e45396. [Google Scholar] [CrossRef] [PubMed]
- Pereira, C.A.D.C. Spirometry. J. Bras. Pneumol. 2002, 28, S1–S82. [Google Scholar]
- Sim, Y.S.; Lee, J.; Lee, W.; Suh, D.I.; Oh, Y.; Yoon, J.; Lee, J.H.; Cho, J.H.; Kwon, C.S.; Chang, J.H. Spirometry and Bronchodilator Test. Tuberc. Respir. Dis. 2017, 3536, 105–112. [Google Scholar] [CrossRef]
- Ansarin, K.; Chatkin, J.M.; Ferreira, I.M.; Gutierrez, C.A.; Zamel, N.; Chapman, K.R. Exhaled nitric oxide in chronic obstructive pulmonary disease: Relationship to pulmonary function. Eur. Respir. J. 2001, 17, 934–938. [Google Scholar] [CrossRef]
- Santos, U.P.; Garcia, M.L.S.B.; Braga, A.L.F.; Pereira, L.A.A.; Lin, C.A.; André, P.A.; André, C.D.S.; Singer, J.M.; Saldiva, P.H.N. Association between Traffic Air Pollution and Reduced Forced Vital Capacity: A Study Using Personal Monitors for Outdoor Workers. PLoS ONE 2016, 11, e0163225. [Google Scholar] [CrossRef]
- Panis, L.I.; Provost, E.B.; Cox, B.; Louwies, T.; Laeremans, M.; Standaert, A.; Dons, E.; Holmstock, L.; Nawrot, T.; Boever, P. Short-term air pollution exposure decreases lung function: A repeated measures study in healthy adults. Environ. Health 2017, 16, 1–7. [Google Scholar] [CrossRef]
- Makwana, A.H.; Solanki, J.D.; Gokhale, P.A.; Mehta, H.B.; Shah, C.J.; Gadhavi, B.P. Study of computerized spirometric parameters of traffic police personnel of Saurashtra region, Gujarat, India. Lung India 2015, 32, 457–461. [Google Scholar] [CrossRef]
- Börekçi, S.; Demir, T.; Dilektaşlı, A.G.; Uygun, A.G.; Yıldırım, N. A Simple Measure to Assess Hyperinflation and Air Trapping: 1-Forced Expiratory Volume in Three Second/Forced Vital Capacity. Balk. Med. J. 2017, 34, 113–118. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, L.J.; Ellis, E.R. The effect on expiratory flow rate of maintaining bag compression during manual hyperinflation. Aust. J. Physiother. 2004, 50, 47–49. [Google Scholar] [CrossRef]
- Schubauer-Berigan, M.K.; Dahm, M.M.; Erdely, A.; Beard, J.D.; Birch, M.E.; Evans, D.E.; Fernback, J.E.; Mercer, R.R.; Bertke, S.J.; Eye, T.; et al. Association of pulmonary, cardiovascular, and hematologic metrics with carbon nanotube and nanofiber exposure among U. S. workers: A cross-sectional study. Part. Fibre Toxicol. 2018, 15, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Oh, A.; Morris, T.A.; Yoshii, I.T.; Morris, T.A. Flow Decay: A Novel Spirometric Index to Quantify Dynamic Airway Resistance. Respir. Care 2017, 62, 928–935. [Google Scholar] [CrossRef]
- Madsen, F.; Frizilund, L.; Ulrik, C.S.; Desken, A. Office spirometry: Temperature conversion of volumes measured by the Vitalograph-R bellows spirometer is not necessary. Respir. Med. 1999, 93, 685–688. [Google Scholar] [CrossRef][Green Version]
- Fan, D.; Yang, J.; Zhang, J.; Lv, Z.; Huang, H.; Qi, J.; Yang, P. Effectively Measuring Respiratory Flow With Portable Pressure Data Using Back Propagation Neural Network. IEEE J. Transl. Eng. Heal. Med. 2018, 6, 1–12. [Google Scholar] [CrossRef]
- Plessis, E.; Swart, F.; Maree, D.; Heydenreich, J.; Heerden, J.V.; Esterhuizen, T.M.; Irusen, E.M.; Koegelenberg, C.N.F. The utility of hand-held mobile spirometer technology in a resource-constrained setting. S. Afr. Med. J. 2019, 109, 219–222. [Google Scholar] [CrossRef]
- Vautz, W.; Baumbach, J.I.; Westhoff, M.; Züchner, K.; Carstens, E.T.H.; Perl, T. Breath sampling control for medical application. Int. J. Ion Mobil. Spec. 2010, 13, 41–46. [Google Scholar] [CrossRef]
- Kecorius, S.; Jakob, L.; Wiedensohler, A.; Pfeifer, S.; Haudek, A.; Mardo, V. A new method to measure real-world respiratory tract deposition of inhaled ambient black carbon. Environ. Pollut. 2019, 248, 295–303. [Google Scholar] [CrossRef]
- Kobler, A.; Hartnack, S.; Sacks, M. Assessing the accuracy of Tafonius® anesthesia machine in vitro and in vivo respiratory volume measurements. Pferdeheilkunde 2016, 32, 449–455. [Google Scholar] [CrossRef][Green Version]
- Wang, T.; Baker, R. Coriolis flowmeters: A review of developments over the past 20 years, and an assessment of the state of the art and likely future directions. Flow Meas. Instrum. 2014, 40, 99–123. [Google Scholar] [CrossRef]
- Patrick, H.; Eisenberg, L. An Electronic Resuscitation Evaluation System. IEEE Trans. Biomed. Eng. 1972, BME-19, 317–320. [Google Scholar] [CrossRef]
- Li, H.N.; Wang, Z.T.; Li, X.B. Hardware design of CPR Simulation Control System based on SCM. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Yichang, China, 16–18 September 2011; pp. 4802–4805. [Google Scholar]
- Leocádio, R.R.V.; Segundo, A.K.R.; Louzada, C.F. Sensor for Measuring the Volume of Air Supplied to the Lungs of Adult Mannequins in Ventilation Maneuvers during Cardiopulmonary Resuscitation. Proceedings 2018, 4, 39. [Google Scholar] [CrossRef]
- Munson, B.R.; Yong, D.F.; Okiishi, T.H. Fundamentals of Fluid Mechanics, 4th ed.; Edgard Bluncher: Ames, IA, USA, 2004. [Google Scholar]
- Mahan, B.M.; Myers, R.J. University Chemistry, 4th ed.; Addison-Wesley: Menlo Park, CA, USA, 1987. [Google Scholar]
- Halliday, D.; Resnick, R.; Krane, K.S. Fundamentals of Physics, 8th ed.; Jearl Walker: Cleveland, OH, USA, 2009; Volumes 1–3. [Google Scholar]
- Perry, R.H.; Green, D.W.; Maloney, J.O. Perry’s Chemical Engineers’ Handbook, 7th ed.; McGraw-Hill: Lawrence, KS, USA, 1997; Volume 27. [Google Scholar]
- Fatehnia, M.; Paran, S.; Kish, S.; Tawfiq, K. Automating double ring infiltrometer with an Arduino microcontroller. Geoderma 2016, 262, 133–139. [Google Scholar] [CrossRef]
- Fahmi, F.; Hizriadi, A.; Khairani, F.; Andayani, U.; Siregar, B. Clean water billing monitoring system using flow liquid meter sensor and SMS gateway. J. Phys. Conf. Ser. 2018, 978. [Google Scholar] [CrossRef]
- Gosavi, G.; Gawde, G.; Gosavi, G. Smart water flow monitoring and forecasting system. In Proceedings of the RTEICT 2017 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology, Bangalore, India, 19–20 May 2017; pp. 1218–1222. [Google Scholar]
- Leocádio, R.R.V.; Segundo, A.K.R.; Louzada, C.F. Sistema de tempo real aplicado a simuladores de Ressuscitação Cardiopulmonar. In 14º Simpósio Brasileiro de Automação Inteligente; Centro de Convenções da UFOP: Ouro Preto, Brazil, 2019; pp. 1–6. [Google Scholar]
- Jamaluddin, A.; Harjunowibowo, D.; Rahardjo, D.T.; Adhitama, E.; Hadi, S. Wireless water flow monitoring based on Android smartphone. In Proceedings of the 2016 2nd International Conference of Industrial, Mechanical, Electrical, and Chemical Engineering (ICIMECE), Yogyakarta, Indonesia, 6–7 October 2016; pp. 243–247. [Google Scholar]
- Jamaluddin, A.; Harjunowibowo, D.; Rahardjo, D.T.; Adhitama, E.; Hadi, S. Wireless water flow monitoring based on Android smartphone. Proc. ImechE. Part I J. Syst. Control Eng. 2017, 220–224. [Google Scholar]
- Mandal, N.; Rajita, G. An accurate technique of measurement of flow rate using rotameter as a primary sensor and an improved op-amp based network. Flow Meas. Instrum. 2017, 58, 38–45. [Google Scholar] [CrossRef]
- Garmabdari, R.; Shafie, S.; Isa, M.M. Sensory system for the electronic water meter. In Proceedings of the ICCAS 2012 IEEE International Conference on Circuits and Systems, Kuala Lumpur, Malaysia, 3–4 October 2012; pp. 223–226. [Google Scholar]
- Garmabdari, R.; Shafie, S.; Wan Hassan, W.Z.; Garmabdari, A. Study on the effectiveness of dual complementary Hall-effect sensors in water flow measurement for reducing magnetic disturbance. Flow Meas. Instrum. 2015, 45, 280–287. [Google Scholar] [CrossRef]
- Sinha, S.; Banerjee, D.; Mandal, N.; Sarkar, R.; Bera, S.C. Design and Implementation of Real-Time Flow Measurement System Using Hall Probe Sensor and PC-Based SCADA. IEEE Sens. J. 2015, 15, 5592–5600. [Google Scholar] [CrossRef]
- Gamage, S.K.; Henderson, H.T. A study on a silicon Hall effect device with an integrated electroplated planar coil for magnetic sensing applications. J. Micromech. Microeng. 2006, 16, 487–492. [Google Scholar] [CrossRef]
- Di Lieto, A.; Giuliano, A.; MacCarrone, F.; Paffuti, G. Hall effect in a moving liquid. Eur. J. Phys. 2012, 33, 115–127. [Google Scholar] [CrossRef]
- Urbański, M.; Nowicki, M.; Szewczyk, R.; Winiarski, W. Flowmeter Converter Based on Hall Effect Sensor. In Automation, Robotics and Measuring Techniques; Springer: Cham, Switzerland, 2015; pp. 265–276. [Google Scholar] [CrossRef]
- Leonov, A.V.; Malykh, A.A.; Mordkovich, V.N.; Pavlyuk, M.I. An autogenerator induction-to-frequency converter circuit based on a field-effect Hall sensor with a regulated frequency. Instruments Exp. Tech. 2015, 58, 637–639. [Google Scholar] [CrossRef]
- GUM, I. Evaluation of Measurement Data: Guide to the Expression of Uncertainty in Measurement—GUM 2008; JCGM: Sevres, France; BIPM: Sevres, France; IEC: Geneva, Switzerland; IFCC: Milano, Italy; ILAC: Toronto ON, Canada; ISO: Geneva, Switzerland; IUPAC: Zurich, Switzerland; IUPAP: Singapore; OIML: Paris, France, 2008. [Google Scholar]
- De Bièvre, P. International Vocabulary of Metrology—Basic and General Concepts and Associated Terms—VIM 2012; JCGM: Sevres, France; BIPM: Sevres, France; IEC: Geneva, Switzerland; IFCC: Milano, Italy; ILAC: Toronto ON, Canada; ISO: Geneva, Switzerland; IUPAC: Zurich, Switzerland; IUPAP: Singapore; OIML: Paris, France, 2012. [Google Scholar]
- Association, A.H. Updating the CPR and ACE Guidelines: Highlights of the American Heart Association 2015; American Heart Association: Dallas, TX, USA, 2015; pp. 4–22. [Google Scholar]
- Jorge, A.d.S.; Ribeiro, A.; Gomes, C.; Frederico, C.; Aragão, D.; Gonçalves, F.; Júnior, F.F.; Dantas, I.; Vale, L.; Serafim, M. Fundamentos de Física e Biofísica, 1st ed.; FTC EaD: Salvador, BA, Brazil, 2008. [Google Scholar]
- Kulish, V. Human Respiration; WIT Press: Billerica, MA, USA, 2006. [Google Scholar]
- Sánchez, R.D.; López-Quintela, M.A.; Rivas, J.; González-Penedo, A.; García-Bastida, A.J.; Ramos, C.A.; Zysler, R.D.; Guevara, S.R. Magnetization and electron paramagnetic resonance of Co clusters embedded in Ag nanoparticles. J. Phys. Condens. Matter 1999, 11, 5643–5654. [Google Scholar] [CrossRef]
- Mitra, S.; Mandal, K.; Kumar, P.A. Temperature dependence of magnetic properties of NiFe2O4 nanoparticles embeded in SiO2 matrix. J. Magn. Magn. Mater. 2006, 306, 254–259. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Mandal, M.; Mandal, K. Preparation and study of NiFe2O4/SiO2 core—Shell nanocomposites. J. Alloy. Compd. 2009, 487, 698–702. [Google Scholar] [CrossRef]
- Ye, S.; Ney, V.; Kammermeier, T.; Ollefs, K.; Zhou, S.; Schmidt, H.; Wilhelm, F.; Rogalev, R.; Ney, A. Absence of ferromagnetic-transport signatures in epitaxial paramagnetic and superparamagnetic Zn0.95Co0.05O films. Phys. Rev. B 2009, 80, 1–7. [Google Scholar] [CrossRef]
- Sakamoto, S.; Anh, L.D.; Hai, P.N.; Shibata, G.; Takeda, Y.; Kobayashi, M.; Takahashi, Y.; Koide, T.; Tanaka, M. Magnetization process of the n-type ferromagnetic semiconductor (In, Fe)As: Be studied by x-ray magnetic circular dichroism. Phys. Rev. B 2016, 93, 1–6. [Google Scholar] [CrossRef]
- Garcı, L.M.; Bartolome, F.; Bartolome, J. Strong Paramagnetism of Gold Nanoparticles Deposited on a Sulfolobus acidocaldarius S Layer. Phys. Rev. Lett. 2012, 247203, 1–5. [Google Scholar] [CrossRef]
- Danielewicz-Ferchmin, I.; Ferchmin, A.R. Static permittivity of water revisited: E in the electric field above 108 Vm−1 and in the temperature range 273 ≤ T ≤ 373 K. Phys. Chem. Chem. Phys. 2004, 6, 1332–1339. [Google Scholar] [CrossRef]
- Capsal, J.; Galineau, J.; Guyomar, D. Evaluation of macroscopic polarization and actuation abilities of electrostrictive dipolar polymers using the microscopic Debye/Langevin formalism. J. Phys. Appl. Phys. 2012, 45, 9. [Google Scholar] [CrossRef]
- Bichurin, M.; Petrov, V.; Zakharov, A.; Kovalenko, D.; Yang, S.C.; Maurya, D.; Bedekar, V.; Shashank, P. Magnetoelectric Interactions in Lead-Based and Lead-Free Composites. Materials 2011, 4, 651–702. [Google Scholar] [CrossRef] [PubMed]
- Boggs, P.T.; Rogers, J.E. Orthogonal Distance Regression Orthogonal Distance Regression; Center for Computing and Applied Mathematics: Fullerton, CA, USA, 1990; NISTIR 89–4197. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimizatio, 2nd ed.; Springer: Evanston, IL, USA, 1996; Volume 17. [Google Scholar]
- Zwolak, J.W.; Boggs, P.T.; Watson, L.T. ODRPACK95: A Weighted Orthogonal Distance Regression Code with Bound Constraints; Virginia Tech: Blacksburg, VA, USA, 2004. [Google Scholar]
- Zwick, D.S. Applications of orthogonal distance regression in metrology. Double Star Res. 2016. Available online: https://www.researchgate.net/publication/262275537 (accessed on 12 June 2019).


| Reference volume(×10−6 m3) ±0.5% | 0 | 300 | 450 | 600 | 750 | 900 | 1050 | 1200 | 1350 | 1500 | 1650 | 1800 |
| Length of the stem(×10−3 m) ±1 × 10−3 m | 0 | 42 | 64 | 85 | 106 | 127 | 148 | 169 | 191 | 212 | 233 | 254 |
| Reference Volume(×10−6 m3) ±0.5% | 300 | 450 | 600 | 750 | 900 | 1050 | 1200 | 1350 | 1500 | 1650 | 1800 |
| Average Indication(×10−6 m3) | 301 | 450 | 601 | 751 | 901 | 1050 | 1201 | 1356 | 1500 | 1650 | 1800 |
| Uncertainty (×10−6 m3) | 22 | 23 | 24 | 26 | 27 | 30 | 33 | 36 | 37 | 45 | 56 |
| Volume (×10−6 m3) | R-Square | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BTZ | LG | ML | Doseresp | Gompertz | Slogistic | LA | ||||||||
| L M | O D R | L M | O D R | L M | O D R | L M | O D R | L M | O D R | L M | O D R | L M | O D R | |
| 300 | I A | N C | I A | N C | I A | 0.99999997354852 | I A | 0.99999996735480 | I A | N C | I A | 0.99999968697100 | I A | N C |
| 450 | 0.99999998774221 | 0.99999998313179 | 0.99999956213635 | |||||||||||
| 600 | 0.99999999387587 | 0.99999998738478 | 0.99999994155838 | |||||||||||
| 750 | 0.99999997787916 | 0.99999998623968 | 0.99999996494737 | |||||||||||
| 900 | 0.99999999363261 | 0.99999999373928 | 0.99999998003168 | |||||||||||
| 1050 | 0.99999998596560 | 0.99999998676343 | 0.99999977894465 | |||||||||||
| 1200 | 0.99999999843628 | 0.99999999853441 | 0.99999994501474 | |||||||||||
| 1350 | 0.99999999976504 | 0.99999999797433 | 0.99999994523958 | |||||||||||
| 1500 | 0.99999999614389 | 0.99999999677671 | 0.99999993443600 | |||||||||||
| 1650 | 0.99999999808238 | 0.99999999767503 | 0.99999680496200 | |||||||||||
| 1800 | 0.99999998519947 | 0.99999998367641 | 0.99999792109656 | |||||||||||
| Volume (×10−6 m3) | Y0 | xc | C | s |
|---|---|---|---|---|
| 300 | 98 ± 21 | 0.30 ± 0.07 | 258 ± 29 | 0.22 ± 0.02 |
| 450 | 182 ± 10 | 0.47 ± 0.02 | 320 ± 14 | 0.19 ± 0.01 |
| 600 | 284 ± 3 | 0.72 ± 0.01 | 372 ± 5 | 0.18 ± 0.01 |
| 750 | 364 ± 6 | 0.89 ± 0.02 | 467 ± 12 | 0.21 ± 0.02 |
| 900 | 515 ± 12 | 1.20 ± 0.03 | 735 ± 39 | 0.38 ± 0.03 |
| 1050 | 535 ± 9 | 1.15 ± 0.03 | 745 ± 33 | 0.33 ± 0.03 |
| 1200 | 608 ± 4 | 1.43 ± 0.01 | 891 ± 15 | 0.45 ± 0.01 |
| 1350 | 672 ± 5 | 1.62 ± 0.01 | 999 ± 19 | 0.51 ± 0.02 |
| 1500 | 709 ± 6 | 1.56 ± 0.02 | 997 ± 14 | 0.47 ± 0.01 |
| 1650 | 881 ± 6 | 2.40 ± 0.02 | 1218 ± 17 | 0.66 ± 0.02 |
| 1800 | 1006 ± 24 | 2.98 ± 0.06 | 1354 ± 54 | 0.77 ± 0.05 |
| Reference (×10−6 m3) | Measured Volume (×10−6 m3) | FVC (×10−6 m3) | tFVC (s) | FEVt=1 s (×10−6 m3) | FEF25–75% (×10−6 m3/s) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| YF-S201 | Koko | YF-S201 | Koko | YF-S201 | Koko | YF-S201 | Koko | YF-S201 | Koko | |
| 300 | 305 ± 22 | 320 ± 23 | 305 ± 22 | 320 ± 23 | 1.4 ± 0.1 | 1.3 ± 0.1 | 274 ± 22 | 260 ± 23 | 355 ± 26 | 230 ± 40 |
| 450 | 450 ± 23 | 450 ± 45 | 450 ± 23 | 450 ± 45 | 1.7 ± 0.1 | 1.6 ± 0.2 | 384 ± 23 | 310 ± 45 | 500 ± 77 | 270 ± 81 |
| 600 | 603 ± 24 | 610 ± 80 | 603 ± 24 | 610 ± 80 | 2.0 ± 0.1 | 2.0 ± 0.3 | 463 ± 24 | 360 ± 80 | 617 ± 87 | 330 ± 143 |
| 750 | 751 ± 26 | 760 ± 100 | 751 ± 26 | 760 ± 100 | 2.1 ± 0.1 | 2.2 ± 0.3 | 414 ± 26 | 390 ± 100 | 565 ± 78 | 330 ± 143 |
| 900 | 922 ± 27 | 890 ± 100 | 922 ± 27 | 890 ± 100 | 2.1 ± 0.1 | 2.1 ± 0.2 | 395 ± 27 | 490 ± 100 | 585 ± 67 | 480 ± 150 |
| 1050 | 1051 ± 30 | 1050 ± 100 | 1051 ± 30 | 1050 ± 100 | 2.4 ± 0.1 | 2.4 ± 0.2 | 419 ± 30 | 490 ± 100 | 635 ± 78 | 420 ± 124 |
| 1200 | 1182 ± 33 | 1200 ± 100 | 1182 ± 33 | 1200 ± 100 | 2.7 ± 0.1 | 2.7 ± 0.2 | 334 ± 33 | 530 ± 100 | 565 ± 75 | 490 ± 139 |
| 1350 | 1326 ± 36 | 1350 ± 100 | 1326 ± 36 | 1350 ± 100 | 3.2 ± 0.1 | 3.2 ± 0.2 | 316 ± 36 | 560 ± 100 | 597 ± 89 | 470 ± 129 |
| 1500 | 1476 ± 37 | 1500 ± 100 | 1476 ± 37 | 1500 ± 100 | 3.6 ± 0.1 | 3.7 ± 0.2 | 372 ± 37 | 570 ± 100 | 610 ± 96 | 440 ± 118 |
| 1650 | 1618 ± 45 | 1650 ± 100 | 1618 ± 45 | 1650 ± 100 | 4.1 ± 0.1 | 4.2 ± 0.3 | 197 ± 45 | 530 ± 100 | 565 ± 107 | 430 ± 156 |
| 1800 | 1786 ± 56 | 1800 ± 100 | 1786 ± 56 | 1800 ± 100 | 4.9 ± 0.1 | 5.0 ± 0.3 | 179 ± 56 | 530 ± 100 | 525 ± 127 | 380 ± 136 |
| Laerdal® (×10−6 m3) | Indicators | This Work (×10−6 m3) |
|---|---|---|
| 0 | Off | 196 ± 2 |
| Orange | 215 ± 2 | |
| Orange | 282 ± 2 | |
| Orange | 328 ± 3 | |
| Orange | 373 ± 3 | |
| ≤400 ± 60 | Orange | 419 ± 3 |
| >400 ± 60 | Green | 557 ± 4 |
| Green | 663 ± 5 | |
| ≤600 ± 90 | Green | 851 ± 6 |
| >600 ± 90 | Red | 1096 ± 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leocádio, R.R.V.; Segundo, A.K.R.; Louzada, C.F. A Sensor for Spirometric Feedback in Ventilation Maneuvers during Cardiopulmonary Resuscitation Training. Sensors 2019, 19, 5095. https://doi.org/10.3390/s19235095
Leocádio RRV, Segundo AKR, Louzada CF. A Sensor for Spirometric Feedback in Ventilation Maneuvers during Cardiopulmonary Resuscitation Training. Sensors. 2019; 19(23):5095. https://doi.org/10.3390/s19235095
Chicago/Turabian StyleLeocádio, Rodolfo Rocha Vieira, Alan Kardek Rêgo Segundo, and Cibelle Ferreira Louzada. 2019. "A Sensor for Spirometric Feedback in Ventilation Maneuvers during Cardiopulmonary Resuscitation Training" Sensors 19, no. 23: 5095. https://doi.org/10.3390/s19235095
APA StyleLeocádio, R. R. V., Segundo, A. K. R., & Louzada, C. F. (2019). A Sensor for Spirometric Feedback in Ventilation Maneuvers during Cardiopulmonary Resuscitation Training. Sensors, 19(23), 5095. https://doi.org/10.3390/s19235095






