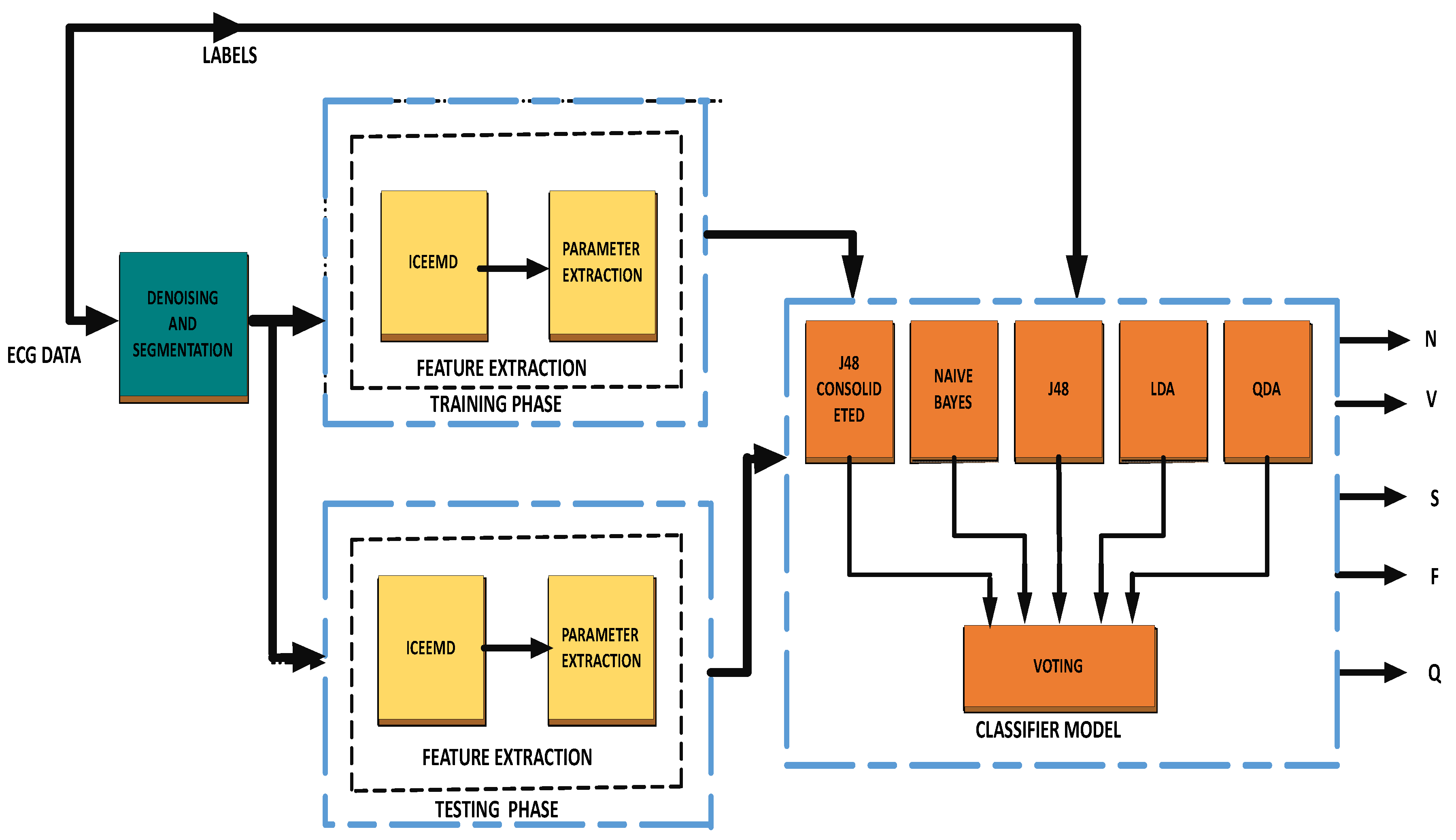
Figure 1.
Block diagram of the proposed methodology.
Figure 1.
Block diagram of the proposed methodology.
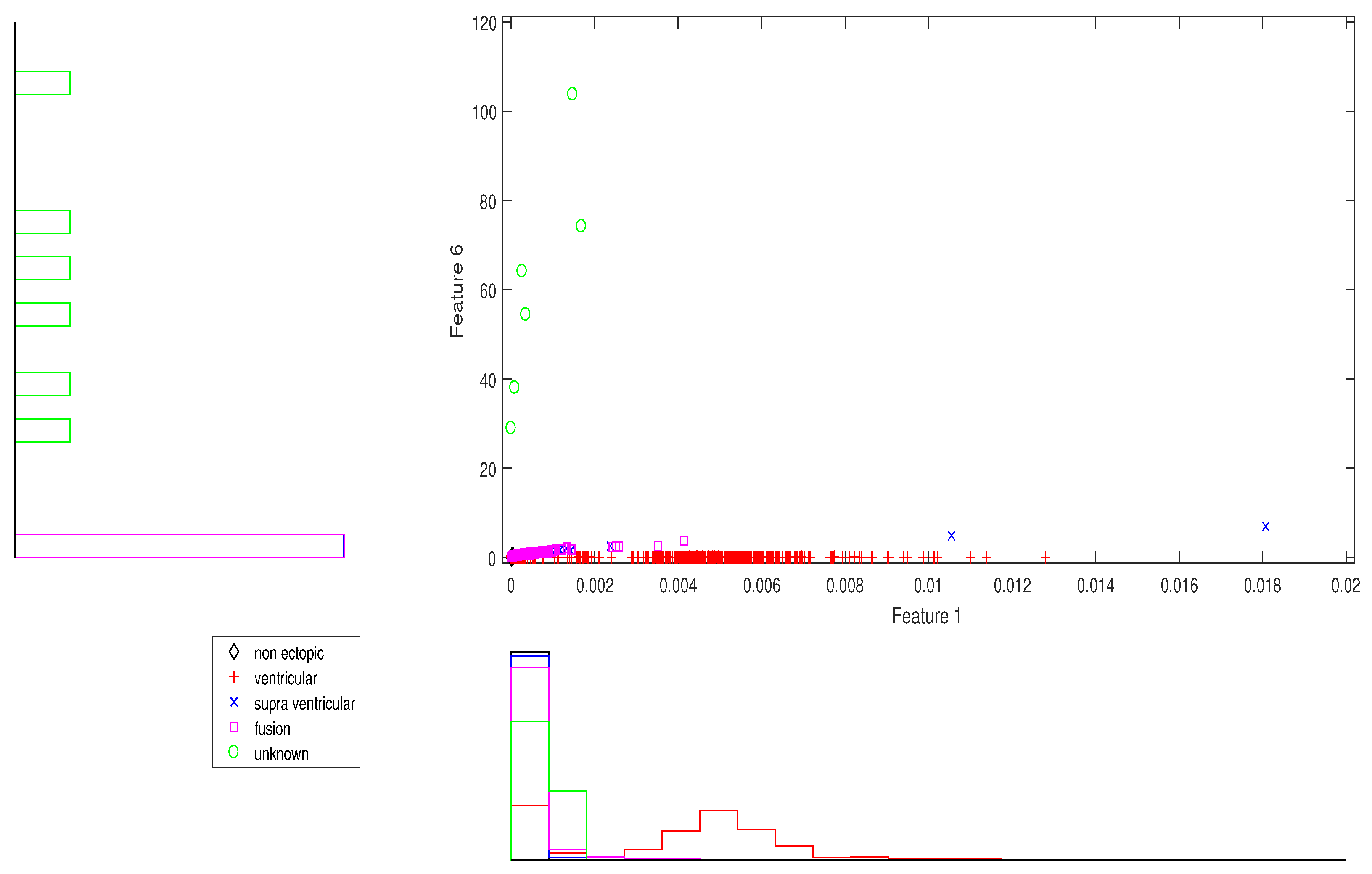
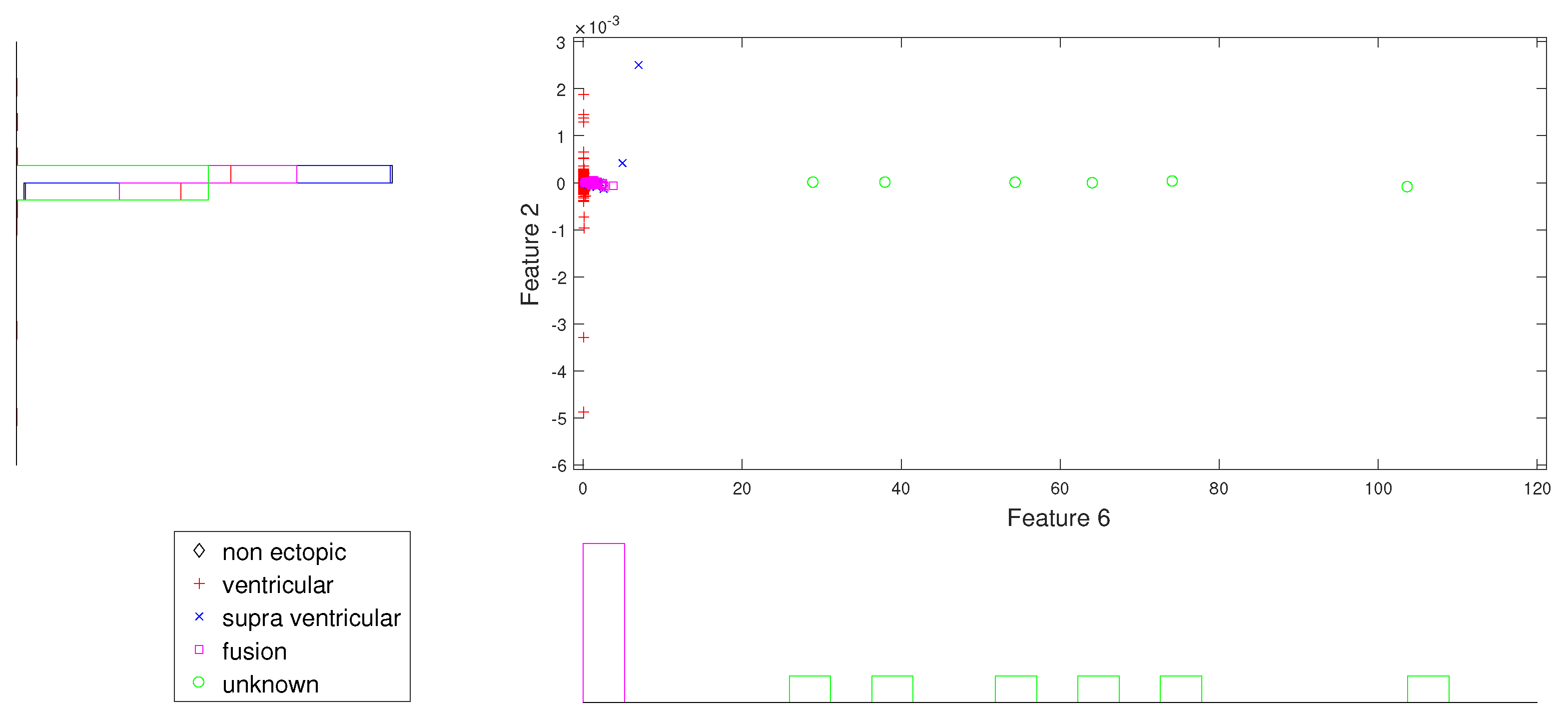
Figure 2.
Scatter plot with marginal histogram for CUM2 (IMF1) vs. norm entropy (IMF1).
Figure 2.
Scatter plot with marginal histogram for CUM2 (IMF1) vs. norm entropy (IMF1).
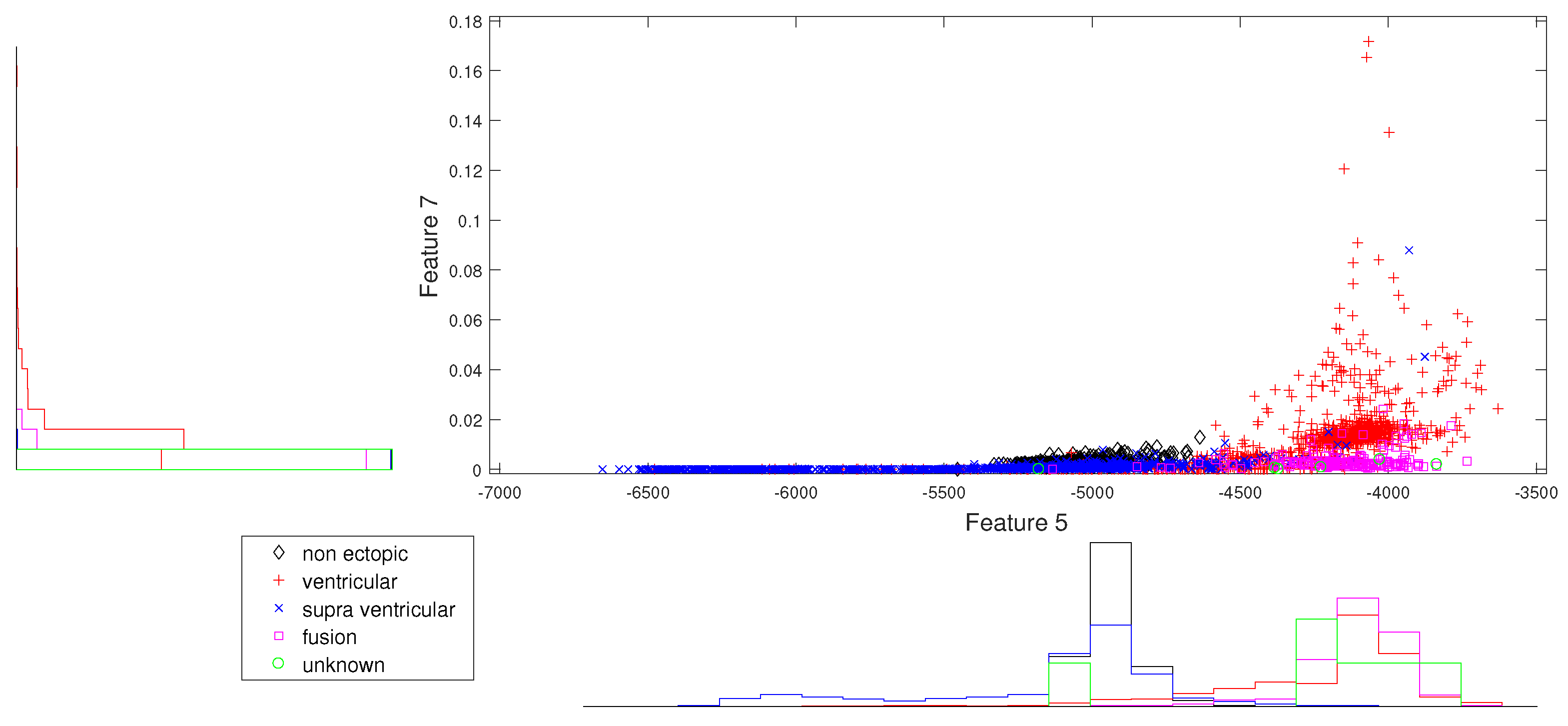
Figure 3.
Scatter plot with marginal histogram for log entropy (IMF1) vs. CUM2 (IMF1).
Figure 3.
Scatter plot with marginal histogram for log entropy (IMF1) vs. CUM2 (IMF1).
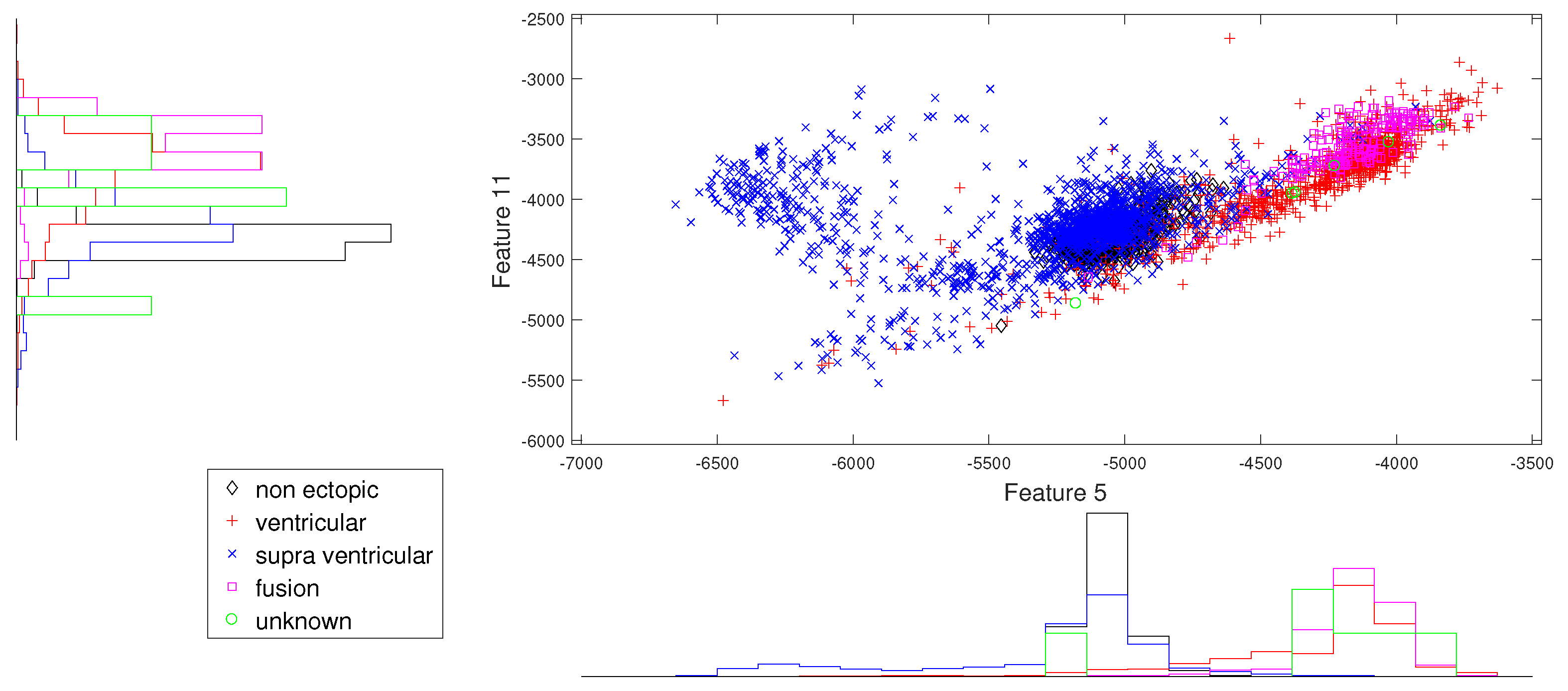
Figure 4.
Scatter plot with marginal histogram for log entropy (IMF1) vs. log entropy (IMF2).
Figure 4.
Scatter plot with marginal histogram for log entropy (IMF1) vs. log entropy (IMF2).
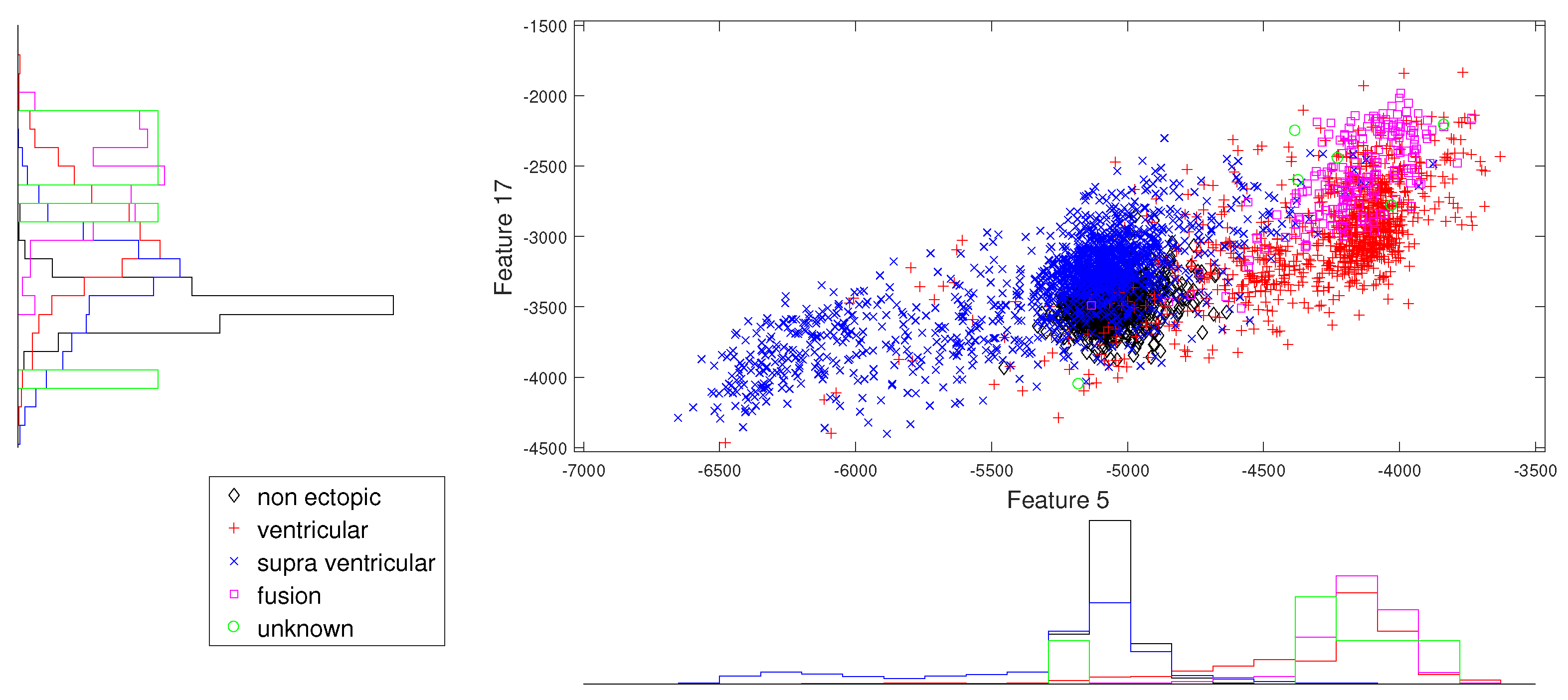
Figure 5.
Scatter plot with marginal histogram for log entropy (IMF1) vs. log entropy (IMF3).
Figure 5.
Scatter plot with marginal histogram for log entropy (IMF1) vs. log entropy (IMF3).
Figure 6.
Scatter plot with marginal histogram for log entropy (IMF1) vs. log entropy (IMF4).
Figure 6.
Scatter plot with marginal histogram for log entropy (IMF1) vs. log entropy (IMF4).
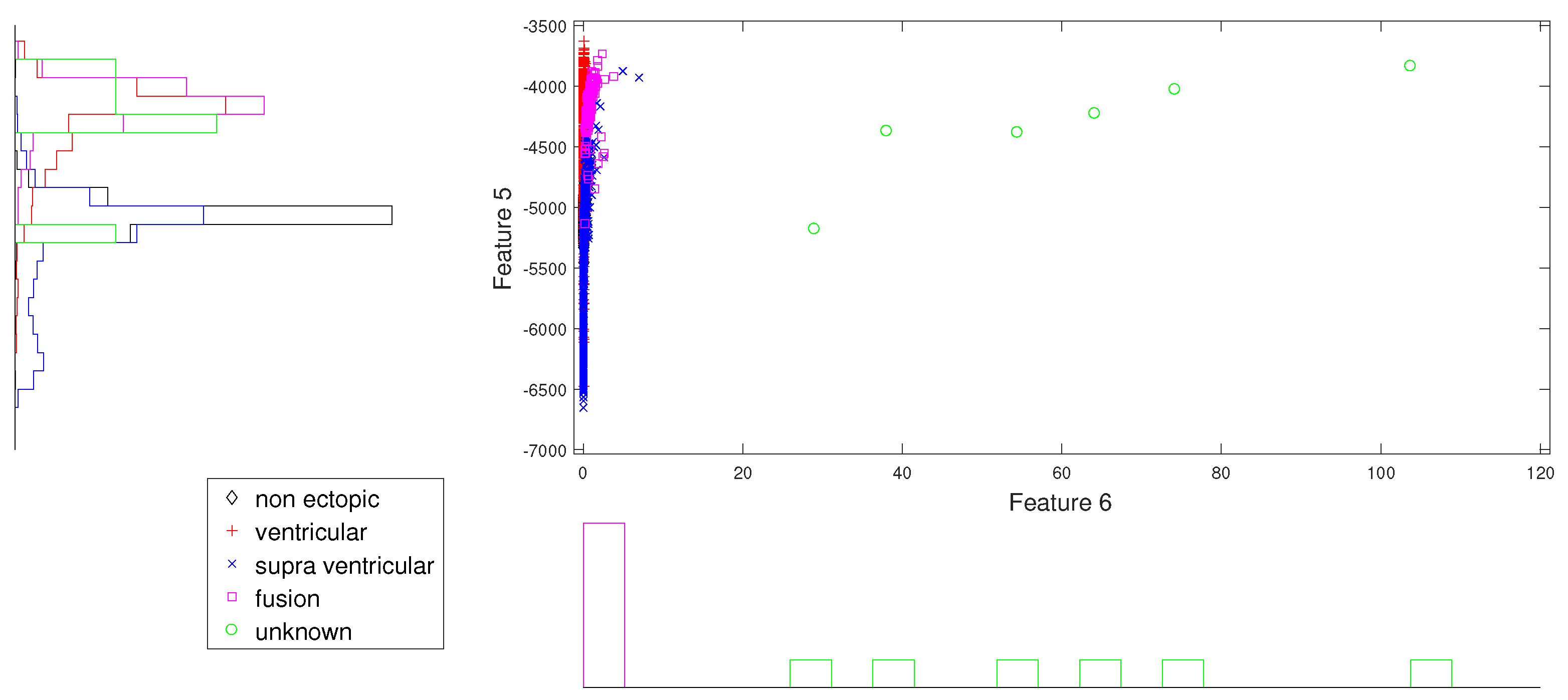
Figure 7.
Scatter plot with marginal histogram for norm entropy (IMF1) vs. CUM2 (IMF1).
Figure 7.
Scatter plot with marginal histogram for norm entropy (IMF1) vs. CUM2 (IMF1).
Figure 8.
Scatter plot with marginal histogram for norm entropy (IMF1) vs. log entropy (IMF1).
Figure 8.
Scatter plot with marginal histogram for norm entropy (IMF1) vs. log entropy (IMF1).
Table 1.
Details of the number of beats selected from each group of AAMI classes.
Table 1.
Details of the number of beats selected from each group of AAMI classes.
| AAMI Classes | MIT-BIH Heartbeats | Total Data | Training (DS1) | Testing (DS2) |
|---|
| N | Normal, left and right bundle branch block | 83,761 | 41,746 | 42,015 |
| | atrial and nodal escape beats | | | | |
| S | atrial premature contraction, Aberrated atrial, | 2614 | 777 | 1837 |
| | supra ventricular and junctional premature beats | | | | |
| V | premature ventricular contraction, ventricular flutter | 6893 | 3787 | 3106 |
| | and escape beats | | | | |
| F | fusion of ventricular and normal | 526 | 266 | 260 |
| | beats | | | | |
| Q | paced, unclassifiable, | 12 | 6 | 6 |
| | fusion of paced and normal beats | | | | |
Table 2.
Naïve Bayes Classifier parameters used in this work.
Table 2.
Naïve Bayes Classifier parameters used in this work.
| Parameters | Naïve Bayes |
|---|
| Use Kernel Estimator | False |
| Use supervise Discretization | True |
Table 3.
LDA and QDA classifier parameters used in this work.
Table 3.
LDA and QDA classifier parameters used in this work.
| Parameters | LDA | QDA |
|---|
| Ridge | | |
Table 4.
J48 and J48-C classifier parameters used in this work.
Table 4.
J48 and J48-C classifier parameters used in this work.
| Parameters | J48 | J48-C |
|---|
| Minimum Objects | 1000 | 1000 |
| Use MDL correction | True | True |
| Number of folds | 3 | 3 |
| Sub-tree raising | True | True |
Table 5.
Confusion matrix.
Table 5.
Confusion matrix.
| | | Predicted Labels | | |
|---|
| Actua Labels | N | V | S | F | Q | Sum |
| N | | | | | | |
| V | | | | | | |
| S | | | | | | |
| F | | | | | | |
| Q | | | | | | |
| Sum | | | | | | |
Table 6.
Confusion matrices for LDA, QDA, naïve Bayes, J48, and J48-C classifiers.
Table 6.
Confusion matrices for LDA, QDA, naïve Bayes, J48, and J48-C classifiers.
| LDA | QDA |
|---|
| | N | V | S | F | Q | | N | V | S | F | Q |
| N | 40,842 | 33 | 47 | 1093 | 0 | | 2777 | 266 | 36,394 | 2578 | 0 |
| V | 319 | 2787 | 0 | 0 | 0 | | 5 | 3101 | 0 | 0 | 0 |
| S | 1831 | 1 | 2 | 3 | 0 | | 95 | 56 | 1675 | 11 | 0 |
| F | 171 | 0 | 0 | 89 | 0 | | 91 | 64 | 20 | 85 | 0 |
| Q | 0 | 0 | 0 | 0 | 6 | | 0 | 6 | 0 | 0 | 0 |
| naïve Bayes | J48 |
| | N | V | S | F | Q | | N | V | S | F | Q |
| N | 36,222 | 745 | 997 | 3289 | 762 | | 41,801 | 214 | 0 | 0 | 0 |
| V | 930 | 1874 | 52 | 231 | 19 | | 363 | 2743 | 0 | 0 | 0 |
| S | 1321 | 3 | 133 | 27 | 353 | | 1819 | 18 | 0 | 0 | 0 |
| F | 8 | 0 | 2 | 245 | 5 | | 259 | 1 | 0 | 0 | 0 |
| Q | 1 | 0 | 0 | 4 | 1 | | 5 | 1 | 0 | 0 | 0 |
| J48-C |
| | | | | N | V | S | F | Q | | | |
| | | | N | 0 | 6941 | 28,966 | 5290 | 818 | | | |
| | | | V | 0 | 2205 | 894 | 6 | 1 | | | |
| | | | S | 0 | 24 | 1785 | 19 | 9 | | | |
| | | | F | 0 | 30 | 23 | 191 | 16 | | | |
| | | | Q | 0 | 0 | 0 | 0 | 6 | | | |
Table 7.
Performance measures for LDA, QDA, naïve Bayes, J48 and J48-C classifiers.
Table 7.
Performance measures for LDA, QDA, naïve Bayes, J48 and J48-C classifiers.
| LDA | QDA |
|---|
| OA = 92.60 | SEN% | FPR% | PPV% | OA = 16.20 | SEN% | FPR% | PPV% |
| N | 97.2 | 44.6 | 94.6 | | 6.6 | 3.7 | 93.6 |
| V | 89.7 | 0.1 | 98.8 | | 99.8 | 0.9 | 88.8 |
| S | 0.1 | 0.1 | 4.1 | | 91.2 | 80.2 | 4.4 |
| F | 34.2 | 2.3 | 7.5 | | 32.7 | 5.5 | 3.2 |
| Q | 100 | 0 | 100 | | 0 | 0 | 0 |
| naïve Bayes | J48 |
| OA = 81.47 | SEN% | FPR% | PPV% | OA = 94.32 | SEN% | FPR% | PPV% |
| N | 86.2 | 43.4 | 94.1 | | 99.5 | 47 | 94.5 |
| V | 60.3 | 1.7 | 71.5 | | 88.3 | 0.5 | 92.1 |
| S | 7.2 | 2.3 | 11.2 | | 0 | 0 | 0 |
| F | 94.2 | 7.6 | 6.5 | | 0 | 0 | 0 |
| Q | 16.7 | 2.4 | 0.1 | | 0 | 0 | 0 |
| J48-C |
| | | | OA = 8.86 | SEN% | FPR% | PPV% | |
| | | | N | 0 | 0 | 0 | |
| | | | V | 71.0 | 15.9 | 24.0 | |
| | | | S | 97.2 | 65.8 | 5.6 | |
| | | | F | 73.5 | 11.3 | 3.5 | |
| | | | Q | 100 | 1.8 | 0.7 | |
Table 8.
Confusion matrix for combining J48, LDA, and naïve Bayes classifiers using a Voting scheme.
Table 8.
Confusion matrix for combining J48, LDA, and naïve Bayes classifiers using a Voting scheme.
| Voting (J48, LDA, naïve Bayes) |
|---|
| | N | V | S | F | Q |
| N | 39,542 | 53 | 489 | 1931 | 0 |
| V | 395 | 2708 | 3 | 0 | 0 |
| S | 1473 | 1 | 353 | 10 | 0 |
| F | 22 | 5 | 1 | 232 | 0 |
| Q | 0 | 0 | 0 | 0 | 6 |
Table 9.
Performance measures for combining J48, LDA, and naïve Bayes classifiers using a Voting scheme.
Table 9.
Performance measures for combining J48, LDA, and naïve Bayes classifiers using a Voting scheme.
| Voting (J48, LDA, naïve Bayes) |
|---|
| OA = 90.71 | SEN% | FPR% | PPV% |
| N | 94.1 | 36.3 | 95.4 |
| V | 87.2 | 0.1 | 97.9 |
| S | 19.2 | 1.1 | 41.7 |
| F | 89.2 | 4.1 | 10.7 |
| Q | 100 | 0 | 100 |
Table 10.
Confusion matrix for combining J48, naïve Bayes, and QDA classifiers using a voting scheme.
Table 10.
Confusion matrix for combining J48, naïve Bayes, and QDA classifiers using a voting scheme.
| Voting ( J48, naïve Bayes, QDA) |
|---|
| | N | V | S | F | Q |
| N | 35,629 | 253 | 3836 | 2297 | 0 |
| V | 11 | 3095 | 0 | 0 | 0 |
| S | 1188 | 11 | 624 | 14 | 0 |
| F | 28 | 61 | 11 | 160 | 0 |
| Q | 0 | 6 | 0 | 0 | 0 |
Table 11.
Performance measures for combining J48, naïve Bayes, and QDA classifiers using a Voting scheme.
Table 11.
Performance measures for combining J48, naïve Bayes, and QDA classifiers using a Voting scheme.
| Voting ( J48, naïve Bayes, QDA) |
|---|
| OA = 83.6 | SEN% | FPR% | PPV% |
| N | 84.8 | 23.6 | 96.7 |
| V | 99.6 | 0.8 | 90.3 |
| S | 34 | 8.5 | 14 |
| F | 61.5 | 4.9 | 6.5 |
| Q | 0 | 0 | 0 |
Table 12.
Confusion matrix for combining J48-C, naïve Bayes, and QDA classifiers using a Voting scheme.
Table 12.
Confusion matrix for combining J48-C, naïve Bayes, and QDA classifiers using a Voting scheme.
| Voting (J48-C, naïve Bayes, QDA) |
|---|
| | N | V | S | F | Q |
| N | 29,730 | 255 | 9089 | 2491 | 0 |
| V | 8 | 3098 | 0 | 0 | 0 |
| S | 1031 | 8 | 779 | 19 | 0 |
| F | 21 | 61 | 12 | 166 | 0 |
| Q | 0 | 6 | 0 | 0 | 0 |
Table 13.
Performance measures for combining J48-C, naïve Bayes, and QDA classifiers using a Voting scheme.
Table 13.
Performance measures for combining J48-C, naïve Bayes, and QDA classifiers using a Voting scheme.
| Voting (J48-C,naïve Bayes, QDA) |
|---|
| OA = 71.51 | SEN% | FPR% | PPV% |
| N | 70.8 | 20.3 | 96.6 |
| V | 99.7 | 0.7 | 90.4 |
| S | 42.4 | 20.1 | 7.9 |
| F | 63.8 | 6.3 | 5.3 |
| Q | 0 | 0 | 0 |
Table 14.
Confusion matrix for combining J48-C, naïve Bayes, and LDA classifiers using a Voting scheme.
Table 14.
Confusion matrix for combining J48-C, naïve Bayes, and LDA classifiers using a Voting scheme.
| Voting (J48-C, naïve Bayes, LDA) |
|---|
| | N | V | S | F | Q |
| N | 38,329 | 66 | 942 | 2678 | 0 |
| V | 553 | 2532 | 20 | 1 | 0 |
| S | 1405 | 2 | 416 | 14 | 0 |
| F | 20 | 4 | 1 | 235 | 0 |
| Q | 0 | 0 | 0 | 0 | 6 |
Table 15.
Performance measures for combining J48-C, naïve Bayes, and LDA classifiers using a Voting scheme.
Table 15.
Performance measures for combining J48-C, naïve Bayes, and LDA classifiers using a Voting scheme.
| Voting (J48-C,naïve Bayes, LDA) |
|---|
| OA = 87.91 | SEN% | FPR% | PPV% |
| N | 91.2 | 38 | 95.1 |
| V | 81.5 | 0.2 | 97.2 |
| S | 22.6 | 2.1 | 30.2 |
| F | 90.4 | 5.7 | 8 |
| Q | 100 | 0 | 100 |
Table 16.
Confusion matrices for various classifiers (N, V, and S classes).
Table 16.
Confusion matrices for various classifiers (N, V, and S classes).
| LDA | QDA |
|---|
| | N | V | S | | N | V | S |
| N | 41,875 | 27 | 113 | | 4569 | 480 | 36,966 |
| V | 280 | 2826 | 0 | | 5 | 3101 | 0 |
| S | 1835 | 0 | 2 | | 105 | 56 | 1676 |
| naïve Bayes | J48 |
| | N | V | S | | N | V | S |
| N | 37,385 | 2968 | 1662 | | 41,998 | 17 | 0 |
| V | 922 | 2120 | 64 | | 1095 | 2011 | 0 |
| S | 1336 | 18 | 483 | | 1837 | 0 | 0 |
| J48-C |
| | | | | N | V | S | |
| | | | N | 34,999 | 7016 | 0 | |
| | | | V | 651 | 2455 | 0 | |
| | | | S | 1585 | 252 | 0 | |
Table 17.
Performance measures for various classifiers (N,V,S classes).
Table 17.
Performance measures for various classifiers (N,V,S classes).
| LDA | QDA |
|---|
| OA = 95.19 | SEN% | FPR% | PPV% | OA = 19.90 | SEN% | FPR% | PPV% |
| N | 99.7 | 42.8 | 95.2 | | 10.9 | 2.2 | 97.6 |
| V | 91.0 | 0.1 | 99.1 | | 99.8 | 1.2 | 85.3 |
| S | 0.1 | 0.3 | 1.7 | | 91.2 | 81.9 | 4.3 |
| naïve Bayes | J48 |
| OA = 85.15 | SEN% | FPR% | PPV% | OA = 93.71 | SEN% | FPR% | PPV% |
| N | 89 | 45.7 | 94.3 | | 100 | 59.3 | 93.5 |
| V | 68.3 | 6.8 | 41.5 | | 64.7 | 0 | 99.2 |
| S | 26.3 | 3.8 | 21.9 | | 0 | 0 | 0 |
| J48-C |
| | | | OA = 79.76 | SEN% | FPR% | PPV% | |
| | | | N | 83.3 | 45.2 | 94 | |
| | | | V | 79 | 16.6 | 25.2 | |
| | | | S | 0 | 0 | 0 | |
Table 18.
Confusion matrix for combining J48, LDA, and naïve Bayes classifiers using a Voting scheme (N,S,V).
Table 18.
Confusion matrix for combining J48, LDA, and naïve Bayes classifiers using a Voting scheme (N,S,V).
| Voting ( J48, LDA, naïve Bayes) |
|---|
| | N | V | S |
| N | 40,918 | 361 | 736 |
| V | 205 | 2897 | 4 |
| S | 1469 | 3 | 365 |
Table 19.
Performance measures for combining J48, LDA, and naïve Bayes classifiers using Voting scheme (N,S,V).
Table 19.
Performance measures for combining J48, LDA, and naïve Bayes classifiers using Voting scheme (N,S,V).
| Voting ( J48, LDA, naïve Bayes) |
|---|
| OA = 94.08 | SEN% | FPR% | PPV% |
| N | 97.4 | 33.9 | 96.1 |
| V | 93.3 | 0.8 | 88.8 |
| S | 19.9 | 1.6 | 33 |
Table 20.
Confusion matrix for combining J48, naïve Bayes, and QDA classifiers using Voting scheme (N,S,V).
Table 20.
Confusion matrix for combining J48, naïve Bayes, and QDA classifiers using Voting scheme (N,S,V).
| Voting ( J48, naïve Bayes, QDA) |
|---|
| | N | V | S |
| N | 37,421 | 574 | 4020 |
| V | 12 | 3094 | 0 |
| S | 1203 | 8 | 626 |
Table 21.
Performance measures for combining J48, naïve Bayes, and QDA classifiers using Voting scheme (N,S,V).
Table 21.
Performance measures for combining J48, naïve Bayes, and QDA classifiers using Voting scheme (N,S,V).
| Voting ( J48, naïve Bayes, QDA) |
|---|
| OA = 87.61 | SEN% | FPR% | PPV% |
| N | 89.1 | 24.6 | 96.9 |
| V | 99.6 | 1.3 | 84.2 |
| S | 34.1 | 8.9 | 13.5 |
Table 22.
Confusion matrix for combining J48-C, naïve Bayes, and QDA classifiers using Voting scheme (N,S,V).
Table 22.
Confusion matrix for combining J48-C, naïve Bayes, and QDA classifiers using Voting scheme (N,S,V).
| Voting ( J48-C, naïve Bayes, QDA) |
|---|
| | N | V | S |
| N | 32011 | 598 | 9406 |
| V | 7 | 3099 | 0 |
| S | 1062 | 8 | 767 |
Table 23.
Performance measures for combining J48-C, naïve Bayes, and QDA classifiers using Voting scheme (N,S,V).
Table 23.
Performance measures for combining J48-C, naïve Bayes, and QDA classifiers using Voting scheme (N,S,V).
| Voting ( J48-C, naïve Bayes, QDA) |
|---|
| OA = 76.40 | SEN% | FPR% | PPV% |
| N | 76.2 | 21.6 | 96.8 |
| V | 99.8 | 1.4 | 83.6 |
| S | 41.8 | 20.8 | 7.5 |
Table 24.
Confusion matrix for combining J48-C, naïve Bayes, and LDA classifiers using Voting scheme (N,S,V).
Table 24.
Confusion matrix for combining J48-C, naïve Bayes, and LDA classifiers using Voting scheme (N,S,V).
| Voting ( J48-C, naïve Bayes, LDA) |
|---|
| | N | V | S |
| N | 40,248 | 688 | 1079 |
| V | 359 | 2735 | 12 |
| S | 1407 | 2 | 428 |
Table 25.
Performance measures for combining J48-C, naïve Bayes, LDA classifiers using Voting scheme (N,S,V).
Table 25.
Performance measures for combining J48-C, naïve Bayes, LDA classifiers using Voting scheme (N,S,V).
| Voting ( J48-C, naïve Bayes, LDA) |
|---|
| OA = 92.44 | SEN% | FPR% | PPV% |
| N | 95.8 | 35.7 | 95.8 |
| V | 88.1 | 1.6 | 79.9 |
| S | 23.3 | 2.4 | 28.2 |
Table 26.
Median ± interquartile range of features extracted on DS1.
Table 26.
Median ± interquartile range of features extracted on DS1.
| Feature Number | Features | N | S | V | F | Q | |
|---|
| 1 | CUM2(IMF1) | 1.0 ± 4.0 | 8.0 ± 4.03 | 7.50 ± 0.00045775 | 0.000162 ± 0.000326 | 0.0001405 ± 0.009121 | |
| 2 | CUM3(IMF1) | 0 ± 0 | 0 ± 0 | 0 ± 2.0 | 0 ± 5.0 | 0 ± 0.000313 | |
| 3 | CUM4(IMF1) | 0 ± 0 | 0 ± 0 | 1.0 ± 2.58 | 2.50 ± 1.1 | 4.5± 0.006113 | |
| 4 | Shan(IMF1) | 0.004769 ± 0.009686 | 0.017643 ± 0.06530625 | 0.112159 ± 0.4199265 | 0.216149 ± 0.330006 | 0.153638 ± 1.47632 | |
| 5 | log(IMF1) | −4792.4962 ± 379.828 | −4735.1172 ± 286.978 | −4532.44 ± 467.507 | −4358.371 ± 271.824 | −4604.445 ± 1783.20 | |
| 6 | norm(IMF1) | 0.1004 ± 0.0726 | 0.1538 ± 0.1719 | 0.0815 ± 0.05794 | 0.5541 ± 0.5434 | 18.1790 ± 20.55612 | |
| 7 | CUM2(IMF2) | 0.001 ± 0.00347 | 0.00109 ± 0.0035 | 0.00028 ± 0.00137 | 0.00107 ± 0.00143 | 0.00411 ± 0.0134 | |
| 8 | CUM3(IMF2) | 8.0± 5.20 | 4.0± 5.10 | 0 ± 6.0 | 5.0± 2.10 | 0 ± 0.000387 | |
| 9 | CUM4(IMF2) | 1.50± 0.000185 | 2.10± 0.000128 | 2.0± 4.20 | 1.60± 5.20 | 0.00046 ± 0.002581 | |
| 10 | Shan(IMF2) | 1.3074 ± 2.9180 | 1.3675 ± 3.4250 | 0.431 ± 1.429 | 1.4044 ± 1.44285 | 2.90440 ± 6.76104 | |
| 11 | log(IMF2) | −4055.72 ± 403.632 | −4045.57 ± 565.833 | −4064.90 ± 479.11 | −3788.21 ± 266.57 | −4023.39 ± 1366.58 | |
| 12 | norm(IMF2) | 2.41 ± 3.81 | 2.57 ± 4.95 | 2.744 ± 1.768 | 2.69 ± 2.04 | 18.17 ± 20.556 | |
| 13 | CUM2(IMF3) | 0.0069 ± 0.0097 | 0.00534 ± 0.009013 | 0.00443 ± 0.00936 | 0.011997 ± 0.00909 | 0.004148 ± 0.008015 | |
| 14 | CUM3(IMF3) | −7.80± 0.000322 | −8.60± 0.0003605 | −3.10± 0.000246 | −0.00019 ± 0.00062 | 8.95± 0.000266 | |
| 15 | CUM4(IMF3) | 0.000235 ± 0.000863 | 0.000104 ± 0.0006515 | 0.000117 ± 0.000747 | 0.0005255 ± 0.000767 | 0.0001945 ± 0.000396 | |
| 16 | Shan(IMF3) | 6.3075515 ± 6.075866 | 5.532014 ± 6.254886 | 4.570122 ± 5.93904725 | 10.002892 ± 5.49255 | 3.8205085 ± 6.888019 | |
| 17 | log(IMF3) | −3114.4106 ± 443.70730 | −3071.71175 ± 705.504 | −3178.659 ± 531.3571 | −2731.2660 ± 467.4692 | −3341.5431 ± 891.0573 | |
| 18 | norm(IMF3) | 9.3564 ± 7.6444 | 8.69133 ± 8.37546 | 7.585 ± 4.1465 | 14.85 ± 7.440 | 18.179 ± 20.55 | |
| 19 | CUM2(IMF4) | 0.013817 ± 0.0210 | 0.01233 ± 0.01653 | 0.0215 ± 0.03611 | 0.0370 ± 0.0297 | 0.0069 ± 0.0102 | |
| 20 | CUM3(IMF4) | −0.00012 ± 0.00081 | −6.80± 0.000469 | −0.00014 ± 0.001305 | −0.001542 ± 0.00207 | 0 ± 0.00039 | |
| 21 | CUM4(IMF4) | 0.000147 ± 0.000734 | 4.60± 0.0003225 | 0.000404 ± 0.00189 | 0.00027 ± 0.00124 | 0.000138 ± 0.00018 | |
| 22 | Shan(IMF4) | 13.05585 ± 12.76457 | 12.2365 ± 11.295 | 16.104 ± 15.135 | 25.934 ± 15.110 | 7.113 ± 10.471 | |
| 23 | log(IMF4) | −2150.494 ± 533.542 | −2143.567 ± 611.308 | −2206.943 ± 794.75 | −1614.17 ± 480.99 | −2593.22 ± 1271.81 | |
| 24 | norm(IMF4) | 19.367 ± 15.509 | 18.686 ± 14.240 | 16.26 ± 9.166 | 35.59 ± 20.941 | 18.179 ± 20.556 | |
| 25 | CUM2(IMF5) | 0.0084 ± 0.018 | 0.0066 ± 0.0156 | 0.033 ± 0.0648 | 0.056 ± 0.058 | 0.0075 ± 0.0149 | |
| 26 | CUM3(IMF5) | 1.0± 0.00017 | 0 ± 0.000103 | −1.0± 0.00146 | 1.40± 0.0022 | 0 ± 0.000405 | |
| 27 | CUM4(IMF5) | −7.00± 0.00012 | −6.0± 0.000127 | −3.0± 0.00193 | −0.00236 ± 0.00621 | −5.50± 0.000287 | |
| 28 | Shan(IMF5) | 10.358 ± 15.6374 | 8.68112 ± 14.823 | 25.882 ± 29.195 | 39.2240 ± 25.737 | 8.992 ± 16.965 | |
| 29 | log(IMF5) | −1917.009 ± 593.83 | −1992.177 ± 872.920 | −1567.422 ± 918.993 | −1216.140± 489.3834 | −2179.500 ± 1495.143 | |
| 30 | norm(IMF5) | 17.118 ± 19.0735 | 14.983 ± 19.2726 | 19.495 ± 14.659 | 52.96 ± 32.190 | 18.179 ± 20.556 | |
| 31 | CUM2(IMF6) | 0.0040 ± 0.0092 | 0.0028 ± 0.00723 | 0.0184 ± 0.04606 | 0.0571 ± 0.0827 | 0.0073 ± 0.01072 | |
| 32 | CUM3(IMF6) | 1.0± 0.00010 | 0 ± 6.80 | 2.0± 0.0011117 | 8.0± 0.00527 | 0 ± 0.0002 | |
| 33 | CUM4(IMF6) | −1.50± 0.00011 | -8.0 6± 6.25 | −0.00024 ± 0.00205 | −0.00389± 0.01428 | −4.40± 0.00017 | |
| 34 | Shan(IMF6) | 6.50405 ± 11.11697 | 5.26119 ± 9.9055 | 20.0112 ± 31.26347 | 44.49 ± 39.5131 | 10.284 ± 13.481 | |
| 35 | log(IMF6) | −1903.169 ± 637.510 | −1983.32 ± 713.457 | −1470.196 ± 744.176 | −1062.5 ± 546.13 | −1682.363 ± 1296.591 | |
| 36 | norm(IMF6) | 13.0914 ± 15.1495 | 11.4410 ± 14.268 | 10.566 ± 12.262 | 57.357 ± 46.317 | 18.179 ± 20.556 | |
Table 27.
Methodology description of recent state-of-the-art compared in our work.
Table 27.
Methodology description of recent state-of-the-art compared in our work.
| Literature | Feature Extraction | Classification |
|---|
| [58] | | |
| method-1 | R–R intervals | Optimum Path Forest (OPF) |
| method-2 | Wavelet based features | OPF |
| method-3 | Mean, standard deviation and average power of wavelet sub-band | OPF |
| method-4 | Auto correlation and energy ratio of wavelet bands | OPF |
| method-5 | Fast-ICA | OPF |
| method-6 | (Wavelet+ICA+RR interval) | OPF |
| [59] | (ECG+VCG) complex network based features | SVM |
| [42] | Wavelet packet decomposition based entropy features | Random Forest |
| [60] | | |
| method-1 | Wavelet based features | Hierarchical Classification (tree approach) |
| method-2 | Mean, standard deviation and average power of wavelet sub-band | Hierarchical Classification (tree approach) |
| method-3 | Auto correlation and energy ratio of wavelet bands | Hierarchical Classification (tree approach) |
| method-4 | Fast-ICA | Hierarchical Classification (tree approach) |
| method-5 | (Wavelet+ICA+RR interval) | Hierarchical Classification (tree approach) |
| [61] | Temporal Vectrcardiogram(TCG) based features | SVM |
| [62] | A combination of projected features | |
| | (features derived from the projected matrix and DCT) and RR intervals | SVM |
| [63] | TCG feature selection by PSO | SVM |
| proposed work | | |
| method-1 | Entropy and statistical features calculated on ICEEMD modes | Voting ( J48, LDA, naïve Bayes) |
| method-2 | Entropy and statistical features calculated on ICEEMD modes | Voting ( J48, QDA, naïve Bayes) |
| method-3 | Entropy and statistical features calculated on ICEEMD modes | Voting ( J48-C, QDA, naïve Bayes) |
| method-4 | Entropy and statistical features calculated on ICEEMD modes | Voting ( J48-C, LDA, naïve Bayes) |
Table 28.
Performance comparison with recent literature (N, S, V, F, and Q classes).
Table 28.
Performance comparison with recent literature (N, S, V, F, and Q classes).
| Literature | N | S | V | F | Q |
|---|
| SEN/FPR/PPV | SEN/FPR/PPV | SEN/FPR/PPV | SEN/FPR/PPV | SEN/FPR/PPV |
|---|
| [58] | | | | | |
| method-1 | 84.5/-/- | 1.0/-/- | 77.7/-/- | 38.4/-/- | 0/-/- |
| method-2 | 86.4/-/- | 2.3/-/- | 40.8/-/- | 0.5/-/- | 0/-/- |
| method-3 | 84.8/-/- | 18.3/-/- | 77.8/-/- | 7.5/-/- | 0/-/- |
| method-4 | 92.5/-/- | 3.0/-/- | 61.8/-/- | 16.8/-/- | 0/-/- |
| method-5 | 95.7/-/- | 17.7/-/- | 74.7/-/- | 3.9/-/- | 0/-/- |
| method-6 | 93.2/-/- | 12.1/-/- | 85.5/-/- | 18.3/-/- | 0/-/- |
| [59] | 89.3/25.2/96.6 | 38.6/6.7/18 | 81.2/4.9/53.6 | 0/0/0 | 0/0/0 |
| [42] | 94.67/3.92/99.73 | 20/3.69/0.16 | 94.20/0.71/89.78 | 50/0.78/0.52 | 0/0/0 |
| [60] | | | | | |
| method-1 | 92.3/22.2/97.1 | 28.5/2.6/29.6 | 83.5/5.51/51.2 | 19.1/1.07/12.3 | 0/0/- |
| method-2 | 93.6/57.1/93.0 | 0.49/0.47/3.81 | 67.9/3.99/54.2 | 0/1.63/0 | 0/0/0 |
| method-3 | 98.2/41.2/95.1 | 4.72/0.71/20.3 | 81.7/1.25/82.0 | 2.58/0.40/4.88 | 0/0/0 |
| method-4 | 98.6/39.8/95.3 | 9.15/0.56/38.6 | 83.2/1.21/82.7 | 0.26/0.38/0.53 | 0/0/- |
| method-5 | 94.7/31.2/96.1 | 37.4/6.19/18.8 | 43.9/1.48/67.4 | 0.52/0.72/0.56 | 0/0/- |
| proposed work | | | | | |
| method-1 | 94.1/36.3/95.4 | 19.2/1.1/41.7 | 87.2/0.1/97.9 | 89.2/4.1/10.7 | 100/0/100 |
| method-2 | 84.8/23.6/96.7 | 34/8.5/14 | 99.6/0.8/90.3 | 61.5/4.9/6.5 | 0/0/0 |
| method-3 | 70.8/20.3/96.6 | 42.4/20.1/7.9 | 99.7/0.7/90.4 | 63.8/6.3/5.3 | 0/0/0 |
| method-4 | 91.2/38/95.1 | 22.6/2.1/30.2 | 81.5/0.2/97.2 | 90.4/5.7/8 | 100/0/100 |
Table 29.
Performance comparison with recent literature (N, S, and V classes).
Table 29.
Performance comparison with recent literature (N, S, and V classes).
| Literature | N | S | V |
|---|
| SEN/FPR/PPV | SEN/FPR/PPV | SEN/FPR/PPV |
|---|
| [61] | 95/27.9/96.5 | 29.6/3.1/26.4 | 85.1/3.01/66.3 |
| [62] | 98.4/-/95.4 | 29.5/-/38.4 | 70.8/-/85.1 |
| [63] | | | |
| method on VCG | 79.1/27.0/96.3 | 31.2/8.4/13.0 | 89.5/7.2/46.1 |
| proposed work | | | |
| method-1 | 97.4/33.9/96.1 | 19.9/1.6/33 | 93.3/0.8/88.8 |
| method-2 | 89.1/24.6/96.9 | 34.1/8.9/13.5 | 99.6/1.3/84.2 |
| method-3 | 76.2/21.6/96.8 | 41.8/20.8/7.5 | 99.8/1.4/83.6 |
| method-4 | 95.8/35.7/95.8 | 23.3/2.4/28.2 | 88.1/1.6/79.9 |