Zero-Error Coding via Classical and Quantum Channels in Sensor Networks
Abstract
:1. Introduction
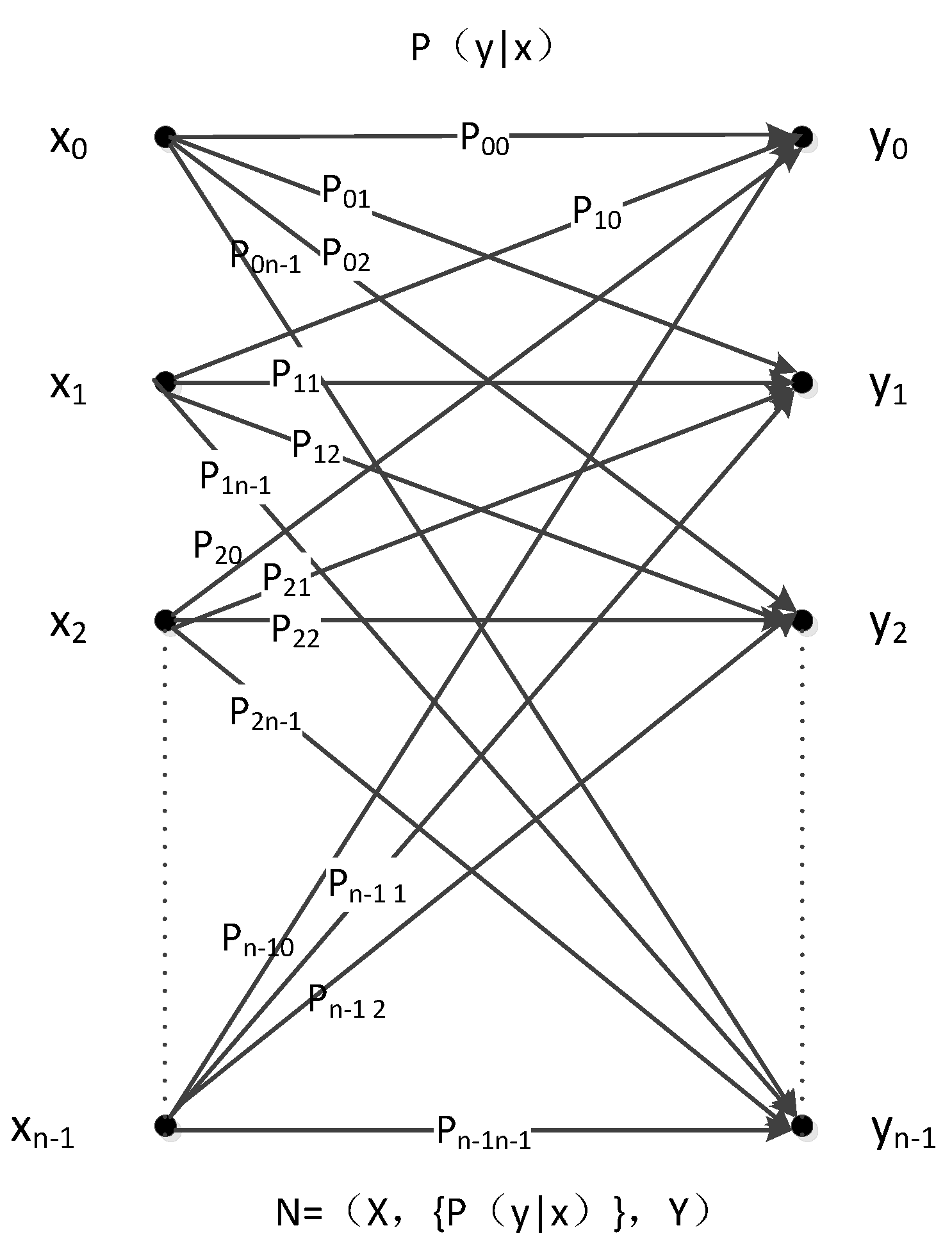
2. Zero-Error Coding via Classical Channel
3. Zero-Error Coding via Quantum Channel
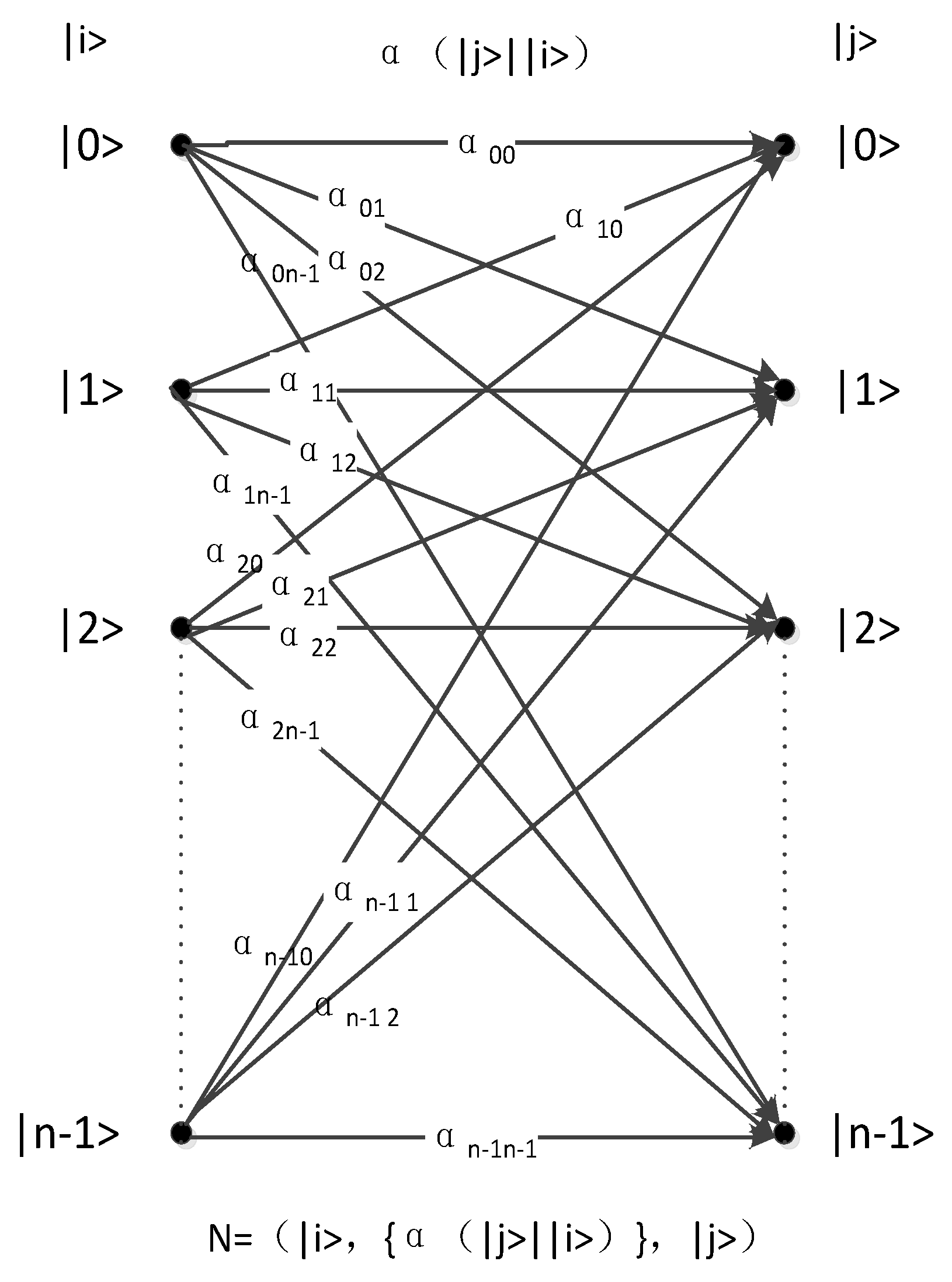
3.1. Quantum n-Symbol Obfuscation Model
3.2. Preliminary Theorems for Zero-Error Coding in Quantum Cases
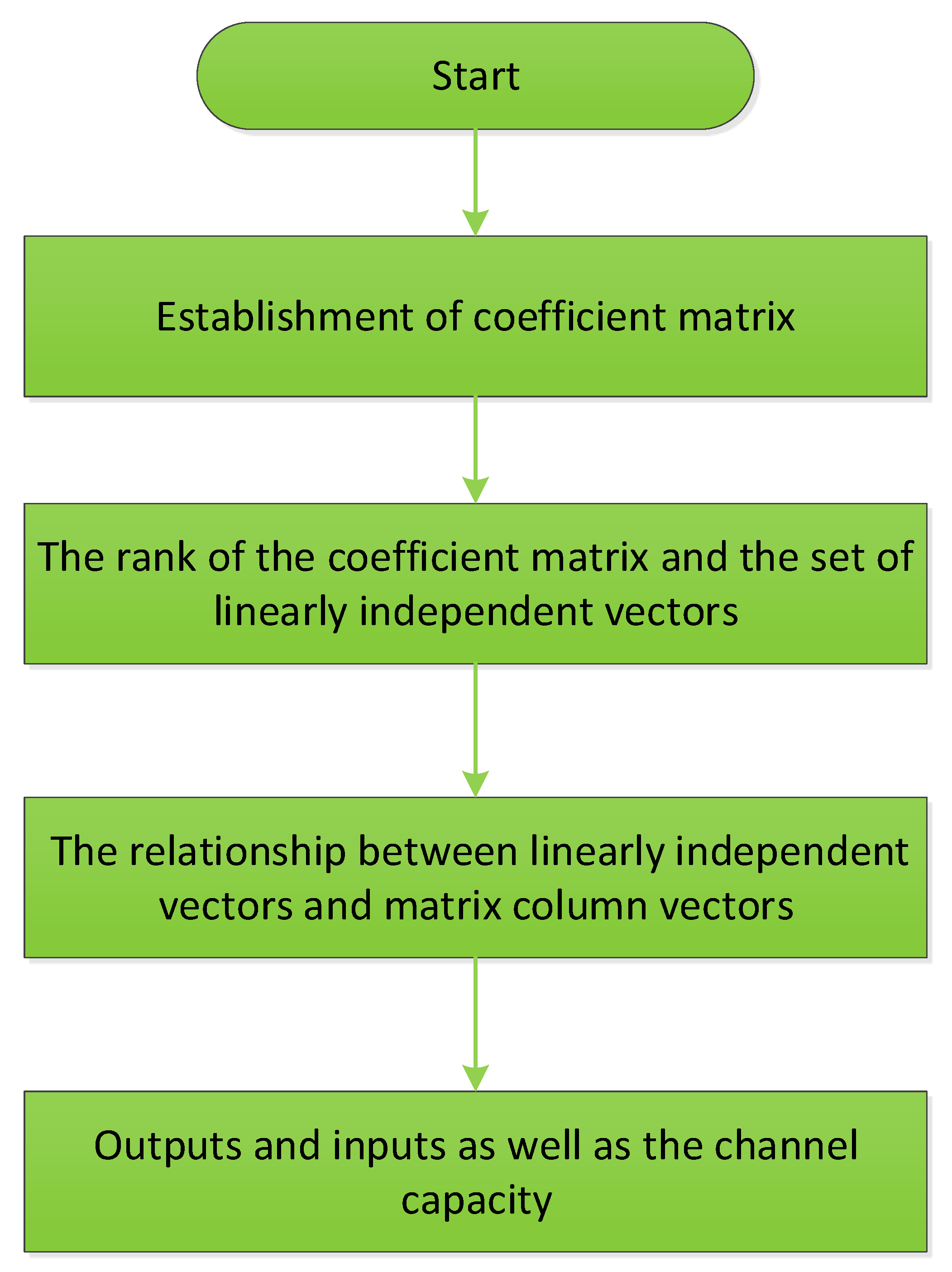
3.3. Quantum Method
4. Examples and Method Analysis
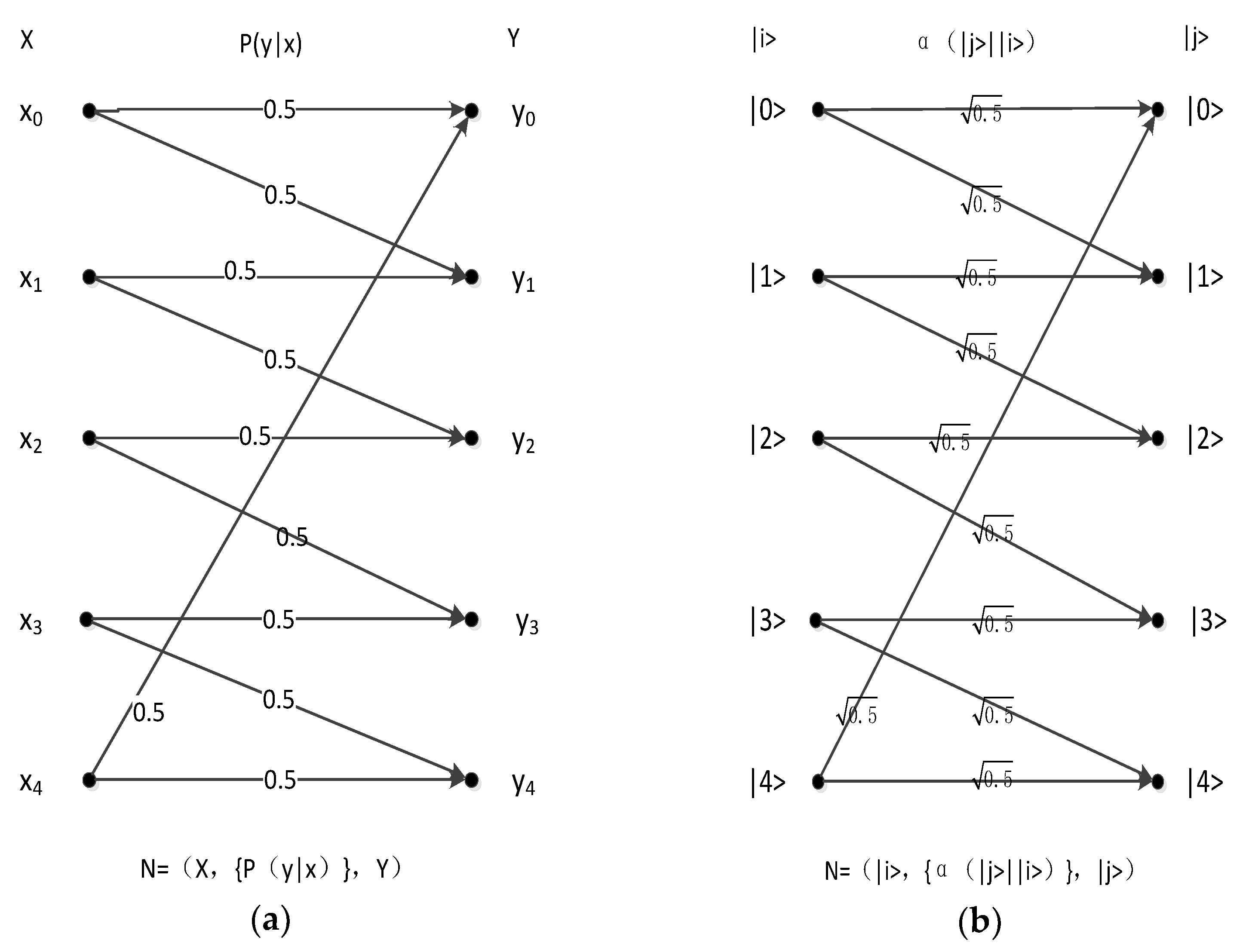
4.1. Pentagon Channel
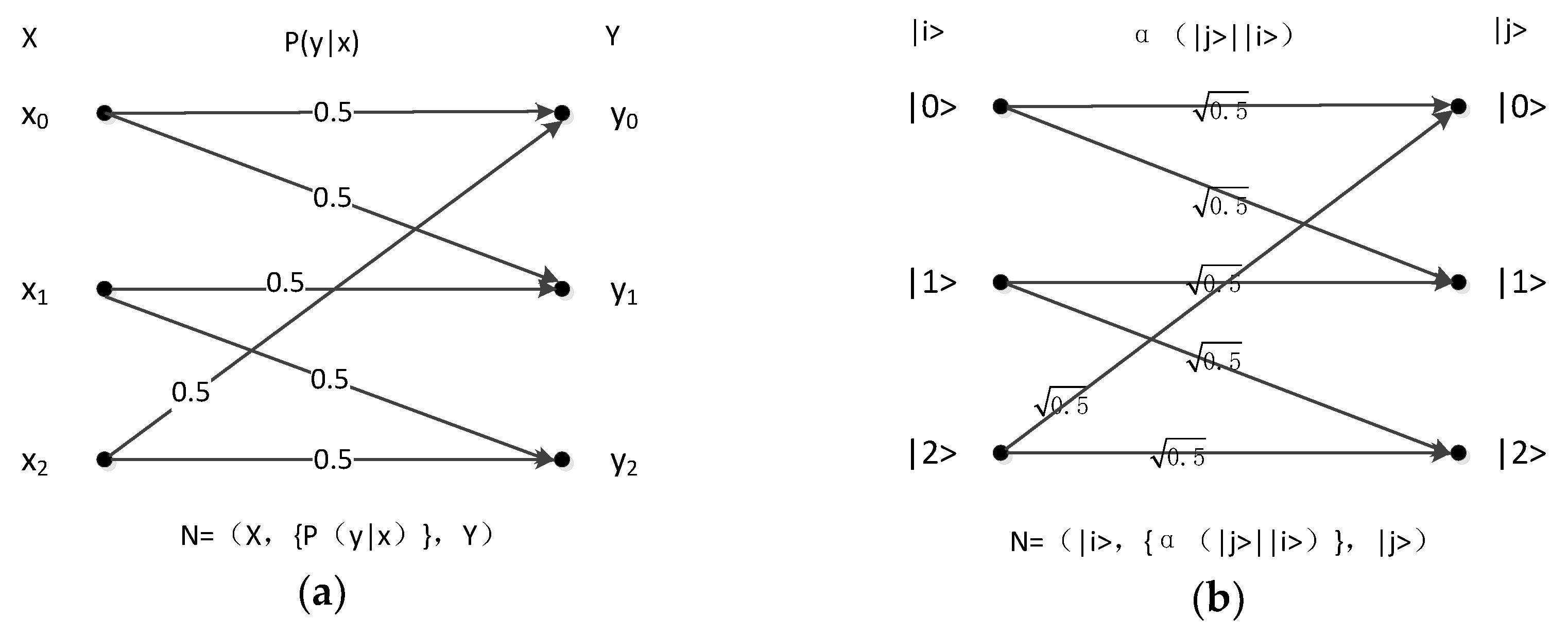
4.2. Triangular Channel
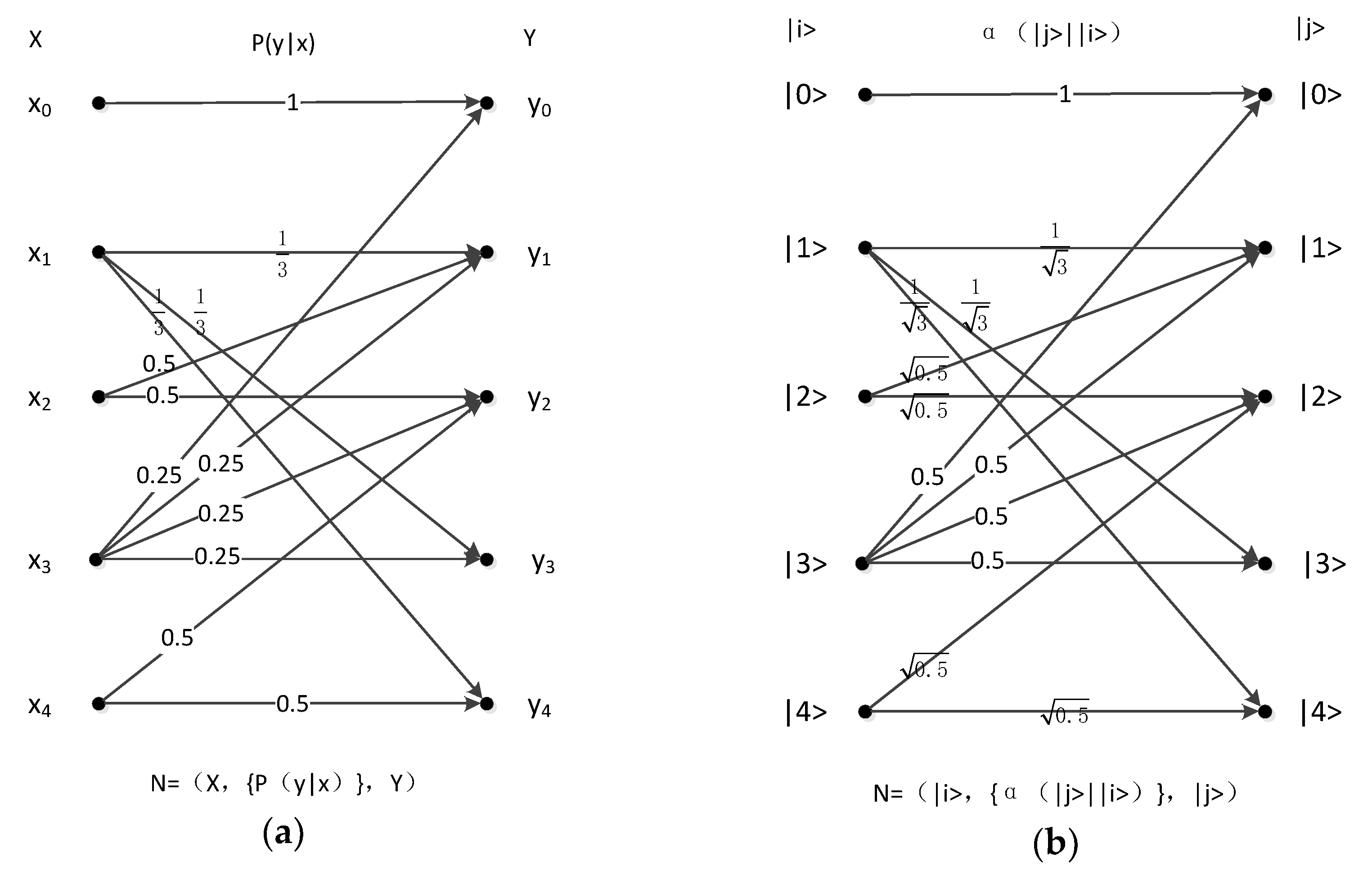
4.3. Five-Symbol Multilateral Obfuscation Channel
4.4. Performance Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Qiu, T.; Wang, X.; Chen, C.; Atiquzzaman, M.; Liu, L. TMED: A Spider Web-Like Transmission Mechanism for Emergency Data in Vehicular Ad Hoc Networks. IEEE Trans. Veh. Technol. 2018, 67, 8682–8694. [Google Scholar] [CrossRef]
- Qiu, T.; Wang, H.; Li, K.; Ning, H.; Sangaiah, A.K.; Chen, B. SIGMM: A Novel Machine Learning Algorithm for Spammer Identification in Industrial Mobile Cloud Computing. IEEE Trans. Ind. Inform. 2019, 15, 2349–2359. [Google Scholar] [CrossRef]
- Qiu, T.; Liu, J.; Si, W.; Wu, D.O. Robustness Optimization Scheme with Multi-Population Co-Evolution for Scale-Free Wireless Sensor Networks. IEEE/ACM Trans. Netw. 2019, 27, 1028–1042. [Google Scholar] [CrossRef]
- Jeong, J.; Ee, C.T. Forward Error Correction in Sensor Networks. In Proceedings of the First International Workshop on Wireless Sensor Networks (WWSN), Marrakesh, Morocco, 4–8 June 2007; p. 4. [Google Scholar]
- Shanon, C.E. The zero-error capacity of a noisy channel. IRE Trans. Inf. Theory 1956, 2, 8–19. [Google Scholar] [CrossRef]
- Lovász, L. On the Shannon Capacity of a Graph. IEEE Trans. Inf. Theory 1979, 25, 1–7. [Google Scholar] [CrossRef]
- Nakano, T.; Wadayama, T. On Zero Error Capacity of Nearest Neighbor Error Channels with Multilevel Alphabet. In Proceedings of the 2016 International Symposium on Information Theory and Its Applications (ISITA), Monterey, CA, USA, 30 October–2 November 2016; pp. 66–70. [Google Scholar]
- He, Y.; Zhu, K. Fano Effect and Quantum Entanglement in Hybrid Semiconductor Quantum Dot-Metal Nanoparticle System. Sensors 2017, 17, 1445. [Google Scholar] [CrossRef]
- Li, J.; Gao, W.; Qian, J.; Guo, Q.; Xi, J.; Ritz, C.H. Robust Entangled-Photon Ghost Imaging with Compressive Sensing. Sensors 2019, 19, 192. [Google Scholar] [CrossRef]
- Qu, Z.; Wu, S.; Wang, M.; Sun, L.; Wang, X. Effect of Quantum Noise on Deterministic Remote State Preparation of an Arbitrary Two-Particle State via Various Quantum Entangled Channels. Quantum Inf. Process. 2017, 16, 306. [Google Scholar] [CrossRef]
- Qu, Z.; Li, Z.; Xu, G.; Wu, S.; Wang, X. Quantum Image Steganography Protocol Based on Quantum Image Expansion and Grover Search Algorithm. IEEE Access 2019, 7, 50849–50857. [Google Scholar] [CrossRef]
- Qu, Z.; Cheng, Z.; Wang, X. Matrix Coding-Based Quantum Image Steganography Algorithm. IEEE Access 2019, 7, 35684–35698. [Google Scholar] [CrossRef]
- Liu, W.; Gao, P.; Yu, W.; Qu, Z.; Yang, C. Quantum Relief algorithm. Quantum Inf. Process. 2018, 17, 280. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Y.; Yang, C.; Gao, P.; Yu, W. An Efficient and Secure Arbitrary N-Party Quantum Key Agreement Protocol Using Bell States. Int. J. Theor. Phys. 2018, 57, 195–207. [Google Scholar] [CrossRef]
- Liu, W.; Wang, H.; Yuan, G.; Xu, Y.; Chen, Z.; An, X.; Ji, F.; Gnitou, G.T. Multiparty Quantum Sealed-Bid Auction Using Single Photons as Message Carrier. Quantum Inf. Process. 2016, 15, 869–879. [Google Scholar] [CrossRef]
- Qu, Z.; Zhu, T.; Wang, J.; Wang, X. A Novel Quantum Steganography Based on Brown States. CMC Comput. Mater. Contin. 2018, 56, 47–59. [Google Scholar]
- Liu, W.; Chen, Z.; Liu, J.; Su, Z.; Chi, L. Full-Blind Delegating Private Quantum Computation. CMC Comput. Mater. Contin. 2018, 56, 211–223. [Google Scholar]
- Wang, M.; Yang, C.; Mousoli, R. Controlled Cyclic Remote State Preparation of Arbitrary Qubit States. CMC Comput. Mater. Contin. 2018, 56, 321–329. [Google Scholar]
- Bennett, C.H.; DiVincenzo, D.P. Quantum Information and Computation. Nature 2000, 404, 247–255. [Google Scholar] [CrossRef]
- Wootters, W.K.; Zurek, W.H. A Single Quantum Cannot Be Cloned. Nature 1982, 299, 802–803. [Google Scholar] [CrossRef]
- Beigi, S.; Shor, P.W. On the Complexity of Computing Zero-Error and Holevo Capacity of Quantum Channels. Available online: https://arxiv.org/abs/0709.2090 (accessed on 13 October 2008).
- Cubitt, T.S.; Chen, J.; Harrow, A.W. Super Activation of the Asymptotic Zero-Error Classical Capacity of a Quantum Channel. Available online: https://arxiv.org/abs/0906.2547 (accessed on 12 September 2011).
- Duan, R. Super-Activation of Zero-Error Capacity of Noisy Quantum Channels. Available online: https://arxiv.org/abs/0906.2527 (accessed on 15 June 2009).
- Duan, R.; Severini, S.; Winter, A. Zero-Error Communication via Quantum Channels, Noncommutative Graphs and a Quantum Lovász Number. IEEE Trans. Inf. Theory 2013, 59, 1164–1174. [Google Scholar] [CrossRef]
- Duan, R.; Severini, S.; Winter, A. On Zero-Error Communication via Quantum Channels in the Presence of Noiseless Feedback. IEEE Trans. Inf. Theory 2016, 62, 5260–5277. [Google Scholar] [CrossRef]
- Stahlke, D. Quantum Zero-Error Source-Channel Coding and Non-Commutative Graph Theory. IEEE Trans. Inf. Theory 2016, 62, 554–577. [Google Scholar] [CrossRef]
- Lancaster, P.; Tismenetsky, M. Theory of Matrices, 2nd ed.; Academic Press: New York, NY, USA; London, UK, 1985. [Google Scholar]
- Jerkovits, T.; Liva, G.; Amat, A.G. Improving the Decoding Threshold of Tailbiting Spatially Coupled LDPC Codes by Energy Shaping. IEEE Commun. Lett. 2018, 22, 660–663. [Google Scholar] [CrossRef]
- Fang, Y.; Bi, G.; Guan, Y.L.; Lau, F.C.M. A Survey on Protograph LDPC Codes and Their Applications. IEEE Commun. Surv. Tutor. 2015, 17, 1989–2016. [Google Scholar] [CrossRef]


| Channel Capacity C | Triangular Channel | Pentagon Channel | Five-Symbol Multilateral Obfuscation Channel |
|---|---|---|---|
| LDPC | 1.405 | ||
| Classical Zero-error Coding | 0 | 1 | |
| Quantum Zero-error Coding | 2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, W.; Xiong, Z.; Dong, Z.; Wang, S.; Li, J.; Liu, G.; Liu, A.X. Zero-Error Coding via Classical and Quantum Channels in Sensor Networks. Sensors 2019, 19, 5071. https://doi.org/10.3390/s19235071
Yu W, Xiong Z, Dong Z, Wang S, Li J, Liu G, Liu AX. Zero-Error Coding via Classical and Quantum Channels in Sensor Networks. Sensors. 2019; 19(23):5071. https://doi.org/10.3390/s19235071
Chicago/Turabian StyleYu, Wenbin, Zijia Xiong, Zanqiang Dong, Siyao Wang, Jingya Li, Gaoping Liu, and Alex X. Liu. 2019. "Zero-Error Coding via Classical and Quantum Channels in Sensor Networks" Sensors 19, no. 23: 5071. https://doi.org/10.3390/s19235071
APA StyleYu, W., Xiong, Z., Dong, Z., Wang, S., Li, J., Liu, G., & Liu, A. X. (2019). Zero-Error Coding via Classical and Quantum Channels in Sensor Networks. Sensors, 19(23), 5071. https://doi.org/10.3390/s19235071





