A Fast, Three-Dimensional, Indirect Geolocation Method Using IAGM and DSM Data without GCPs for Spaceborne SAR Images
Abstract
1. Introduction
2. The Geolocation Theory
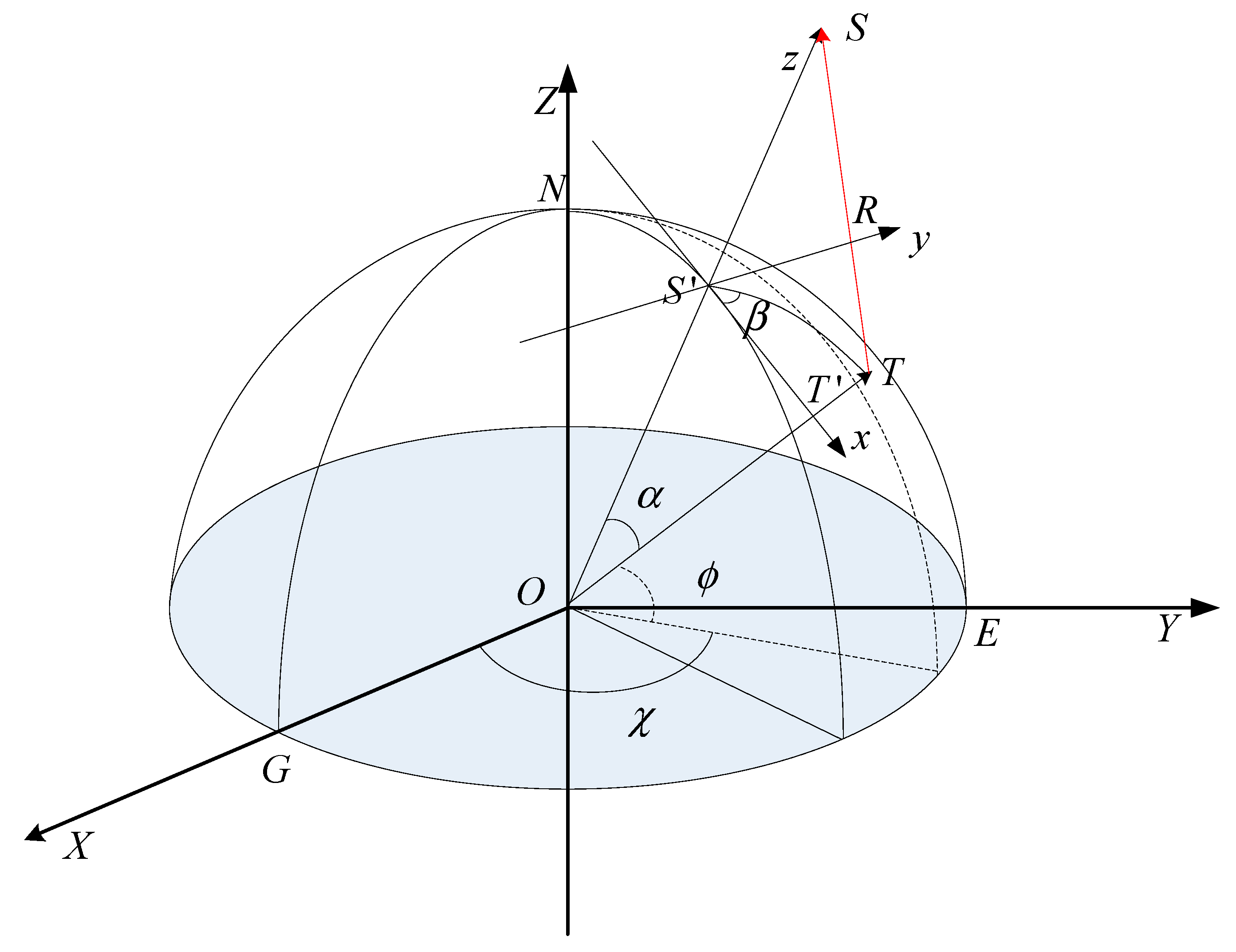
2.1. The Coordinate System and Transformation Formula
2.2. The RD Model for SAR Images
2.2.1. The Earth Model Equation
2.2.2. The SAR Doppler Equation
2.2.3. The SAR Range Equation
2.2.4. The RD Model
2.3. Iterative Analytical Geolocation Method (IAGM)
- (a)
- Calculate the geocentric latitude and longitude of the sub-satellite point :
- (b)
- In the local coordinate system, the vectors , , and in the ECR coordinate system can be transformed to , , and [16]:where .
- (c)
- Calculate the angle from the Doppler equation.
- (d)
- Calculate the geocentric latitude and longitude for the ground point by using the angle and the angle [16].
- Get , , and according to the above method.
- Use Equation (14) to calculate the angle .
- According to the steps from (a) to (d), the position vector can be obtained.
- Calculate the value . If , then stop the iteration and get the final result . Otherwise, let and re-execute step 2.
2.4. Atmospheric Propagation Delay for Microwaves
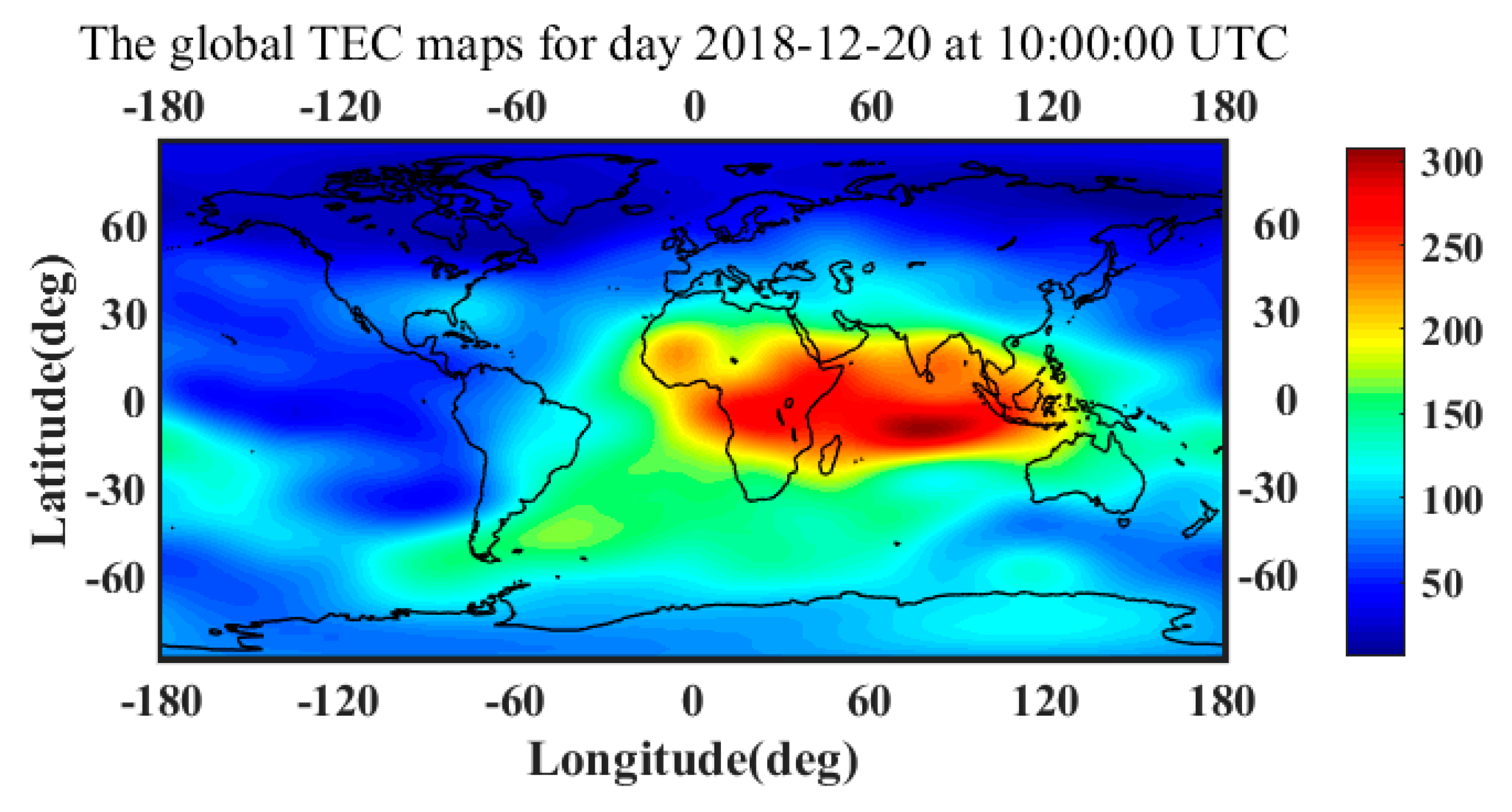
2.4.1. The Ionospheric Delay
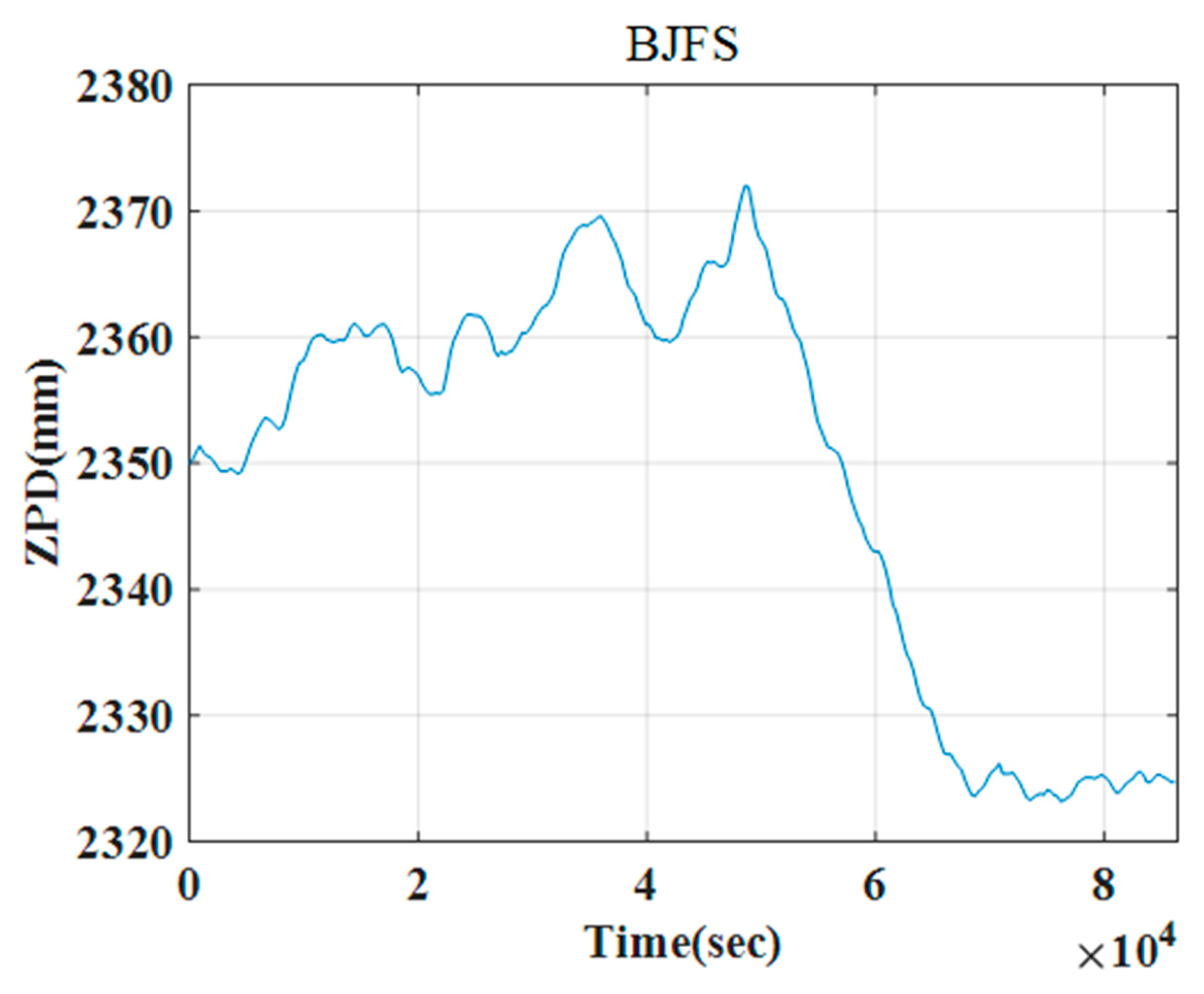
2.4.2. The Tropospheric Delay
2.4.3. Real Data for the Ionosphere and Troposphere
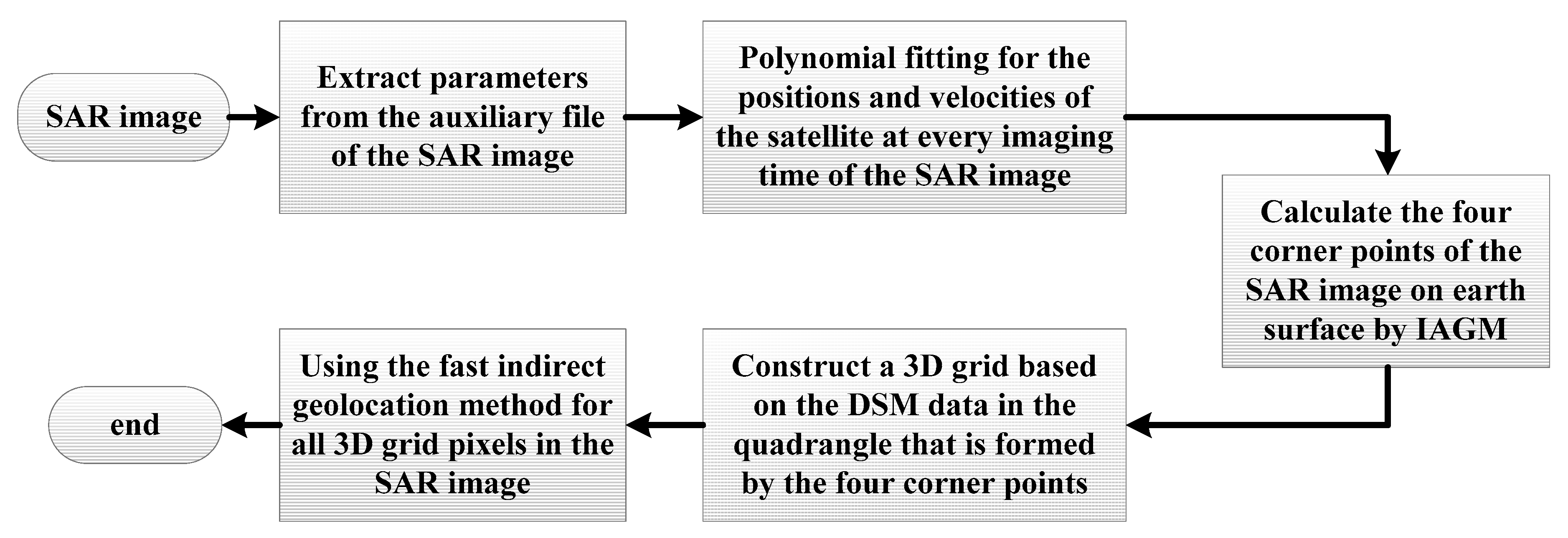
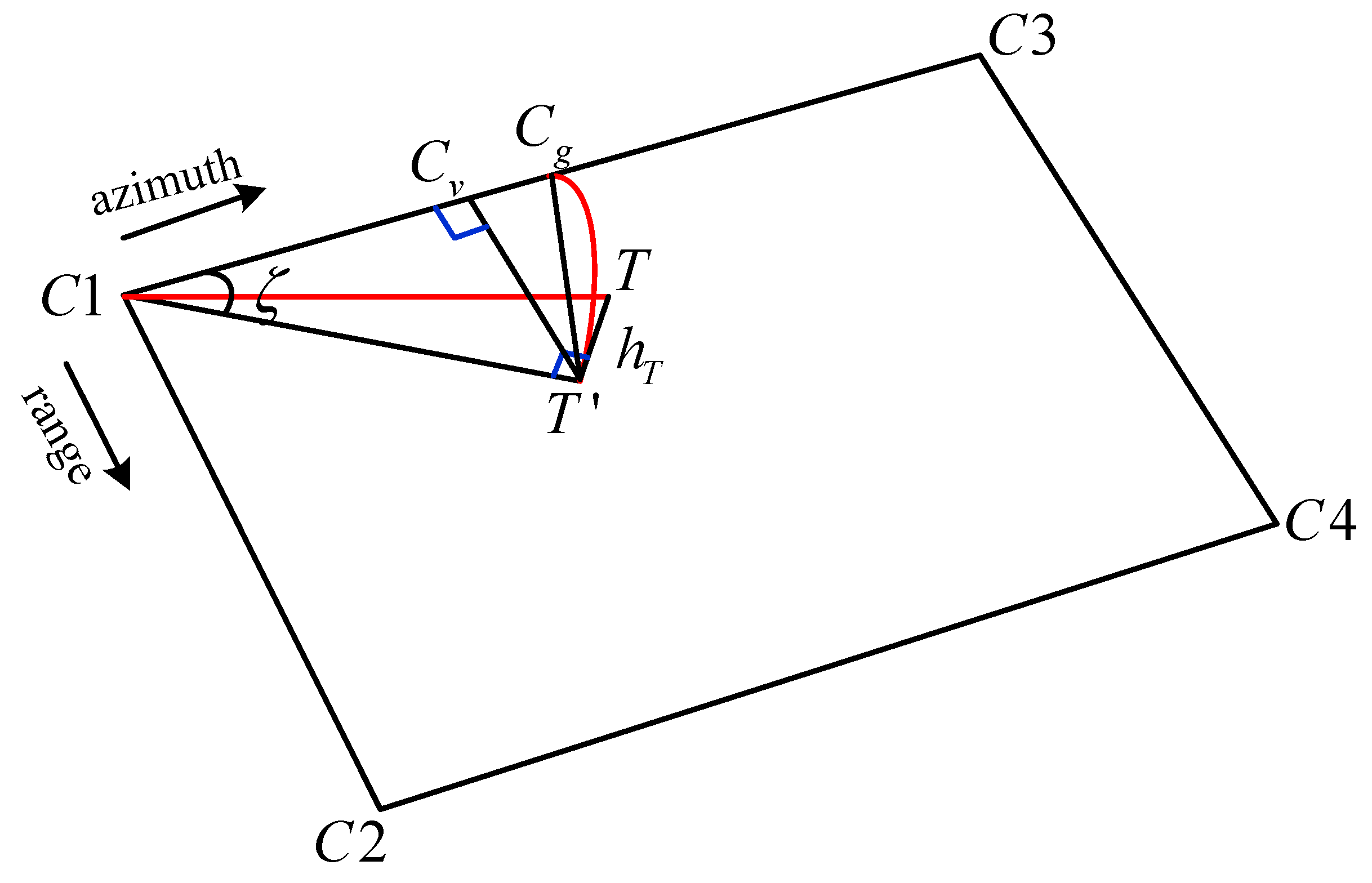
3. A Fast, Three-Dimensional, Indirect Geolocation Method
- (a)
- Calculate the slopes of the latitude and the longitude between the first azimuth time and the last azimuth time at the nearest and furthest slant ranges, respectively.Then, the average values for the slopes of latitude and the longitude are given by:
- (b)
- Calculate the distance between C1 and C3:
- (c)
- As point ’s projection point is , the positions of and are and , respectively. The rectangular space coordinates of point and point are and , respectively. Then calculate the distance between C1 and .
- (d)
- Estimate point on the straight line C1C3, whose geodetic coordinate is given by:
- (e)
- From the ratio relationship, the azimuth time of point can be derived:where is the SAR image generation starting time, is the imaging time interval of the SAR image, and returns the integer part of a decimal number.
- (f)
- Obtain point ’s precise azimuth time . Calculate the Doppler frequency at the estimated azimuth time by Equations (9)–(11).where , , , .
- (g)
- Calculate the slant range of point .where is the satellite position at the azimuth time , is the range spacing.
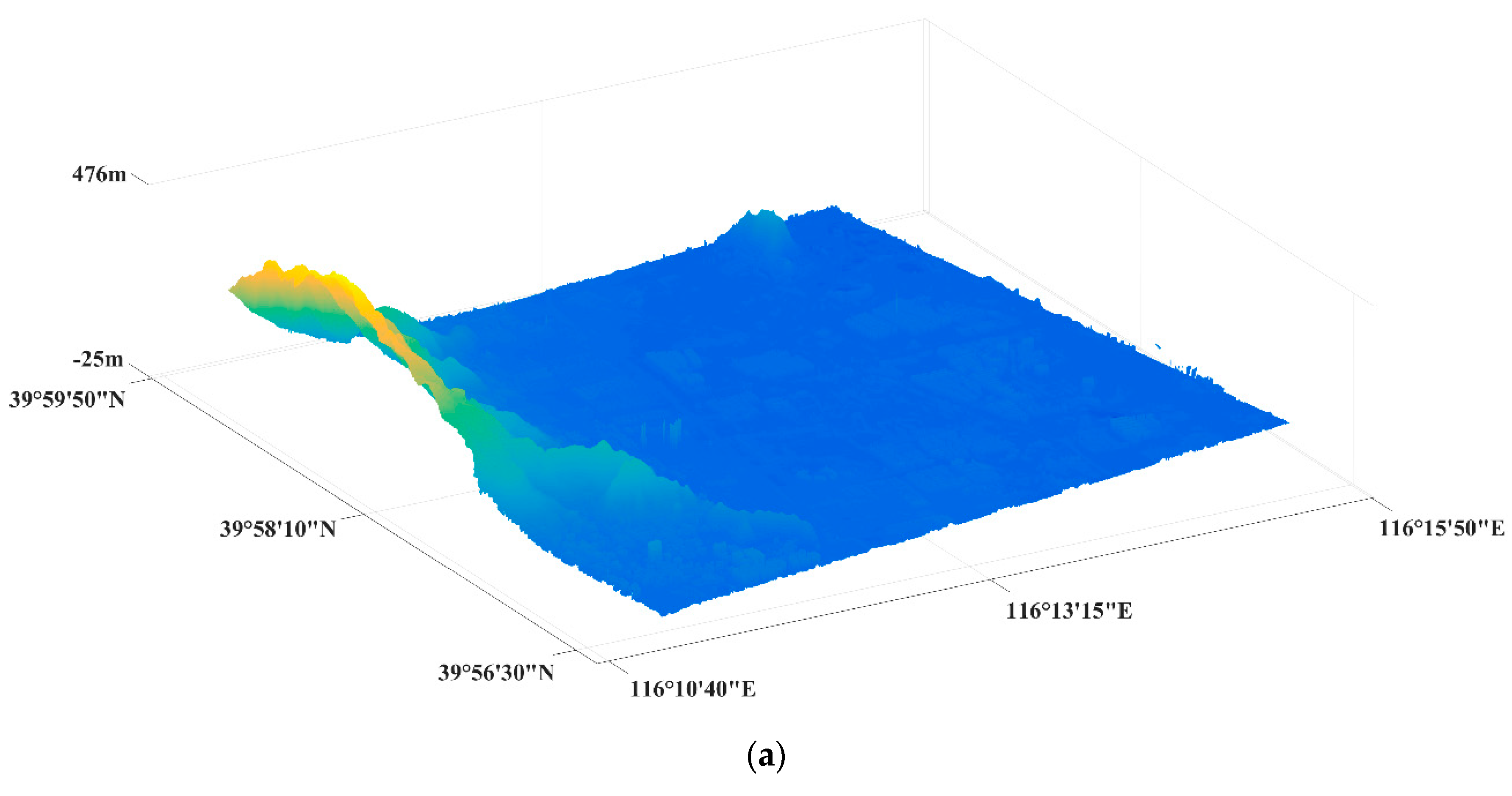
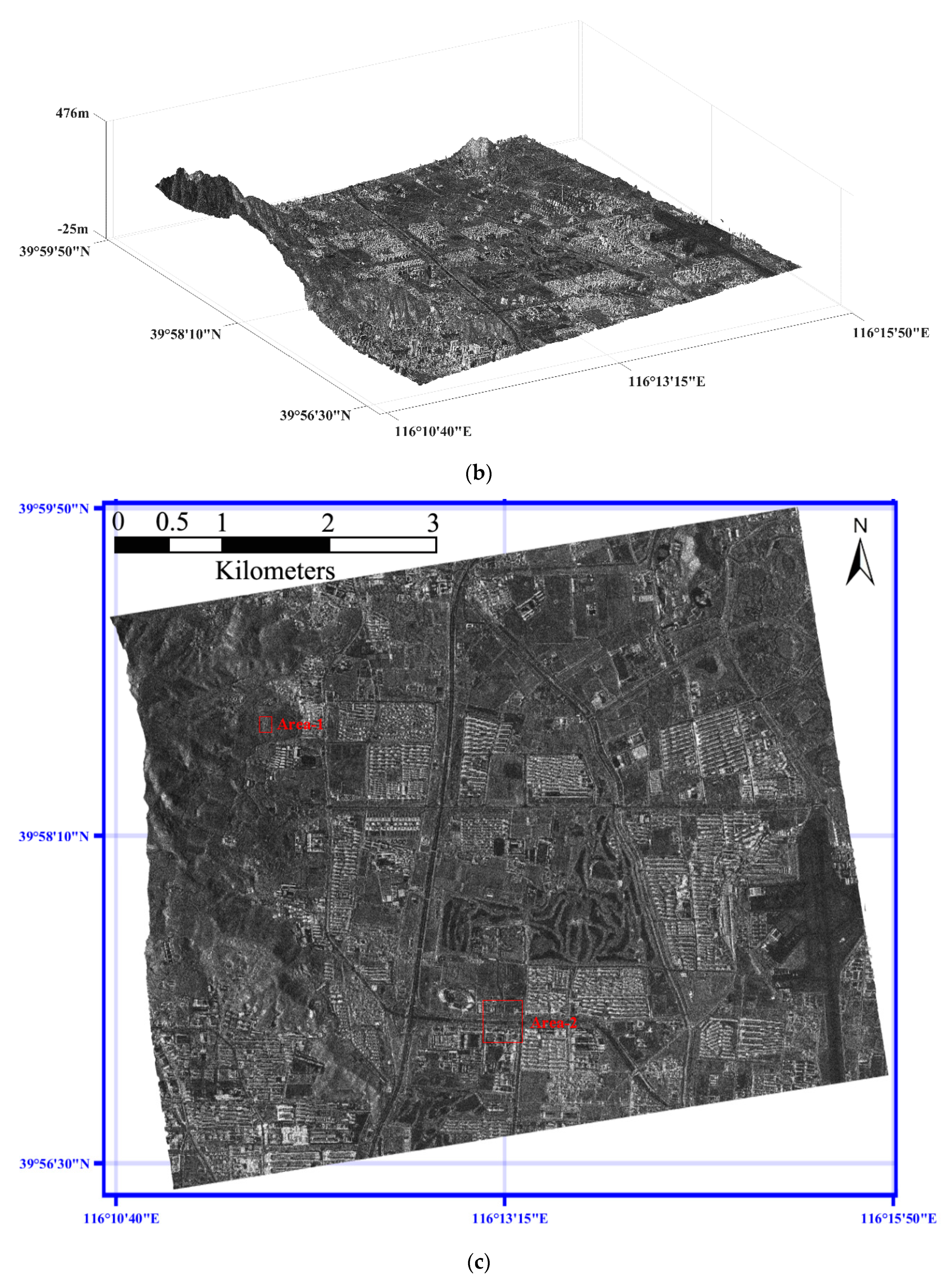
4. Experiments and Analyses
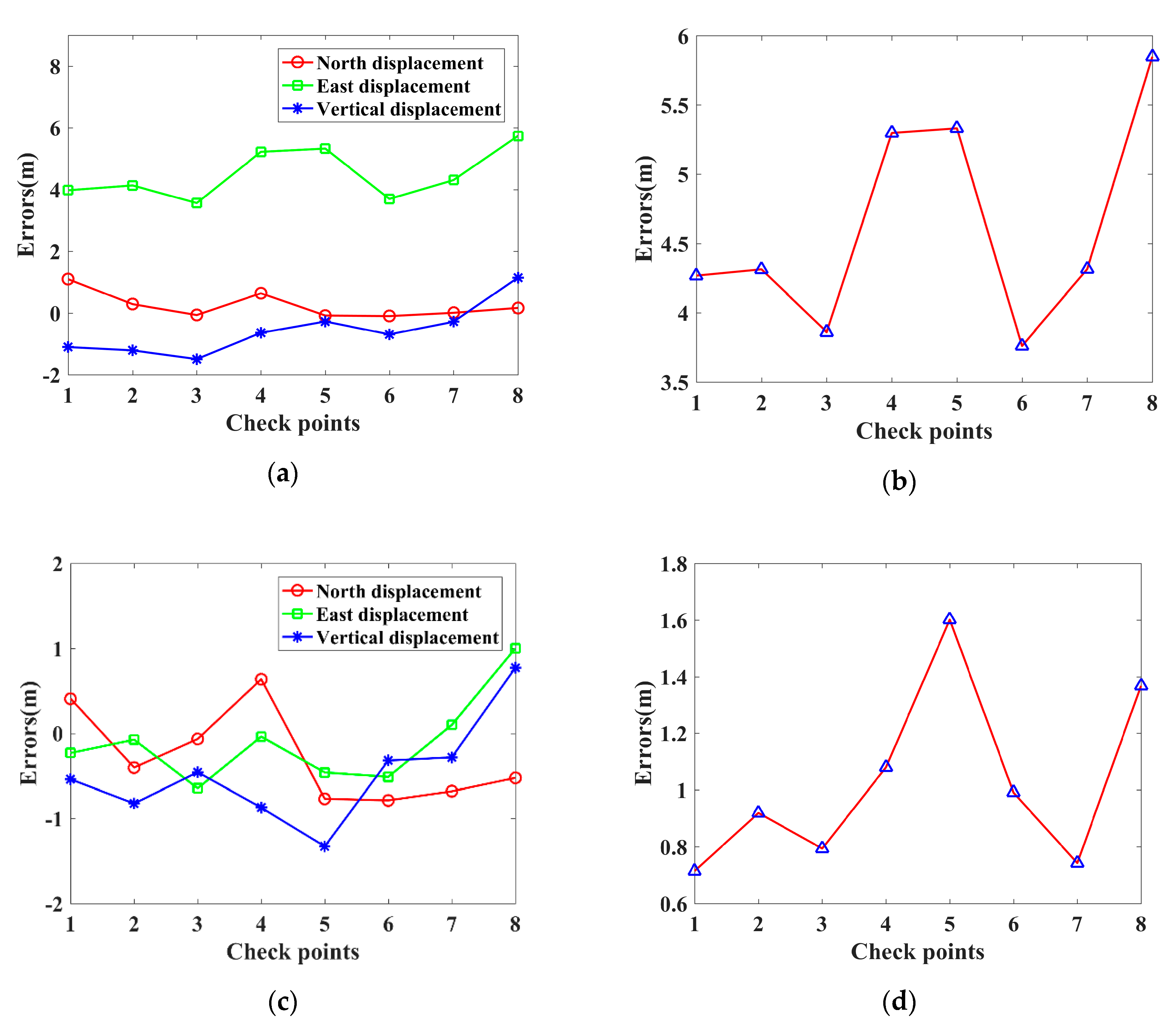
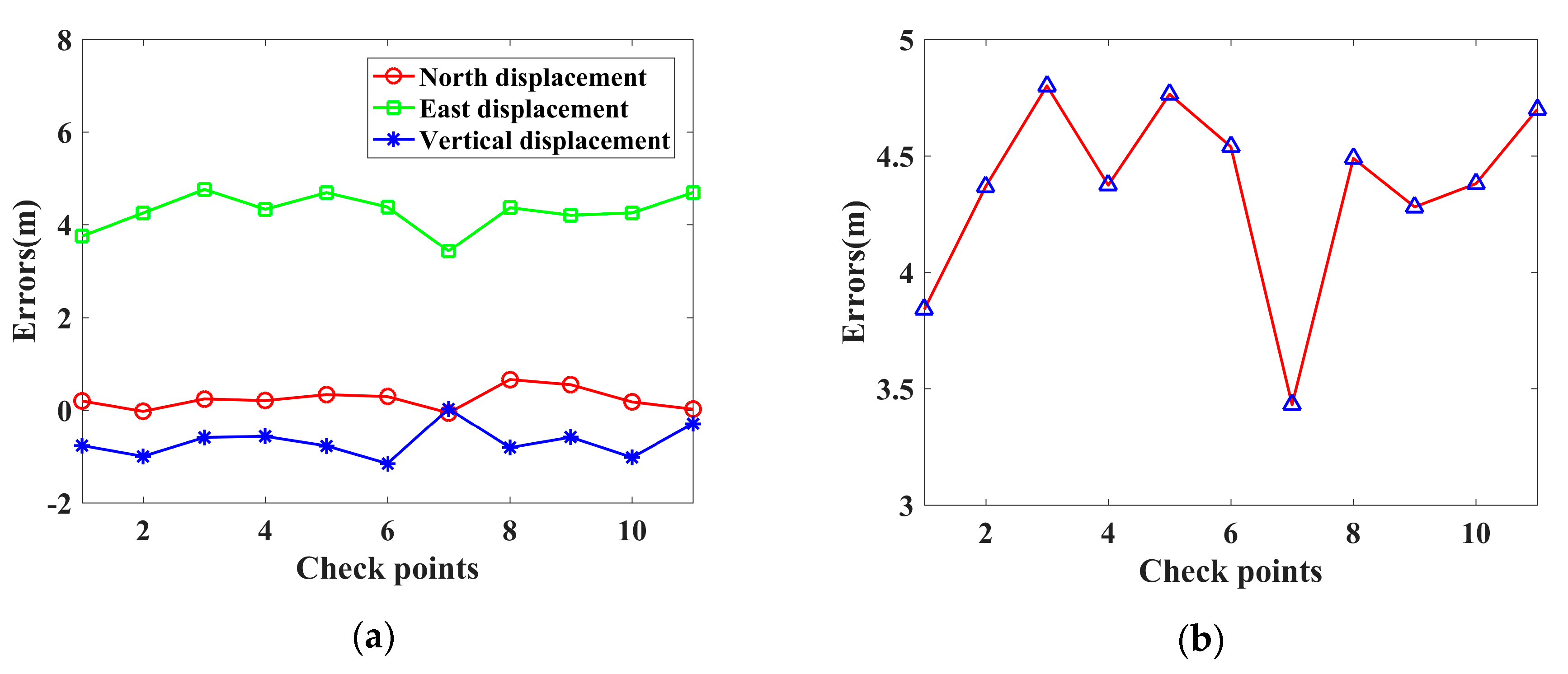
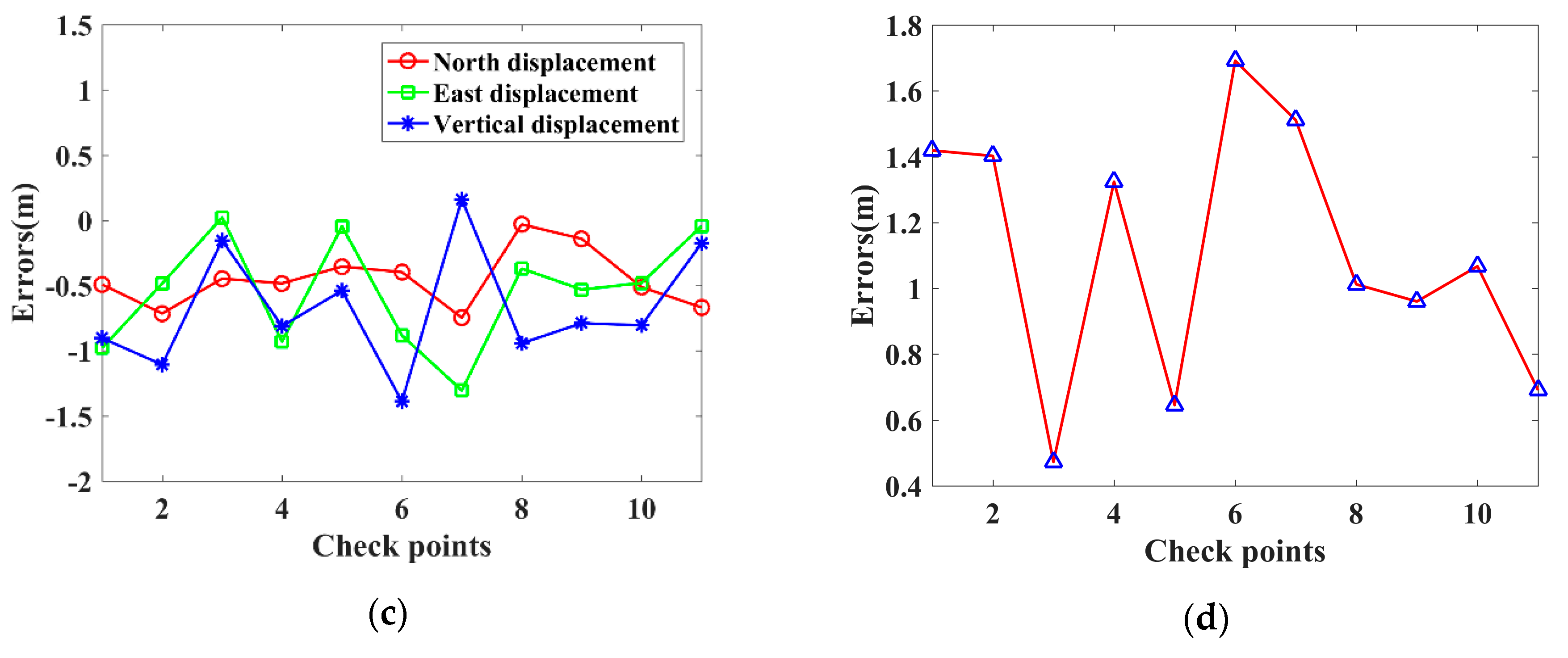
4.1. Geolocation Results
4.2. Computational Efficiency and Accuracy
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Curlander, J.C.; Mcdonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Blass, U.; Cong, X.Y.; Brcic, R.; Rexer, M.; Minet, C.; Breit, H.; Eineder, M.; Fritz, T. High precision measurement on the absolute localization accuracy of TerraSAR-X. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 1625–1628. [Google Scholar]
- Schubert, A.; Jehle, M.; Small, D.; Meier, E. Mitigation of atmospheric perturbations and solid Earth movements in a TerraSAR-X time-series. J. Geod. 2011, 86, 257–270. [Google Scholar] [CrossRef]
- Ding, C.; Liu, J.; Lei, B.; Qiu, X. Preliminary exploration of systematic geolocation accuracy of GF-3 SAR satellite system. J. Radar 2017, 6, 11–16. [Google Scholar]
- Balss, U.; Eineder, M.; Fritz, T.; Breit, H.; Minet, C. Techniques for high accuracy relative and absolute localization of TerraSAR-X/TanDEM-X data. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 2464–2467. [Google Scholar]
- Eineder, M.; Minet, C.; Steigenberger, P.; Cong, X.; Fritz, T. Imaging geodesy—Toward centimeter-level ranging accuracy with TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2011, 49, 661–671. [Google Scholar] [CrossRef]
- Cong, X.; Balss, U.; Eineder, M.; Fritz, T. Imaging geodesy—Centimeter-level ranging accuracy with TerraSAR-X: An update. IEEE Geosci. Remote Sens. Lett. 2012, 9, 948–952. [Google Scholar] [CrossRef]
- Chen, E. Study on Ortho-Rectification Methodology of Space-Borne Synthetic Aperture Radar Imagery. Ph.D. Thesis, Chinese Academy of Forestry, Beijing, China, 2004. [Google Scholar]
- Song, Z.; Zhang, J.; Huang, G. Research on airborne SAR indirect geocoding method based on correction of slant range measurement error. Remote Sens. Inf. 2011, 4, 23–27. [Google Scholar]
- Wang, D.; Liu, A.; Xia, X. Error model based on range-doppler indirect positioning. Electron. Meas. Technol. 2018, 41, 139–144. [Google Scholar]
- Blass, U.; Gisinger, C.; Cong, X.; Eineder, M.; Brcic, R. Precise 2-D and 3-D ground target localization with TerraSAR-X. Int. Arch. Photogramm. Remote Sens. 2013, 40, 23–28. [Google Scholar] [CrossRef]
- Blass, U.; Gisinger, C.; Eineder, M. Measurements on the absolute 2-D and 3-D localization accuracy of TerraSAR-X. Remote Sens. 2018, 10, 656. [Google Scholar] [CrossRef]
- Curlander, J.C. Utilization of Spaceborne SAR Data for Mapping. IEEE Trans. Geosci. Remote Sens. 1984, 22, 106–112. [Google Scholar] [CrossRef]
- Balz, T.; Zhang, L.; Liao, M. Fast geocoding of spaceborne synthetic-aperture radar images using graphics processing units. J. Appl. Remote Sens. 2012, 6, 063553. [Google Scholar]
- Liu, X.; Ma, H.; Sun, W. Study on the Geolocation Algorithm of Space-Borne SAR Image. Advances in Machine Vision, Image Processing, and Pattern Analysis; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Zhou, G.; He, C.; Yue, T.; Huang, W.; Huang, Y.; Li, X.; Chen, Y. An improved method of AGM for high precision geolocation of SAR images. Int. Arch. Photogramm. Remote Sens. 2018, 42, 2479–2484. [Google Scholar] [CrossRef]
- Yang, S.; Huang, G.; Zhou, Z. Generation of SAR stereo image pair. In Proceedings of the IET International Radar Conference, Guilin, China, 20–22 April 2009; p. 646. [Google Scholar]
- Wan, Z.; Shao, Y.; Xie, C.; Zhang, F. Ortho-rectification of high-resolution SAR image in mountain area by DEM. In Proceedings of the 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010. [Google Scholar]
- Xu, G. GPS: Theory, Algorithms and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems; Springer: Mörlenbach, Germany, 2008. [Google Scholar]
- Li, Y. Direct and Indirect Ortho-Rectification of Space-Borne SAR Image. Ph.D. Thesis, University of Chinese Academy of Sciences, Beijing, China, 2017. [Google Scholar]
- Wang, Q.; Huang, H.; Dong, Z.; Yu, A.; He, F.; Liang, D. High-precision, fast geolocation method for spaceborne synthetic aperture radar. Chin. Sci. Bull. 2012, 57, 287–293. [Google Scholar] [CrossRef]
- Curlander, J.C. Location of spaceborne SAR imagery. IEEE Trans. Geosci. Remote Sens. 1982, 20, 359–364. [Google Scholar] [CrossRef]
- Zanin, K.A. Quality analysis of image geolocation for a space synthetic aperture radar. Solar Syst. Res. 2014, 48, 555–560. [Google Scholar] [CrossRef]
- Wang, W.; Liu, J.; Qiu, X. Decimeter-level geolocation accuracy updated by a parametric tropospheric model with GF-3. Sensors 2018, 18, 2197. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The geometry-free GPS ambiguity search space with a weighted ionosphere. J. Geod. 1997, 71, 370–383. [Google Scholar] [CrossRef]
- Alizadeh, M.M.; Wijaya, D.D.; Hobiger, T.; Weber, R.; Schuh, H. Ionospheric Effects on Microwave Signals. In Atmospheric Effects in Space Geodesy; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- IONEX File Containing IGS Combined Ionosphere Maps Provided by CDDIS. Available online: Ftp://cddis.gsfc.nasa.gov/pub/gps/products/ionosphere/2018/354/igsg3540.18i.Z (accessed on 5 August 2019).
- Nilsson, T.; Böhm, J.; Wijaya, D.D.; Tresch, A.; Nafisi, V.; Schuh, H. Path Delays in the Neutral Atomosphere. In Atmospheric Effects in Space Geodesy; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Baldysz, Z.; Nykiel, G.; Araszkiewicz, A.; Figurski, M.; Szafranek, K. Comparison of GPS tropospheric delays derived from two consecutive EPN reprocessing campaigns from the point of view of climate monitoring. Atmos. Meas. Tech. 2016, 9, 4861–4877. [Google Scholar] [CrossRef]
- Lannes, A.; Teunissen, P.J.G. GNSS algebraic structures. J. Geod. 2011, 85, 273–290. [Google Scholar] [CrossRef][Green Version]
- Maciuk, K. GPS-only, GLONASS-only and Combined GPS+GLONASS Absolute Positioning under Different Sky View Conditions. Teh. Vjesn. 2018, 25, 933–939. [Google Scholar]
- Nordman, M.; Eresmaa, R.; Boehm, J.; Poutanen, M.; Koivula, H.; Järvinen, H. Effect of troposphere slant delays on regional double difference GPS processing. Earth Planets Space 2009, 61, 845–852. [Google Scholar] [CrossRef]
- Wang, K.; Rothacher, M. Stochastic modeling of high-stability ground clocks in GPS analysis. J. Geod. 2013, 87, 427–437. [Google Scholar] [CrossRef]
- Tropospheric Delay in ZPD Format Provided by CDDIS. Available online: Ftp://cddis.gsfc.nasa.gov/pub/gps/products/troposphere/zpd/2018/354/bjfs3540.18zpd.gz (accessed on 5 August 2019).
- Technical Information Elevation1 Digital Surface Model. Available online: https://www.intelligence-airbusds.com/files/pmedia/public/r49249_9_elevation1_dsm.pdf (accessed on 2 July 2019).
- Fraczek, W. Mean Sea Level, GPS, and the Geoid. Available online: https://www.esri.com/news/arcuser/0703/geoid1of3.html (accessed on 2 July 2019).
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. An Earth gravitational model to degree 2160: EGM2008. In Proceedings of the General Assembly of the European Geosciences Union, Vienna, Austria, 13–18 April 2008. [Google Scholar]



| Parameter Name | Value | Units |
|---|---|---|
| Image size | − | |
| Azimuth spacing | 0.8705 | m |
| Range spacing | 0.4547 | m |
| Slant range to the first pixel | 706,315.7084 | m |
| Pulse repetition frequency | 3720.4126 | Hz |
| Radar frequency | 9649.998153 | MHz |
| The number of orbit state vectors | 12 | − |
| Date of acquisition(UTC) | 20 December 2018 | − |
| Acquisition mode | Spotlight | − |
| Producttype | SSC_HS_S | − |
| Descending/Ascending | Ascending | − |
| Look direction | Right | − |
| Check Points | N (m) | E (m) | H (m) | Spatial (m) |
|---|---|---|---|---|
| P1-M1 | 1.0942 | 3.9758 | −1.1020 | 4.2684 |
| P1-M2 | 0.4080 | −0.2308 | −0.5400 | 0.7151 |
| P2-M1 | 0.2842 | 4.1319 | −1.2079 | 4.3143 |
| P2-M2 | −0.4020 | −0.0747 | −0.8236 | 0.9195 |
| P3-M1 | −0.0664 | 3.5610 | −1.4886 | 3.8602 |
| P3-M2 | −0.0664 | −0.6456 | −0.4571 | 0.7938 |
| P4-M1 | 0.6374 | 5.2201 | −0.6411 | 5.2978 |
| P4-M2 | 0.6374 | −0.0382 | −0.8710 | 1.0800 |
| P5-M1 | −0.0816 | 5.3240 | −0.2730 | 5.3316 |
| P5-M2 | −0.7678 | −0.4600 | −1.3277 | 1.6012 |
| P6-M1 | −0.1002 | 3.6949 | −0.6922 | 3.7605 |
| P6-M2 | −0.7864 | −0.5117 | −0.3195 | 0.9912 |
| P7-M1 | 0.0063 | 4.3063 | −0.2809 | 4.3155 |
| P7-M2 | −0.6799 | 0.0998 | −0.2821 | 0.7429 |
| P8-M1 | 0.1632 | 5.7325 | 1.1457 | 5.8481 |
| P8-M2 | −0.5230 | 1.0001 | 0.7717 | 1.3672 |
| Check Points | N (m) | E (m) | H (m) | Spatial (m) |
|---|---|---|---|---|
| P1-M1 | 0.1944 | 3.7567 | −0.7724 | 3.8402 |
| P1-M2 | −0.4918 | −0.9774 | −0.9034 | 1.4189 |
| P2-M1 | −0.0275 | 4.2506 | −1.0030 | 4.3674 |
| P2-M2 | −0.7137 | −0.4836 | −1.1060 | 1.4023 |
| P3-M1 | 0.2397 | 4.7571 | −0.5951 | 4.8002 |
| P3-M2 | −0.4465 | 0.0229 | −0.1541 | 0.4729 |
| P4-M1 | 0.2034 | 4.3313 | −0.5728 | 4.3737 |
| P4-M2 | −0.4828 | −0.9289 | −0.8107 | 1.3240 |
| P5-M1 | 0.3324 | 4.6884 | −0.7787 | 4.7642 |
| P5-M2 | −0.3538 | −0.0458 | −0.5379 | 0.6455 |
| P6-M1 | 0.2901 | 4.3786 | −1.1601 | 4.5390 |
| P6-M2 | −0.3961 | −0.8816 | −1.3881 | 1.6915 |
| P7-M1 | −0.0604 | 3.4302 | 0.0244 | 3.4308 |
| P7-M2 | −0.7466 | −1.3040 | 0.1605 | 1.5111 |
| P8-M1 | 0.6558 | 4.3651 | −0.8153 | 4.4888 |
| P8-M2 | −0.0304 | −0.3691 | −0.9421 | 1.0123 |
| P9-M1 | 0.5451 | 4.2038 | −0.5918 | 4.2801 |
| P9-M2 | −0.1411 | −0.5304 | −0.7880 | 0.9603 |
| P10-M1 | 0.1747 | 4.2544 | −1.0270 | 4.3801 |
| P10-M2 | −0.5115 | −0.4798 | −0.8043 | 1.0671 |
| P11-M1 | 0.0195 | 4.6897 | −0.2976 | 4.6992 |
| P11-M2 | −0.6667 | −0.0445 | −0.1763 | 0.6911 |
| SN | Scale | Traditional | Proposed |
|---|---|---|---|
| i | 1024 × 1024 | 59.15 s | 4.69 s |
| ii | 2048 × 2048 | 232.82 s | 18.58 s |
| SN | Scale | Traditional | Proposed |
|---|---|---|---|
| i | 1024 × 1024 | 1.026 m | 1.026 m |
| ii | 2048 × 2048 | 1.108 m | 1.108 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Xiao, P. A Fast, Three-Dimensional, Indirect Geolocation Method Using IAGM and DSM Data without GCPs for Spaceborne SAR Images. Sensors 2019, 19, 5062. https://doi.org/10.3390/s19235062
Liu M, Xiao P. A Fast, Three-Dimensional, Indirect Geolocation Method Using IAGM and DSM Data without GCPs for Spaceborne SAR Images. Sensors. 2019; 19(23):5062. https://doi.org/10.3390/s19235062
Chicago/Turabian StyleLiu, Min, and Peng Xiao. 2019. "A Fast, Three-Dimensional, Indirect Geolocation Method Using IAGM and DSM Data without GCPs for Spaceborne SAR Images" Sensors 19, no. 23: 5062. https://doi.org/10.3390/s19235062
APA StyleLiu, M., & Xiao, P. (2019). A Fast, Three-Dimensional, Indirect Geolocation Method Using IAGM and DSM Data without GCPs for Spaceborne SAR Images. Sensors, 19(23), 5062. https://doi.org/10.3390/s19235062






