Development of an Image Grating Sensor for Position Measurement
Abstract
:1. Introduction
2. Experimental Setup
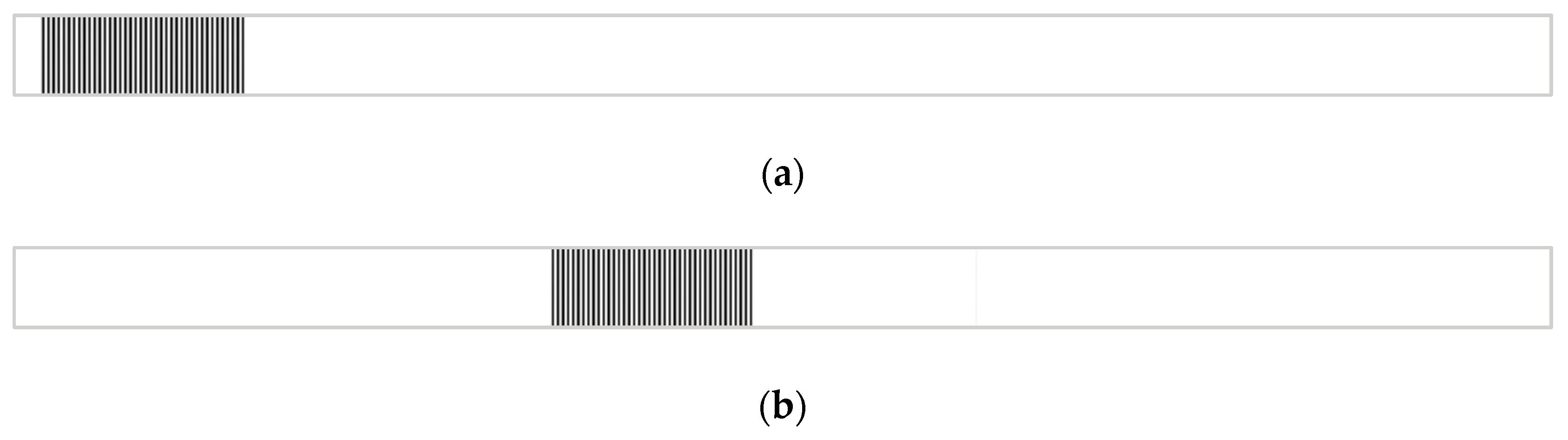
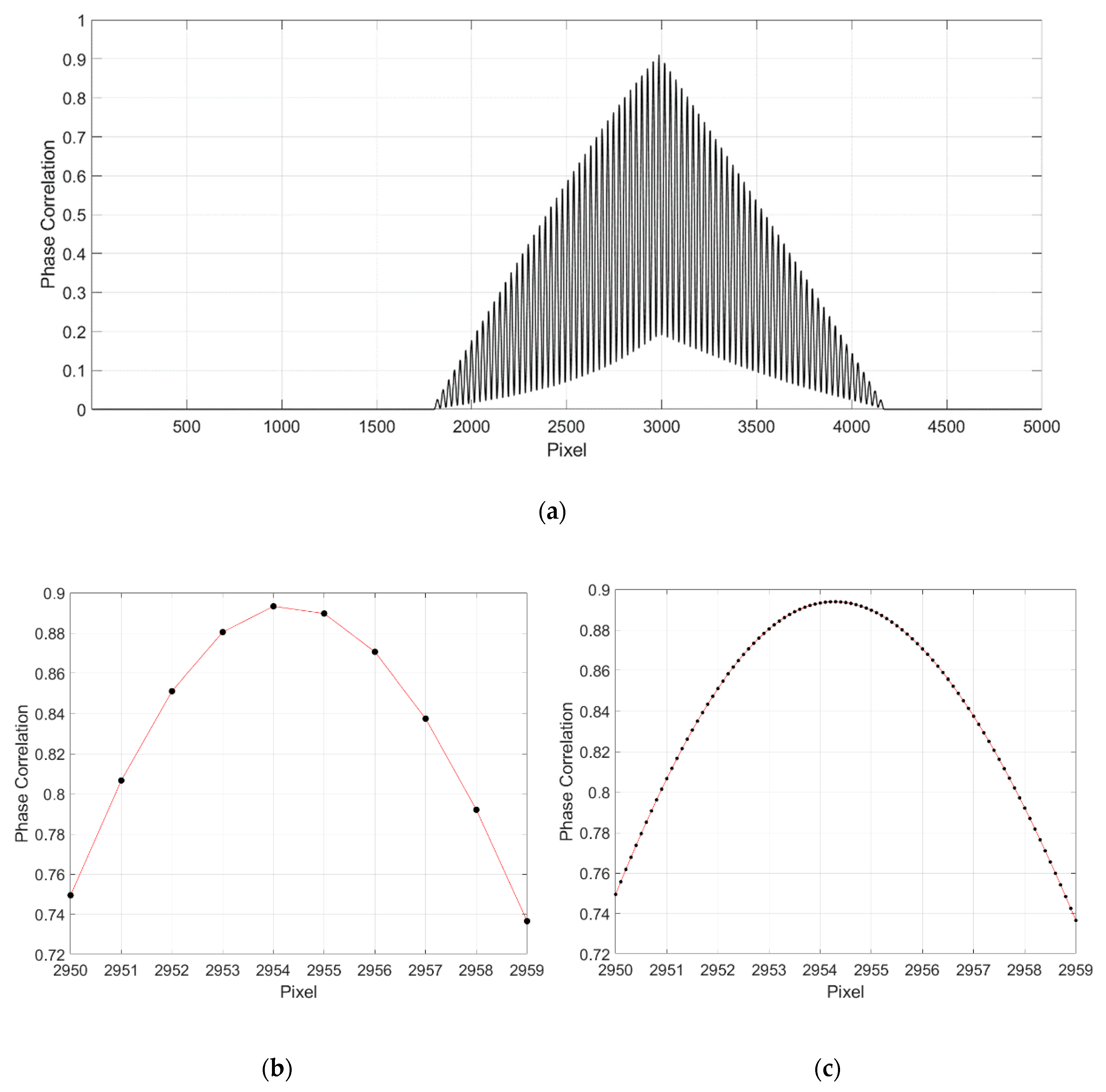
3. Subpixel Image Registration Based on 1D Single-Step Discrete Fourier Transform
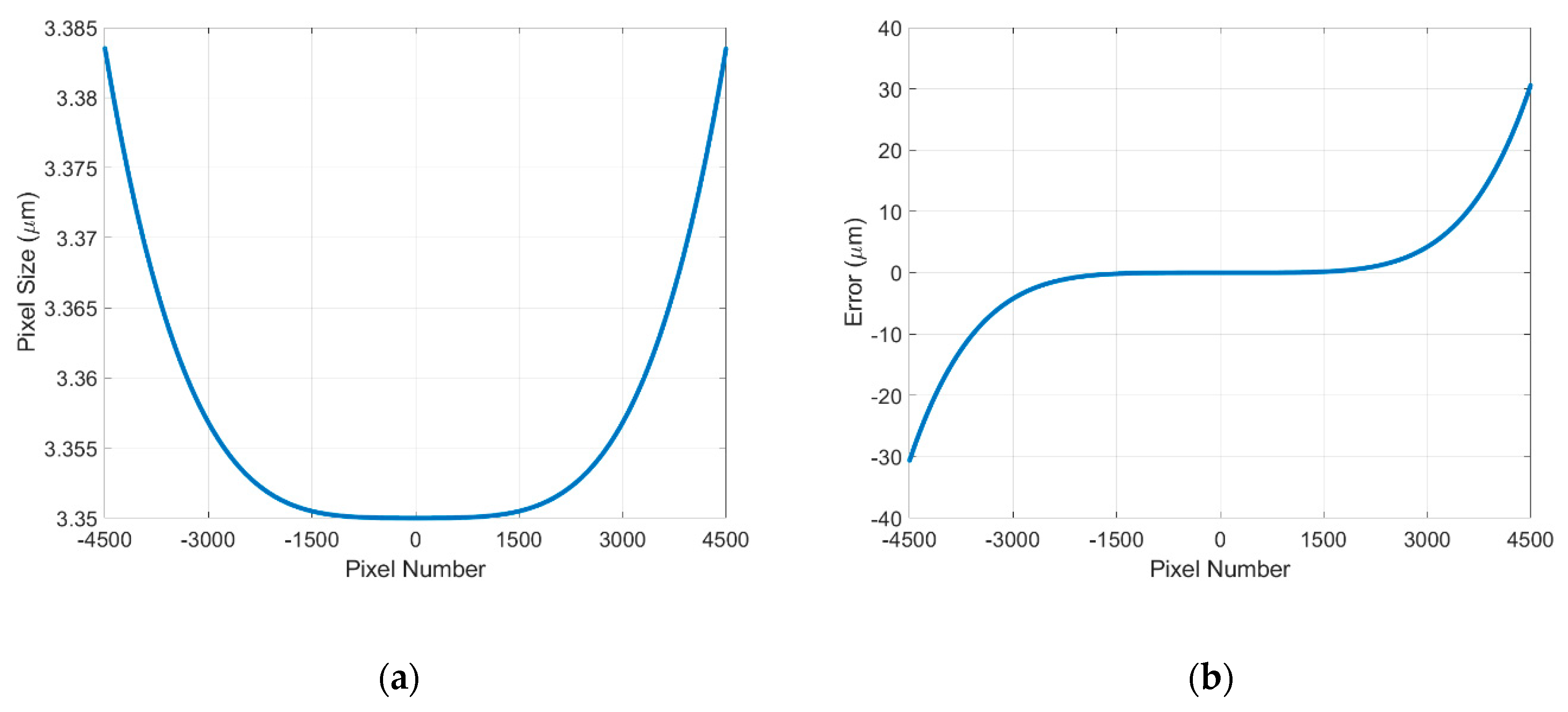
4. Error Correction Based on Lens Distortion
4.1. Theoretical Modelling
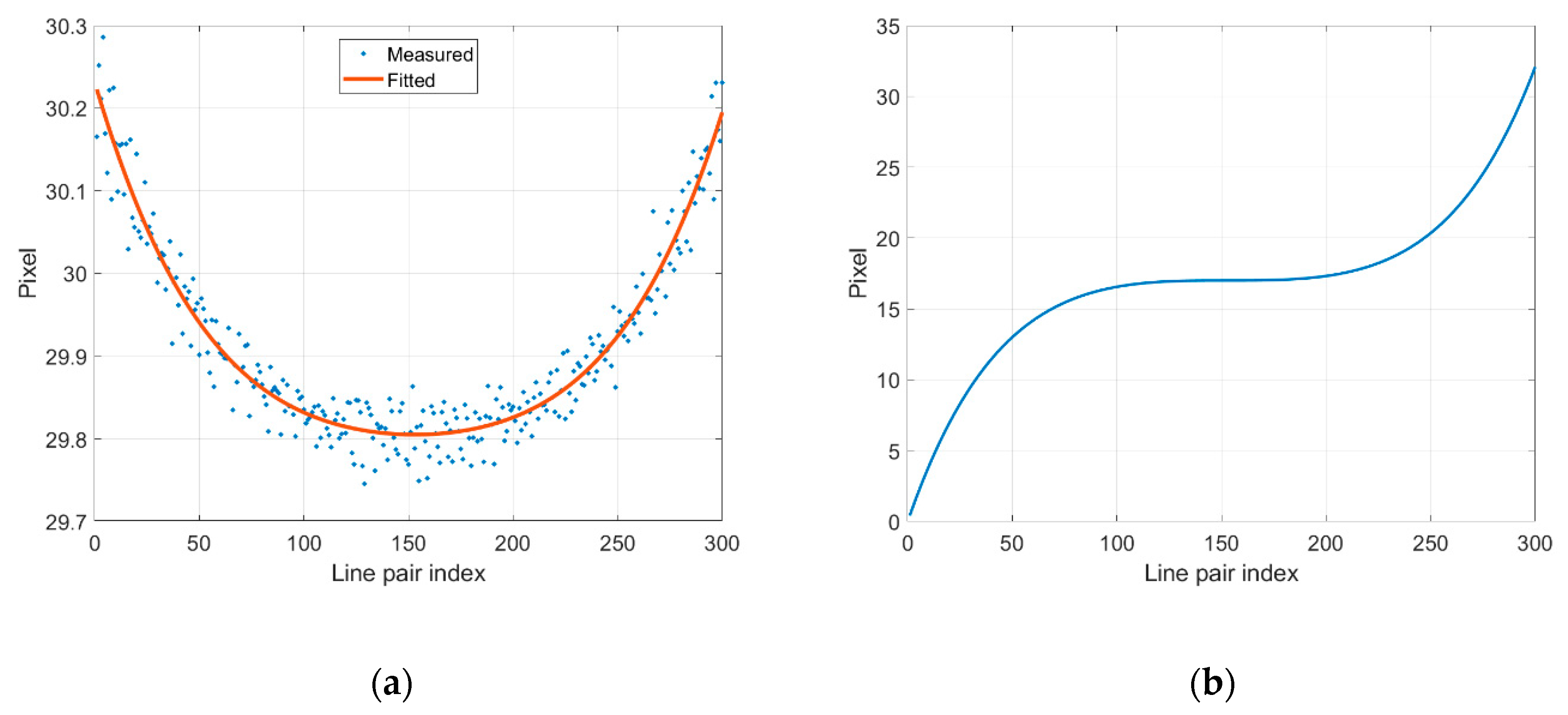
4.2. Experimental Verification
5. Experimental Results
5.1. Measurement Results
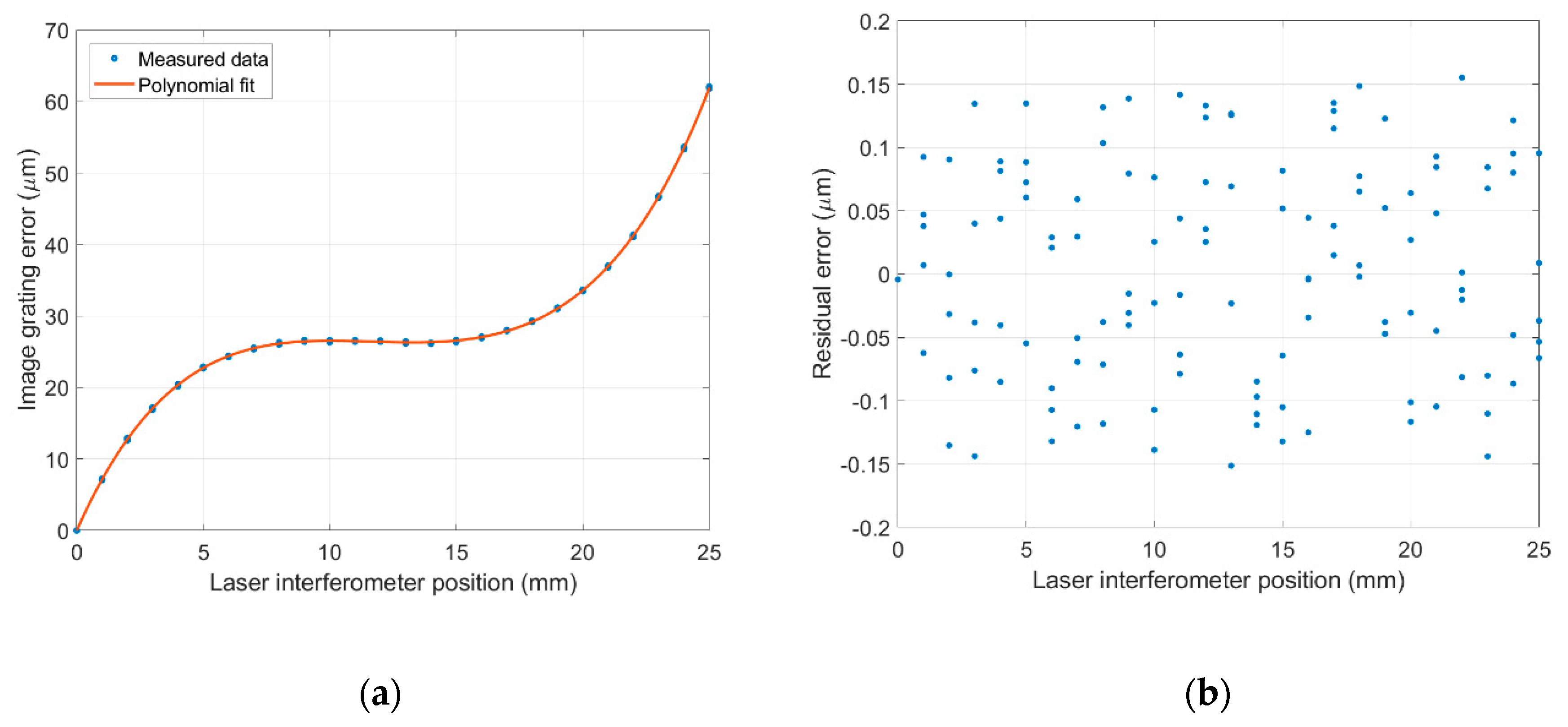
5.2. Fifth-Degree Polynomial Fitting
5.3. Position Measurement and Error Compensation
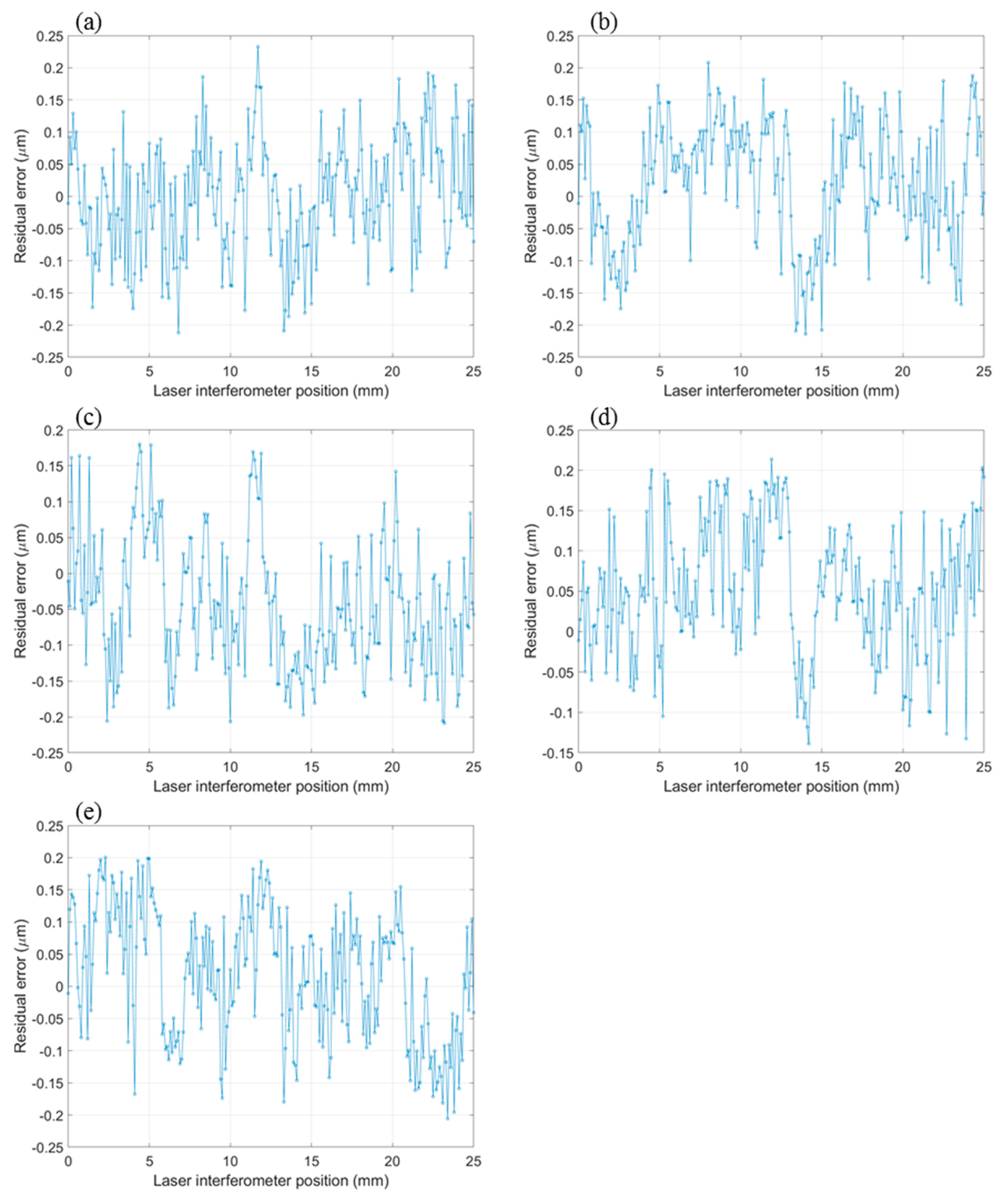
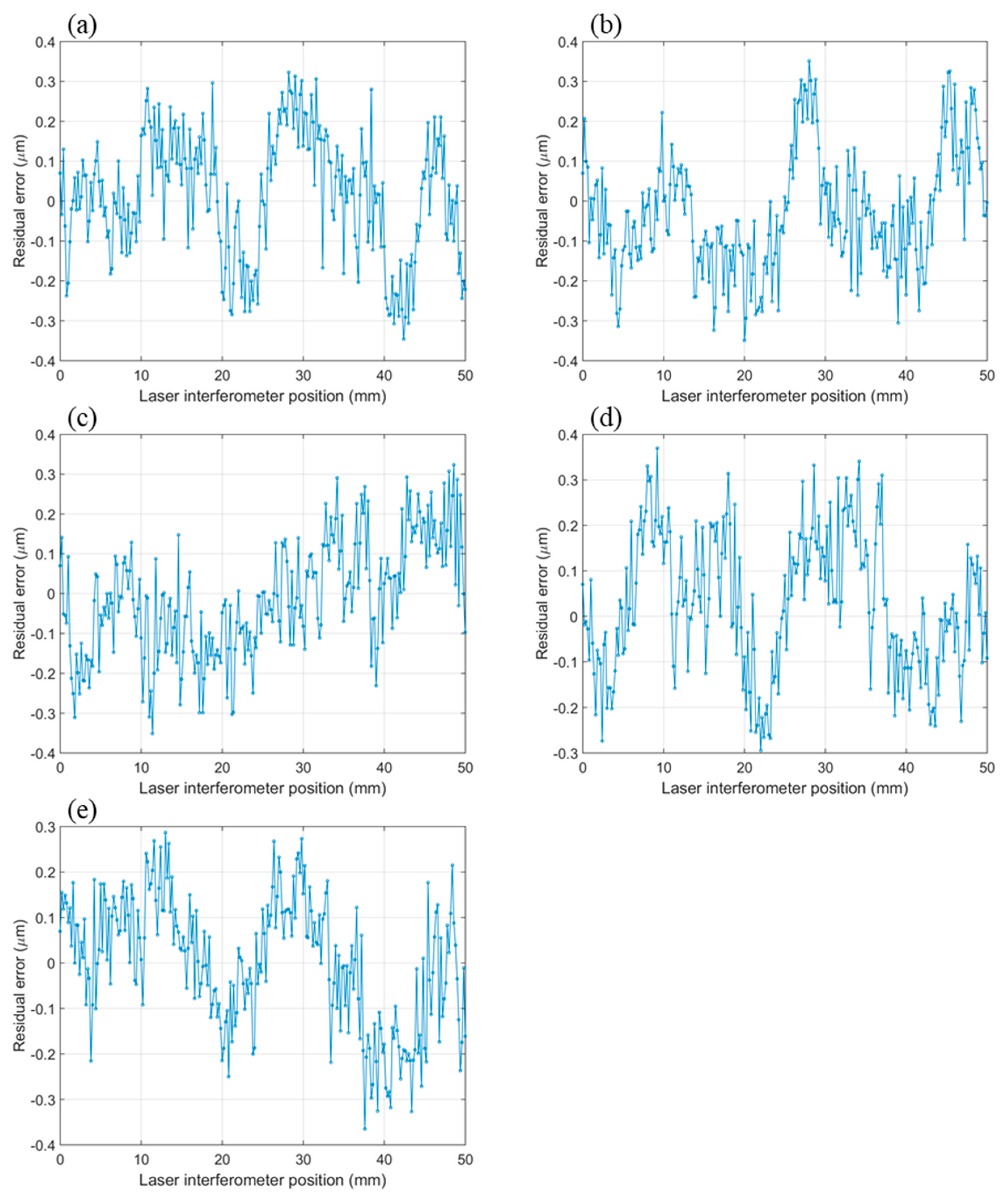
5.4. Measurement Repeatability Study
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Whitehouse, D. A new look at surface metrology. Wear 2009, 266, 560–565. [Google Scholar] [CrossRef]
- Fu, S.; Cheng, F.; Tjahjowidodo, T.; Zhou, Y.; Butler, D. A Non-Contact Measuring System for In-Situ Surface Characterization Based on Laser Confocal Microscopy. Sensors 2018, 18, 2657. [Google Scholar] [CrossRef]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.L.; Lu, X.D.; Knapp, W.; Weckenmann, A.; Estler, W.T.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Cheng, F.; Fan, K.-C. Linear diffraction grating interferometer with high alignment tolerance and high accuracy. Appl. Opt. 2011, 50, 4550. [Google Scholar] [CrossRef]
- Kunzmann, H.; Pfeifer, T.; Flügge, J. Scales vs. Laser Interferometers Performance and Comparison of Two Measuring Systems. CIRP Ann. 1993, 42, 753–767. [Google Scholar] [CrossRef]
- Chen, Z.; Pu, H.; Liu, X.; Peng, D.; Yu, Z. A Time-Grating Sensor for Displacement Measurement With Long Range and Nanometer Accuracy. IEEE Trans. Instrum. Meas. 2015, 64, 3105–3115. [Google Scholar] [CrossRef]
- Yu, Z.; Peng, K.; Liu, X.; Pu, H.; Chen, Z. A new capacitive long-range displacement nanometer sensor with differential sensing structure based on time-grating. Meas. Sci. Technol. 2018, 29, 054009. [Google Scholar] [CrossRef]
- Zhou, P. Subpixel displacement and deformation gradient measurement using digital image/speckle correlation (DISC). Opt. Eng. 2001, 40, 1613. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Huang, S.-H.; Pan, Y.-C. Automated visual inspection in the semiconductor industry: A survey. Comput. Ind. 2015, 66, 1–10. [Google Scholar] [CrossRef]
- Yamahata, C.; Sarajlic, E.; Krijnen, G.J.M.; Gijs, M.A.M. Subnanometer Translation of Microelectromechanical Systems Measured by Discrete Fourier Analysis of CCD Images. J. Microelectromech. Syst. 2010, 19, 1273–1275. [Google Scholar] [CrossRef]
- Dalsa, T. Line Scan Primer. Available online: http://www.teledynedalsa.com/en/learn/knowledge-center/line-scan-primer/ (accessed on 29 August 2018).
- Novus Light Technologies Today Line-Scan vs. Area-Scan: What Is Right for Machine Vision Applications? Available online: https://www.novuslight.com/line-scan-vs-area-scan-what-is-right-for-machine-vision-applications_N6824.html (accessed on 29 August 2018).
- Douini, Y.; Riffi, J.; Mahraz, A.M.; Tairi, H. An image registration algorithm based on phase correlation and the classical Lucas–Kanade technique. Signal Image Video Process. 2017, 11, 1321–1328. [Google Scholar] [CrossRef]
- Foroosh, H.; Zerubia, J.B.; Berthod, M. Extension of phase correlation to subpixel registration. IEEE Trans. Image Process. 2002, 11, 188–200. [Google Scholar] [CrossRef]
- Takita, K.; Aoki, T.; Sasaki, Y.; Higuchi, T.; Kobayashi, K. High-Accuracy Subpixel Image Registration Based on Phase-Only Correlation. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2003, E86-A, 1925–1934. [Google Scholar]
- Zitová, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Szeliski, R. Image Alignment and Stitching: A Tutorial. Found. Trends® Comput. Graph. Vis. 2006, 2, 1–104. [Google Scholar] [CrossRef]
- Pan, B.; Xie, H.; Xu, B.; Dai, F. Performance of sub-pixel registration algorithms in digital image correlation. Meas. Sci. Technol. 2006, 17, 1615–1621. [Google Scholar]
- Riha, L.; Fischer, J.; Smid, R.; Docekal, A. New interpolation methods for image-based sub-pixel displacement measurement based on correlation. In Proceedings of the 2007 IEEE Instrumentation & Measurement Technology Conference IMTC 2007, Warsaw, Poland, 1–3 May 2007; pp. 1–5. [Google Scholar]
- Wang, H.; Zhao, J.; Zhao, J.; Dong, F.; Pan, Z.; Feng, Y. Position detection method of linear motor mover based on extended phase correlation algorithm. IET Sci. Meas. Technol. 2017, 11, 921–928. [Google Scholar] [CrossRef]
- Fienup, J.R. Invariant error metrics for image reconstruction. Appl. Opt. 1997, 36, 8352. [Google Scholar] [CrossRef]
- Guizar-Sicairos, M.; Thurman, S.T.; Fienup, J.R. Efficient Image Registration Algorithms for Computation of Invariant Error Metrics. In Proceedings of the Adaptive Optics: Analysis and Methods/Computational Optical Sensing and Imaging/Information Photonics/Signal Recovery and Synthesis Topical Meetings on CD-ROM, OSA, Washington, DC, USA, 18–20 June 2007; p. SMC3. [Google Scholar]
- Wang, C.; Jing, X.; Zhao, C. Local Upsampling Fourier Transform for accurate 2D/3D image registration. Comput. Electr. Eng. 2012, 38, 1346–1357. [Google Scholar] [CrossRef]
- Galeano-Zea, J.-A.; Sandoz, P.; Gaiffe, E.; Prétet, J.-L.; Mougin, C. Pseudo-Periodic Encryption of Extended 2-D Surfaces for High Accurate Recovery of any Random Zone by Vision. Int. J. Optomechatronics 2010, 4, 65–82. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.; Ozer, E.; Fukuda, Y. A Vision-Based Sensor for Noncontact Structural Displacement Measurement. Sensors 2015, 15, 16557–16575. [Google Scholar] [CrossRef]
- Li, X. High-Accuracy Subpixel Image Registration With Large Displacements. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6265–6276. [Google Scholar] [CrossRef]
- Stone, H.S.; Orchard, M.T.; Ee-Chien, C.; Martucci, S.A. A fast direct Fourier-based algorithm for subpixel registration of images. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2235–2243. [Google Scholar] [CrossRef]
- Guelpa, V.; Laurent, G.; Sandoz, P.; Zea, J.; Clévy, C. Subpixelic Measurement of Large 1D Displacements: Principle, Processing Algorithms, Performances and Software. Sensors 2014, 14, 5056–5073. [Google Scholar] [CrossRef]
- Jaramillo, J.; Zarzycki, A.; Galeano, J.; Sandoz, P. Performance Characterization of an xy-Stage Applied to Micrometric Laser Direct Writing Lithography. Sensors 2017, 17, 278. [Google Scholar] [CrossRef]
- Hibino, K.; Oreb, B.F.; Farrant, D.I.; Larkin, K.G. Phase-shifting algorithms for nonlinear and spatially nonuniform phase shifts. J. Opt. Soc. Am. A 1997, 14, 918. [Google Scholar] [CrossRef]
- Vergara, M.A.; Jacquot, M.; Laurent, G.J.; Sandoz, P. Digital holography as computer vision position sensor with an extended range of working distances. Sensors 2018, 18, 2005. [Google Scholar] [CrossRef]
- Guizar-Sicairos, M.; Thurman, S.T.; Fienup, J.R. Efficient subpixel image registration algorithms. Opt. Lett. 2008, 33, 156. [Google Scholar] [CrossRef]
- Almonacid-Caballer, J.; Pardo-Pascual, J.E.; Ruiz, L.A. Evaluating fourier cross-correlation sub-pixel registration in Landsat images. Remote Sens. 2017, 9, 1051. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, Y.; Zhao, C. Robust Subpixel Registration for Image Mosaicing. In Proceedings of the 2009 Chinese Conference on Pattern Recognition, Nanjing, China, 4–6 November 2009; pp. 1–5. [Google Scholar]
- Antoš, J.; Nežerka, V.; Somr, M. Real-Time Optical Measurement of Displacements Using Subpixel Image Registration. Exp. Tech. 2019, 43, 315–323. [Google Scholar] [CrossRef]
- Thorlabs, I. Motorized 2″ (50 mm) Linear Translation Stages. Available online: https://www.thorlabs.com/navigation.cfm?guide_id=2081 (accessed on 29 August 2018).
- ZOLIX INSTRUMENTS Motorized Linear Stages. Available online: http://www.zolix.com.cn/en/products3_371_384_418.html (accessed on 29 August 2018).
- Physik Instrumente (PI) GmbH & Co. KG Linear Stages with Motor/Screw-Drives; Physik Instrumente (PI) GmbH & Co.: Karlsruhe, Germany, 2017. [Google Scholar]
- Soummer, R.; Pueyo, L.; Sivaramakrishnan, A.; Vanderbei, R.J. Fast computation of Lyot-style coronagraph propagation. Opt. Express 2007, 15, 15935. [Google Scholar] [CrossRef]
- Brown, D. Decentering Distortion of Lenses. Photom. Eng. 1966, 32, 444–462. [Google Scholar]
- Brown, D.C. Close-range camera calibration. Photogramm. Eng. 1971, 37, 855–866. [Google Scholar]
- Weng, J.; Cohen, P.; Herniou, M. Camera calibration with distortion models and accuracy evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 965–980. [Google Scholar] [CrossRef]








| SSDFT Method | Image Translation (pixel) | Computational Time (s) |
|---|---|---|
| 1D | 2984.180 | 2.9693 |
| 2D | 2984.180 | 4.9092 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, S.; Cheng, F.; Tjahjowidodo, T.; Liu, M. Development of an Image Grating Sensor for Position Measurement. Sensors 2019, 19, 4986. https://doi.org/10.3390/s19224986
Fu S, Cheng F, Tjahjowidodo T, Liu M. Development of an Image Grating Sensor for Position Measurement. Sensors. 2019; 19(22):4986. https://doi.org/10.3390/s19224986
Chicago/Turabian StyleFu, Shaowei, Fang Cheng, Tegoeh Tjahjowidodo, and Mengjun Liu. 2019. "Development of an Image Grating Sensor for Position Measurement" Sensors 19, no. 22: 4986. https://doi.org/10.3390/s19224986
APA StyleFu, S., Cheng, F., Tjahjowidodo, T., & Liu, M. (2019). Development of an Image Grating Sensor for Position Measurement. Sensors, 19(22), 4986. https://doi.org/10.3390/s19224986






