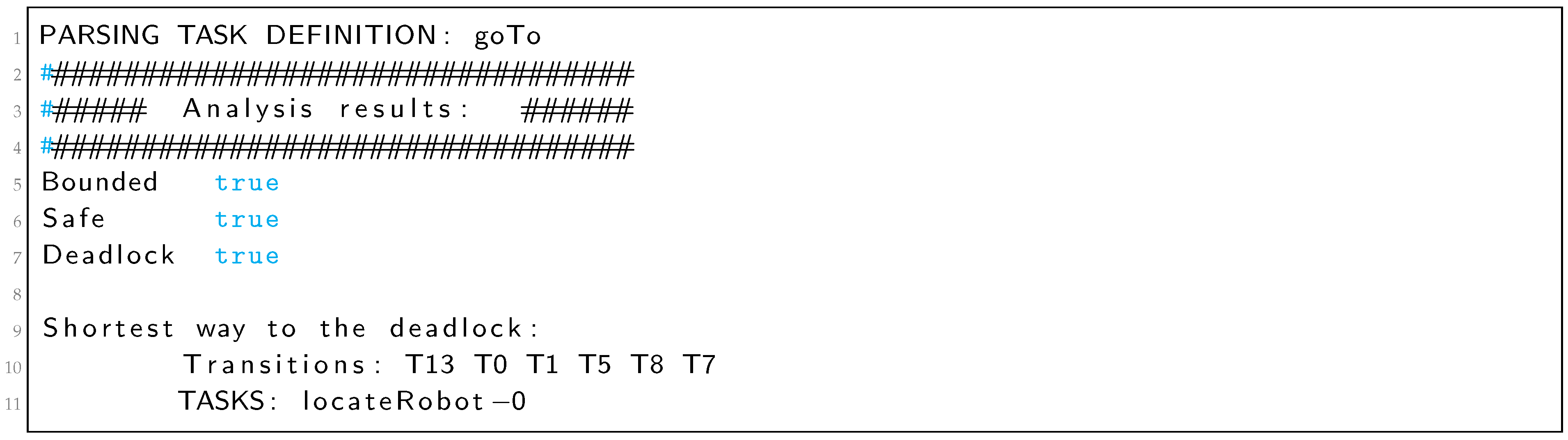
Petri nets provide a balance between modeling power and analyzability because many properties about asynchronous systems can be automatically determined using Petri nets. The study of some Petri net properties has proved to be a powerful technique for investigating properties of the modeled systems. Two important criteria in the study of Petri net models are liveness and safeness.
5.1. Basic Definitions
One of the properties of the Petri nets that we will use later is liveness, which is related to the complete absence of deadlocks. Liveness indicates the capability of transitions to be fired again. A transition is said to be live with respect to an initial marking if, from any reachable marking , there exists a sequence of transition firings that grants can be enabled and fired again. Otherwise, it is said to be dead. A PN is live if and only if all its transitions are said to be live. Therefore, a Petri net is said to be live if, no matter what marking has been reached from the initial marking, it is always possible to fire any transition of the net by progressing through some further firing sequence.
The concept of liveness is closely related to the absence of deadlocks. This means that a live Petri net guarantees deadlock-free operation, no matter what firing sequence is chosen. However, liveness is a more restrictive condition than deadlock-freeness.
As shown before, we use a hierarchical representation of Petri nets by obtaining a Petri net for the main program and all the Petri nets for the goals spawned in the main and subsequent goals. This decomposition into simpler Petri nets can simplify the analysis if we prove that these properties (deadlock-freeness and liveness) are preserved by the decomposition. In that case, we can reduce the problem of checking that a system holds these properties to the study of the properties for each Petri net (main and spawned goals).
There are several studies that deal with some kind of hierarchical Petri nets [
39] and Petri net refinements [
40,
41]. In all these cases, each refinement step in the hierarchical representation consists on the replacement of one transition by a subnet that represents its behavior in more detail. In the solution proposed here, the spawn goal structure defined in
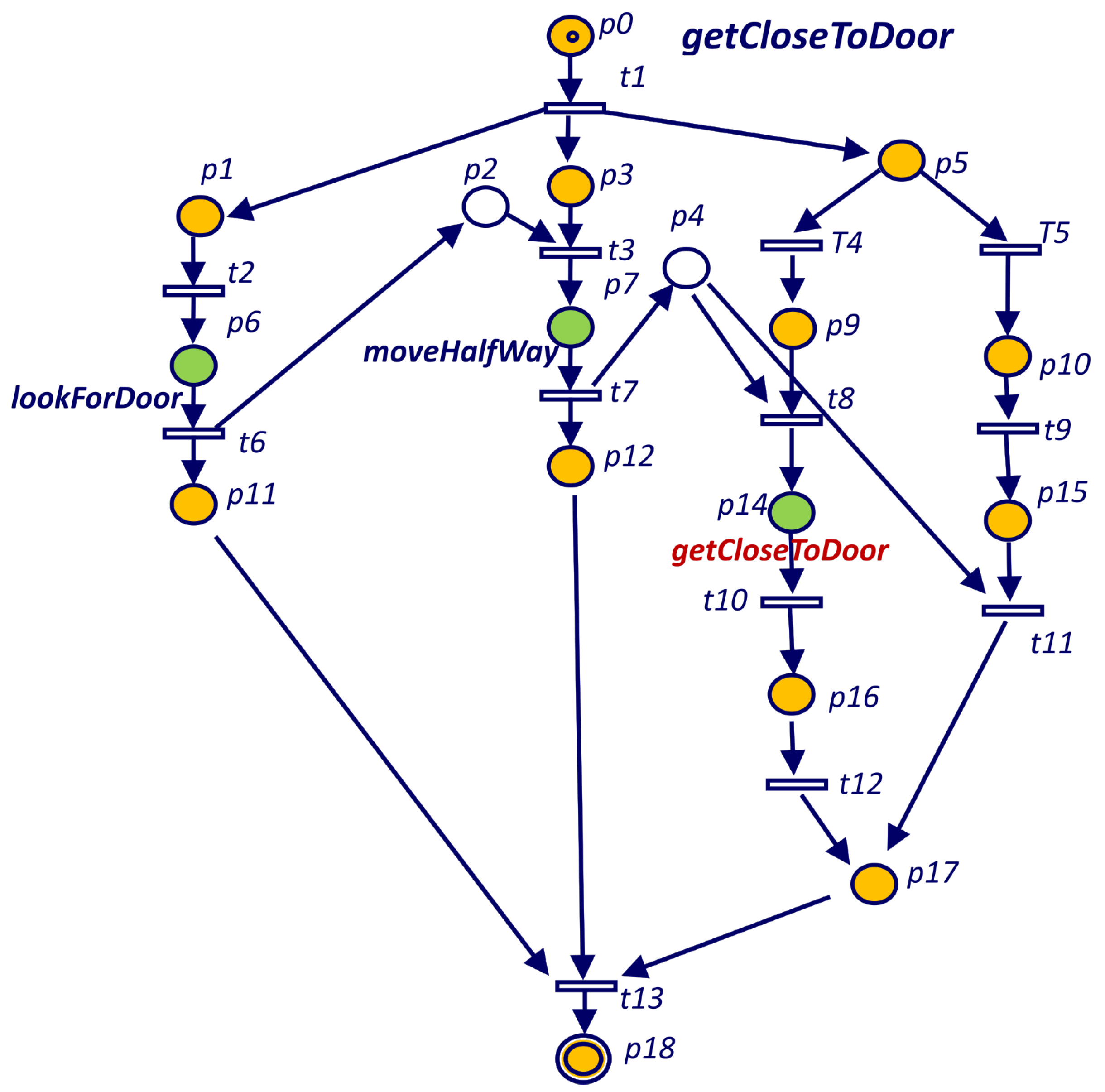
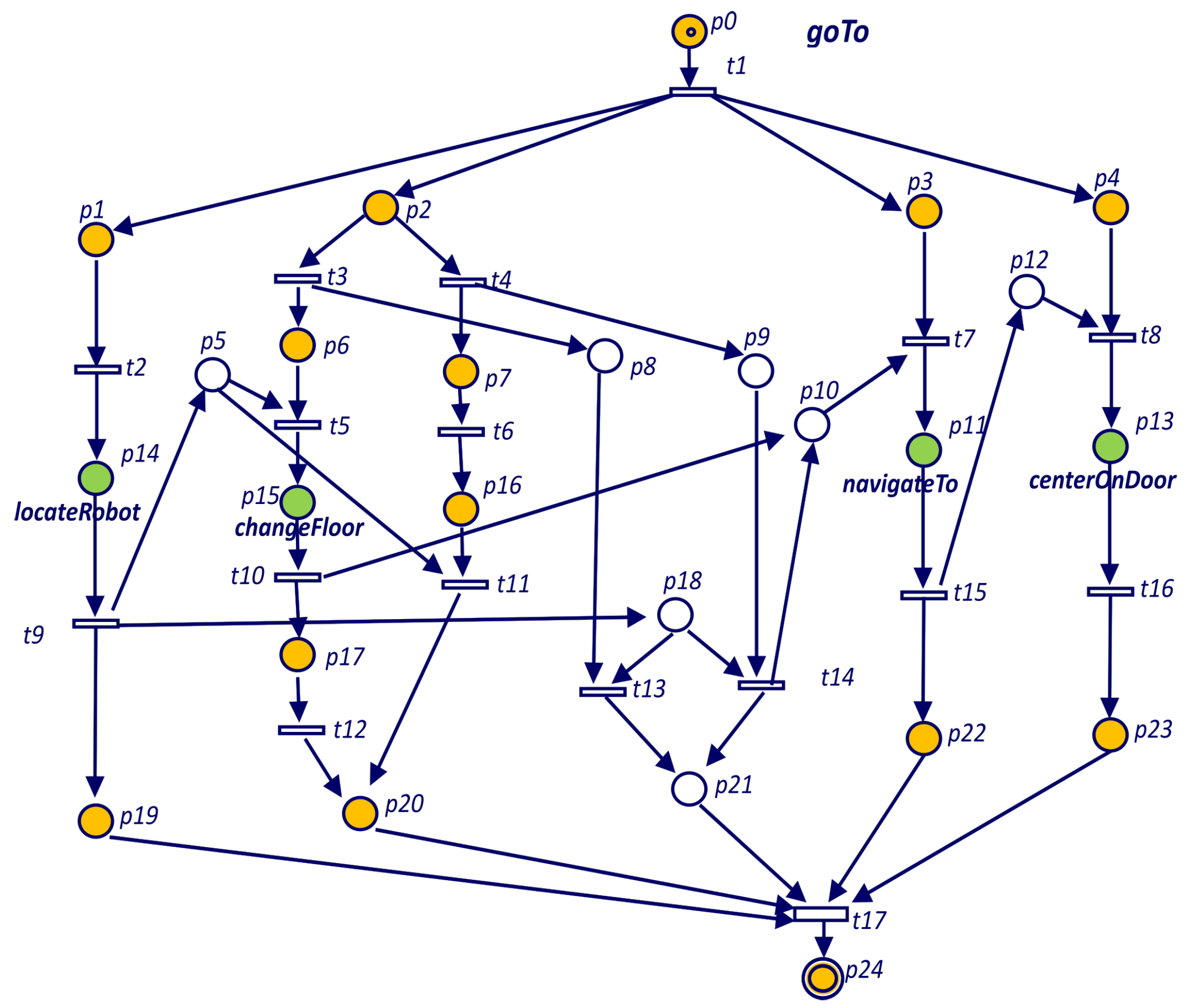
Section 3 is replaced by the goal PN. The spawn goal structure in this case is represented by a place (execution of the subgoal) and a transition (end of subgoal execution) instead of only a transition.
5.2. Terminability Analysis
Petri nets have been used to model and analyze different kinds of systems such as communication protocols and factory processes where liveness is a very important property. However, in robotic task-modeling systems, most tasks and subtask should finish. For that kind of systems, the terminability property plays a very important role.
Definition 1. A terminable Petri net (TPN) is a Petri net with a final marking. This is, =(P, T, F, ,) where:
are the final places, with (i.e., {}). Whenever all tokens of current marking are within the final places () or there are no tokens left at all () the execution of the TPN terminates.
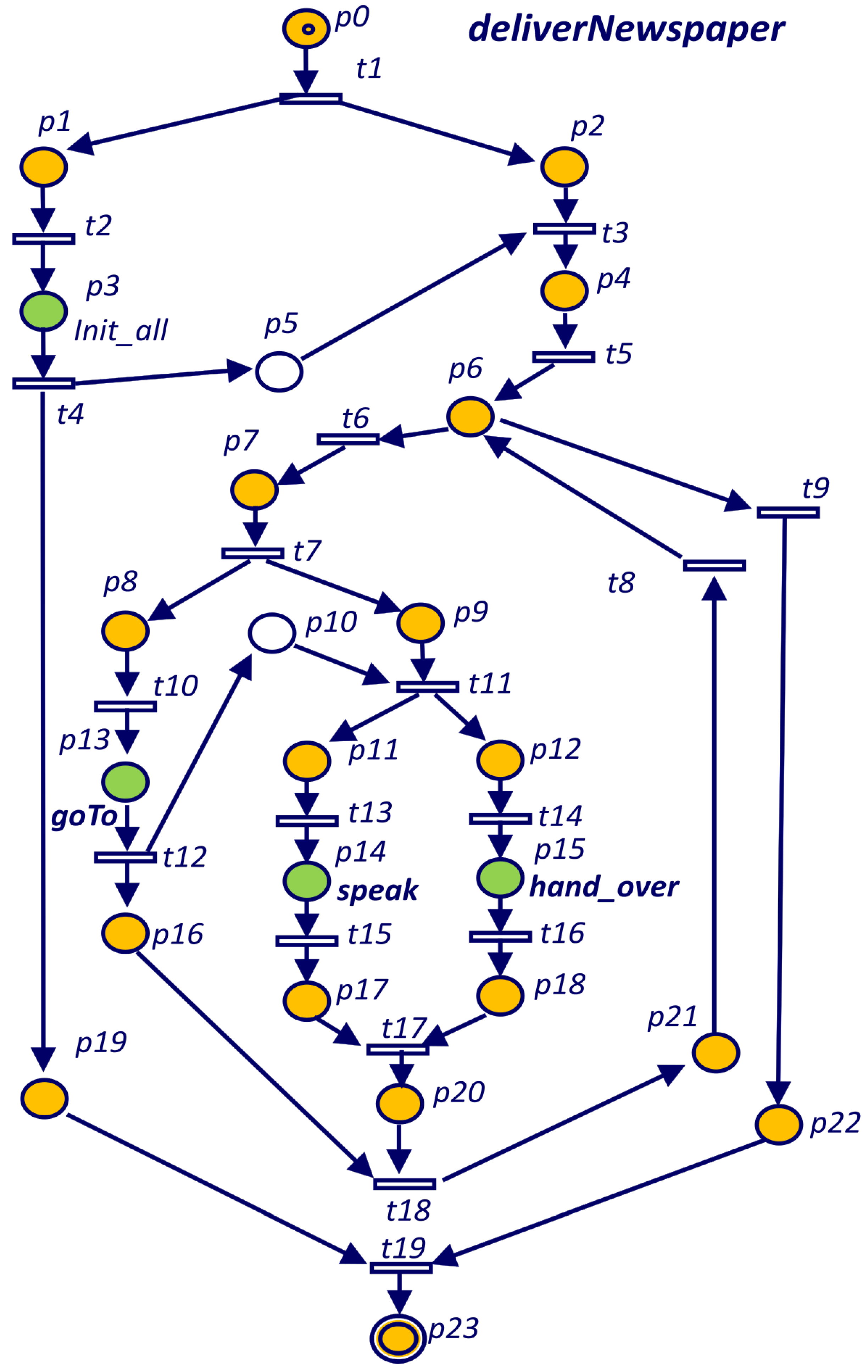
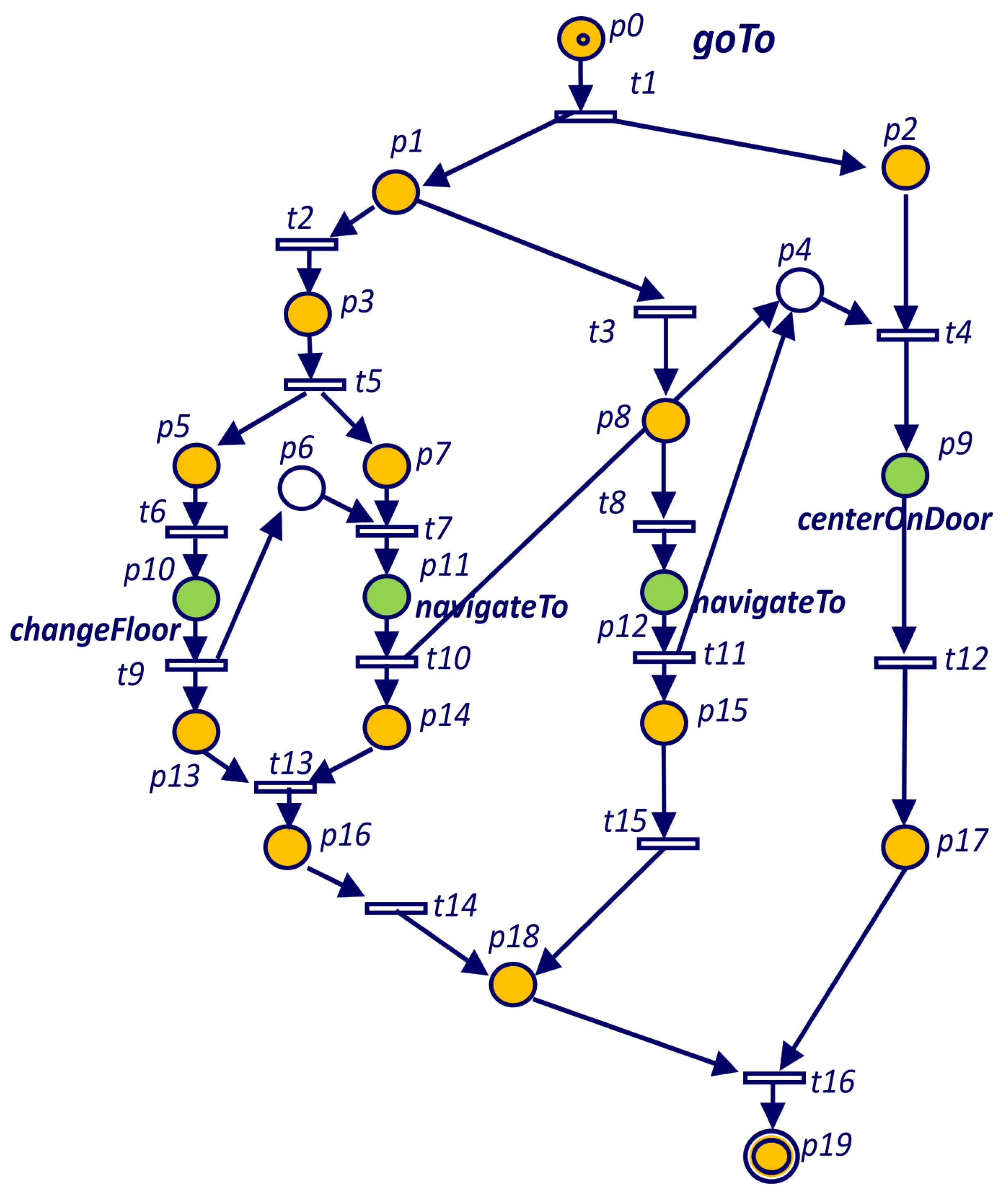
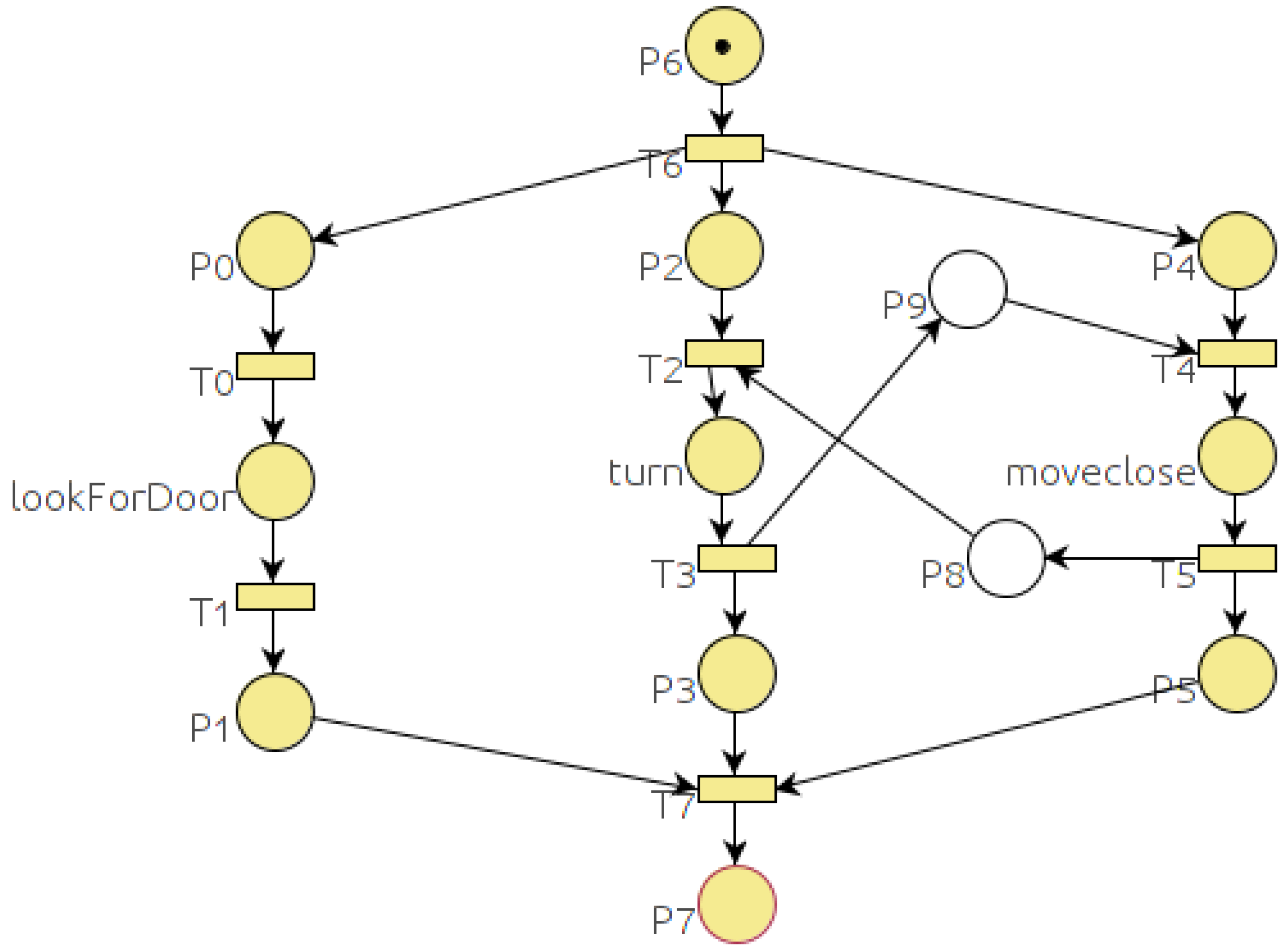
These final places are a new feature introduced in the model and allows the system to control the actual termination of any task. Graphically, all the final places in
are represented by a double border circle. For example, in
Figure 8 place labelled as “End B” is the only place for Task B in the final places
={
}. Therefore, whenever there are no tokens in the net or there is only one token in place “End B”, the execution terminates.
Definition 2. A marking is considered a terminal marking if fulfills the termination condition: {}. This is, all tokens of current marking are within the final places or there are no tokens left at all, given that {}. Whenever the execution of a net reaches a terminal marking, it will terminate.
Definition 3. A Hierarchic Terminable Petri net is a terminable net that might include terminable subnets. The hierarchical tree of a net A represented as is the tree of nets under A. This is, all the PNs that are started directly or indirectly from A including A.
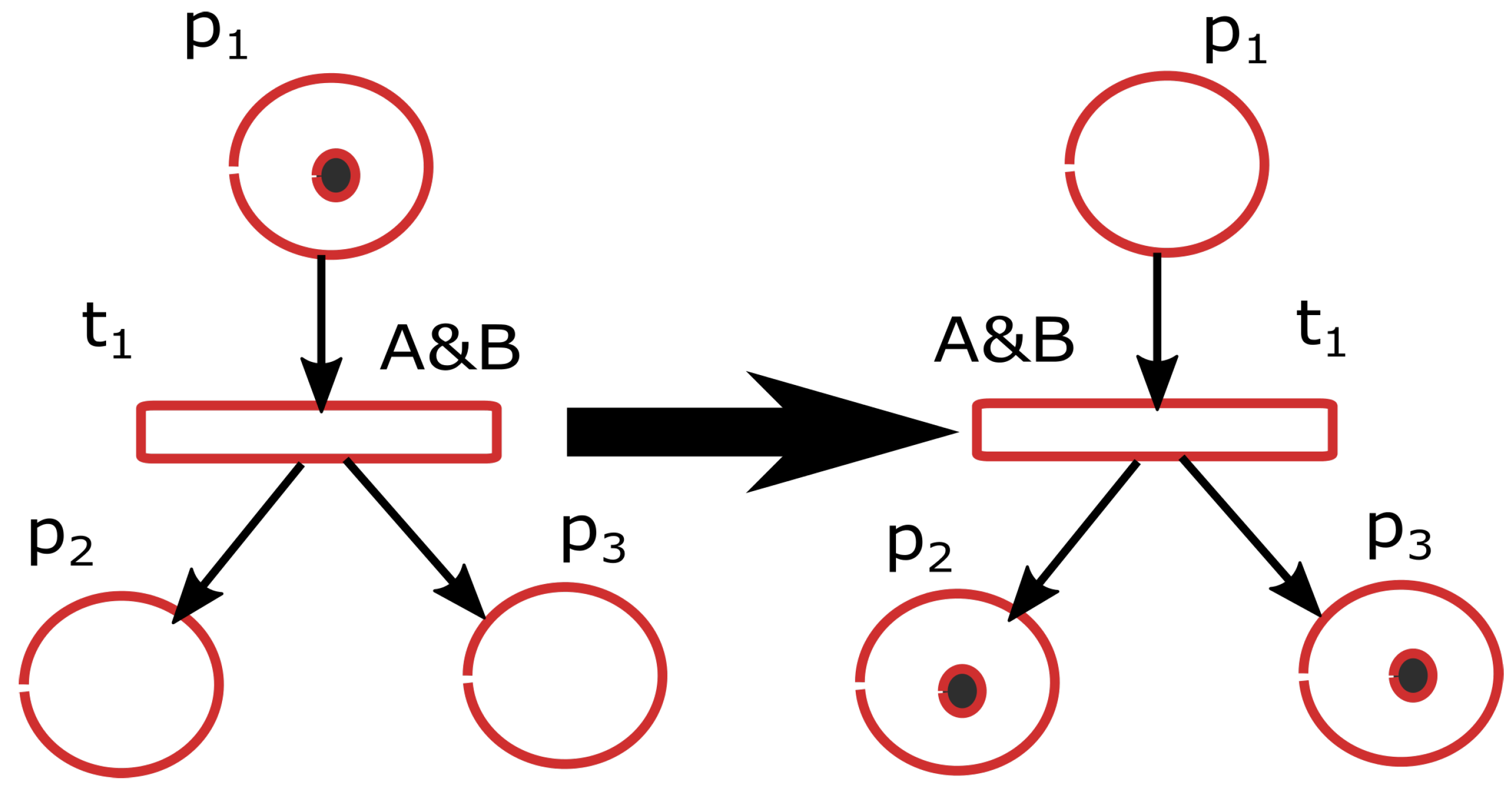
The execution of a PN (subtask B) inside another one (task A) is represented as a sequence of a place and a transition (
Figure 8). When the first transition is fired (
in
Figure 8), the subnet (Task B) will start with the initial marking. The place in the main task (labeled “Task B” in
Figure 8) would have a token while the subnet is running. The condition associated to the final transition (
transition in
Figure 8) is that the subnet (Task B) reaches a terminal marking
.
Definition 4. Terminability condition : A TPN holds the terminability condition if for any marking () derived from the initial marking {} exists some sequence of firings that ends in a terminal marking of the TPN {} This condition grants the termination of a net regardless of the marking evolution, i.e., it is free of deadlocks and some termination marking is always reachable.
Since we work with interpretable Petri nets, it is very important to notice that all transitions of the net must be firable to guarantee the terminability condition of the net. This is, it might exist a firing sequence that ends in a terminal marking. However, if there is a transition in the firing sequence that cannot be fired, the TPN will never terminate.
Theorem 1. If all the nets in a hierarchy tree hold the terminability condition, then the task A is also terminable.
Proof. Since the main TPN associated to task A is terminable, there is at least a sequence that leads to a terminal marking. If that sequence includes some transition associated to a subnet, we have to make sure that the transition is firable. In other words, the condition associated to the transition will eventually become true. According to Definition 3, the condition associated to the subnet transition is the termination of the subnet. However, since all the subnets hold the terminability condition, can eventually terminate and the condition will eventually become true. □
From the last theorem we can determine that the task represented by the hierarchic net A is free of deadlocks since it will always end regardless of the transition firing sequence of the main net and subnets.
According to Theorem 1, we need to analyze all the PNs in the hierarchy (
) in order to find out if they hold the terminability condition. For this analysis, we propose the use of the state space represented by the Coverability Tree [
30].
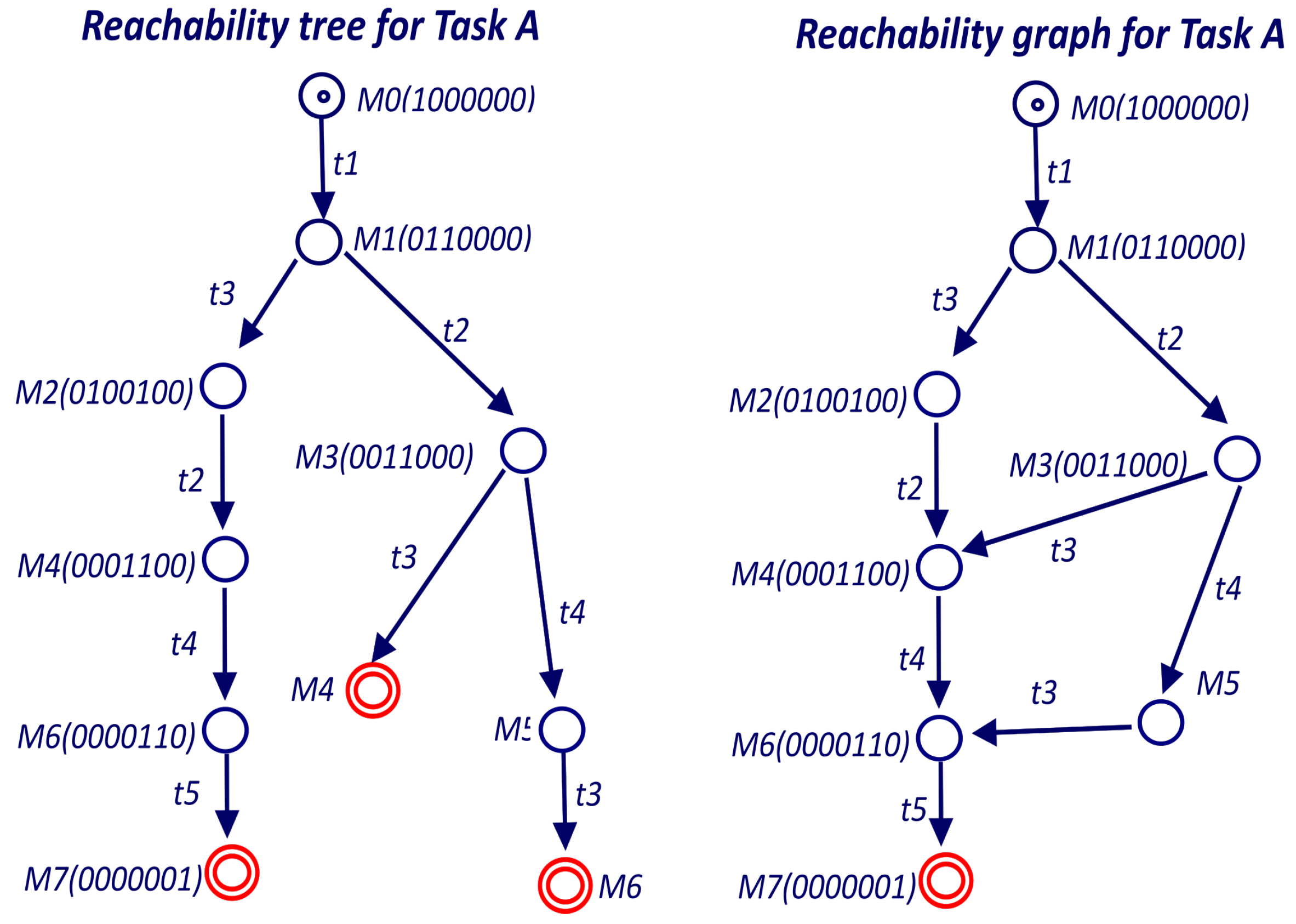
In the case of bounded nets, the Coverability Tree is called Reachability Tree (RT) [
30] since it contains all possible reachable markings. The coverability tree is a tree representation of its possible firing sequences. Nodes represent markings generated from the initial marking
(root) and its successors as shown in
Figure 9. Each arc in the tree represents a transition firing, which transforms one marking to another. The Reachability Graph (RG) is obtained from the RT by merging the nodes with the same marking as shown in
Figure 9. The RT can be obtained by the Karp and Miller algorithm [
42] that for the case of binary Petri nets is reduced to Algorithm 1.
| Algorithm 1 Algorithm to obtain the reachability tree |
| 1: Label initial marking as the root of the tree and tag it as new. |
| 2: for each new marking do |
| 3: select a new marking M. |
| 4: if M is identical to a marking on the tree then |
| 5: tag M as old |
| 6: go to another new marking |
| 7: end if |
| 8: if no transitions are enabled at M then |
| 9: tag M as dead-end. |
| 10: end if |
| 11: for each enabled transitions at M do |
| 12: obtain the marking M’ that results from firing t at M. |
| 13: introduce M’ as a node, draw an arc with label t from M to M’ and tag M’ as new. |
| 14: end for |
| 15: end for |
Theorem 2. In order to verify the terminability of a single TPN, its RG must fulfill the following:
Proof. Since the RG represents all possible firing sequences, the terminal nodes represent all the possible markings where it can stop. If the markings of all those terminal nodes are terminal markings it fulfils the terminability condition. □
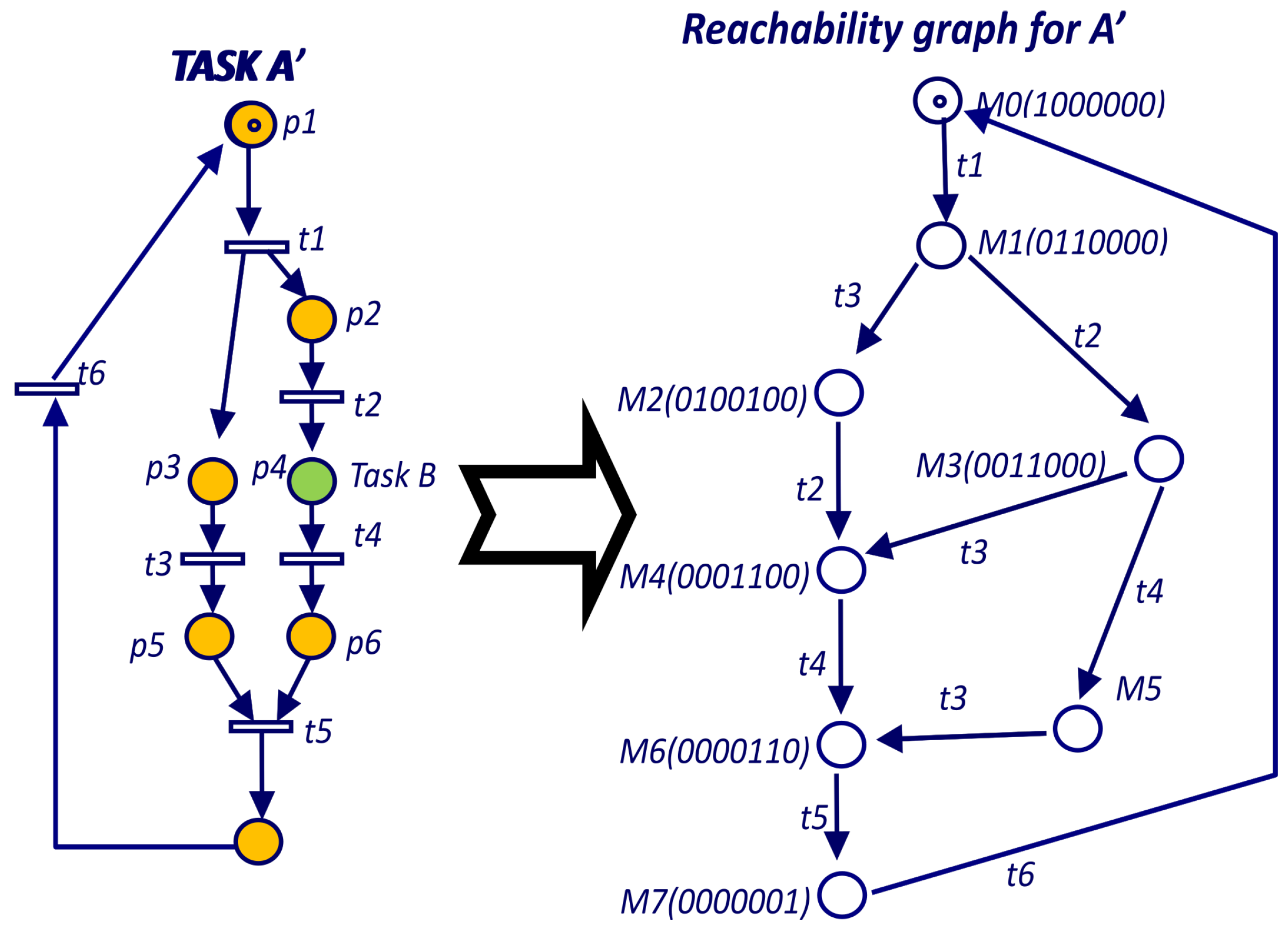
In the example of
Figure 9 the Reachability Tree has three leave nodes. The leave on the left has marking
, which is a terminal marking according to Definition 2. The other two leaves have markings (
and
) that are included in the left branch and therefore hold Theorem 2.
Even though this is an exhaustive method, the hierarchic decomposition allows for small nets whose reachability tree can be easily obtained with the aforementioned algorithm. In
Section 6 we will quantify the time and memory reduction obtained with the hierarchic decomposition.
5.3. Liveness Analysis
Some of the tasks that an autonomous robot system can execute can also be cyclic. For example, a surveillance robot can execute a cyclic patrol task. The analysis of that kind of Petri nets is very similar to the nets on other applications such as discrete process control in manufacturing systems. For that kind of systems the Petri nets are desirable to be deadlock-free and live. If a net is live it is known to be free of deadlocks, as every transition can always be fired again, no matter the firing sequence [
30].
Theorem 3. If all the nets in a hierarchy tree hold the terminability condition and the main Petri net holds the liveness condition, then the task A is live.
Proof. This theorem is a direct consequence of applying Theorems 1 and 2. □
From the last theorem, we can determine that the task represented by the hierarchic net A is live and therefore also free of deadlocks. This means that every transition within A will be always fireable again and its subnets, if any, will not block its evolution. Also, every transition within every subnet (at every level) are also always fireable again. In this case, the hierarchic system of TPNs works similar as a bigger single live net.
As in the terminability case, the liveness analysis of the main PN is based on the state space constructing the RG. First, the PN of the subtasks are analyzed for terminability as described above and second, the liveness of the main (root) PN needs to be analyzed.
A possible method to analyze liveness from the RG can be derived from former publications such as [
43]. The nodes (possible markings) of the RG can be partitioned into strongly connected components (i.e., maximal set of mutually reachable states). For liveness, the
ergodic or
absorbing components are the maximal set of states (nodes) mutually reachable so that there are no paths going out of the component. Once constructed the ergodic components, a transition
T is live if and only if an arc
t appears in all the ergodic components. The PN is live if all the transitions are live.
The Petri net for Task A (
Figure 9) is not live because is terminable and liveness and terminable are mutually exclusive. However, a live version of Task A (Task A’ in
Figure 10) can be obtained changing the termination condition of place
and adding a loop back to the initial place (
). For the RG of
Figure 9, the
ergodic component is the hole RG since it is not possible to make a smaller set of nodes mutually reachable. Since the RG includes all the transitions, all of them are inside the unique
ergodic component and therefore all of them are live.