Trajectory Planning for Data Collection of Energy-Constrained Heterogeneous UAVs
Abstract
1. Introduction
- Each UAV has different energy constraints and power efficiency. Thus, it is difficult to plan trajectory and assign tasks under their respective energy constraints.
- The value of data collected from each sensor is different, which depends on the importance of the monitoring area of the sensor and elapsed time after the previous collecting time (i.e., the freshness of collected data).
- Joint consideration of communication scheduling and trajectory optimization is a variant of the multiple knapsack problem, which is a classical NP-hard problem.
- Considering the different values of data and different energy constraints of heterogeneous UAVs, we focus on using multiple heterogeneous UAVs to collect data from sensors. Our objective is to maximize the data collection utility by jointly optimizing the communication scheduling and trajectories of UAVs. This problem is a variant of the multiple knapsack problem, which is a classical NP-hard problem [18,19].
- We prove that the data collection utility function is a submodular function, and transform the initial problem into the problem of maximizing a submodular function under energy constraints, and then we propose a novel trajectory planning algorithm to maximize the data collection utility, while accounting for different energy constraints of heterogeneous UAVs.
- Sufficient simulations are performed to demonstrate the validity and applicability of the proposed algorithm. The data collection utility of our algorithm can be increased by at most, and the proposed algorithm is the closest to the optimal scheme compared with other algorithms.
2. Related Work
2.1. UAV-Enabled Data Collection
2.2. Trajectory Planning
3. System Model and Problem Formulation
3.1. System Model
3.1.1. Network Model
3.1.2. Propulsion Energy Consumption Model
3.1.3. Communication-Related Energy Consumption Model
3.1.4. Utility Model
3.2. Problem Formulation
4. Solution
4.1. Hardness Analysis
4.2. Submodular Analysis
- for all or equivalently: for all and (monotonicity);
- and for all (nonnegativity);
- , for any or equivalently: , (submodularity).
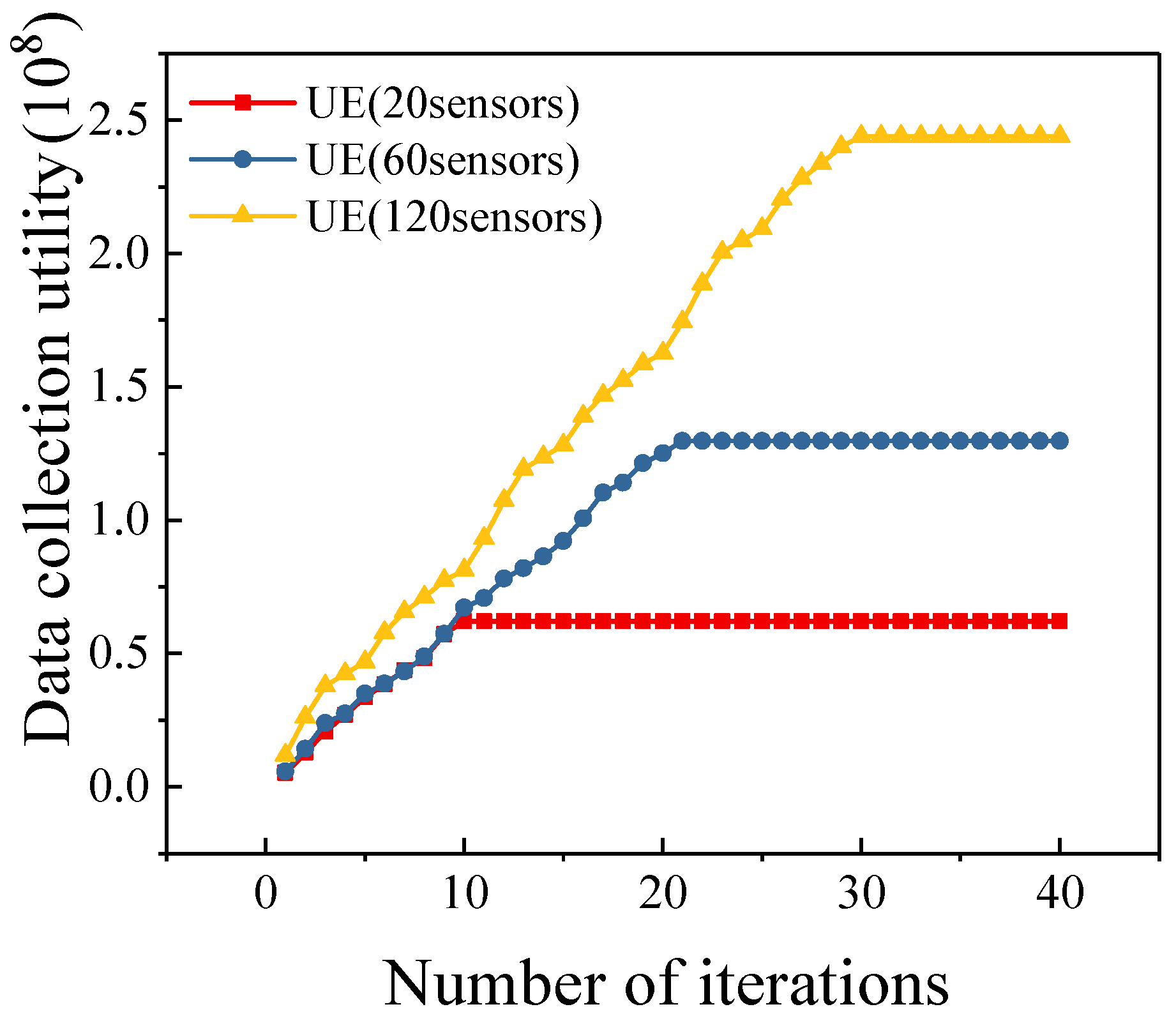
4.3. Algorithm
| Algorithm 1 Cluster Head Selection and Trajectory Planning Algorithm |
|
| Algorithm 2 Multiple Energy-constrained Heterogeneous UAV Trajectory Planning Algorithm |
|
5. Simulation Results
5.1. Simulation Setup
5.2. Baseline Setup
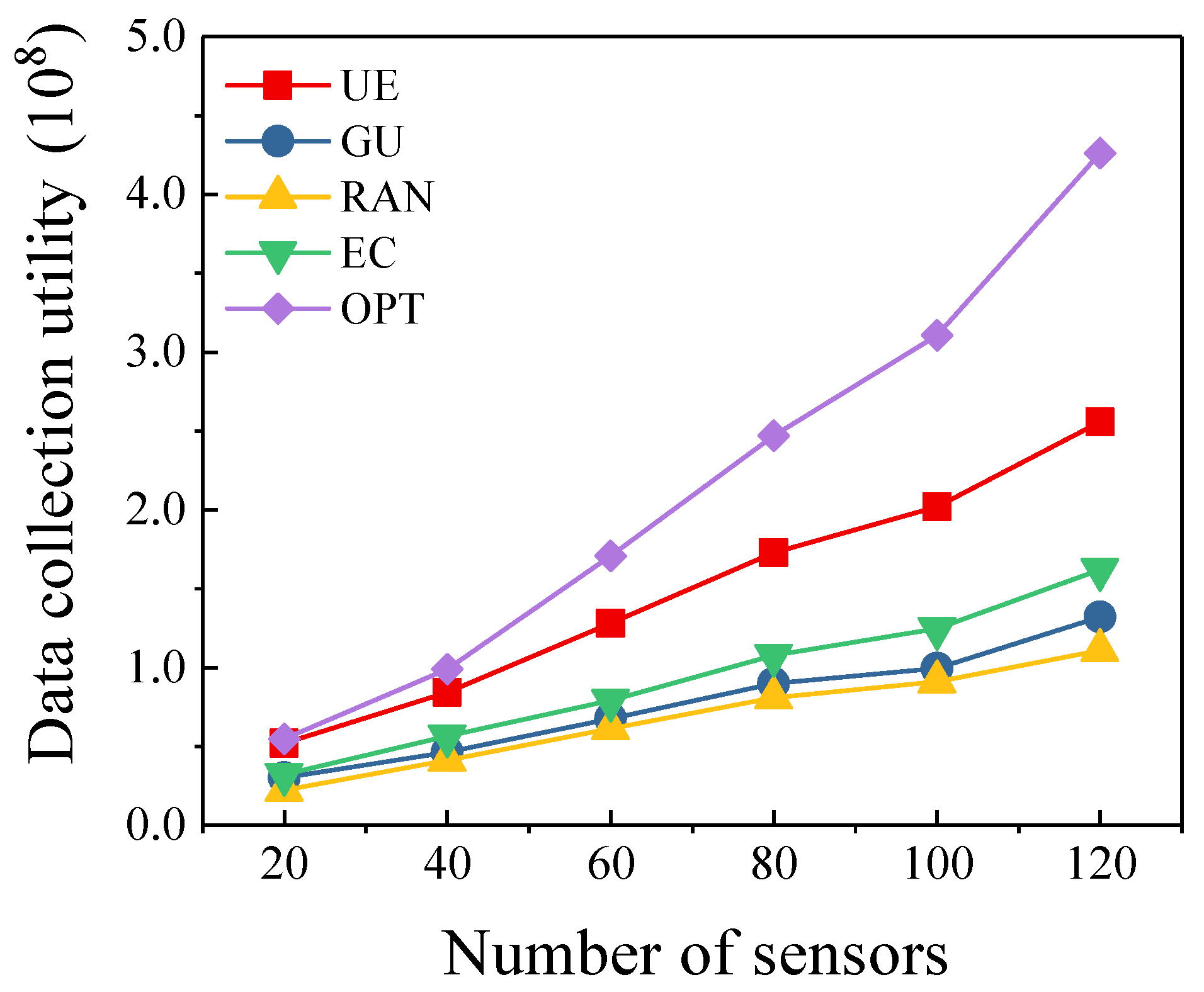
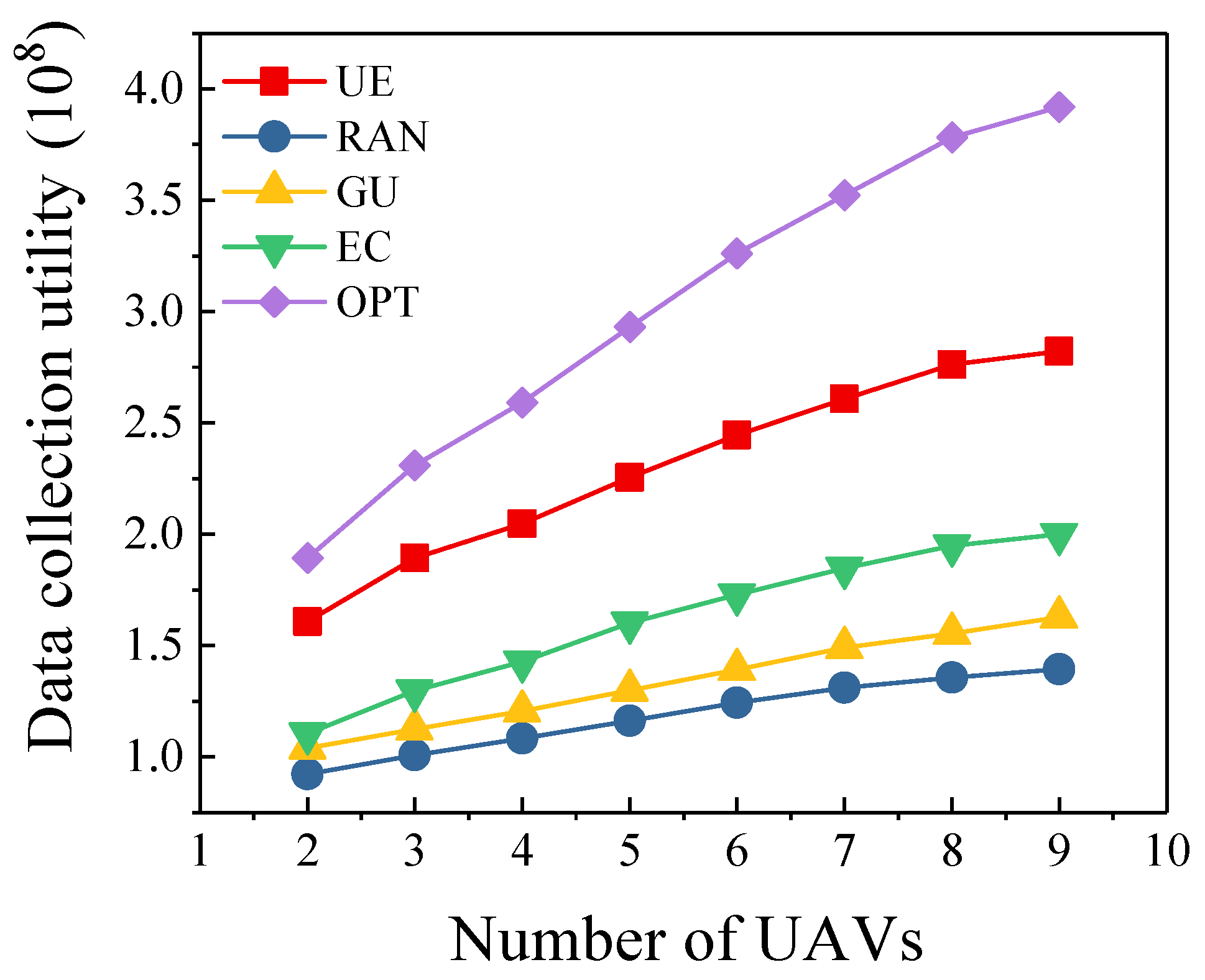
- Optimal scheme (OPT): To evaluate how the proposed algorithm approaches the optimal performance, we use brute-force searching method to get the optimal scheme which maximizes the data collection utility.
- RAN algorithm: Multi-UAV randomly select cluster heads for data collection. Based on the selected data collection points, we consider the energy constraint of each UAV to plan the trajectories.
- EC algorithm: The main purpose of this algorithm is to collect as much data as possible from sensors. However, it does not take into account the value of data.
- GU algorithm: This algorithm selects a cluster head which has maximum data collection utility in each iteration. However, the algorithm does not consider the energy consumption of the UAV when it selects cluster heads.
5.3. Different Number of Sensors
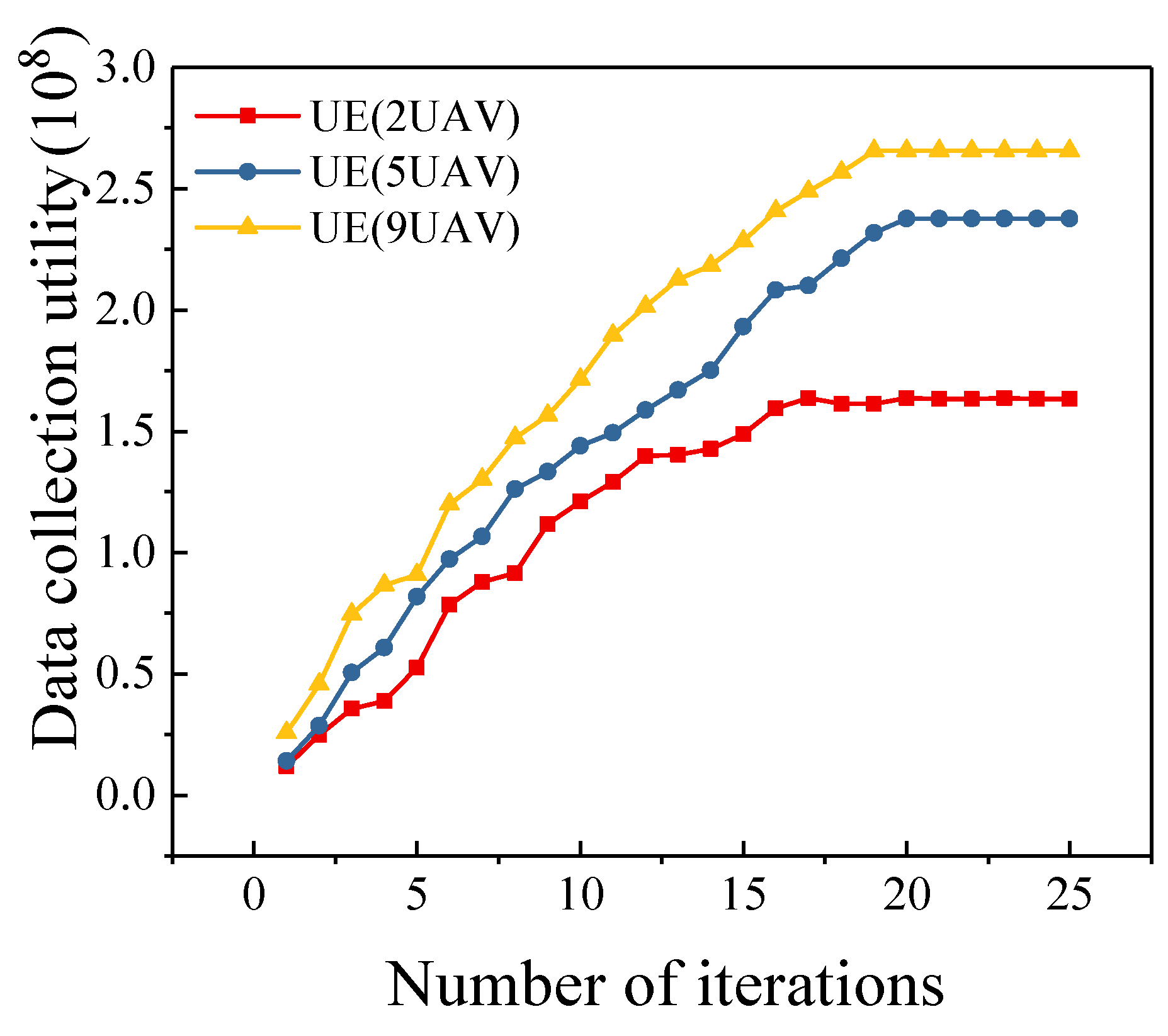
5.4. Different Number of UAVs
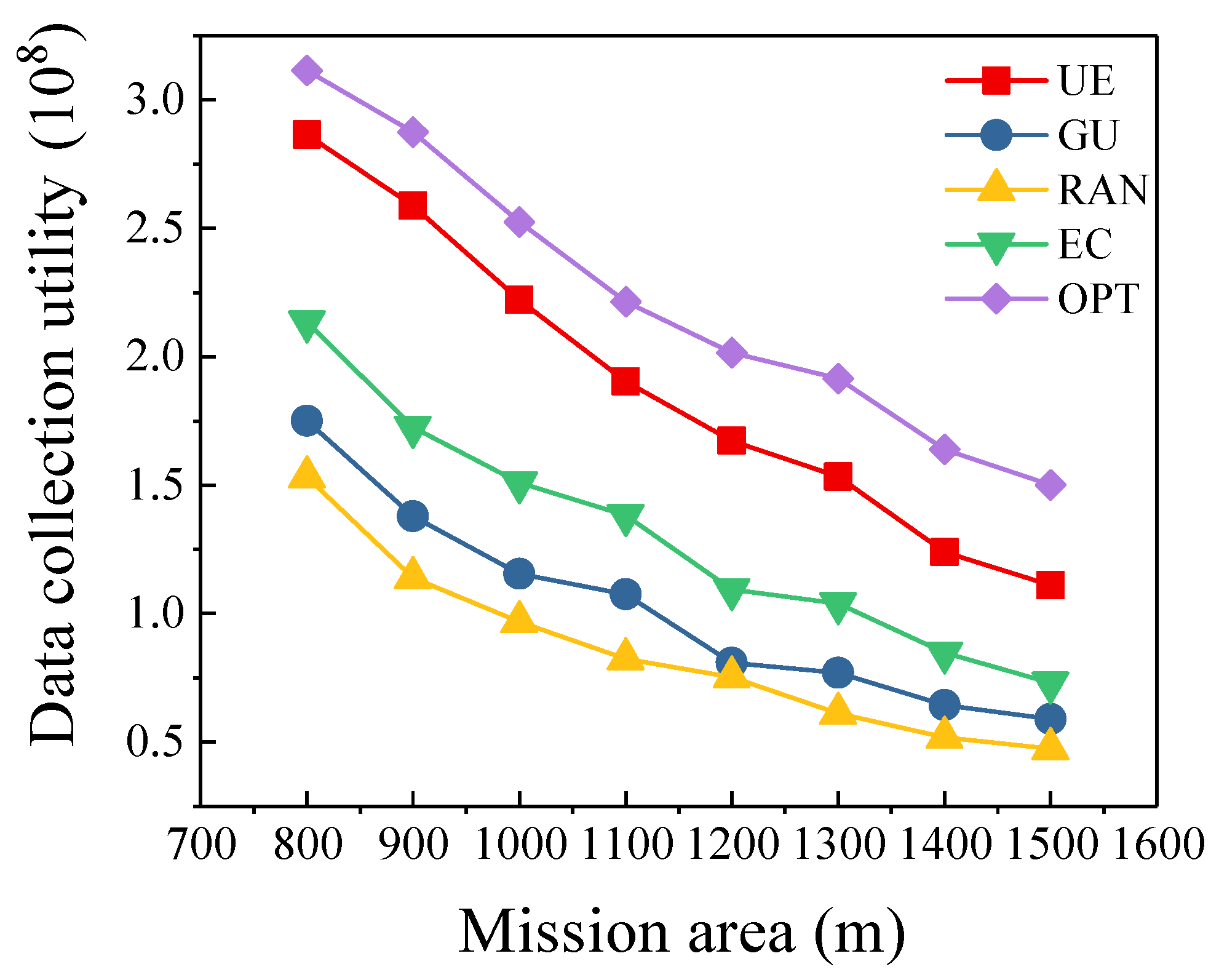
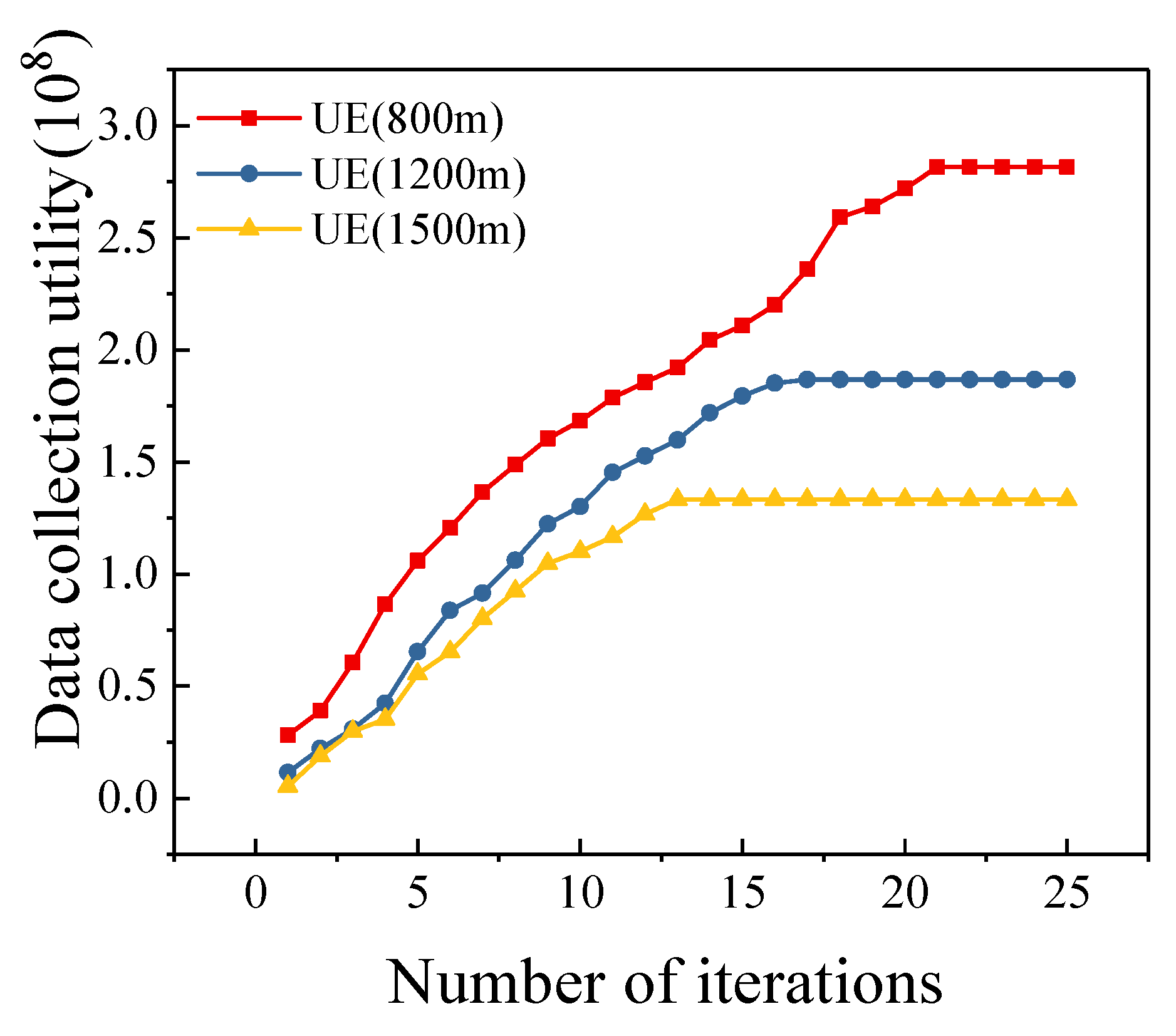
5.5. Different Mission Area Sizes
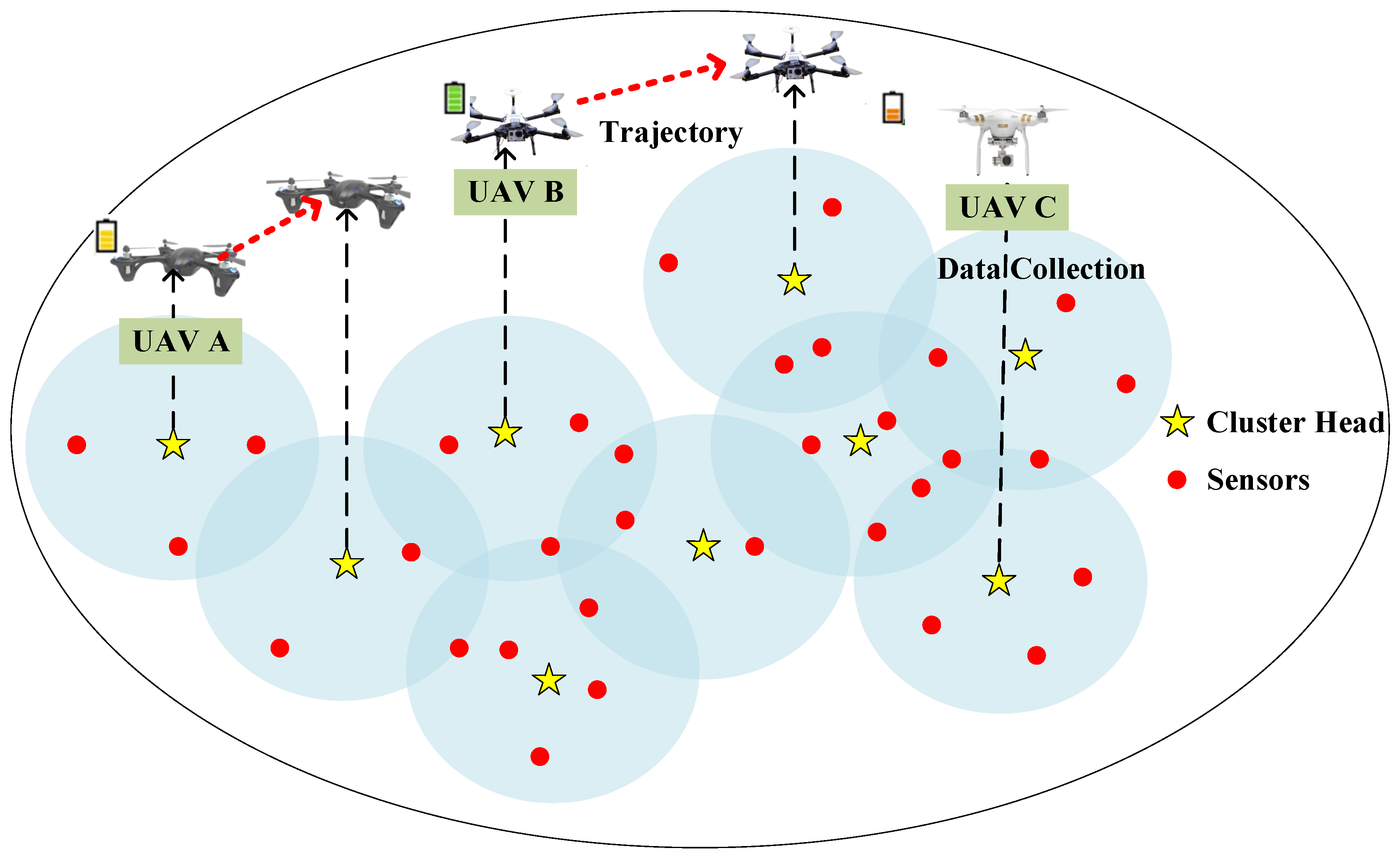
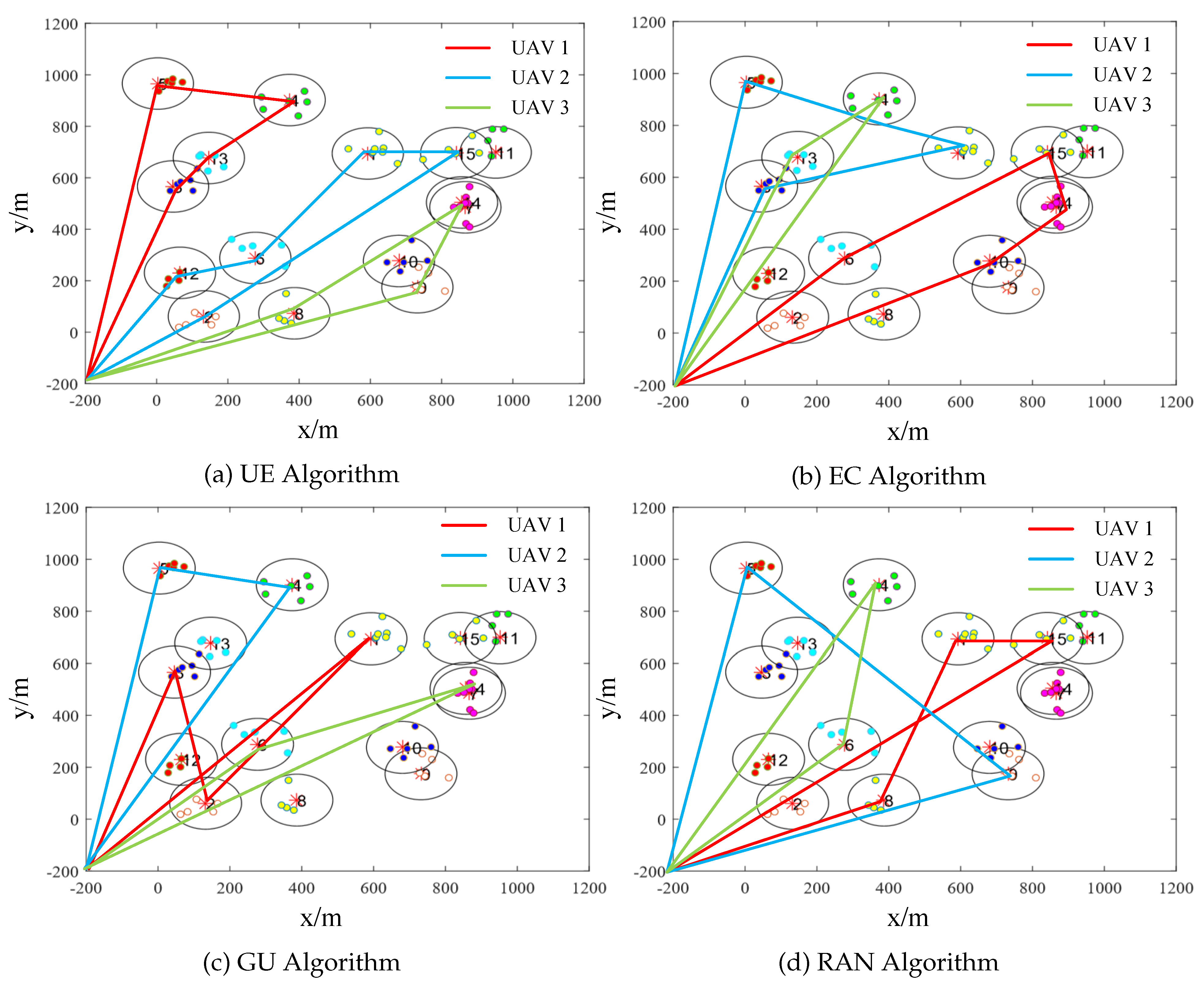
5.6. Trajectories of UAVs
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, F.; Yang, J.; Gui, G. DSF-NOMA: UAV-assisted emergency communication technology in a heterogeneous Internet of things. IEEE Internet Things J. 2019, 6, 5508–5519. [Google Scholar] [CrossRef]
- Al-Fuqaha, A.; Guizani, M.; Mohammadi, M.; Aledhari, M.; Ayyash, M. Internet of things: A survey on enabling technologies, protocols, and applications. IEEE Commun. Surv. Tutorials 2015, 17, 2347–2376. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, M.; Shen, X.; Xie, L.L. Probabilistic analysis on QoS provisioning for Internet of things in LTE-A heterogeneous networks with partial spectrum usage. IEEE Internet Things J. 2016, 3, 354–365. [Google Scholar] [CrossRef]
- Liu, J.; Nishiyama, H.; Kato, N.; Guo, J. On the outage probability of device-to-device communication enabled multi-channel cellular networks: A RSS threshold-based perspective. IEEE J. Sel. Areas Commun. 2016, 34, 163–175. [Google Scholar] [CrossRef]
- Jiang, B.; Yang, J.; Xu, H.; Song, H.; Zheng, G. Multimedia data throughput maximization in Internet-of-things system based on optimization of cache-enabled UAV. IEEE Internet Things J. 2018, 6, 3525–3532. [Google Scholar] [CrossRef]
- Ebrahimi, D.; Sharafeddine, S.; Ho, P.; Assi, C. UAV-aided projection-based compressive data gathering in Wireless Sensor Networks. IEEE Internet Things J. 2018, 6, 1893–1905. [Google Scholar] [CrossRef]
- Li, G.; He, J.; Peng, S.; Jia, W.; Wang, C.; Niu, J.; Yu, S. Energy efficient data collection in large-scale Internet of things via computation offloading. IEEE Internet Things J. 2018, 6, 4176–4187. [Google Scholar] [CrossRef]
- Kim, H.; Ben-othman, J. On collision-free reinforced barriers for multi domain IoT with heterogeneous UAVs. IEEE Commun. Lett. 2018, 22, 2587–2590. [Google Scholar] [CrossRef]
- Eiaz, W.; Naeem, M.; Shahid, A.; Anpalagan, A.; Jo, M. Efficient energy management for the Internet of things in smart cities. IEEE Commun. Mag. 2017, 55, 84–91. [Google Scholar]
- Motlagh, N.H.; Taleb, T.; Arouk, O. Low-altitude Unmanned Aerial Vehicles-based Internet of things services: Comprehensive survey and future perspectives. IEEE Internet Things J. 2016, 3, 899–922. [Google Scholar] [CrossRef]
- Yang, D.; Wu, Q.; Zeng, Y.; Zhang, R. Energy trade-off in Ground-to-UAV communication via trajectory design. IEEE Trans. Veh. Techn. 2018, 67, 6721–6726. [Google Scholar] [CrossRef]
- Zhan, C.; Zeng, Y.; Zhang, R. Energy-efficient data collection in UAV enabled Wireless Sensor Network. IEEE Commun. Lett. 2017, 7, 328–331. [Google Scholar] [CrossRef]
- Hu, Q.; Cai, Y.; Yu, G.; Qin, Z.; Zhao, M.; Li, G. Joint offloading and trajectory design for UAV-enabled mobile edge computing systems. IEEE Internet Things J. 2018, 6, 1879–1892. [Google Scholar] [CrossRef]
- Zhan, C.; Lai, H. Energy minimization in Internet-of-things system based on rotary-wing UAV. IEEE Wirel. Commun. Lett. 2019. [Google Scholar] [CrossRef]
- You, C.; Zhang, R. 3D trajectory optimization in rician fading for UAV-enabled data harvesting. IEEE Trans. Wirel. Commun. 2019, 18, 3192–3207. [Google Scholar] [CrossRef]
- Gong, J.; Chang, T.-H.; Shen, C.; Chen, X. Flight time minimization of UAV for data collection over wireless sensor networks. IEEE J. Sel. Areas Commun. 2018, 36, 1942–1954. [Google Scholar] [CrossRef]
- Zhan, C.; Zeng, Y. Completion time minimization for multi-UAV enabled data collection. IEEE Trans. Wirel. Commun. 2019, 18, 4859–4872. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, C.; Zhang, Z.; Lu, Y.; Chen, S.; Liang, M.; Tao, L. Solving NP-hard problems with physarum-based ant colony system. IEEE/ACM Trans. Comput. Biol. Bioinf. 2015, 14, 108–120. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Hao, J. Memetic search for the generalized quadratic multiple knapsack problem. IEEE Trans. Evol. Comput. 2016, 20, 908–923. [Google Scholar] [CrossRef]
- Rovira-Sugranes, A.; Afghah, F.; Razi, A. Optimized compression policy for flying ad hoc networks. In Proceedings of the 2019 16th IEEE Annual Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 11–14 January 2019; pp. 1–2. [Google Scholar]
- Yang, S.; Deng, Y.; Tang, X.; Ding, Y.; Zhou, J. Energy efficiency optimization for UAV-assisted backscatter communications. IEEE Commun. Lett. 2019. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Zhang, N.; Wu, W.; Liu, A. Optimizing trajectory of Unmanned Aerial Vehicles for efficient data acquisition: A matrix completion approach. IEEE Internet Things J. 2019, 6, 1829–1840. [Google Scholar] [CrossRef]
- Samir, M.; Sharafeddine, S.; Assi, C.; Nguyen, T.M.; Ghrayeb, A. Trajectory planning and resource allocation of multiple UAVs for data delivery in vehicular networks. IEEE Networking Lett. 2019, 1, 107–110. [Google Scholar] [CrossRef]
- Sharafeddine, S.; Islambouli, R. On-demand deployment of multiple aerial base stations for traffic offloading and network recovery. Comput. Networks 2019, 156, 52–61. [Google Scholar] [CrossRef]
- Samir, M.; Sharafeddine, S.; Assi, C.; Nguyen, T.M.; Ghrayeb, A. UAV trajectory planning for data collection from time-constrained IoT devices. IEEE Trans. Wirel. Commun. 2019. [Google Scholar] [CrossRef]
- Hu, Y.; Yuan, X.; Xu, J.; Schmeink, A. Optimal 1D trajectory design for UAV-enabled multiuser wireless power transfer. IEEE Trans. Commun. 2017, 67, 5674–5688. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, X.; Zhang, R. Trajectory design for completion time minimization in UAV-enabled multicasting. IEEE Trans. Wirel. Commun. 2018, 17, 2233–2246. [Google Scholar] [CrossRef]
- Stefano, P.; Giorgio, G.; Alessandro, R. A risk-aware path planning strategy for UAVs in urban environments. J. Intell. Rob. Syst. 2018, 95, 629–643. [Google Scholar]
- Islam, S.; Razi, A. A path planning algorithm for collective monitoring using autonomous drones. In Proceedings of the 2019 53rd Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 20–22 March 2019; pp. 1–6. [Google Scholar]
- Babel, L. Coordinated target assignment and UAV path planning with timing constraints. J. Intell. Rob. Syst. 2019, 94, 857–869. [Google Scholar] [CrossRef]
- Christian, Z.; Kampen, E.V. Advancements for A* and RRT in 3D path planning of UAVs. Available online: https://arc.aiaa.org/doi/abs/10.2514/6.2019-0920 (accessed on 8 September 2019).
- Hu, J.; Zhang, H.; Song, L. Reinforcement learning for decentralized trajectory design in cellular UAV networks with sense-and-send protocol. IEEE Internet Things J. 2018, 6, 6177–6189. [Google Scholar] [CrossRef]
- Wu, Q.; Zeng, Y.; Zhang, R. Joint trajectory and communication design for multi-UAV enabled wireless networks. IEEE Trans. Wirel. Commun. 2018, 17, 2109–2121. [Google Scholar] [CrossRef]
- Youssef, M.; Youssef, A.; Younis, M. Overlapping multihop clustering for Wireless Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2009, 20, 1844–1856. [Google Scholar] [CrossRef]
- Youssef, A.; Younis, M.; Youssef, M.; Agrawala, A. Distributed formation of overlapping multi-hop clusters in Wireless Sensor Networks. In Proceedings of the 2006 IEEE Global Communications Conference, San Francisco, CA, USA, 27 November–1 December 2006. [Google Scholar]
- Zeng, Y.; Xu, J.; Zhang, R. Energy minimization for wireless communication with rotary-wing UAV. IEEE Trans. Wirel. Commun. 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Thammawichai, M.; Baliyarasimhuni, S.P.; Kerrigan, E.C. Optimizing communication and computation for multi-UAV information gathering applications. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 601–615. [Google Scholar] [CrossRef]
- Monwar, M.; Semiari, O.; Saad, W. Optimized path planning for inspection by Unmanned Aerial Vehicles swarm with energy constraints. In Proceedings of the 2018 IEEE Global Communications Conference, Abu Dhabi, UAE, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Stolaroff, J.K.; Samaras, C.; Oneill, E.R.; Lubers, A.; Mitchell, A.S.; Ceperley, D. Energy use and life cycle greenhouse gas emissions of drones for commercial package delivery. Nature Commun. 2018, 9, 1–13. [Google Scholar]
- Driessens, S.; Pounds, P.E.I. Towards a more efficient quadrotor configuration. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1–7. [Google Scholar]
- Tang, C.; Mckinley, P.K. Energy optimization under informed mobility. IEEE Trans. Parallel Distrib. Syst. 2016, 17, 947–962. [Google Scholar] [CrossRef]
- Ruan, L.; Wang, J.; Chen, J.; Xu, Y.; Yang, Y.; Jiang, H.; Zhang, Y.; Xu, Y. Energy-efficient multi-UAV coverage deployment in UAV networks: A game-theoretic framework. China Commun. 2018, 15, 194–209. [Google Scholar] [CrossRef]
- Na, H.J.; Yoo, S. PSO-based dynamic UAV positioning algorithm for sensing information acquisition in Wireless Sensor Networks. IEEE Access 2019, 7, 77499–77513. [Google Scholar] [CrossRef]
- Wu, T.; Yang, P.; Dai, H.; Xu, W.; Xu, M. Collaborated tasks-driven mobile charging and scheduling: A near optimal result. In Proceedings of the IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; pp. 1–9. [Google Scholar]
- Zhang, H.; Vorobeychik, Y. Submodular optimization with routing constraints. In Proceedings of the AAAI, Phoenix, AZ, USA, 12–17 February 2016; pp. 1–9. [Google Scholar]
- Zeng, Y.; Zhang, R.; Teng, J.L. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
| Notation | Definition |
|---|---|
| U | UAV set |
| S | Sensor set |
| C | Cluster head set |
| L | UAV trajectory set |
| UAV i | |
| Sensor j | |
| Cluster head a | |
| Trajectory of UAV i | |
| k | Number of UAVs, or number of trajectories |
| n | Number of sensors |
| m | Number of cluster heads |
| Energy budget of UAV i | |
| Minimum motion power | |
| Motion energy consumption of UAV i | |
| Actual motion power of UAV i | |
| Length of trajectory | |
| Velocity of UAV i | |
| Power efficiency of UAV i | |
| Hovering energy consumption of UAV i | |
| Amount of data collected by UAV i in cluster head a | |
| Minimum hovering power | |
| Actual hovering power of UAV i | |
| Data transmission rate between UAV i and cluster head a | |
| Communication energy consumption of UAV i | |
| Path loss exponent | |
| Communication energy consumption parameter | |
| Value of data collected from sensor j | |
| Recovery interval of sensor j | |
| Time of previous data collection from sensor j | |
| Data utility of cluster head a collected by UAV i | |
| Data collection utility of UAV i | |
| Q | Overall data collection utility |
| Maximum velocity | |
| trajectory projected on the ground | |
| Time derivative of | |
| Minimum inter-UAV distance | |
| H | Altitude of UAVs |
| Definition | Parameters | Values |
|---|---|---|
| Area size | D | 1 km× 1 km |
| Minimum inter-UAV distance | 100 m | |
| Altitude of UAVs | H | 50 m |
| Maximum velocity | 20 m/s | |
| Minimum motion power | 388.32 J/s | |
| Minimum hovering power | 308 J/s | |
| Power efficiency of UAV | 70%–80% | |
| Data transmission rate | R | 2 Mbps |
| Path loss exponent | 2 | |
| Communication energy consumption parameter | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, Z.; Dong, C.; Wang, H.; Li, A.; Dai, H.; Sun, W.; Xu, Z. Trajectory Planning for Data Collection of Energy-Constrained Heterogeneous UAVs. Sensors 2019, 19, 4884. https://doi.org/10.3390/s19224884
Qin Z, Dong C, Wang H, Li A, Dai H, Sun W, Xu Z. Trajectory Planning for Data Collection of Energy-Constrained Heterogeneous UAVs. Sensors. 2019; 19(22):4884. https://doi.org/10.3390/s19224884
Chicago/Turabian StyleQin, Zhen, Chao Dong, Hai Wang, Aijing Li, Haipeng Dai, Weihao Sun, and Zhengqin Xu. 2019. "Trajectory Planning for Data Collection of Energy-Constrained Heterogeneous UAVs" Sensors 19, no. 22: 4884. https://doi.org/10.3390/s19224884
APA StyleQin, Z., Dong, C., Wang, H., Li, A., Dai, H., Sun, W., & Xu, Z. (2019). Trajectory Planning for Data Collection of Energy-Constrained Heterogeneous UAVs. Sensors, 19(22), 4884. https://doi.org/10.3390/s19224884






