Chaotic Signatures Exhibited by Plasmonic Effects in Au Nanoparticles with Cells
Abstract
1. Introduction
2. Materials and Methods
2.1. Synthesis of the Au NPs in a TiO2 Film
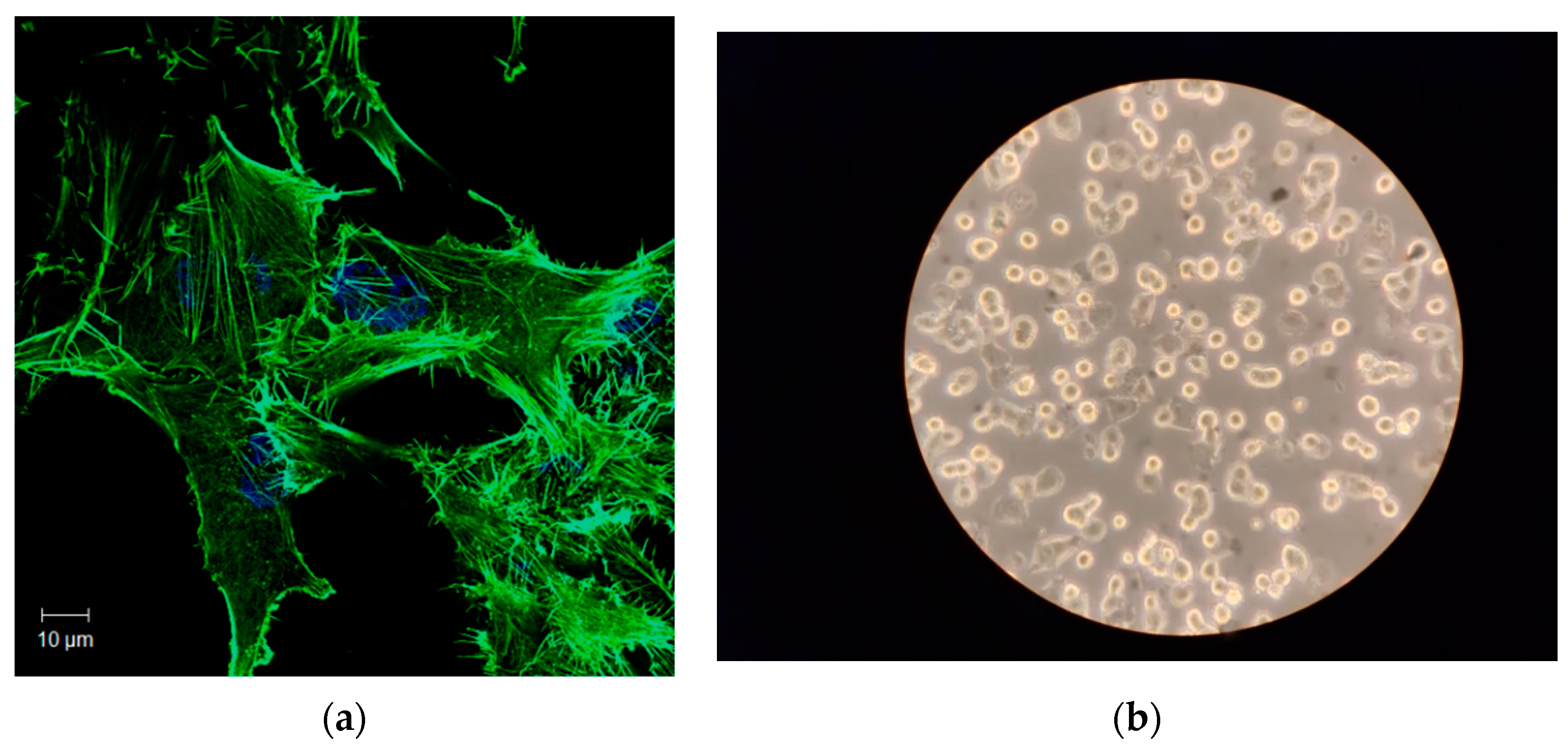
2.2. Preparation of the Biological Sample
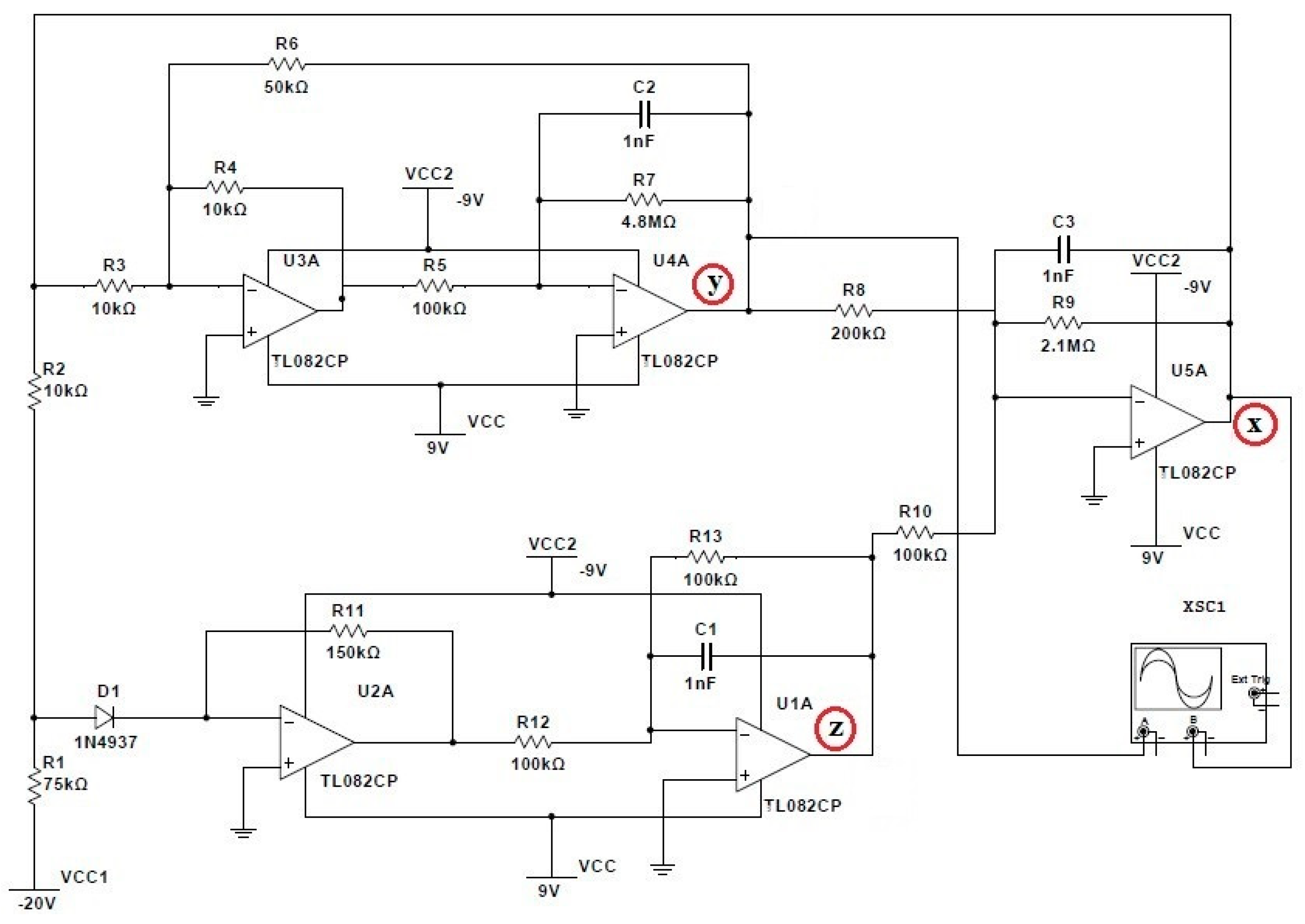
2.3. Modeling of Chaotic Electronic Rössler System
2.4. Modification of the LSPR of the Sample by Nanosecond Pulses
2.5. Biosensing Assisted by Au NPs and Steady-State Rössler Attractors
2.6. Laser Ablation Threshold in the Biomarkers under a Vectorial Two-Wave Mixing Irradiation
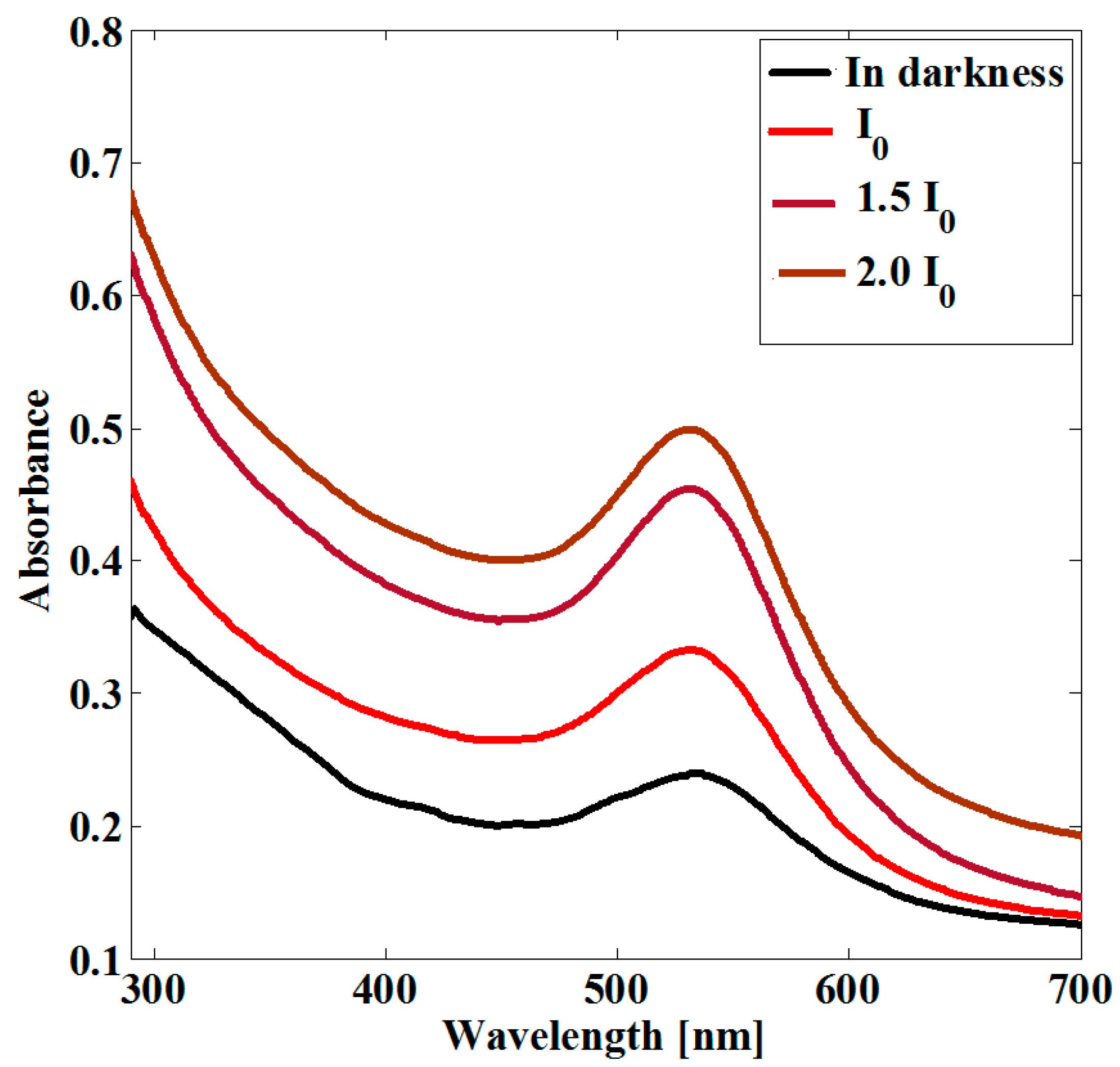
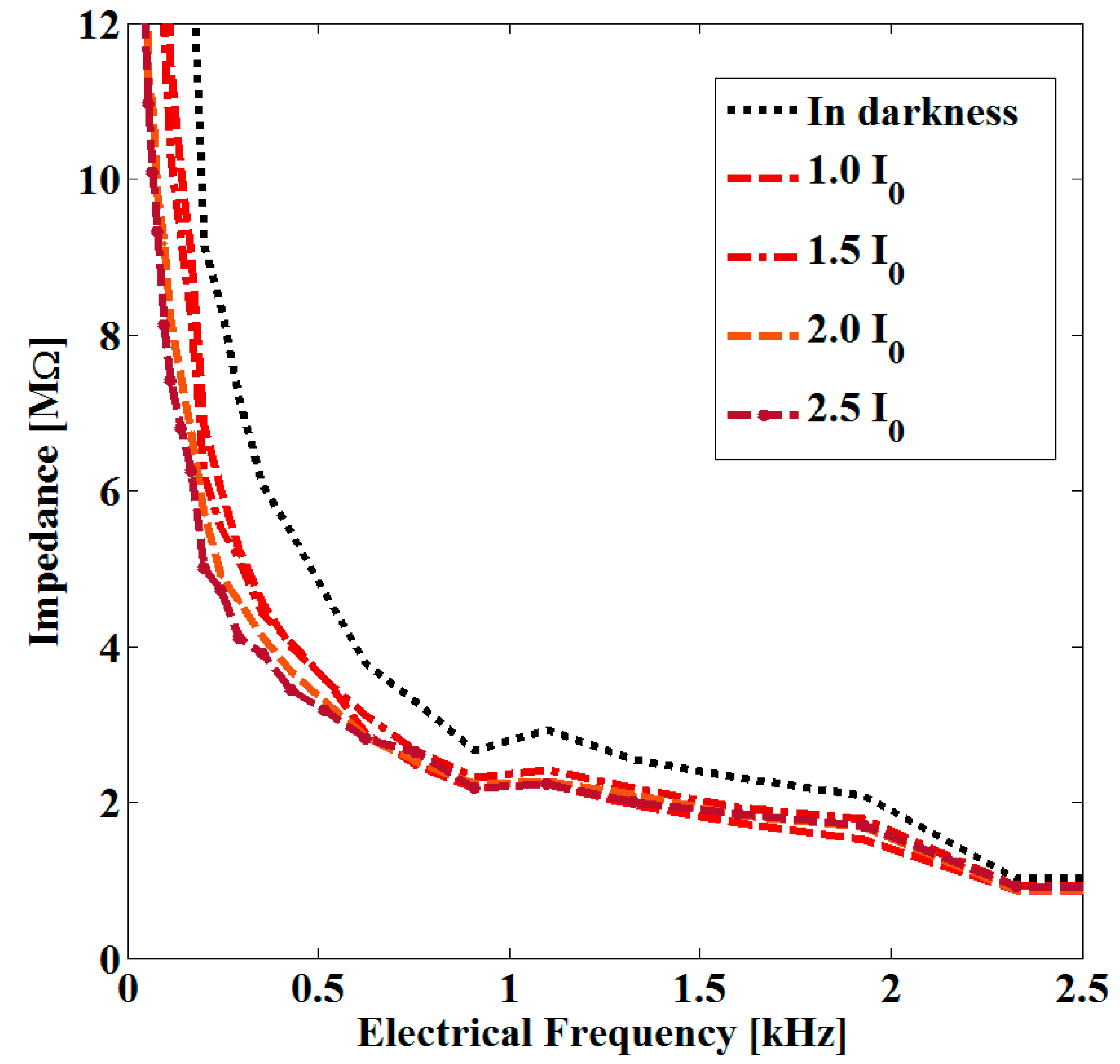
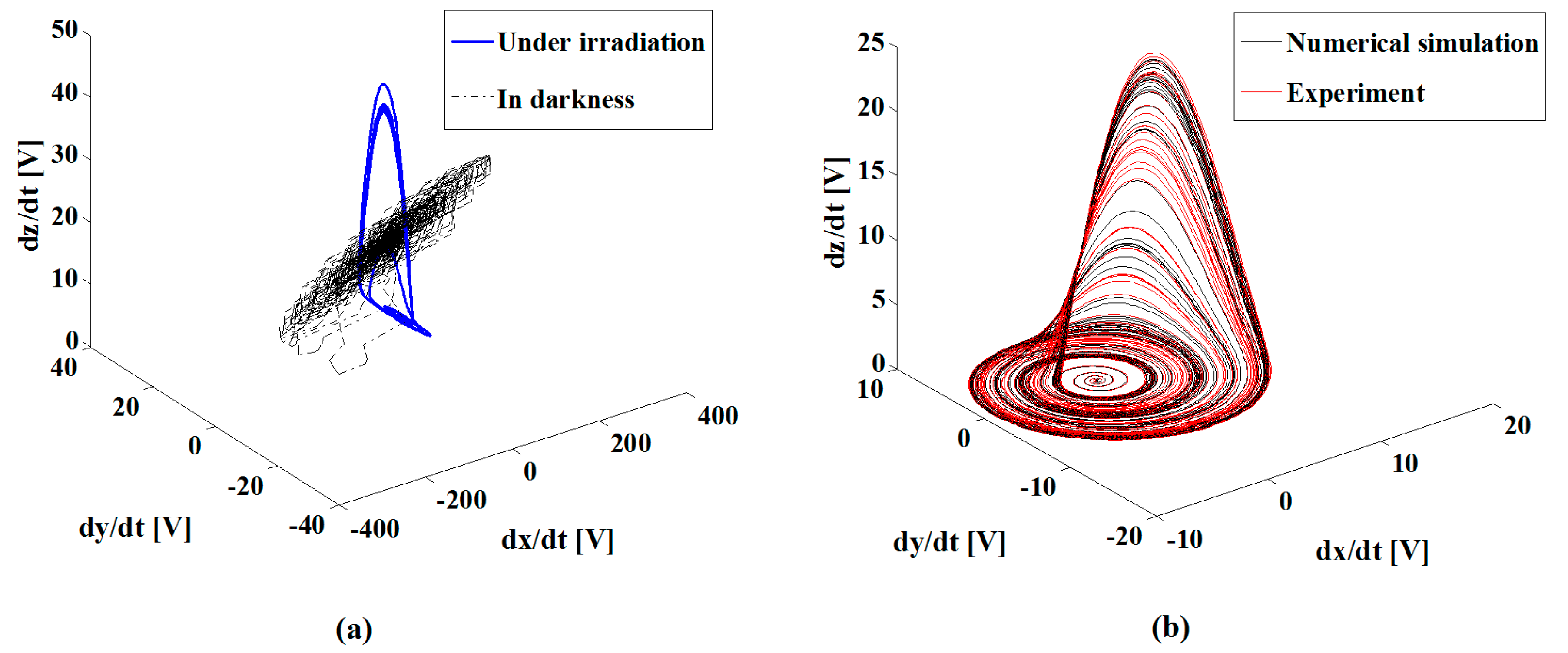
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rosalie, M. Templates and subtemplates of Rössler attractors from a bifurcation diagram. J. Phys. A Math. Theor. 2016, 49, 315101. [Google Scholar] [CrossRef]
- Rosalie, M.; Letellier, C. Toward a general procedure for extracting templates from chaotic attractors bounded by high genus torus. Int. J. Bifurc. Chaos 2014, 24, 1450045. [Google Scholar] [CrossRef]
- Vinay, V.; Pavan, T. Shape distributions of nonlinear dynamical systems for video-based inference. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2531–2543. [Google Scholar]
- Jeter, R.; Belykh, I. Synchronization in on-off stochastic networks: Windows of opportunity. IEEE Trans. Circuits Syst. 2015, 62, 1260–1269. [Google Scholar] [CrossRef]
- Mirzaei, O.; Yaghoobi, M.; Irani, H. A new image encryption method: Parallel sub-image encryption with hyper chaos. Nonlinear Dynam. 2012, 67, 557–566. [Google Scholar] [CrossRef]
- Shekhar, S.C.; Gary, R.; Jin, J.; Mingyan, L.; Andrew, M.K.; Imants, D.S.; Stuart, C. Chaotic Sensing. IEEE Trans. Image Process. 2018, 27, 6079–6092. [Google Scholar]
- Behrouz, V.; Mohammad, A.P.; Saleh, M. Finite-time chaos synchronization and its application in wireless sensor networks. Trans. Inst. Meas. Control. 2018, 40, 3788–3799. [Google Scholar]
- Rémi, M.; Andreas, W. Materials learning from life: Concepts for active, adaptive and autonomous molecular systems. Chem. Soc. Rev. 2017, 46, 5588–5619. [Google Scholar]
- Velmurugan, G.; Rakkiyappan, R.; Jinde, C. Finite-time synchronization of fractional-order memristor-based neural networks with time delays. Neural Netw. 2016, 73, 36–46. [Google Scholar] [CrossRef]
- Barrio, R.; Blesa, F.; Serrano, S. Bounds for the chaotic region in the Lorenz model. Physica D 2009, 238, 1087–1100. [Google Scholar] [CrossRef]
- Botha, A.E.; Dednam, W. Computer assisted ‘proof’ of the global existence of periodic orbits in the Rössler system. In Proceedings of the 59th Annual Conference of the SAIP, Johannesburg, South Africa, 7–11 July 2014; Volume 59, p. 571. [Google Scholar]
- Makoto, N.; Yuta, T.; Atsushi, U.; Song-Ju, K. Ultrafast photonic reinforcement learning based on laser chaos. Sci. Rep. 2017, 7, 8772. [Google Scholar]
- Ye, G.; Huang, X. A novel block chaotic encryption scheme for remote sensing image. Multimed. Tools Appl. 2016, 75, 11433–11446. [Google Scholar] [CrossRef]
- Huang, X.; Ye, G. An image encryption algorithm based on hyper-chaos and DNA sequence. Multimed. Tools Appl. 2014, 72, 57–70. [Google Scholar] [CrossRef]
- Chang, C.Y.; Choi, D.; Locquet, A.; Wishon, M.J.; Merghem, K.; Ramdane, A.; Lelarge, F.; Martinez, A.; Citrin, D.S. A multi-GHz chaotic optoelectronic oscillator based on laser terminal voltage. Appl. Phys. Lett. 2016, 108, 191109. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, J.; Xie, T. Cryptanalyzing a RGB image encryption algorithm based on DNA encoding and chaos map. Opt. Laser Technol. 2014, 60, 111–115. [Google Scholar] [CrossRef]
- González-Salas, J.S.; Shbat, M.S.; Ordaz-Salazar, F.C.; Simón, J. Analyzing Chaos Systems and Fine Spectrum Sensing Using Detrended Fluctuation Analysis Algorithm. Math. Probl. Eng. 2016, 2016, 2865195. [Google Scholar] [CrossRef]
- Xi, T.; Zheng-Mao, W.; Jia-Gui, W.; Tao, D.; Jian-Jun, C.; Li, F.; Zhu-Qiang, Z.; Guang-Qiong, X. Tbits/s physical random bit generation based on mutually coupled semiconductor laser chaotic entropy source. Opt. Express 2015, 23, 33130–33141. [Google Scholar]
- Bueno, J.; Maktoobi, S.; Froehly, L.; Fischer, I.; Jacquot, M.; Larger, L.; Brunner, D. Reinforcement learning in a large-scale photonic recurrent neural network. Optica 2018, 5, 756–760. [Google Scholar] [CrossRef]
- Gustavo, T.; Wayne, K.; Luke, J.; Raymundo, A.; Ibrahim, K.; Alaa, E. Uncertainty Propagation Analysis of Computational Models in Laser Powder Bed Fusion Additive Manufacturing Using Polynomial Chaos Expansions. J. Manuf. Sci. Eng. 2018, 140, 121006. [Google Scholar]
- Dumeige, Y.; Raineri, F. Nonlinear optics in nano-and microstructures. In Nanophotonics; ISTE Ltd.: Newport Beach, CA, USA, 2006. [Google Scholar]
- Ozba, E. Plasmonics: Merging photonics and electronics at nanoscale dimensions. Science 2006, 311, 189–193. [Google Scholar] [CrossRef]
- Hagymási, I.; Vancsó, P.; Pálinkás, A.; Osváth, Z. Interaction effects in a chaotic graphene quantum billiard. Phys. Rev. B 2017, 95, 075123. [Google Scholar] [CrossRef]
- Hampson, K.M.; Cufflin, M.P.; Mallen, E.A. Sensitivity of Chaos Measures in Detecting Stress in the Focusing Control Mechanism of the Short-Sighted Eye. Bull. Math. Biol. 2017, 79, 1870–1887. [Google Scholar] [CrossRef] [PubMed]
- Torres-Torres, C.; López-Suárez, A.; Can-Uc, B.; Rangel-Rojo, R.; Tamayo-Rivera, L.; Oliver, A. Collective optical Kerr effect exhibited by an integrated configuration of silicon quantum dots and gold nanoparticles embedded in ion-implanted silica. Nanotechnology 2015, 26, 295701. [Google Scholar] [CrossRef] [PubMed]
- Mitta, S.B.; Reddeppa, M.; Vellampatti, S.; Dugasani, S.R.; Yoo, S.; Lee, S.; Kim, M.; Ha Park, S. Gold nanoparticle-embedded DNA thin films for ultraviolet photodetectors. Sens. Actuators B Chem. 2018, 275, 137–144. [Google Scholar] [CrossRef]
- Morales-Bonilla, S.; Martines-Arano, H.; Torres-Torres, D.; Ochoa-Ortega, G.; Carrillo-Delgado, C.; Trejo-Valdez, M.; Torres-Torres, C. Dynamic and plasmonic response exhibited by Au nanoparticles suspended in blood plasma and cerebrospinal fluids. J. Mol. Liq. 2019, 281, 1–8. [Google Scholar] [CrossRef]
- Huakang, Y.; Yusi, P.; Yong, Y.; Zhi-Yuan, L. Plasmon-enhanced light–matter interactions and applications. npj Comput. Mater. 2019, 5, 45. [Google Scholar]
- Saha, K.; Agasti, S.S.; Kim, C.; Li, X.; Rotello, V.M. Gold nanoparticles in chemical and biological sensing. Chem. Rev. 2012, 112, 2739–2779. [Google Scholar] [CrossRef]
- Notariannia, M. Plasmonic effect of gold nanoparticles in organic solar cells. Sol. Energy 2014, 106, 23–37. [Google Scholar] [CrossRef]
- Thompson, D.T. Using gold nanoparticles for catalysis. Nano Today 2007, 2, 40–43. [Google Scholar] [CrossRef]
- Tiwari, P.M.; Vig, K.; Dennis, V.A.; Singh, S.R. Functionalized gold nanoparticles and their biomedical applications. Nanomaterials 2011, 1, 31–63. [Google Scholar] [CrossRef]
- Trejo-Valdez, M.; Torres-Martínez, R.; Peréa-López, N.; Santiago-Jacinto, P.; Torres-Torres, C. Contribution of the two-photon absorption to the third order nonlinearity of Au nanoparticles embedded in TiO2 films and in ethanol suspension. J. Phys. Chem. C 2010, 114, 10108–10113. [Google Scholar] [CrossRef]
- Bell, J.G. Nonlinear Instabilities in Chemical and Electrochemical Systems. Ph.D. Thesis, University of Windsor, Windsor, ON, Canada, 2017; p. 5967. [Google Scholar]
- Sambas, A.; Sanjaya, M.; Mamat, M. Halimatussadiyah. Design and Analysis Bidirectional Chaotic Synchronization of Rossler Circuit and Its Application for Secure Communication. Appl. Math. Sci. 2013, 1, 11–21. [Google Scholar]
- Ibrahim, K.M.; Jamal, R.K.; Ali, F.H. Chaotic behaviour of the Rossler model and its analysis by using bifurcations of limit cycles and chaotic attractors. J. Phys. Conf. Ser. 2018, 1003, 012099. [Google Scholar] [CrossRef]
- Torres-Torres, C.; Khomenko, A.V.; Tamayo-Rivera, L.; Rangel-Rojo, R.; Mao, Y.; Watson, W.H. Measurements of nonlinear optical refraction and absorption in an amino-triazole push-pull derivative by a vectorial self-diffraction method. Opt. Commun. 2008, 281, 3369–3374. [Google Scholar] [CrossRef]
- Hecht, E. Optics, 4th ed.; Addison Wesley: San Francisco, CA, USA, 2002. [Google Scholar]
- Nikolov, A.S.; Nedyalkov, N.N.; Nikov, R.G.; Atanasov, P.A.; Alexandro, M.T. Characterization of Ag and Au nanoparticles created by nanosecond pulsed laser ablation in double distilled water. Appl. Surf. Sci. 2011, 257, 5278–5282. [Google Scholar] [CrossRef]
- Zhaohui, W.; Siwen, L.; Min, Z.; Yi, M.; Yuxi, L.; Weidong, G.; Jiaqi, Z.; Yueqing, G. Laser-Triggered Small Interfering RNA Releasing Gold Nanoshells against Heat Shock Protein for Sensitized Photothermal Therapy. Adv. Sci. 2017, 4, 1600327. [Google Scholar]
- Sina, N.S.; Jalil, J.; Mostafa, K.M. Electrical Conductivity, Viscosity, and Density of Different Nanofluids: An Experimental Study. Exp. Therm. Fluid Sci. 2016, 74, 339–346. [Google Scholar]
- Bornacelli, J.; Torres-Torres, C.; Silva-Pereyra, H.G.; Labrada-Delgado, G.J.; Crespo-Sosa, A.; Cheang-Wong, J.C.; Oliver, A. Superlinear photoluminescence by ultrafast laser pulses in dielectric matrices with metal nanoclusters. Sci. Rep. 2019, 9, 5699. [Google Scholar] [CrossRef]
- Nie, W.J.; Zhang, Y.X.; Yu, H.H.; Li, R.; He, R.Y.; Dong, N.N.; Wang, J.; Hübner, R.; Böttger, R.; Zhou, S.Q.; et al. Plasmonic nanoparticles embedded in single crystals synthesized by gold ion implantation for enhanced optical nonlinearity and efficient Q-switched lasing. Nanoscale 2018, 10, 4228–4236. [Google Scholar] [CrossRef]
- Jagannath, G.; Eraiah, B.; NagaKrishnakanth, K.; Rao, S.V. Linear and nonlinear optical properties of gold nanoparticles doped borate glasses. J. Non-Cryst. Solids 2018, 482, 160–169. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, T.; Jorgens, D.M.; Nickerson, A.; Lin, L.-J.; Pelz, J. Quantitating morphological changes in biological samples during scanning electron microscopy sample preparation with correlative superresolution microscopy. PLoS ONE 2017, 12, e0176839. [Google Scholar]
- Chen, J.; Wang, D.; Xi, J.; Au, L.; Siekkinen, A.; Warsen, A.; Li, Z.-Y.; Zhang, H.; Xia, Y.; Li, X. Immuno Gold Nanocages with Tailored Optical Properties for Targeted Photothermal Destruction of Cancer Cells. Nano Lett. 2007, 7, 1318–1322. [Google Scholar] [CrossRef] [PubMed]
- Gómez, F.R.; Rubira, R.J.G.; Camacho, S.A.; Martin, C.S.; da Silva, R.R.; Constantino, C.J.L.; Alessio, P.; Oliveira, O.N.; Mejía-Salazar, J.R. Surface Plasmon Resonances in Silver Nanostars. Sensors 2018, 18, 3821. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Li, X.; He, R.; Wu, L.; Zhang, L.; Zeng, J. Chloride-induced shape transformation of silver nanoparticles in a water environment. Environ. Pollut. 2015, 204, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Kulkarni, V.N.; Sood, D.K. Pulsed laser heating calculations incorporating vapourization. Appl. Phys. 1981, 25, 127–133. [Google Scholar] [CrossRef]
- Torres-Torres, D.; Torres-Torres, C.; Vega-Becerra, O.; Cheang-Wong, J.C.; Rodríguez-Fernández, L.; Crespo-Sosa, A.; Oliver, A. Structured strengthening by two-wave optical ablation in silica with gold nanoparticles. Opt. Laser Technol. 2015, 75, 115–122. [Google Scholar] [CrossRef]
- Wu, T.; Nieminen, T.A.; Mohanty, S.; Miotke, J.; Meyer, R.L.; Rubinsztein-Dunlop, H.; Berns, M.W. A photon-driven micromotor can direct nerve fibre growth. Nat. Photonics 2011, 6, 62–67. [Google Scholar] [CrossRef]
- Bintoro, S.N.; Alexander, A.I.; Victor, A.M.; Jasper, K. Instabilities in the optical response of a semiconductor quantum dot—Metal nanoparticle heterodimer: Self-oscillations and chaos. J. Opt. 2017, 19, 015004. [Google Scholar]
- Ka, S.W.; Ori Henderson-Sapir Peter, J.V.; Murray, H.; Jesper, M.; David, J.O. Self-pulsing in Tm-doped YAlO3 lasers: Excited-state absorption and chaos. Phys. Rev. A 2015, 91, 043819. [Google Scholar]
- Lingzhen, Y.; Jianjun, Y.; Yi, Y.; Zongwei, Z.; Juanfen, W.; Zhaoxia, Z.; Pingping, X.; Yongkang, G.; Nigel, C. Optical sensors using chaotic correlation fiber loop ring down. Opt. Express 2017, 25, 2031–2037. [Google Scholar]
- Lei, Z.; Fengchun, T.; David, Z. Chaotic Time Series-Based Sensor Drift Prediction. In Electronic Nose: Algorithmic Challenges; Springer: Singapore, 2018; pp. 135–146. [Google Scholar]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martines-Arano, H.; García-Pérez, B.E.; Vidales-Hurtado, M.A.; Trejo-Valdez, M.; Hernández-Gómez, L.H.; Torres-Torres, C. Chaotic Signatures Exhibited by Plasmonic Effects in Au Nanoparticles with Cells. Sensors 2019, 19, 4728. https://doi.org/10.3390/s19214728
Martines-Arano H, García-Pérez BE, Vidales-Hurtado MA, Trejo-Valdez M, Hernández-Gómez LH, Torres-Torres C. Chaotic Signatures Exhibited by Plasmonic Effects in Au Nanoparticles with Cells. Sensors. 2019; 19(21):4728. https://doi.org/10.3390/s19214728
Chicago/Turabian StyleMartines-Arano, Hilario, Blanca Estela García-Pérez, Mónica Araceli Vidales-Hurtado, Martín Trejo-Valdez, Luis Héctor Hernández-Gómez, and Carlos Torres-Torres. 2019. "Chaotic Signatures Exhibited by Plasmonic Effects in Au Nanoparticles with Cells" Sensors 19, no. 21: 4728. https://doi.org/10.3390/s19214728
APA StyleMartines-Arano, H., García-Pérez, B. E., Vidales-Hurtado, M. A., Trejo-Valdez, M., Hernández-Gómez, L. H., & Torres-Torres, C. (2019). Chaotic Signatures Exhibited by Plasmonic Effects in Au Nanoparticles with Cells. Sensors, 19(21), 4728. https://doi.org/10.3390/s19214728






