Identification of Bicycling Periods Using the MicroPEM Personal Exposure Monitor
Abstract
1. Introduction
1.1. Motivation
1.2. Related Work
2. Data
2.1. Device Description
2.2. Data Collection
2.3. Dataset Description
2.4. Data Preprocessing and Feature Creation
3. Methods
3.1. Biking Recognition Models
3.2. Model Evaluation
4. Results
4.1. Model Performance
4.2. Feature Importance
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Model | Specification |
|---|---|
| Mode Smoothed | Window length: 11 Window orientation: Centered on current observation |
| Stacked Ensemble | Classifier type: Gradient boosted trees classifier Features: Base model predicted probabilities Number of boosting stages: 40 Learning rate: 0.1 |
| Gradient Boosted Trees | Number of boosting stages: 80 Learning rate: 0.1 |
| K-Nearest Neighbors | K: 5 Weight function: Points weighted by inverse of their distance Distance metric: Euclidean |
| Logistic Regression | Regularization: L1-norm C (inverse of regularization strength): 0.0008 Class weights: balanced Optimization Solver: SAGA [31] |
References
- Cohen, A.J.; Brauer, M.; Burnett, R.; Anderson, H.R.; Frostad, J.; Estep, K.; Balakrishnan, K.; Brunekreef, B.; Dandona, L.; Dandona, R.; et al. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the Global Burden of Diseases Study 2015. Lancet 2017, 389, 1907–1918. [Google Scholar] [CrossRef]
- Rodes, C.E.; Lawless, P.A.; Thornburg, J.W.; Williams, R.W.; Croghan, C.W. DEARS particulate matter relationships for personal, indoor, outdoor, and central site settings for a general population. Atmos. Environ. 2010, 44, 1386–1399. [Google Scholar] [CrossRef]
- Rodes, C.E. Breathing zone exposure assessment. In Aerosols Handbook; CRC Press: Boca Raton, FL, USA, 2004; pp. 69–81. [Google Scholar]
- Rodes, C.E.; Chillrud, S.N.; Haskell, W.L.; Intille, S.S.; Albinali, F.; Rosenberger, M.E. Predicting adult pulmonary ventilation volume and wearing complianceby on-board accelerometry during personal level exposure assessments. Atmos. Environ. 2012, 57, 126–137. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Chillrud, S.N.; Pitiranggon, M.; Ross, J.; Ji, J.; Yan, B. Development of an approach to correcting MicroPEM baseline drift. Environ. Res. 2018, 164, 39–44. [Google Scholar] [CrossRef] [PubMed]
- Zuurbier, M.; Hoek, G.; van den Hazel, P.; Brunekreef, B. Minute ventilation of cyclists, car and bus passengers: An experimental study. Environ. Health 2009, 8, 48. [Google Scholar] [CrossRef]
- Fajardo, O.A.; Rojas, N.Y. Particulate matter exposure of bicycle path users in a high-altitude city. Atmos. Environ. 2012, 46, 675–679. [Google Scholar] [CrossRef]
- Int Panis, L.; de Geus, B.; Vandenbulcke, G.; Willems, H.; Degraeuwe, B.; Bleux, N.; Mishra, V.; Thomas, I.; Meeusen, R. Exposure to particulate matter in traffic: A comparison of cyclists and car passengers. Atmos. Environ. 2010, 44, 2263–2270. [Google Scholar] [CrossRef]
- Minet, L.; Stokes, J.; Scott, J.; Xu, J.; Weichenthal, S.; Hatzopoulou, M. Should traffic-related air pollution and noise be considered when designing urban bicycle networks? Transp. Res. Part D Transp. Environ. 2018, 65, 736–749. [Google Scholar] [CrossRef]
- Lee, K.; Sener, I.N. Understanding Potential Exposure of Bicyclists on Roadways to Traffic-Related Air Pollution: Findings from El Paso, Texas, Using Strava Metro Data. Int. J. Environ. Res. Public Health 2019, 16, 371. [Google Scholar] [CrossRef]
- Tribby, C.P.; Tharp, D.S. Examining urban and rural bicycling in the United States: Early findings from the 2017 National Household Travel Survey. J. Transp. Health 2019, 13, 143–149. [Google Scholar] [CrossRef]
- Poppe, R. A survey on vision-based human action recognition. Image Vis. Comput. 2010, 28, 976–990. [Google Scholar] [CrossRef]
- Lara, O.D.; Labrador, M.A. A Survey on Human Activity Recognition using Wearable Sensors. IEEE Commun. Surv. Tutor. 2013, 15, 1192–1209. [Google Scholar] [CrossRef]
- Parkka, J.; Ermes, M.; Korpipaa, P.; Mantyjarvi, J.; Peltola, J.; Korhonen, I. Activity Classification Using Realistic Data From Wearable Sensors. IEEE Trans. Inf. Technol. Biomed. 2006, 10, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Bao, L.; Intille, S.S. Activity Recognition from User-Annotated Acceleration Data. In Pervasive Computing; Ferscha, A., Mattern, F., Eds.; Springer Berlin Heidelberg: Berlin, Germany, 2004; pp. 1–17. [Google Scholar]
- Riboni, D.; Bettini, C. COSAR: Hybrid Reasoning for Context-aware Activity Recognition. Pers. Ubiquitous Comput. 2011, 15, 271–289. [Google Scholar] [CrossRef]
- Yang, J. Toward Physical Activity Diary: Motion Recognition Using Simple Acceleration Features with Mobile Phones. In Proceedings of the 1st International Workshop on Interactive Multimedia for Consumer Electronics, Beijing, China, 23 October 2009; pp. 1–10. [Google Scholar]
- Jordao, A.; Nazare Jr, A.C.; Sena, J.; Schwartz, W.R. Human activity recognition based on wearable sensor data: A standardization of the state-of-the-art. arXiv preprint 2018, arXiv:1806.05226v3. [Google Scholar]
- Dehghani, A.; Glatard, T.; Shihab, E. Subject Cross Validation in Human Activity Recognition. arXiv e-print 2009, arXiv:1904.02666. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. The Elements of Statistical Learning; Springer series in statistics: New York, NY, USA, 2001; Volume 1. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 1189–1232. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Polley, E.C.; Rose, S.; Van der Laan, M.J. Super learning. In Targeted learning; Springer: New York, NY, USA, 2011; pp. 43–66. [Google Scholar]
- Van der Laan, M.J.; Polley, E.C.; Hubbard, A.E. Super learner. Stat. Appl. Genet. Mol. Biol. 2007, 6. [Google Scholar] [CrossRef]
- Mannini, A.; Intille, S.S.; Rosenberger, M.; Sabatini, A.M.; Haskell, W. Activity recognition using a single accelerometer placed at the wrist or ankle. Med. Sci. Sports Exerc. 2013, 45, 2193. [Google Scholar] [CrossRef] [PubMed]
- Ramasamy Ramamurthy, S.; Roy, N. Recent trends in machine learning for human activity recognition—A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1254. [Google Scholar] [CrossRef]
- Janidarmian, M.; Roshan Fekr, A.; Radecka, K.; Zilic, Z. A comprehensive analysis on wearable acceleration sensors in human activity recognition. Sensors 2017, 17, 529. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, Y.; Hao, S.; Peng, X.; Hu, L. Deep learning for sensor-based activity recognition: A survey. Pattern Recognit. Lett. 2019, 119, 3–11. [Google Scholar] [CrossRef]
- Cook, D.; Feuz, K.D.; Krishnan, N.C. Transfer learning for activity recognition: A survey. Knowl. Inf. Syst. 2013, 36, 537–556. [Google Scholar] [CrossRef] [PubMed]
- Defazio, A.; Bach, F.; Lacoste-Julien, S. SAGA: A fast incremental gradient method with support for non-strongly convex composite objectives. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 16 December 2014; pp. 1646–1654. [Google Scholar]
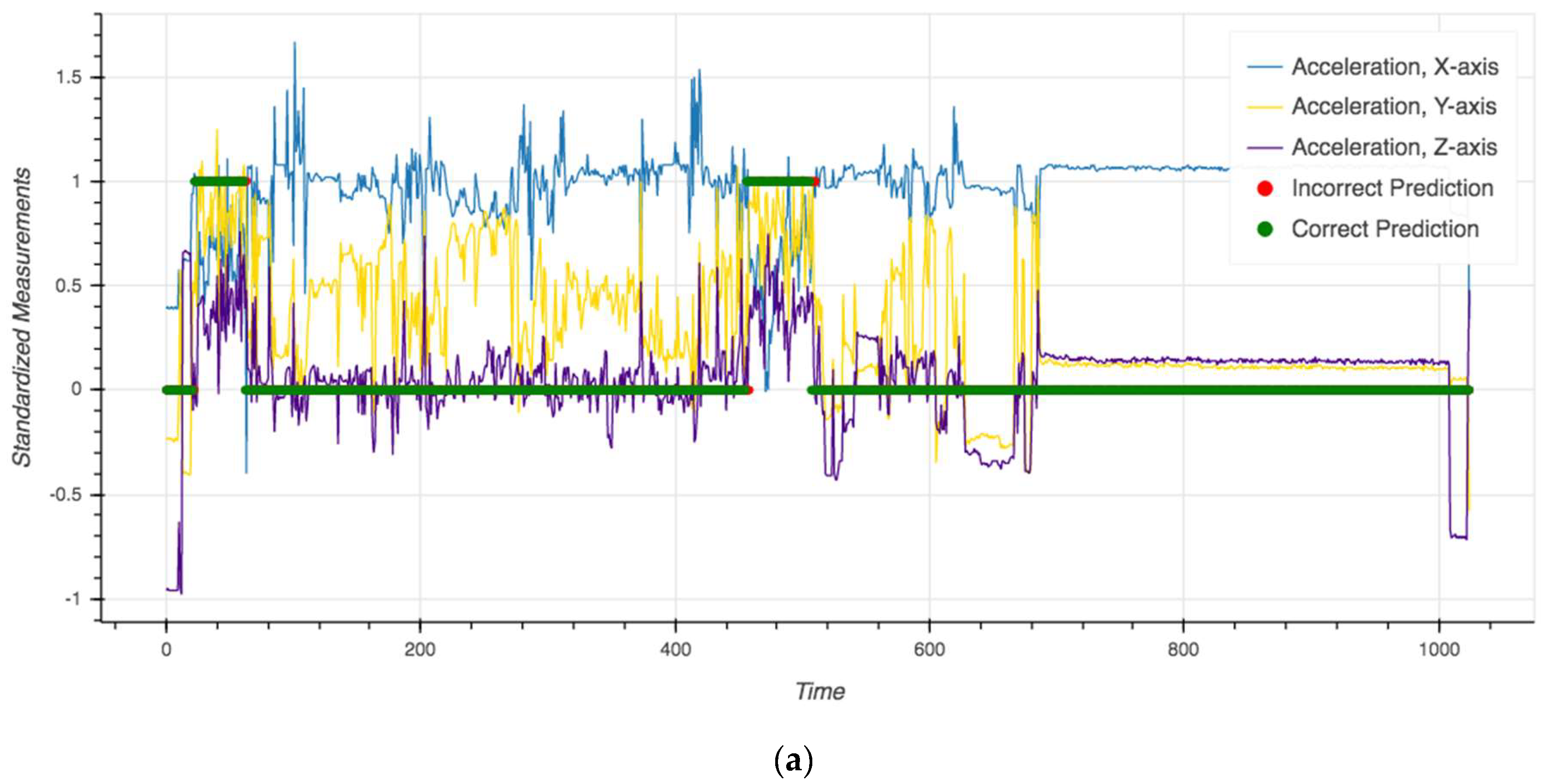
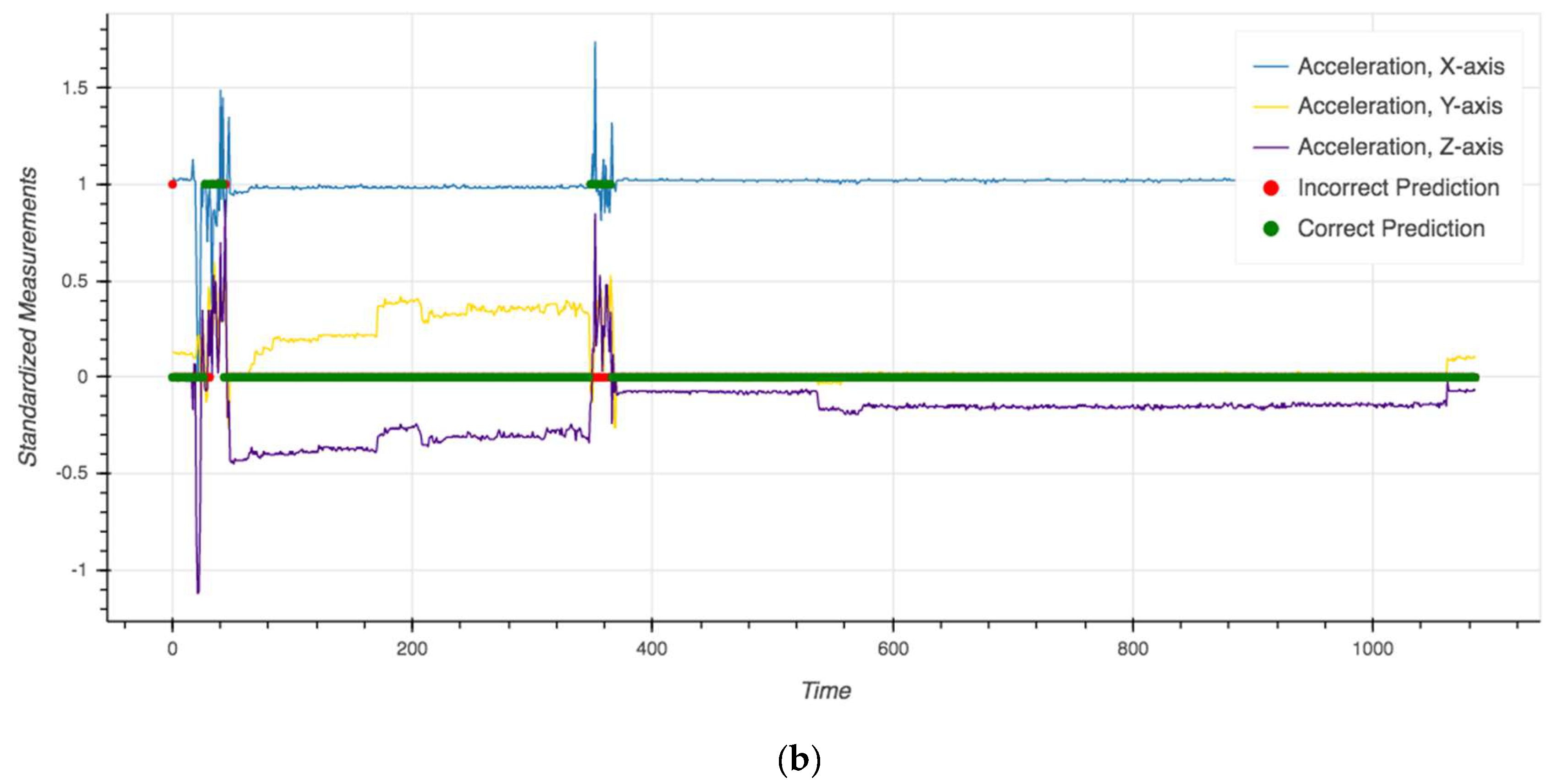

| Statistics Per Session | Mean | Median | Min | Max |
|---|---|---|---|---|
| Records | 992 | 989 | 916 | 1087 |
| Percent Biking | 7.4% | 6.7% | 3.1% | 11.8% |
| X-axis acceleration (m2/s) | 0.84 | 0.95 | –0.95 | 2.26 |
| Y-axis acceleration (m2/s) | 0.06 | 0.02 | –1.81 | 1.33 |
| Z-axis acceleration (m2/s) | 0.02 | 0.03 | –1.37 | 1.82 |
| Temperature (C) | 24.8 | 24.4 | 9.0 | 33.5 |
| Relative Humidity (%) | 50.0 | 50.2 | 17.9 | 94.5 |
| PM2.5 (µg/m3) | 22.4 | 3.0 | 0.0 | 1640.0 |
| Model | F1 | Precision | Recall | |||
|---|---|---|---|---|---|---|
| Raw | Weighted | Raw | Weighted | Raw | Weighted | |
| Mode Smoothed | 0.832 | 0.979 | 0.884 | 0.980 | 0.801 | 0.980 |
| (0.117) | (0.011) | (0.063) | (0.011) | (0.166) | (0.010) | |
| Stacked Ensemble | 0.767 | 0.970 | 0.791 | 0.971 | 0.767 | 0.970 |
| (0.115) | (0.012) | (0.115) | (0.011) | (0.115) | (0.012) | |
| Gradient Boosted Trees | 0.746 | 0.969 | 0.810 | 0.970 | 0.714 | 0.970 |
| (0.151) | (0.011) | (0.103) | (0.010) | (0.193) | (0.010) | |
| K-Nearest Neighbors | 0.744 | 0.965 | 0.780 | 0.967 | 0.732 | 0.965 |
| (0.115) | (0.017) | (0.137) | (0.015) | (0.138) | (0.018) | |
| Logistic Regression | 0.656 | 0.936 | 0.542 | 0.961 | 0.909 | 0.923 |
| (0.141) | (0.038) | (0.182) | (0.015) | (0.074) | (0.051) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chew, R.; Thornburg, J.; Jack, D.; Smith, C.; Yang, Q.; Chillrud, S. Identification of Bicycling Periods Using the MicroPEM Personal Exposure Monitor. Sensors 2019, 19, 4613. https://doi.org/10.3390/s19214613
Chew R, Thornburg J, Jack D, Smith C, Yang Q, Chillrud S. Identification of Bicycling Periods Using the MicroPEM Personal Exposure Monitor. Sensors. 2019; 19(21):4613. https://doi.org/10.3390/s19214613
Chicago/Turabian StyleChew, Robert, Jonathan Thornburg, Darby Jack, Cara Smith, Qiang Yang, and Steven Chillrud. 2019. "Identification of Bicycling Periods Using the MicroPEM Personal Exposure Monitor" Sensors 19, no. 21: 4613. https://doi.org/10.3390/s19214613
APA StyleChew, R., Thornburg, J., Jack, D., Smith, C., Yang, Q., & Chillrud, S. (2019). Identification of Bicycling Periods Using the MicroPEM Personal Exposure Monitor. Sensors, 19(21), 4613. https://doi.org/10.3390/s19214613





