Fault Detection and Diagnosis Using Combined Autoencoder and Long Short-Term Memory Network
Abstract
1. Introduction
2. Related Works
3. Combined Autoencoder and LSTM Network
3.1. Autoencoder-Based Anomaly Detection
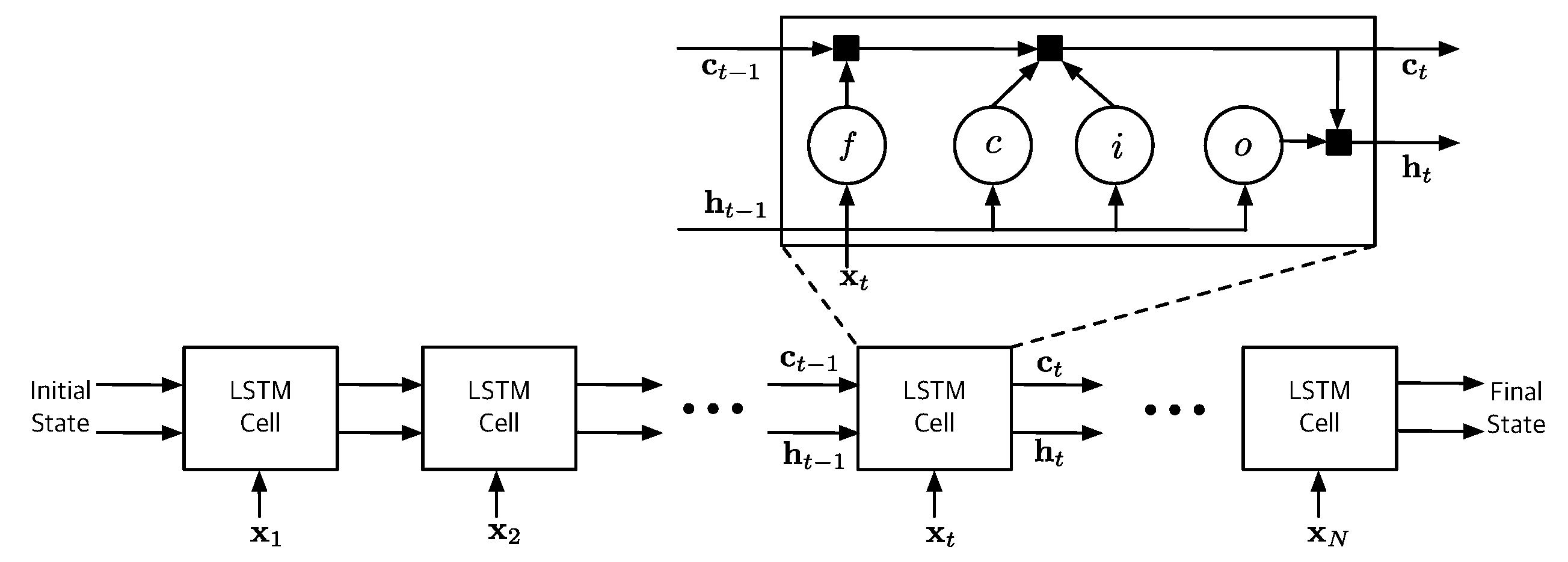
3.2. LSTM-Based Fault Diagnosis
4. Evaluation Setup
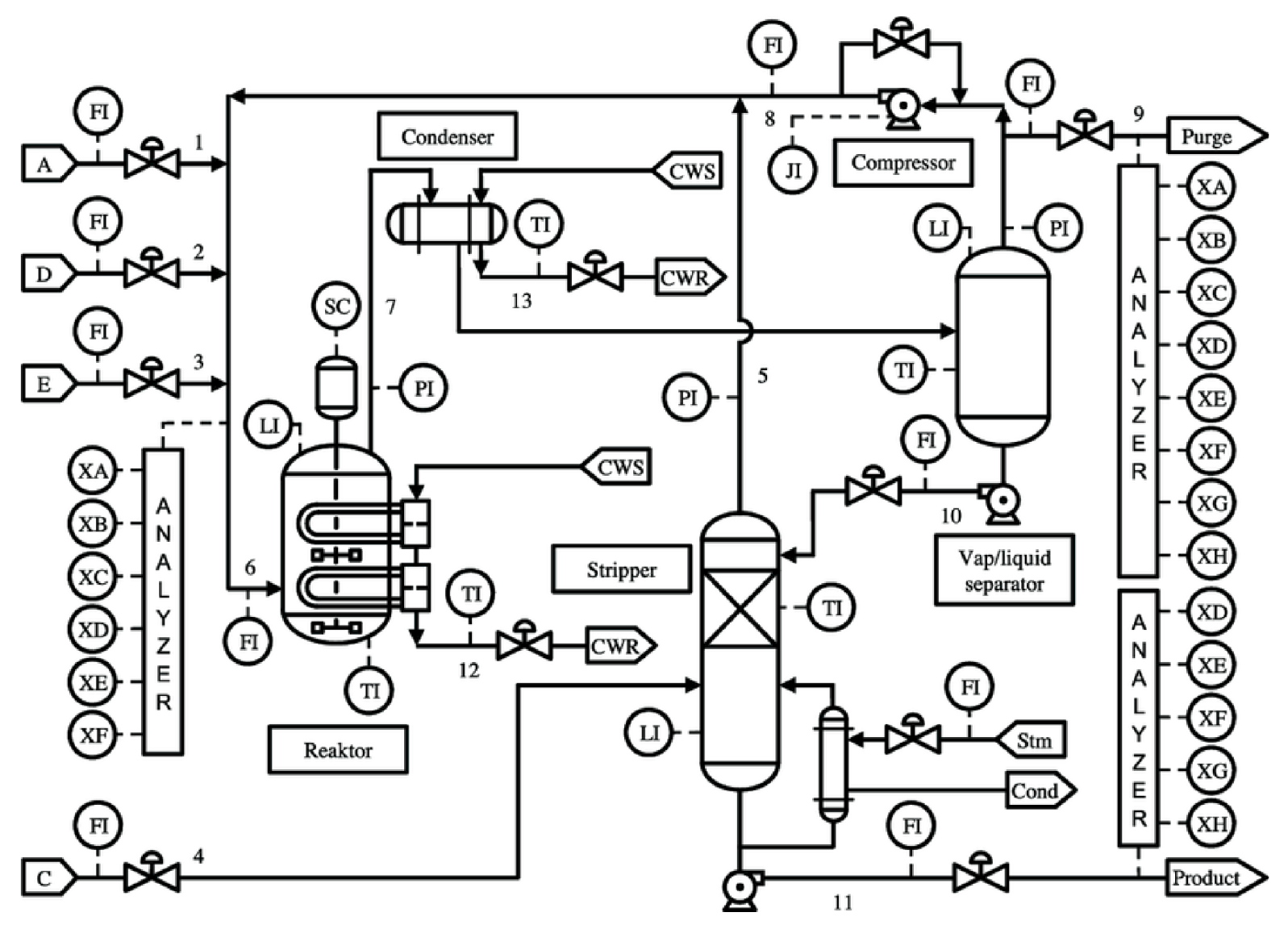
4.1. Tennessee Eastman Challenge Problem
4.2. DCNN
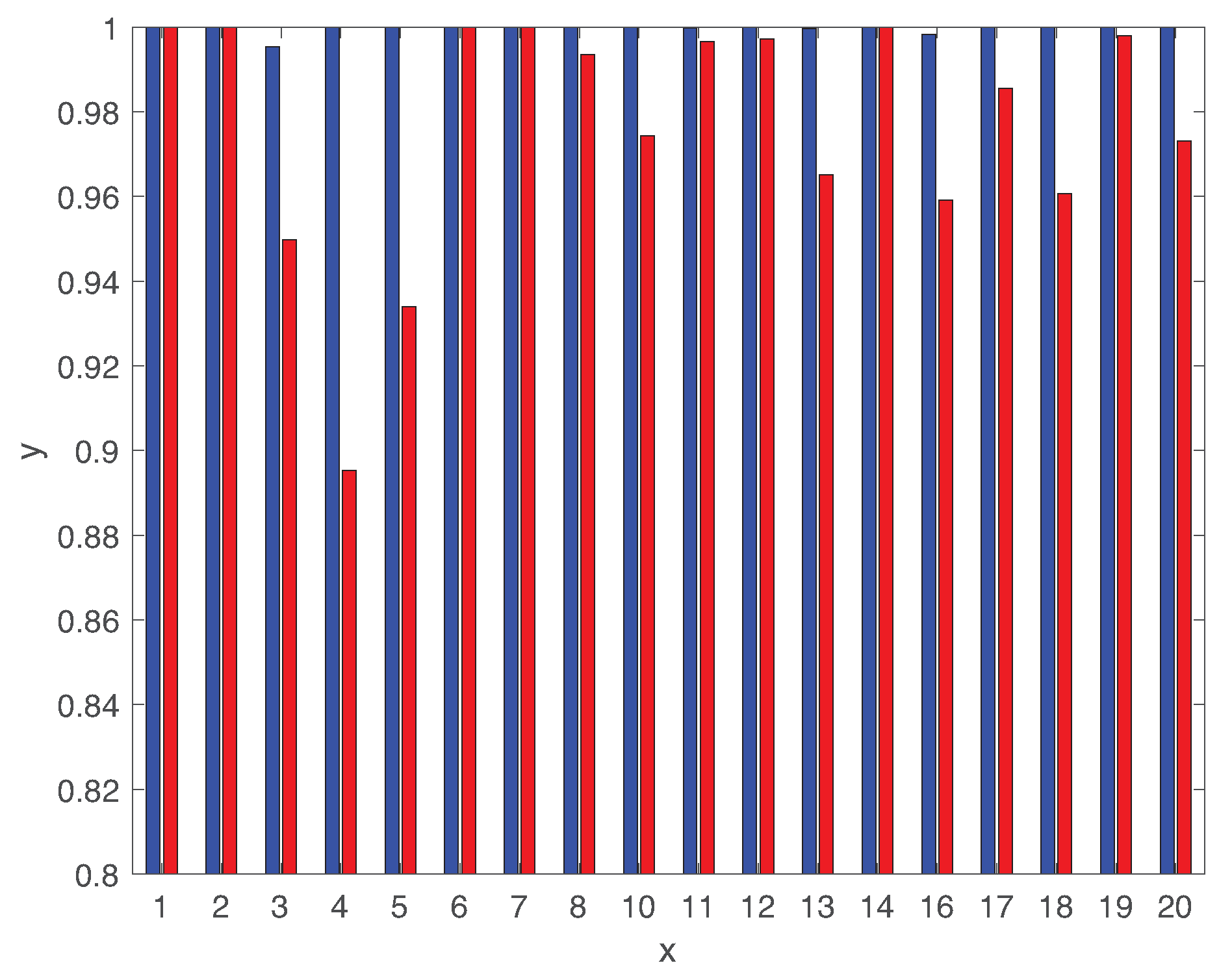
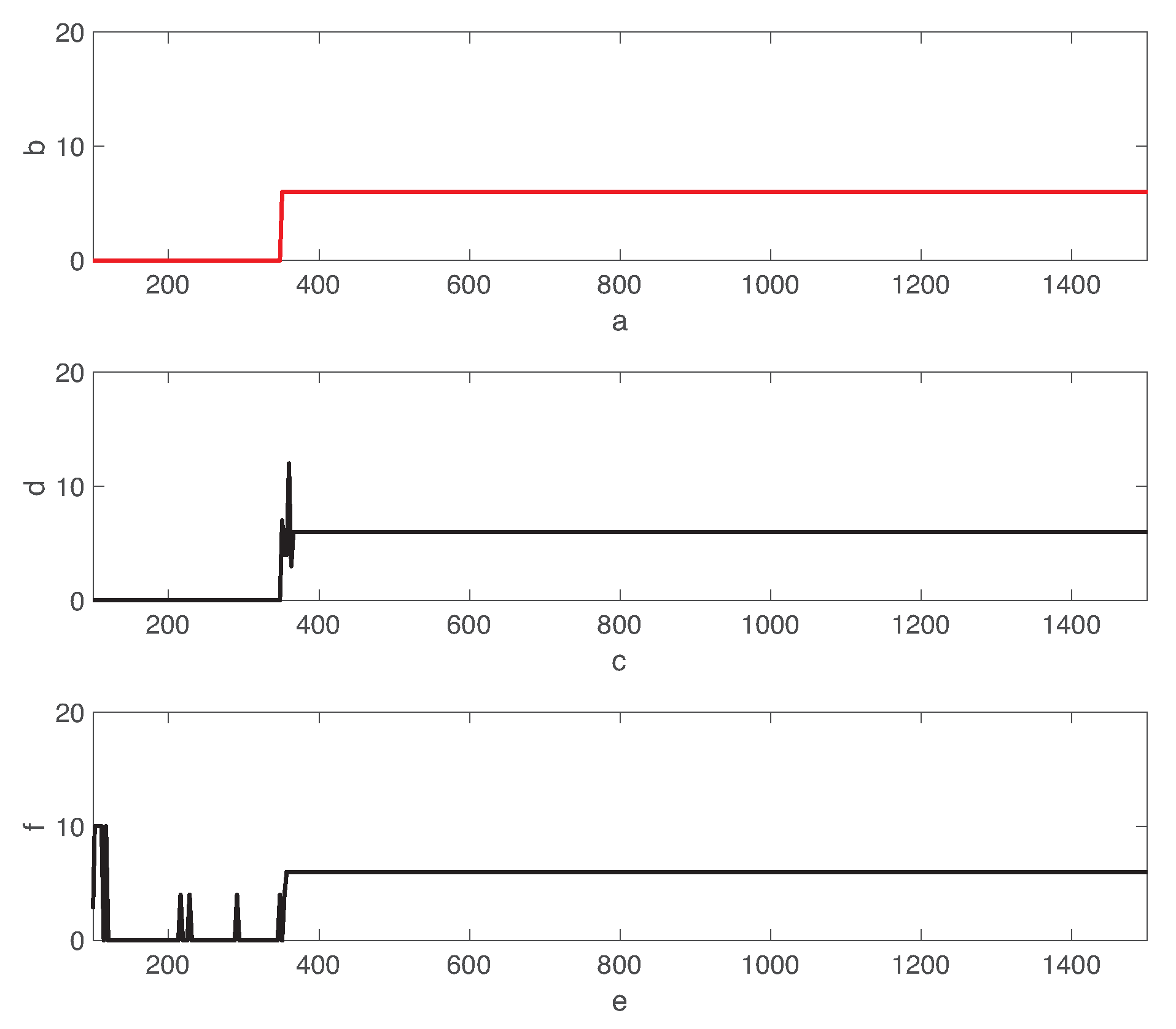
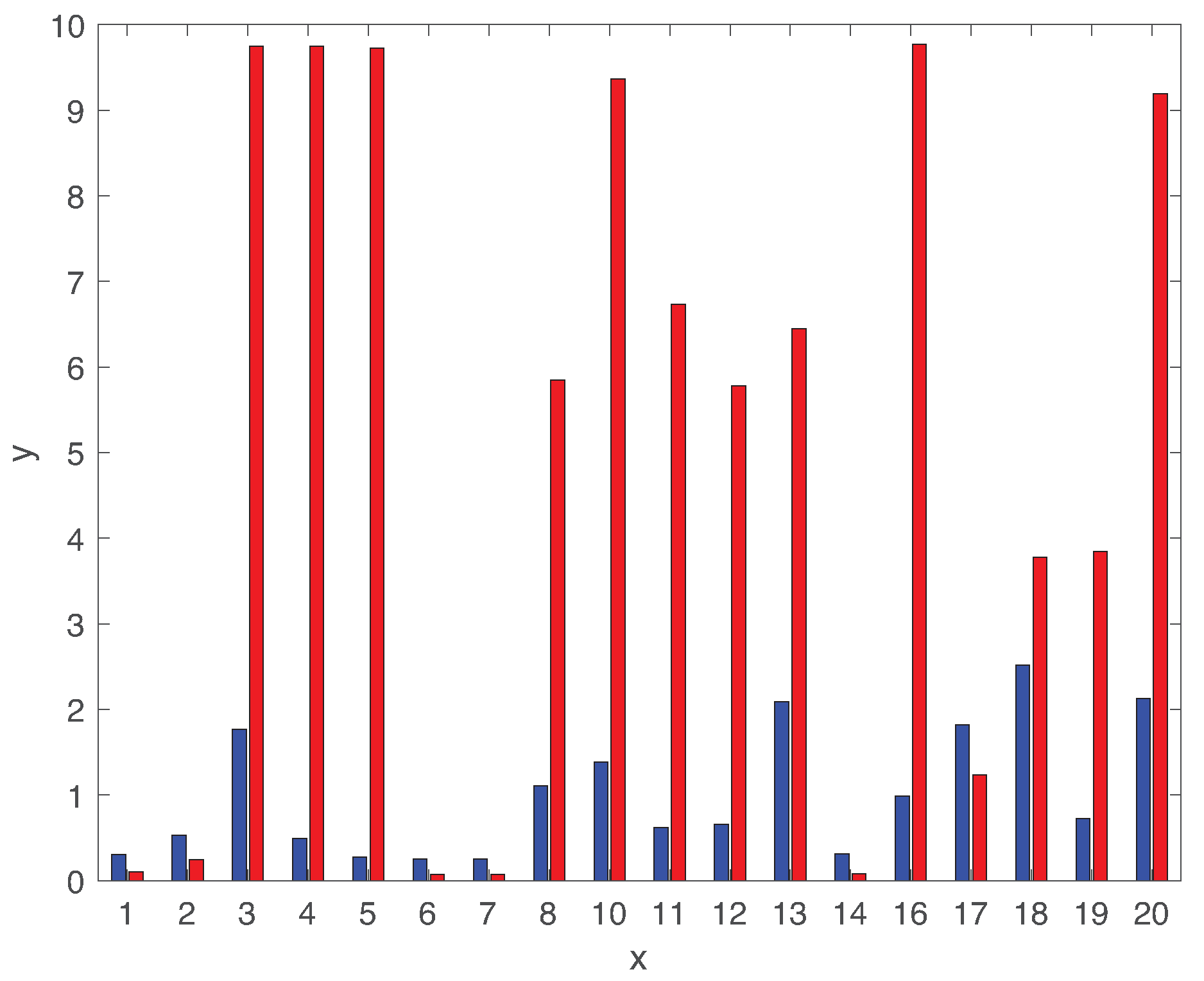
5. Performance Evaluation
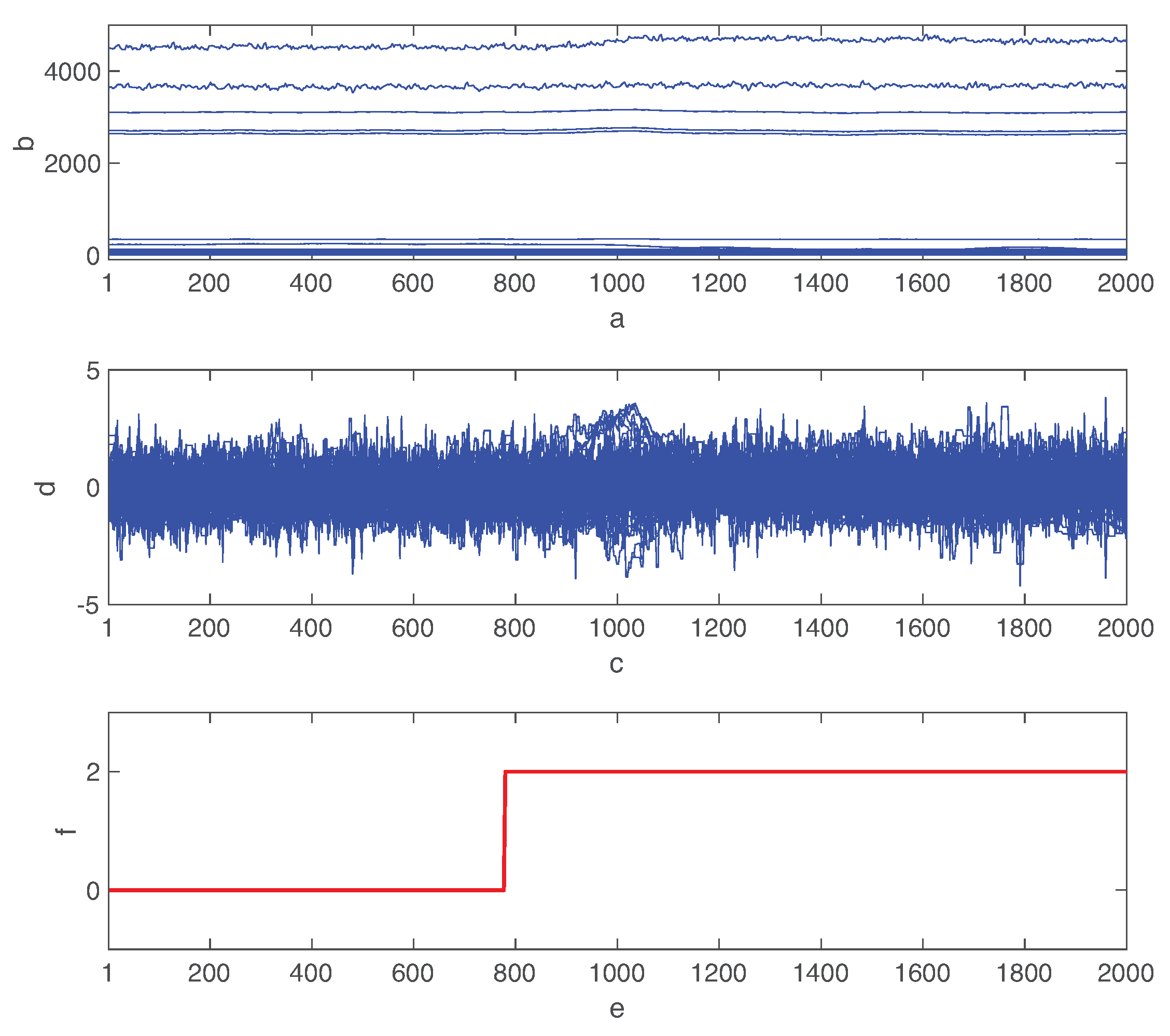
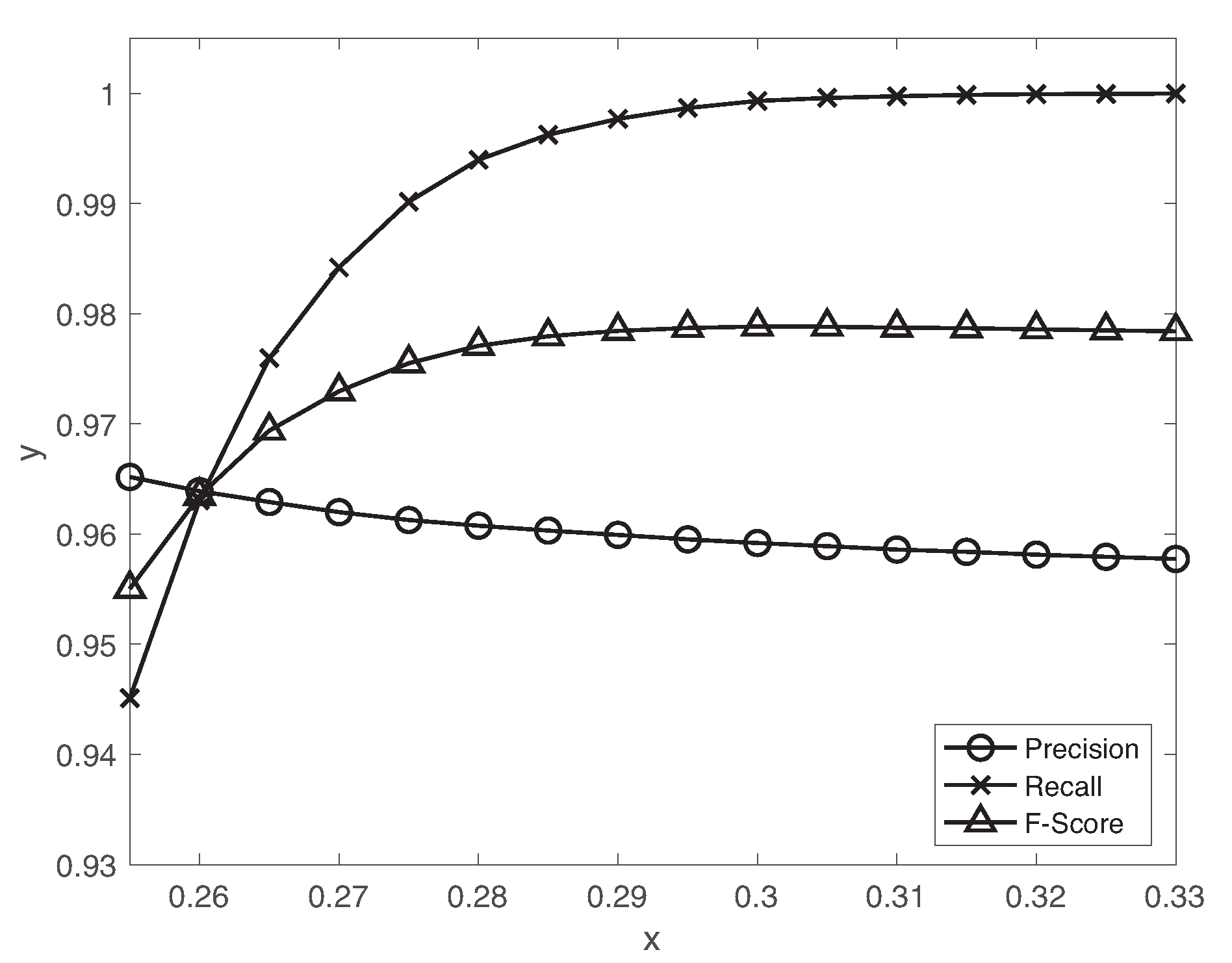
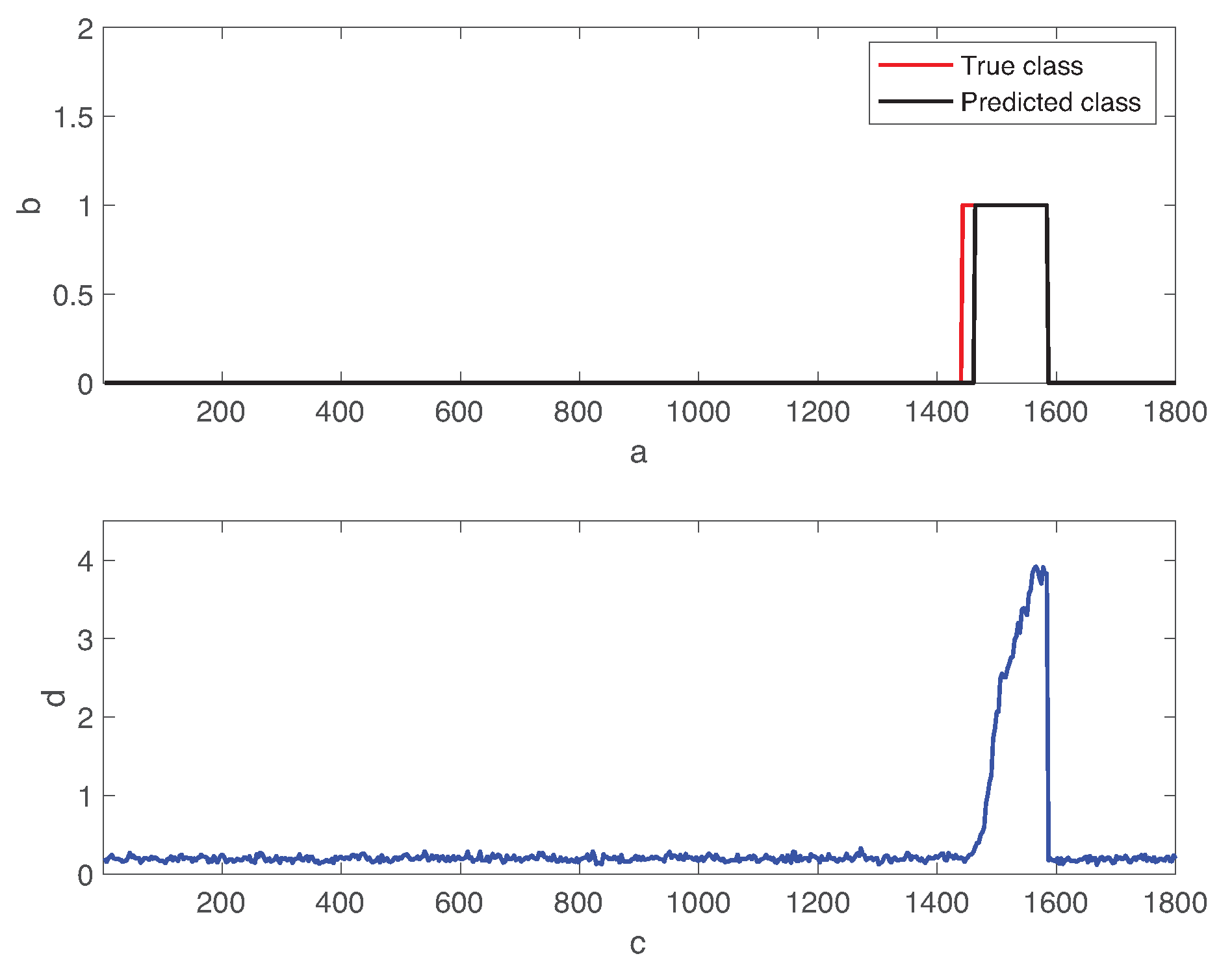
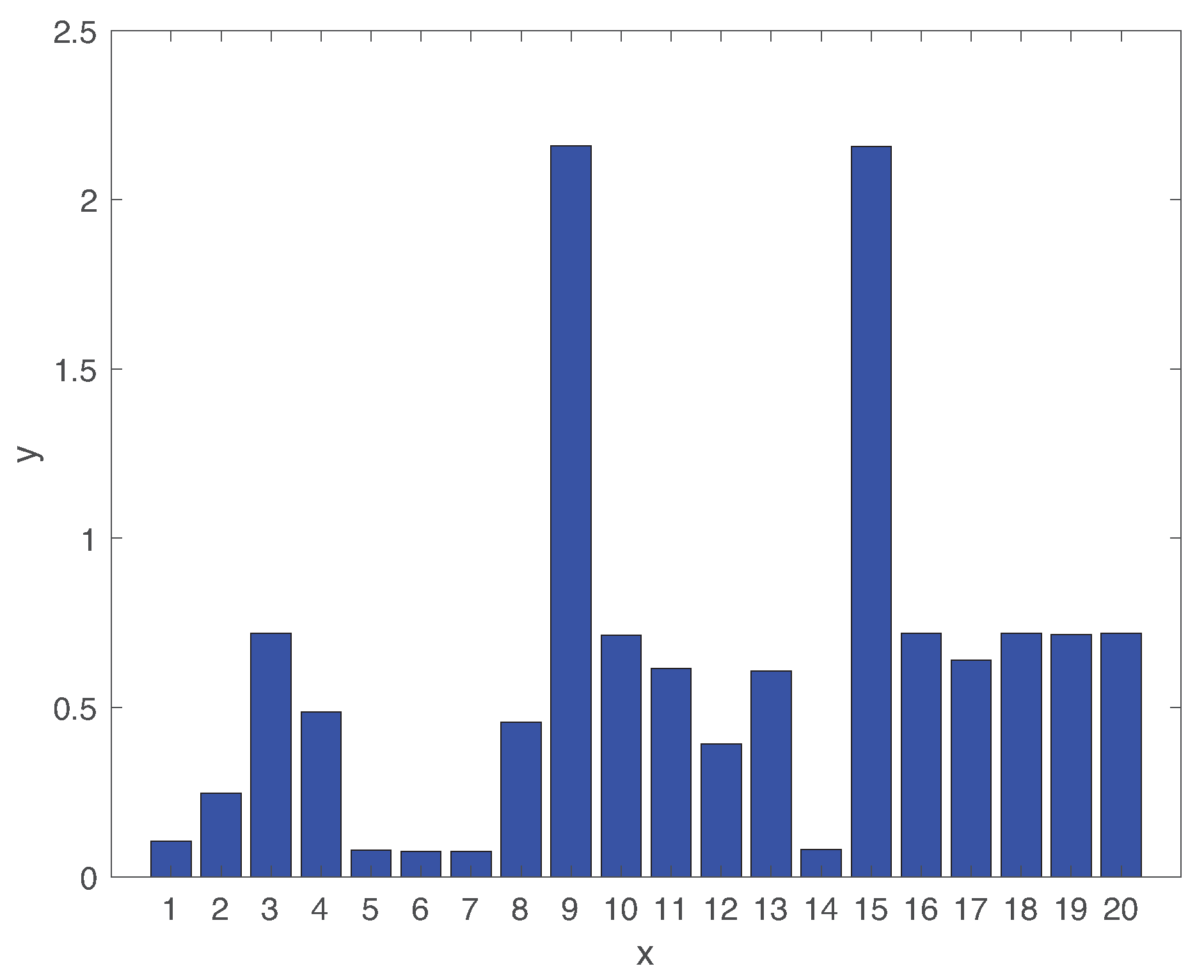
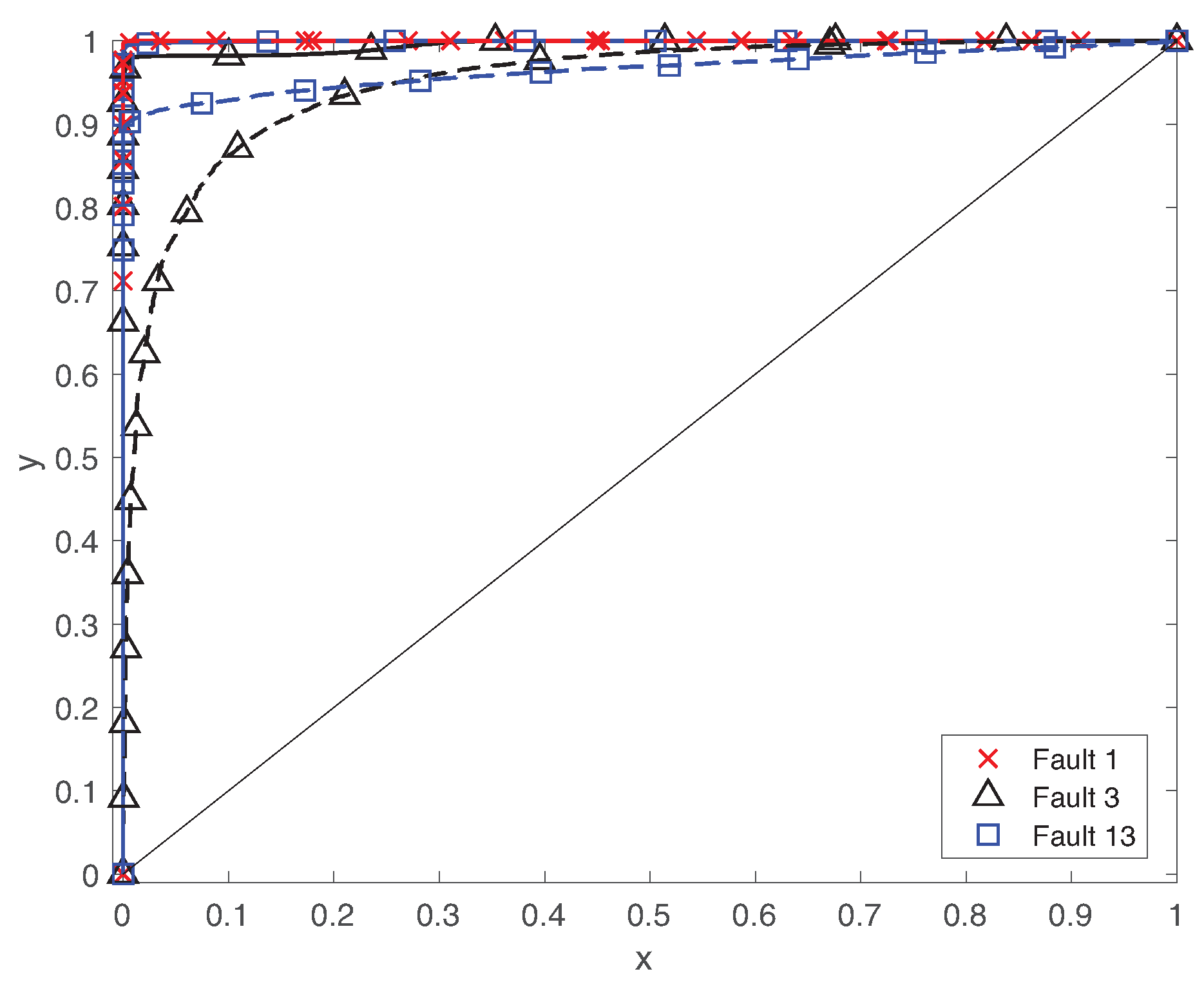
5.1. Fault Detection
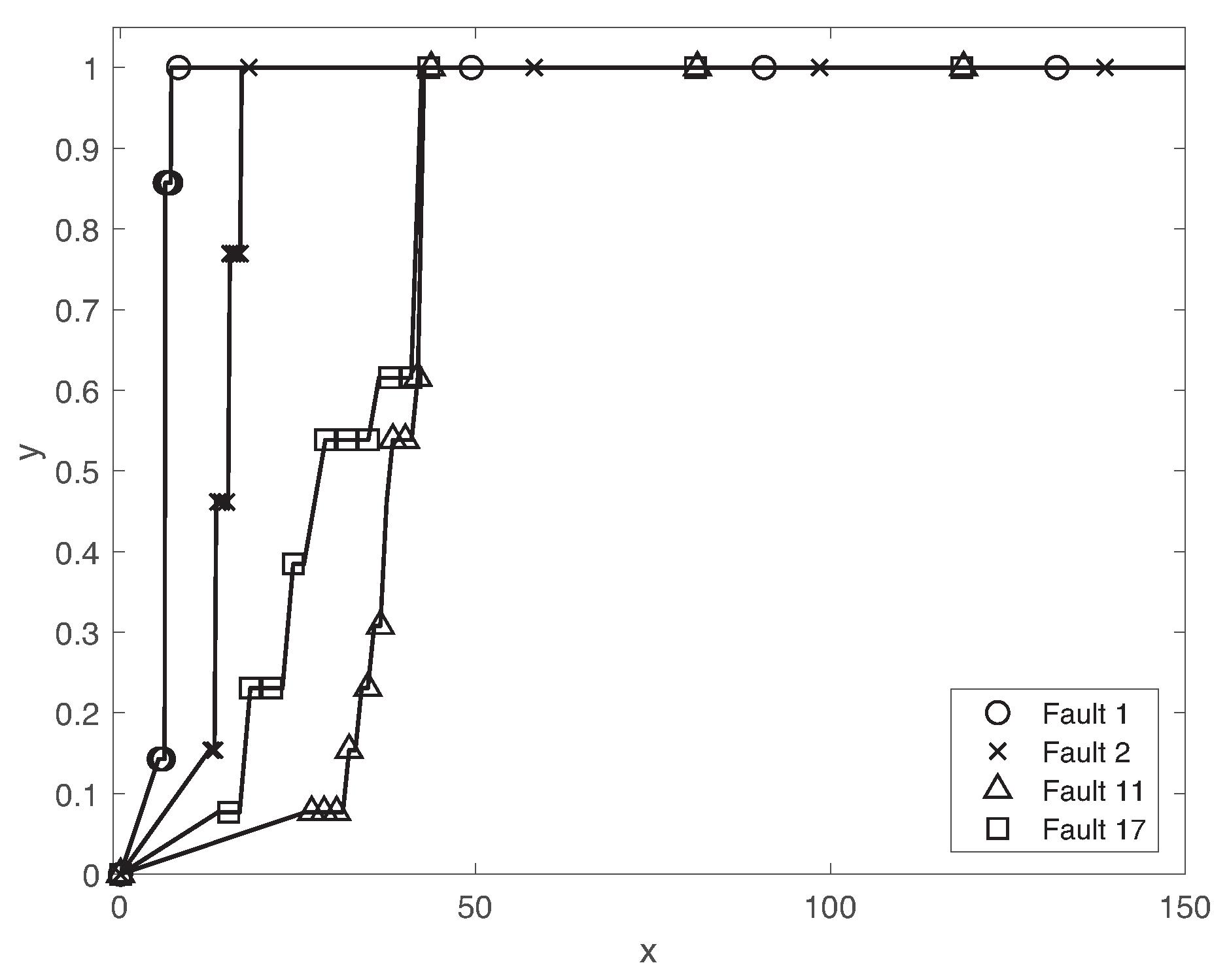
5.2. Fault Diagnosis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Khalastchi, E.; Kalech, M. On Fault Detection and Diagnosis in Robotic Systems. ACM Comput. Surv. 2018, 51, 1–24. [Google Scholar] [CrossRef]
- Patel, P.; Ali, M.I.; Sheth, A. From Raw Data to Smart Manufacturing: AI and Semantic Web of Things for Industry 4.0. IEEE Intell. Syst. 2018, 33, 79–86. [Google Scholar] [CrossRef]
- Park, P.; Ergen, S.C.; Fischione, C.; Lu, C.; Johansson, K.H. Wireless network design for control systems: A survey. IEEE Commun. Surv. Tutor. 2018, 20, 978–1013. [Google Scholar] [CrossRef]
- Dai, X.; Gao, Z. From Model, Signal to Knowledge: A Data-Driven Perspective of Fault Detection and Diagnosis. IEEE Trans. Ind. Inform. 2013, 9, 2226–2238. [Google Scholar] [CrossRef]
- Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Lim, M.H. Challenges and Opportunities of Deep Learning Models for Machinery Fault Detection and Diagnosis: A Review. IEEE Access 2019, 7, 122644–122662. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z.; Ding, S.X.; Huang, B. Data Mining and Analytics in the Process Industry: The Role of Machine Learning. IEEE Access 2017, 5, 20590–20616. [Google Scholar] [CrossRef]
- Hoffmann, J.B.; Heimes, P.; Senel, S. IoT Platforms for the Internet of Production. IEEE Internet Things J. 2019, 6, 4098–4105. [Google Scholar] [CrossRef]
- Park, P.; Marco, P.D.; Johansson, K.H. Cross-Layer Optimization for Industrial Control Applications Using Wireless Sensor and Actuator Mesh Networks. IEEE Trans. Ind. Electron. 2017, 64, 3250–3259. [Google Scholar] [CrossRef]
- Ranjan, C.; Reddy, M.; Mustonen, M.; Paynabar, K.; Pourak, K. Dataset: Rare Event Classification in Multivariate Time Series; Tech. Rep.; ProcessMiner Inc.: Atlanta, GA, USA, 2019. [Google Scholar]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part II: Fault Diagnosis With Knowledge-Based and Hybrid/Active Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Yin, S.; Ding, S.X.; Haghani, A.; Hao, H.; Zhang, P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process Control 2012, 22, 1567–1581. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X.; Chen, S. Modified kernel principal component analysis based on local structure analysis and its application to nonlinear process fault diagnosis. Chemom. Intell. Lab. Syst. 2013, 127, 195–209. [Google Scholar] [CrossRef]
- Gao, X.; Hou, J. An improved SVM integrated GS-PCA fault diagnosis approach of Tennessee Eastman process. Neurocomputing 2016, 174, 906–911. [Google Scholar] [CrossRef]
- Rad, M.A.A.; Yazdanpanah, M.J. Designing supervised local neural network classifiers based on EM clustering for fault diagnosis of Tennessee Eastman process. Chemom. Intell. Lab. Syst. 2015, 146, 149–157. [Google Scholar]
- Yin, S.; Zhu, X.; Kaynak, O. Improved PLS focused on key- performance-indicator-related fault diagnosis. IEEE Trans. Ind. Electron. 2015, 62, 1651–1658. [Google Scholar] [CrossRef]
- Hyvarinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Fan, J.; Wang, Y. Fault detection and diagnosis of non-linear non-Gaussian dynamic processes using kernel dynamic independent component analysis. Inf. Sci. 2014, 259, 369–379. [Google Scholar] [CrossRef]
- Lee, J.-M.; Yoo, C.; Lee, I.-B. Statistical process monitoring with independent component analysis. J. Process Control 2004, 14, 467–485. [Google Scholar] [CrossRef]
- Scholkopf, B.; Smola, A.; Muller, K. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Lee, J.-M.; Qin, S.J.; Lee, I.-B. Fault detection of non-linear processes using kernel independent component analysis. Can. J. Chem. Eng. 2007, 85, 526–536. [Google Scholar] [CrossRef]
- Chiang, L.H.; Kotanchek, M.E.; Kordon, A.K. Fault diagnosis based on Fisher discriminant analysis and support vector machines. Comput. Chem. Eng. 2004, 28, 1389–1401. [Google Scholar] [CrossRef]
- Jan, S.U.; Lee, Y.; Shin, J.; Koo, I. Sensor fault classification based on support vector machine and statistical time-domain features. IEEE Access 2017, 5, 8682–8690. [Google Scholar] [CrossRef]
- Guo, J.; Qi, L.; Li, Y. Fault detection of batch process using dynamic multi-way orthogonal locality preserving projections. J. Comput. Inf. Syst. 2015, 11, 577–586. [Google Scholar]
- Eslamloueyan, R. Designing a hierarchical neural network based on fuzzy clustering for fault diagnosis of the Tennessee Eastman process. Appl. Soft Comput. 2011, 11, 1407–1415. [Google Scholar] [CrossRef]
- Lau, C.; Ghosh, K.; Hussain, M.; Hassan, C.C. Fault diagnosis of Tennessee Eastman process with multi-scale PCA and ANFIS. Chemom. Intell. Lab. Syst. 2013, 120, 1–14. [Google Scholar] [CrossRef]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Xie, D.; Bai, L. A hierarchical deep neural network for fault diagnosis on Tennessee-Eastman process. In Proceedings of the IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 745–748. [Google Scholar]
- Funahashi, K.; Nakamura, Y. Approximation of dynamical systems by continuous time recurrent neural networks. Neural Netw. 1993, 6, 801–806. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Greff, K.; Srivastava, R.K.; Koutnk, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef]
- Yuan, M.; Wu, Y.; Lin, L. Fault diagnosis and remaining useful life estimation of aero engine using LSTM neural network. In Proceedings of the IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 135–140. [Google Scholar]
- De Bruin, T.; Verbert, K.; Babuska, R. Railway track circuit fault diagnosis using recurrent neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 523–533. [Google Scholar] [CrossRef] [PubMed]
- Le, Q.V.; Ranzato, M.; Monga, R.; Devin, M.; Chen, K.; Corrado, G.S.; Dean, J.; Ng, A.Y. Building high-level features using large scale unsupervised learning. In Proceedings of the International Conference on International Conference on Machine Learning, Edinburgh, Scotland, UK, 26 June–1 July 2012; pp. 507–514. [Google Scholar]
- Rifai, S.; Vincent, P.; Muller, X.; Glorot, X.; Bengio, Y. Contractive auto-encoders: Explicit invariance during feature extraction. In Proceedings of the International Conference on International Conference on Machine Learning, Washington, DC, USA, 28 June–2 July 2011; pp. 833–840. [Google Scholar]
- Zhao, H.; Sun, S.; Jin, B. Sequential fault diagnosis based on LSTM neural network. IEEE Access 2018, 6, 12929–12939. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Liu, M.; Bao, Z. Data-based line trip fault prediction in power systems using LSTM networks and SVM. IEEE Access 2018, 6, 7675–7686. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.-A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Krishnapuram, B.; Carin, L.; Figueiredo, M.A.T.; Hartemink, A.J. Sparse multinomial logistic regression: Fast algorithms and generalization bounds. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 957–968. [Google Scholar] [CrossRef]
- Bengio, Y. Practical Recommendations for Gradient-Based Training of Deep Architectures; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Downs, J.; Vogel, E. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Lawrence Ricker, N. Tennessee Eastman Challenge Archive. University of Washington. 2015. Available online: https://depts.washington.edu/control/LARRY/TE/download.html (accessed on 20 October 2019).
- Rieth, C.A.; Amsel, B.D.; Tran, R.; Cook, M.B. Additional Tennessee Eastman Process Simulation Data for Anomaly Detection Evaluation. Harvard Dataverse. 2017. Available online: https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/6C3JR1 (accessed on 20 October 2019).
- Park, B.; Nah, J.; Choi, J.Y.; Yoon, I.J.; Park, P. Transmission Scheduling Schemes of Industrial Wireless Sensors for Heterogeneous Multiple Control Systems. Sensors 2018, 18, 4284. [Google Scholar] [CrossRef]
- Park, B.; Nah, J.; Choi, J.Y.; Yoon, I.J.; Park, P. Robust Wireless Sensor and Actuator Networks for Networked Control Systems. Sensors 2019, 19, 1535. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, J. A deep belief network based fault diagnosis model for complex chemical processes. Comput. Chem. Eng. 2017, 107, 395–407. [Google Scholar] [CrossRef]
- Russell, E.L.; Chiang, L.H.; Braatz, R.D. Data-Driven Methods for Fault Detection and Diagnosis in Chemical Processes; Springer: New York, NY, USA, 2000. [Google Scholar]
- Wu, H.; Zhao, J. Deep convolutional neural network model based chemical process fault diagnosis. Comput. Chem. Eng. 2018, 115, 185–197. [Google Scholar] [CrossRef]
- Russell, E.L.; Chiang, L.H.; Braatz, R.D. Fault detection in industrial processes using canonical variate analysis and dynamic principal component analysis. Chemom. Intell. Lab. Syst. 2000, 51, 81–93. [Google Scholar] [CrossRef]

| Fault Number | Description | Type |
|---|---|---|
| 1 | feed ratio, B composition constant (Stream 4) | Step |
| 2 | B composition, ratio constant (Stream 4) | Step |
| 3 | D feed temperature (Stream 2) | Step |
| 4 | Reactor cooling water inlet temperature | Step |
| 5 | Condenser cooling water inlet temperature | Step |
| 6 | A feed loss (Stream 1) | Step |
| 7 | C header pressure loss-reduced availablity (Stream 4) | Step |
| 8 | A, B, C feed composition (Stream 4) | Random variation |
| 9 | D feed temperature (Stream 2) | Random variation |
| 10 | C feed temperature (Stream 4) | Random variation |
| 11 | Reactor cooling water inlet temperature | Random variation |
| 12 | Condenser cooling water inlet temperature | Random variation |
| 13 | Reaction kinetics | Slow drift |
| 14 | Reactor cooling water valve | Sticking |
| 15 | Condenser cooling water valve | Sticking |
| 16 | Unknown | Unknown |
| 17 | Unknown | Unknown |
| 18 | Unknown | Unknown |
| 19 | Unknown | Unknown |
| 20 | Unknown | Unknown |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, P.; Marco, P.D.; Shin, H.; Bang, J. Fault Detection and Diagnosis Using Combined Autoencoder and Long Short-Term Memory Network. Sensors 2019, 19, 4612. https://doi.org/10.3390/s19214612
Park P, Marco PD, Shin H, Bang J. Fault Detection and Diagnosis Using Combined Autoencoder and Long Short-Term Memory Network. Sensors. 2019; 19(21):4612. https://doi.org/10.3390/s19214612
Chicago/Turabian StylePark, Pangun, Piergiuseppe Di Marco, Hyejeon Shin, and Junseong Bang. 2019. "Fault Detection and Diagnosis Using Combined Autoencoder and Long Short-Term Memory Network" Sensors 19, no. 21: 4612. https://doi.org/10.3390/s19214612
APA StylePark, P., Marco, P. D., Shin, H., & Bang, J. (2019). Fault Detection and Diagnosis Using Combined Autoencoder and Long Short-Term Memory Network. Sensors, 19(21), 4612. https://doi.org/10.3390/s19214612







