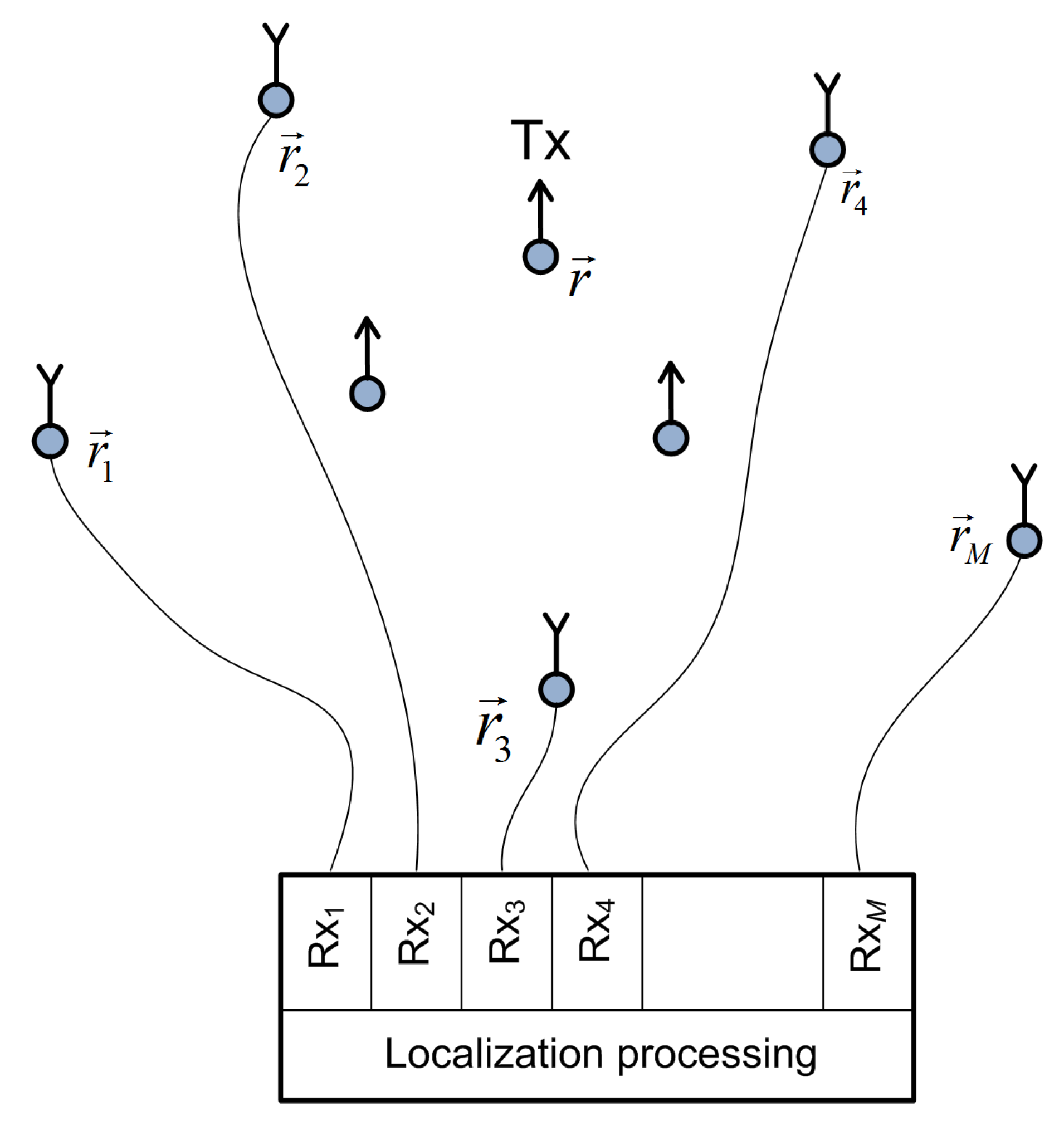
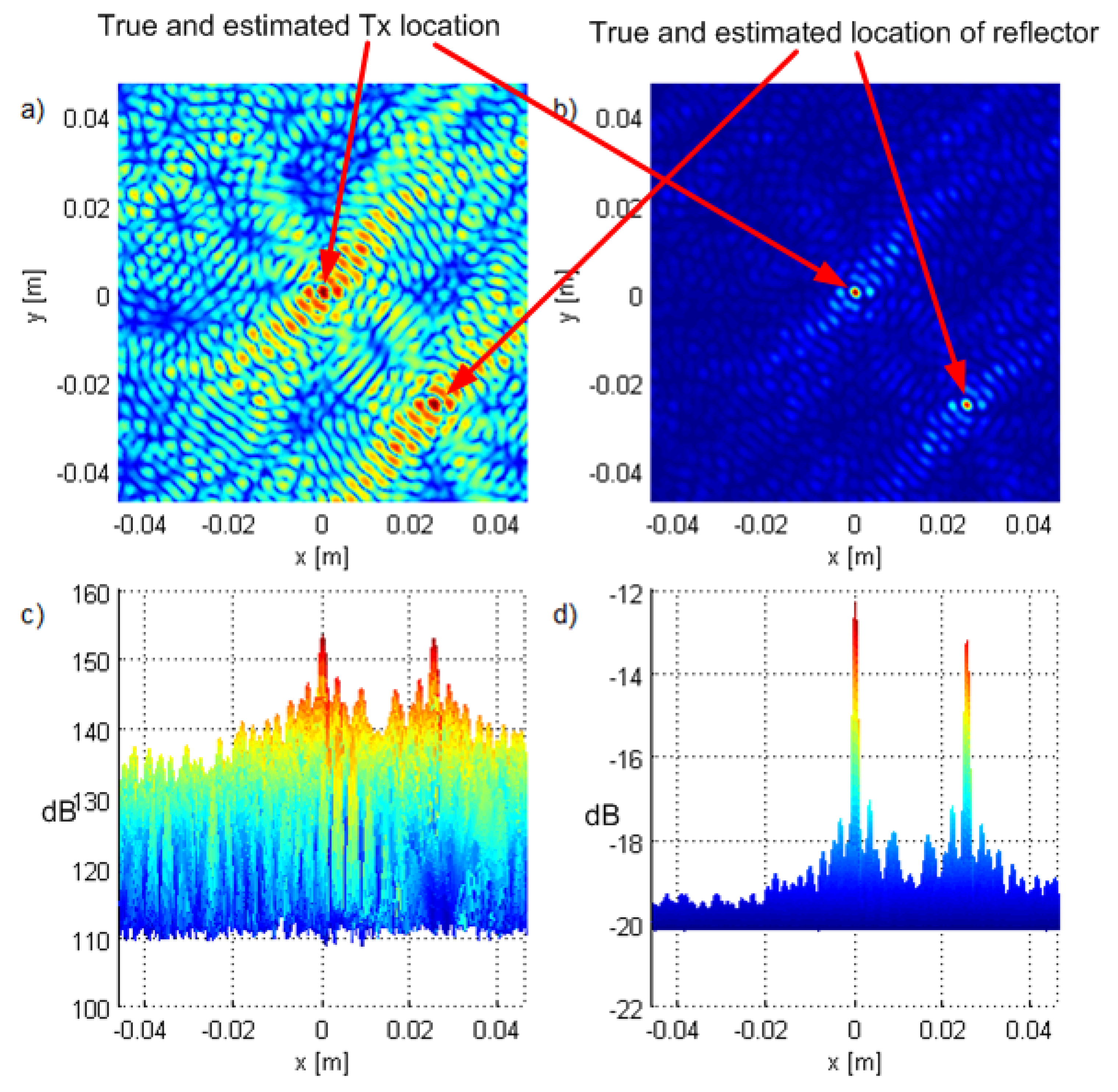
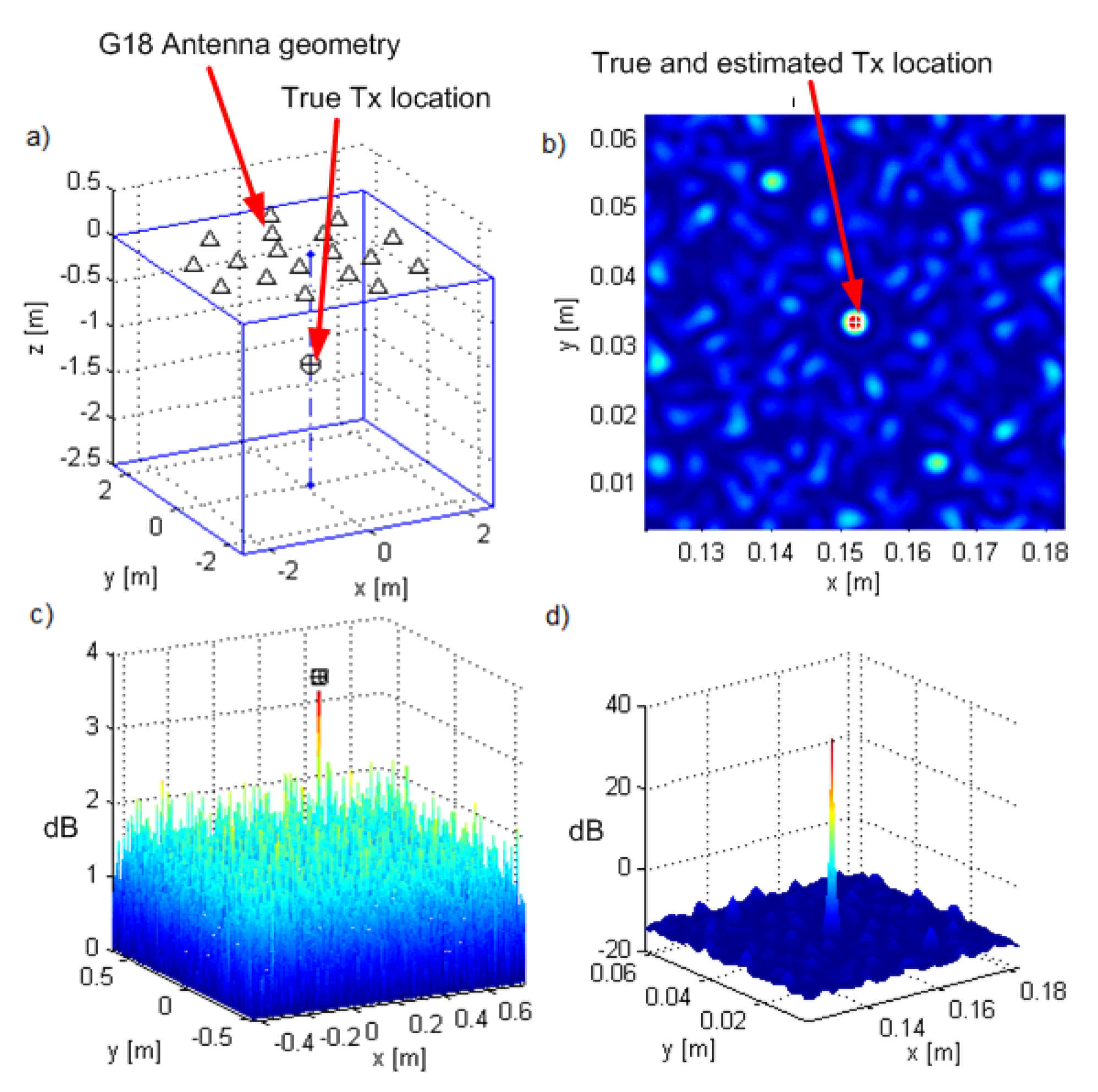
2.1. System Model
A distributed receiving antenna array that performs the localization has
M stationary elements/channels,
,
, where the antenna
is at a known position
; see
Figure 1. An active stationary transmitter,
, is at an unknown position
. All receive and transmit antennas are arbitrarily distributed in the 3D area of interest for which we assume spatial coherence of the LoS components across the entire distributed receiving array. The coherence can be established if the carrier phase difference between any two of the receiving antennas,
and
, can be obtained from the difference in the distances between them and the
. In mathematical terms, we have:
where
and
are the carrier phases of the
and
receiving antennas, respectively;
is the carrier frequency in Hz;
is the distance between
and
antennas,
,
, where
is the Euclidean norm;
is the speed of propagation (
). The distributed receiving antennas are connected to
M collocated receiving channels (front-ends) by calibrated cables (coaxial or fiber optic) for two reasons. The first is that fine time, frequency, and phase synchronization between the receiving channels is easier to achieve with collocated than with distributed front-ends. The second reason it that a centralized (specifically, direct or one-step) localization algorithm is a natural choice in this setup. All antennas act as “isotropic”, and their polarizations are aligned. Deviations from this in practice can be taken into account if there are additional attenuations and phase shifts and whose values are determined by the antenna design. The positions of the receiving antennas,
, are known in the sense that the antennas must be positioned with accuracy greater than the localization accuracy itself (with an error much smaller than the carrier wavelength). In the proposed system model, in practice, some antennas could be used for localization and the others for down-link communication with
.
2.2. Signal Model
The
transmits an RF signal (approximately) band-limited to
, where
B is the signal bandwidth in Hz, i.e., the complex form of the transmitted sequence/waveform is band-limited to
. The signal received at the
antenna,
, which is an attenuated and delayed version of the transmitted signal, after down-conversion and A/D conversion at the Nyquist rate
, is represented in a complex form
as:
where
n denotes discretized time normalized with
, i.e.,
;
is a real-valued attenuation factor for the LoS component;
,
are the normalized angular and natural carrier frequencies, respectively; the unknown value
models the fact that the
is not time synchronized with the
system (we always use the
time axis); the normalized propagation delays from the Tx to the antenna
are
, where the normalized propagation speed is
;
denotes all of the multipath components of the Tx signal except the LoS;
is the noise;
is an unknown complex-valued attenuation factor of the
component received by the
Rx channel, and
is an appropriate time delay; the acquired samples are
. Note that
,
, and
are fractional dimensionless values (the propagation time delays do not have to be integer multiples of the sampling interval) and that the sequence/waveform
is defined in the entire (continuous) range
since it has been transformed into a continuous waveform inside the
.
A signal model on a large antenna array can be frequency- and spatial-wideband, and the effects of these phenomena are discussed in detail in [
21]. The model has to be spatially wideband, if the propagation time across the aperture of the receiving array is greater than the inverse of the signal bandwidth,
. It models envelope shifts between the signals in the receiving channels in addition to carrier phase shifts (Strictly speaking, the signals have to be modeled as spatially wideband, if the approximation
does not hold for some
. The signal is spatially narrowband if
,
.). It is well known that, if the signal model is spatially wideband, then the localization methods have to be formulated in the spectral domain. Our signal model does not limit the signal bandwidth, so, in the context of [
21], our model is both frequency-wideband and spatial-wideband (Consider a numerical example in the mmWave band. If a signal with bandwidth
at a carrier frequency
is transmitted in a conference room equipped with an antenna array with an aperture of, say,
, then the propagation time across the array would be two sampling intervals. This shows the importance of wideband modeling.).
We scale the signal
in a preprocessing step by
to obtain
. We note that the signal-to-noise ratios (SNRs) and noise powers are considered known to the receivers. Thereby, the useful signals in all the receiving channels have the same power. Then, we have:
where
,
,
is a circular-complex zero-mean Gaussian random process (the noise) with variance
, independent across time samples and channels and independent of the useful signal
. The variabilities of the propagation attenuations are modeled by
, but the model considers that no information about the transmitter location is contained in the attenuations. We assumed this because, in practice, location estimation based on phases is more robust than estimation based on attenuations. Additionally, this reduces the number of dimensions of the search grid in the proposed algorithms. However, the algorithms use the SNRs for channel weighting. We define the SNR in channel
m as
.
We implement the time shifting of an RF signal by performing operations in the discrete Fourier transform (DFT) domain on its complex envelope, and therefore, strictly speaking, the signal has to be periodic with period N (the length of the observation interval). However, this does not have to be the case if the error created by a cyclic time shift, compared to the regular time shift, is negligible, which is important for the random sequence scenario.
If the
entry of a matrix
is
, define the
entry of
as
. Furthermore, for any vector
, let
be the diagonal matrix whose elements on the main diagonal are the elements of
. Then, the discrete-time matrix form of the signal model (
3) is:
where
,
, and
;
is a modified Fourier transform matrix;
is the delay-by-
operator, for any
;
and
denote transpose and conjugate transpose, respectively. In the known signal scenario, the conditions that the continuous waveform
is band-limited to
and that it is periodic with period
N imply that, given the samples in
, the signal in the entire (continuous) range
is
, where
. In the random signal scenario,
,
, is a circular-complex zero-mean Gaussian random process with variance
, so that
.
The goal is to estimate given the observations , .