1. Introduction
Pulse-compression technology is used to compress a long pulse chirp signal into a narrow pulse in time by convolution [
1]. Since the pulse is greatly compressed, the energy is concentrated in a narrow pulse, so the signal-to-noise ratio (SNR) and resolution are increased significantly. Therefore, this system only requires the transmitting peak power of mW magnitude.
It is worth noting that some pulse-compression systems are exactly the same as standard frequency modulated continuous wave (FMCW) scheme [
2,
3,
4], except that their signals are pulsed. Both of them obtain the target distance through beat frequency between local oscillator and echo light, so they can only utilize the overlap part in one sweep period. The farther the target is, the less overlap there will be. But our pulse-compression scheme has no such limitations, because it compresses a long pulse into a much narrower pulse whose peak position indicates the target distance through matched filter, namely local chirp to convolving with signal, therefore it is more advantageous for long-distance detection.
The compression ratio is equal to the time bandwidth product (TBP) of the chirp pulse. Some chirp pulse-compression lidar systems chirp laser through frequency modulation (FM) [
4,
5,
6,
7,
8,
9,
10,
11]. But each FM system has its own limitation: In ref [
4], the system uses the acoustic optical modulator (AOM) to chirp laser. Since its bandwidth is only 14 MHz, the TBP is small, so the resolution is limited; In refs [
5,
6], these systems use a ceramic piezoelectric transducer (PZT) to modulate the length of laser cavity to chirp laser. PZT has the drawback of instability and nonlinearity of modulation, so the ranging results will fluctuate and the SNR is small. In refs [
7,
8], these systems use dispersive element to chirp laser, which is only suitable for fiber sensing because free space will greatly deteriorate the linearity of the chirp optical signal; Other systems are either complicated or bulky [
9,
10,
11]. In contrast, AM system based on electro-optic modulator (EOM) has great agility, such as large bandwidth and fast response speed.
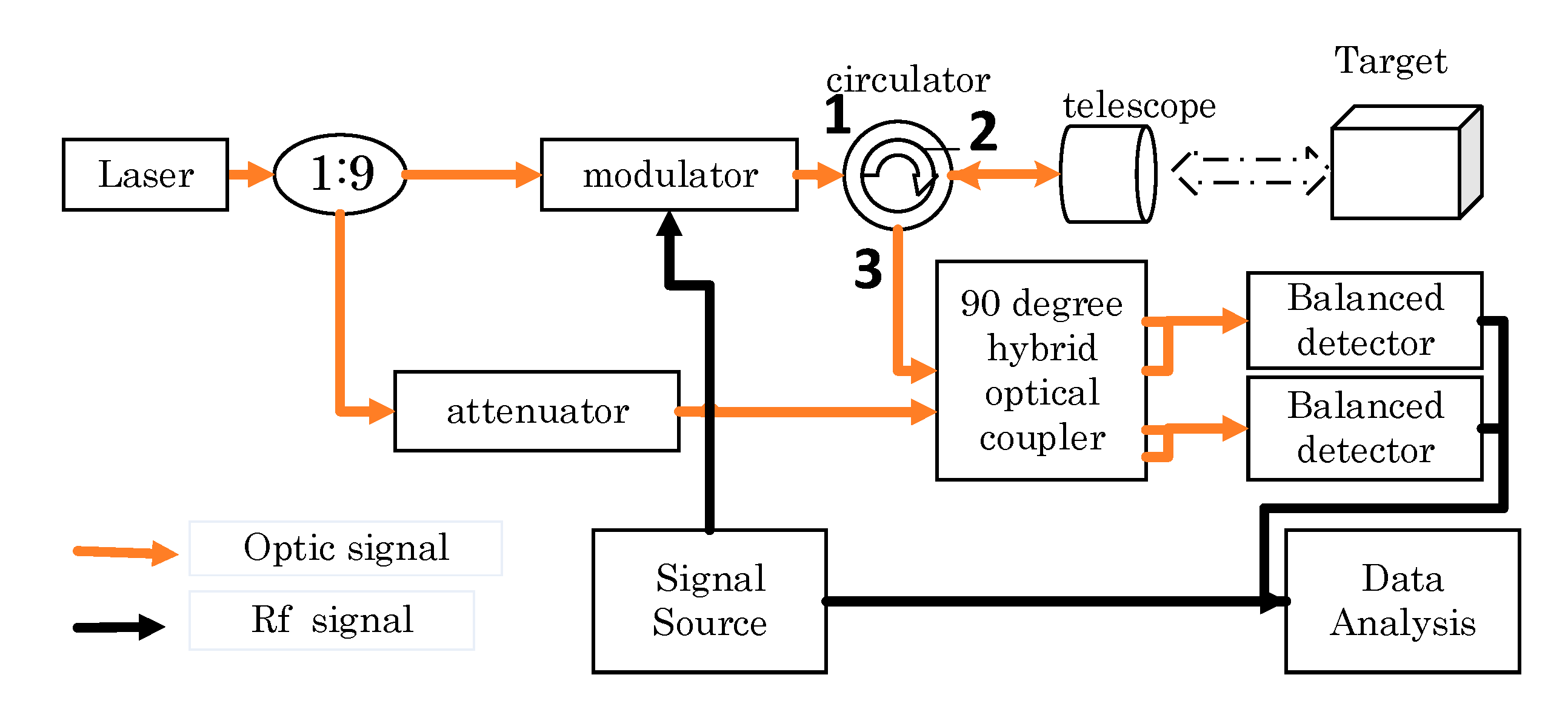
Our system based on EOM has a small size, simple structure, and is suitable for measuring long-distance hard target in free space. In our system, there is a random phase difference between the echo and local oscillator light, which is caused by atmospheric turbulence, laser phase noise, and target vibration, so it is a random variable. The random phase difference makes the amplitude of the detected electrical chirp signal randomly fluctuate, sometimes smaller than noise even after compression, so the detection probability is small. Detection probability means the probability we determine that we detect a target under a certain SNR when a target does exist. In order to solve this problem, we use a 90-degree optical hybrid at the receiver [
12]. Connecting the hybrid with two balanced detectors, we obtain two orthogonal electrical signals, I and Q—if one signal is weakened, the other one will be enhanced, so we can use them to stabilize the ranging results.
In addition, comparing with other coding ranging system [
13], our system can also be used to detect the radial velocity and distance of the target easily at the same time without any change, which has been verified in our previous work [
14].
3. Results
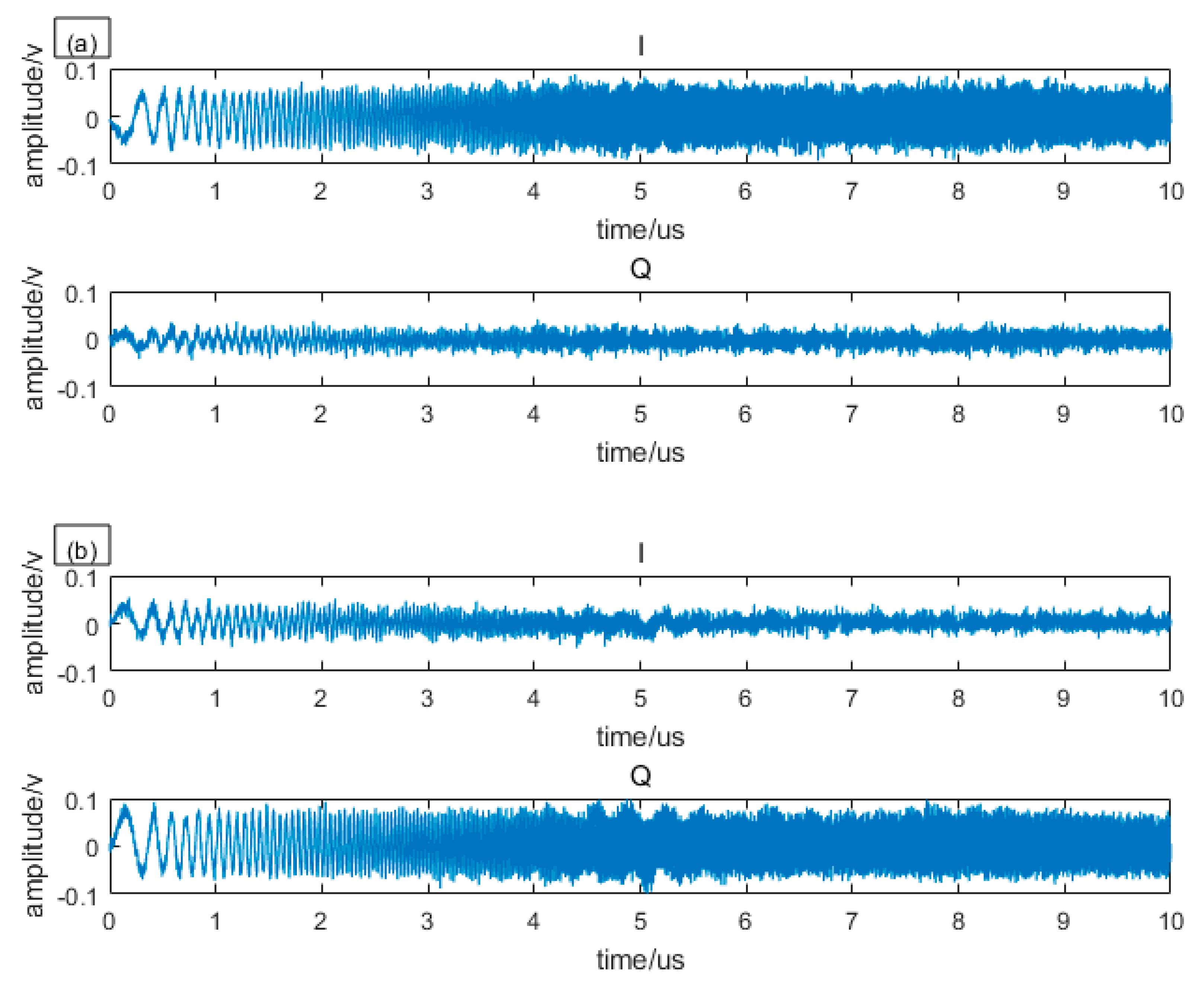
A digital oscilloscope (TELEDYNE LECROY Waverunner 610ZI) samples the two channel electrical signals of balance detectors. Then the digital signals were sent to the computer. After data processing through, the distance can be obtained in real time. We sampled and processed the detected electrical signals for 800 times. Three of them are shown in
Figure 3.
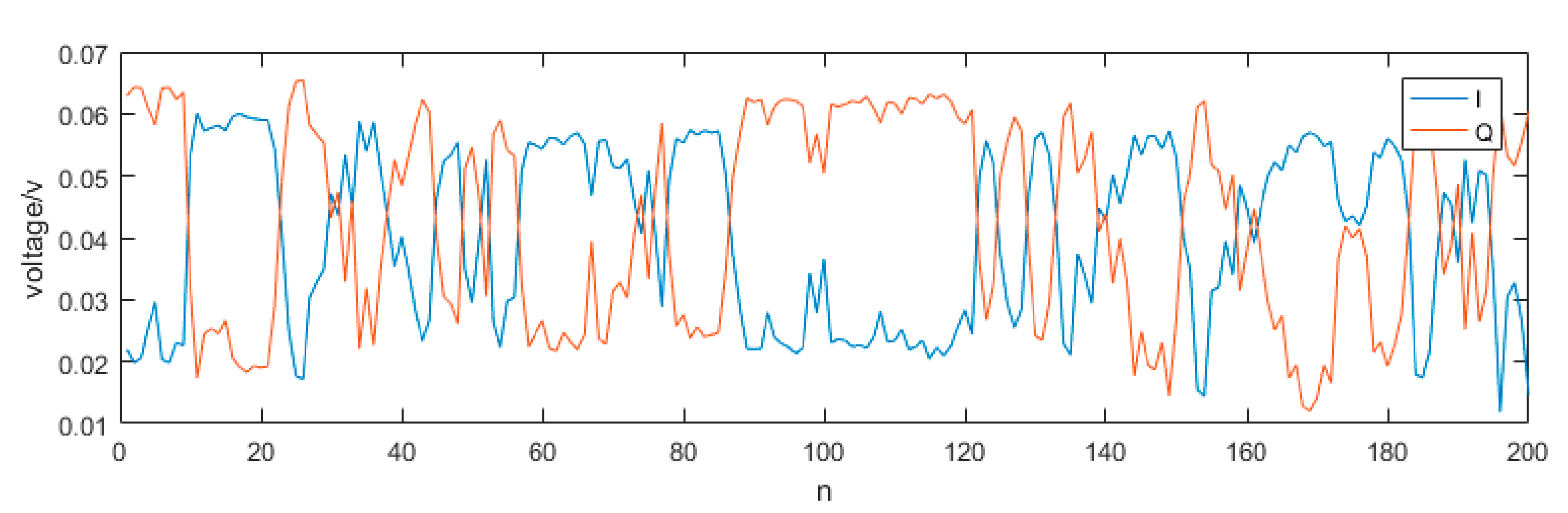
The chirp pulse consists of crosstalk and echo. Since the time delay between echo and crosstalk is very short compared to the pulse duration, the crosstalk and echo almost overlap in time. In addition, the echo is smaller than the crosstalk that the echo cannot be seen by the naked eye. So, when we explore the trend, we can treat the above signal as crosstalk, and the echo contained in it can be ignored. We can see that I and Q signals are complementary, when one is weakened the other is enhanced. The amplitude of 200 I and Q signals are shown in
Figure 4.
In order to more clearly show the complementary characteristics of I and Q, we only show the amplitude of 200 pairs of signals. We can see that their trend is completely in keeping with the law described in Equation (9) and the phase difference
changes irregularly, so it is a random variable and varies sharply between two consecutive samples, but it can be seen from
Figure 3 that within one sample, it has not changed much. So, within one pulse, the
can be considered unchanged.
One of the data processing method for I and Q channels are as follows: first sum the squares of I and Q, then compress the sum signal, and then make Hilbert transform to the compressed signal to get the envelope. But this method has limitations which will be demonstrated by following analysis.
Although the random phase difference can be eliminated theoretically by adding the squares of I and Q channels, in fact, since crosstalk and echo generated almost overlap in time, the sum of the squares of the two signals is
In Equation (12), the first term is echo, the second term is crosstalk, the third term is coherent sum of them, and the rest are direct current (DC) term and random noise term. Only the first and third terms contain , so only they can be used to measure the distance of the wall.
Because the sweeping rate of the first term is twice of that of third term, and one local chirp can only match one term, we can only utilize one of them to measure the distance. Firstly, since the local oscillator light is much larger than the crosstalk and the crosstalk is much larger than the echo, namely
, if we use first term, the other much bigger term will be a non-negligible noise. Secondly, since the third term contains the multiplier:
in Equation (12), and we have
so the amplitude of the third term varies randomly from zero to its maximum, the detection probability cannot be 100% because there is always system noise. After normalization, when the amplitude of noise is 80% of the sum envelope and if the SNR is bigger than 3 dB, we determined that the target is detected, the detection probability is easily calculated as
It can be seen from above analysis that the squaring method has its shortcomings, therefore we try another method: first compress I and Q, and then sum their envelope. The data processing steps are as follows: first, the two signals are respectively compressed, and then we make Hilbert transform to each compressed signal to obtain respective envelopes, and then sum the two envelopes. In this method, since there is no nonlinear process of squaring, there are only signal and crosstalk and no other coherent terms like Equation (12) act as noise so the SNR will be bigger. Besides, the detection probability will be improved because
which means the amplitude of the sum envelope will vary randomly from its minimum instead of zero to maximum. After normalization, when the noise is small than 1, the detection probability is 100%. When the amplitude of noise is 80% of the sum signal, the detection probability is
Which is bigger than 20% as calculated in Equation (14).
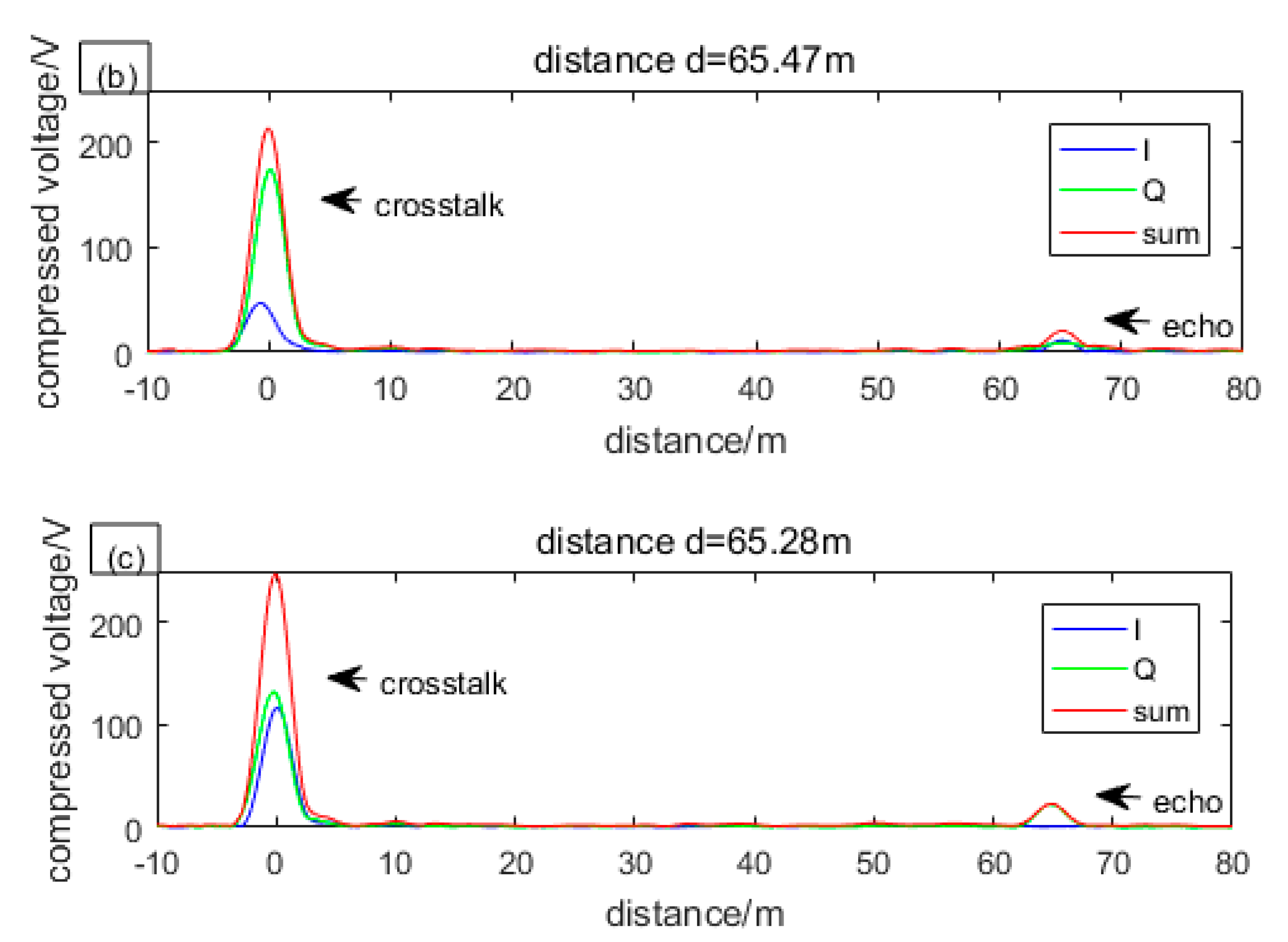
In order to reduce the side lobes, we multiplied local chirp with a Hamming window, at the expense of broadening the main lobe. The compressed envelopes of I, Q, and sum in
Figure 3 are as shown in
Figure 5.
As can be seen from
Figure 5, the crosstalk and echo that almost overlap before compression are completely separated after compression. It can be seen from both crosstalk and echo that when one channel is weak, the other is strong, so that the amplitude of sum envelope can always be greater than the noise. It is worth noting that the random phase difference between crosstalk and echo do not change synchronously because they walk different paths, thereby, when one channel of crosstalk is strong, the echo is not likely to be strong. From the crosstalk, we can see that the sum envelope is still unstable, as is described by Equation (15).
By compression, the magnitude of the crosstalk increases from about 0.04 V to about 208 V and the echo signal that is invisible to the naked eye increases to about 17 V. The data of 208 V and 17 V are obtained by averaging the results of 800 compressions.
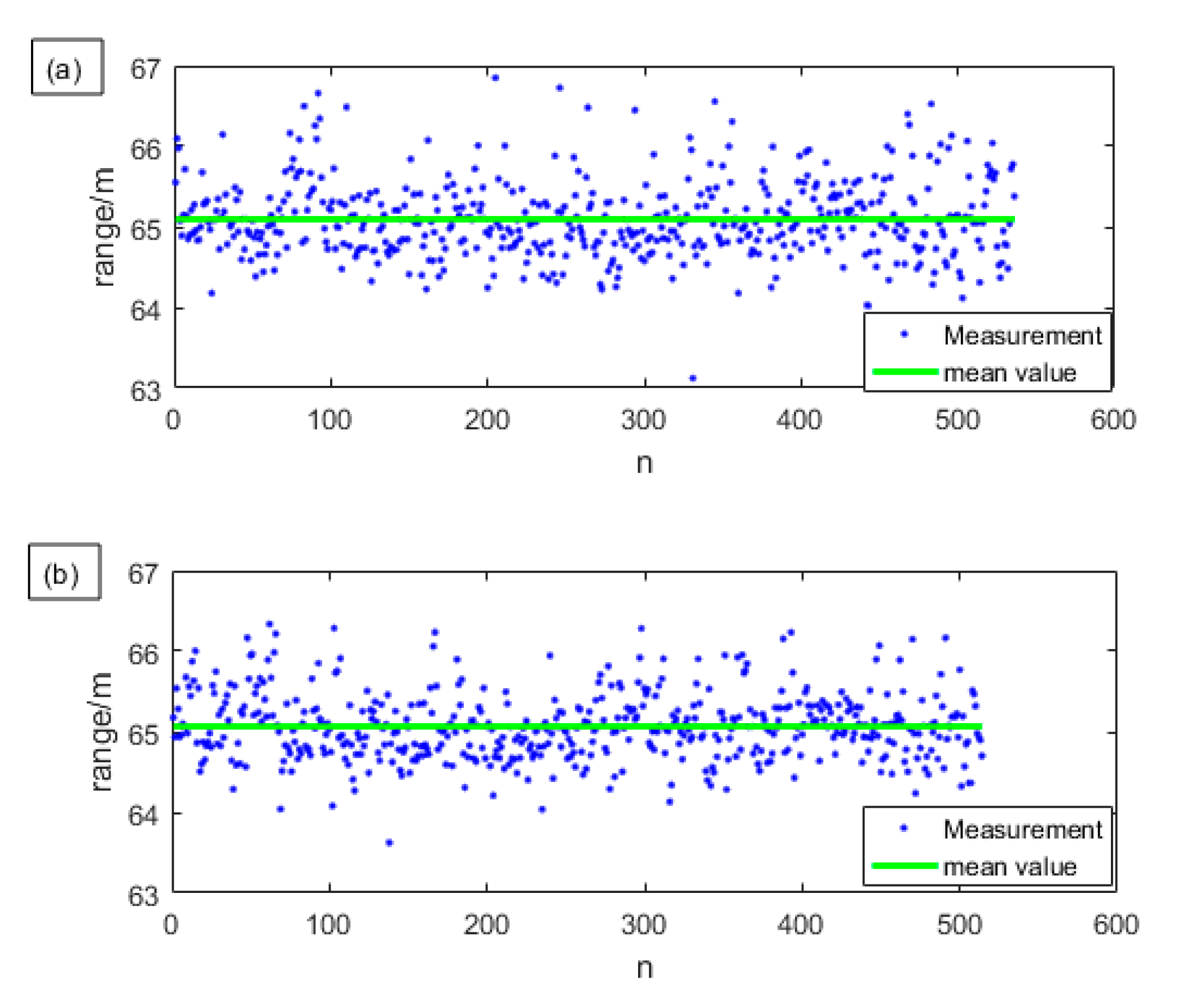
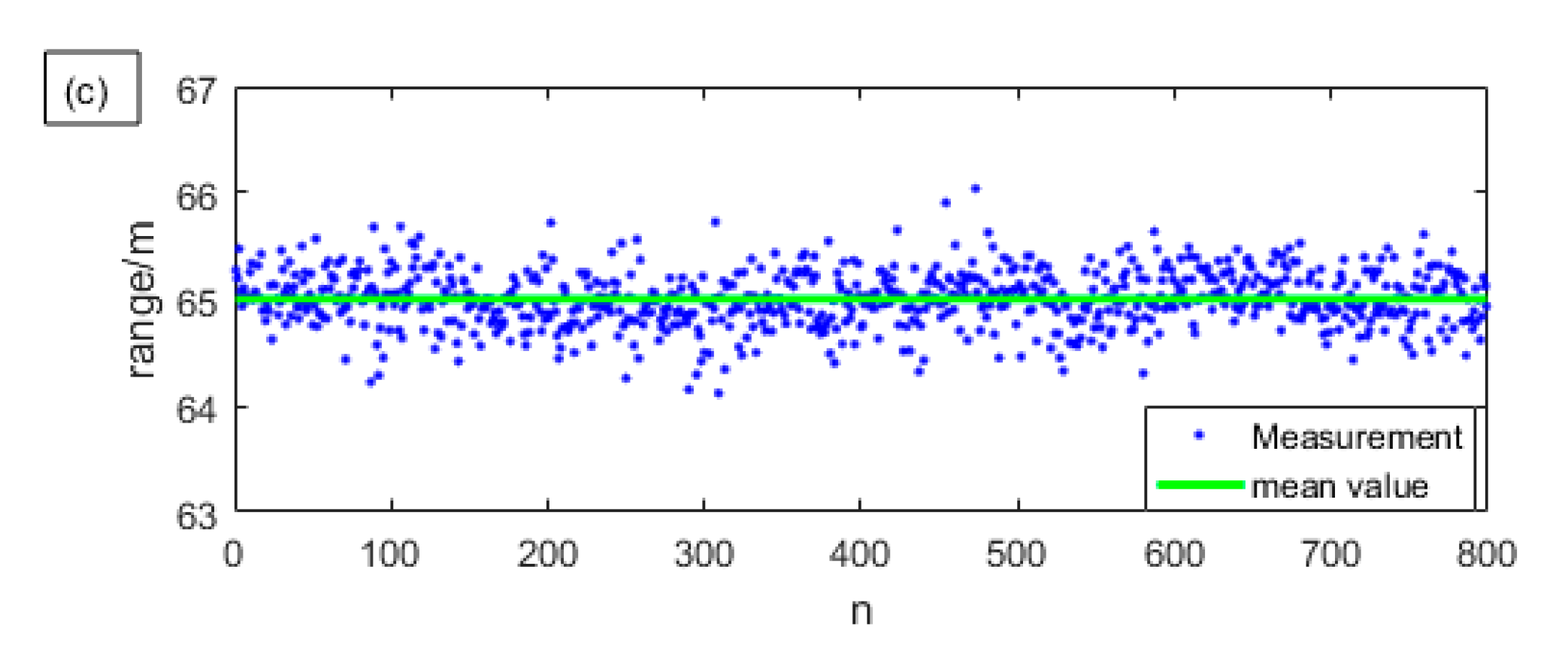
In order to illustrate the improvement of 90-degree optical hybrid in ranging performance, we use 800 sets of I and Q signals to separately measure the distance and compare their results with using the sum. We only keep those measurement results whose SNR are greater than or equal to 13 dB. The results are shown in
Figure 6. The blue points are the valid distance measurement results, and the green line is the mean of the distance.
4. Discussion
The detection probability increases by about 35% by using the 90-degree optical hybrid. It can be seen from the
Figure 6 that when measuring with one channel alone, due to the random phase difference, the signal amplitude may be so small that the SNR after compression is still lower than 13 dB, so the detection probability is no bigger than 70%. When measuring with sum signal, it is greatly improved by up to 99.88%. The reason why the detection probability of the latter method is not 100% is that sometimes the atmospheric turbulence is so strong that the echo is not almost coherent with the local light, causing the detected two radio frequency (RF) echo chirps to both be so weak that the SNR is less than 13 dB. Still, this is a low probability event since it only happens once in 800 results. We can also see that when measured with the sum signal, the distribution of the blue points is more compact, and the standard deviation reduces from about 0.42 m to about 0.27 m. So, the precision, which means the reproducibility between the results obtained by repeated measurements using the same system set-up, is improved.
Limitation factors of the system ranging precision mainly are: TBP and sampling frequency. Chirp signal of larger TBP and sampling instrument of higher sampling frequency can contribute to higher precision.
We can use the scheme of transmitting and receiving with different telescopes to avoid the crosstalk effect of the circulator, so that the squaring method can be used to make the signal completely stable. However, this scheme needs to match the field of view of the two telescopes. The receiving field of view is typically larger than the transmitting field of view, therefore more noise is introduced. More notably, there is no circulator to act as a zero-time base, therefore we need an additional one, which makes the system more complicated.