Optimal Target Assignment with Seamless Handovers for Networked Radars
Abstract
:1. Introduction
2. Preliminaries
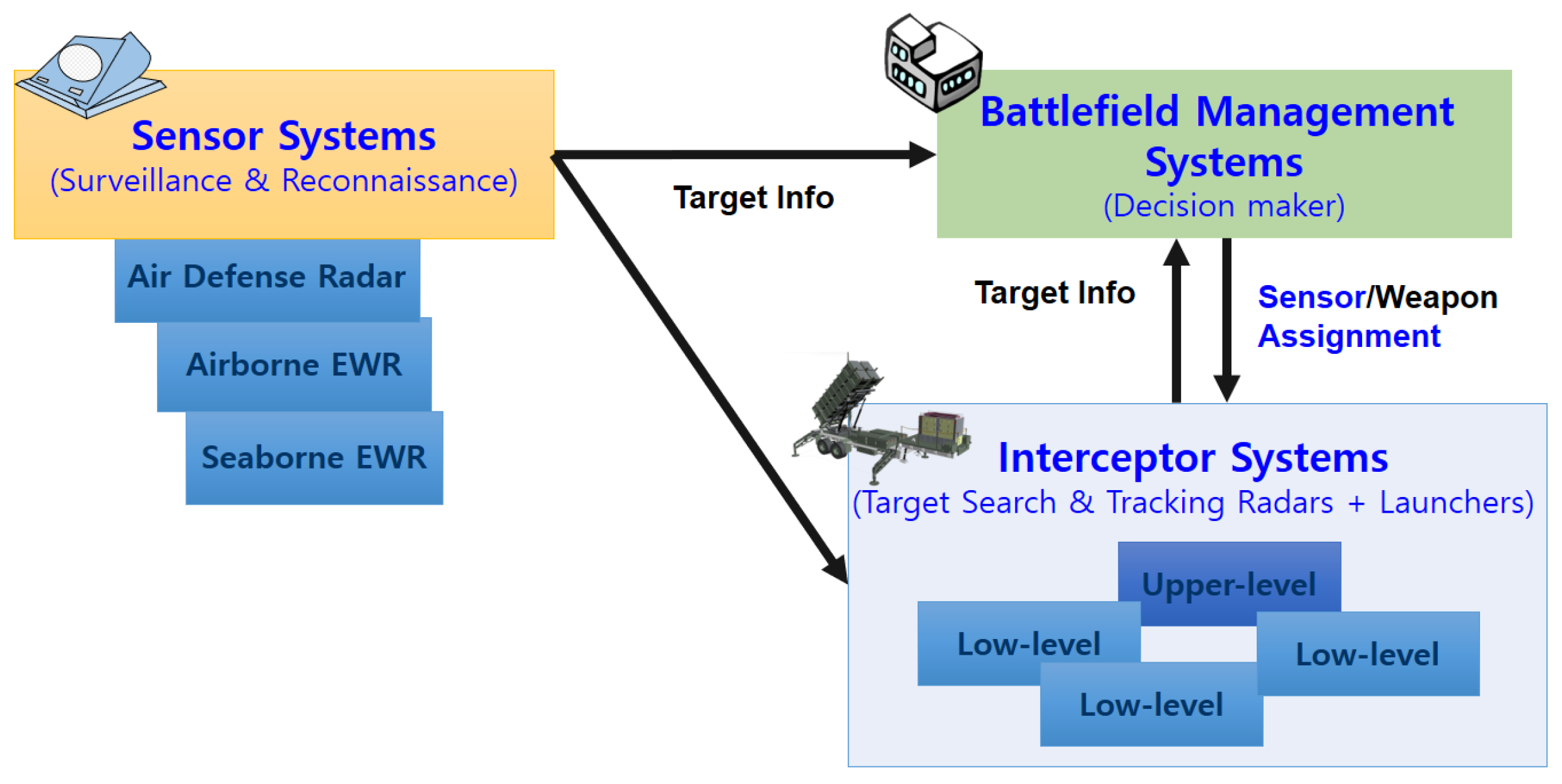
2.1. Mission Overview
2.2. Key Notions in Scheduling
2.2.1. Radar
2.2.2. Target Priority
2.2.3. Ballistic Target
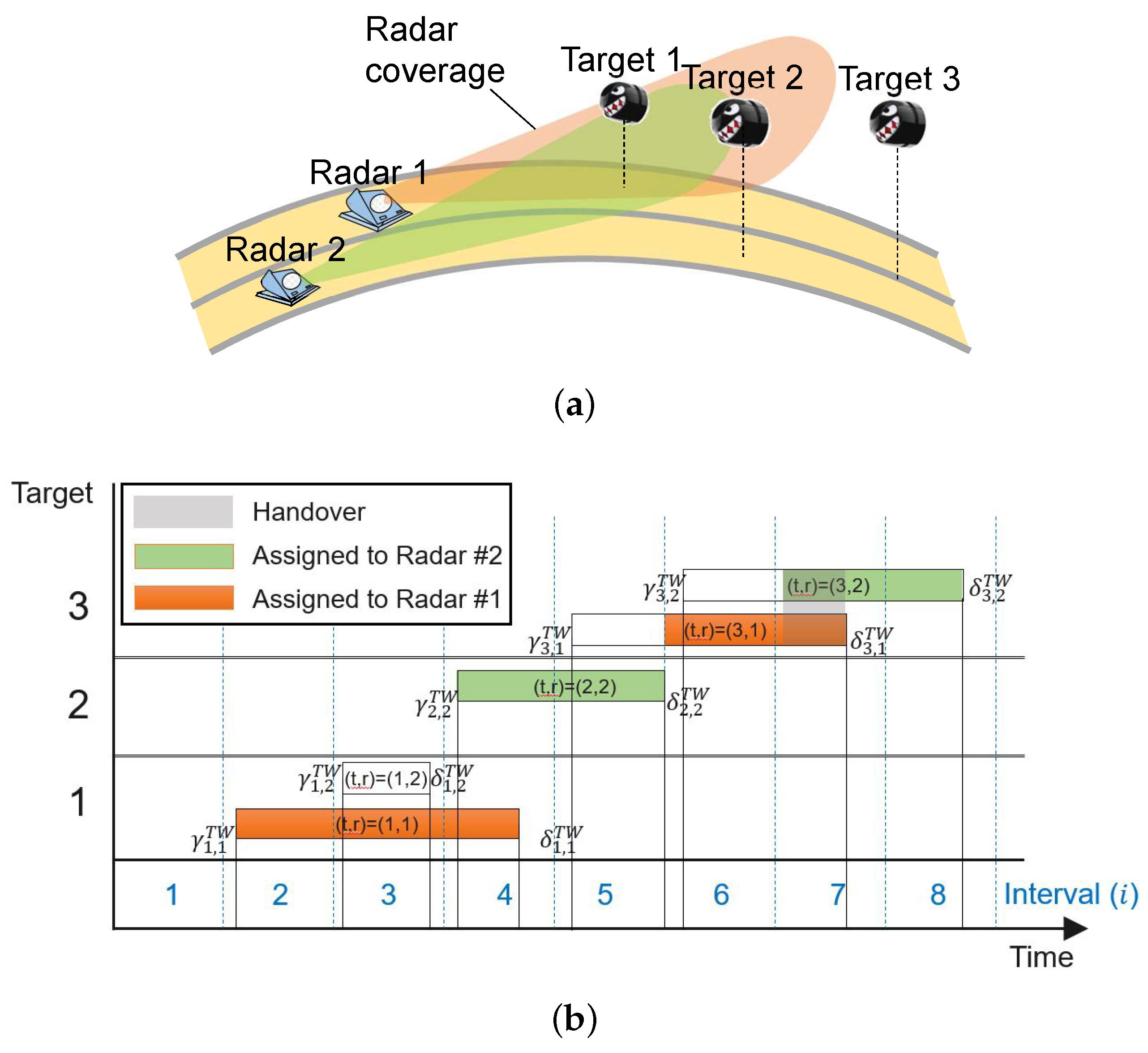
2.2.4. Time Window
2.2.5. Handover
2.3. Toy Model Implementation
2.4. Assumptions
- First, communication between the radars is fast enough to ensure appropriate information sharing. Communication connections using satellites or terrestrial optical cables should be a prerequisite.
- Second, since numerous researches have been conducted on sensor fusion and data association techniques for the handover of ballistic target information [23,24,27,28,29,30], it is regarded that the targets are handed over smoothly, and filtering problems related to target processing and sensor fusion that occurs are not covered in this study. The methodological and technical problems that may arise in the process of handing over targets between radars are not discussed. Please note that there is an early warning radar (EWR) featuring handover capability has recently been introduced in the market [31].
- Third, it is assumed that ballistic missile information is provided by EWR so that the time window for each missile is within the entire mission planning horizon. In addition, the EWR is equipped with a target separation and data association capability in the ground-to-air-level clutter environment.
3. Problem Formulation
4. Results and Discussion
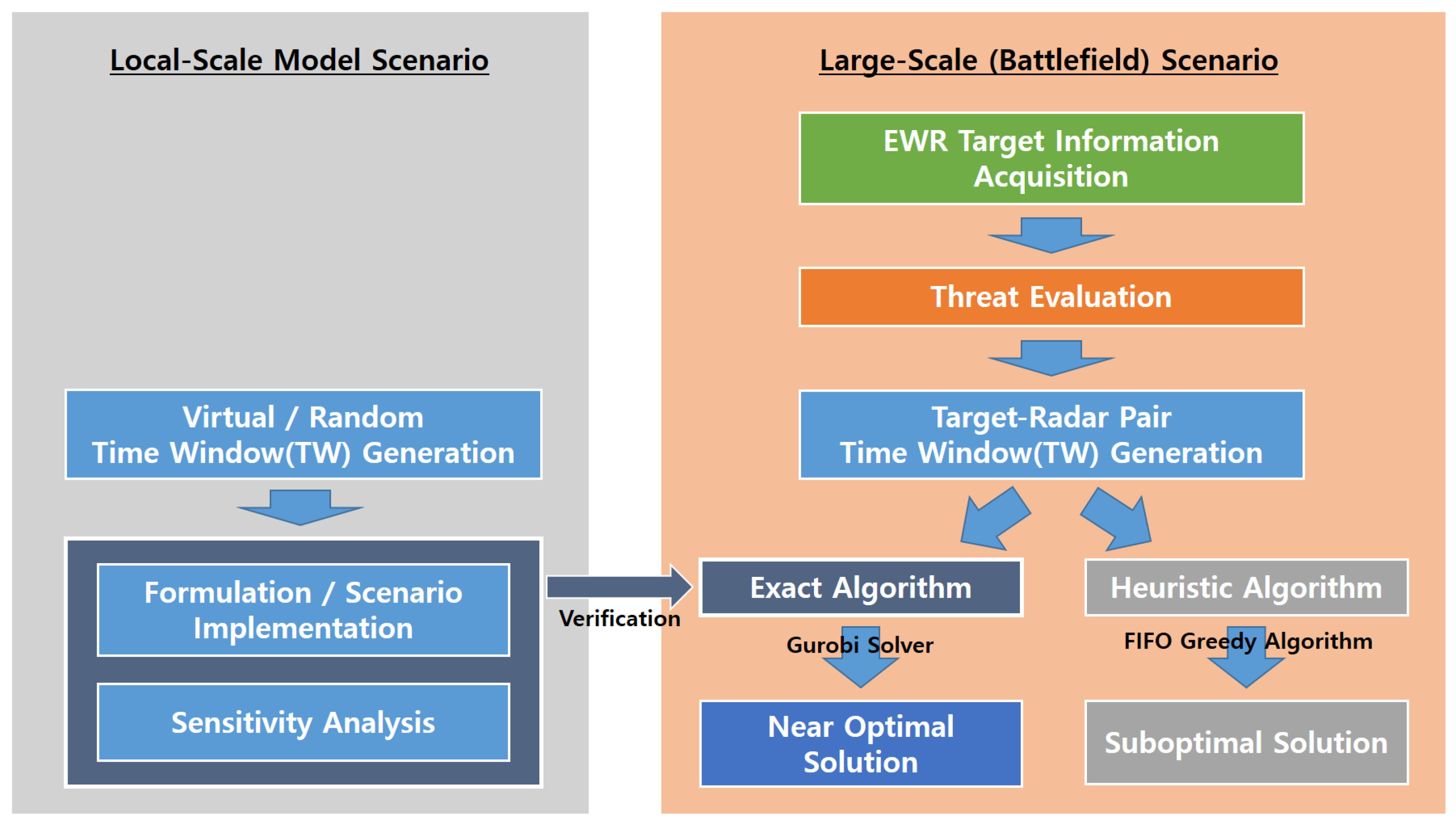
4.1. Local Scale Scenario Experiment
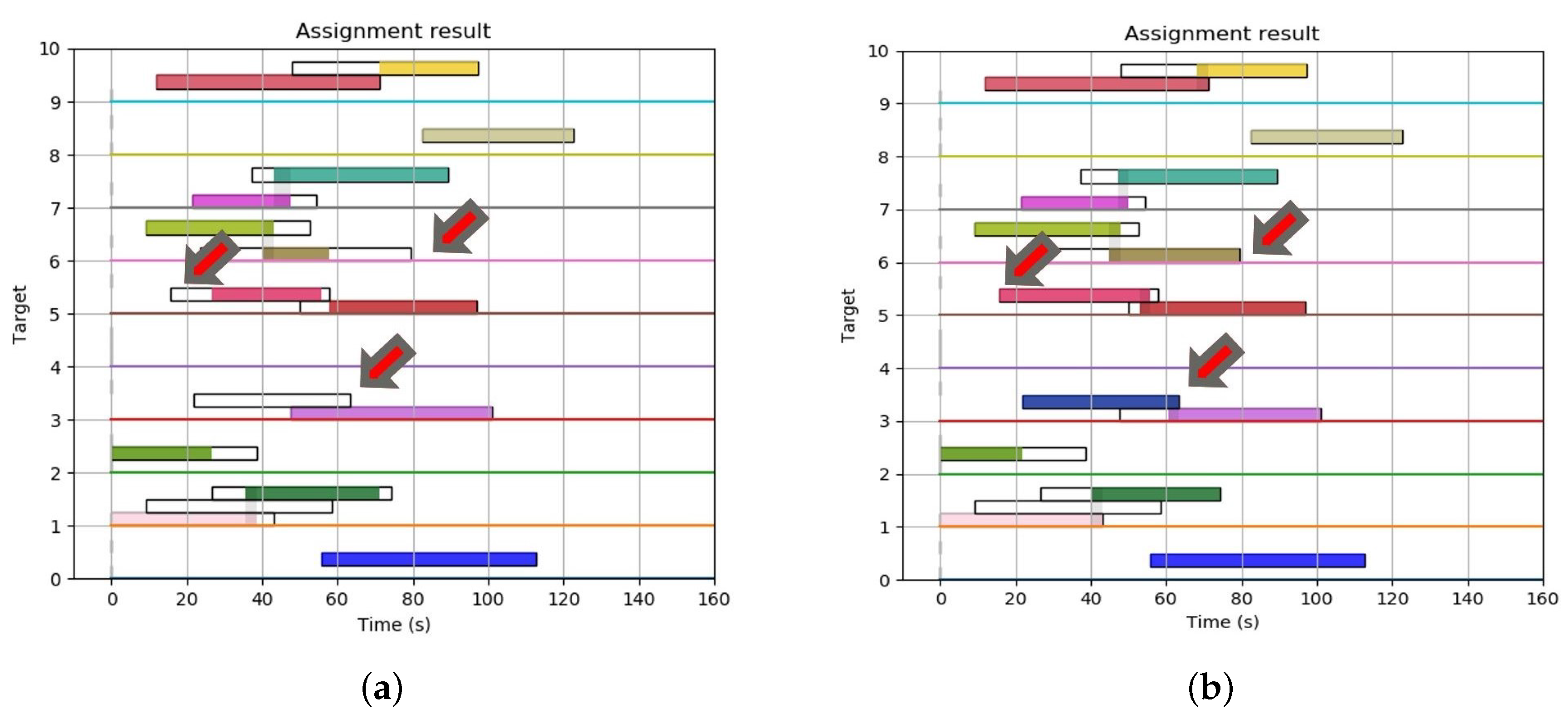
4.1.1. Algorithm Verification
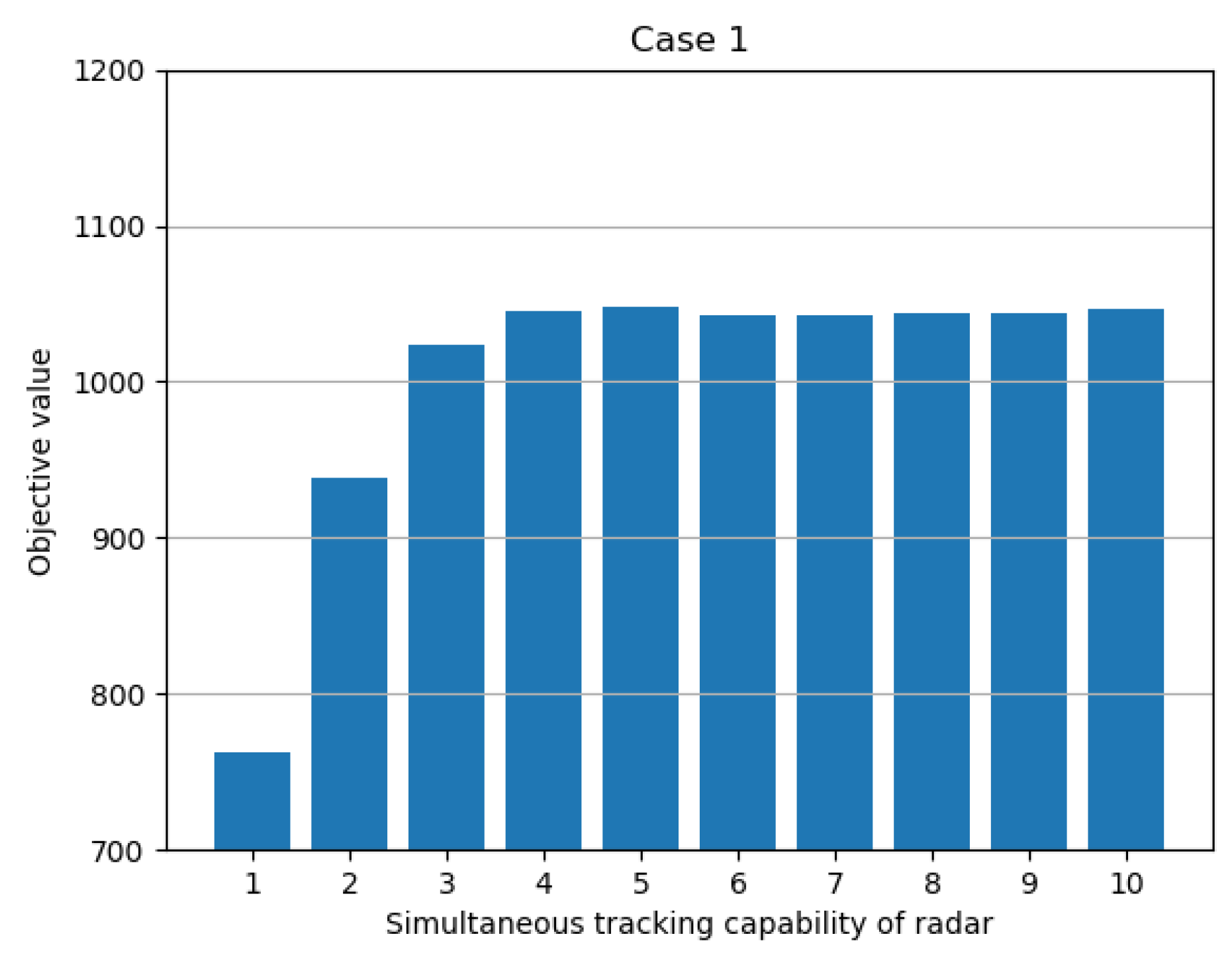
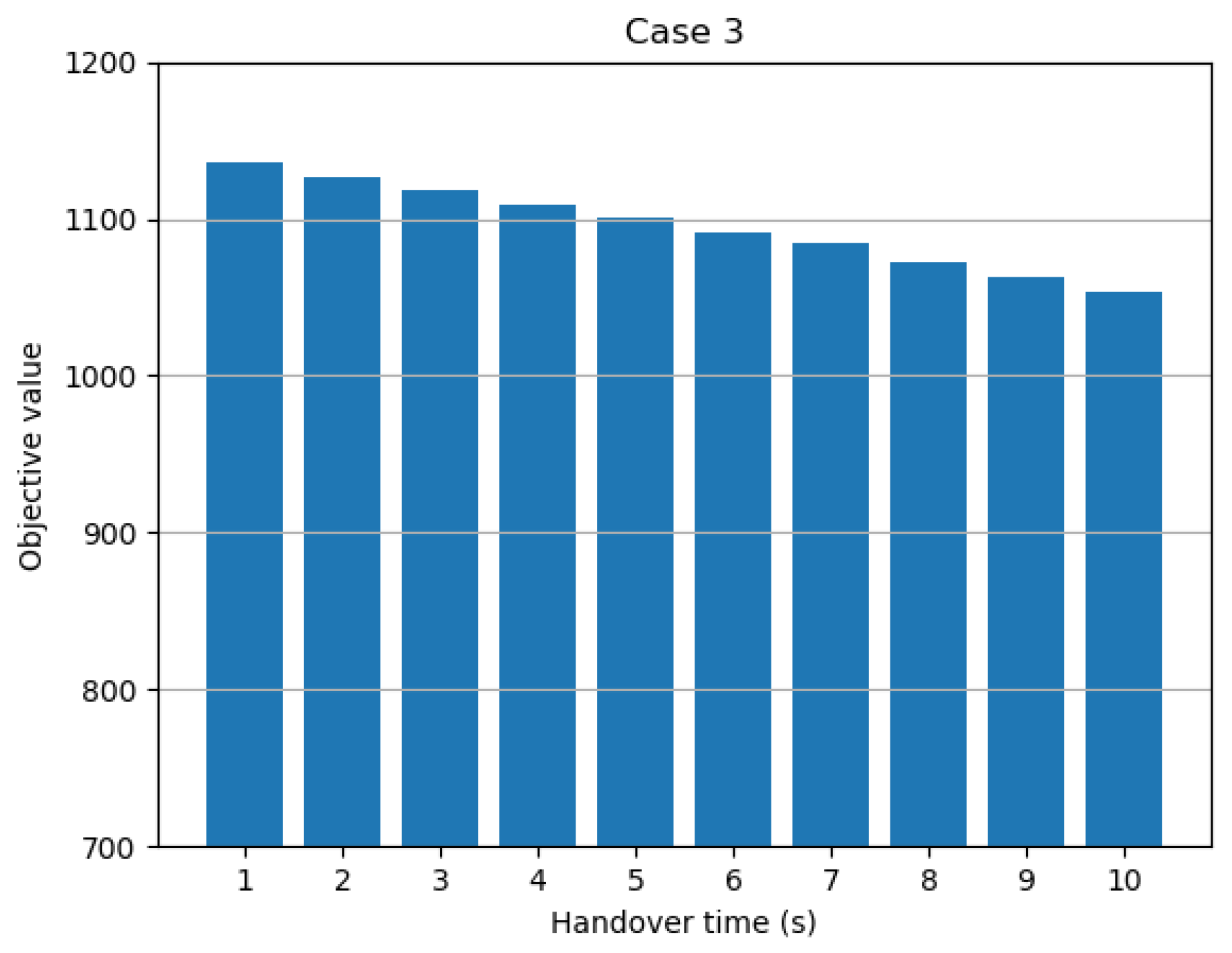
4.1.2. Parameter Sensitivity Analysis
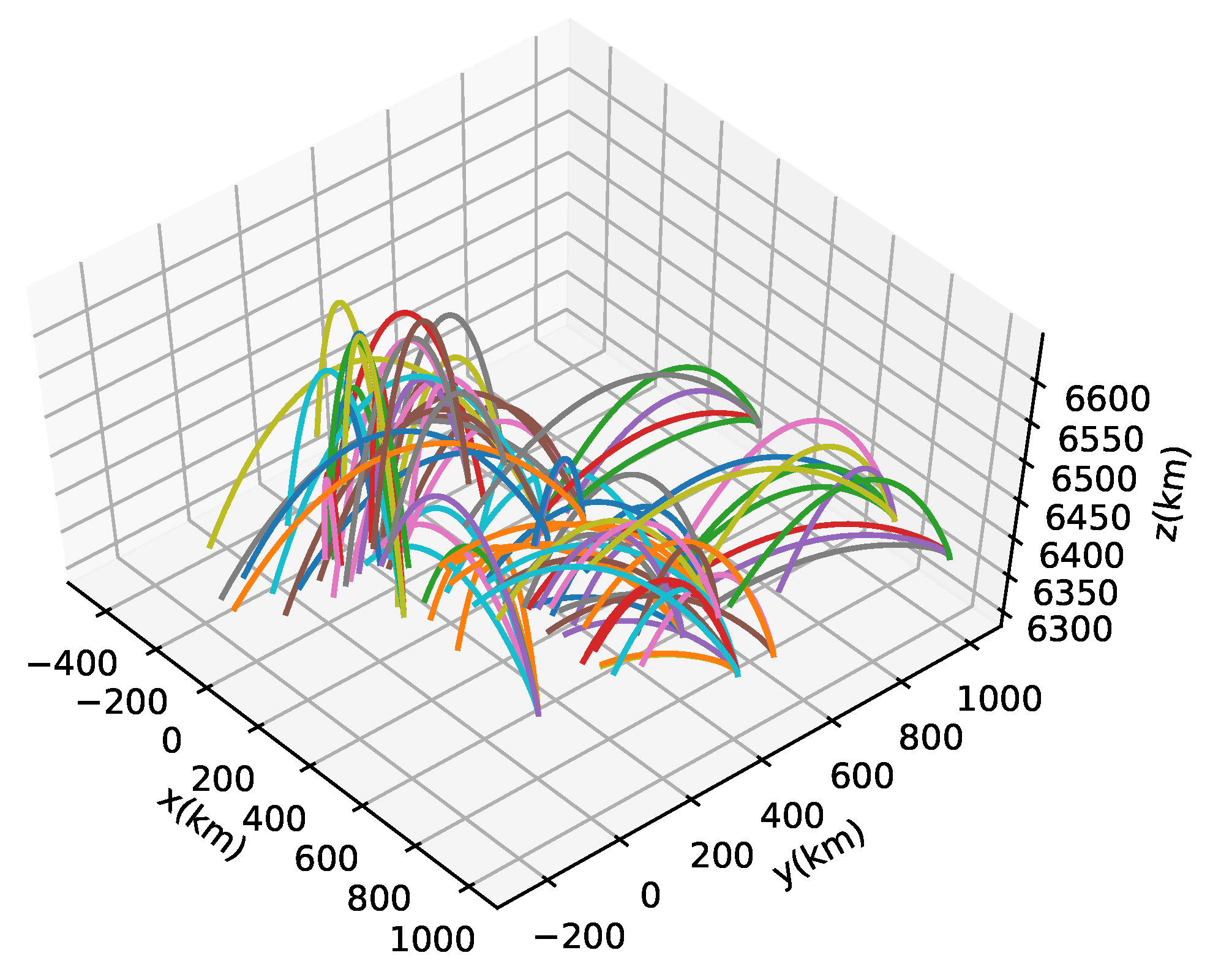
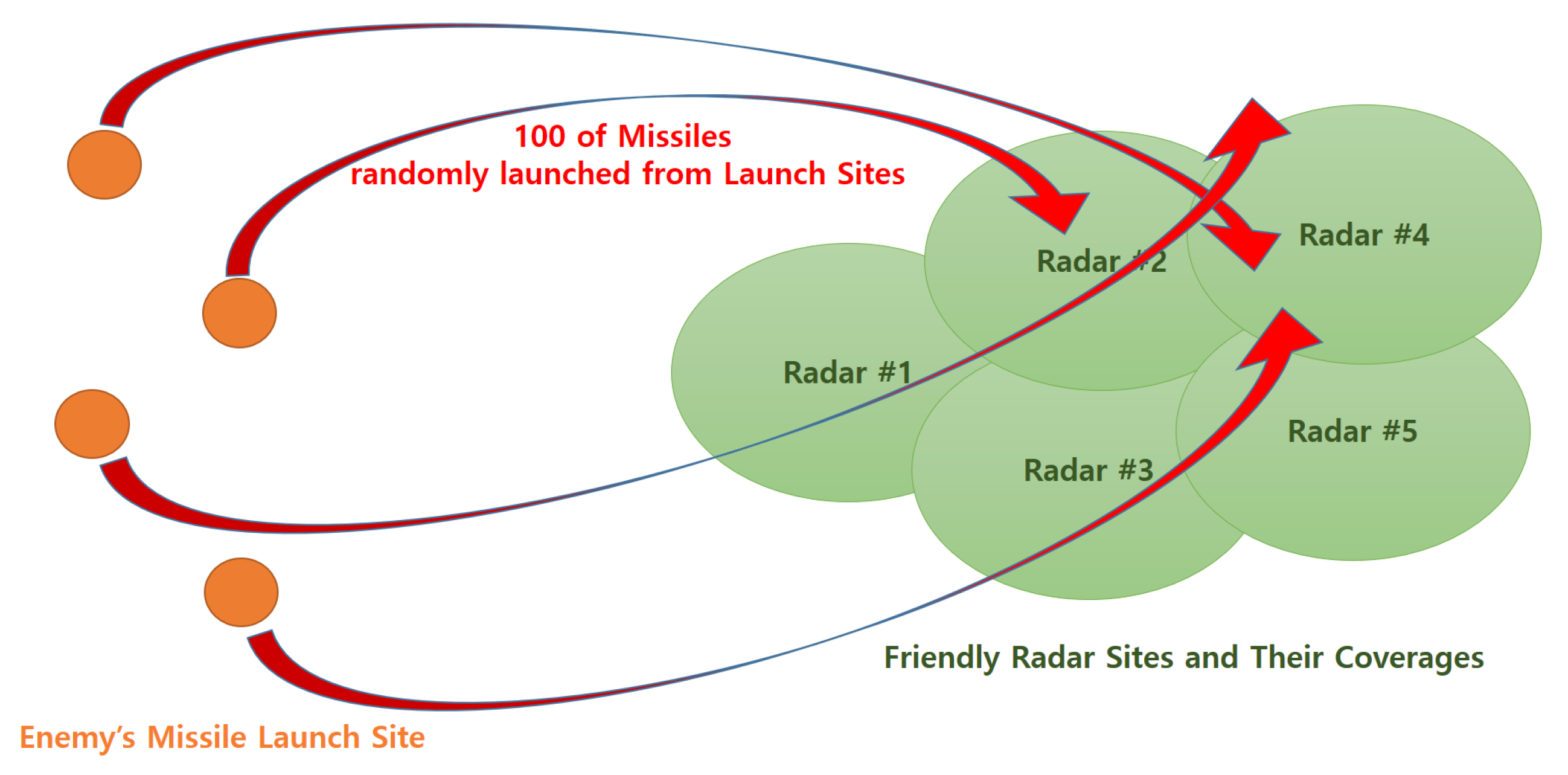
4.2. Battlefield Scenario Experiment
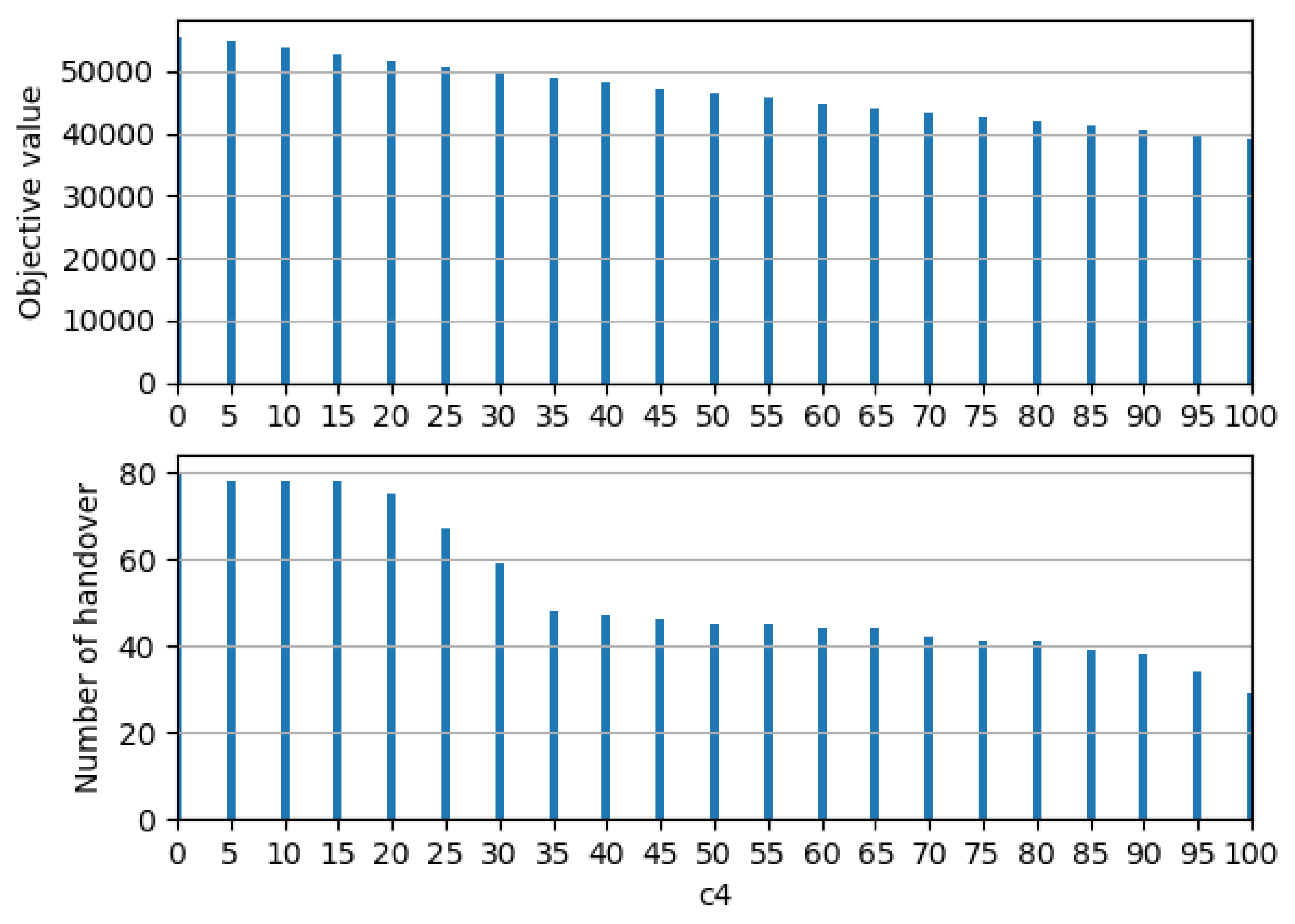
4.2.1. Weights of Objective Function Sensitivity Analysis
4.2.2. Complexity Analysis
4.2.3. Numerical Simulations for Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Pseudo-Code of FIFO Greedy Algorithm
| Algorithm A1 FIFO greedy algorithm |
| Input: Target information, Time windows information, Radar tracking capability |
| Output: Target tracking schedules for each radar |
|
References
- Owens, W.A. The Emerging U.S. System-of-Systems. Naval Inst. Proc. 1996, 121, 7. [Google Scholar]
- Alberts, D.S.; Garstka, J.J.; Stein, F.P. Network Centric Warfare: Developing and Leveraging Information Superiority; Assistant Secretary of Defense (C3I/Command Control Research Program): Washington, DC, USA, 2000; pp. 87–114. [Google Scholar]
- Dahmann, J.S.; Baldwin, K.J. Understanding the current state of US defense systems of systems and the implications for systems engineering. In Proceedings of the 2008 2nd Annual IEEE Systems Conference, Montreal, QC, Canada, 7–10 April 2008; pp. 1–7. [Google Scholar]
- Barcio, B.T.; Ramaswamy, S.; Macfadzean, R.; Barber, K.S. Object-oriented analysis, modeling, and simulation of a notional air defense system. Simulation 1996, 66, 5–21. [Google Scholar] [CrossRef]
- Countering Air and Missile Threats; Joint Publication 3-01; United States Joint Chief of Staff: Washington, DC, USA, 2018.
- Cho, D.H.; Kim, J.H.; Choi, H.L.; Ahn, J. Optimization-Based Scheduling Method for Agile Earth-Observing Satellite Constellation. J. Aerosp. Inf. Syst. 2018, 15, 611–626. [Google Scholar] [CrossRef]
- Khalafa, A.; Djouania, K.; Hamama, Y.; Alaylid, Y. Mixed-integer linear programming (MILP) for optimisation of medical equipment maintenance schedules. In Proceedings of the 2015 22nd Iranian Conference on Biomedical Engineering (ICBME), Tehran, Iran, 25–27 November 2015; pp. 205–209. [Google Scholar]
- Zakaria, R.; Moalic, L.; Caminada, A.; Dib, M. Greedy Algorithm for Relocation Problem in One-Way Carsharing Systems. In Proceedings of the MOSIM 2014, 10ème Conférence Francophone de Modélisation, Optimisation et Simulation, Nancy, France, 5–7 November 2014. [Google Scholar]
- Che, A.; Zeng, Y.; Lyu, K. An efficient greedy insertion heuristic for energy-conscious single machine scheduling problem under time-of-use electricity tariffs. J. Clean. Prod. 2016, 129, 565–577. [Google Scholar] [CrossRef]
- Eles, A.; Cabezas, H.; Heckl, I. Heuristic algorithm utilizing mixed-integer linear programming to schedule mobile workforce. Chem. Eng. Trans. 2018, 70, 895–900. [Google Scholar]
- Johnson, B.W.; Green, J.M. Naval network-centric sensor resource management. In 7th ICCRTS; Naval Postgraduate School: Monterey, CA, USA, 2002. [Google Scholar]
- Narykov, A.S.; Krasnov, O.A.; Yarovoy, A. Algorithm for resource management of multiple phased array radars for target tracking. In Proceedings of the IEEE 16th International Conference on Information Fusion, Istanbul, Turkey, 9–12 July 2013; pp. 1258–1264. [Google Scholar]
- Lian, F.; Hou, L.; Wei, B.; Han, C. Sensor Selection for Decentralized Large-Scale Multi-Target Tracking Network. Sensors 2018, 18, 4115. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Ling, Q.; Tian, Z. Distributed sensor allocation for multi-target tracking in wireless sensor networks. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3538–3553. [Google Scholar] [CrossRef]
- Yan, J.; Pu, W.; Liu, H.; Zhou, S.; Bao, Z. Cooperative target assignment and dwell allocation for multiple target tracking in phased array radar network. Signal Proc. 2017, 141, 74–83. [Google Scholar] [CrossRef]
- Sherwani, H.; Griffiths, H.D. Tracking parameter control in multifunction radar network incorporating information sharing. In Proceedings of the IEEE 2016 19th International Conference on Information Fusion (FUSION), Heidelberg, Germany, 5–8 July 2016; pp. 319–326. [Google Scholar]
- Severson, T.A.; Paley, D.A. Distributed multi-target search and track assignment using consensus-based coordination. In Proceedings of the IEEE SENSORS, Baltimore, MD, USA, 3–6 November 2013; pp. 1–4. [Google Scholar]
- Severson, T.A.; Paley, D.A. Optimal sensor coordination for multitarget search and track assignment. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2313–2320. [Google Scholar] [CrossRef]
- Ying, C.; Wang, Y.; He, J. Study on time window of track tasks in multifunction phased array radar tasks scheduling. In Proceedings of the IET International Radar Conference, Guilin, China, 20–22 April 2009; pp. 20–22. [Google Scholar]
- Jang, D.S.; Choi, H.L.; Roh, J.E. A time-window-based task scheduling approach for multi-function phased array radars. In Proceedings of the IEEE 2011 11th International Conference on Control, Automation and Systems, Gyeonggi-do, Korea, 26–29 October 2011; pp. 1250–1255. [Google Scholar]
- Duan, Y.; Tan, X.S.; Qu, Z.G.; Wang, J.; Peng, X.Y. A scheduling algorithm for phased array radar based on adaptive time window. In Proceedings of the 2017 IEEE 3rd Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 3–5 October 2017; pp. 935–941. [Google Scholar]
- Qiang, S.W.; Xing, H.; Jian, G. A task scheduling simulation for phased array radar with time windows. In Proceedings of the 2017 IEEE 6th International Conference on Computer Science and Network Technology (ICCSNT), Dalian, China, 21–22 October 2017; pp. 165–169. [Google Scholar]
- Maurer, D.E. Information handover for track-to-track correlation. Inf. Fus. 2003, 4, 281–295. [Google Scholar] [CrossRef]
- Lewis, B.M.; Tabaczynski, J.A. The Role of Serious Games in Ballistic Missile Defense. Lincoln Lab. J. 2019, 23, 11–24. [Google Scholar]
- Jang, D.S.; Cho, D.H.; Choi, H.L. An approach to multiple radar resource assignment problem for managing highspeed multi target. In Proceedings of the KSAS 2016 Fall Conference, Jeju, Korea, 16–18 November 2016; pp. 910–911. [Google Scholar]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking: II. Ballistic target models. In Proceedings of the International Symposium on Optical Science and Technology, San Diego, CA, USA, 29 July–3 August 2001; Volume 4473, pp. 559–581. [Google Scholar]
- Maurer, D.E.; Schirmer, R.W.; Kalandros, M.K.; Peri, J.S. Sensor fusion architectures for ballistic missile defense. Johns Hopkins APL Tech. Digest 2006, 27, 19–31. [Google Scholar]
- Serakos, D. On BMD Target Tracking: Data Association and Data Fusion. arXiv 2014, arXiv:1408.3596. [Google Scholar]
- Song, T.L. Multi-target tracking filters and data association: A survey. J. Inst. Control Robot. Syst. 2014, 20, 313–322. [Google Scholar] [CrossRef]
- Zhang, Z.; Fu, K.; Sun, X.; Ren, W. Multiple Target Tracking Based on Multiple Hypotheses Tracking and Modified Ensemble Kalman Filter in Multi-Sensor Fusion. Sensors 2019, 19, 3118. [Google Scholar] [CrossRef] [PubMed]
- ELM-2090 TERRA Strategic Early Warning Dual Band Radar System. Available online: https://www.iai.co.il/p/elm-2090-terra (accessed on 29 September 2019).
- Griva, I.; Nash, S.G.; Sofer, A. Linear and Nonlinear Optimization; Siam: Philadelphia, PA, USA, 2009; Volume 108. [Google Scholar]
- Till, J.; Engell, S.; Panek, S.; Stursberg, O. Applied hybrid system optimization: An empirical investigation of complexity. Control Eng. Pract. 2004, 12, 1291–1303. [Google Scholar] [CrossRef]
- Cho, D.H.; Choi, H.L. Greedy Maximization for Asset-Based Weapon—Target Assignment with Time-Dependent Rewards. In Cooperative Control of Multi-Agent Systems; John Wiley & Sons, Ltd.: New York, NY, USA, 2017; Chapter 5; pp. 115–138. [Google Scholar]
- Vazirani, V.V. Approximation Algorithms; Springer GmbH: Berlin/Heidelberg, Germany, 2003. [Google Scholar]





| Notation | Physical Meaning |
|---|---|
| Start time of time window | |
| End time of time window | |
| Start time of Interval i | |
| End time of Interval i | |
| Minimum tracking assignment time | |
| Target handover time | |
| Target priority(importance of target) | |
| Number of radars | |
| Number of targets | |
| Simultaneous tracking capability of each radar |
| Notation | Value | Physical Meaning |
|---|---|---|
| Start time of tracking | ||
| Tracking duration time | ||
| Whether Target t is being allocated (tracked) or not | ||
| Whether Radar r tracks the target t or not | ||
| Whether Radar and handover the target t or not | ||
| Support variable for | ||
| Whether Radar r tracks the Target t in interval i or not |
| Planning horizon | 160 s |
| Minimum tracking assignment time | 7 s |
| Target handover time | 3 s |
| Simultaneous tracking capability of each radar | 2 |
| Target Number | Total Tracking Duration (s) | ||
|---|---|---|---|
| Increments | |||
| Target 1 | 56.8 | 56.8 | 0 |
| Target 2 | 71.1 | 74.3 | +3.2 |
| Target 3 | 26.7 | 21.8 | −4.9 |
| Target 4 | 53.4 | 79.2 | +25.8 |
| Target 5 | 0 | 0 | 0 |
| Target 6 | 70.2 | 81 | +10.8 |
| Target 7 | 48.8 | 70.1 | +21.3 |
| Target 8 | 67.9 | 67.9 | 0 |
| Target 9 | 40.2 | 40.2 | 0 |
| Target 10 | 85.4 | 85.4 | 0 |
| Parameters | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| Simultaneous tracking capability | 1 to 10 | 5 | 5 |
| Minimum tracking assignment time | 10 | 1 to 10 | 10 |
| Handover time | 10 | 10 | 1 to 10 |
| Number of target | 100 |
| Number of radar | 5 |
| Planning horizon | 1000 s |
| Minimum tracking assignment time | 7 s |
| Target handover time | 3 s |
| Simultaneous tracking capability of each radar | 20 |
| Term | Opt. of Ind. Objective | Coeff. Value for Normalization |
|---|---|---|
| Target priority | 18,610.8 | |
| Maximization of tracking time | 7621.6 | |
| Maximization of the number of tracked target | 98.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Cho, D.-H.; Lee, W.-C.; Park, S.-S.; Choi, H.-L. Optimal Target Assignment with Seamless Handovers for Networked Radars. Sensors 2019, 19, 4555. https://doi.org/10.3390/s19204555
Kim J, Cho D-H, Lee W-C, Park S-S, Choi H-L. Optimal Target Assignment with Seamless Handovers for Networked Radars. Sensors. 2019; 19(20):4555. https://doi.org/10.3390/s19204555
Chicago/Turabian StyleKim, Juhyung, Doo-Hyun Cho, Woo-Cheol Lee, Soon-Seo Park, and Han-Lim Choi. 2019. "Optimal Target Assignment with Seamless Handovers for Networked Radars" Sensors 19, no. 20: 4555. https://doi.org/10.3390/s19204555
APA StyleKim, J., Cho, D.-H., Lee, W.-C., Park, S.-S., & Choi, H.-L. (2019). Optimal Target Assignment with Seamless Handovers for Networked Radars. Sensors, 19(20), 4555. https://doi.org/10.3390/s19204555





