Efficient Parameter Estimation for Sparse SAR Imaging Based on Complex Image and Azimuth-Range Decouple
Abstract
1. Introduction
2. Signal Model and Automatic Parameter Estimation Method
2.1. Signal Model
2.1.1. Azimuth-Range Decouple-Based Sparse SAR Imaging
2.1.2. Complex Image-Based Sparse SAR Imaging
2.2. Automatic Parameter Estimation Method
3. Efficient Adaptive Parameter Estimation for Sparse SAR Imaging
3.1. The Adaptive Parameter Estimation Method Based on Azimuth-Range Decouple
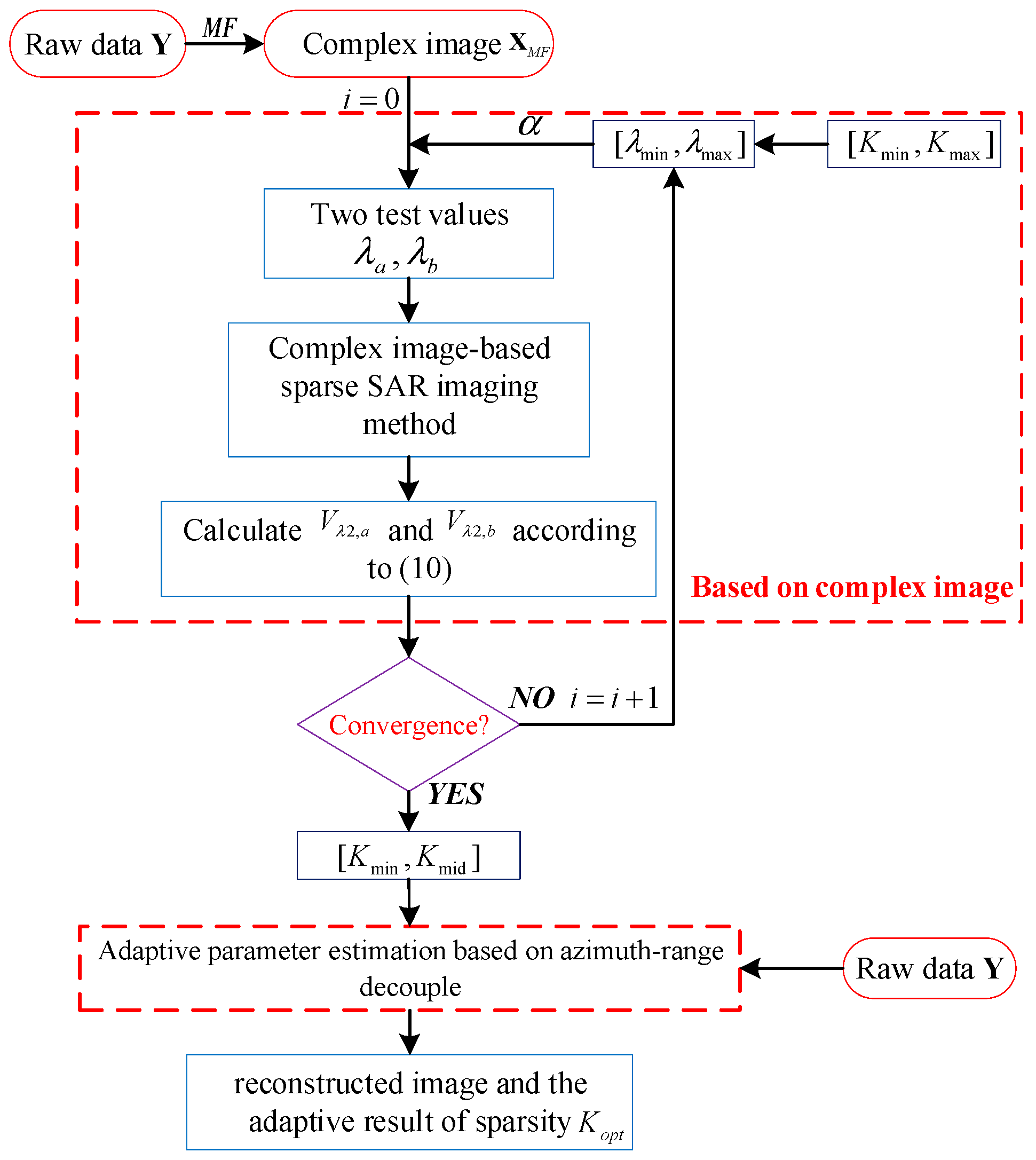
3.2. The Adaptive Parameter Estimation Method Based on Complex Image
3.3. The Proposed Method
| Algorithm 1: The adaptive parameter estimation method based on azimuth-range decouple |
| 1: Input: downsampled SAR raw data , parameter , |
| 2: Initialization: , , |
| 3: while and |
| 1) ; |
| 2) ; |
| 3) ; |
| 4) Calculate and according to (9) |
| 5) if else |
| 6) |
| 4: end while |
| 5: Output: the reconstructed image and the adaptive parameter |
3.4. Analysis of Computational Complexity
4. Experiments
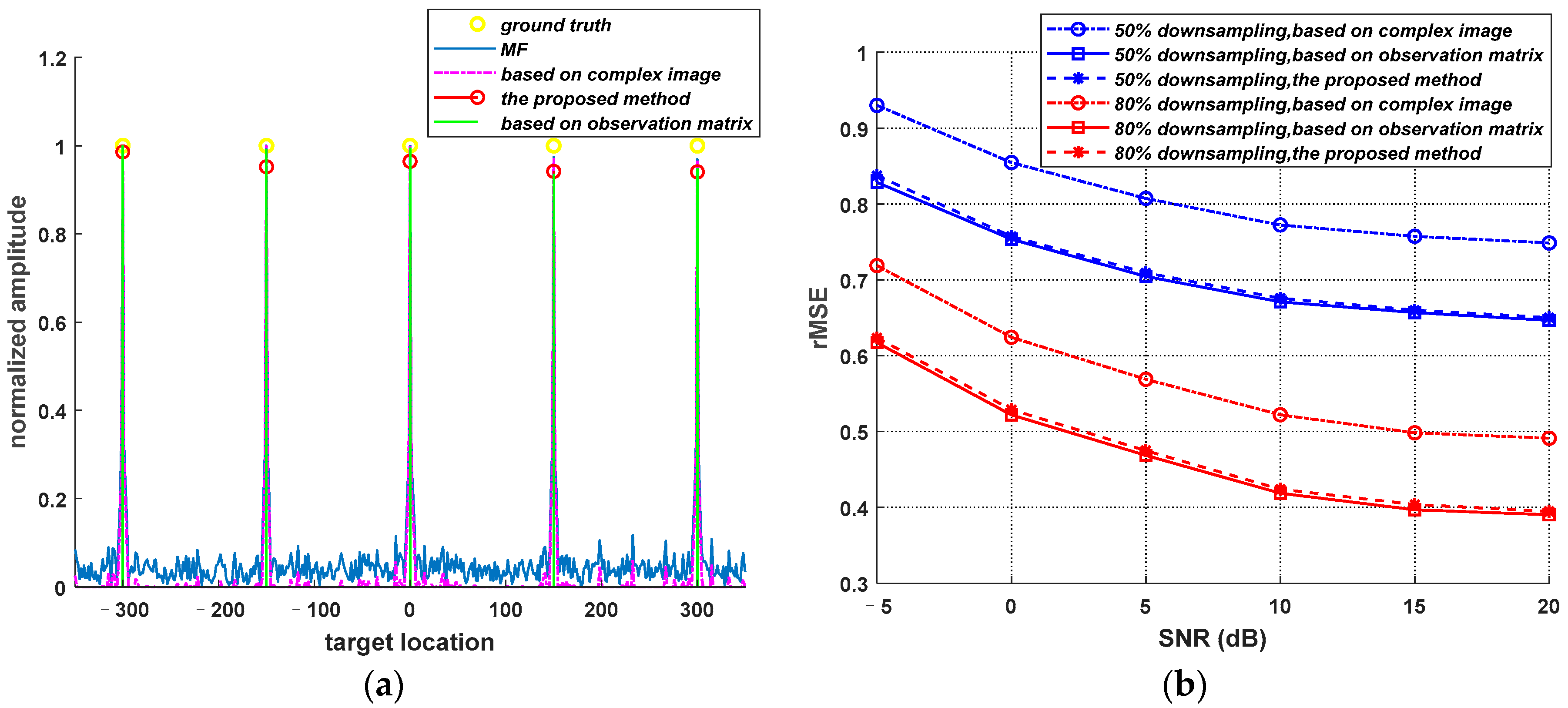
4.1. 1D Simulation
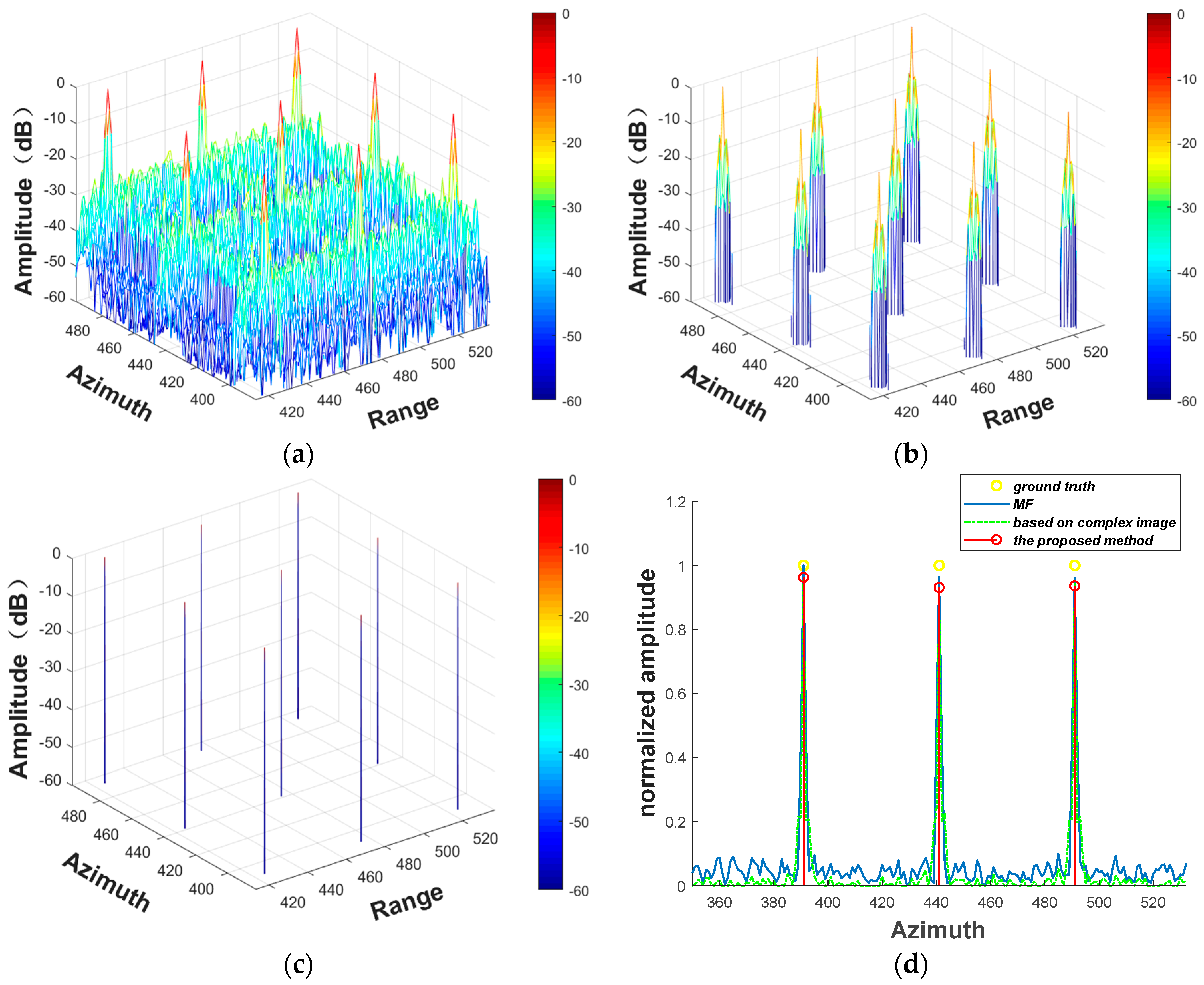
4.2. 2D Simulation
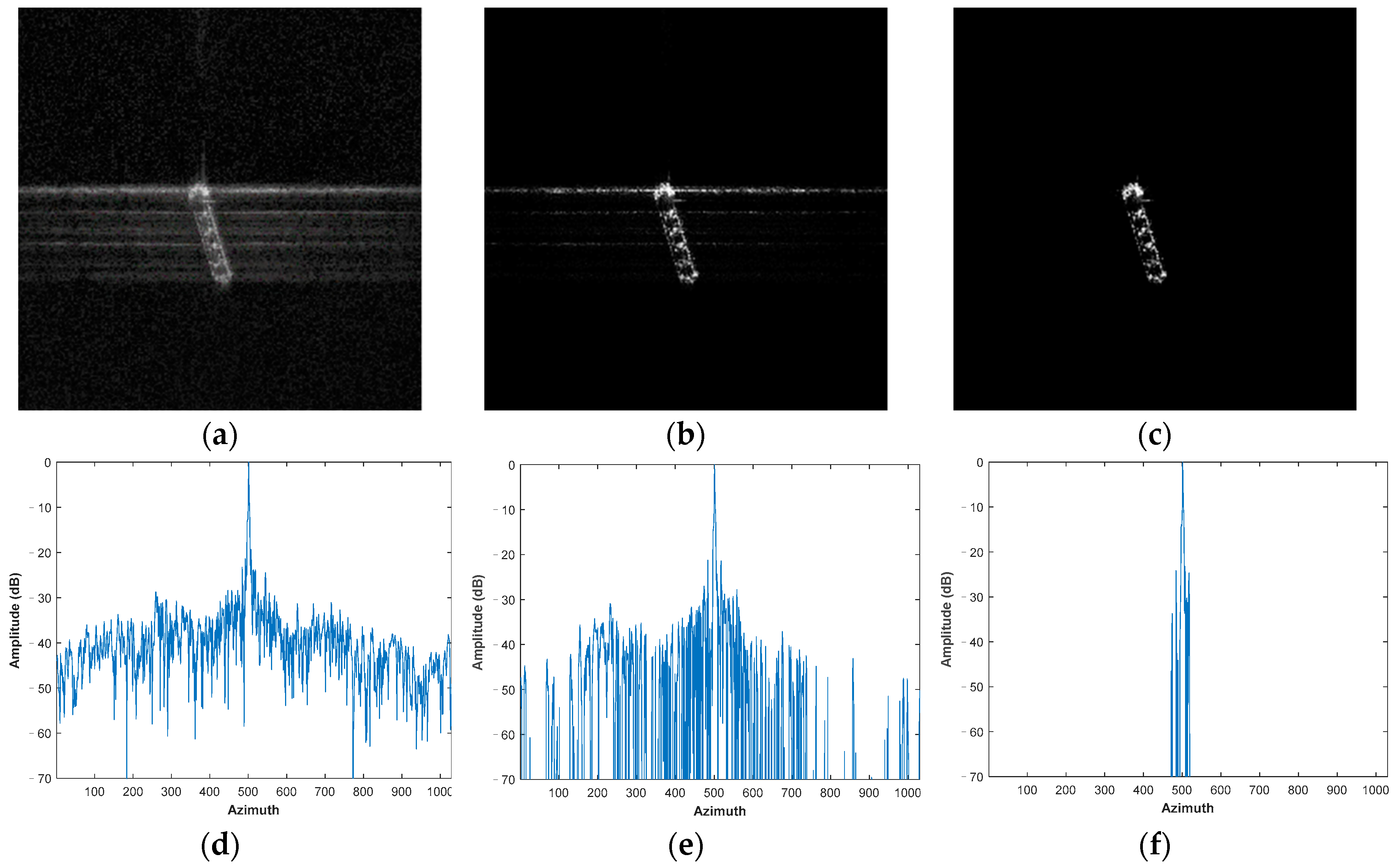
4.3. Airborne Data
4.4. Gaofen-3 Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar-Systems and Signal Processing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1991. [Google Scholar]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithm and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Potter, L.C.; Ertin, E.; Parker, J.T.; Cetin, M. Sparsity and Compressed Sensing in Radar Imaging. Proc. IEEE 2010, 98, 1006–1020. [Google Scholar] [CrossRef]
- Ender, J. A brief review of compressive sensing applied to radar. In Proceedings of the 14th International Radar Symposium (IRS), Dresden, Germany, 19–21 May 2013; IEEE: Piscataway, NJ, USA, 2013; Volume 1, pp. 3–16. [Google Scholar]
- Cetin, M.; Stojanovic, I.; Onhon, O.; Varshney, K.; Samadi, S.; Karl, W.C.; Willsky, A.S. Sparsity-driven synthetic aperture radar imaging: Reconstruction, autofocusing, moving targets, and compressed sensing. IEEE Signal Process. Mag. 2014, 31, 27–40. [Google Scholar] [CrossRef]
- Zhang, B.C.; Hong, W.; Wu, Y.R. Sparse microwave imaging: Principles and applications. Sci. China Inf. Sci. 2012, 55, 1722–1754. [Google Scholar] [CrossRef]
- Patel, V.M.; Easley, G.R.; Healy, D.M., Jr.; Chellappa, R. Compressed synthetic aperture radar. IEEE J. Sel. Top. Signal Process. 2010, 4, 244–254. [Google Scholar] [CrossRef]
- Luo, H.; Li, Z.; Dong, Z.; Yu, A.; Zhang, Y.; Zhu, X. Super-Resolved Multiple Scatterers Detection in SAR Tomography Based on Compressive Sensing Generalized Likelihood Ratio Test (CS-GLRT). Remote Sens. 2019, 11, 1930. [Google Scholar] [CrossRef]
- Aghababaee, H.; Ferraioli, G.; Ferro-Famil, L.; Schirinzi, G.; Huang, Y. Sparsity Based Full Rank Polarimetric Reconstruction of Coherence Matrix T. Remote Sens. 2019, 11, 1288. [Google Scholar] [CrossRef]
- Zhu, X.X.; Wang, Y.; Montazeri, S.; Ge, N. A review of ten-year advances of multi-baseline SAR interferometry using TerraSAR-X data. Remote Sens. 2018, 10, 1374. [Google Scholar] [CrossRef]
- Zhang, S.; Dong, G.; Kuang, G. Superresolution downward-looking linear array three-dimensional SAR imaging based on two-dimensional compressive sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2184–2196. [Google Scholar] [CrossRef]
- Zhu, X.; He, F.; Ye, F.; Dong, Z.; Wu, M. Sidelobe Suppression with Resolution Maintenance for SAR Images via Sparse Representation. Sensors 2018, 18, 1589. [Google Scholar] [CrossRef]
- Batu, O.; Çetin, M. Parameter selection in sparsity-driven SAR imaging. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 3040–3050. [Google Scholar] [CrossRef]
- Fang, J.; Xu, Z.; Zhang, B.; Hong, W.; Wu, Y. Fast compressed sensing SAR imaging based on approximated observation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 352–363. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, Z.; Jiang, C.; Zhao, Y.; Hong, W.; Wu, Y. System design and first airborne experiment of sparse microwave imaging radar: Initial results. Sci. China Inf. Sci. 2015, 58, 1–10. [Google Scholar] [CrossRef]
- Bi, H.; Zhang, B.; Zhu, X.X.; Jiang, C.; Hong, W. Extended chirp scaling-baseband azimuth scaling-based azimuth-range decouple L1 regularization for TOPS SAR imaging via CAMP. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3748–3763. [Google Scholar] [CrossRef]
- Bi, H.; Zhang, B.; Zhu, X.; Hong, W. Azimuth-range decouple-based L1 regularization method for wide ScanSAR imaging via extended chirp scaling. J. Appl. Remote Sens. 2017, 11, 015007. [Google Scholar] [CrossRef]
- Quan, X.; Zhang, B.; Zhu, X.X.; Wu, Y. Unambiguous SAR Imaging for Nonuniform DPC Sampling: ℓq Regularization Method Using Filter Bank. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1596–1600. [Google Scholar] [CrossRef]
- Wei, Z.; Zhang, B.; Wu, Y. Accurate Wide Angle SAR Imaging Based on LS-CS-Residual. Sensors 2019, 19, 490. [Google Scholar] [CrossRef]
- Ender, J. Multi-Channel GMTI via Approximated Observation. In Proceedings of the 20th International Radar Symposium (IRS), Bonn, Germany, 20–22 June 2018; IEEE: Piscataway, NJ, USA, 2019; pp. 1–9. [Google Scholar]
- Bi, H.; Bi, G.; Zhang, B.; Hong, W. Complex-image-based sparse SAR imaging and its equivalence. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5006–5014. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, B.; Bi, H.; Wu, C.; Wei, Z. Comparison of Raw Data-Based and Complex Image-Based Sparse SAR Imaging Methods. Sensors 2019, 19, 320. [Google Scholar] [CrossRef]
- Candès, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- Kim, S.J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An interior-point method for large-scale ℓ1-regularized least. IEEE J. Sel. Top. Sign. Proces. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346. [Google Scholar] [CrossRef]
- Chartrand, R. Exact reconstruction of sparse signals via nonconvex minimization. IEEE Signal Process. Lett. 2007, 14, 707–710. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, H.; Wang, Y.; Chang, X.; Liang, Y. L1/2 regularization. Sci. China Inf. Sci. 2010, 53, 1159–1169. [Google Scholar] [CrossRef]
- Tropp, J.A. Greed is good: Algorithmic results for sparse approximation. IEEE Trans. Inf. Theory 2004, 50, 2231–2242. [Google Scholar] [CrossRef]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Daubechies, I.; Defrise, M.; De Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. J. Issued Courant Inst. Math. Sci. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Anitori, L.; Maleki, A.; Otten, M.; Baraniuk, R.G.; Hoogeboom, P. Design and analysis of compressed sensing radar detectors. IEEE Trans. Signal Process. 2012, 61, 813–827. [Google Scholar] [CrossRef]
- Maleki, A.; Anitori, L.; Yang, Z.; Baraniuk, R.G. Asymptotic analysis of complex LASSO via complex approximate message passing (CAMP). IEEE Trans. Inf. Theory 2013, 59, 4290–4308. [Google Scholar] [CrossRef]
- Bi, H.; Zhang, B.; Zhu, X.X.; Hong, W.; Sun, J.; Wu, Y. L1-regularization-based SAR imaging and CFAR detection via complex approximated message passing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3426–3440. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR processing using chirp scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Osher, S.; Ruan, F.; Xiong, J.; Yao, Y.; Yin, W. Sparse recovery via differential inclusions. Appl. Comput. Harmon. Anal. 2016, 41, 436–469. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. The Dantzig selector: Statistical estimation when p is much larger than n. Ann. Stat. 2007, 35, 2313–2351. [Google Scholar] [CrossRef]
- Çetin, M.; Karl, W.C.; Castanón, D.A. Feature enhancement and ATR performance using nonquadratic optimization-based SAR imaging. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1375–1395. [Google Scholar]
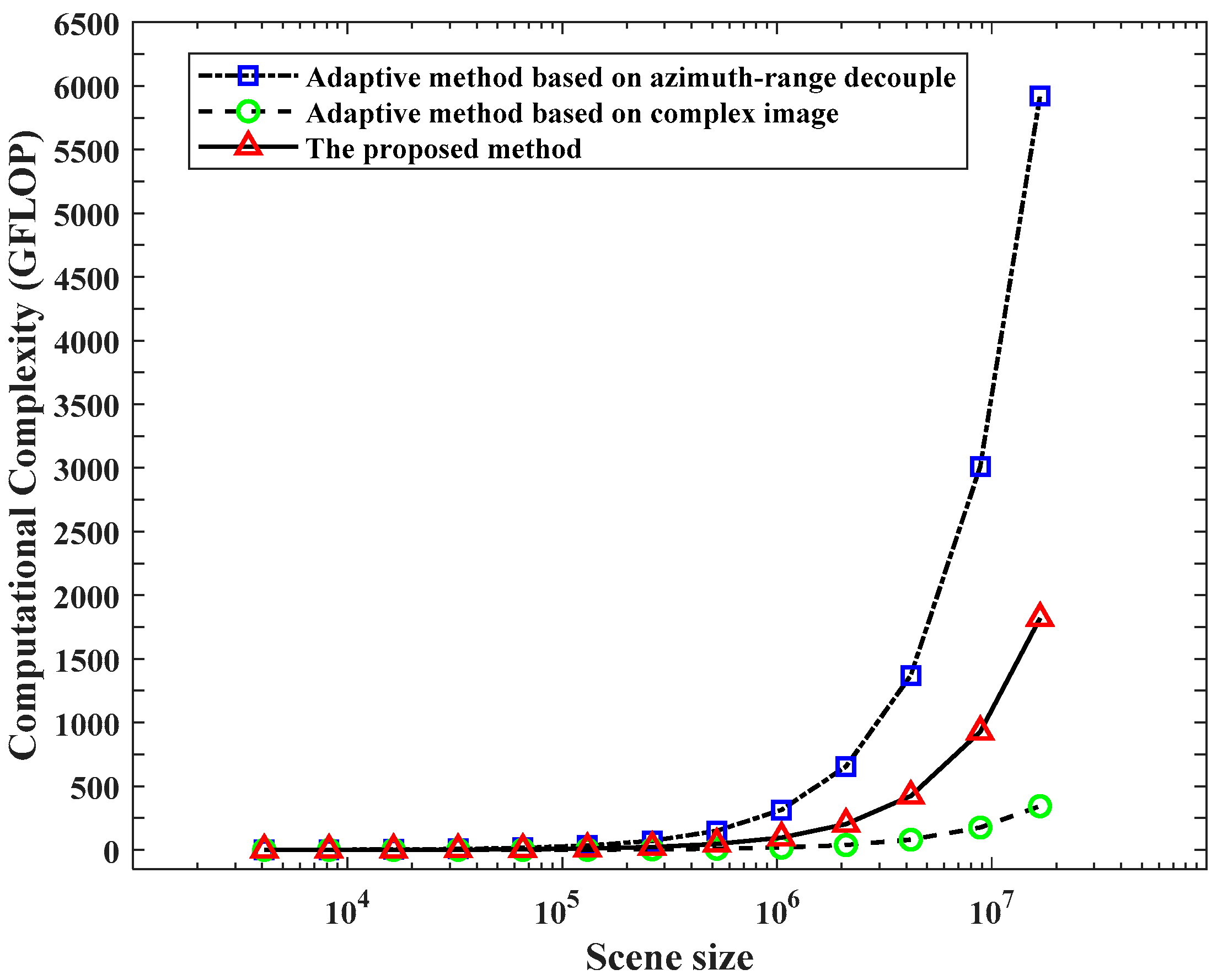
| Adaptive Parameter Estimation Methods | Computational Complexity (FLOP) | Example (GFLOP) |
|---|---|---|
| Observation Matrix | ||
| Azimuth-Range Decouple | ||
| Complex Image | ||
| The Proposed Method |
| Parameters | Value |
|---|---|
| Center frequency | 5.3 GHz |
| Pulse duration | 2.5 |
| Velocity | 70 m/s |
| Bandwidth | 50 MHz |
| Sampling rate | 60 MHz |
| Pulse repetition frequency (PRF) | 130 Hz |
| Minimum slant range | 3500 m |
| Downsampling Rate | SNR (dB) | Adaptive and RMSE of Different Adaptive Parameter Estimation Methods | |||||
|---|---|---|---|---|---|---|---|
| Azimuth-Range Decouple | Complex Image | The Proposed Method | |||||
| RMSE | RMSE | RMSE | |||||
| 80% | 5 | 0.3178 | 0.6714 | 0.0734 | 0.8329 | 0.3190 | 0.6685 |
| 10 | 0.3204 | 0.5932 | 0.0895 | 0.7762 | 0.3216 | 0.5833 | |
| 15 | 0.3216 | 0.5265 | 0.1282 | 0.6822 | 0.3221 | 0.5254 | |
| 20 | 0.3235 | 0.4887 | 0.1755 | 0.6345 | 0.3242 | 0.4855 | |
| 25 | 0.3237 | 0.4793 | 0.2130 | 0.6109 | 0.3245 | 0.4720 | |
| 60% | 5 | 0.2950 | 0.7944 | 0.0586 | 0.9364 | 0.3031 | 0.7883 |
| 10 | 0.3082 | 0.7146 | 0.0842 | 0.8507 | 0.3127 | 0.7071 | |
| 15 | 0.3128 | 0.6231 | 0.1153 | 0.7926 | 0.3159 | 0.6205 | |
| 20 | 0.3194 | 0.5654 | 0.1483 | 0.7218 | 0.3206 | 0.5611 | |
| 25 | 0.3203 | 0.5590 | 0.1967 | 0.7023 | 0.3211 | 0.5528 | |
| Methods | Target-to-Background Ratio (dB) | ||||
|---|---|---|---|---|---|
| Ship 1 | Ship 2 | Ship 3 | Ship 4 | Ship 5 | |
| MF | 32.09 | 37.28 | 35.30 | 38.53 | 38.48 |
| Based on azimuth-range decouple | 47.61 | 52.26 | 49.72 | 54.08 | 55.71 |
| Based on complex image | 42.24 | 44.46 | 41.71 | 46.74 | 47.57 |
| The proposed method | 47.49 | 51.89 | 49.46 | 53.76 | 55.31 |
| Methods | Azimuth Ambiguity-to-Signal Ratio (dB) | ||||
|---|---|---|---|---|---|
| Ship 1 | Ship 2 | Ship 3 | Ship 4 | Ship 5 | |
| MF | −11.32 | −12.02 | −12.13 | −11.30 | −11.36 |
| Based on azimuth-range decouple | −19.62 | −20.10 | −18.95 | −21.66 | −22.23 |
| Based on complex image | −12.75 | −13.92 | −13.45 | −12.70 | −13.10 |
| The proposed method | −19.43 | −20.23 | −18.62 | −21.25 | −22.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Zhang, B.; Xu, Z.; Wu, Y. Efficient Parameter Estimation for Sparse SAR Imaging Based on Complex Image and Azimuth-Range Decouple. Sensors 2019, 19, 4549. https://doi.org/10.3390/s19204549
Liu M, Zhang B, Xu Z, Wu Y. Efficient Parameter Estimation for Sparse SAR Imaging Based on Complex Image and Azimuth-Range Decouple. Sensors. 2019; 19(20):4549. https://doi.org/10.3390/s19204549
Chicago/Turabian StyleLiu, Mingqian, Bingchen Zhang, Zhongqiu Xu, and Yirong Wu. 2019. "Efficient Parameter Estimation for Sparse SAR Imaging Based on Complex Image and Azimuth-Range Decouple" Sensors 19, no. 20: 4549. https://doi.org/10.3390/s19204549
APA StyleLiu, M., Zhang, B., Xu, Z., & Wu, Y. (2019). Efficient Parameter Estimation for Sparse SAR Imaging Based on Complex Image and Azimuth-Range Decouple. Sensors, 19(20), 4549. https://doi.org/10.3390/s19204549





