Sub-Wavelength Focusing in Inhomogeneous Media with a Metasurface Near Field Plate
Abstract
1. Introduction
2. Design of Near Field Plates
2.1. Underlying Concept and Analytic Treatment
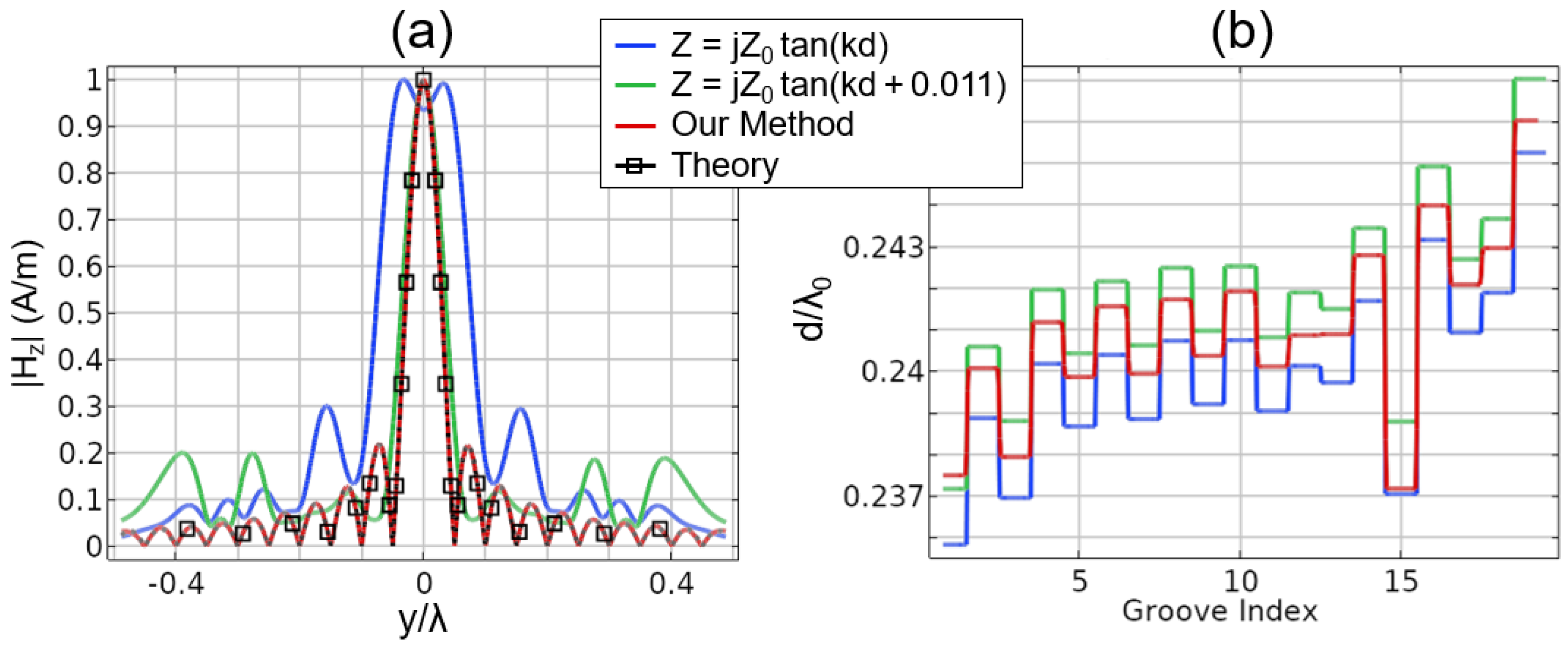
2.2. Rigorous FEM and Lagrange Multiplier Model
2.3. Model Implementation
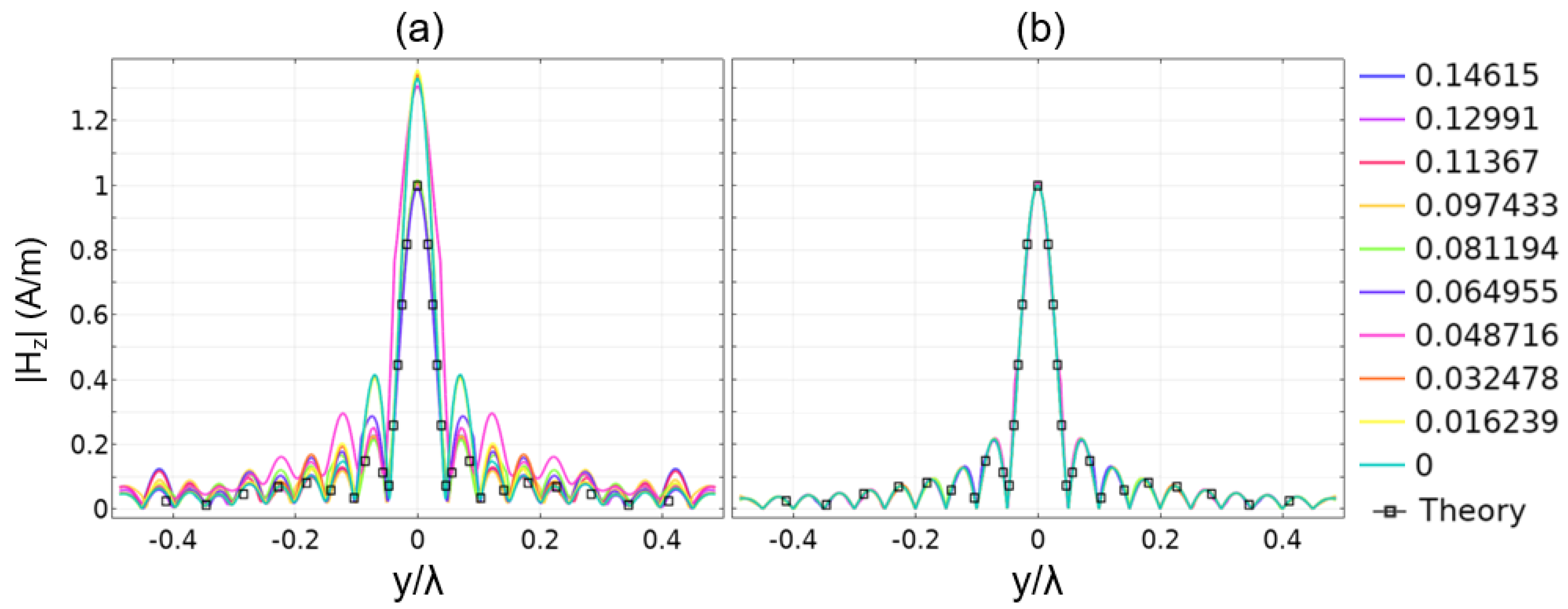
3. Results for the 2D Planar Geometry
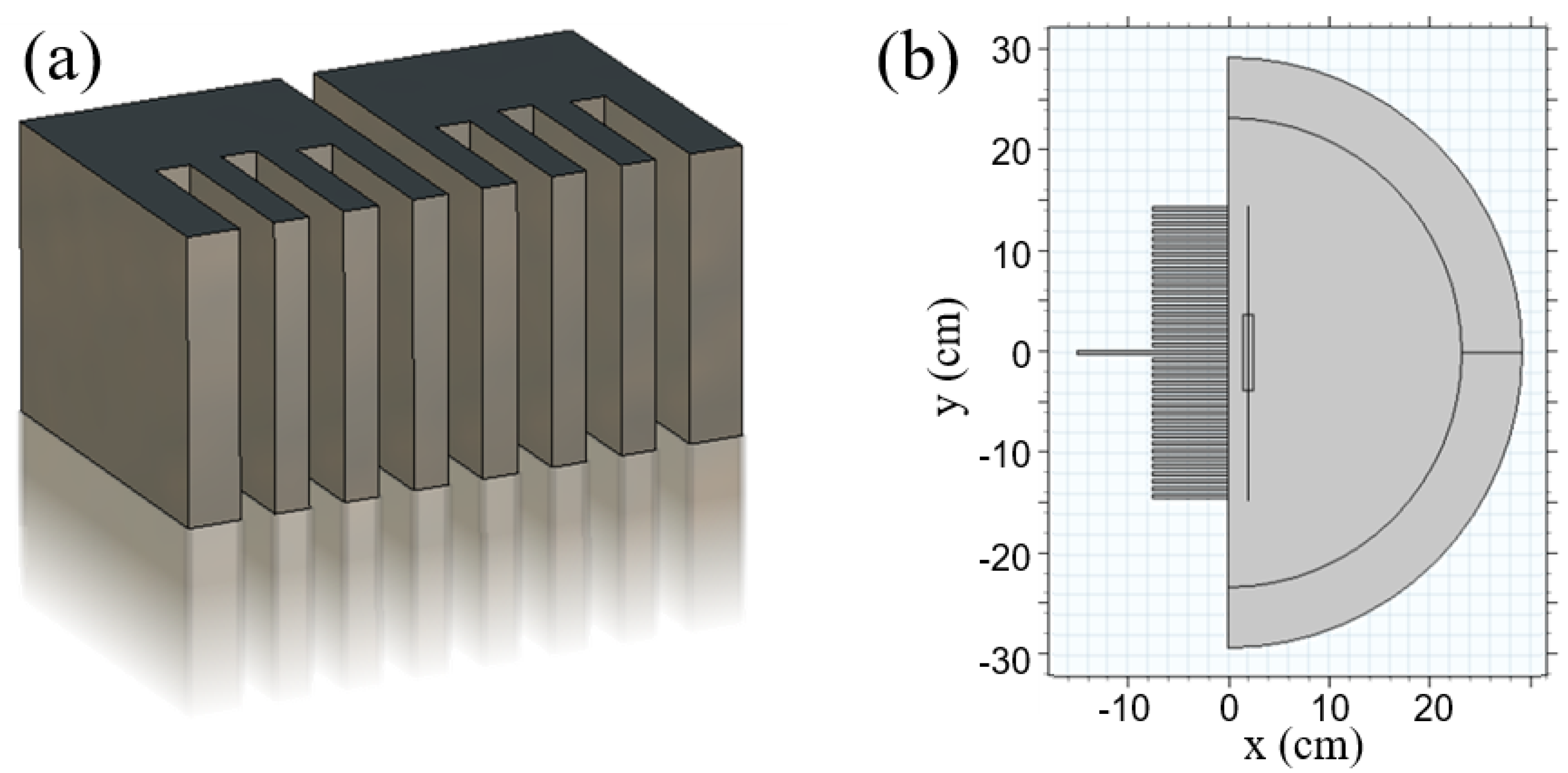
4. Flat, Axisymmetric Near Field Plate
4.1. NFP with Grooves
4.2. NFP with Printed Circuit Board
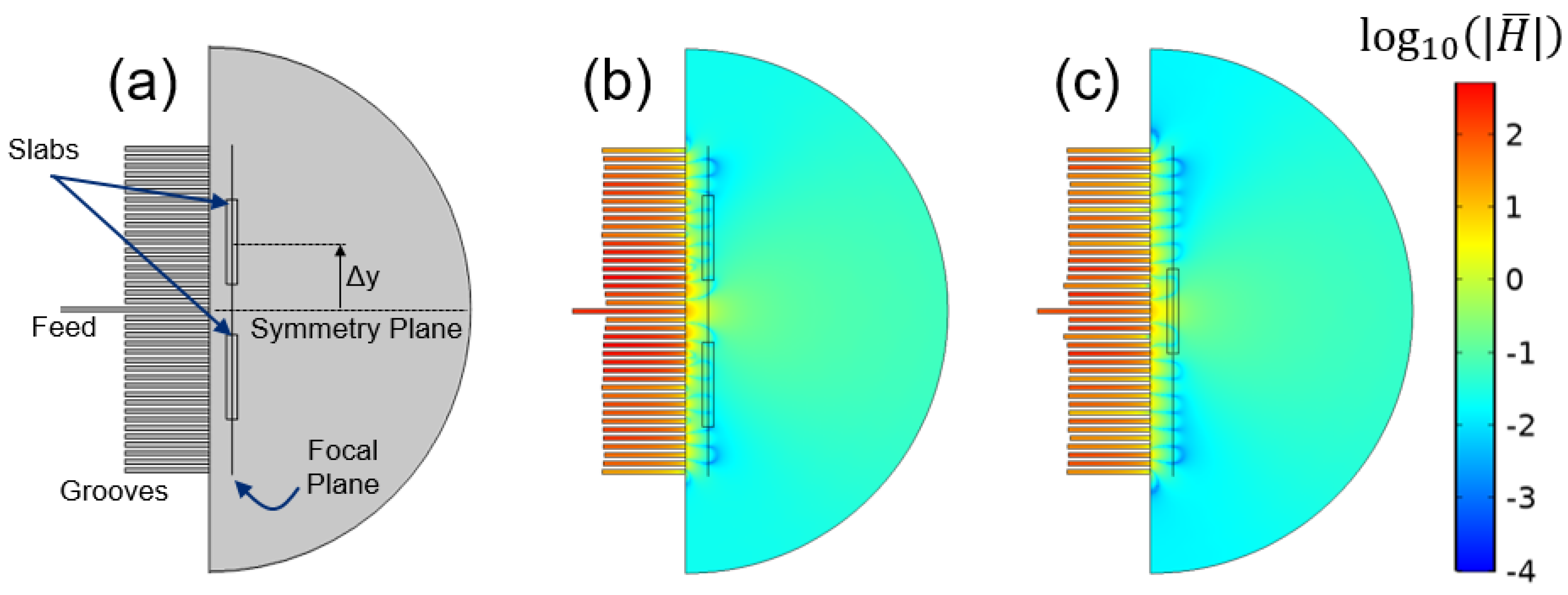
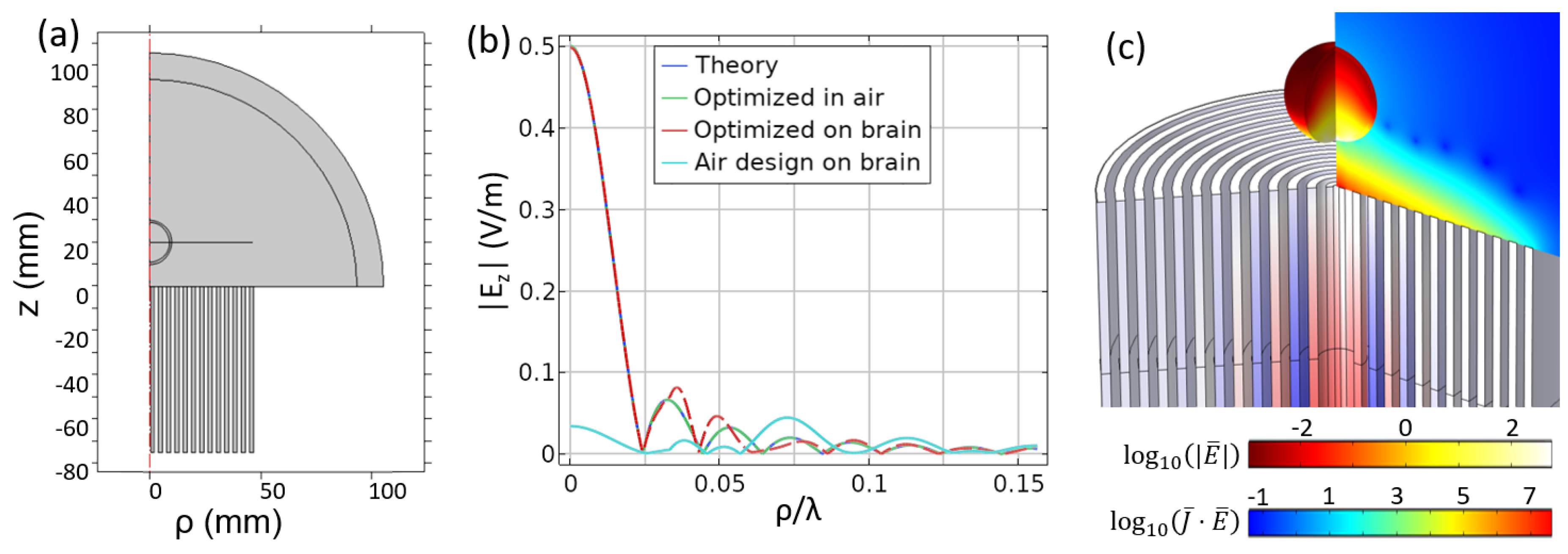
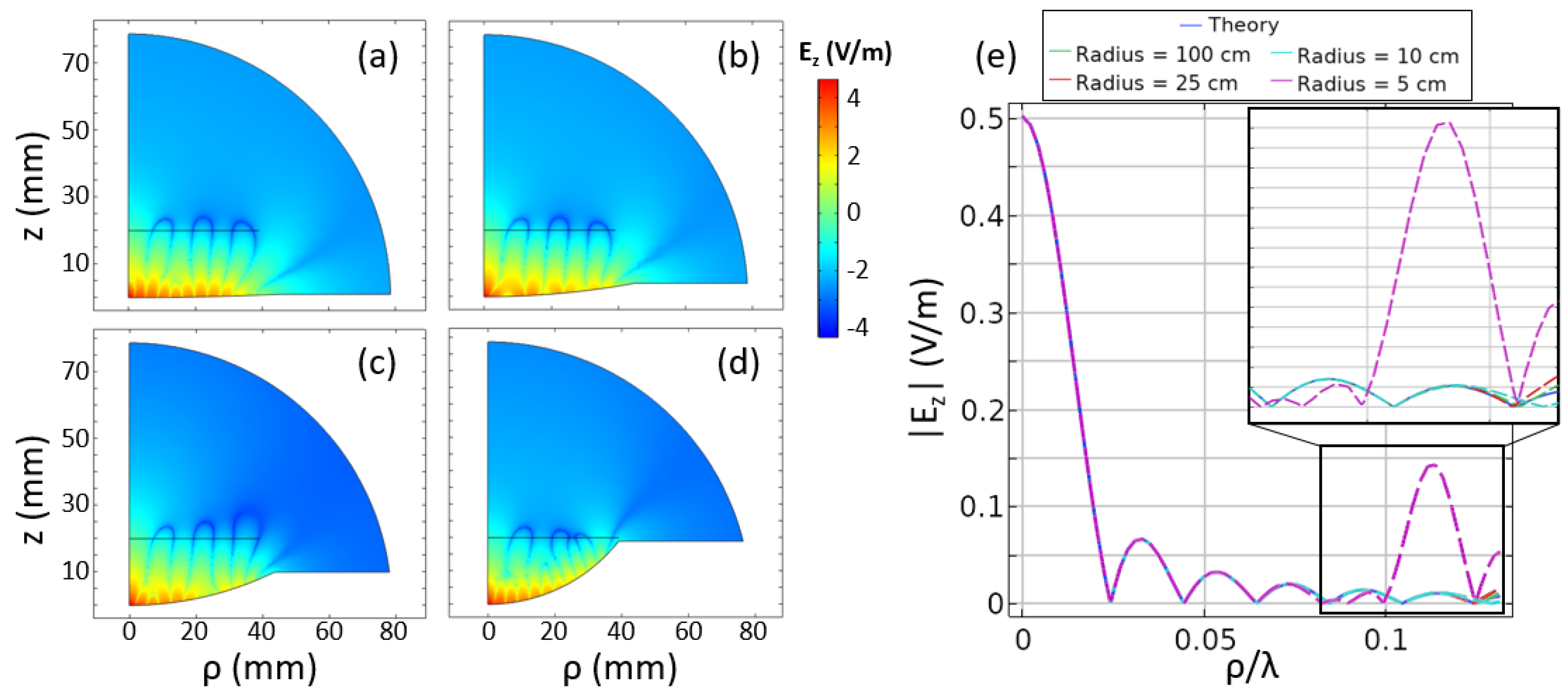
5. Curved, Axisymmetric Near Field Plate
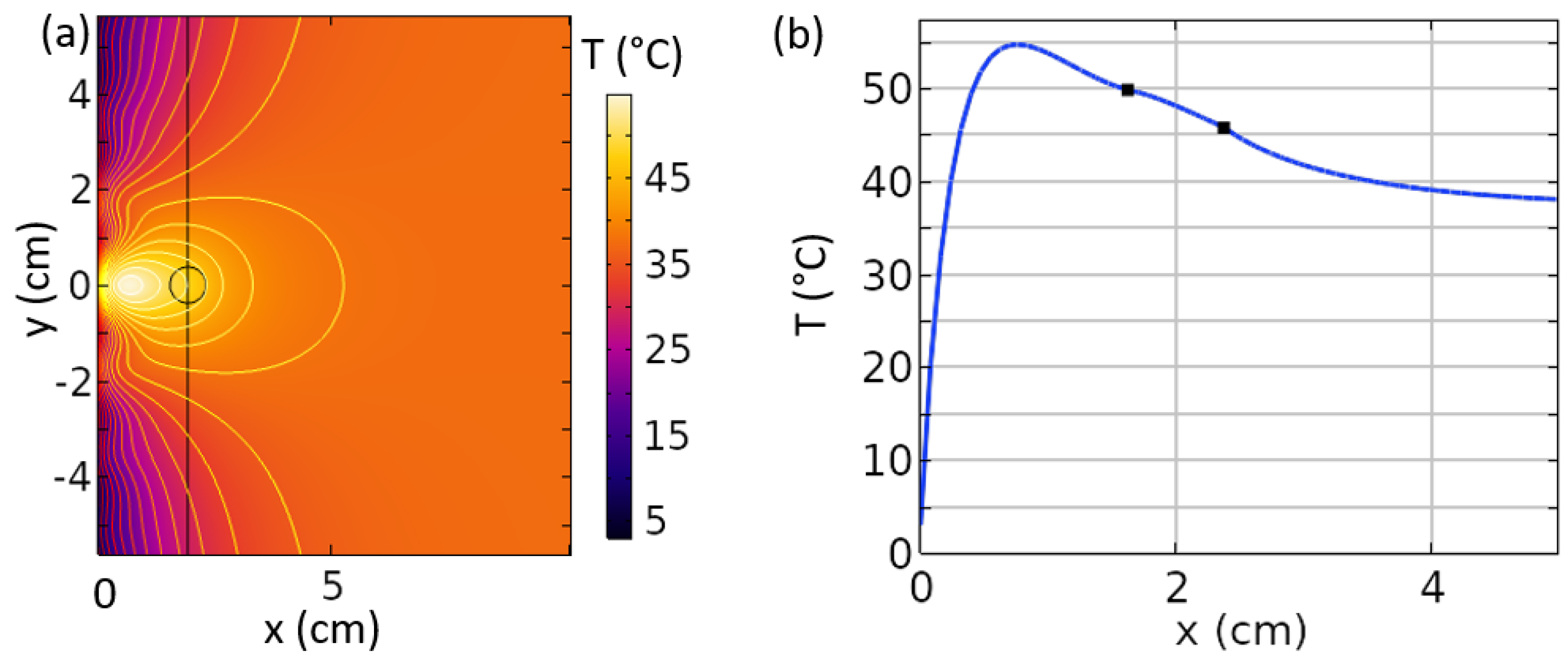
6. Heating Effects and Ablation
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Novotny, L. The history of near-field optics. Prog. Opt. 2007, 50, 137. [Google Scholar]
- Lezec, H.J.; Degiron, A.; Devaux, E.; Linke, R.; Martin-Moreno, L.; Garcia-Vidal, F.; Ebbesen, T. Beaming light from a subwavelength aperture. Science 2002, 297, 820–822. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.; Johnson, S.G.; Joannopoulos, J.; Pendry, J. Subwavelength imaging in photonic crystals. Phys. Rev. B 2003, 68, 045115. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966. [Google Scholar] [CrossRef] [PubMed]
- Fang, N.; Lee, H.; Sun, C.; Zhang, X. Sub–diffraction-limited optical imaging with a silver superlens. Science 2005, 308, 534–537. [Google Scholar] [CrossRef] [PubMed]
- Merlin, R. Radiationless electromagnetic interference: evanescent-field lenses and perfect focusing. Science 2007, 317, 927–929. [Google Scholar] [CrossRef]
- Grbic, A.; Jiang, L.; Merlin, R. Near-field plates: Subdiffraction focusing with patterned surfaces. Science 2008, 320, 511–513. [Google Scholar] [CrossRef]
- Keilmann, F.; Hillenbrand, R.; Zayats, A.; Richard, D. Near-field nanoscopy by elastic light scattering from a tip. In Nano-Optics and Near-Field Optical Microscopy; Artech House: Norwood, MA, USA, 2009; pp. 235–265. [Google Scholar]
- Kim, S.; Ho, J.S.; Chen, L.Y.; Poon, A.S. Wireless power transfer to a cardiac implant. Appl. Phys. Lett. 2012, 101, 073701. [Google Scholar] [CrossRef]
- Converse, M.; Bond, E.J.; Veen, B.; Hagness, C. A computational study of ultra-wideband versus narrowband microwave hyperthermia for breast cancer treatment. IEEE Trans. Microw. Theory Tech. 2006, 54, 2169–2180. [Google Scholar] [CrossRef]
- Converse, M.; Bond, E.J.; Hagness, S.C.; Van Veen, B.D. Ultrawide-band microwave space-time beamforming for hyperthermia treatment of breast cancer: A computational feasibility study. IEEE Trans. Microw. Theory Tech. 2004, 52, 1876–1889. [Google Scholar] [CrossRef]
- Chew, W.C.; Wang, Y.M. Reconstruction of two-dimensional permittivity distribution using the distorted Born iterative method. IEEE Trans. Med. Imaging 1990, 9, 218–225. [Google Scholar] [CrossRef] [PubMed]
- Chen, X. Computational Methods for Electromagnetic Inverse Scattering; Wiley Online Library: Hoboken, NJ, USA, 2018. [Google Scholar]
- Jiang, J.; Sell, D.; Hoyer, S.; Hickey, J.; Yang, J.; Fan, J.A. Free-form diffractive metagrating design based on generative adversarial networks. ACS Nano 2019, 13, 8872–8878. [Google Scholar] [CrossRef] [PubMed]
- Hughes, T.W.; Minkov, M.; Williamson, I.A.; Fan, S. Adjoint method and inverse design for nonlinear nanophotonic devices. ACS Photonics 2018, 5, 4781–4787. [Google Scholar] [CrossRef]
- Logothetis, N.K. The neural basis of the blood–oxygen–level–dependent functional magnetic resonance imaging signal. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2002, 357, 1003–1037. [Google Scholar] [CrossRef]
- Durduran, T.; Yu, G.; Burnett, M.G.; Detre, J.A.; Greenberg, J.H.; Wang, J.; Zhou, C.; Yodh, A.G. Diffuse optical measurement of blood flow, blood oxygenation, and metabolism in a human brain during sensorimotor cortex activation. Opt. Lett. 2004, 29, 1766–1768. [Google Scholar] [CrossRef]
- Grbic, A.; Merlin, R.; Thomas, E.M.; Imani, M.F. Near-field plates: Metamaterial surfaces/arrays for subwavelength focusing and probing. Proc. IEEE 2011, 99, 1806–1815. [Google Scholar] [CrossRef]
- Grbic, A.; Merlin, R. Near-field focusing plates and their design. IEEE Trans. Antennas Propag. 2008, 56, 3159–3165. [Google Scholar] [CrossRef]
- Imani, M.F.; Grbic, A. Near-field focusing with a corrugated surface. IEEE Antennas Wirel. Propag. Lett. 2009, 8, 421–424. [Google Scholar] [CrossRef]
- Imani, M.F.; Grbic, A. Planar near-field plates. IEEE Trans. Antennas Propag. 2013, 61, 5425–5434. [Google Scholar] [CrossRef]
- Imani, M.F.; Grbic, A. Generating evanescent Bessel beams using near-field plates. IEEE Trans. Antennas Propag. 2012, 60, 3155–3164. [Google Scholar] [CrossRef]
- Holloway, C.L.; Kuester, E.F.; Gordon, J.A.; O’Hara, J.; Booth, J.; Smith, D.R. An overview of the theory and applications of metasurfaces: The two-dimensional equivalents of metamaterials. IEEE Antennas Propag. Mag. 2012, 54, 10–35. [Google Scholar] [CrossRef]
- Achouri, K.; Salem, M.A.; Caloz, C. General metasurface synthesis based on susceptibility tensors. IEEE Trans. Antennas Propag. 2015, 63, 2977–2991. [Google Scholar] [CrossRef]
- Tretyakov, S.A.; Maslovski, S.; Belov, P.A. An analytical model of metamaterials based on loaded wire dipoles. IEEE Trans. Antennas Propag. 2003, 51, 2652–2658. [Google Scholar] [CrossRef]
- Pulido-Mancera, L.; Bowen, P.T.; Imani, M.F.; Kundtz, N.; Smith, D. Polarizability extraction of complementary metamaterial elements in waveguides for aperture modeling. Phys. Rev. B 2017, 96, 235402. [Google Scholar] [CrossRef]
- Johnson, M.; Bowen, P.; Kundtz, N.; Bily, A. Discrete-dipole approximation model for control and optimization of a holographic metamaterial antenna. Appl. Opt. 2014, 53, 5791–5799. [Google Scholar] [CrossRef] [PubMed]
- Elliott, R. On the theory of corrugated plane surfaces. Trans. IRE Prof. Group Antennas Propag. 1954, 2, 71–81. [Google Scholar] [CrossRef]
- Jones, E. An annular corrugated-surface antenna. Proc. IRE 1952, 40, 721–725. [Google Scholar] [CrossRef]
- Pfeiffer, C.; Grbic, A. Metamaterial Huygens’ surfaces: Tailoring wave fronts with reflectionless sheets. Phys. Rev. Lett. 2013, 110, 197401. [Google Scholar] [CrossRef]
- Reddy, J.N. Introduction to the Finite Element Method, 3rd ed.; McGraw-Hill Education: New York, NY, USA, 2006. [Google Scholar]
- Gowda, V.R.; Imani, M.F.; Sleasman, T.; Yurduseven, O.; Smith, D.R. Focusing Microwaves in the Fresnel Zone with a Cavity-Backed Holographic Metasurface. IEEE Access 2018, 6, 12815–12824. [Google Scholar] [CrossRef]
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues. Version 4.0. Available online: https://itis.swiss/database (accessed on 15 May 2018).
- F. Imani, M.; Sleasman, T.; Gollub, J.N.; Smith, D.R. Analytical modeling of printed metasurface cavities for computational imaging. J. Appl. Phys. 2016, 120, 144903. [Google Scholar] [CrossRef]
- Boyarsky, M.; Sleasman, T.; Pulido-Mancera, L.; Diebold, A.V.; Imani, M.F.; Smith, D.R. Single-frequency 3D synthetic aperture imaging with dynamic metasurface antennas. Appl. Opt. 2018, 57, 4123–4134. [Google Scholar] [CrossRef] [PubMed]
- Sleasman, T.; Boyarsky, M.; Imani, M.F.; Fromenteze, T.; Gollub, J.N.; Smith, D.R. Single-frequency microwave imaging with dynamic metasurface apertures. JOSA B 2017, 34, 1713–1726. [Google Scholar] [CrossRef]
- Agrawal, D.R.; Tanabe, Y.; Weng, D.; Ma, A.; Hsu, S.; Liao, S.Y.; Zhen, Z.; Zhu, Z.Y.; Sun, C.; Dong, Z.; et al. Conformal phased surfaces for wireless powering of bioelectronic microdevices. Nat. Biomed. Eng. 2017, 1, 0043. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Ren, Z.; Boybay, M.S.; Ramahi, O.M. Waveguide probe loaded with split-ring resonators for crack detection in metallic surfaces. IEEE Trans. Microw. Theory Tech. 2014, 62, 871–878. [Google Scholar] [CrossRef]



| Background | Tumor | |
|---|---|---|
| Relative Permittivity | 15.66 | 50.74 |
| Electrical Conductivity, S/m | 1.03 | 4.82 |
| Density, kg/m3 | 1069 | 1182 |
| Heat Capacity, J/(kg·K) | 2279 | 3049 |
| Thermal Conductivity, W/(m·K) | 0.306 | 0.496 |
| Metabolic Heat Source, W/m3 | 350 | 5500 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strikwerda, A.C.; Sleasman, T.; Anderson, W.; Awadallah, R. Sub-Wavelength Focusing in Inhomogeneous Media with a Metasurface Near Field Plate. Sensors 2019, 19, 4534. https://doi.org/10.3390/s19204534
Strikwerda AC, Sleasman T, Anderson W, Awadallah R. Sub-Wavelength Focusing in Inhomogeneous Media with a Metasurface Near Field Plate. Sensors. 2019; 19(20):4534. https://doi.org/10.3390/s19204534
Chicago/Turabian StyleStrikwerda, Andrew C., Timothy Sleasman, William Anderson, and Ra’id Awadallah. 2019. "Sub-Wavelength Focusing in Inhomogeneous Media with a Metasurface Near Field Plate" Sensors 19, no. 20: 4534. https://doi.org/10.3390/s19204534
APA StyleStrikwerda, A. C., Sleasman, T., Anderson, W., & Awadallah, R. (2019). Sub-Wavelength Focusing in Inhomogeneous Media with a Metasurface Near Field Plate. Sensors, 19(20), 4534. https://doi.org/10.3390/s19204534





