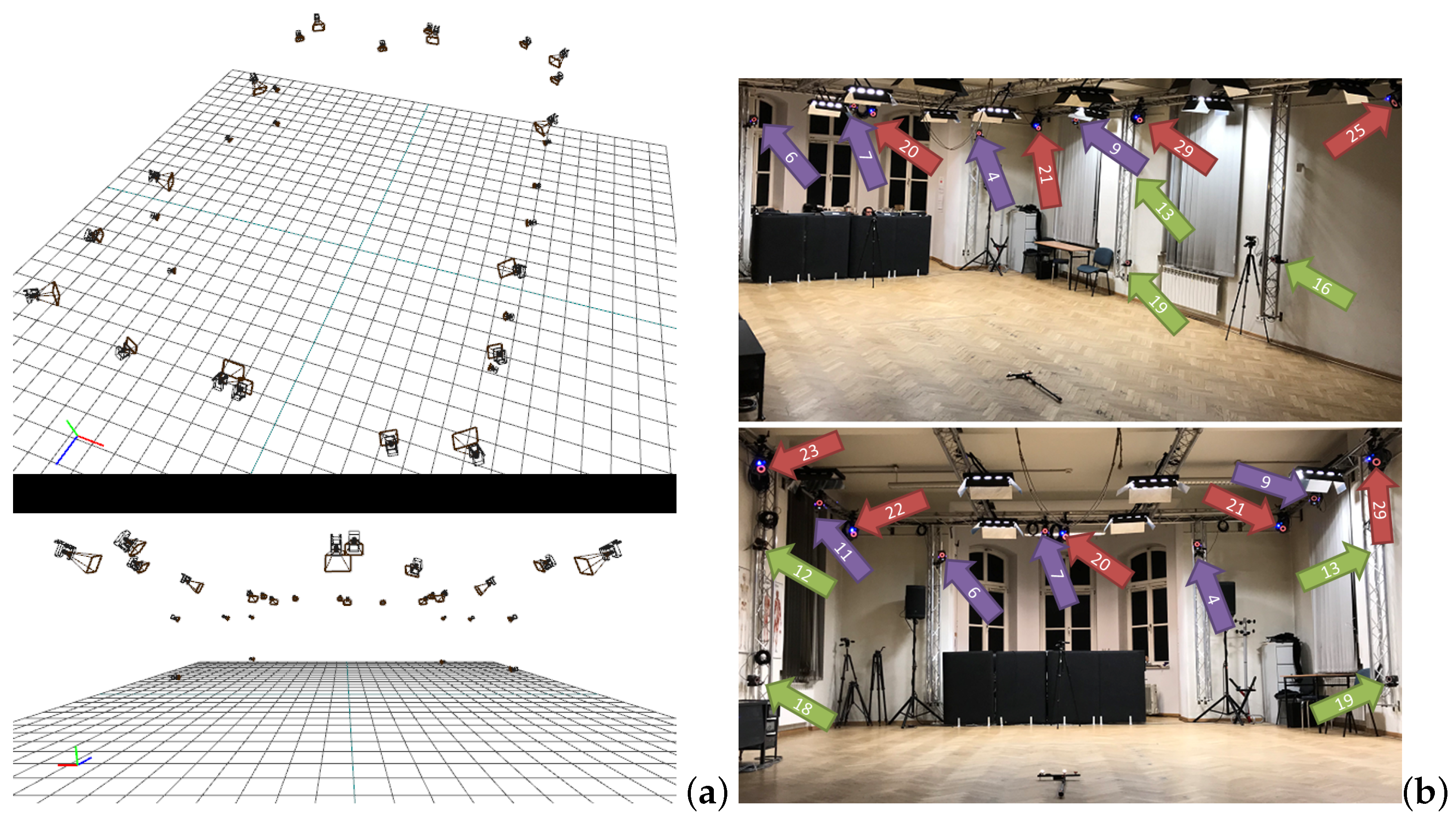
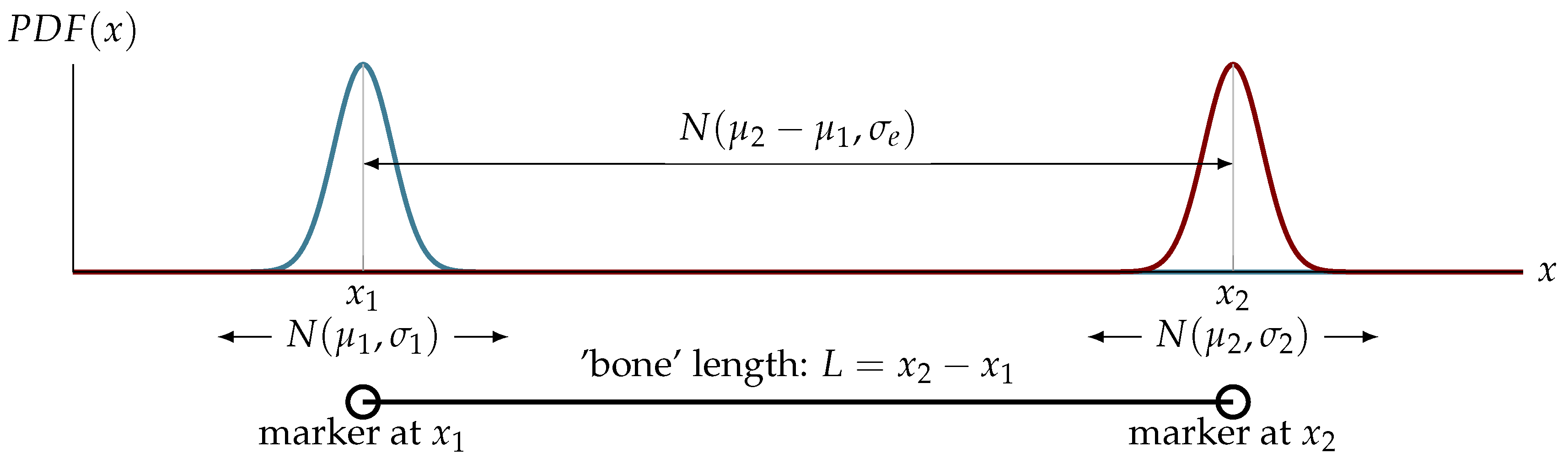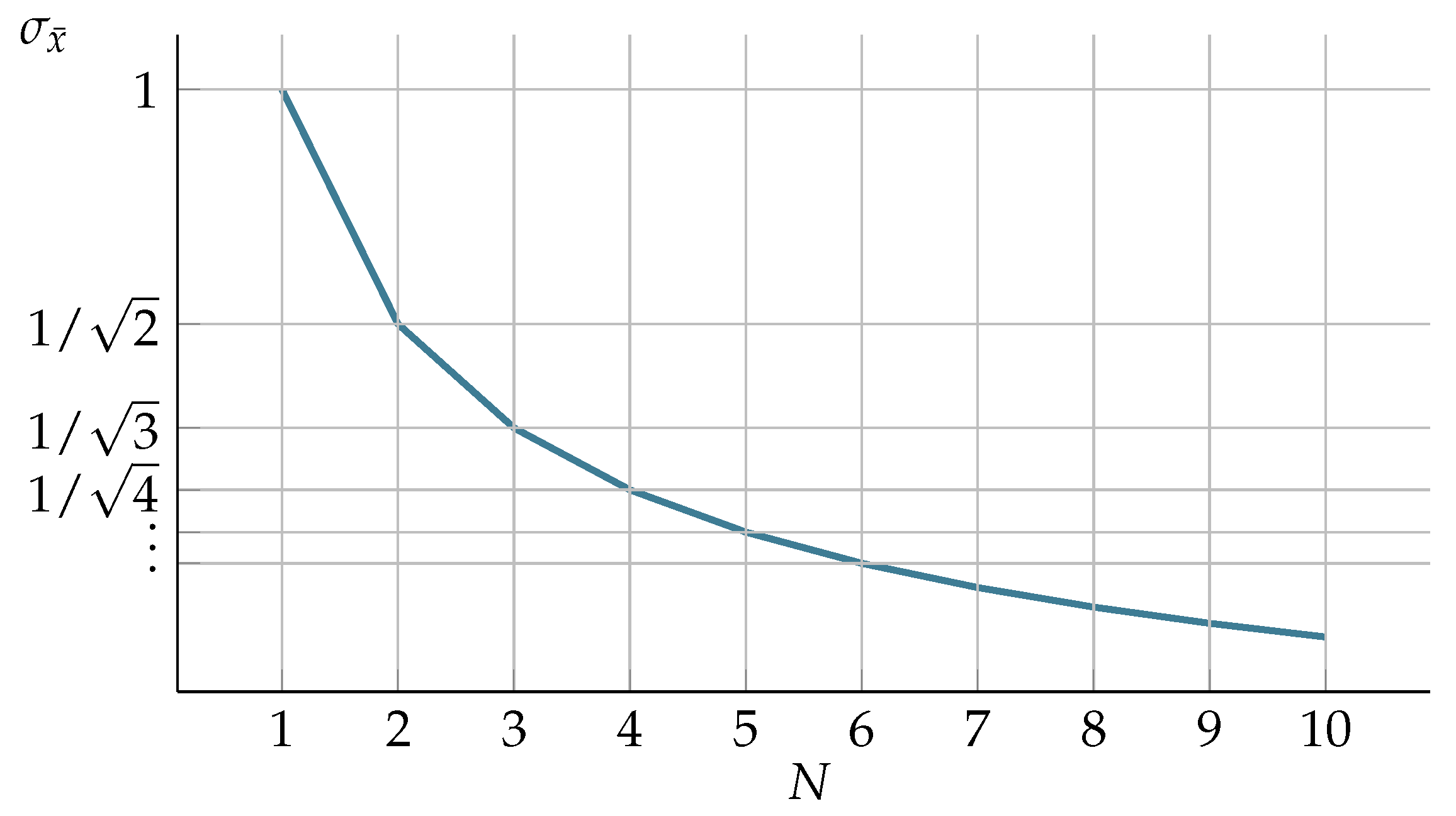2.1. Previous Works
The accuracy and precision in different OMCs were subject to analysis in several works [
10,
11,
12,
13]. In those works, the most frequently studied OMCs are one of Vicon System (MX, Bonita, and V-series), or the OptiTrack system. Regardless of the system used, the authors of these studies agree that the most important factor that influences the data is camera calibration. Camera calibration originates from photogrammetry [
14], it relies on positioning the cameras in a virtual 3D space so that they correspond to the cameras positions in the laboratory. This position and several (minimum two) 2D camera projections of markers are used to reconstruct markers in 3D space [
15]. The calibration quality is determined using average re-projection error. This is the mean distance between the 2D image of the markers on camera and 3D reconstructions of those markers projected back to the camera’s sensor in pixels.
Early works modeled the noise in frequency-based fashion for signal processing needs. Values of a high frequency were considered to be noise that needed to be removed. They were identified or as residuals from the ‘right’ motion modeled by slowly varying curves (low-order polynomials, splines, or Fourier series of low order) [
16,
17], or by conventional Butterworth filtering [
18,
19], where the cut-off frequency was identified by the lack of autocorrelation in the filtered-out residuals.
Windolf et al. [
11] reported that performance of OMC strongly depends on their individual setup and that accuracy and precision should be determined for an individual laboratory installation. They tested both accuracy as a root-mean-square (RMS) error from ground truth and precision as a standard deviation of measured positions in a four camera Vicon 460 system. As a ground truth they employed a custom-built robot mounted L-shaped template. They verified the influence of changing the camera setup, calibration volume, marker size and lens filter application. In the best case they report 63 ± 5 μm accuracy and 15 μm precision.
In another study, Jensenius et al. [
13] tested two OMC systems: Optitrack and Qualisys. They used constancy of position as a quality criterion and identified marker position drifting over the time. They measured drifting velocity (in mm/s) and drifting range (in mm) that identifies volume of uncertainty for marker position. They also emphasize role of proper calibration for the performance of OMC, and coverage of the area within the calibration procedure.
In the work of Carse et al. [
12], three optical 3D motion analysis systems were compared, one of which was a new low-cost system (Optitrack), and two which were considerably more expensive (Vicon 612 and Vicon MX). They used a rigid cluster of markers and measured inter-marker distance and its standard deviation (SD) as a quality criterion for a walking task in an unknown, but adequately large volume. They reached SD values between 0.11–3.7 mm depending on the OMC system.
Results confirming high quality position measurement, using Vicon MX with 5 Vicon F-40 cameras, were obtained in the work by Yang et al. [
20]. They considered whether the OMC could be used for the subtle bone deformation during exercises; the task required accuracy better than 20 μm. As a test template they used markers mounted on the computer numerical controlled (CNC) milling machine with 1 μm spatial resolution. They tested influence of marker size for cameras located very close to the observed, quite small, volume (0.4 × 0.3 × 0.3 m). They confirmed that it is possible to achieve the RMSE accuracy and precision to be 1.2–1.8 μm and 1.5–2.5 μm respectively.
Eichelberger et al. [
10] investigated the influence of various recording parameters on the accuracy using Vicon Bonita cameras. These are the number of cameras (6, 8 and 10), measurement height (foot, knee and hip) and movement (static and dynamic). All these affected the system accuracy significantly.
Another notable work was conducted by Merriaux et al. [
21]. They performed two experimental error estimations in 8 Vicon T40 camera OMC in moderate volume 2 × 1.5 × 1 m. They used two sophisticated robotic templates for static and dynamic (fast rotating blade) cases. In the static case, the estimated errors are mean absolute error (MAE) 0.15 mm for accuracy and RMSE of 0.015 mm for precision. In the dynamic case, the observed accuracy was larger, yet still satisfying, it achieved values between 0.3 mm to <2 mm. They demonstrated also that it depends on the object velocity and sampling frequency.
Slightly different, yet interesting study on noise [
22] involved aquatic OMC based on Vicon T40 cameras, where the scene was a water-filled tank, cameras are located externally in dry locations and the markers made of dedicated reflective tape (SOLAS) are submerged. They demonstrated no significant difference in accuracy and precision due to various mediums in the optical path.
The technological side of an OMC is not the only source of distortions in the system. In the work of Capozzo et al. [
23], the mechanics of markers placed on the skin was emphasized as a source of distortions in OMC. Further, it has been practically considered in the work of Alexander and Andriacchi [
24], where skin motion-based distortions were suppressed. Clusters of marker positions were observed in a non-disclosed OMC. Bone orientation was estimated and evaluated, but marker positions were also analyzed; however, they were not the main quality criterion. They were able to reduce marker location error from 0.025 to 0.008 cm and the average bone orientation error from 0.370 to 0.083 degrees.
Various requirements towards the system uncertainty were specified in the literature. They depend on the applications and recorded tasks [
1]. Some applications may require very high accuracy and precision achievable in a small volume, whereas most of the motion capture labs need larger observed volume at the expense of quality for practical purposes [
25]. Moreover, due to various process dynamics and to avoid motion blur, some tasks may require much higher sampling frequency than 100–120 Hz, which is typically used. Detailed handwriting analysis for subtle symptoms of cognitive issues requires small volume but high accuracy and frequent sampling [
26], whereas for some sports activities the volumes might be huge but the accuracy of meters is enough [
27]. Even the same area of applications may require very different parameters of motion acquisition. Exemplarily, in medical applications, the aforementioned [
20] bone deformation acquisition needs high accuracy in small volume; whereas the behavioral study of the surgery staff [
28], which took place in 6 × 6 m operating room, resulted in 10% of recordings, which were inconclusive for identification of a subject.
2.2. Simple Preliminary Gaussian Model
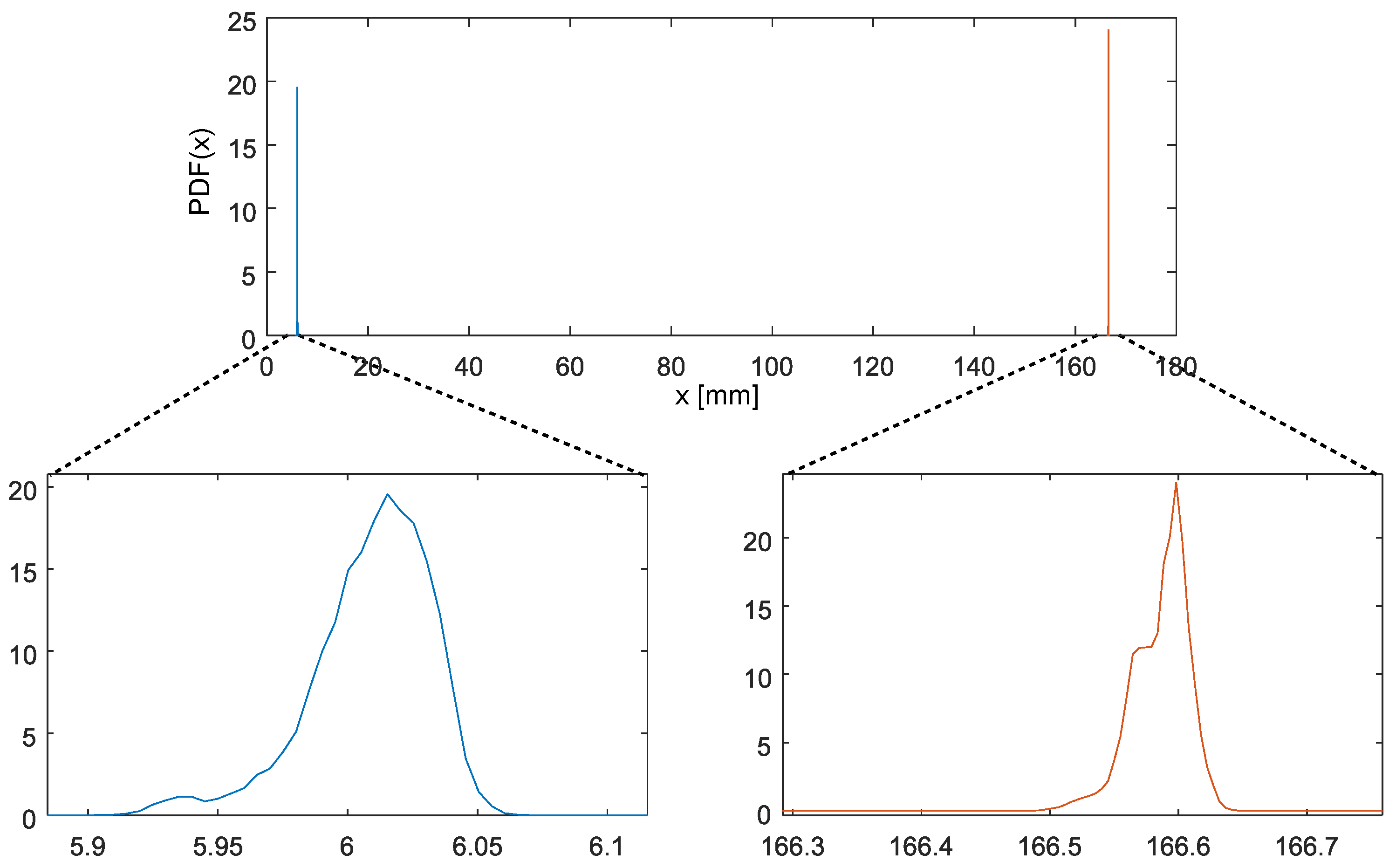
Locating markers in a scene is a continuous process occurring frame-by-frame at the requested sampling frequency. The measurement of the location of a marker can be presumed to be an actual location signal plus additive Gaussian white noise, consequently, locating of each marker location is an independent statistical process. One dimensional case, as depicted in
Figure 1, can be described with normal probability density function:
where:
denotes actual location of
kth marker in a scene.
denotes normal (Gaussian) distribution, which for real location at
is estimated as a mean
, and standard deviation
, that (at best) should be common for all the same markers (of a same size).
The typical uncertainty analysis in measurements employs two factors accuracy and precision [
29]—the accuracy that describes how close the estimate
is to actual location
and describes the systematic error, whereas
reflects the precision of measurement and describes random part of the error.
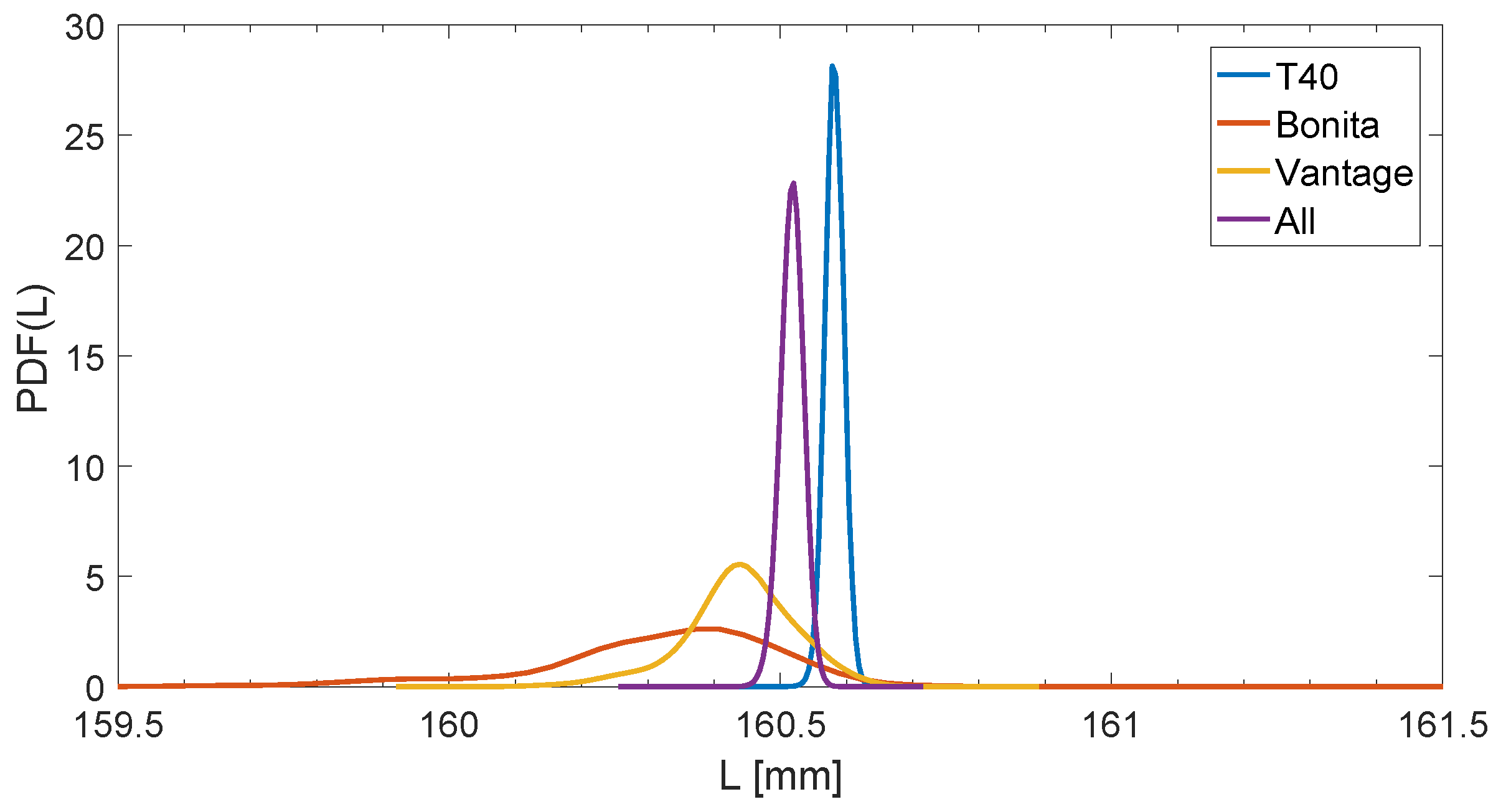
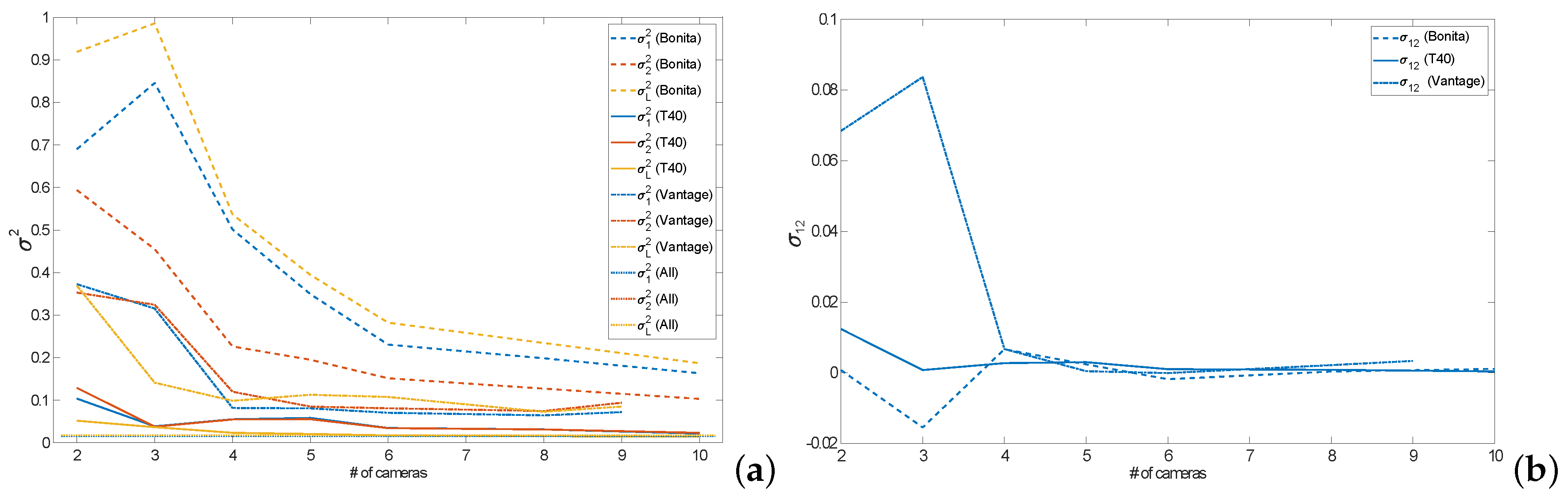
Extending the estimation of a marker model to the estimation of a length (
L) of a bone, it yields a difference of double marker location measurements, hence its probability density function is described:
where:
—expected (in common sense) mean value,
—expected standard deviation, which might take different forms, depending on the case:
—for two identical (), independent variances (covariance ),
—for two different (), independent variances (),
—for two different (), correlated variances ().
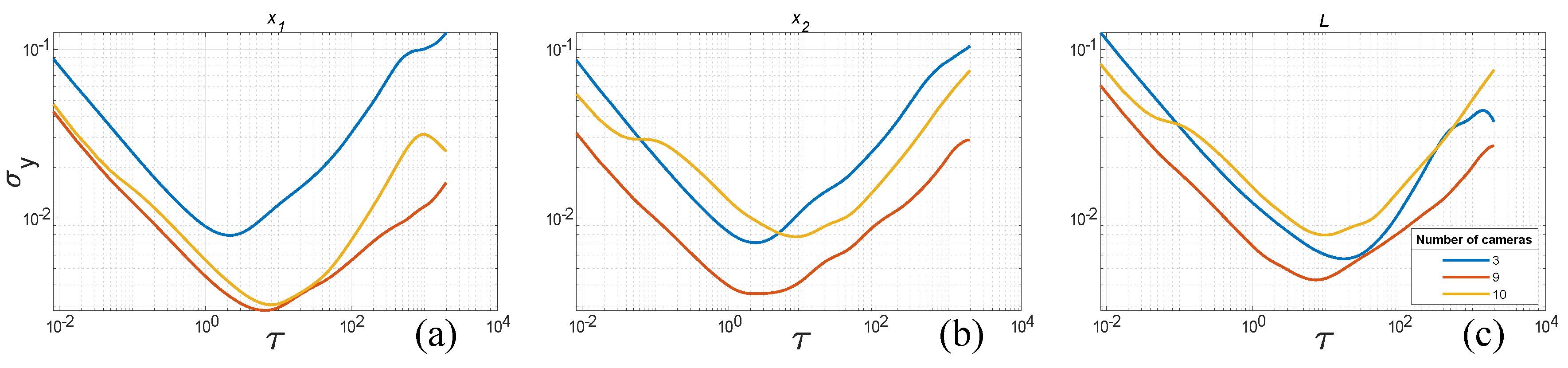
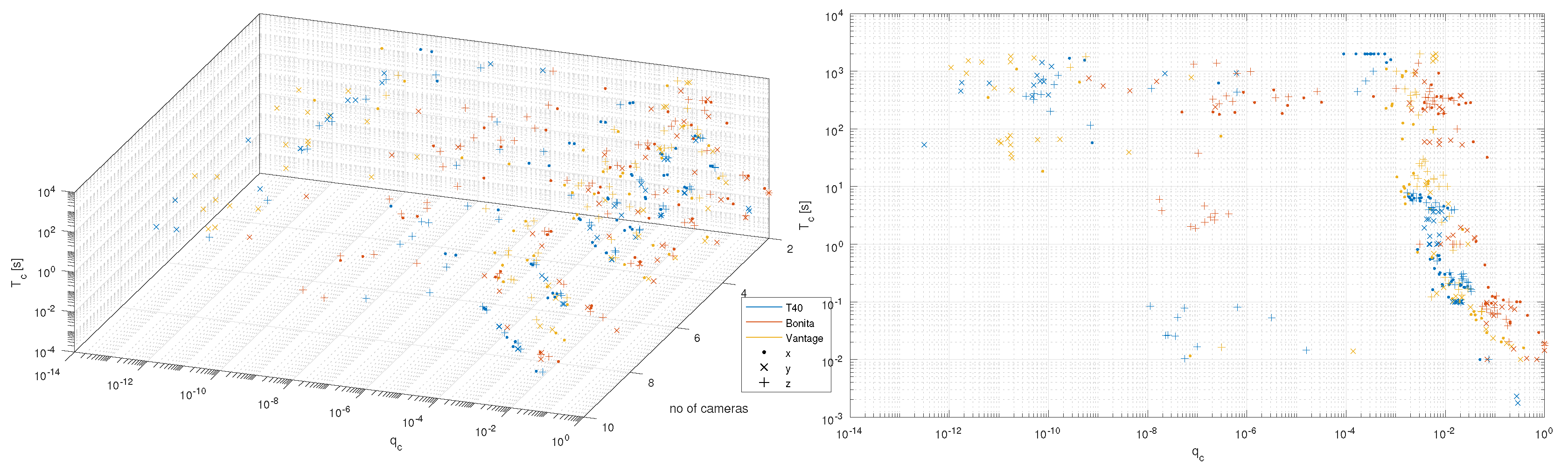
The number of cameras used for position reconstruction is another factor that has a significant influence on the uncertainty of measured position. In the system which takes multiple samples of the measured value (such as position) and results in a mean value of these, the perceived precision can be described as standard error (SE) [
30]. In our case, the increasing number of cameras used for reconstruction could be considered to be taking successive samples of the position. With the increasing number of samples, the SE value falls as the variability of measured value reduces. SE calculation is based on standard deviation:
where:
N is several observations,
σ—standard deviation. This theoretic, quasi-hyperbolic relationship is depicted in
Figure 2. Such a description is just a kind of approximation of the uncertainty variation in the multicamera triangulation process, since we do not exactly know all the nuances of implementation by OMC vendor; furthermore it does not take into consideration spatial location of cameras.
The other issue of the error quantification is the lack of reliable ground truth. The Vicon systems return their results with 1/100 mm resolution, though it is known (see
Section 2) that the actual accuracy of OMCs in real installations is lower. Yet still, the uncertainty of reference has to be much better than the tested system. According to the meteorology standards, reference uncertainty should be smaller between 4 and 10 times than the system under test [
30]. It is difficult to obtain necessary physical template (like the T-frame) manufactured with precision and accuracy sufficient to reliably calibrate OMCs. For this reason, it is hardly feasible to evaluate the accuracy (bias) of the length estimation with mean values without sophisticated equipment. Fortunately, this aspect is of lesser concern as it describes the systematic error, which is easy to compensate.
However, all above considerations would not be enough if the input location measurements are correlated. According to metrology guidelines [
29] simple experimental mean or standard deviation are not adequate to describe the uncertainty in the system with correlated noises. In such a situation a dedicated tool, namely Allan variance, is recommended.
2.3. Allan Variance
Allan variance (AVAR) a two-sample variance and its square root—Allan deviation (ADEV) are statistical descriptors that were developed for the evaluation of the stability of the time and oscillation in clocks. A notable advantage of this approach that there is no need to provide reference value or ground truth.
Presently, the measure is effectively used for quantifying the noises in the measurement of other quantities [
31,
32], but it is particularly useful for evaluation of inertial motion capture sensors [
33,
34]. Allan variance [
9] is defined as:
where
is the time intersample spacing,
denotes expected value.
The AVAR analysis consists of identifying the linear parts of certain slopes of the log-log plot of
τ steps versus ADEV (square root of AVAR). It is demonstrated in the schematic ADEV plot in
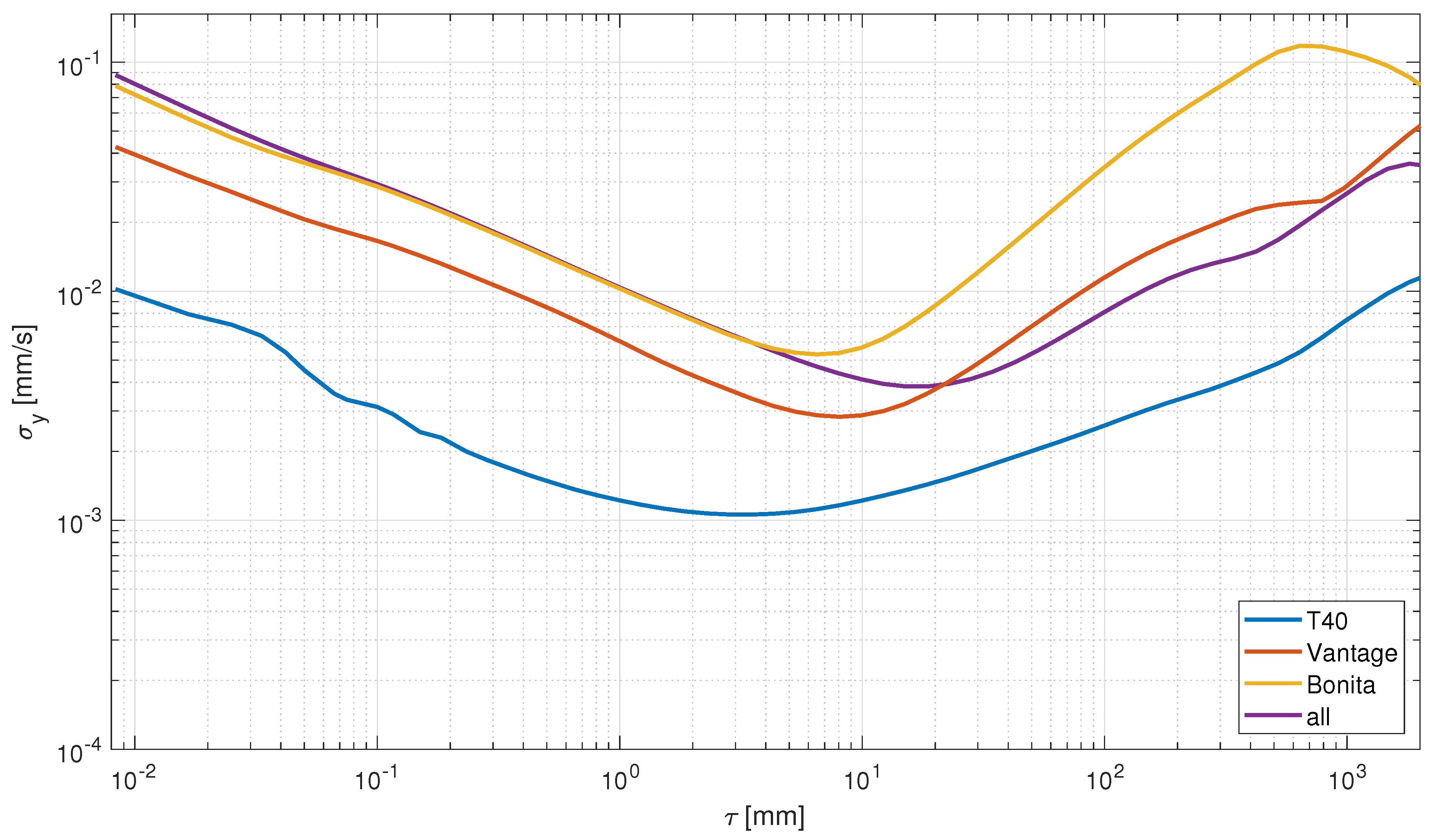
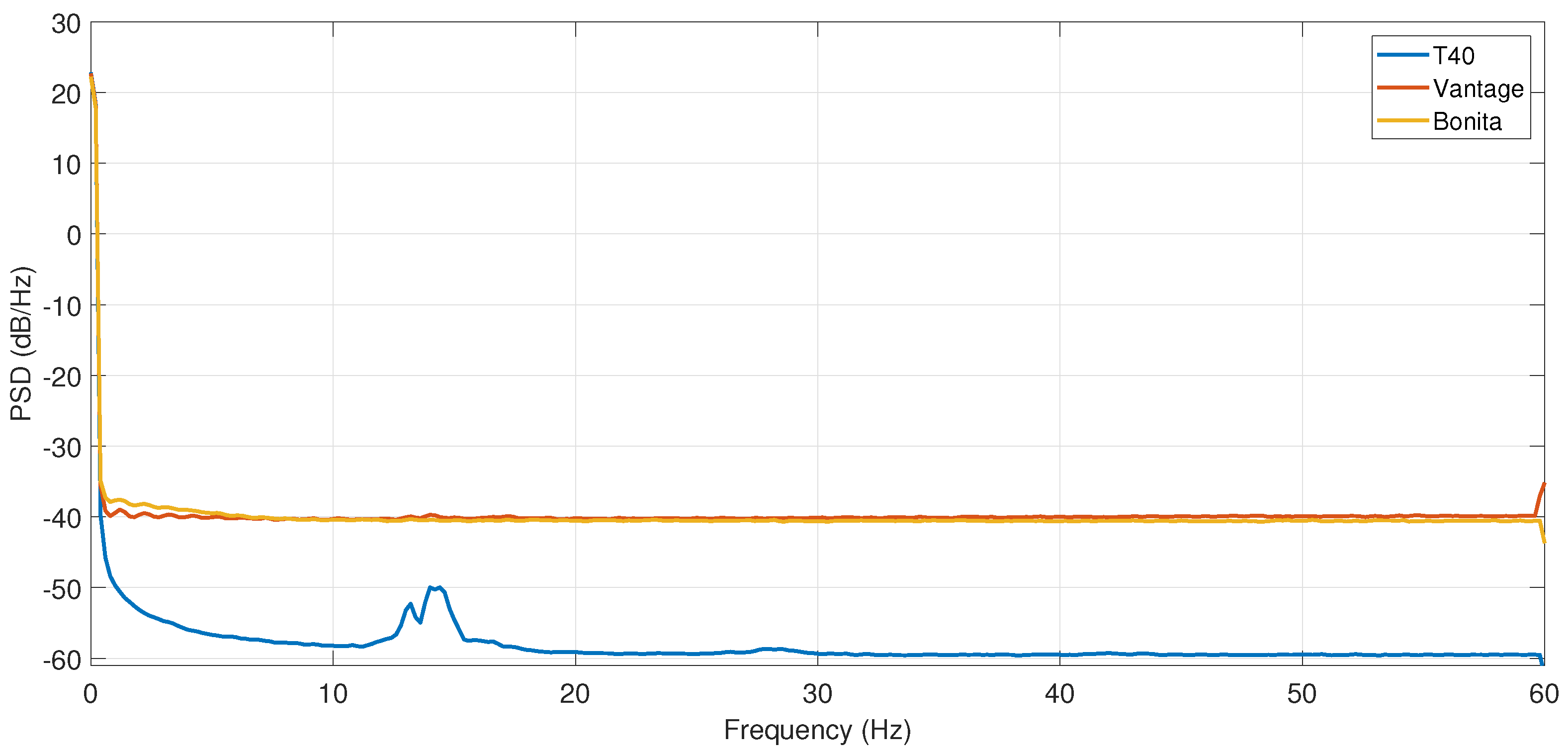
Figure 3. It is a highly beneficial advantage of the AVAR noise quantification over the power spectral density (PSD), which has the capability not to clutter different noise processes and to precisely discriminate several types at once. However, there are also disadvantages. AVAR is sensitive to the outliers and requires considering outlier cleaning to obtain reliable results. The second issue is a necessity to record quite a long sequence for the analysis of a longer term processes.
The conventional types of noise can be identified by their PSD distribution with the power law and respective ADEV slopes [
35]. The ’color’ is given as power relation with respect to frequency (
). Therefore, overall noise characteristics, comprising different basic noise types are:
It corresponds to:
which for a conventional set of noises yields:
Conventional (color) noise types are gathered in
Table 1,
where is bandwidth limit for the measurement system. respective scaling factors .
Additionally, two complex distortions, exponentially correlated (Markovian) and sinusoidal, can be identified using Allan variance [
36]. The Markovian noise is visible in the Allan deviation plot as a single ’bump’ with slopes
. Periodic (sinusoidal) distortion is represented in respective plot as a decaying series of bumps with left-sided slope 1 and right side bump series with constant envelope of a slope −1; however, it is the only case that is more convenient to be observed and to analyze the distortion in the Fourier spectral domain.
Correlated noise PSD is given as:
and corresponding Allan variance has a form:
where:
is the noise amplitude,
is the correlation time.
Sinusoidal noise PSD has a form of two peaks, modeled with Dirac delta:
and respective Allan variance form:
here:
is the amplitude,
is the frequency,
is Dirac delta peak.