Distributed Acoustic Sensing Using Chirped-Pulse Phase-Sensitive OTDR Technology
Abstract
1. Introduction
2. Principle of Operation of CP-ΦOTDR
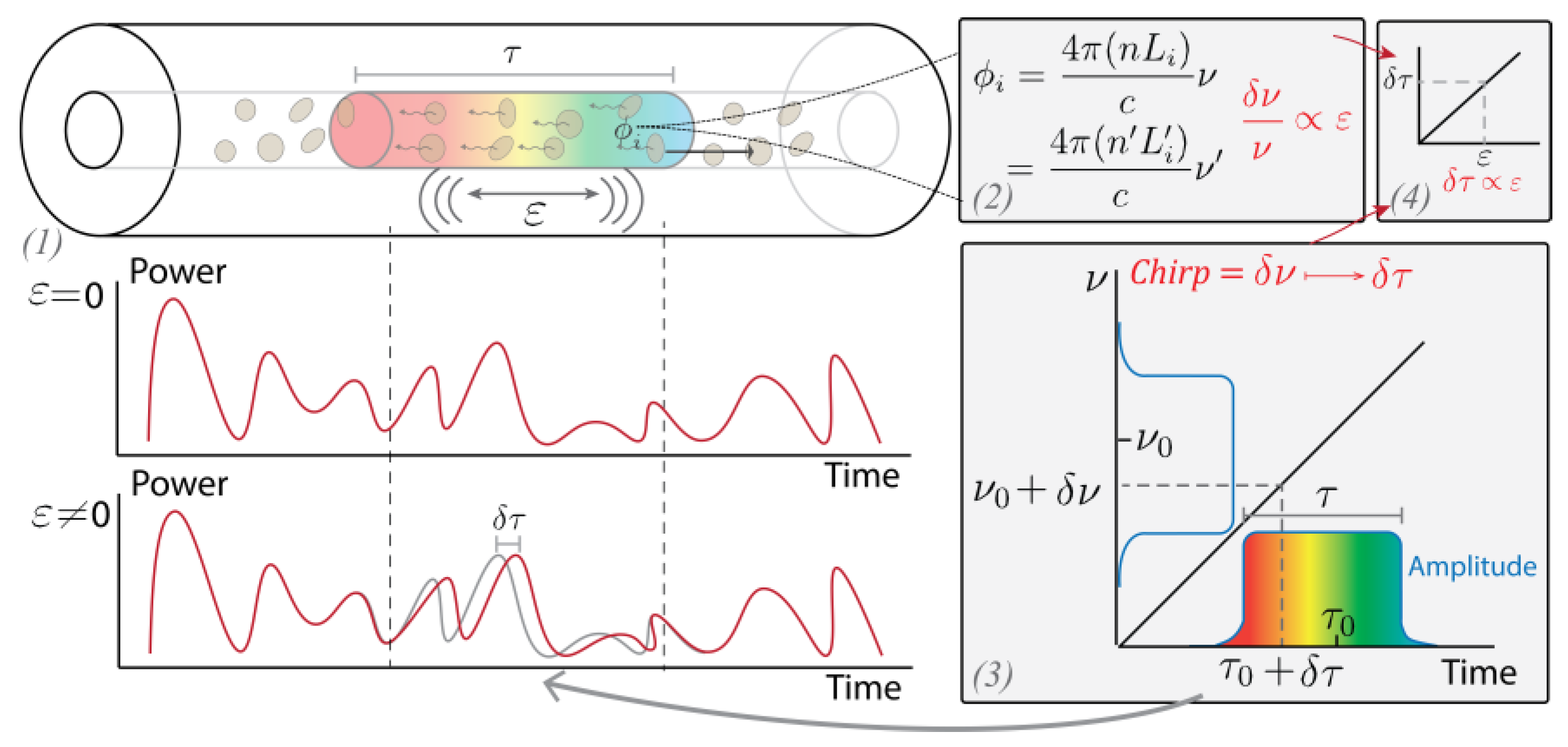
2.1. Mathematical Description
2.2. Typical Setup
2.3. Basic Measurement Settings
2.3.1. Acoustic Sampling
2.3.2. Spatial Resolution and Gauge Length
2.3.3. Sensing Range
2.4. Detection Bandwidth Considerations
2.5. Type of Measurement: Local Measurement (vs. Spatially Differentiated)
3. Pulse Propagation and Optical Trace
3.1. Dispersion
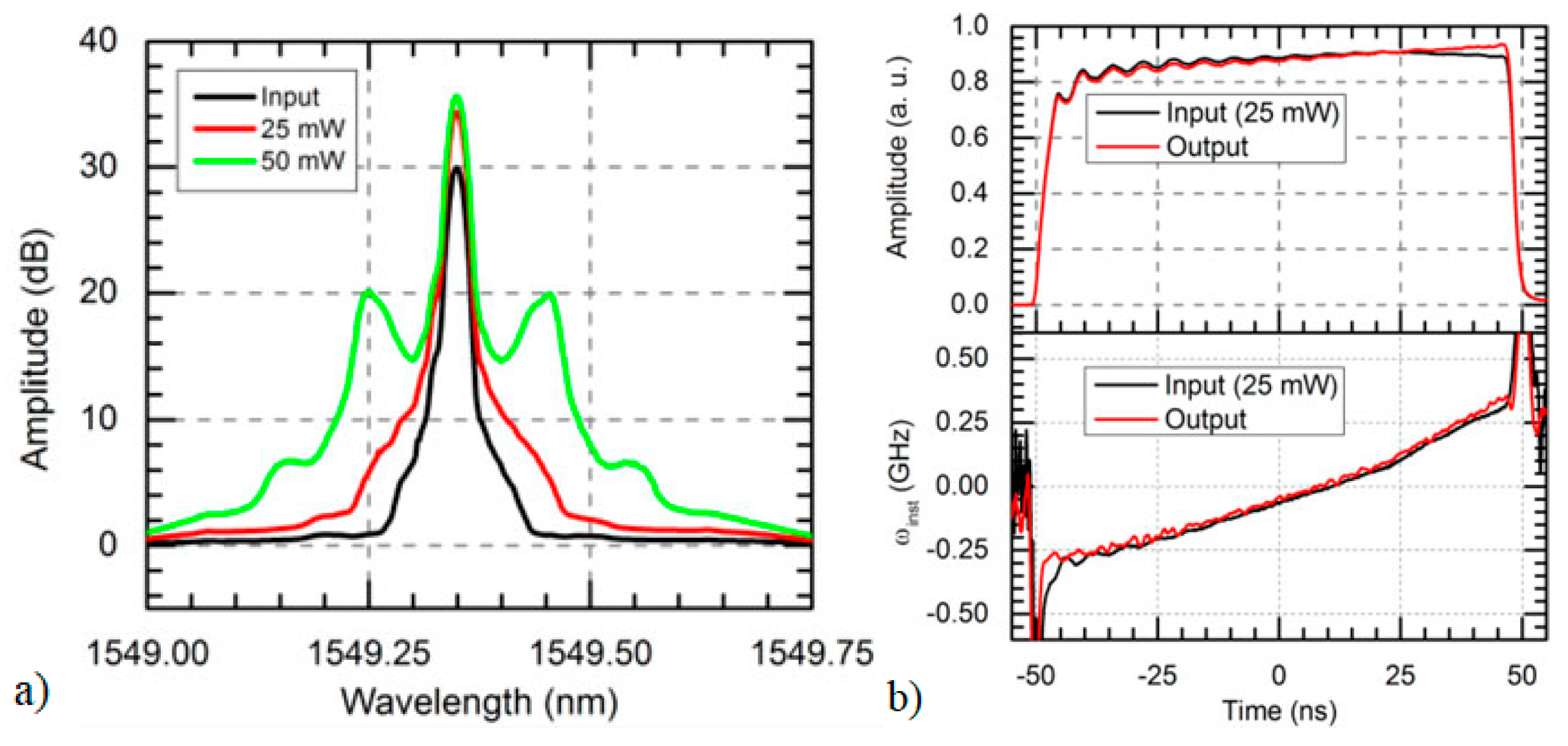
3.2. Nonlinearities—Modulation Instability
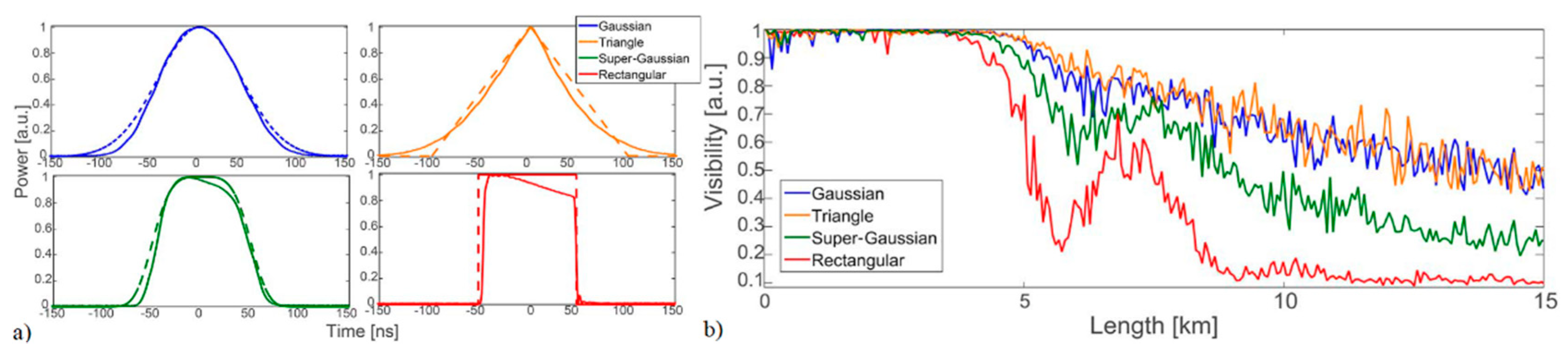
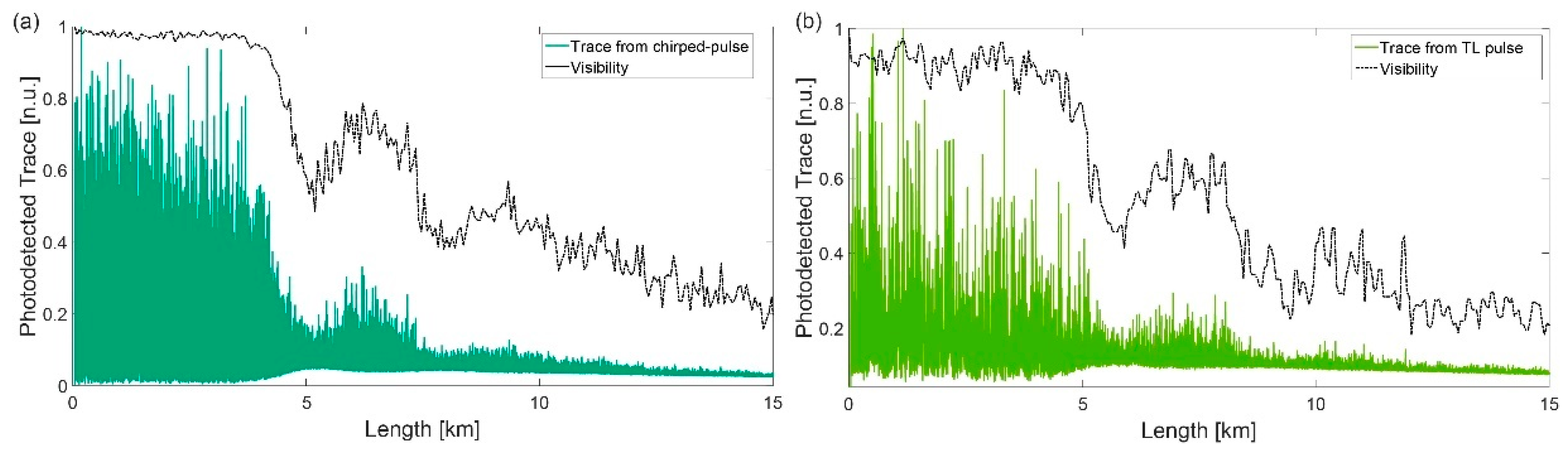
Mitigation of MI in ΦOTDR
3.3. Distributed Optical Amplification
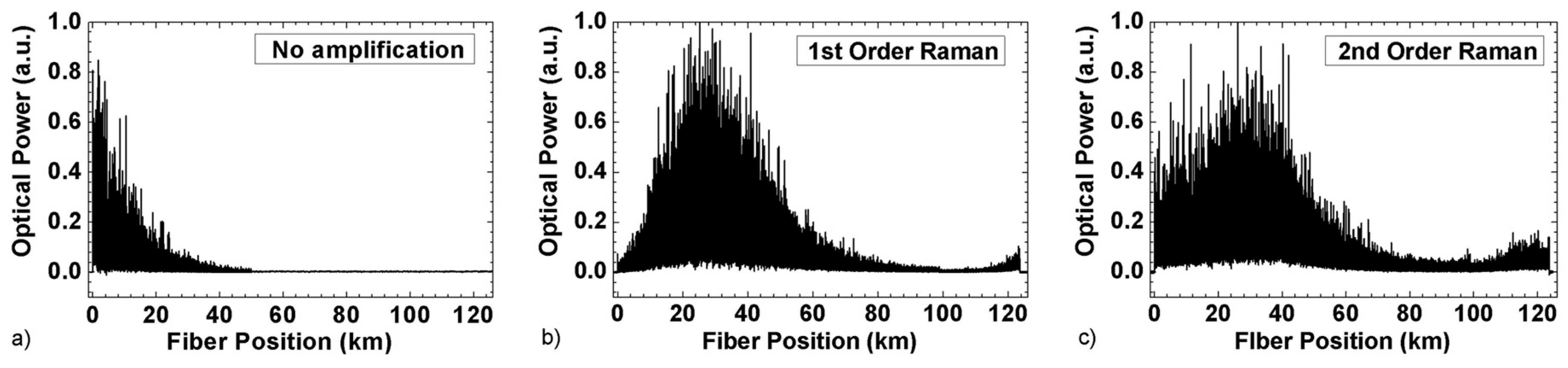
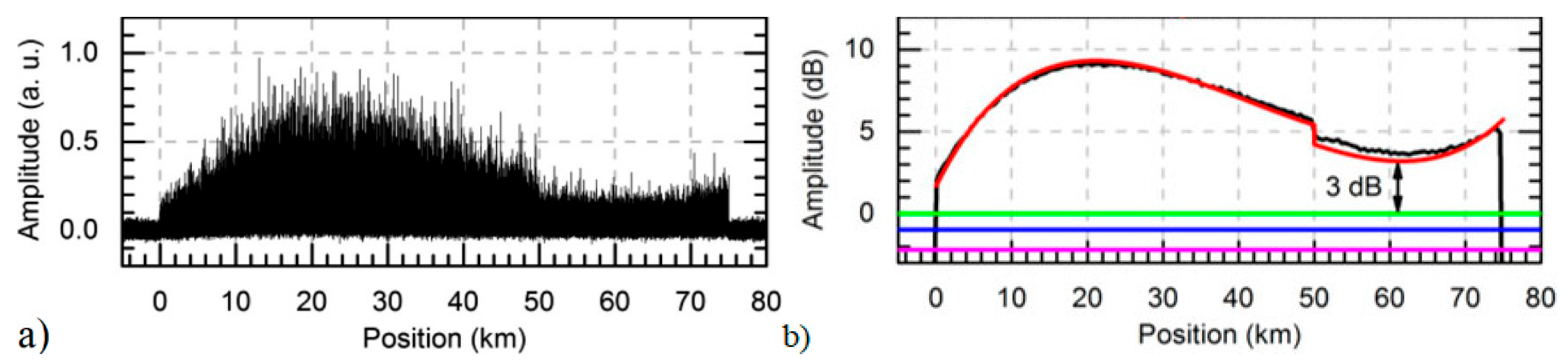
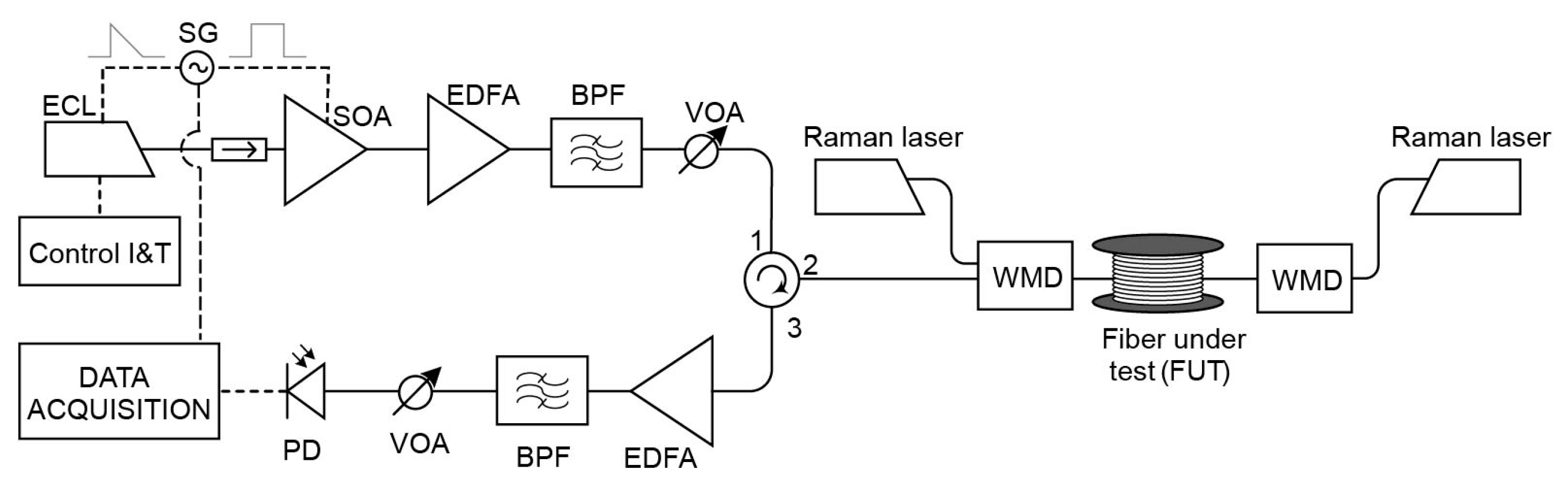
Distributed Raman Amplification in CP-ΦOTDR
4. Strain Signal Properties
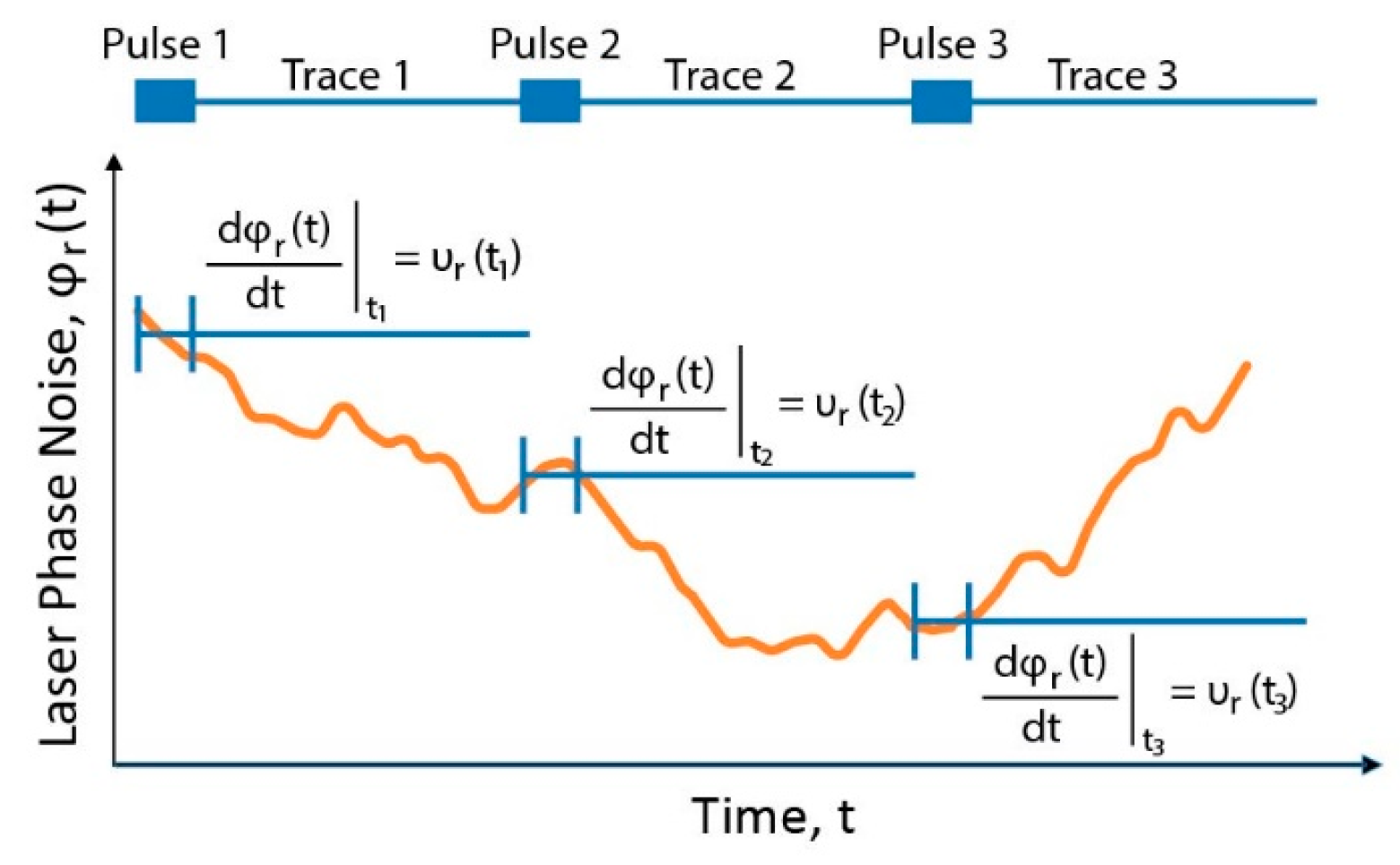
4.1. Laser Noise
4.1.1. Laser Phase/Frequency Noise Affecting Strain Measurement
4.1.2. Laser Noise Compensation
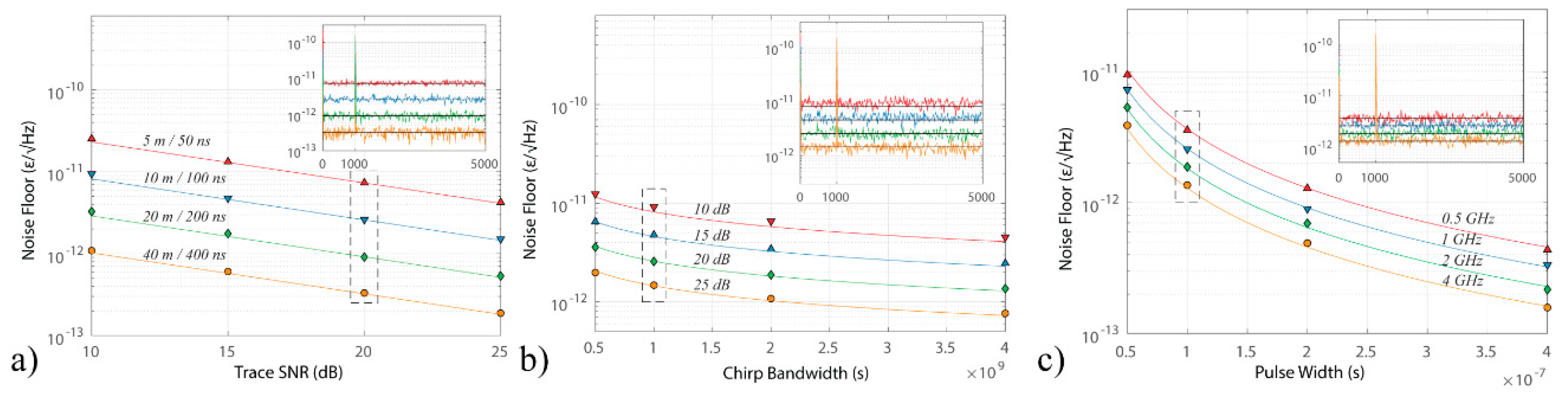
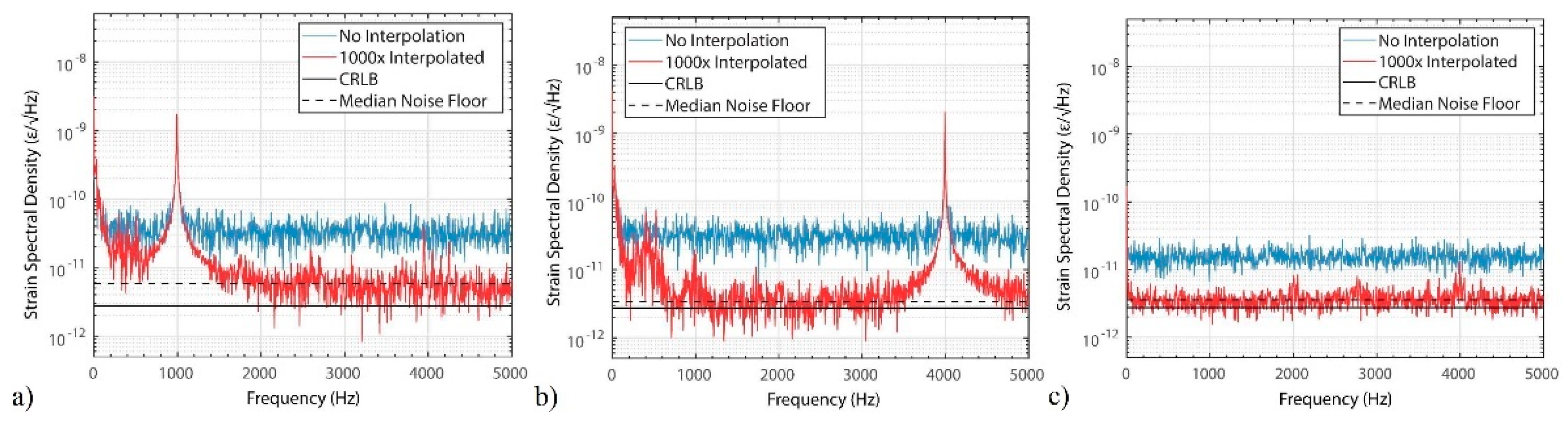
4.2. Theoretical Strain Sensitivity Limit
4.2.1. TDE Problem in Intensity CP-ΦOTDR
4.2.2. Minimum Required Optical Trace SNR
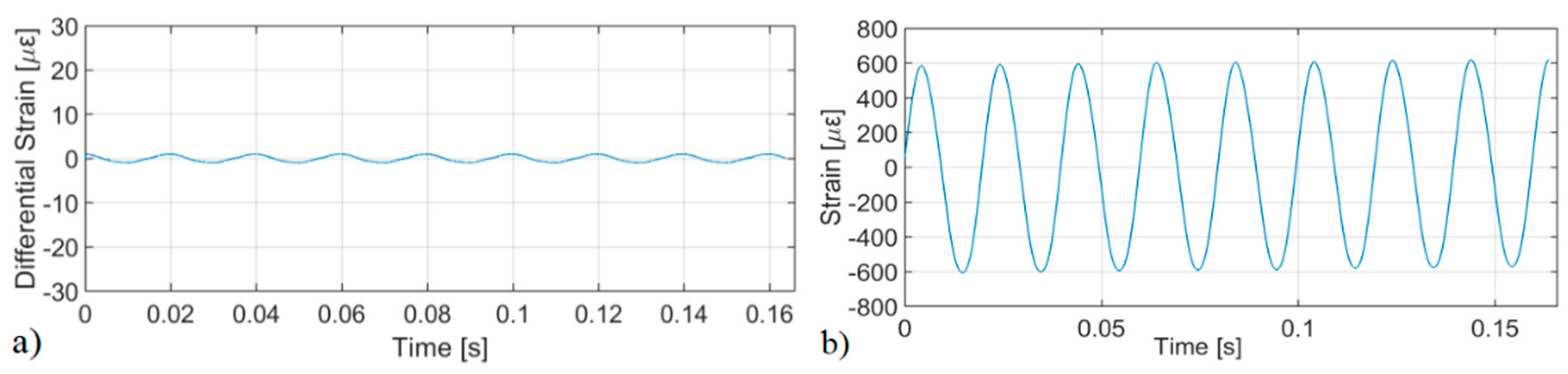
4.3. Maximum Measurable Strain: Shot-to-Shot Limit
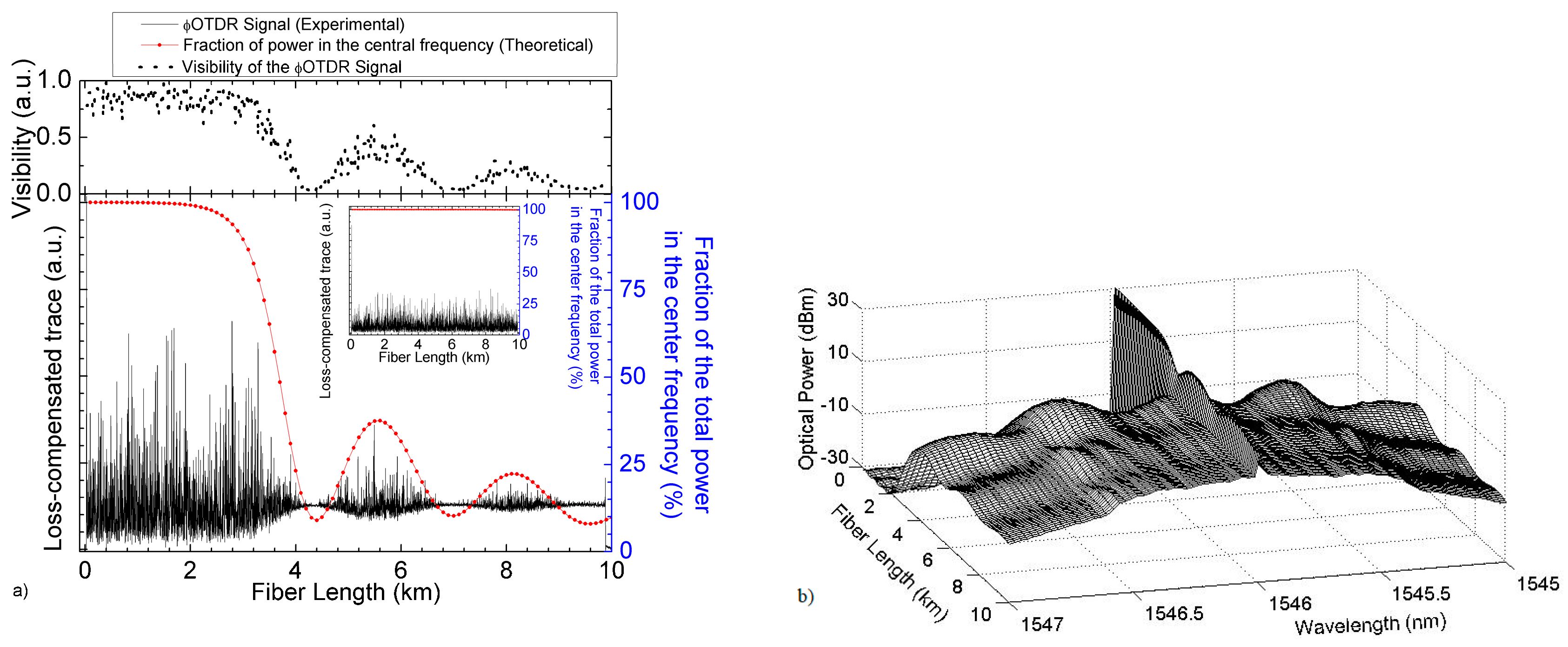
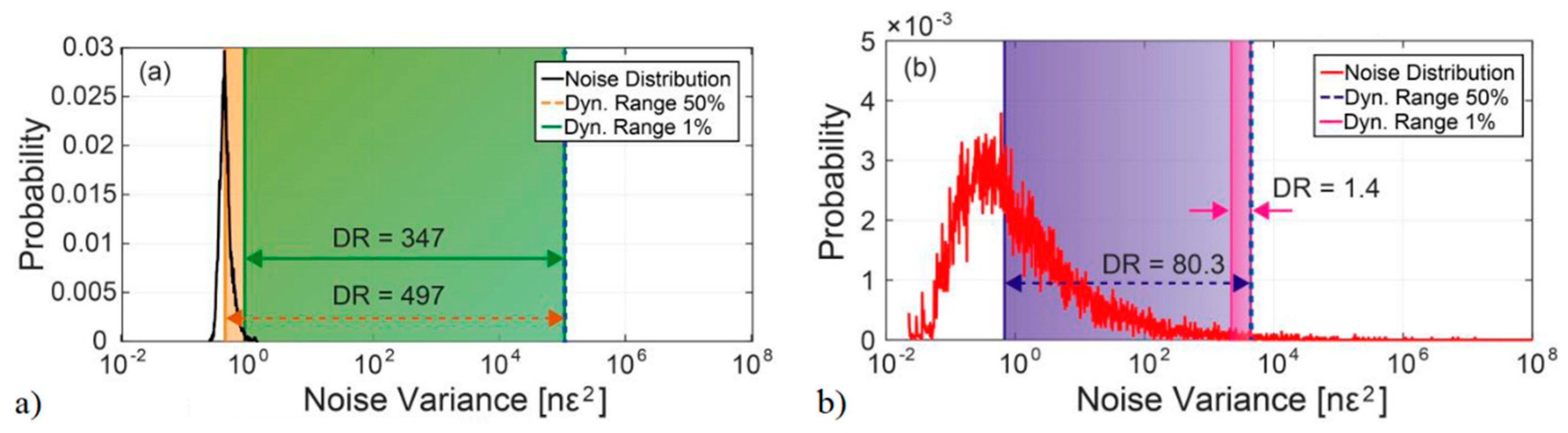
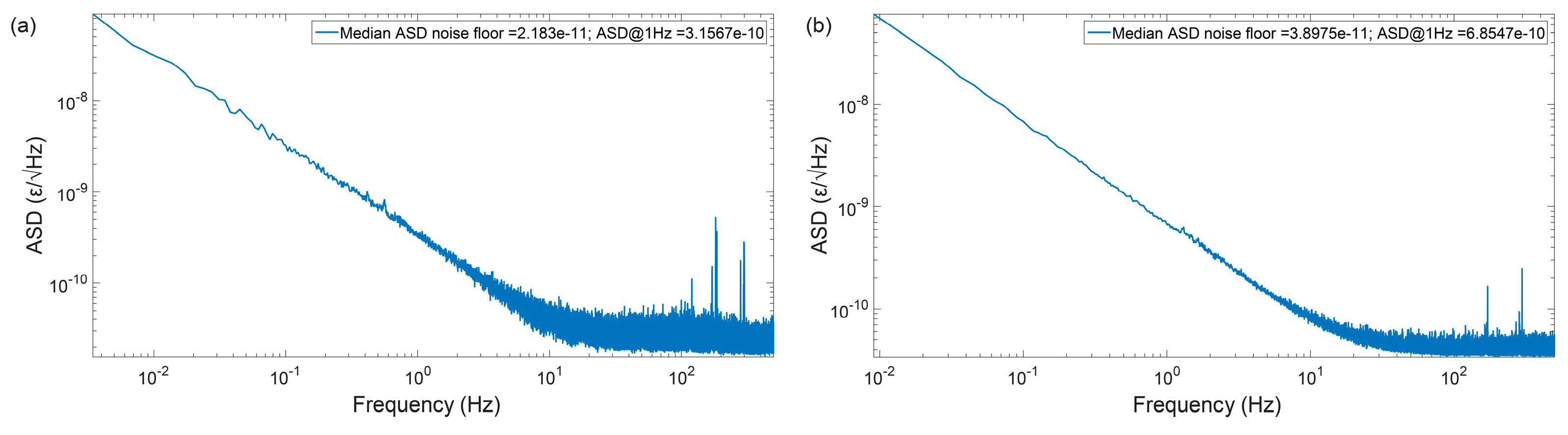
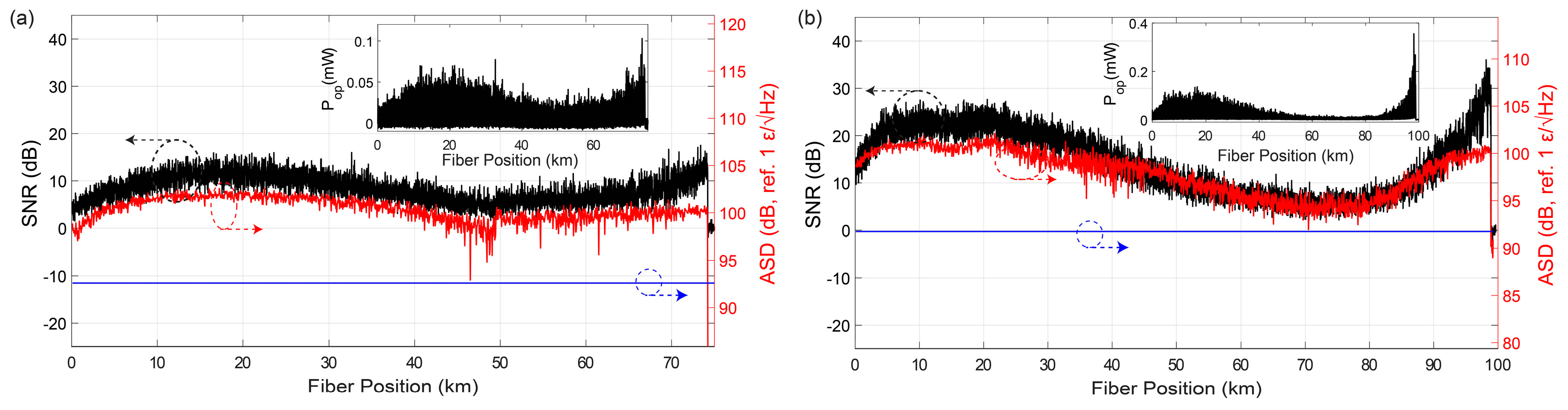
4.4. Reliability and Sensitivity Variability (Fading Free Measurement)
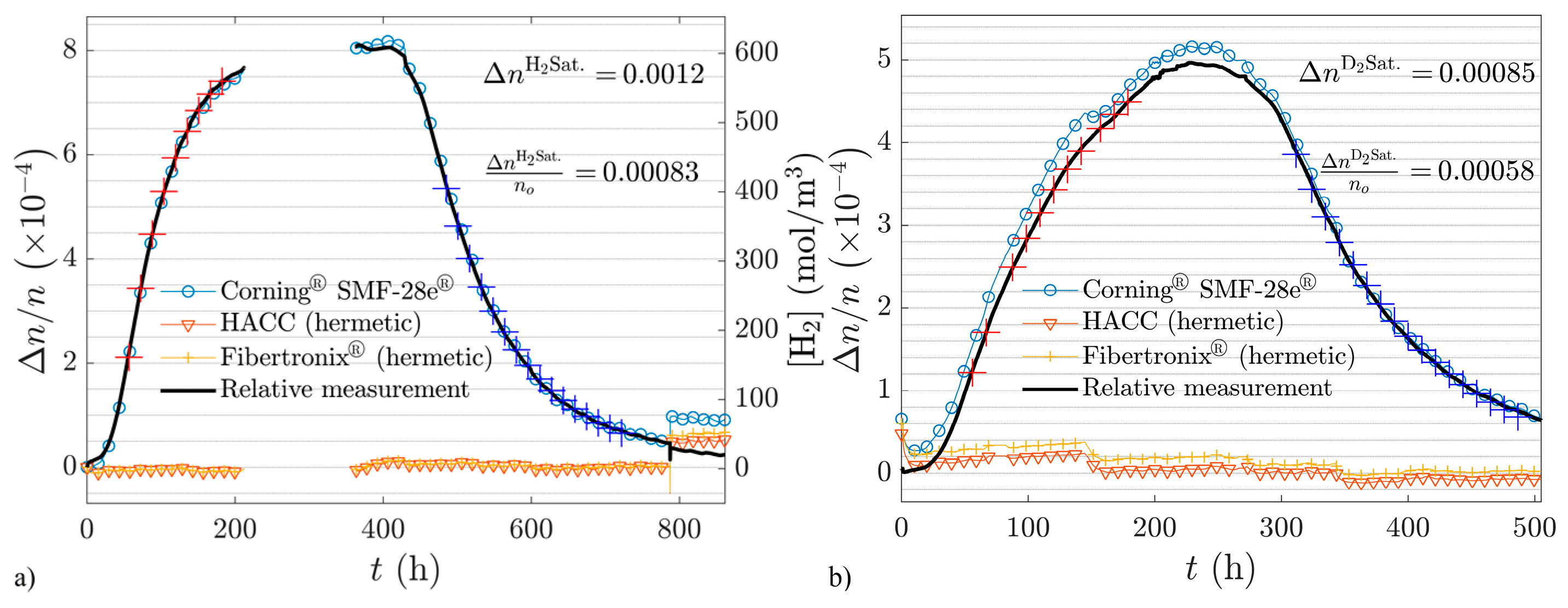
4.5. Long Term Stability and Temperature Measurements
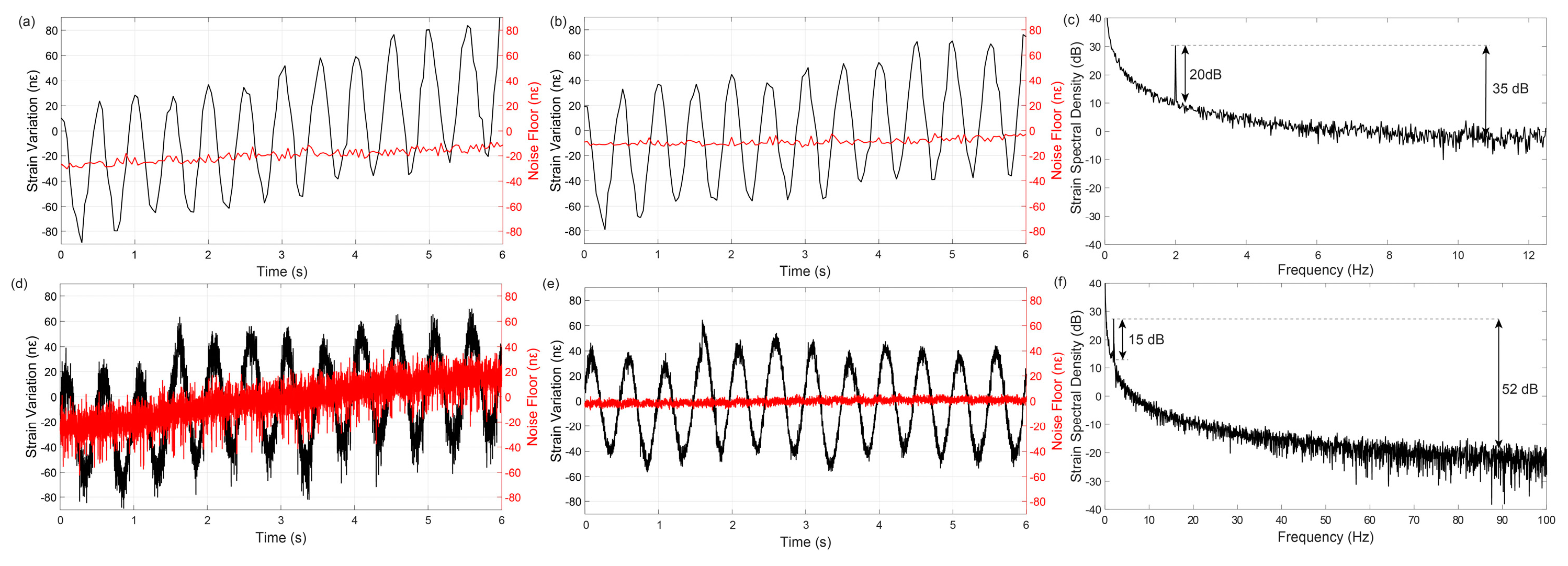
5. Experimental Results
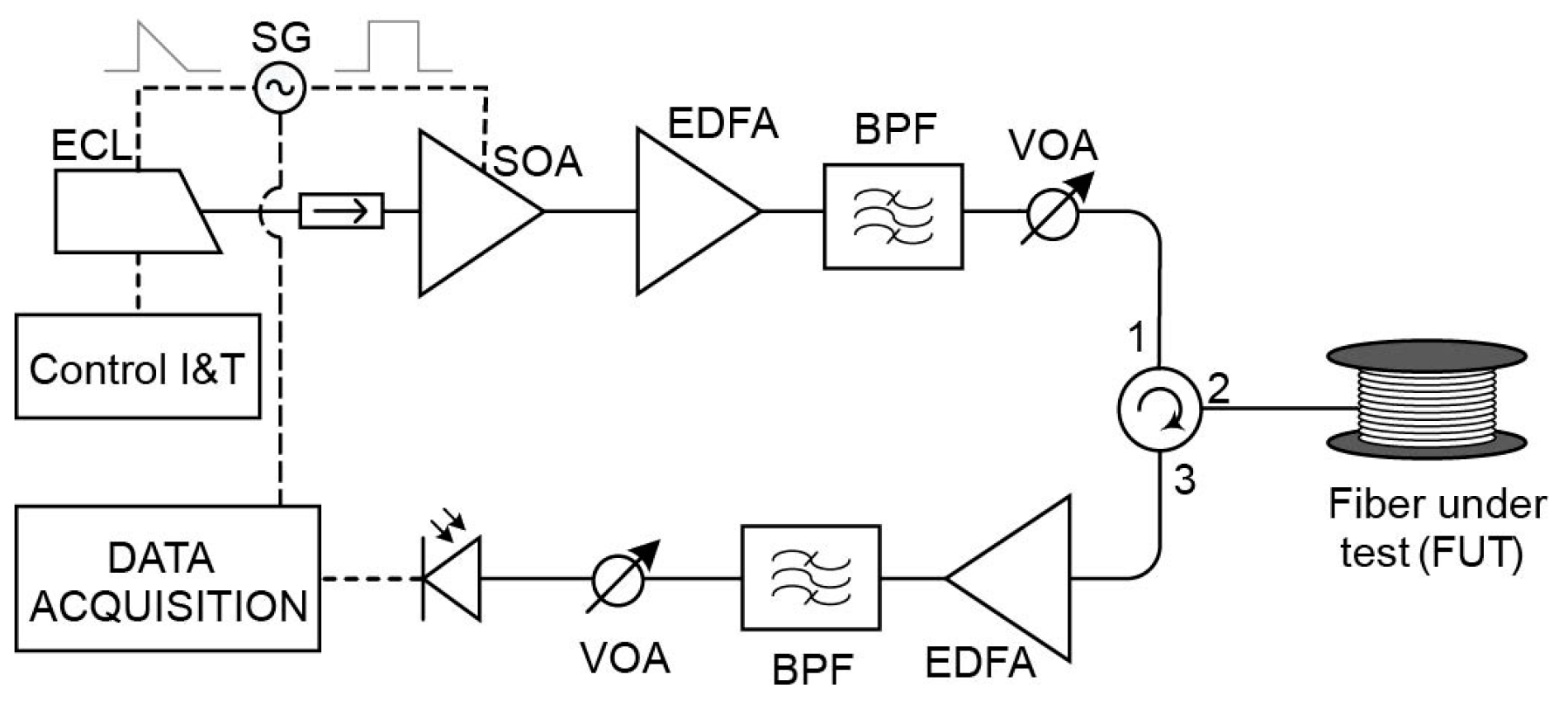
Experimental Setup
6. Comparison of Performance with Respect to Alternative Distributed Sensors
7. Applications
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dakin, J.P.; Pratt, D.J.; Bibby, G.W.; Ross, J.N. Distributed optical fibre Raman temperature sensor using a semiconductor light source and detector. Electron. Lett. 1985, 21, 569–570. [Google Scholar] [CrossRef]
- Dominguez-Lopez, A.; Soto, M.; Martin-Lopez, S.; Thevenaz, L.; Gonzalez-Herraez, M. Resolving 1 million sensing points in an optimized differential time-domain Brillouin sensor. Opt. Lett. 2017, 42, 1903–1906. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.; He, Q.; Xiao, X.; Bao, X. Modulated pulses based distributed vibration sensing with high frequency response and spatial resolution. Opt. Express 2013, 21, 2953–2963. [Google Scholar] [CrossRef] [PubMed]
- Kersey, A.D. A review of recent developments in fiber optic sensor technology. Opt. Fiber Technol. 1996, 2, 291–317. [Google Scholar] [CrossRef]
- Yuksel, K.; Wuilpart, M.; Moeyaert, V.; Mégret, P. Optical frequency domain reflectometry: A review. In Proceedings of the 2009 11th International Conference on Transparent Optical Networks, S. Miguel, Azores, Portugal, 28 June–2 July 2009; pp. 2–7. [Google Scholar]
- Barrias, A.; Casas, J.R.; Villalba, S. A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef] [PubMed]
- Galindez-Jamioy, C.A.; Lopez-Higuera, J.M. Brillouin Distributed Fiber Sensors: An Overview and Applications. J. Sens. 2012, 2012, 1–17. [Google Scholar] [CrossRef]
- Muanenda, Y. Recent Advances in Distributed Acoustic Sensing based on Phase-Sensitive Optical Time Domain Reflectometry. J. Sens. 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent Progress in Distributed Fiber Optic Sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef]
- Pastor-Graells, J.; Martins, H.F.; Garcia-Ruiz, A.; Martin-Lopez, S.; Gonzalez-Herraez, M. Single-shot distributed temperature and strain tracking using direct detection phase-sensitive OTDR with chirped pulses. Opt. Express 2016, 24, 13121–13133. [Google Scholar] [CrossRef]
- Fernández-Ruiz, M.R.; Pastor-Graells, J.; Martins, H.F.; Garcia-Ruiz, A.; Martin-Lopez, S.; Gonzalez-Herraez, M. Laser Phase-Noise Cancellation in Chirped-Pulse Distributed Acoustic Sensors. J. Lightwave Technol. 2018, 36, 979–985. [Google Scholar] [CrossRef]
- Costa, L.; Martins, H.F.; Martin-Lopez, S.; Fernández-Ruiz, M.R.; Gonzalez-Herraz, M. Fully distributed optical fiber strain sensor with 10^{-12} ε/√ Hz sensitivity. J. Lightwave Technol. 2019, 99, 1–9. [Google Scholar]
- Wang, Z.; Zhang, L.; Wang, S.; Xue, N.; Peng, F.; Fan, M.; Sun, W.; Qian, X.; Rao, J.; Rao, Y. Coherent Φ-OTDR based on I/Q demodulation and homodyne detection. Opt. Express 2016, 24, 853–858. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Chen, J.; Wang, T.; Liu, H.; Pang, F.; Lv, L.; Mei, X.; Song, Y.; Chen, J.; Wang, T. True Phase Measurement of Distributed Vibration Sensors Based on Heterodyne ϕ -OTDR True Phase Measurement of Distributed Heterodyne ϕ-OTDR. IEEE Photonics J. 2018, 10, 1–9. [Google Scholar]
- Koyamada, Y.; Imahama, M.; Kubota, K.; Hogari, K. Fiber-optic distributed strain and temperature sensing with very high measurand resolution over long range using coherent OTDR. J. Lightwave Technol. 2009, 27, 1142–1146. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Martins, H.F.; Martin-Lopez, S.; Corredera, P.; Filograno, M.L.; Frazao, O.; Gonzalez-Herraez, M. Coherent noise reduction in high visibility phase-sensitive optical time domain reflectometer for distributed sensing of ultrasonic waves. J. Lightwave Technol. 2013, 31, 3631–3637. [Google Scholar] [CrossRef]
- Marcon, L.; Soto, M.A.; Soriano-amat, M.; Costa, L.; Martins, H.F.; Palmieri, L.; Gonzalez-herraez, M. Boosting the spatial resolution in chirped pulse ϕ -OTDR using sub-band processing. In Proceedings of the European Workshop on Optical Fibre Sensors (EWOFS), Limassol, Cyprus, 1–4 October 2019; Volume 1, pp. 1–4. [Google Scholar]
- Zhang, L.; Costa, L.; Yang, Z.; Soto, M.A.; Gonzalez-herráez, M.; Member, S.; Thévenaz, L. Analysis and Reduction of Large Errors in Rayleigh-based Distributed Sensor. J. Lightwave Technol. 2019, 37, 1–11. [Google Scholar] [CrossRef]
- Ianniello, J.P. Time Delay Estimation Via Cross-Correlation in the Presence of Large Estimation Errors. IEEE Trans. Acoust. 1982, 30, 998–1003. [Google Scholar] [CrossRef]
- Soriano-Amat, M.; Marcon, L.; Costa, L.; Garcia-Ruiz, A.; Martins, H.F.; Martin-Lopez, S.; Palmieri, L.; Gonzalez-Herraez, M. Characterization and modelling of induced “virtual” perturbations in chirped pulse φ -OTDR. In Proceedings of the European Workshop on Optical Fibre Sensors (EWOFS), Limassol, Cyprus, 1–4 October 2019; pp. 1–4. [Google Scholar]
- Incorporated, C. Corning® SMF-28® Ultra Optical Fiber; Product Information; Corning Inc.: Corning, NY, USA, 2014. [Google Scholar]
- Martins, H.F.; Martin-Lopez, S.; Corredera, P.; Salgado, P.; Frazão, O.; González-Herráez, M. Modulation instability-induced fading in phase-sensitive optical time-domain reflectometry. Opt. Lett. 2013, 38, 872–874. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics, 5th ed.; Academic Press: Cambridge, MA, USA, 2007; ISBN 9780123970237. [Google Scholar]
- Van Simaeys, G.; Emplit, P. Experimental demonstration of the Fermi-Pasta-Ulam recurrence in a modulationally unstable optical wave. Phys. Rev. Lett. 2001, 87, 33902-1–33902-4. [Google Scholar] [CrossRef]
- Fernández-Ruiz, M.R.; Martins, H.F.; Pastor-Graells, J.; Martin-Lopez, S.; Gonzalez-Herraez, M. Phase-sensitive OTDR probe pulse shapes robust against modulation-instability fading. Opt. Lett. 2016, 41, 5756–5759. [Google Scholar] [CrossRef]
- Pastor-Graells, J.; Nuno, J.; Fernández-Ruiz, M.R.; Garcia-Ruiz, A.; Martins, H.F.; Martin-Lopez, S.; Gonzalez-Herraez, M. Chirped-Pulse Phase-Sensitive Reflectometer Assisted by First-Order Raman Amplification. J. Lightwave Technol. 2017, 35, 4677–4683. [Google Scholar] [CrossRef]
- Wang, Z.N.; Li, J.; Fan, M.Q.; Zhang, L.; Peng, F.; Wu, H.; Zeng, J.J.; Zhou, Y.; Rao, Y.J. Phase-sensitive optical time-domain reflectometry with Brillouin amplification. Opt. Lett. 2014, 39, 4313–4316. [Google Scholar] [CrossRef] [PubMed]
- Martins, H.F.; Martin-Lopez, S.; Corredera, P.; Filograno, M.L.; Frazao, O.; Gonzalez-Herraez, M. Phase-sensitive optical time domain reflectometer assisted by first-order raman amplification for distributed vibration sensing over >100 km. J. Lightwave Technol. 2014, 32, 1510–1518. [Google Scholar] [CrossRef]
- Peng, F.; Wu, H.; Jia, X.; Rao, Y.; Wang, Z.; Peng, Z. Ultra-long high-sensitivity Φ -OTDR for high spatial resolution intrusion detection of pipelines. Opt. Express 2014, 22, 13804–13810. [Google Scholar] [CrossRef]
- Wang, Z.N.; Zeng, J.J.; Li, J.; Fan, M.Q.; Wu, H.; Peng, F.; Zhang, L.; Zhou, Y.; Rao, Y.J. Ultra-long phase-sensitive OTDR with hybrid distributed amplification. Opt. Lett. 2014, 39, 5866–5869. [Google Scholar] [CrossRef] [PubMed]
- Martins, H.F.; Martin-Lopez, S.; Corredera, P.; Ania-Castañon, J.D.; Frazao, O.; Gonzalez-Herraez, M. Distributed vibration sensing over 125 km with enhanced SNR using Phi-OTDR over a URFL cavity. J. Lightwave Technol. 2015, 33, 2628–2632. [Google Scholar] [CrossRef]
- Gyger, F.; Rochat, E.; Chin, S. Extending the sensing range of Brillouin optical time-domain analysis up to 325 km combining four optical repeaters. In Proceedings of the Optical Fiber Sensors (OFC) Conference, San Francisco, CA, USA, 9–13 March 2014; Volume 9157, p. 91576. [Google Scholar]
- Camatel, S.; Ferrero, V. Narrow linewidth CW laser phase noise characterization methods for coherent transmission system applications. J. Lightwave Technol. 2008, 26, 3048–3055. [Google Scholar] [CrossRef]
- Costa, L.; Martins, H.F.; Martin-lopez, S.; Fernández-Ruiz, M.R.; González-, M. Optimization of first-order phase noise cancellation in CP-φOTDR. In Proceedings of the European Workshop on Optical Fibre Sensors (EWOFS), Limassol, Cyprus, 1–4 October 2019; pp. 3–6. [Google Scholar]
- Carter, G.C. Coherence and time delay estimation. Proc. IEEE 1987, 75, 236–255. [Google Scholar] [CrossRef]
- Carter, G.C. Time Delay Estimation for Passive Sonar Signal Processing. IEEE Trans. Acoust. 1981, 29, 463–470. [Google Scholar] [CrossRef]
- Quazi, A.H. An Overview on the Time Delay Estimate in Active and Passive Systems for Target Localization. IEEE Trans. Acoust. 1981, 29, 527–533. [Google Scholar] [CrossRef]
- Bhatta, H.D.; Costa, L.; Garcia-ruiz, A.; Fernández-Ruiz, M.R.; Martins, H.F.; Tur, M.; Gonzalez-Herraez, M. Dynamic Measurements of 1000 microstrains using Chirped-pulse Phase Sensitive Optical Time Domain Reflectometry ( CP-ΦOTDR). J. Lightwave Technol. 2019. [Google Scholar] [CrossRef]
- Hen, D.; Liu, Q.; He, Z. High-fidelity distributed fiber-optic acoustic sensor with fading noise suppressed and sub-meter spatial resolution. Opt. Express 2018, 26, 16138–16146. [Google Scholar]
- Chen, D.; Liu, Q.; He, Z. Phase-detection distributed fiber-optic vibration sensor without fading-noise based on time-gated digital OFDR. Opt. Express 2017, 25, 8315–8325. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wu, H.; Zheng, H.; Huang, J.; Yin, G.; Zhu, T.; Qiu, F.; Huang, X.; Qu, D.; Bai, Y. 80 km fading free phase-sensitive reflectometry based on multi-carrier NLFM pulse without distributed amplification. J. Lightwave Technol. 2019, 37, 1–7. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, Z.; Ye, Q.; Cai, H.; Qu, R.; Fang, Z. Characteristics and Explanations of Interference Fading of a -OTDR With a Multi-Frequency Source. J. Lightwave Technol. 2013, 31, 2947–2954. [Google Scholar] [CrossRef]
- Fernández-Ruiz, M.R.; Martins, H.F.; Costa, L.; Martin-Lopez, S.; Gonzalez-Herraez, M. Steady-Sensitivity Distributed Acoustic Sensors. J. Lightwave Technol. 2018, 36, 5690–5696. [Google Scholar] [CrossRef]
- Gabai, H.; Eyal, A. On the sensitivity of distributed acoustic sensing. Opt. Lett. 2016, 41, 5648–5651. [Google Scholar] [CrossRef]
- Motil, A.; Bergman, A.; Tur, M. State of the art of Brillouin fiber-optic distributed sensing. Opt. Laser Technol. 2016, 78, 81–103. [Google Scholar] [CrossRef]
- Garcia-ruiz, A.; Morana, A.; Martins, H.F.; Martin-lopez, S.; Gonzalez-Herraez, M.; Delepine-Lesoille, S.; Boukenter, A.; Ouerdane, Y.; Girard, S. Hydrogen and deuterium distributed sensing using Chirped-Pulse φOTDR. In Proceedings of the European Workshop on Optical Fibre Sensors (EWOFS), Limassol, Cyprus, 1–4 October 2019; Volume 3, pp. 1–4. [Google Scholar]
- Angulo-Vinuesa, X.; Martin-Lopez, S.; Nuño, J.; Corredera, P.; Ania-Castañón, J.D.; Thévenaz, L.; González-Herráez, M. Raman-Assisted Brillouin Distributed Temperature Sensor Over 100 km Featuring 2 m Resolution. J. Lightwave Technol. 2012, 30, 1060–1065. [Google Scholar] [CrossRef]
- Peled, Y.; Motil, A.; Yaron, L.; Tur, M. Slope-assisted fast distributed sensing in optical fibers with arbitrary Brillouin profile. Opt. Express 2011, 19, 19845–19854. [Google Scholar] [CrossRef]
- Mompó, J.J.; Martin-Lopez, S.; Gonzalez-Herraez, M.; Loayssa, A. Sidelobe apodization in optical pulse compression reflectometry for fiber optic distributed acoustic sensing. Opt. Express 2018, 43, 1499–1502. [Google Scholar] [CrossRef] [PubMed]
- Martins, H.F.; Shi, K.; Thomsen, B.C.; Martin-Lopez, S.; Gonzalez-Herraez, M.; Savory, S.J. Real time dynamic strain monitoring of optical links using the backreflection of live PSK data. Opt. Express 2016, 24, 22303–22317. [Google Scholar] [CrossRef] [PubMed]
- Qin, Z.; Chen, L.; Bao, X. Wavelet denoising method for improving detection performance of distributed vibration sensor. IEEE Photonics Technol. Lett. 2012, 24, 542–544. [Google Scholar] [CrossRef]
- Zou, W.; Yu, L.; Yang, S.; Chen, J. Optical pulse compression reflectometry based on single-sideband modulator driven by electrical frequency-modulated pulse. Opt. Commun. 2016, 367, 155–160. [Google Scholar] [CrossRef]
- Lu, X.; Soto, M.A.; Thévenaz, L. Temperature-strain discrimination in distributed optical fiber sensing using phase-sensitive optical time-domain reflectometry. Opt. Express 2017, 25, 16059–16071. [Google Scholar] [CrossRef]
- Soto, M.A.; Lu, X.; Martins, H.F.; Gonzalez-Herraez, M.; Thévenaz, L. Distributed phase birefringence measurements based on polarization correlation in phase-sensitive optical time-domain reflectometers. Opt. Express 2015, 23, 24923–24936. [Google Scholar] [CrossRef] [PubMed]
- Zou, W.; Yang, S.; Long, X.; Chen, J. Optical pulse compression reflectometry: Proposal and proof-of-concept experiment. Opt. Express 2015, 23, 512–522. [Google Scholar] [CrossRef]
- Wu, M.; Fan, X.; Liu, Q.; He, Z. High Performance Distributed Acoustic Sensor Based on Ultra-Weak FBG Array. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; IEEE: Piscatawa, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Lu, B.; Pan, Z.; Wang, Z.; Zheng, H.; Ye, Q.; Qu, R.; Cai, H. High spatial resolution phase-sensitive optical time domain reflectometer with a frequency-swept pulse. Opt. Lett. 2017, 42, 391–394. [Google Scholar] [CrossRef]
- Tejedor, J.; Macias-Guarasa, J.; Martins, H.F.; Pastor-Graells, J.; Martin-Lopez, S.; Corredera, P.; De Pauw, G.; De Smet, F.; Postvoll, W.; Ahlen, C.H.; et al. Real Field Deployment of a Smart Fiber-Optic Surveillance System for Pipeline Integrity Threat Detection: Architectural Issues and Blind Field Test Results. J. Lightwave Technol. 2018, 36, 1052–1062. [Google Scholar] [CrossRef]
- Daley, T.M.; Miller, D.E.; Dodds, K.; Cook, P.; Freifeld, B.M. Field testing of modular borehole monitoring with simultaneous distributed acoustic sensing and geophone vertical seismic profiles at Citronelle, Alabama. Geophys. Prospect. 2016, 64, 1318–1334. [Google Scholar] [CrossRef]
- Peng, F.; Duan, N.; Rao, Y.; Li, J. Real-Time Position and Speed Monitoring of Trains Using Phase-Sensitive OTDR. IEEE Photonics J. 2014, 26, 2055–2057. [Google Scholar] [CrossRef]
- Jousset, P.; Reinsch, T.; Ryberg, T.; Blanck, H.; Clarke, A.; Aghayev, R.; Hersir, G.P.; Henninges, J.; Weber, M.; Krawczyk, C.M. Dynamic strain determination using fibre-optic cables allows imaging of seismological and structural features. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Martins, H.F.; Fernández-Ruiz, M.R.; Costa, L.; Williams, E.; Zhan, Z.; Martin, S.; Gonzalez-herraez, M. Monitoring of remote seismic events in metropolitan area fibers using distributed acoustic sensing (DAS) and spatio-temporal signal processing. In Proceedings of the Optical Fiber Communications (OFC), San Diego, CA, USA, 3–7 March 2019; pp. 1–3. [Google Scholar]
- Garcia-Ruiz, A.; Dominguez-Lopez, A.; Pastor-Graells, J.; Martins, H.F.; Martin-Lopez, S.; Gonzalez-Herraez, M. Long-range distributed optical fiber hot-wire anemometer based on chirped-pulse ΦOTDR. Opt. Express 2018, 26, 463–476. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Ruiz, A.; Pastor-Graells, J.; Martins, H.F.; Tow, K.H.; Thévenaz, L.; Martin-Lopez, S.; Gonzalez-Herraez, M. Distributed photothermal spectroscopy in microstructured optical fibers: Towards high-resolution mapping of gas presence over long distances. Opt. Express 2017, 25, 1789–1805. [Google Scholar] [CrossRef] [PubMed]
- Magalhães, R.; Garcia-Ruiz, A.; Martins, H.F.; Pereira, J.; Margulis, W.; Martin-Lopez, S.; Gonzalez-Herraez, M. Fiber-based distributed bolometry. Opt. Express 2019, 27, 4317–4328. [Google Scholar] [CrossRef] [PubMed]
- Magalhães, R.; Pereira, J.; Margulis, W.; Martin-Lopez, S.; Gonzalez-Herráez, M.; Martins, H.F. Distributed Detection of quadratic Kerr effect in silica fibers using chirped-pulse φOTDR. In Proceedings of the European Workshop on Optical Fibre Sensors (EWOFS), Limassol, Cyprus, 1–4 October 2019; pp. 1–4. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
R. Fernández-Ruiz, M.; Costa, L.; F. Martins, H. Distributed Acoustic Sensing Using Chirped-Pulse Phase-Sensitive OTDR Technology. Sensors 2019, 19, 4368. https://doi.org/10.3390/s19204368
R. Fernández-Ruiz M, Costa L, F. Martins H. Distributed Acoustic Sensing Using Chirped-Pulse Phase-Sensitive OTDR Technology. Sensors. 2019; 19(20):4368. https://doi.org/10.3390/s19204368
Chicago/Turabian StyleR. Fernández-Ruiz, María, Luis Costa, and Hugo F. Martins. 2019. "Distributed Acoustic Sensing Using Chirped-Pulse Phase-Sensitive OTDR Technology" Sensors 19, no. 20: 4368. https://doi.org/10.3390/s19204368
APA StyleR. Fernández-Ruiz, M., Costa, L., & F. Martins, H. (2019). Distributed Acoustic Sensing Using Chirped-Pulse Phase-Sensitive OTDR Technology. Sensors, 19(20), 4368. https://doi.org/10.3390/s19204368





