Infrared-Inertial Navigation for Commercial Aircraft Precision Landing in Low Visibility and GPS-Denied Environments
Abstract
1. Introduction
2. Methodology
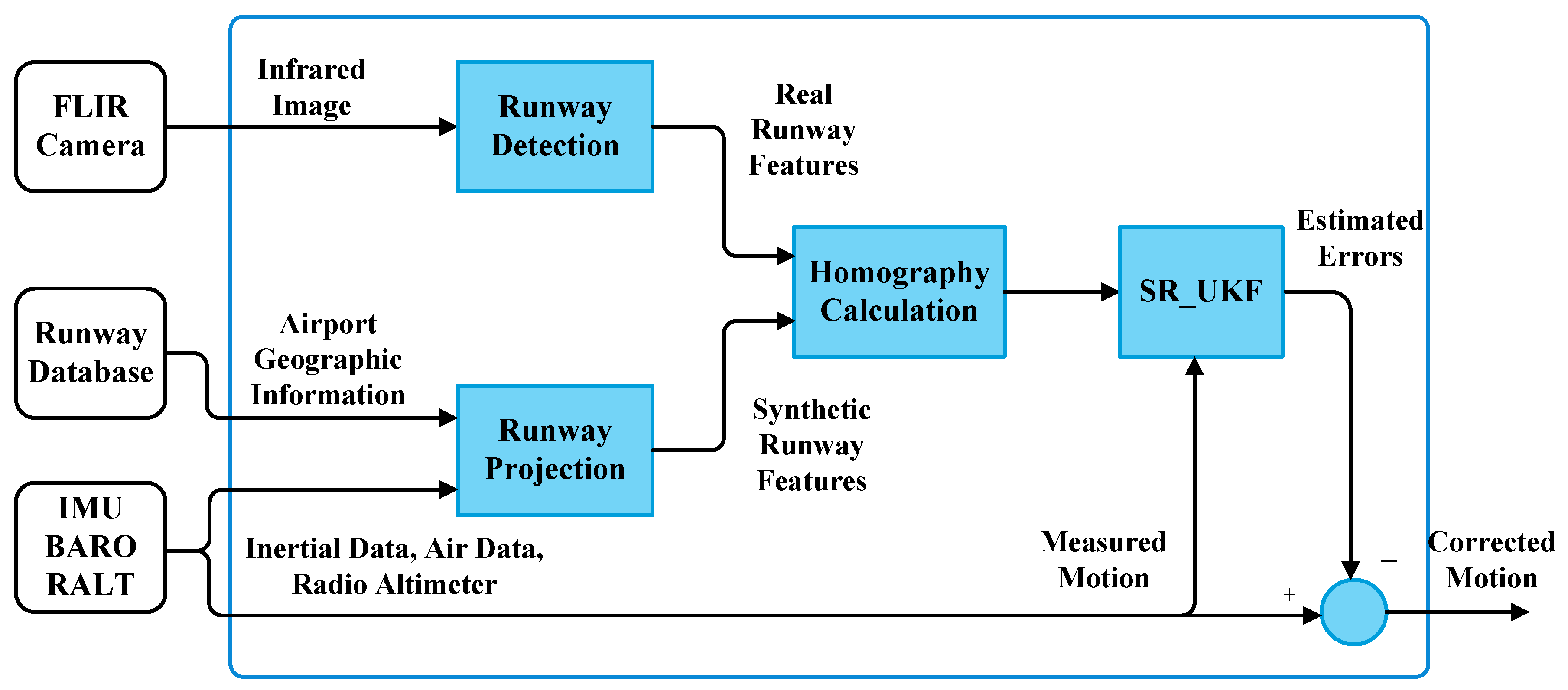
2.1. Framework of Infrared-Inertial Landing Navigation
2.2. Vision Observation
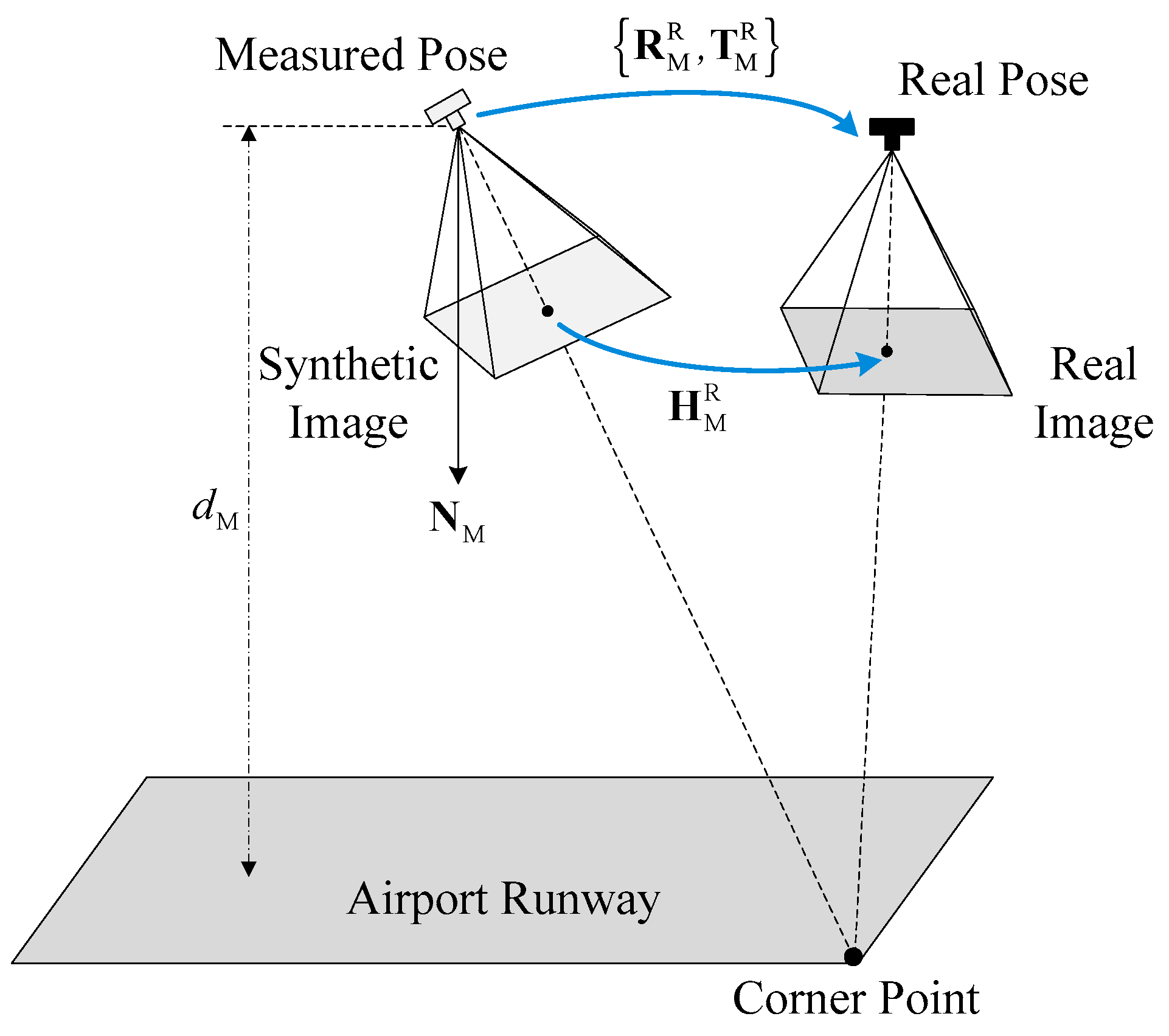
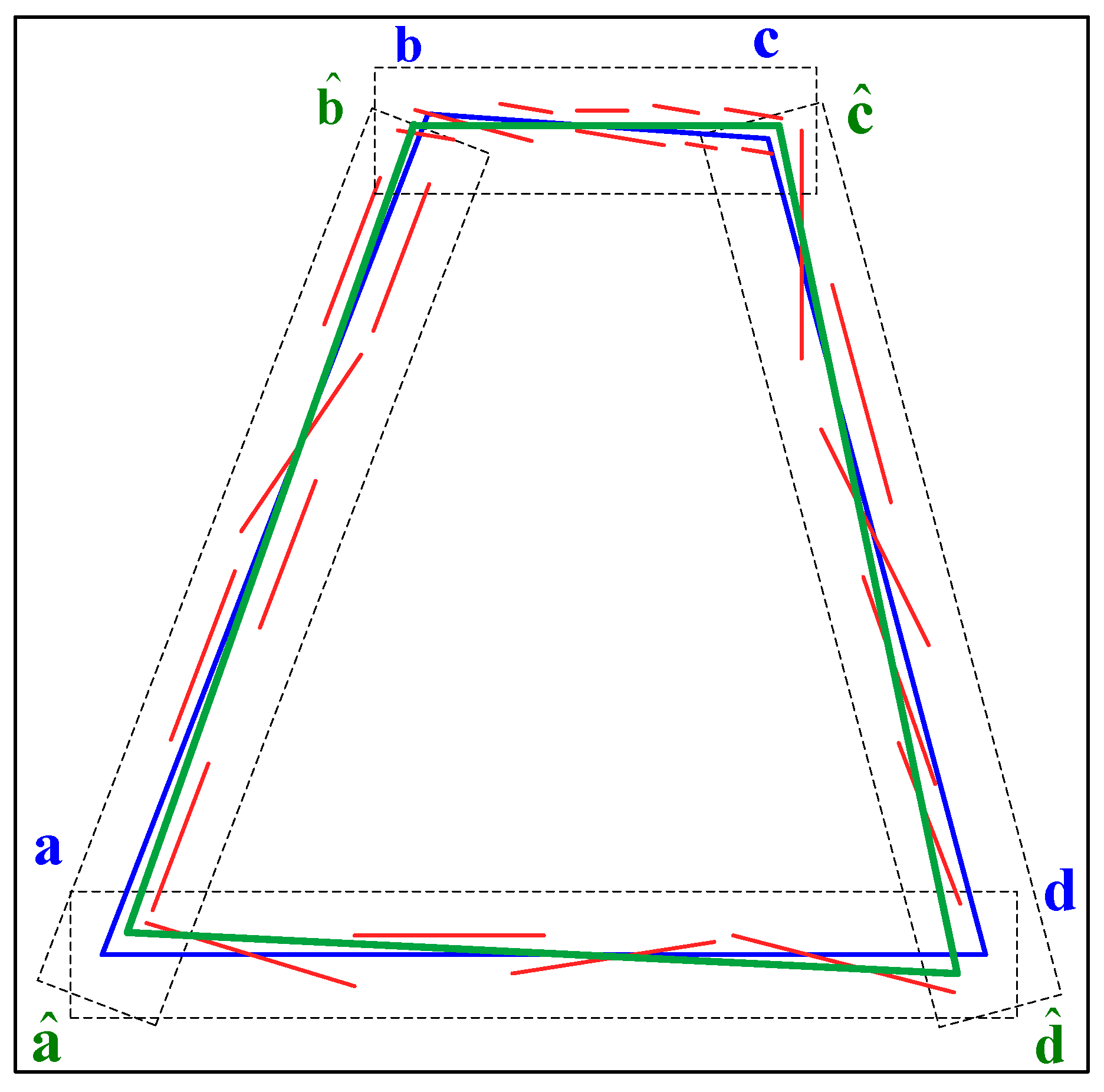
2.2.1. Homography between Synthetic and Real Images
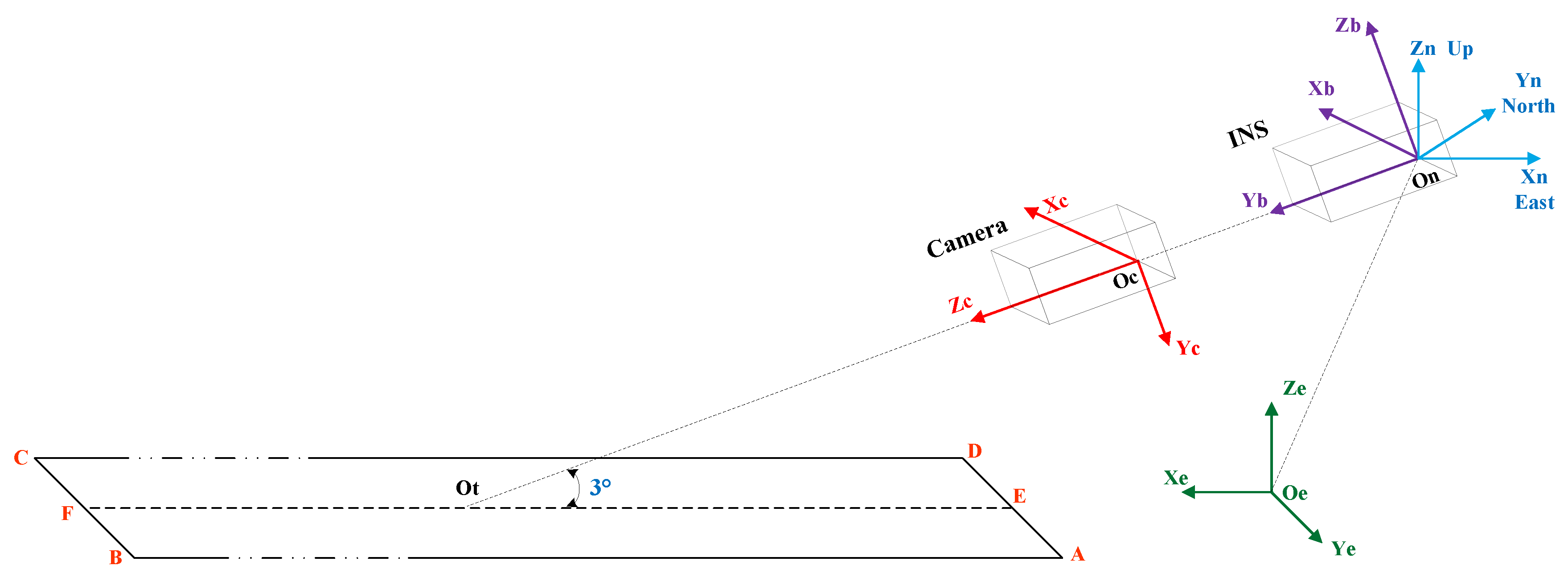
2.2.2. Synthetic Runway Features
2.2.3. Real Runway Features
2.3. Visual-Inertial Navigation
2.3.1. Process Modeling
2.3.2. Vision Measurement Model
2.3.3. Other Observations
2.4. Observability
2.4.1. Nonlinear Observability
2.4.2. Observability Analysis
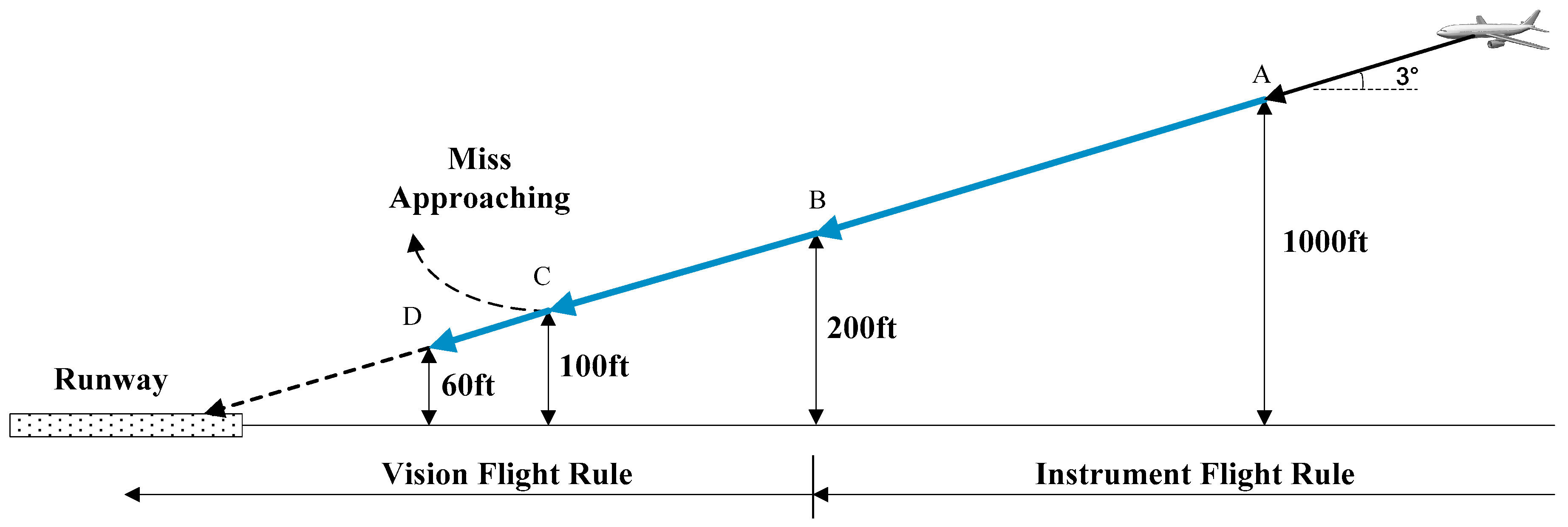
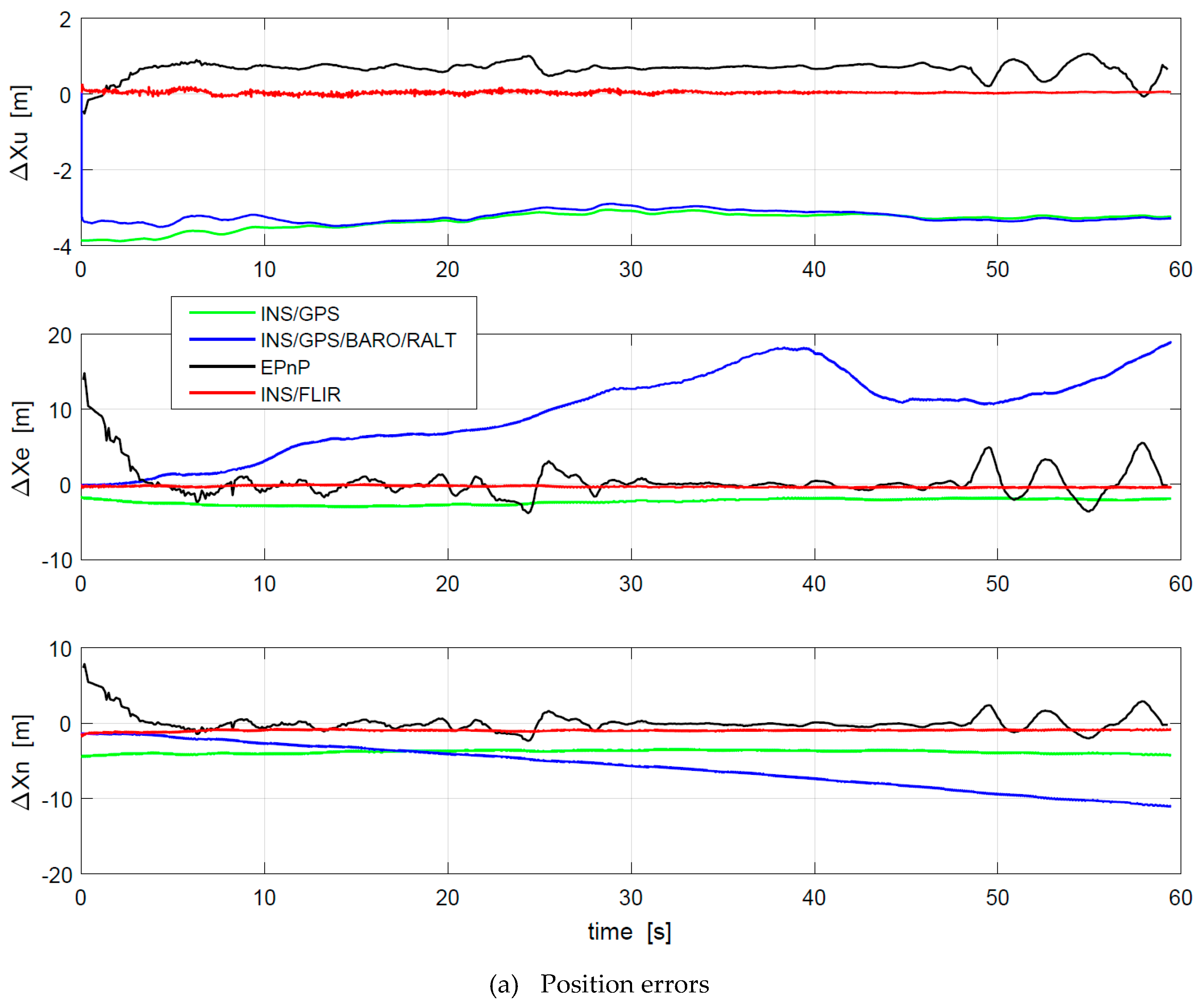
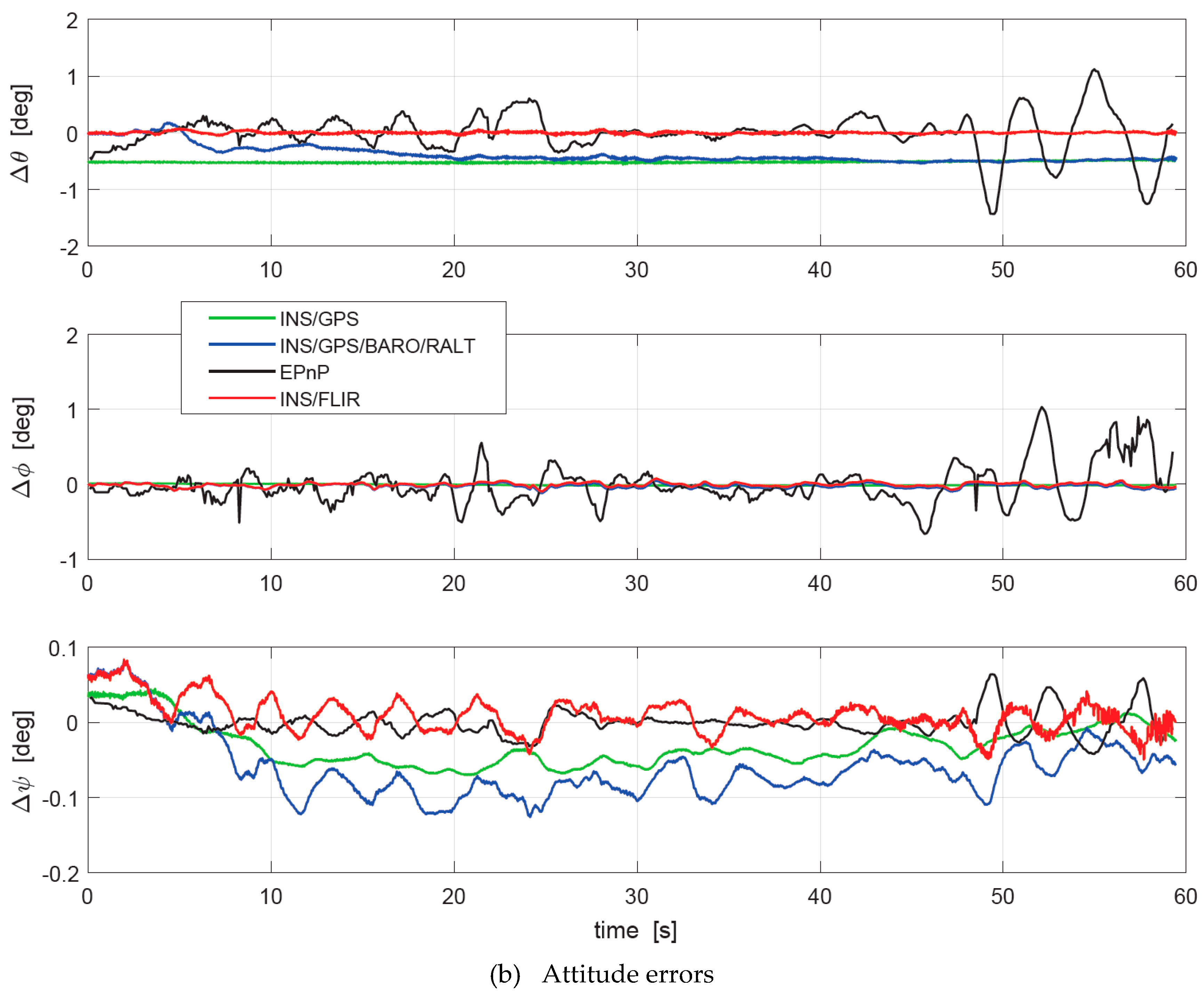
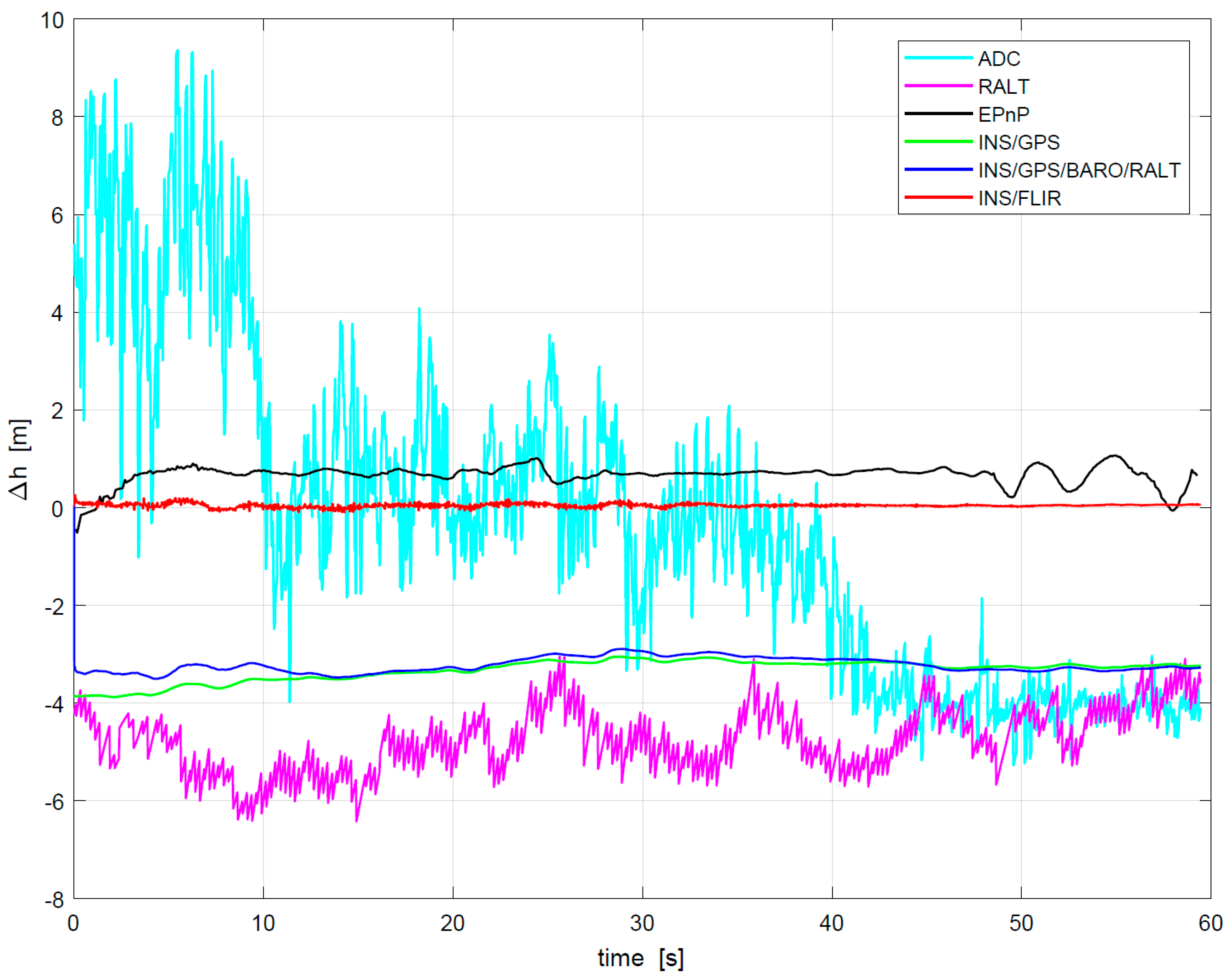
3. Experimental Section and Discussion
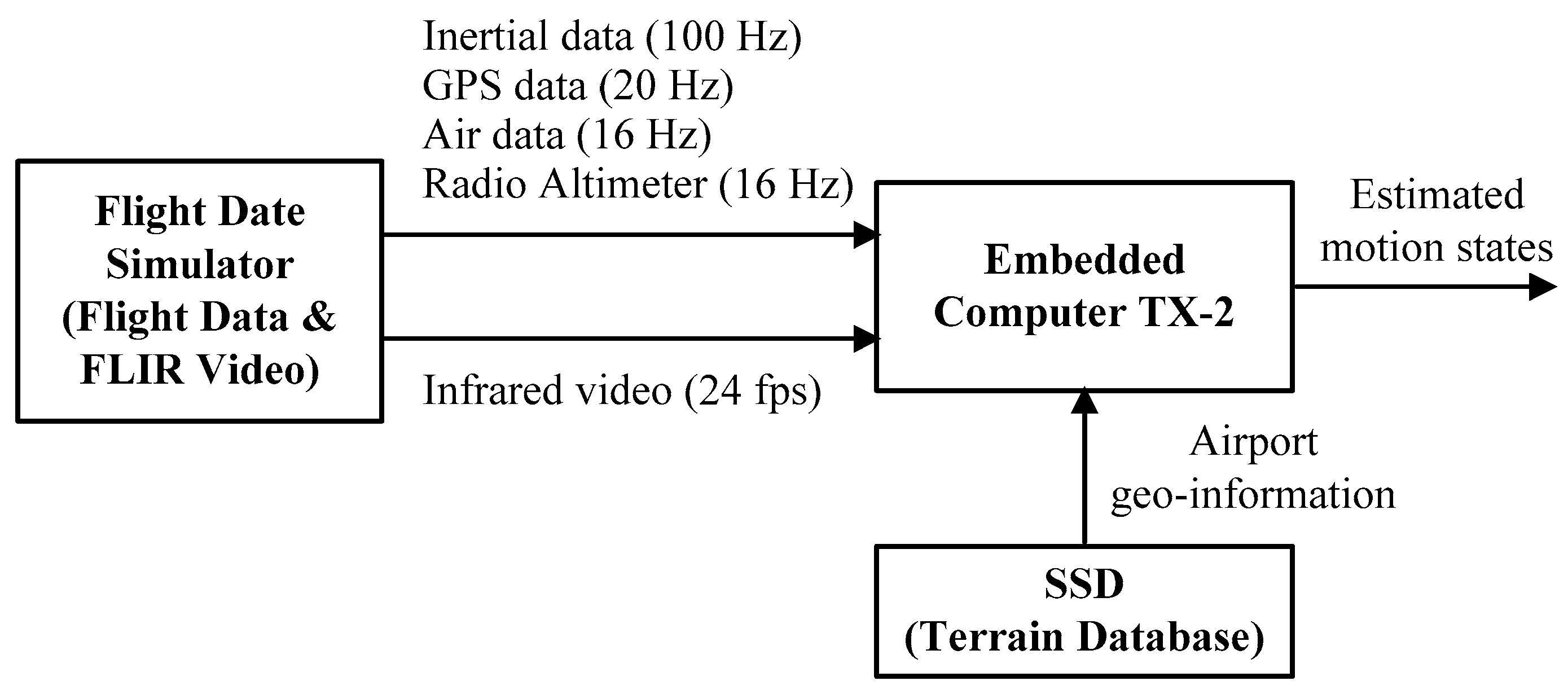
3.1. Experiments Preparation
3.2. Runway Detection Experiment
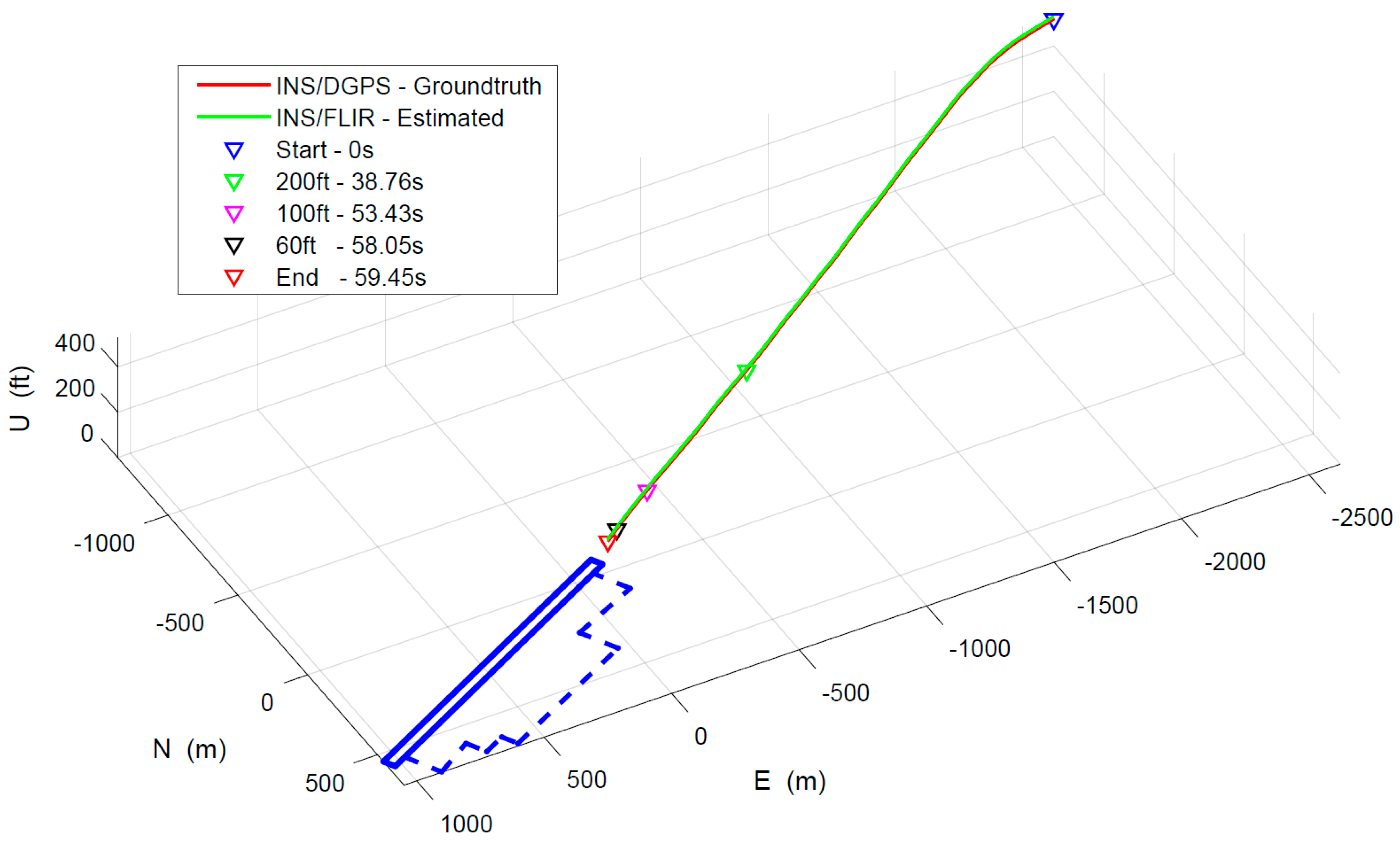
3.3. Motion Estimation Experiment
3.4. Discussions
4. Conclusions and Future Works
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Jiyun, L.; Minchan, K. Optimized GNSS Station Selection to Support Long-Term Monitoring of Ionospheric Anomalies for Aircraft Landing Systems. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 236–246. [Google Scholar] [CrossRef]
- Alvika, G.; Sujit, P.B.; Srikanth, S. A Survey of Autonomous Landing Techniques for UAVs. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 1210–1218. [Google Scholar]
- Kong, W.; Zhou, D.; Zhang, D.; Zhang, J. Vision-based Autonomous Landing System for Unmanned Aerial Vehicle: A Survey. In Proceedings of the International Conference on Multisensor Fusion and Information Integration for Intelligent Systems (MFI), Beijing, China, 28–29 September 2014; pp. 1–8. [Google Scholar]
- Martínez, C.; Mondragón, I.; Olivares-Méndez, M.; Compoy, P. On-board and Ground Visual Pose Estimation Techniques for UAV Control. J. Intell. Robot. Syst. 2011, 61, 301–320. [Google Scholar] [CrossRef]
- Kong, W.; Zhang, D.; Wang, X.; Xian, Z.; Zhang, J. Autonomous Landing of an UAV with a Ground-Based Actuated Infrared Stereo Vision System. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 2963–2970. [Google Scholar]
- Kong, W.; Zhou, D.; Zhang, Y.; Zhang, D.; Zhang, J. A Ground-Based Optical System for Autonomous Landing of a Fixed Wing UAV. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems (IROS), Chicago, IL, USA, 14–18 September 2014; pp. 4797–4804. [Google Scholar]
- Kong, W.; Hu, T.; Zhang, D.; Shen, L.; Zhang, J. Localization Framework for Real-Time UAV Autonomous Landing: An On-Ground Deployed Visual Approach. Sensors 2017, 17, 1437–1453. [Google Scholar] [CrossRef] [PubMed]
- Tang, D.; Hu, T.; Shen, L.; Zhang, D.; Kong, W.; Low, K. Ground Stereo Vision-based Navigation for Autonomous Take-off and Landing of UAVs: A Chan-Vese Model Approach. Int. J. Adv. Robot. Syst. 2016, 13, 67–80. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, T.; Shen, L. Stereo Vision Guiding for the Autonomous Landing of Fixed-wing UAVs: A Saliency-inspired Approach. Int. J. Adv. Robot. Syst. 2016, 13, 43–55. [Google Scholar] [CrossRef]
- Yang, T.; Li, G.; Li, J.; Zhang, Y.; Zhang, X.; Zhang, Z.; Li, Z. A Ground-Based Near Infrared Camera Array System for UAV Auto-Landing in GPS-Denied Environment. Sensors 2016, 16, 1393–1412. [Google Scholar] [CrossRef] [PubMed]
- Coutard, L.; Chaumette, F.; Pflimlin, J. Automatic landing on aircraft carrier by visual servoing. In Proceedings of the IEEE Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011; pp. 2843–2848. [Google Scholar]
- Coutard, L.; Chaumette, F. Visual detection and 3D model-based tracking for landing on an aircraft carrier. Proceedings of IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1746–1751. [Google Scholar]
- Ding, Z.; Li, K.; Meng, Y.; Wang, L. FLIR/INS/RA Integrated Landing Guidance for Landing on Aircraft Carrier. Int. J. Adv. Robot. Syst. 2015, 12, 60–68. [Google Scholar] [CrossRef]
- Jia, N.; Lei, Z.; Yan, S. An Independently Carrier Landing Method Using Point and Line Features for Fixed-Wing UAVs. Commun. Comput. Inf. Sci. 2016, 634, 176–183. [Google Scholar] [CrossRef]
- Muskardin, T.; Balmer, G.; Wlach, S.; Kondak, K.; Laiacker, M.; Ollero, A. Landing of a Fixed-wing UAV on a Mobile Ground Vehicle. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1237–1242. [Google Scholar]
- Hans-Ullrich, D.; Bernd, R. Autonomous infrared-based guidance system for approach and landing. In Proceedings of the Enhanced and Synthetic Vision, Orlando, FL, USA, 12–13 April 2004; pp. 140–147. [Google Scholar]
- Goncalves, T.; Azinheira, J.; Rives, P. Vision-Based Automatic Approach and Landing of Fixed-Wing Aircraft Using a Dense Visual Tracking. Inform. Control Autom. Robot. 2011, 85, 269–282. [Google Scholar] [CrossRef]
- Gui, Y.; Guo, P.; Zhang, H.; Lei, Z.; Zhou, X.; Du, J.; Yu, Q. Airborne Vision-Based Navigation Method for UAV Accuracy Landing Using Infrared Lamps. J. Intell. Robot. Syst. 2013, 72, 197–218. [Google Scholar] [CrossRef]
- Guo, P.; Li, X.; Gui, Y.; Zhou, X.; Zhang, H.; Zhang, X. Airborne Vision-Aided Landing Navigation System for Fixed-Wing UAV. In Proceedings of the IEEE International Conference on Signal Processing (ICSP), Hangzhou, China, 19–23 October 2014; pp. 1215–1220. [Google Scholar]
- Bras, F.; Hamel, T.; Mahony, R.; Barat, C.; Thadasack, J. Approach Maneuvers for Autonomous Landing Using Visual Servo Control. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1051–1065. [Google Scholar] [CrossRef]
- Fan, Y.; Ding, M.; Cao, Y. Vision algorithms for fixed-wing unmanned aerial vehicle landing system. Sci. China Technol. Sci. 2017, 60, 434–443. [Google Scholar] [CrossRef]
- Burlion, L.; Plinval, H. Toward vision-based landing of a fixed-wing UAV on an unknown runway under some fov constrains. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017; pp. 1824–1832. [Google Scholar]
- Gibert, V.; Burlion, L.; Chriette, A.; Boada, J.; Plestan, F. Nonlinear observers in vision system: Application to civil aircraft landing. In Proceedings of the European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 1818–1823. [Google Scholar]
- Gibert, V.; Burlion, L.; Chriette, A.; Boada, J.; Plestan, F. New pose estimation scheme in perspective vision system during civil aircraft landing. IFAC-PapersOnLine 2015, 48, 238–243. [Google Scholar] [CrossRef]
- Gibert, V.; Plestan, F.; Burlion, L.; Boada, J.; Chriette, A. Visual estimation of deviations for the civil aircraft landing. Control Eng. Pract. 2018, 75, 17–25. [Google Scholar] [CrossRef]
- Ruchanurucks, M.; Rakprayoon, P.; Kongkaew, S. Automatic Landing Assist System Using IMU+PnP for Robust Positioning of Fixed-Wing UAVs. J. Intell. Robot. Syst. 2018, 90, 189–199. [Google Scholar] [CrossRef]
- Santoso, F.; Garratt, M.; Anavatti. Visual Inertial Navigation Systems for Aerial Robotics Sensor Fusion and Technology. IEEE Trans. Autom. Sci. Eng. 2017, 14, 260–275. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, F.; Shen, S.J. Real-time Monocular Dense Mapping on Aerial Robots Using Visual-Inertial Fusion. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Marina Bay Sands, Singapore, 29 May–3 June 2017; pp. 4552–4559. [Google Scholar]
- Mur-Artal, R.; Tardos, J. Visual-Inertial monocular SLAM with Map Reuse. IEEE Trans. Autom. Lett. 2017, 2, 796–803. [Google Scholar] [CrossRef]
- Sun, K.; Mohta, K.; Pfrommer, B.; Watterson, M.; Liu, S.; Mulgaonkar, Y.; Taylor, C.J.; Kumar, V. Robust Stereo Visual Inertial Odometry for Fast Autonomous Flight. IEEE Robot. Autom. Lett. 2018, 3, 965–972. [Google Scholar] [CrossRef]
- Borges, P.; Vidas, S. Practical Infrared Visual Odometry. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2205–2213. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, Q.; Zhang, Y.; Tan, K. Runway Extraction in Low Visibility Conditions Based on Sensor Fusion Method. IEEE Sens. J. 2016, 14, 1980–1987. [Google Scholar] [CrossRef]
- Kumar, V.; Kashyao, S.; Kumar, N. Detection of Runway and Obstacles using Electro-optical and Infrared Sensors before Landing. Def. Sci. J. 2014, 64, 67–76. [Google Scholar] [CrossRef]
- Wu, W.; Xia, R.; Xiang, W.; Hui, B.; Chang, Z.; Liu, Y.; Zhang, Y. Efficient Airport Detection Using Line Segment Detector and Fisher Vector Representation. IEEE Geosci. Remote Sens. 2016, 13, 1079–1083. [Google Scholar] [CrossRef]
- Lei, Z.; Cheng, Y.; Zhengjun, Z. Real-time Accurate Runway Detection based on Airborne Multi-sensors Fusion. Def. Sci. J. 2017, 67, 48–56. [Google Scholar] [CrossRef]
- Hermann, R.; Krener, A. Nonlinear controllability and observability. IEEE Trans. Autom. Control 1977, 22, 728–740. [Google Scholar] [CrossRef]
- Kelly, J.; Sukhatme, G. Visual-Inertial Sensor Fusion: Localization, Mapping and Sensor-to-Sensor Self-Calibration. Int. J. Robot. Res. 2010, 5, 56–79. [Google Scholar] [CrossRef]
- Weiss, S. Vision Based Navigation for Micro Helicopters. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2012. [Google Scholar]
- RTCA DO-315B. Minimum Aviation System Performance Standard (MASPS) for Enhanced Vision Systems, Synthetic Vision Systems, Combine Vision Systems and Enhanced Flight Vision Systems; RTCA: Washington, DC, USA, 2013. [Google Scholar]
- Ma, Y.; Soatto, S.; Kosecka, J.; Sastry, S. An Invitation to 3-D Vision: From Images to Geometric Models; Springer: New York, NY, USA, 2004; pp. 131–139. [Google Scholar]
- Ezio, M.; Manuel, V. Deeper Understanding of the Homography Decomposition for Vision-Based Control; RR-6303; INRIA: Sophia Antipolis, France, 2007. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003; pp. 325–339. [Google Scholar]
- Akinlar, C.; Topal, C. EDLines: A real-time line segment detector with a false detection control. Pattern Recognit. Lett. 2011, 32, 1633–1642. [Google Scholar] [CrossRef]
- Rudolph, V.D.; Eric., A.W. The Square-root Unscented Kalman Filter for State and Parameter-estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing 2001, Salt Lake City, UT, USA, 7–11 May 2001; pp. 3461–3464. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Khalaf, W.; Chouaib, I.; Wainakh, M. Novel adaptive UKF for tightly-coupled INS/GPS integration with experimental validation on an UAV. Gyrosc. Navig. 2017, 8, 259–269. [Google Scholar] [CrossRef]
- Gay, R.; Maybeck, P. An Integrated GPS/INS/BARO and Radar Altimeter System for Aircraft Precision Approach Landings. In Proceedings of the IEEE National Aerospace and Electronics Conference, Dayton, OH, USA, 22–26 May 1995; pp. 161–168. [Google Scholar]
- Huang, B.; Bi, D.; Wu, D. Infrared and Visible Image Fusion Based on Different Constraints in the Non-Subsampled Shearlet Transform Domain. Sensors 2018, 18, 1169–1182. [Google Scholar] [CrossRef]
- Ma, J.; Ma, Y.; Li, C. Infrared and Visible Image Fusion methods and Applications: A Survey. Inform. Fusion 2019, 45, 153–178. [Google Scholar] [CrossRef]
- Dong, J.; Fei, X.; Soatto, S. Visual-Inertial-Semantic Scene Representation for 3D Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3567–3577. [Google Scholar]
- Yang, Z.F.; Shen, S.J. Monocular Visual-Inertial State Estimation with Online Initialization and Camera-IMU Extrinsic Calibration. IEEE Trans. Autom. Sci. Eng. 2017, 14, 39–51. [Google Scholar] [CrossRef]
- Kaiser, J.; Martinelli, A.; Fontana, F.; Scraramuzza, D. Simultaneous State Initialization and Gyroscope Bias Calibration in Visual Inertial Aided Navigation. IEEE Robot. Autom. Lett. 2017, 2, 18–25. [Google Scholar] [CrossRef]
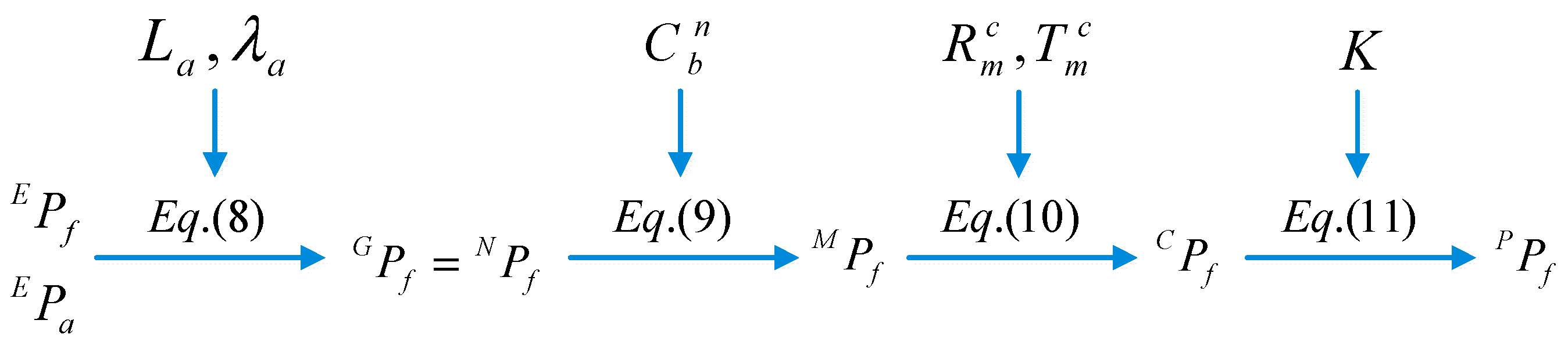




| FLIR Camera Intrinsic Parameters | pixel size | 0.025 µm |
| focal length | fx = 1010.7 pixel, fy = 1009.5 pixel | |
| principal point | u0 = 316.376 pixel, v0 = 237.038 pixel | |
| radial distortion | k1 = −0.3408, k2 = 0.1238 | |
| spectral response | 0.9–1.7 μm | |
| CCD resolution | 640 × 512 | |
| field of view | 20°(H) × 30°(V) | |
| FLIR Camera Installation | position | [−0.002, 0.094, −12.217] m [−0.0181, −0.0824, −0.0049] rad |
| attitude | ||
| INS Installation | position | [0.0704, −0.4742, −7.2863] m [0.0789, 0.0003, −0.0088] rad |
| attitude |
| Scenarios | Flight Height (Ft) | ROI (pixels) | ROI/CCD Ratio | Lines |
|---|---|---|---|---|
| 1 | 200 | 49 × 77 | 0.0115 | 16 |
| 2 | 100 | 106 × 214 | 0.0692 | 58 |
| 3 | 60 | 164 × 488 | 0.2442 | 173 |
| Height | Method | Δθ (deg) | Δϕ (deg) | Δψ (deg) | ΔVe (m/s) | ΔVn (m/s) | ΔVu (m/s) | ΔXe (m) | ΔXn (m) | ΔXu (m) |
|---|---|---|---|---|---|---|---|---|---|---|
| 500–200 ft | A | 0.0222 | 0.0275 | 0.0275 | 0.1384 | 0.2344 | 0.1180 | 0.2544 | 1.0091 | 0.0638 |
| B | 0.5252 | 0.0118 | 0.0478 | 0.1300 | 0.1205 | 0.1118 | 2.5186 | 3.8128 | 3.3936 | |
| C | 0.3686 | 0.0345 | 0.0808 | 0.0980 | 0.6693 | 0.1159 | 9.3157 | 4.3762 | 3.2143 | |
| D | 0.2056 | 0.1645 | 0.0118 | — | — | — | 2.4090 | 1.3071 | 0.6973 | |
| 200–100 ft | A | 0.0133 | 0.0275 | 0.0151 | 0.1096 | 0.1709 | 0.0748 | 0.3938 | 0.6297 | 0. 4013 |
| B | 0.5063 | 0.0151 | 0.0303 | 0.0916 | 0.1164 | 0.0754 | 1.9192 | 3.7881 | 3.2277 | |
| C | 0.4934 | 0.0364 | 0.0650 | 0.1001 | 0.4617 | 0.0780 | 12.952 | 8.6355 | 3.2394 | |
| D | 0.4415 | 0.3349 | 0.0207 | — | — | — | 1.5185 | 0.7632 | 0.6902 | |
| 100–60 ft | A | 0.0122 | 0.0268 | 0.0203 | 0.0793 | 0.1228 | 0.0601 | 0.4051 | 0.8981 | 0.0531 |
| B | 0.4869 | 0.0135 | 0.0080 | 0.0802 | 0.1093 | 0.0619 | 2.0229 | 4.0380 | 3.2476 | |
| C | 0.4773 | 0.0346 | 0.0375 | 0.1173 | 0.3777 | 0.0631 | 14.617 | 10.401 | 3.3094 | |
| D | 0.6914 | 0.5275 | 0.0304 | — | — | — | 2.5647 | 1.3917 | 0.7617 | |
| 60–47 ft | A | 0.0190 | 0.0379 | 0.0131 | 0.1187 | 0.1282 | 0.1189 | 0.4038 | 0.8795 | 0.0567 |
| B | 0.4762 | 0.0596 | 0.0141 | 0.0769 | 0.1525 | 0.1221 | 1.9263 | 4.1950 | 3.2373 | |
| C | 0.4703 | 0.0800 | 0.0486 | 0.1390 | 0.5439 | 0.1224 | 18.051 | 10.948 | 3.2825 | |
| D | 0.7734 | 0.4161 | 0.0202 | — | — | — | 3.3010 | 1.7121 | 0.4384 |
| Height | INS/FLIR | INS/GPS | INS/GPS/BARO/RALT | EPnP | BARO | Radio Altimeter |
|---|---|---|---|---|---|---|
| 500–200 ft | 0.0638 | 3.3936 | 3.2143 | 0.6973 | 3.0746 | 4.9590 |
| 200–100 ft | 0.0413 | 3.2277 | 3.2394 | 0.6902 | 3.6841 | 4.7333 |
| 100–60 ft | 0.0531 | 3.2476 | 3.3094 | 0.7617 | 4.0300 | 4.1154 |
| 60–47 ft | 0.0567 | 3.2373 | 3.2825 | 0.4384 | 4.1483 | 3.6150 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhai, Z.; He, L.; Wen, P.; Niu, W. Infrared-Inertial Navigation for Commercial Aircraft Precision Landing in Low Visibility and GPS-Denied Environments. Sensors 2019, 19, 408. https://doi.org/10.3390/s19020408
Zhang L, Zhai Z, He L, Wen P, Niu W. Infrared-Inertial Navigation for Commercial Aircraft Precision Landing in Low Visibility and GPS-Denied Environments. Sensors. 2019; 19(2):408. https://doi.org/10.3390/s19020408
Chicago/Turabian StyleZhang, Lei, Zhengjun Zhai, Lang He, Pengcheng Wen, and Wensheng Niu. 2019. "Infrared-Inertial Navigation for Commercial Aircraft Precision Landing in Low Visibility and GPS-Denied Environments" Sensors 19, no. 2: 408. https://doi.org/10.3390/s19020408
APA StyleZhang, L., Zhai, Z., He, L., Wen, P., & Niu, W. (2019). Infrared-Inertial Navigation for Commercial Aircraft Precision Landing in Low Visibility and GPS-Denied Environments. Sensors, 19(2), 408. https://doi.org/10.3390/s19020408





