Real-Time Model-Free Minimum-Seeking Autotuning Method for Unmanned Aerial Vehicle Controllers Based on Fibonacci-Search Algorithm
Abstract
1. Introduction
2. State of the Art
3. UAV Applications—Practical Problems
4. Fibonacci-Search Gain Tuning
4.1. Preliminaries and Notation
- the model/mathematical description of the dynamical system is unknown/imprecise or does not simply allow tuning the controller parameters by analytical calculations;
- there is no formula describing the cost function based on which it can be verified whether the solution to the problem, i.e., controller parameters, is optimal;
- the value of the cost function is based on observing a performance index in a given time horizon, and can be obtained repeatedly by performing consecutive experiments during the same flight;
- the optimal solution (minimizer) in the form of optimal parameters of a controller is obtained in an iterative manner;
- a zero-order iterative algorithm (a branch and bound algorithm) has been chosen to find the solution.
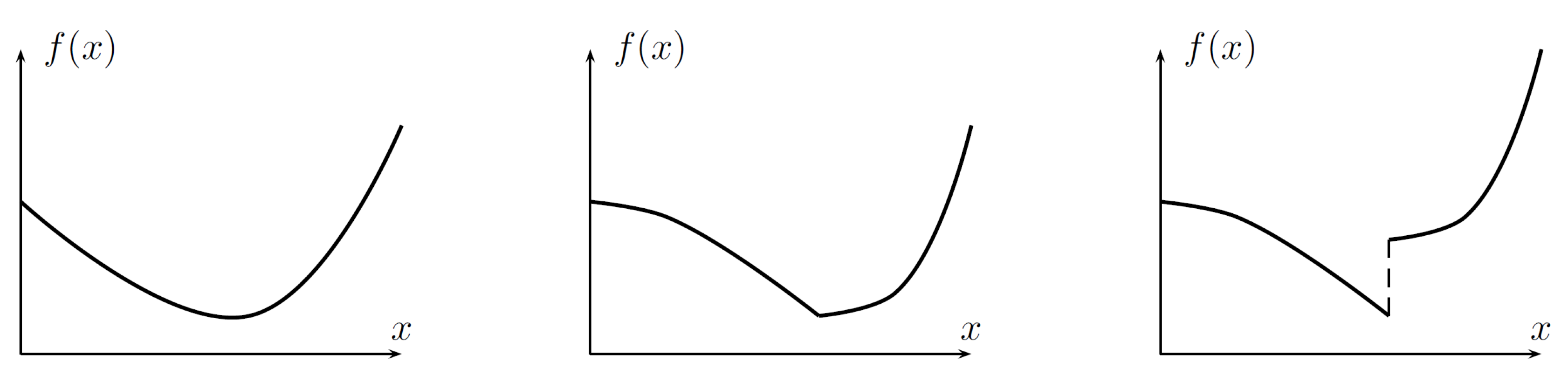
4.2. The Idea behind Zero-Order Iterative Methods for Finding Minimum Points
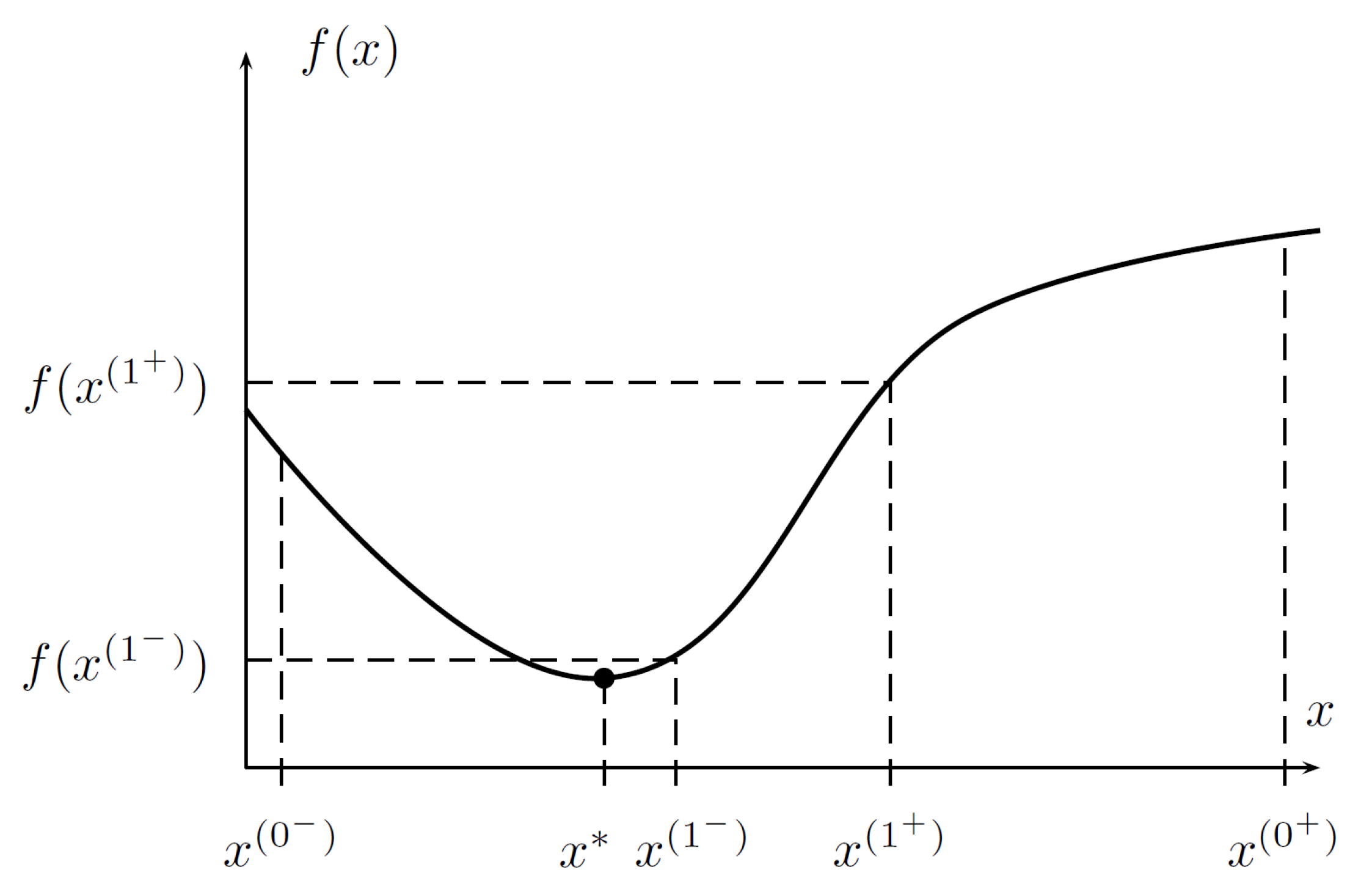
- → the minimum is in the range (see Figure 4);
- → the minimum is in the range .
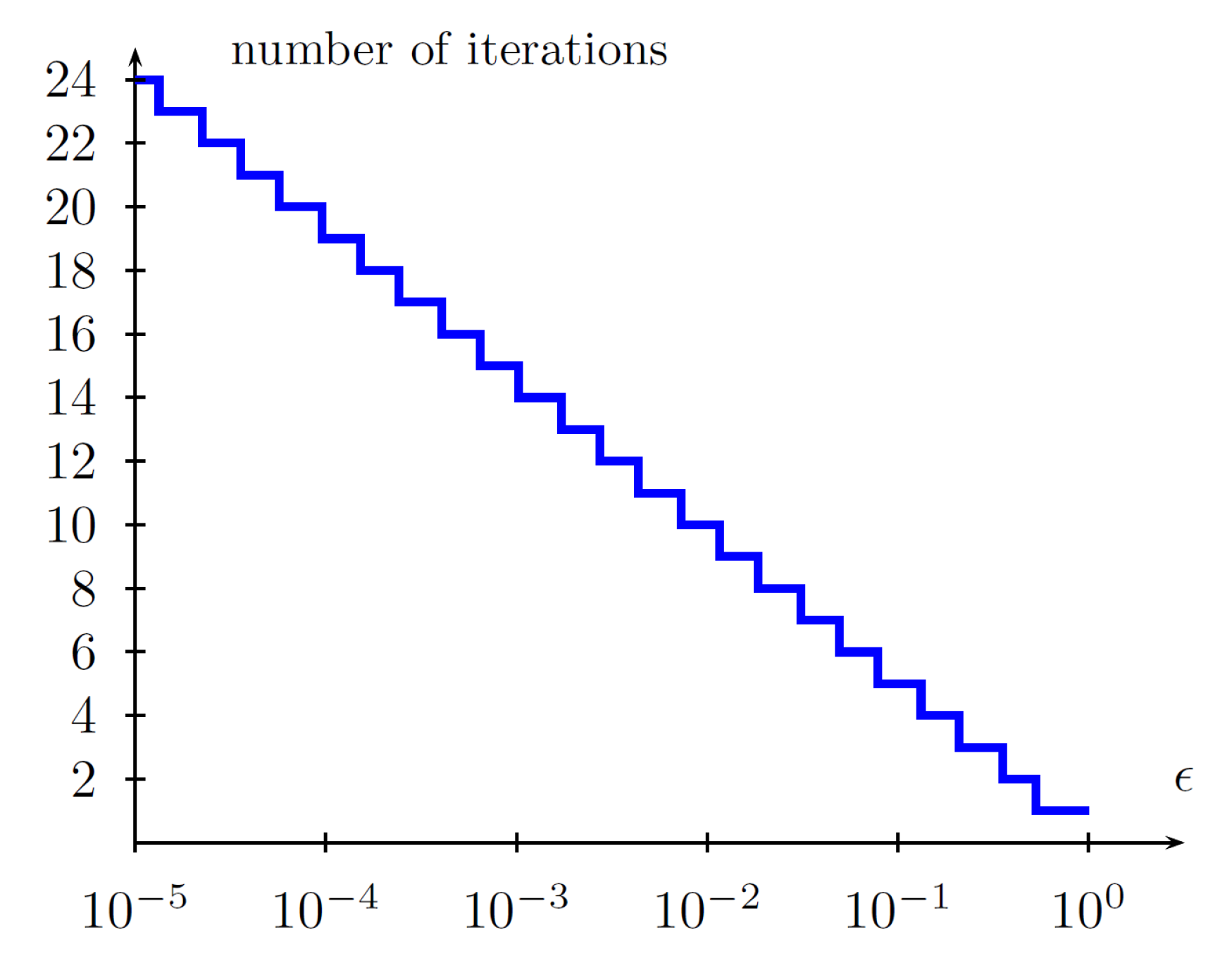
- evaluate the minimal number of iterations N for which the difference between true minimum and iterative solution (it is assumed that it is in the middle of the range ) does not exceed the prescribed relative accuracy ϵ, where
- for :
- (1)
- pick two intermediate points , (, ) from the current range ;
- (2)
- obtain the new range selecting its limits as:
- (a)
- for , ;
- (b)
- for , ;
- (3)
- put ;
- assume that is the solution to the problem.
4.3. Fibonacci-Search Method Concept
4.4. Sketch of the Algorithm for Optimal Tuning of a Two-Parameter Controller
- (0)
- calculate/estimate allowable ranges of and for the given dynamical system, ensuring stability of the closed-loop system (see Remark 3);
- (1)
- define initial value of ;
- (2)
- using a sequence of Fibonacci-search iterations for defined tolerance ϵ and , implement the followingbootstrappingtechnique (put ):
- (2a)
- starting with the initial range for and fixed , find by means of the Fibonacci method the optimal , and proceed to the step 2b;
- (2b)
- starting with the initial range for and fixed , find by means of the Fibonacci method the optimal , and proceed to the step 2c;
- (2c)
- if the updated point has already been found in the past iterations, stop the algorithm (no improvement is possible anymore); otherwise, enter and proceed to the step 2a.
- (1)
- (2)
- for a simulation-developed model of the UAV, as used in the paper in ROS-Gazebo environment, obtained, e.g., by designing a model of the UAV in such software as Autodesk Inventor Professional 2015 (Dyson, 9.0.23.0, Autodesk, San Rafael, CA, USA), perform a series of simulations to observe the behaviour of the model in a simulation environment, as in [56],
- (3)
- obtain a linearized model of the UAV for the expected motion, assume possible disturbances, such as wind gusts, as bounded, an obtain stability analysis as in [57] considering ranges for controller parameters,
- (4)
- heuristic approach: set the ranges close to the nominal parameters of the controller, which proved to stabilise the UAV in real-world experiments.
4.5. Stopping Criteria for Iterative Algorithms
- theoretical tests (in general, for )
- practical stopping criteriaor
4.6. Outline of the Implementation of the Algorithm
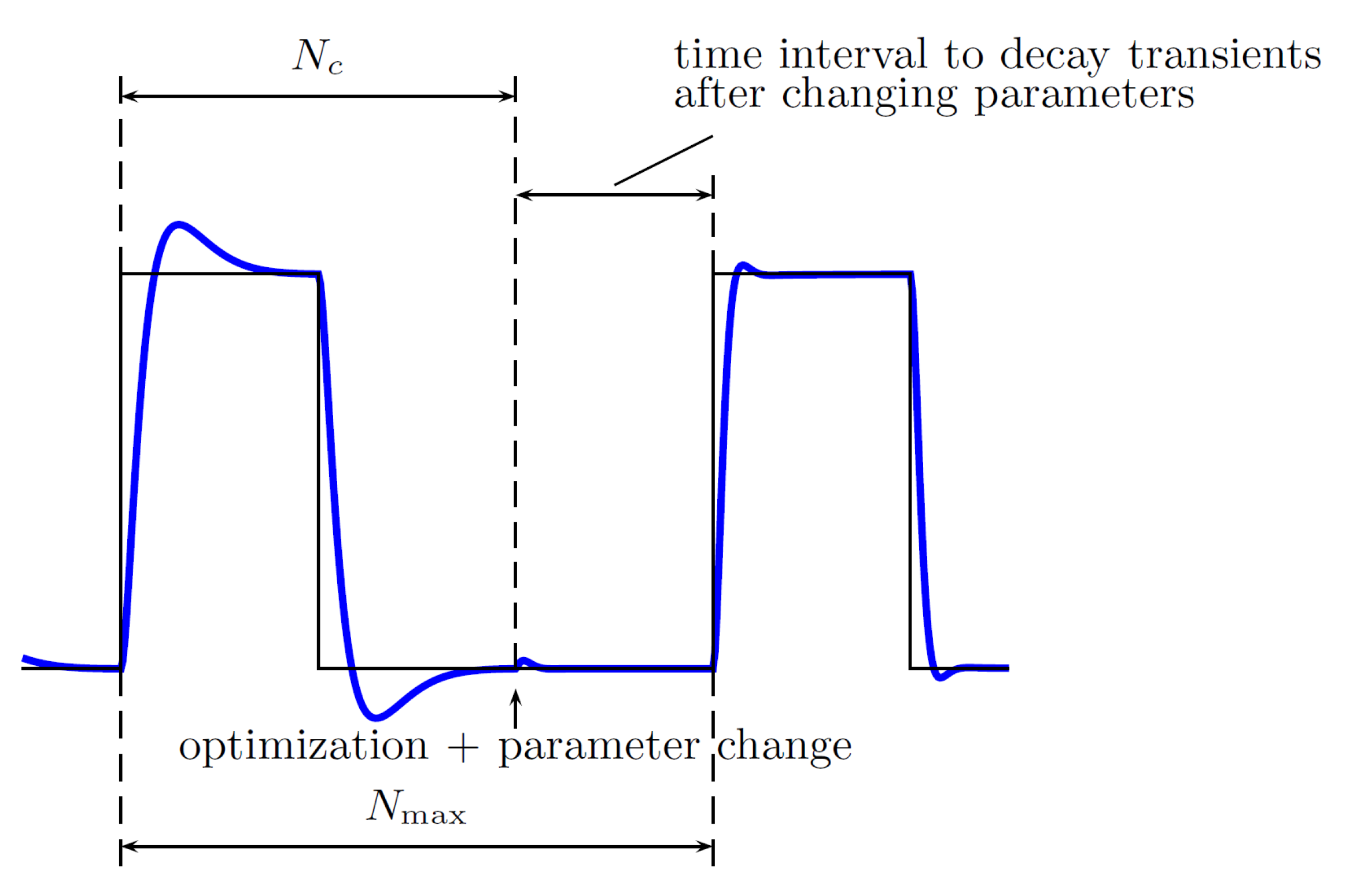
- for and with the controller parameters updated in the previous iteration, the performance index is evaluated aswhere might be, e.g., chosen as corresponding to the i-th sample of the tracking error at time or corresponding to the sum squared values of the tracking error and control input to the plant;
- for , a single iteration of the Fibonacci method is initialized—the cost function (performance index) value is stored, and if it is possible to compare the values of cost functions in a given range, i.e., either if the two intermediate points have been evaluated, the range has been reduced or the optimal solution has been found and bootstrapping takes place—either way at this point controller parameters change (are updated), which results in transient behavior of the dynamical system,
- for no action is taken (the parameters of the controller have been updated, no performance index is collected), and these steps are intended to allow the closed-loop system to stabilize at some point (to decay the transients), in order to allow performance index evaluation during the next main iteration (starting again from ).
5. Experimental Platform
6. Experimental Results
6.1. Introduction
6.2. ROS Implementation of the FGT Algorithm
update_parameters_FIB(input,main_iteration_counter,P1_range,P2_range,N_c,N_max,Par_initial,method,output)with the following parameters:
- input—the current value of the increment of the performance index, i.e., the tracking error or the low-pass filtered tracking error;
- main_iteration_counter—the variable referring to the number of iterations of the algorithm, here: 48;
- P1_range—the range for the first tuned parameter, here ;
- P2_range—the range for the second tuned parameter, here ;
- N_c—the number of samples when the performance index is collected (see Figure 9), here 50;
- N_max—the number of samples corresponding to the length of the trajectory primitive, here 60;
- Par_initial—the initial value for the second parameter, here treated as variable;
- method:
- 0—the performance index is calculated at every step;
- 1—the performance index is averaged over all past measurements with the same parameters;
- 2—the performance index is evaluated only for parameters that have been unconsidered before (the length of the tuning procedure is reduced);
- output—the vector of output variables, including tuned gains.
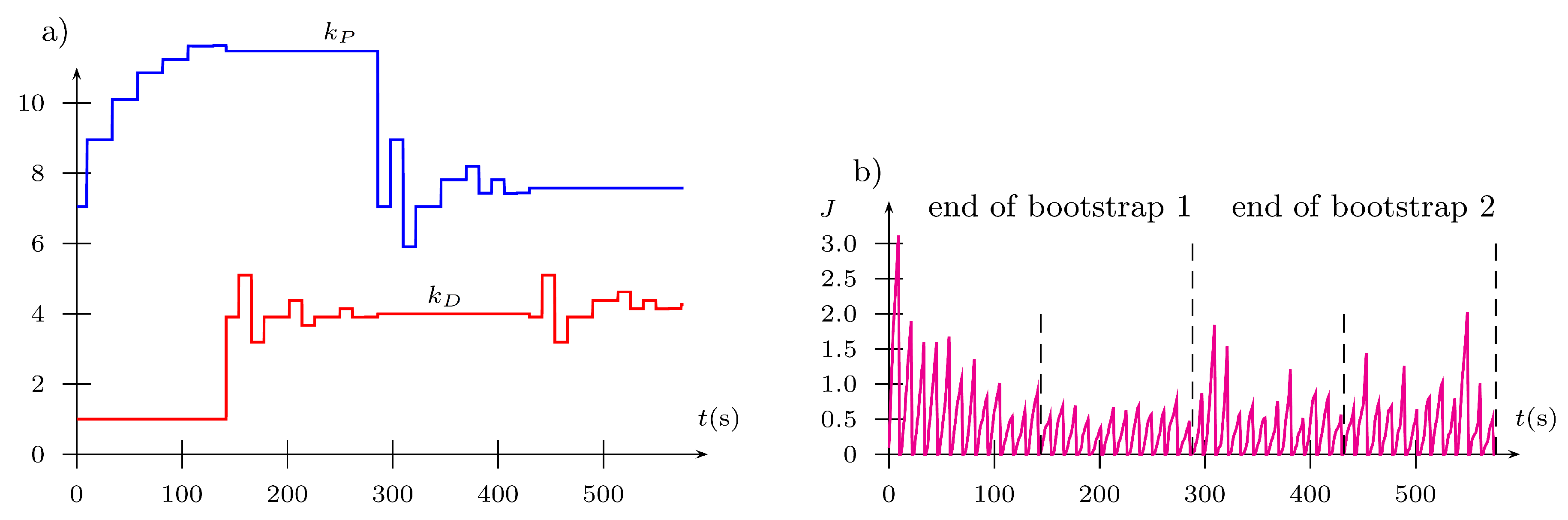
- comprises two bootstraps;
- (see Figure 10);
- the number of iterations in a single bootstrap is (each iteration is composed of two evaluations of performance indices);
- (Fibonacci–search);
- requires 48 loops of a single trajectory primitive.
6.3. ROS Gazebo Simulation Results
- (i)
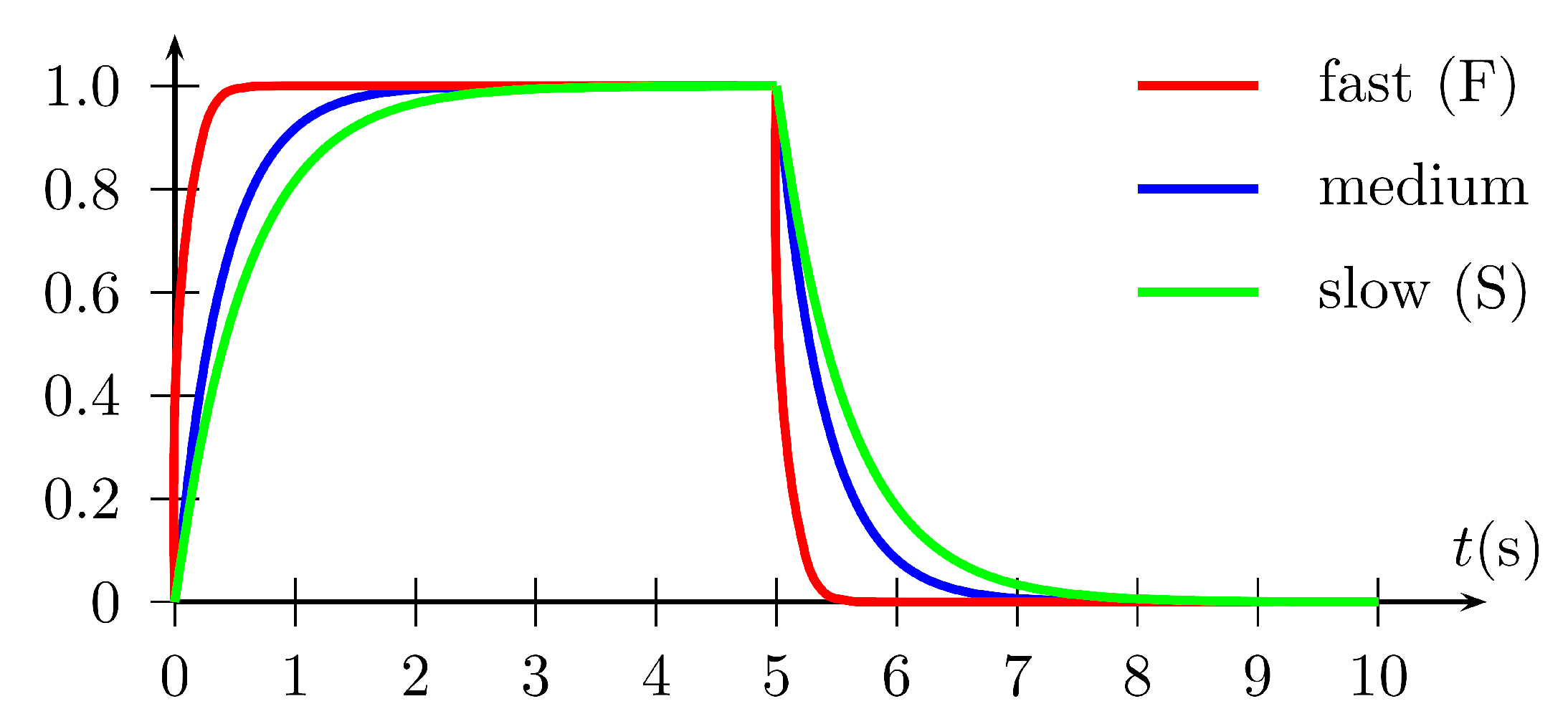
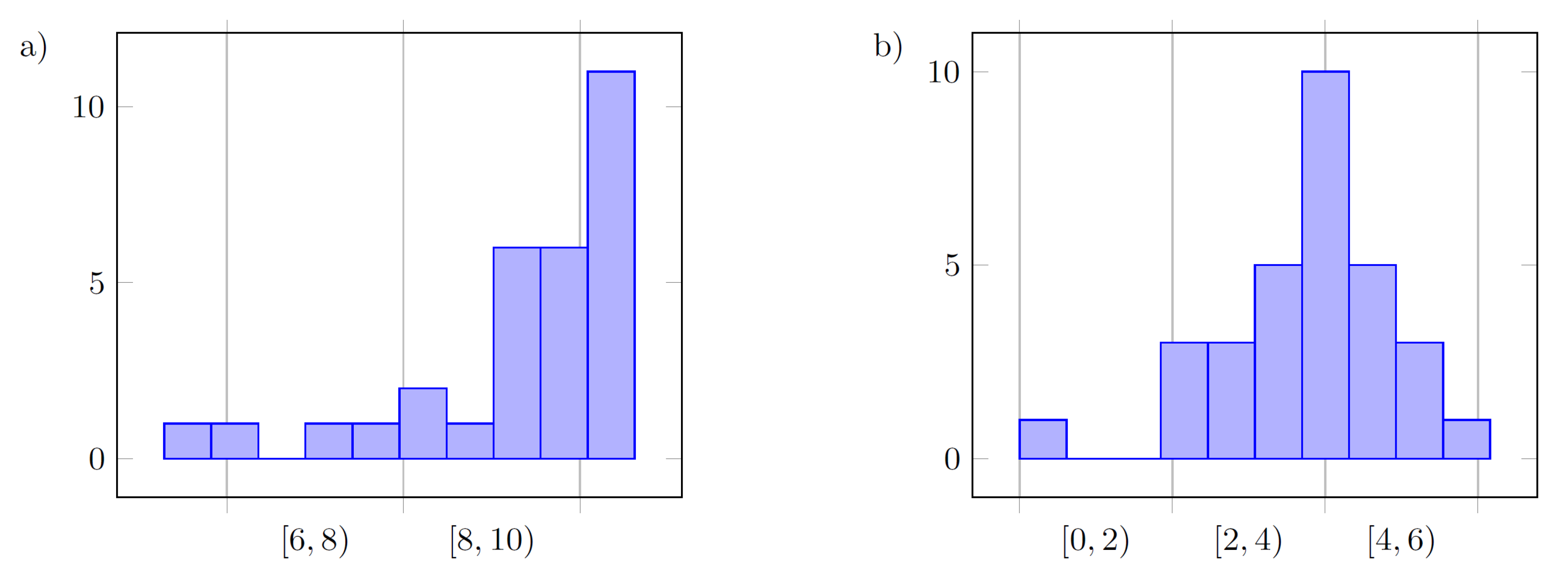
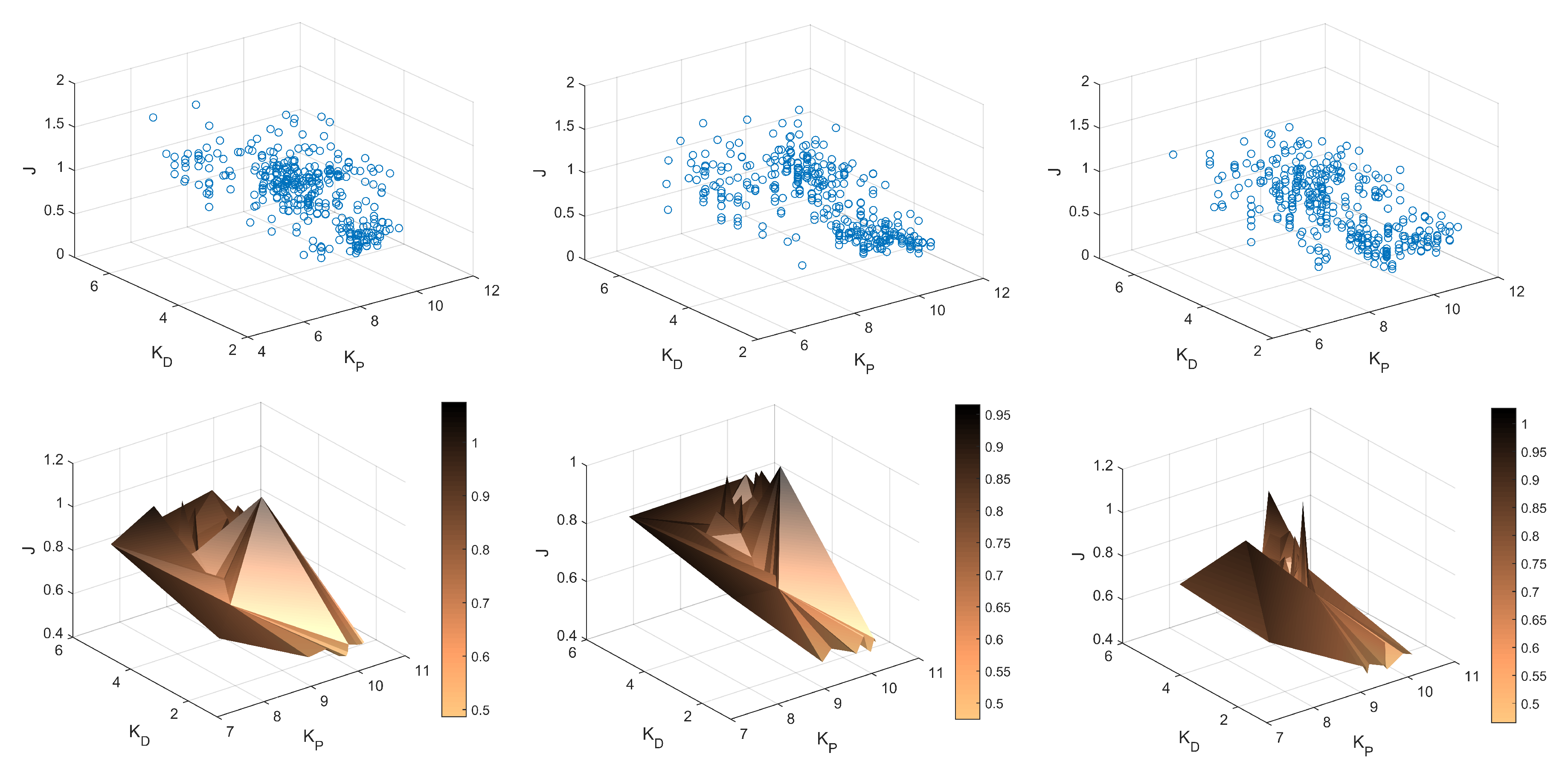
- accuracy of the obtained controller parameters for reference primitives with different dynamics: fast (, ), medium (, ), slow (, ) reference primitives,
- (ii)
- the impact of the initial value of the second parameter of the controller (Par_initial) on the convergence of the FGT procedure,
- (iii)
- ability to reduce tuning errors using a low-pass first-order filter in the variants listed above where a low-pass filter recursive equation is proposed to diminish the impact of the measurement noise on the results of optimization.
- method = 1,
- filter = 1,
- Par_initial = 1,
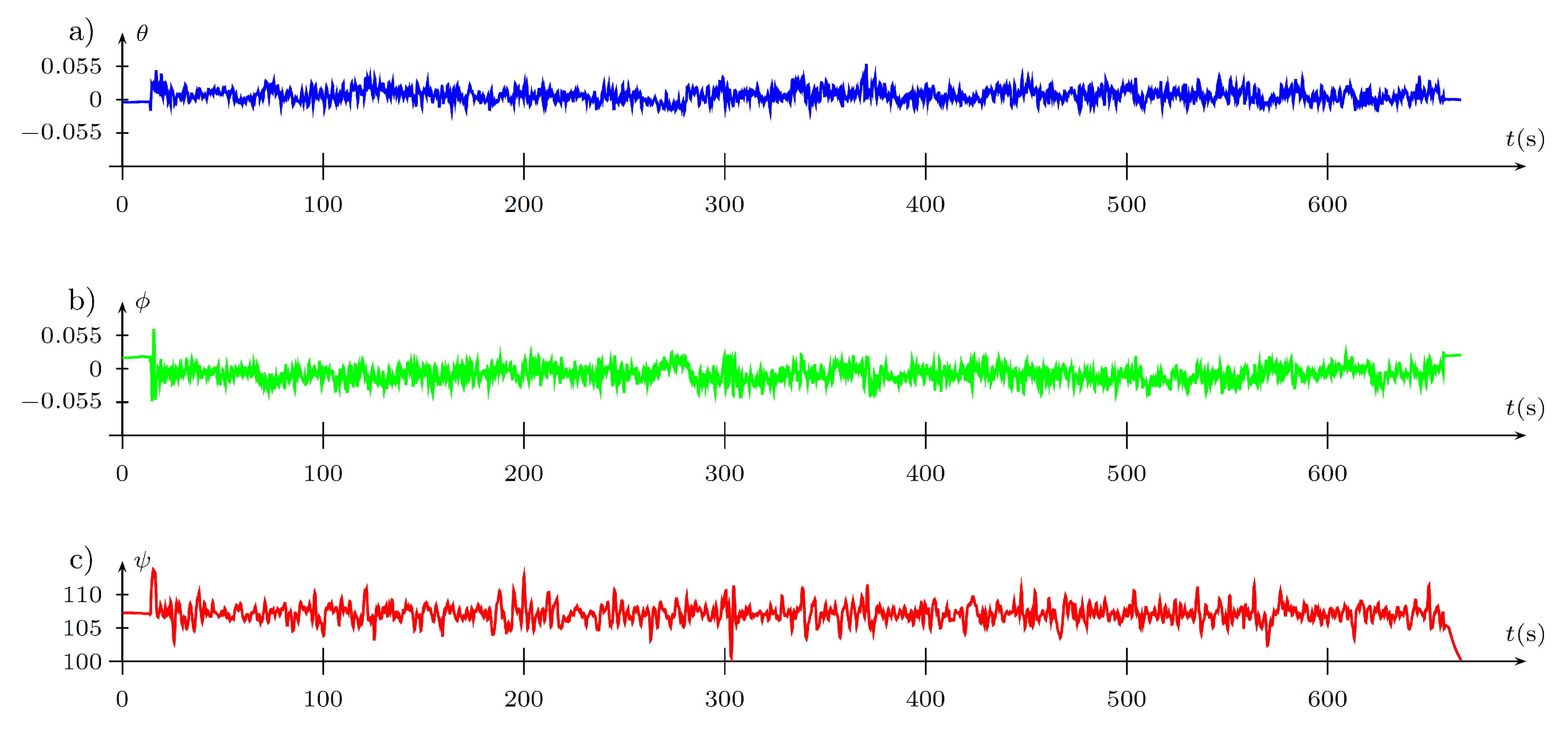
6.4. Tests in Flight Conditions
- method = 1,
- filter = 1,
- Par_initial = 1,
- trajectory primitive (M).
7. Conclusions
- it allows automatic tuning, in predefined ranges, of parameters of a controller that is widely used with a low number of parameters, such as of PD or PID type (if the method is extended to 3-parameter framework, which is not discussed in the paper, though, is the topic of the current research);
- the resulting solution from the FGT algorithm is optimal in the sense of the optimality of a function, with respect to the prescribed accuracy, and the cost function might be, in general, arbitrarily chosen;
- with respect to multirotor UAV altitude controllers, the optimal tuning process is carried out in real time and can be conducted either using a model of a UAV, or using a real robot—to the best knowledge of the authors, there are no such results reported in the literature up until now;
- two-parameter controller tuning due to the use of the proposed Fibonacci-search algorithm is characterized with rapid convergence, as has been observed during experiments even past several iterations of the algorithm; the obtained controller parameters ensure visible improvement in the reference altitude tracking task in comparison to nominal controller parameters; the time required to obtain optimal parameters is considerably shorter in comparison to bio-inspired batch methods;
- due to the structure of the algorithm, the FGT method can be used in a single run or performed in stages, in separate flights taking the maximum flight time limited by capabilities of the voltage source in a particular UAV; from authors’ observations, it can be said that provided the UAV has a maximum time of flight approximately equal to 20 min, and the tuning experiment takes about 9.5 min to terminate ( for smooth reference altitude tracking, the experiment can be performed in a single run; however, if a visible voltage drop is observed, resulting in a loss in the effective thrust force of the used driving units, the FGT approach should be used in stages, e.g., the first bootstrap in the first stage, and the second one in the next flight with new batteries;
- the last and obvious feature of the FGT algorithm that has appeared as the result of the experiments is the safety of this method during autotuning process of the altitude controller of the hexacopter UAV in flight conditions; in all the tests, independently of the initial value of the second parameter, no stability loss of the UAV has been noted, which could be a potential threat for the operator, environment or the very robot; naturally, any initial/expert knowledge concerning nominal parameters of the controller that can be used during flight is of importance. These parameters can be fine-tuned in selected ranges using the FGT method; intuitively, to obtain these ranges for parameters can be extended in consecutive experiments or to use any rapid prototyping methods prior to the experimental stage.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EKF | Extended Kalman Filter |
| FGT | Fibonacci-search Gain Tuning |
| GPS | Global Positioning System |
| IAE | Integral Absolute Error |
| IFT | Iterative Feedback Tuning |
| ILA | Iterative Learning Approach |
| IMU | Inertial Measurement Unit |
| ISE | Integral Squared Error |
| ITAE | Integral Time-weighted Absolute Error |
| ITSE | Integral Time-weighted Squared Error |
| LKF | Linear Kalman Filter |
| MBZIRC | Mohamed Bin Zayed International Robotics Challenge |
| MPC | Model Predictive Control |
| MMD | Mathematical Models Database |
| PD | Proportional-Derivative type controller |
| PI | Proportional-Integral controller |
| PID | Proportional-Integral-Derivative type controller |
| PSO | Particle Swarm Optimization |
| SITL | Simulation-In-The-Loop |
| UAV | Unmanned Aerial Vehicle |
Appendix A
Appendix B
References
- Liu, Y.; Rajappa, S.; Montenbruck, J.M.; Stegagno, P.; Bülthoff, H.; Allgöwer, F.; Zell, A. Robust nonlinear control approach to nontrivial maneuvers and obstacle avoidance for quadrotor UAV under disturbances. Robot. Auton. Syst. 2017, 98, 317–332. [Google Scholar] [CrossRef]
- Pounds, P.E.I.; Bersak, D.R.; Dollar, A.M. Stability of small-scale UAV helicopters and quadrotors with added payload mass under PID control. Auton. Robot. 2012, 33, 129–142. [Google Scholar] [CrossRef]
- Mahony, R.; Kumar, V.; Corke, P. Multirotor Aerial Vehicles: Modeling, Estimation, and Control of Quadrotor. IEEE Robot. Autom. Mag. 2012, 19, 20–32. [Google Scholar] [CrossRef]
- Chovancová, A.; Fico, T.; Hubinský, P.; Duchoň, F. Comparison of various quaternion-based control methods applied to quadrotor with disturbance observer and position estimator. Robot. Auton. Syst. 2016, 79, 87–98. [Google Scholar] [CrossRef]
- Espinoza, T.; Dzul, A.; Llama, M. Linear and nonlinear controllers applied to fixed-wing UAV. Int. J. Adv. Robot. Syst. 2013, 10, 1–10. [Google Scholar] [CrossRef]
- Espinoza-Fraire, T.; Dzul, A.; Cortés-Martínez, F.; Giernacki, W. Real-Time Implementation and Flight Tests using Linear and Nonlinear Controllers for a Fixed-Wing Miniature Aerial Vehicle (MAV). Int. J. Control Autom. Syst. 2017, 16, 392–396. [Google Scholar] [CrossRef]
- Loianno, G.; Spurny, V.; Thomas, J.; Baca, T.; Thakur, D.; Hert, D.; Penicka, R.; Krajnik, T.; Zhou, A.; Cho, A.; et al. Localization, grasping, and transportation of magnetic objects by a team of MAVs in challenging desert like environments. IEEE Robot. Autom. Lett. 2018, 3, 1576–1583. [Google Scholar] [CrossRef]
- Spurný, V.; Báča, T.; Saska, M.; Pěnička, R.; Krajník, T.; Loianno, G.; Thomas, J.; Thakur, D.; Kumar, V. Cooperative Autonomous Search, Grasping and Delivering in Treasure Hunt Scenario by a Team of UAVs. J. Field Robot. 2018. [Google Scholar] [CrossRef]
- Kohout, P. A system for Autonomous Grasping and Carrying of Objects by a Pair of Helicopters. Master’s Thesis, Czech Technical University in Prague, Prague, Czech Republic, 2017. [Google Scholar]
- Gąsior, P.; Bondyra, A.; Gardecki, S.; Giernacki, W.; Kasiński, A. Thrust estimation by fuzzy modeling of coaxial propulsion unit for multirotor UAVs. In Proceedings of the 2016 IEEE International Conference in Multisensor Fusion and Integration for Intelligent Systems (MFI), Baden-Baden, Germany, 19–21 September 2016; pp. 418–423. [Google Scholar] [CrossRef]
- Ziegler, J.G.; Nichols, N.B. Optimum settings for automatic controllers. Trans. ASME 1942, 64, 759–768. [Google Scholar] [CrossRef]
- Cohen, G.; Coon, G. Theoretical consideration of retarded control. Trans. ASME 1953, 75, 827–834. [Google Scholar]
- Panda, R. Introduction to PID Controllers—Theory, Tuning and Application to Frontier Areas; In-Tech: Rijeka, Croatia, 2012. [Google Scholar]
- O’Dwyer, A. Handbook of PI and PID Controller Tuning Rules, 3rd ed.; Imperial College Press: London, UK, 2009. [Google Scholar]
- Gautam, D.; Ha, C. Control of a Quadrotor Using a Smart Self-Tuning Fuzzy PID Controller. Int. J. Adv. Robot. Syst. 2013, 10, 1–9. [Google Scholar] [CrossRef]
- Zemalache, K.M.; Beji, L.; Maaref, H. Control of a Drone: Study and Analysis of the Robustness. J. Autom. Mob. Robot. Intell. Syst. 2008, 2, 33–42. [Google Scholar]
- Huang, S.N.; Tan, K.K.; Lee, T.H. Adaptive friction compensation using neural network approximations. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2000, 30, 551–557. [Google Scholar] [CrossRef]
- Huang, S.N.; Tan, K.K.; Lee, T.H. Adaptive motion control using neural network approximations. Automatica 2002, 38, 227–233. [Google Scholar] [CrossRef]
- Spall, J.C.; Cristion, J.A. Model-Free Control of Nonlinear Stochastic Systems with Discrete-Time Measurements. IEEE Trans. Autom. Control 1998, 43, 1198–1210. [Google Scholar] [CrossRef]
- Fister, D.; Fister, I., Jr.; Fister, J.; Šafarič, R. Parameter tuning of PID controller with reactive nature-inspired algorithms. Robot. Auton. Syst. 2016, 84, 64–75. [Google Scholar] [CrossRef]
- Giernacki, W.; Gośliński, J. Coaxial Quadrotor—From the most important physical aspects to a useful mathematical model for control purposes. In review.
- Duan, H.; Li, P. Bio-inspired Computation in Unmanned Aerial Vehicles; Springer-Verlag: Berlin, Germany, 2014. [Google Scholar]
- Hjalmarsson, H.; Gunnarsson, S.; Gevers, M. A convergent iterative restricted complexity control design scheme. In Proceedings of the 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; pp. 1735–1740. [Google Scholar] [CrossRef]
- Hjalmarsson, H.; Gevers, M.; Gunnarsson, S.; Lequin, O. Iterative feedback tuning: Theory and applications. IEEE Control Syst. Mag. 1998, 18, 26–41. [Google Scholar] [CrossRef]
- Lequin, O. Optimal closed-loop PID tuning in the process industry with the “Iterative Feedback Tuning” scheme. In Proceedings of the 1997 European Control Conference (ECC), Brussels, Belgium, 1–7 July 1997; pp. 3931–3936. [Google Scholar] [CrossRef]
- Soma, S.; Kaneko, O.; Fujii, T. A new method of a controller parameter tuning based on input-output data Fictitious Reference Iterative Tuning. In Proceedings of the 2nd IFAC Workshop on Adaptation and Learning in Control and Signal Processing (ALCOSP 2004), Yokohama, Japan, 30 August–1 September 2004; pp. 789–794. [Google Scholar] [CrossRef]
- Julkananusart, A.; Nilkhamhang, I. Quadrotor Tuning for Attitude Control based on Double-Loop PID Controller using Fictitious Reference Iterative Tuning (FRIT). In Proceedings of the 41st Annual Conference of the IEEE Industrial Electronics Society IECON 2015, Yokohama, Japan, 9–12 November 2015; pp. 4865–4870. [Google Scholar] [CrossRef]
- Julkananusart, A.; Nilkhamhang, I.; Vanijjirattikhan, R.; Takahashi, A. Quadrotor Tuning for Attitude Control based on PID Controller using Fictitious Reference Iterative Tuning (FRIT). In Proceedings of the 2015 6th International Conference of Information and Communication Technology for Embedded Systems (IC-ICTES), Hua-Hin, Thailand, 22–24 March 2015; pp. 56–60. [Google Scholar] [CrossRef]
- Bien, Z.; Xu, J.X. Iterative Learning Control—Analysis, Design, Integration and Applications; Kluwer Academic Press: Boston, MA, USA, 1998. [Google Scholar]
- Xu, J.X.; Huang, D. Optimal Tuning of PID Parameters Using Iterative Learning Approach. In Proceedings of the IEEE Multi-conference on Systems and Control, Singapore, 1–3 October 2007; pp. 226–231. [Google Scholar] [CrossRef]
- Campi, M.C.; Lecchini, A.; Savaresi, S.M. Virtual Reference Feedback Tuning (VRFT): A direct method for the design of feedback controllers. Automatica 2002, 18, 1337–1346. [Google Scholar] [CrossRef]
- Junell, J.; Mannucci, T.; Zhou, Y.; Kampen, E.J. Self-tuning Gains of a Quadrotor using a Simple Model for Policy Gradient Reinforcement Learning. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA; pp. 1–15. [CrossRef]
- Killingsworth, N.J.; Krstic, M. PID Tuning Using Extremum Seeking. Model-free for online performance optimization. IEEE Control Syst. 2006, 26, 70–79. [Google Scholar] [CrossRef]
- Skoglar, P.; Nygards, J.; Ulvklo, M. Concurrent Path and Sensor Planning for a UAV—Towards an Information Based Approach Incorporating Models of Environment and Sensor. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 2436–2442. [Google Scholar] [CrossRef]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J.; Wibisono, A. Optimal Rates for Zero-Order Convex Optimization: The Power of Two Function Evaluations. IEEE Trans. Inf. Theory 2015, 61, 2788–2806. [Google Scholar] [CrossRef]
- Agarwal, A.; Foster, D.P.; Hsu, D.; Kakade, S.M.; Rakhlin, A. Stochastic convex optimization with bandit feedback. SIAM J. Optim. 2013, 23, 213–240. [Google Scholar] [CrossRef]
- Ghadimi, S.; Lan, G. Stochastic First- and Zeroth-Order Methods for Nonconvex Stochastic Programming; University of Florida, Department of Industrial and Systems Engineering: Gainesville, FL, USA, 2013. [Google Scholar]
- Flaxman, A.D.; Kalai, A.T.; McMahan, H.B. Online convex optimization in the bandit setting: Gradient descent without a gradient. In Proceedings of the Sixteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), Vancouver, BC, Canada; 2005; pp. 385–394. [Google Scholar]
- Ahmed, N.A.; Miyatake, M. A novel maximum power point tracking for photovoltaic applications under partially shaded insolation conditions. Electr. Power Syst. Res. 2008, 78, 777–784. [Google Scholar] [CrossRef]
- Pai, N.S.; Chang, S.C.; Huang, C.T. Tuning PI/PID controllers for integrating processes with deadtime and inverse response by simple calculations. J. Process Control 2010, 20, 726–733. [Google Scholar] [CrossRef]
- Litt, J. An expert system to perform online controller tuning. IEEE Control Syst. 1991, 11, 18–23. [Google Scholar] [CrossRef]
- Pěnička, R.; Faigl, J.; Vaňa, P.; Saska, M. Dubins Orienteering Problem. IEEE Robot. Autom. Lett. 2017, 2, 1210–1217. [Google Scholar] [CrossRef]
- Saska, M.; Báča, T.; Thomas, J.; Chudoba, J.; Preucil, L.; Krajník, T.; Faigl, J.; Loianno, G.; Kumar, V. System for deployment of groups of unmanned micro aerial vehicles in GPS-denied environments using onboard visual relative localization. Auton. Robot. 2017, 41, 919–944. [Google Scholar] [CrossRef]
- Saska, M.; Vonásek, V.; Chudoba, J.; Thomas, J.; Loianno, G.; Kumar, V. Swarm Distribution and Deployment for Cooperative Surveillance by Micro-Aerial Vehicles. J. Intell. Robot. Syst. 2016, 84, 469–492. [Google Scholar] [CrossRef]
- Saska, M.; Vonásek, V.; Krajník, T.; Přeučil, L. Coordination and navigation of heterogeneous MAV-UGV formations localized by a ‘hawk-eye’-like approach under a model predictive control scheme. Int. J. Robot. Res. 2014, 33, 1393–1412. [Google Scholar] [CrossRef]
- Saska, M.; Krajník, T.; Vonásek, V.; Kasl, Z.; Spurný, V.; Přeučil, L. Fault-Tolerant Formation Driving Mechanism Designed for Heterogeneous MAVs-UGVs Groups. J. Intell. Robot. Syst. 2014, 73, 603–622. [Google Scholar] [CrossRef]
- Maher, A.; Taha, H.; Zhang, B. Realtime multi-aircraft tracking in aerial scene with deep orientation network. J. Real-Time Image Proc. 2018, 15, 495–507. [Google Scholar] [CrossRef]
- Chong, E.K.P.; Zak, S.H. An Introduction to Optimization, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Horla, D. Computational Methods in Optimization, 2nd ed.; Publishing House of Poznan University of Technology: Poznan, Poland, 2016. (In Polish) [Google Scholar]
- Horla, D. Performance evaluation of iterative methods to unconstrained single variable minimization problems. Stud. Autom. Inf. Eng. 2013, 38, 7–34. [Google Scholar]
- Lee, K.U.; Yun, Y.H.; Chang, W.; Park, J.B.; Choi, Y.H. Modeling and altitude control of quad-rotor UAV. In Proceedings of the 2011 11th International Conference on Control, Automation and Systems, Gyeonggi-do, South Korea, 26–29 October 2011; pp. 1897–1902. [Google Scholar]
- Ackermann, J. Robust Control—Systems with Uncertain Physical Parameters; Springer-Verlag: London, UK, 1993. [Google Scholar]
- Barmish, B.R. New Tools for Robustness of Linear Systems; Macmillan: New York, NY, USA, 1994. [Google Scholar]
- Bhattacharyya, S.P.; Chapellat, H.; Keel, L.H. Robust Control: The Parametric Approach; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Sanchez-Pena, R.; Sznaier, M. Robust Systems: Theory and Applications; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Zietkiewicz, J.; Horla, D.; Owczarkowski, A. Sparse in the Time Stabilization of a Bicycle Robot Model: Strategies for Event- and Self-Triggered Control Approaches. Robotics 2018, 77. [Google Scholar] [CrossRef]
- Tarbouriech, S.; Gomes da Silva, J.M.; Garcia, J. Stability and disturbance tolerance for linear systems with bounded controls. In Proceedings of the 2001 European Control Conference (ECC), Porto, Portugal, 4–7 September 2001; pp. 3219–3224. [Google Scholar] [CrossRef]
- Vrabie, D.; Pastravanu, O.; Abu-Khalaf, M. Adaptive optimal control for continuous-time linear systems based on policy iteration. Automatica 2009, 45, 477–484. [Google Scholar] [CrossRef]
- Vrabie, D.; Lewis, F.L. Adaptive optimal control algorithm for continuous-time nonlinear systems based on policy iteration. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008; pp. 73–79. [Google Scholar] [CrossRef]
- Lewis, F.L.; Vrabie, D.; Syrmos, V.L. Optimal Control, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Báča, T.; Štepán, P.; Spurný, V.; Saska, M.; Pěnička, R.; Loianno, G.; Thomas, J.; Kumar, V. Autonomous Landing on a Moving Vehicle with Unmanned Aerial Vehicle. J. Fied Robot. 2017. in review. Available online: http://mrs.felk.cvut.cz/data/papers/mbzirc-landing2017.pdf (accessed on 13 January 2019).
- Lee, T.; Leok, M.; McClamroch, N.H. Nonlinear Robust Tracking Control of a Quadrotor UAV on SE(3). Asian J. Control 2013, 15, 391–408. [Google Scholar] [CrossRef]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar] [CrossRef]
- Giernacki, W.; Horla, D.; Sadalla, T. Mathematical models database (MMD ver. 1.0) non-commercial proposal for researchers. In Proceedings of the 21st International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 29 August–1 September 2016; pp. 555–558. [Google Scholar] [CrossRef]
- Saska, M.; Baca, T.; Spurný, V.; Loianno, G.; Thomas, J.; Krajník, T.; Stepan, P.; Kumar, V. Vision-based high-speed autonomous landing and cooperative objects grasping—Towards the MBZIRC competition. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems—Vision-based High Speed Autonomous Navigation of UAVs (Workshop), Daejeon, South Korea, 9–14 October 2016; pp. 1–5. [Google Scholar]
- Saska, M.; Krátký, V.; Spurný, V.; Báča, T. Documentation of Dark Areas of Large Historical Buildings by a Formation of Unmanned Aerial Vehicles using Model Predictive Control. In Proceedings of the IEEE Conference on Emerging Technologies and Factory Automation (ETFA’17), Limassol, Cyprus, 12–15 September 2017; pp. 1–8. [Google Scholar] [CrossRef]


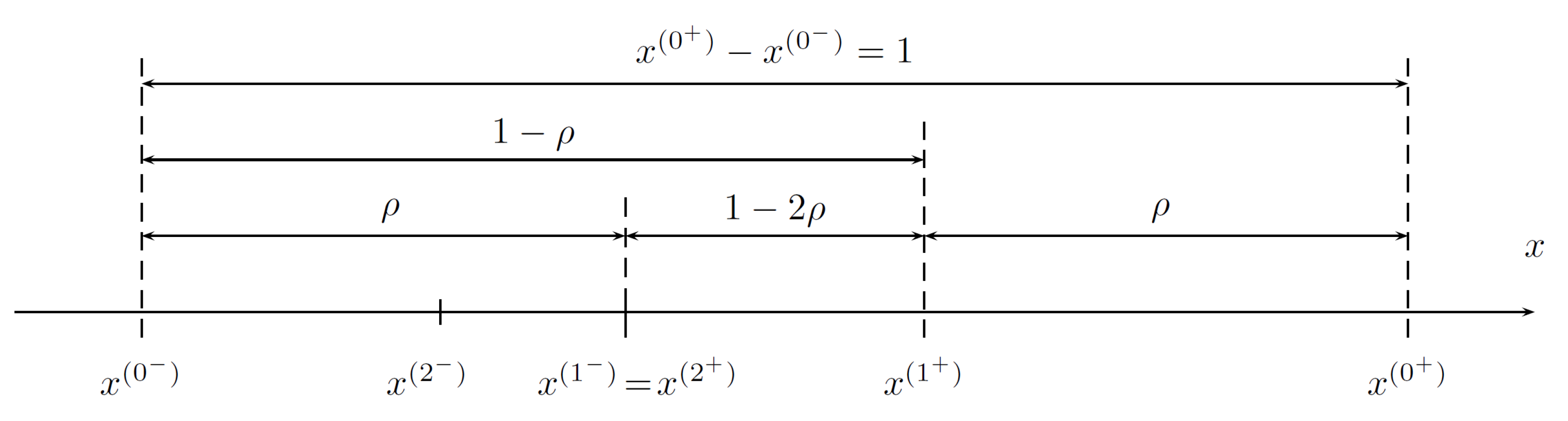




| lower bound for a parameter at k-th iteration | |
| upper bound for a parameter at k-th iteration | |
| candidate point in branch-and-bound procedure | |
| cost function | |
| considered range of a parameter at k-th iteration | |
| iterative estimate of the optimal solution |
| Slow (S) | Medium (M) | Fast (F) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| method | filter | Par_init | J | J | J | ||||||
| 0 | 0 | 1 | 8.34 | 5.45 | 1.07 | 11.76 | 2.36 | 0.75 | 9.86 | 3.55 | 0.61 |
| 0 | 0 | 3 | 8.34 | 4.50 | 1.01 | 9.48 | 2.36 | 0.67 | 10.62 | 4.03 | 0.88 |
| 0 | 0 | 5 | 4.50 | 9.86 | 0.85 | 10.62 | 4.03 | 0.87 | 10.62 | 5.45 | 0.78 |
| 0 | 0 | 7 | 10.62 | 6.16 | 0.64 | 11.00 | 4.50 | 0.73 | 9.86 | 2.35 | 0.68 |
| 0 | 0 | 9 | 9.96 | 5.69 | 0.73 | 9.95 | 4.26 | 0.70 | 9.86 | 3.55 | 0.73 |
| Total J for S, M, F: 11.713 | |||||||||||
| 0 | 1 | 1 | 7.57 | 3.55 | 0.80 | 8.04 | 3.21 | 0.53 | 9.86 | 6.16 | 0.68 |
| 0 | 1 | 3 | 10.62 | 2.12 | 0.52 | 5.76 | 2.84 | 1.15 | 9.86 | 4.50 | 0.75 |
| 0 | 1 | 5 | 6.43 | 4.26 | 0.78 | 10.62 | 2.12 | 0.46 | 10.33 | 4.02 | 0.56 |
| 0 | 1 | 7 | 9.48 | 4.74 | 0.73 | 9.95 | 3.78 | 0.56 | 10.62 | 3.55 | 0.60 |
| 0 | 1 | 9 | 11.76 | 5.93 | 0.66 | 10.33 | 4.02 | 0.72 | 9.86 | 5.45 | 0.85 |
| Total J for S, M, F: 10.368 | |||||||||||
| 1 | 0 | 1 | 8.72 | 4.74 | 0.96 | 8.72 | 2.59 | 0.55 | 10.62 | 2.36 | 0.59 |
| 1 | 0 | 3 | 10.24 | 3.07 | 0.76 | 10.33 | 4.26 | 0.88 | 5.29 | 4.26 | 0.83 |
| 1 | 0 | 5 | 6.05 | 2,59 | 0.91 | 10.24 | 2.35 | 0.63 | 10.62 | 3.79 | 0.79 |
| 1 | 0 | 7 | 9.10 | 2.83 | 0.60 | 8.81 | 5.93 | 1.16 | 9.10 | 3.78 | 0.80 |
| 1 | 0 | 9 | 8.72 | 2.60 | 0.94 | 9.48 | 2.60 | 0.76 | 9.48 | 3.79 | 0.86 |
| Total J for S, M, F: 12.041 | |||||||||||
| 1 | 1 | 1 | 7.28 | 4.50 | 0.94 | 10.33 | 4.02 | 0.61 | 10.62 | 4.26 | 0.63 |
| 1 | 1 | 3 | 10.62 | 2.12 | 0.43 | 10.24 | 3.31 | 0.46 | 9.10 | 3.31 | 0.66 |
| 1 | 1 | 5 | 10.24 | 2.60 | 0.61 | 8.72 | 2.60 | 0.63 | 10.24 | 4.50 | 0.55 |
| 1 | 1 | 7 | 8.72 | 2.60 | 0.72 | 11.38 | 2.12 | 0.64 | 10.62 | 2.12 | 0.55 |
| 1 | 1 | 9 | 10.33 | 2.12 | 0.56 | 10.24 | 5.69 | 0.66 | 7.19 | 3.55 | 0.59 |
| Total J for S, M, F: 9.227 | |||||||||||
| 2 | 0 | 1 | 10.33 | 4.02 | 0.83 | 11.47 | 2.35 | 0.68 | 8.71 | 4.74 | 0.94 |
| 2 | 0 | 3 | 11.76 | 3.31 | 0.74 | 9.19 | 4.26 | 0.73 | 9.48 | 3.07 | 0.69 |
| 2 | 0 | 5 | 9.86 | 3.31 | 0.82 | 9.95 | 2.84 | 0.62 | 9.10 | 4.02 | 0.73 |
| 2 | 0 | 7 | 10.33 | 2.84 | 0.67 | 9.19 | 4.02 | 0.62 | 7.57 | 4.26 | 1.00 |
| 2 | 0 | 9 | 8.34 | 2.36 | 0.79 | 9.19 | 3.55 | 0.66 | 9.19 | 4.50 | 0.74 |
| Total J for S, M, F: 11.261 | |||||||||||
| 2 | 1 | 1 | 8.33 | 2.59 | 0.80 | 9.19 | 5.45 | 0.79 | 10.62 | 2.83 | 0.47 |
| 2 | 1 | 3 | 10.24 | 3.07 | 0.54 | 9.86 | 3.78 | 0.54 | 10.24 | 3.07 | 0.54 |
| 2 | 1 | 5 | 7.66 | 3.55 | 0.90 | 10.33 | 3.07 | 0.47 | 8.43 | 4.02 | 0.58 |
| 2 | 1 | 7 | 11.38 | 2.84 | 0.44 | 10.33 | 2.35 | 0.42 | 8.34 | 5.22 | 1.14 |
| 2 | 1 | 9 | 11.09 | 3.31 | 0.42 | 8.04 | 2.35 | 0.52 | 6.14 | 4.50 | 0.92 |
| Total J for S, M, F: 9.490 | |||||||||||
| – | Slow (S) | Medium (M) | Fast (F) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| mean value | 9.221 | 3.335 | 0.640 | 9.230 | 3.095 | 0.670 | 8.689 | 3.478 | 0.740 |
| std deviation | 1.190 | 1.100 | 0.170 | 1.230 | 1.050 | 0.210 | 1.130 | 1.090 | 0.200 |
| min value | 7.190 | 2.120 | 0.379 | 7.190 | 2.120 | 0.477 | 6.430 | 2.360 | 0.572 |
| max value | 11.000 | 4.980 | 0.935 | 10.620 | 5.210 | 1.153 | 10.240 | 4.980 | 1.278 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giernacki, W.; Horla, D.; Báča, T.; Saska, M. Real-Time Model-Free Minimum-Seeking Autotuning Method for Unmanned Aerial Vehicle Controllers Based on Fibonacci-Search Algorithm. Sensors 2019, 19, 312. https://doi.org/10.3390/s19020312
Giernacki W, Horla D, Báča T, Saska M. Real-Time Model-Free Minimum-Seeking Autotuning Method for Unmanned Aerial Vehicle Controllers Based on Fibonacci-Search Algorithm. Sensors. 2019; 19(2):312. https://doi.org/10.3390/s19020312
Chicago/Turabian StyleGiernacki, Wojciech, Dariusz Horla, Tomáš Báča, and Martin Saska. 2019. "Real-Time Model-Free Minimum-Seeking Autotuning Method for Unmanned Aerial Vehicle Controllers Based on Fibonacci-Search Algorithm" Sensors 19, no. 2: 312. https://doi.org/10.3390/s19020312
APA StyleGiernacki, W., Horla, D., Báča, T., & Saska, M. (2019). Real-Time Model-Free Minimum-Seeking Autotuning Method for Unmanned Aerial Vehicle Controllers Based on Fibonacci-Search Algorithm. Sensors, 19(2), 312. https://doi.org/10.3390/s19020312








