Knowledge Extraction and Improved Data Fusion for Sales Prediction in Local Agricultural Markets †
Abstract
1. Introduction
- Local Market Information (LMI): geographical position, name of products, number of sellers, quantity of population that uses the local market, etc.
- For each sale and for each product, the quantity of product acquired in each sale.
2. Related Works
- (1)
- Monitoring system will be able to guarantee timely and accurate information on current food production;
- (2)
- More accurate forecasting techniques for better understanding the key risks in food supply
- The Global Information and Early Warning System (GIEWS) from the Food and Agriculture Organization (FAO) of the United Nations.
- The Famine Early Warning Systems Network (FEWSNET) from the United States Agency for International Development (USAID).
- The Monitoring Agriculture with Remote Sensing (MARS) system from the European Commission (EC).
- CropWatch in China.
- The Crop Explorer service, which provides remote-sensing-based information used by agricultural economists and researchers to predict global crop production.
- GEOGLAM6, a flagship initiative from GEO (Group on Earth Observations), which was endorsed by the G20 in 2011.
- Seasonal Monitor System of the World Food Programme (WFP).
- Anomaly Hot Spots of Agricultural Production (ASAP)9, launched by the Joint Research Centre (JRC) of the European Commission (EC) in June 2017.
- (1)
- In previous works, authors have tried to forecast the production of some specific products and tried to correlate the amount of production with external conditions. In this paper, we work with several products that could be correlated.
- (2)
- In this work, the monitoring system is modeled as a Data Fusion System, where information from several farms is aligned in time and space and then fused to obtain a global view of production.
- (3)
- Besides an analysis of contextual information (meteorological and close population), a measure of the improvement of using this information is included.
- (4)
- In this work, a “Monitoring Agriculture Fairs System” is proposed which systematically analyzes the relationships among variables based on sales (transactions) in order to improve the accuracy of prediction models for agricultural production.
3. Spatial Predictions Based on Data Fusion
- A soft sensor able to measure the climatic floors for each geographic region where the market is located. This is a software process applied over data coming from hard sensors (pressure, humidity, luminosity, etc.):i-th source from market j of type t (e.g., for temperature, humidity, etc.)
- A soft sensor able to measure the population in each one of the cantons of the study.
4. Methodology Based on Data Mining to Improve the Fusion Process
- (1)
- Clean and Transform Information
- 1.1. Records with no values are deleted
- 1.2. Similar values on records are standardized
- 1.3. Units are defined for all measurements
- 1.4. The set of products are selected for the study
- 1.5. Generate spatial structures:
- 1.5.1. Create common spatial structures (grids for extrapolation)
- 1.5.2. Transform data to a common coordinate system (the same reference for all sources)
- 1.6. Final database is generated and prepared for pattern search
- (2)
- Extract best association rules
- 2.1. The database of sold products is discretized from transactional data
- 2.2. Association algorithms are applied to mine the best association rules
- 2.3. Establish the set of products with strongest associations
- (3)
- Estimate future predictions applying geostatistical fusion techniques and validate the hypothesis of strongest conditional dependencies found by data association mining
- 3.1. Comparison of the fusion results using the set of most associated variables
- 3.2. Comparison of the results using climatic floors
- 3.3. Comparison of the results using population
- 3.4. Comparison of the results using the rest of the variables
- (4)
- Finally, the improvement of the proposal is analyzed by comparing predictions with a single product vs the data fusion results (using residuals as evaluation metrics with Leave-one-out cross-validation, LOOCV)
- Support (of a rule) is evaluated as the number of instances (register in the data set) the rule covers related to the whole set (of registers in the dataset).where D is the total set of transactions.
- Confidence (of a rule) is evaluated as the number (percentage) of times that consequent B appears among the instances that are selected by the antecedent A. The meaning of this concept is the accuracy of its prediction; it is defined as:
- Lift (of a rule) is evaluated as the ratio of observed support considering that A and B were independent:
- (1)
- Generate all item sets L with a single element; this set is used to form a new set with two, three, or more elements. All possible pairs are taken so that their support equals minsup
- (2)
- For every frequent item set L’ found:
- Determine all association rules of the form:
- If L’-J→J
- Select those rules whose confidence is greater than or equal to minconf
5. Case Study
5.1. Data Preparation
5.1.1. Spatial Data
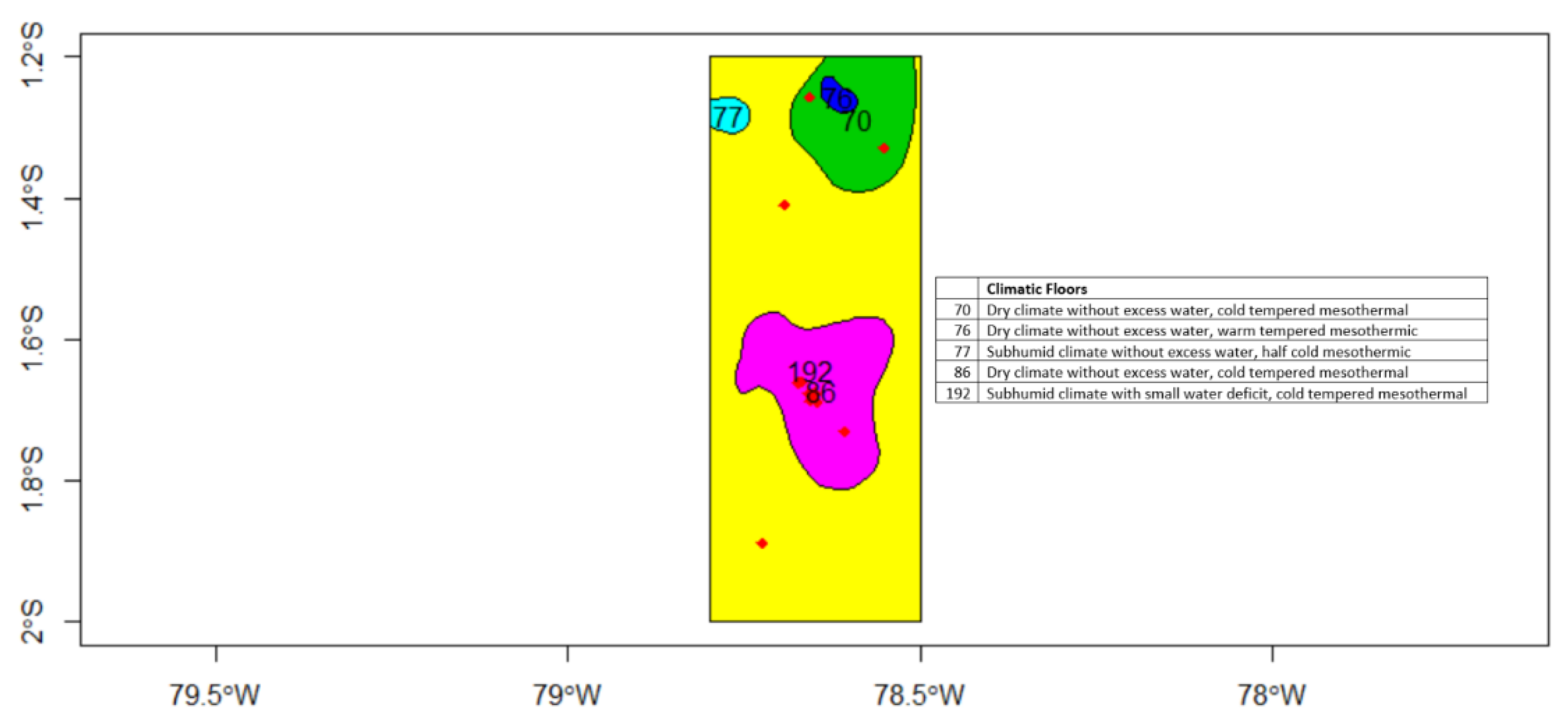
5.1.2. Climatic Zones
5.2. Association Rules Mining
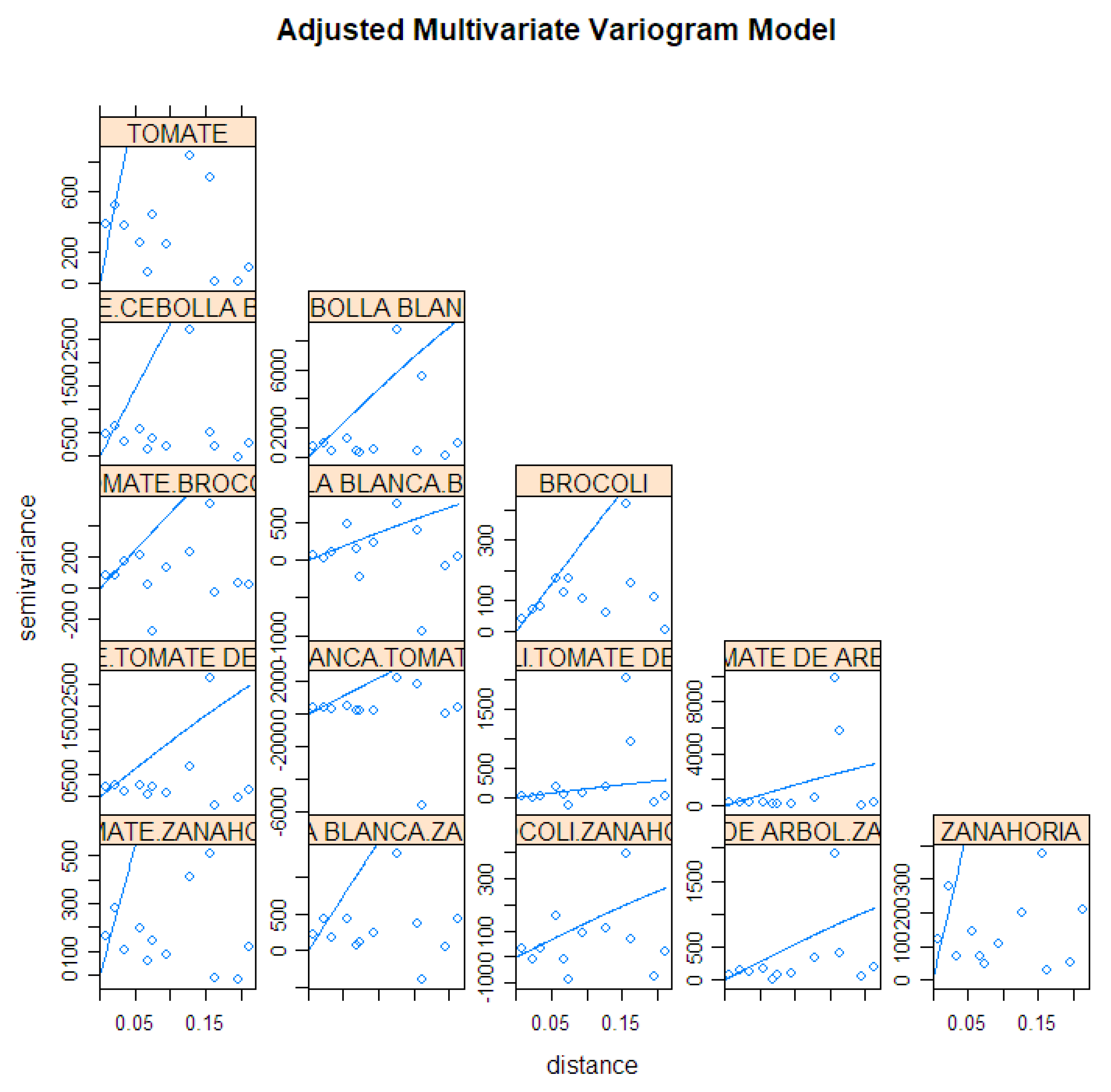
- The strongest association was found between white onion and tomato products, with a confidence of 87%. The next strongest were the association rules for tamarillo (86%), carrot (83%), and broccoli (82%). These products were selected as the multivariable set, as indicated in Figure 6.
- The product with the highest commercial ratio of the study sample is tomato.
5.3. Spatial Prediction
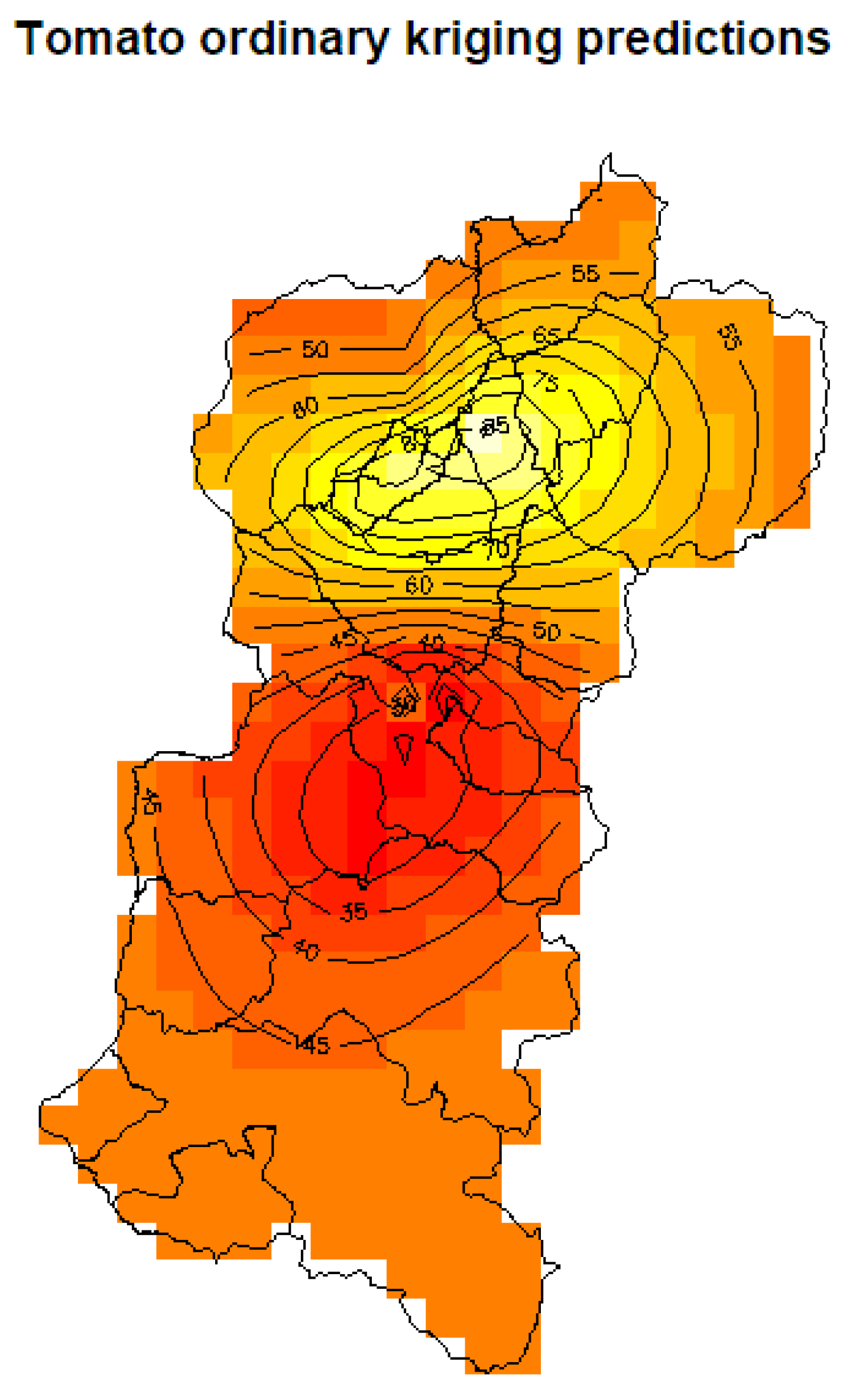
5.3.1. Kriging Prediction
5.3.2. Co-kriging Prediction
5.4. Discussion of Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Padilla, W.R.; García, H.J. CIALCO: Alternative marketing channels. Commun. Comput. Inf. Sci. 2016, 616, 313–321. [Google Scholar]
- Padilla, W.R.; García, J.; Molina, J.M. Improving Forecasting Using Information Fusion in Local Agricultural Markets. In International Conference on Hybrid Artificial Intelligence Systems; Springer: Cham, Switzerland, 2018; pp. 479–489. [Google Scholar]
- Padilla, W.R.; García, J.; Molina, J.M. Information Fusion and Machine Learning in Spatial Prediction for Local Agricultural Markets. In International Conference on Practical Applications of Agents and Multi-Agent Systems; Springer: Cham, Switzerland, 2018; pp. 235–246. [Google Scholar]
- Padilla, W.R.; Garcia, J.; Molina, J.M. Model Learning and Spatial Data Fusion for Predicting Sales in Local Agricultural Markets. In Proceedings of the 21st International Conference on Information Fusion (FUSION), Cambridge, UK, 10–13 July 2018. [Google Scholar]
- Gomede, E.; Gaffo, F.H.; Briganó, G.U.; Miranda, R.; de Souza, L. Application of Computational Intelligence to Improve Education in Smart Cities. Sensors 2018, 18, 267. [Google Scholar] [CrossRef] [PubMed]
- Costa, D.G.; Duran-Faundez, C.; Andrade, D.C.; Rocha-Junior, J.B.; Just, J.P. TwitterSensing: An Event-Based Approach for Wireless Sensor Networks Optimization Exploiting Social Media in Smart City Applications. Sensors 2018, 18, 1080. [Google Scholar] [CrossRef] [PubMed]
- Miori, V.; Russo, D.; Concordia, C. Meeting People’s Needs in a Fully Interoperable Domotic Environment. Sensors 2012, 12, 6802–6824. [Google Scholar] [CrossRef] [PubMed]
- United Nations. Transforming our World: The 2030 Agenda for Sustainable Development. Available online: https://sustainabledevelopment.un.org/post2015/transformingourworld/publication (accessed on 15 July 2015).
- Fritza, S.; Seea, L.; Bayasa, J.C.L.; Waldner, F.; Jacquesc, D.; Becker-Reshefd, I.; Whitcraftd, A.; Baruthe, B.; Bonifaciof, R.; Crutchfieldg, J.; et al. A comparison of global agricultural monitoring systems and current gaps. Agric. Syst. 2019, 168, 258–272. [Google Scholar] [CrossRef]
- Gemtos, T.A.; Markinos, A.; Nassiou, T. Cotton Lint Quality Spatial Variability and Correlation with Soil Properties and Yield. In Proceedings of the 5th European Conference on Precision Agiculture, Uppsala, Sweden, 9–12 June 2005. [Google Scholar]
- Wendroth, O.; Jurschik, P.; Giebel, A.; Nielsen, D.R. Spatial Statistical Analysis of On-site Crop Yield and Soil Observations for Site-specific Management. In Proceedings of the Fourth International Conference on Precision Agriculture, St. Paul, MN, USA, 19–22 July 1998. [Google Scholar]
- Papageorgiou, E.I.; Aggelopoulou, K.D.; Gemtos, T.A.; Nanos, G.D. Yield Prediction in Apples Using Fuzzy Cognitive Map Learning Approach. Comput. Electron. Agric. 2013, 91, 19–29. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Markinos, A.T.; Gemtos, T.A. Fuzzy Cognitive Map Based Approach for Predicting Yield in Cotton Crop Production as a Basis for Decision Support System in Precision Agriculture Application. Appl. Soft Comput. 2011, 11, 3643–3657. [Google Scholar] [CrossRef]
- Browna, J.N.; Hochmanb, Z.; Holzworthc, D.; Horanb, H. Seasonal climate forecasts provide more definitive and accurate crop yield predictions. Agric. For. Meteorol. 2018, 260, 247–254. [Google Scholar] [CrossRef]
- Llinas, J.; Bowman, C.; Rogova, G.; Steinberg, A.; Waltz, E.; White, F. Revisiting the JDL Data Fusion Model II; Space and Naval Warfare Systems Command: San Diego, CA, USA, 2004. [Google Scholar]
- Celemín, J.P. Autocorrelación espacial e indicadores locales de asociación espacial: Importancia, estructura y aplicación. Rev. Univ. Geogr. 2009, 18, 11–31. [Google Scholar]
- Tonye, E.; Fotsing, J.; Zobo, B.E.; Tankam, N.T.; Kanaa, T.F.N.; Rudant, J.P. Contribution of Variogram and Feature Vector of Texture for the Classification of Big Size SAR Images. In Proceedings of the Seventh International Conference on Signal Image Technology Internet-Based Systems, Dijon, France, 28 November–1 December 2011. [Google Scholar]
- Bivand, R.S.; Pebesma, E.; Gómez-Rubio, V. Applied Spatial Data Analysis with R; Springer: New York, NY, USA, 2013. [Google Scholar]
- Doligez, B.; Beucher, H.; Lerat, O.; Souza, O. Use of a Seismic Derived Constraint: Different Steps and Joined Uncertainties in the Construction of a Realistic Geological Model. Oil Gas Sci. Technol. Rev. IFP 2007, 62, 237–248. [Google Scholar] [CrossRef]
- Kanevski, M.; Maignan, M. Analysis and Modelling of Spatial Environmental Data; EPFL Press: Lausanne, Switzerland, 2004. [Google Scholar]
- Agrawal, R.; Imielinski, T.; Swami, A. Mining association rules between sets of items in large databases. In Proceedings of the ACM SIGMOD International Conference on Management of Data, Washington, DC, USA, 25–28 May 1993. [Google Scholar]
- Agrawal, R.; Srikant, R. Fast Algorithms for Mining Association Rules. In Proceedings of the 20th International Conference on Very Large Data Bases, Santiago, Chile, 12–15 September 1994. [Google Scholar]
- Zulfikar, W.B.; Wahana, A.; Uriawan, W.; Lukman, N. Implementation of association rules with apriori algorithm for increasing the quality of promotion. In Proceedings of the 4th International Conference on Cyber and IT Service Management, Bandung, Indonesia, 26–27 April 2016. [Google Scholar]
- Chang, C.-C.; Li, Y.-C.; Lee, J.-S. An efficient algorithm for incremental mining of association rules. In Proceedings of the 15th International Workshop on Research Issues in Data Engineering: Stream Data Mining and Applications, Tokyo, Japan, 3–4 April 2005. [Google Scholar]
- Han, J.; Pei, J.; Yiwen, Y.; Fraser, S. Mining Frequent Patterns without Candidate Generation: A Frequent-Pattern Tree Approach. Data Min. Knowl. Discov. 2004, 8, 53–87. [Google Scholar] [CrossRef]
- Hipp, J.; Güntzer, U.; Nakhaeizadeh, G. Algorithms for Association Rule Mining—A General Survey and Comparison. ACM Sigkdd Explor. Newsl. 2000, 2, 58–64. [Google Scholar] [CrossRef]
- Agrawal, R.; Srikant, R. Mining sequential patterns. In Proceedings of the Eleventh International Conference on Data Engineering, Taipei, Taiwan, 6–10 March 1996. [Google Scholar]
- Zaki, M.J. SPADE: An efficient algorithm for mining frequent sequences. Mach. Learn. 2001, 42, 31–60. [Google Scholar] [CrossRef]
- Ayres, J.; Flannick, J.; Gehrke, J.; Yiu, T. Sequential pattern mining using a bitmap representation. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002. [Google Scholar]
- Spiliopoulou, M.; Roddick, J.F. Higher Order Mining: Modelling and Mining the Results of Knowledge Discovery. In WIT Transactions on Information and Communication Technologies; Ebecken, N.F., Brebbia, C.A., Eds.; WIT press: Ashurst, UK, 2000. [Google Scholar]
- Asadifar, S.; Kahani, M. Semantic association rule mining: A new approach for stock market prediction. In Proceedings of the 2nd Conference on Swarm Intelligence and Evolutionary Computation, Kerman, Iran, 7–9 March 2017. [Google Scholar]
- Mane, R.V.; Ghorpade, V.R. Predicting student admission decisions by association rule mining with pattern growth approach. In Proceedings of the International Conference on Electrical, Electronics, Communication, Computer and Optimization Techniques, Mysuru, India, 9–10 December 2016. [Google Scholar]
- Kumar, P.S.V.V.S.R.; Maddireddi, L.R.D.P.; Lakshmi, V.A.; Dirisala, J.N.K. Novel fuzzy classification approaches based on optimisation of association rules. In Proceedings of the 2nd International Conference on Applied and Theoretical Computing and Communication Technology, Bangalore, India, 21–23 July 2016. [Google Scholar]
- Instituto Nacional de Meteorología e Hidrología. Geoinformación Hidrometeorológica. Quito, Ecuador, 2018. Available online: http://www.serviciometeorologico.gob.ec/geoinformacion-hidrometeorologica/ (accessed on 14 March 2018).
- Instituto Nacional de Estadística y Censos. Población y Demografía; Quito, Ecuador, 2018. Available online: http://www.ecuadorencifras.gob.ec/censo-de-poblacion-y-vivienda/ (accessed on 14 March 2018).
- Weka 3—Data Mining with Open Source Machine Learning Software in Java. Available online: http://www.cs.waikato.ac.nz/ml/weka/ (accessed on 28 September 2017).
- RStudio—Open Source and Enterprise-Ready Professional Software for R. Available online: https://www.rstudio.com/ (accessed on 8 December 2017).
- Zhang, Y.; Yang, Y. Cross-validation for selecting a model selection procedure. J. Econ. 2015, 187, 95–112. [Google Scholar] [CrossRef]
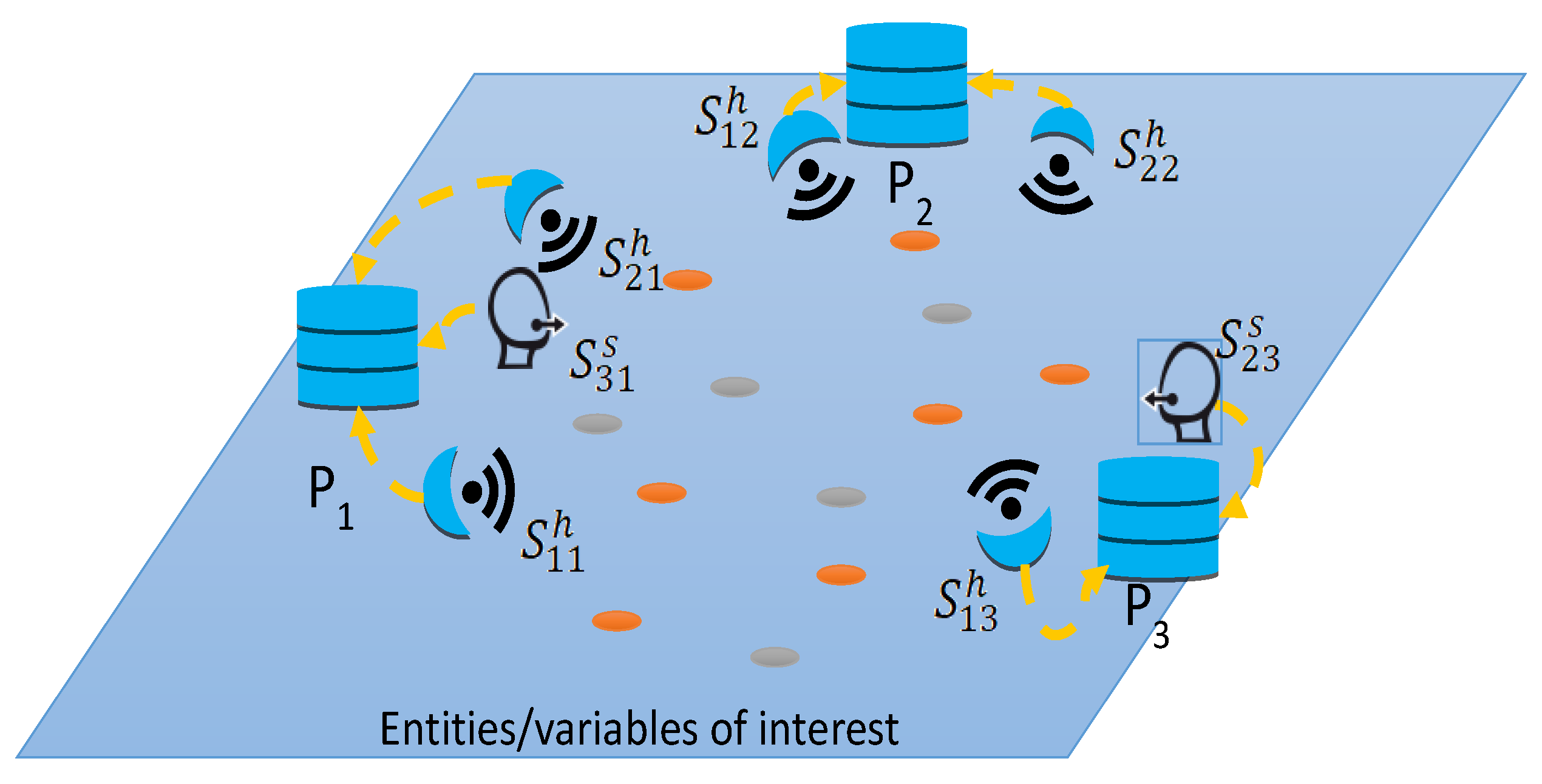





| Time Stamp | Platform | Sensor | Type of Sensor | Value |
|---|---|---|---|---|
| 0.1 s | P1 | S11 | Hard | (x,y) |
| 0.2 s | P2 | S12 | Hard | (x,y) |
| 0.4 s | P1 | S31 | Soft | ID |
| 0.6 s | P3 | S31 | Hard | (x,y) |
| 0.7 s | P3 | S23 | Soft | ID |
| 0.9 s | P1 | S11 | Hard | (x,y) |
| … | … | … | … | … |
| Spanish Name | Scientific Name | English Name |
|---|---|---|
| Acelga | Beta vulgaris var. cicla | Chard |
| Ajo | Allium sativum | Garlic |
| Arveja | Pisum sativum | Vetch |
| Babaco | Carica pentagona | Babaco |
| Brócoli | Brassica oleracea italica | Broccoli |
| Cebolla blanca | Allium fistulosum | White onion |
| Cebolla paiteña | Allium fistulosum | Onion |
| Choclo | Zea mays | Corn |
| Col | Brassica oleracea | Cabbage |
| Col verde | Brassica oleracea var. Sabellica | Green cabbage |
| Coliflor | Brassica oleracea var. Botrytis | Cauliflower |
| Espinaca | Spinacia oleracea | Spinach |
| Frejol | Phaseolus vulgaris | Frejol |
| Frutilla | Fragaria | Strawberry |
| Habas | Vicia faba | Broad beans |
| Hierbas | Coriandrum sativum, Petroselinum crispum | Weeds |
| Lechuga | Lactuca sativa | Lettuce |
| Melloco | Ullucus tuberosus | Melloco |
| Nabo | Brassica rapa | Turnip |
| Papas | Solanum tuberosum | Potatoes |
| Pepinillo | Cucumis sativus | Pickle |
| Pepino | Cucumis sativus | Cucumber |
| Pimiento | Capsicum annuum | Pepper |
| Rábano | Raphanus sativus | Radish |
| Remolacha | Beta vulgaris | Beet |
| Tomate de árbol | Solanum betaceum | Tamarillo |
| Tomate Riñón | Solanum lycopersicum | Tomato |
| Vainita | Phaseolus vulgaris L | Vainita |
| Zanahoria | Daucus carota | Carrot |
| Zapallo | Cucurbita maxima | Squash |
| FAIR | BROCCOLI | WHITE ONION | TOMATO | TAMARILLO | CARROT | X | Y |
|---|---|---|---|---|---|---|---|
| Colta | 6 | 60 | 26 | 30 | 30 | –78.7238 | –1.888 |
| Tisaleo | 37.9 | 36 | 88.25 | 185 | 47.5 | –78.6923 | –1.40951 |
| Riobamba1 | 8 | 9.6 | 18 | 0 | 0 | –78.6737 | –1.66153 |
| Riobamba2 | 26 | 42.5 | 60 | 15 | 17.5 | –78.673 | –1.66089 |
| Riobamba3 | 0 | 10 | 8 | 8 | 5 | –78.6687 | –1.66025 |
| Riobamba4 | 2.5 | 74 | 60 | 35 | 29.5 | –78.6588 | –1.67626 |
| Cevallos | 9 | 9.6 | 51 | 45 | 20 | –78.6566 | –1.25714 |
| Riobamba5 | 7.2 | 50 | 30 | 35 | 20 | –78.6558 | –1.6871 |
| Riobamba6 | 6 | 65 | 42 | 27 | 29 | –78.6538 | –1.67599 |
| Riobamba7 | 2 | 0 | 10 | 0 | 5 | –78.65 | –1.67803 |
| Riobamba8 | 6 | 26.5 | 33 | 0 | 36 | –78.6497 | –1.67468 |
| Riobamba9 | 2.5 | 0 | 6.9 | 0 | 3 | –78.6463 | –1.68942 |
| Chambo | 21 | 50 | 30 | 20 | 20 | –78.6077 | –1.7303 |
| Pillaro | 20.1 | 141.5 | 92 | 78 | 40 | –78.551 | –1.32836 |
| FAIR | BROCCOLI | WHITE ONION | TOMATO | TAMARILLO | CARROT | X | Y | POPULATION | PCLIMATICO |
|---|---|---|---|---|---|---|---|---|---|
| Colta | 6 | 60 | 26 | 30 | 30 | –78.7238 | –1.888 | 44.701 | 192 |
| Tisaleo | 37.9 | 36 | 88.25 | 185 | 47.5 | –78.6923 | –1.40951 | 10.565 | 192 |
| RIOBAMBA1 | 8 | 9.6 | 18 | 0 | 0 | –78.6737 | –1.66153 | 193.315 | 86 |
| RIOBAMBA2 | 26 | 42.5 | 60 | 15 | 17.5 | –78.673 | –1.66089 | 193.315 | 86 |
| RIOBAMBA3 | 0 | 10 | 8 | 8 | 5 | –78.6687 | –1.66025 | 193.315 | 86 |
| RIOBAMBA4 | 2.5 | 74 | 60 | 35 | 29.5 | –78.6588 | –1.67626 | 193.315 | 86 |
| Cevallos | 9 | 9.6 | 51 | 45 | 20 | –78.6566 | –1.25714 | 6.8730 | 70 |
| RIOBAMBA5 | 7.2 | 50 | 30 | 35 | 20 | –78.6558 | –1.68710 | 193.315 | 86 |
| RIOBAMBA6 | 6 | 65 | 42 | 27 | 29 | –78.6538 | –1.67599 | 193.315 | 86 |
| RIOBAMBA7 | 2 | 0 | 10 | 0 | 5 | –78.6500 | –1.67803 | 193.315 | 86 |
| RIOBAMBA8 | 6 | 26.5 | 33 | 0 | 36 | –78.6497 | –1.67468 | 193.315 | 86 |
| RIOBAMBA9 | 2.5 | 0 | 6.9 | 0 | 3 | –78.6463 | –1.68942 | 193.315 | 86 |
| CHAMBO | 21 | 50 | 30 | 20 | 20 | –78.6077 | –1.7303 | 10.541 | 86 |
| Pillaro | 20.1 | 141.5 | 92 | 78 | 40 | –78.551 | –1.32836 | 34.925 | 70 |
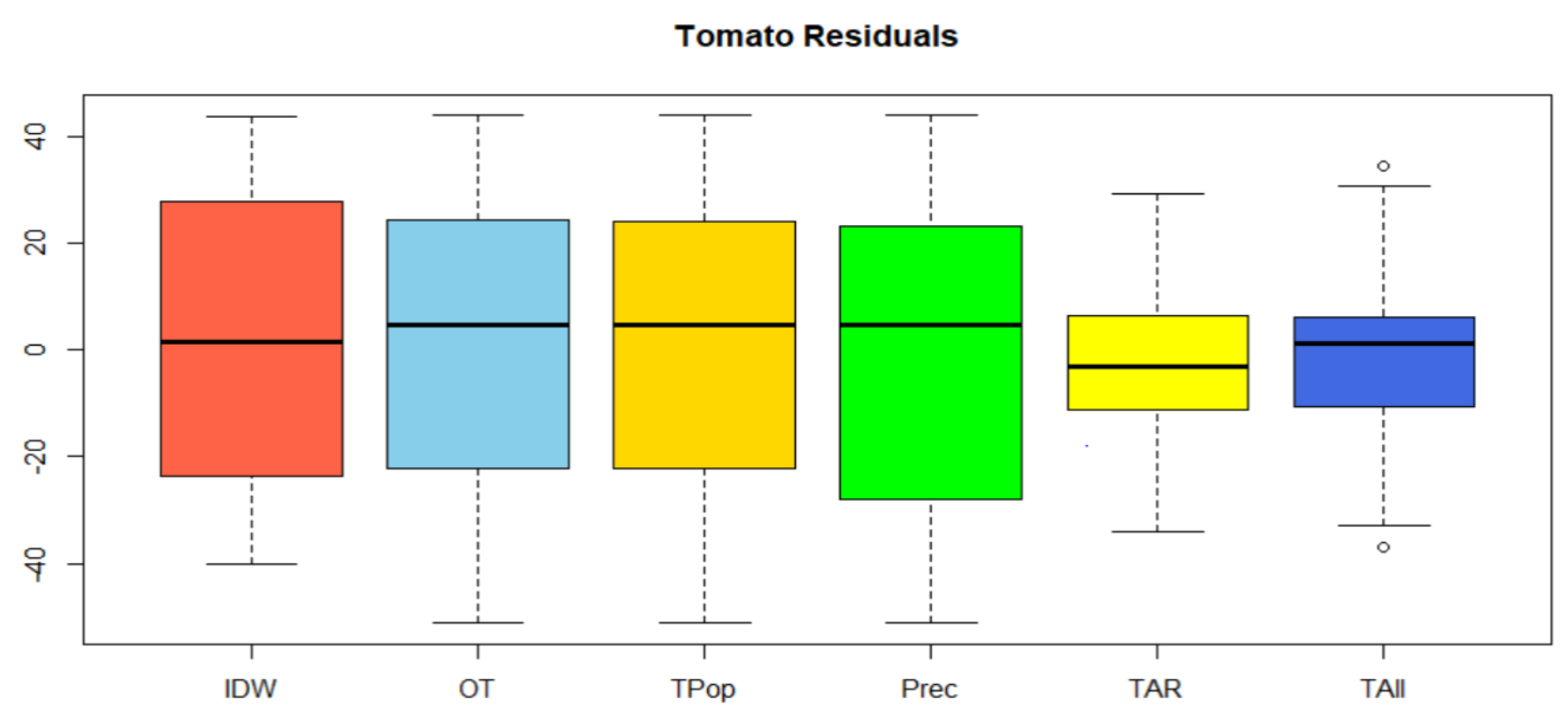
| Process | Min | 1Q | Median | Mean | 3Q | Max | RMSE |
|---|---|---|---|---|---|---|---|
| IDW | −40.1610 | –21.955 | 1.669 | 2.259 | 23.613 | 44 | 27.804 |
| Tom (kriging) | –51.2331 | –21.1409 | 4.8034 | –0.0194 | 23.5698 | 43.9355 | 29.440 |
| Tom/Population (cK) | –51.2289 | 4.8066 | –0.0945 | 23.3578 | 43.9361 | 29.370 | |
| Tom/Prec (cK) | –51.2170 | –26.465 | 4.87 | –0.731 | 23.097 | 43.944 | 29.320 |
| Tom/AR (cK) | –34.1243 | –11.1405 | –3.151 | –0.9209 | 6.2992 | 29.2215 | 16.550 |
| Tom/All Var (cK) | –36.8303 | –9.4598 | 1.3216 | 0.1151 | 5.5997 | 34.6041 | 19.420 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Padilla, W.R.; García, J.; Molina, J.M. Knowledge Extraction and Improved Data Fusion for Sales Prediction in Local Agricultural Markets. Sensors 2019, 19, 286. https://doi.org/10.3390/s19020286
Padilla WR, García J, Molina JM. Knowledge Extraction and Improved Data Fusion for Sales Prediction in Local Agricultural Markets. Sensors. 2019; 19(2):286. https://doi.org/10.3390/s19020286
Chicago/Turabian StylePadilla, Washington R., Jesús García, and José M. Molina. 2019. "Knowledge Extraction and Improved Data Fusion for Sales Prediction in Local Agricultural Markets" Sensors 19, no. 2: 286. https://doi.org/10.3390/s19020286
APA StylePadilla, W. R., García, J., & Molina, J. M. (2019). Knowledge Extraction and Improved Data Fusion for Sales Prediction in Local Agricultural Markets. Sensors, 19(2), 286. https://doi.org/10.3390/s19020286






