A Self-Adaptive 1D Convolutional Neural Network for Flight-State Identification
Abstract
:1. Introduction
2. Problem Statement
- (1)
- A tailored 1D deep CNN structure with multiple input channels using DTCWPT is developed for automatic feature learning instead of feature extraction and selection by human experts.
- (2)
- A self-adaptive CNN is proposed by combining the 1D CNN with a swarm-based GWO for automatic parameter determination instead of relying on human experience.
- (3)
- The flight-state identification of the self-sensing wing is treated as a classification problem by directly establishing the mapping relationship from the raw data to the physical space characterized by varying angle of attack and airspeed through wind tunnel experiments.
- (4)
- The application on stall detection and alerting with high identification accuracy provides new perspectives for autonomous flight control towards the “fly-by-feel” air vehicles.
3. Methodology Development
3.1. Basic CNN Theory
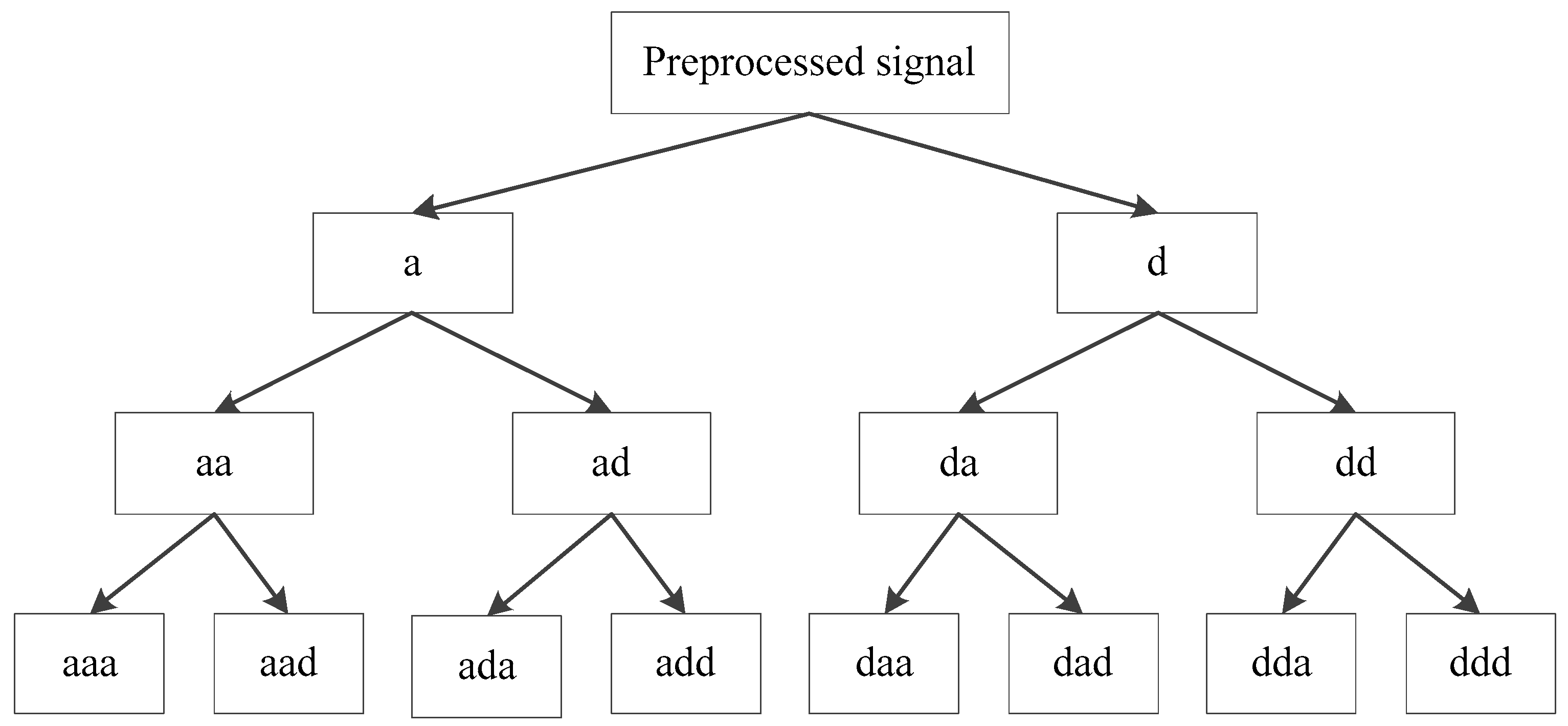
3.2. 1D CNN with DTCWPT
3.3. Parameter Optimization by GWO
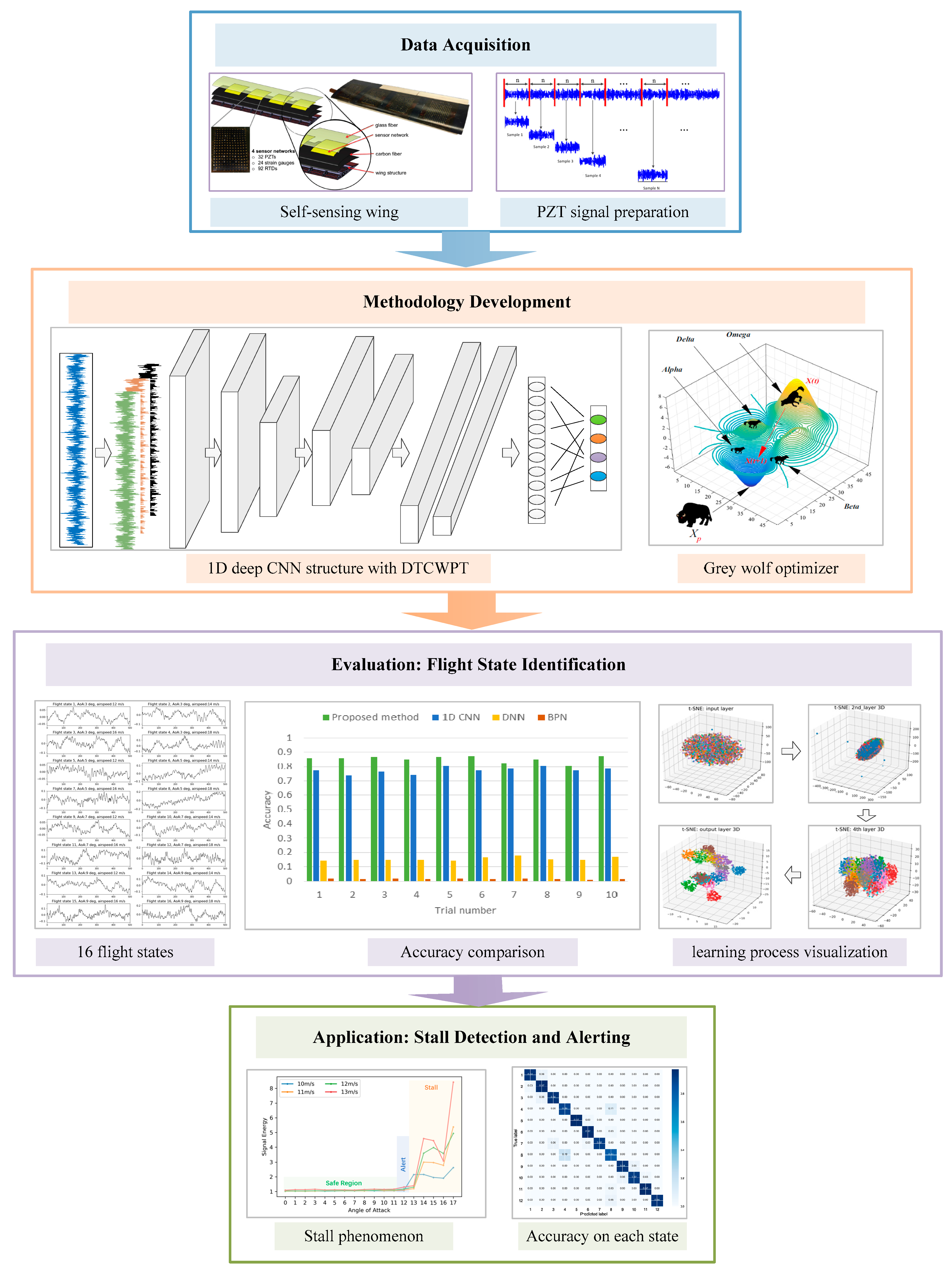
4. Case Study
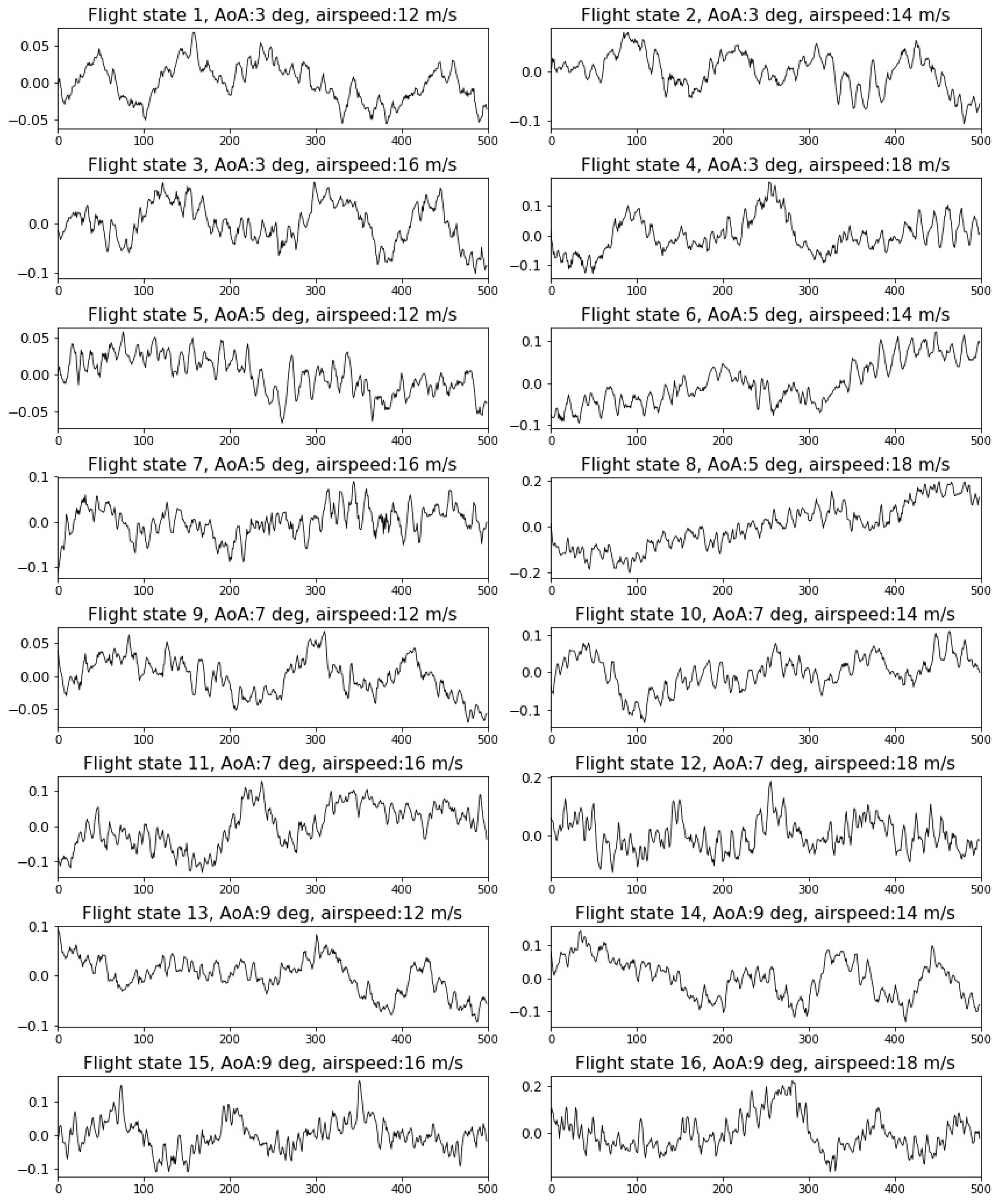
4.1. Wind-Tunnel Experiment and Data Preparation
4.2. General Flight-State Identification
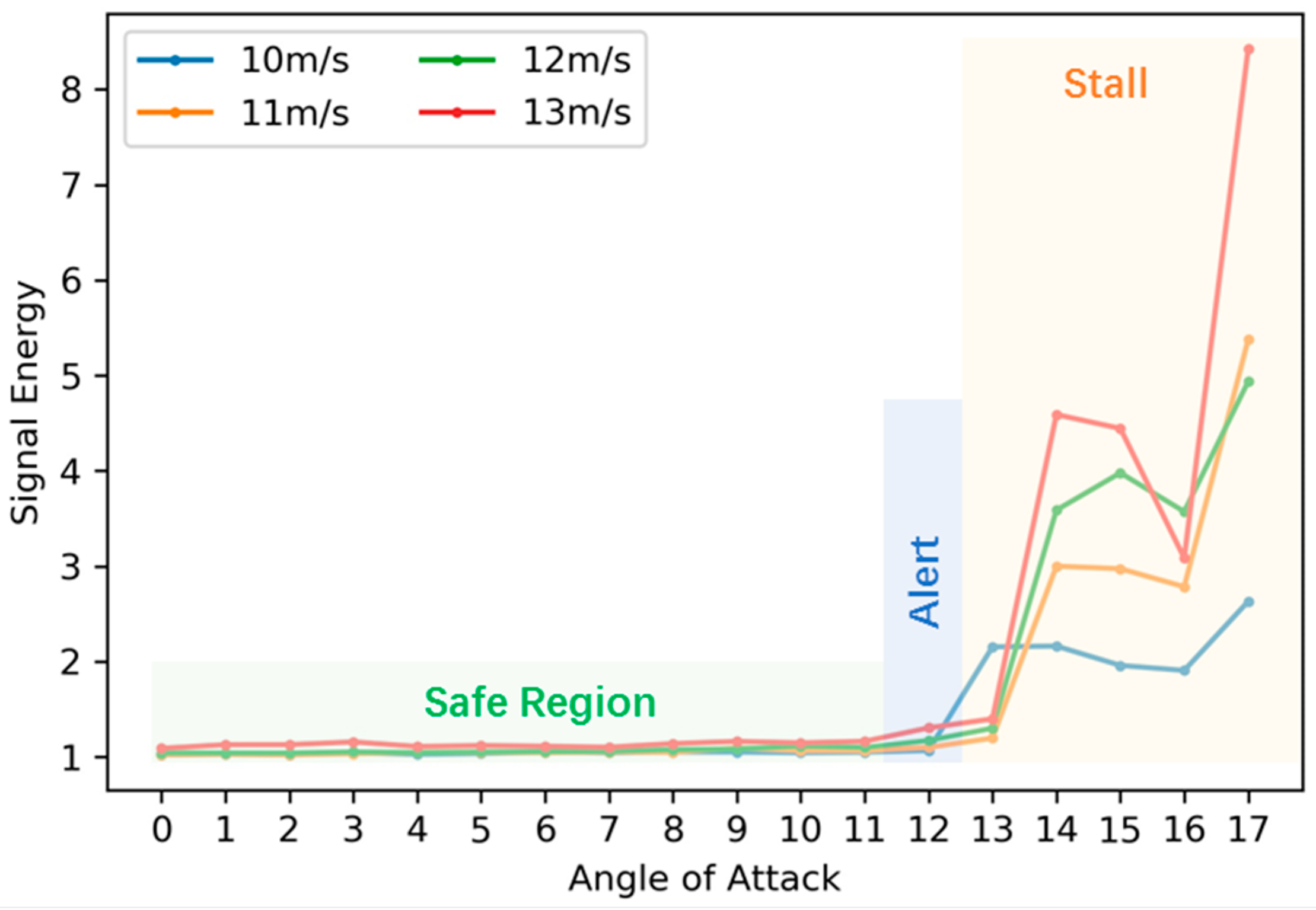
4.3. Stall Detection and Alerting
5. Results and Discussion
5.1. General Flight-State Identification
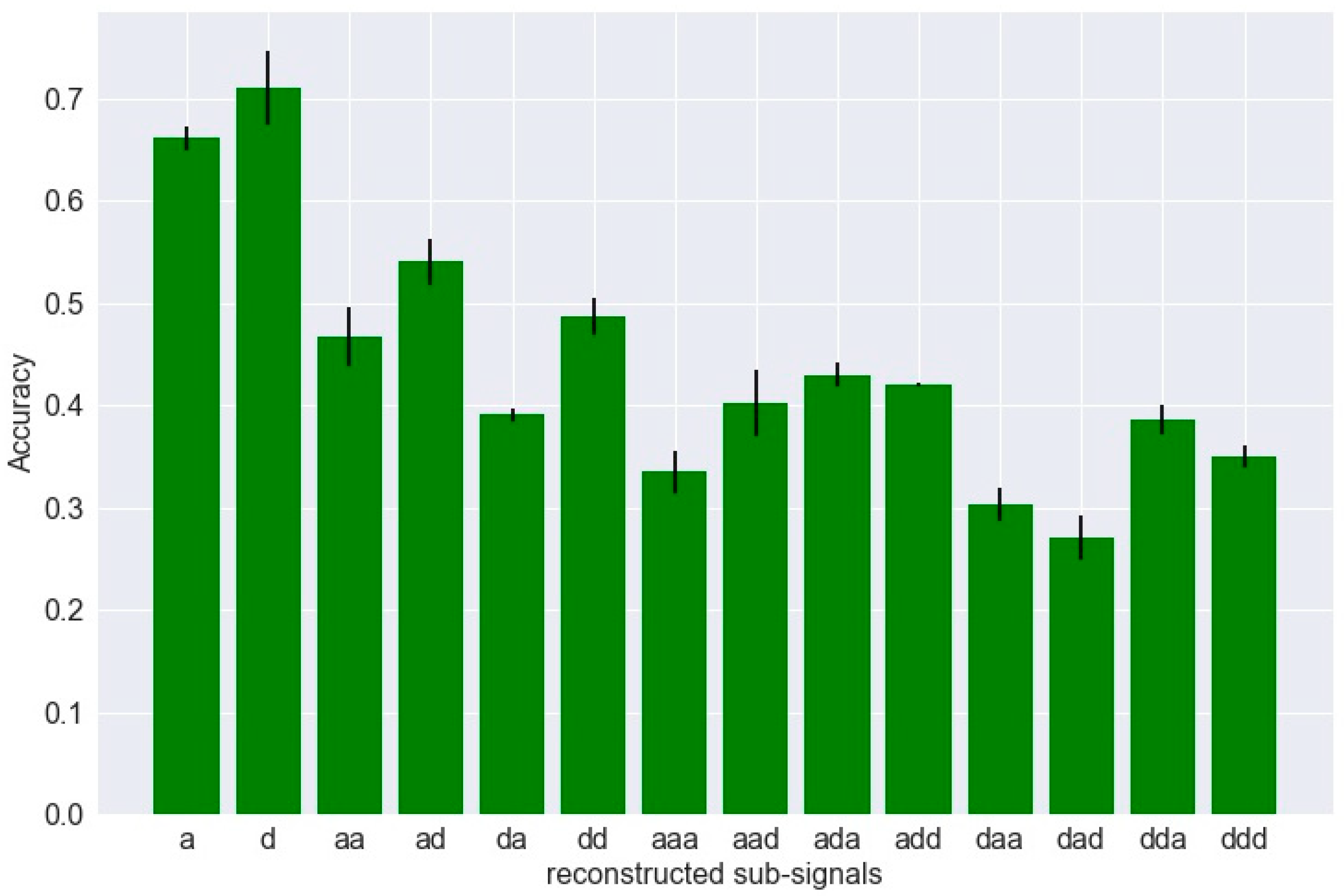
5.1.1. Signal Decomposition and Reconstructed-Signal Selection
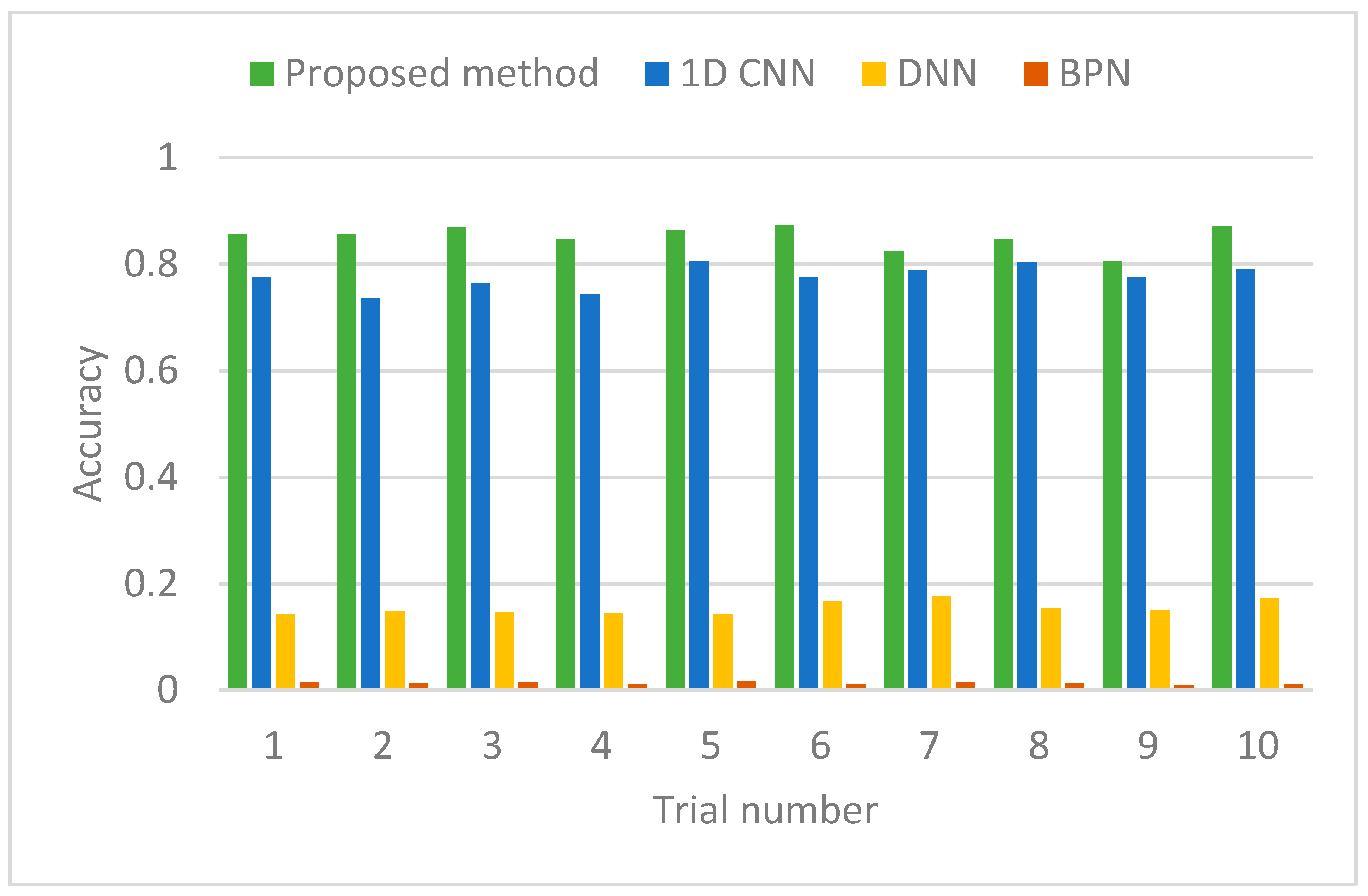
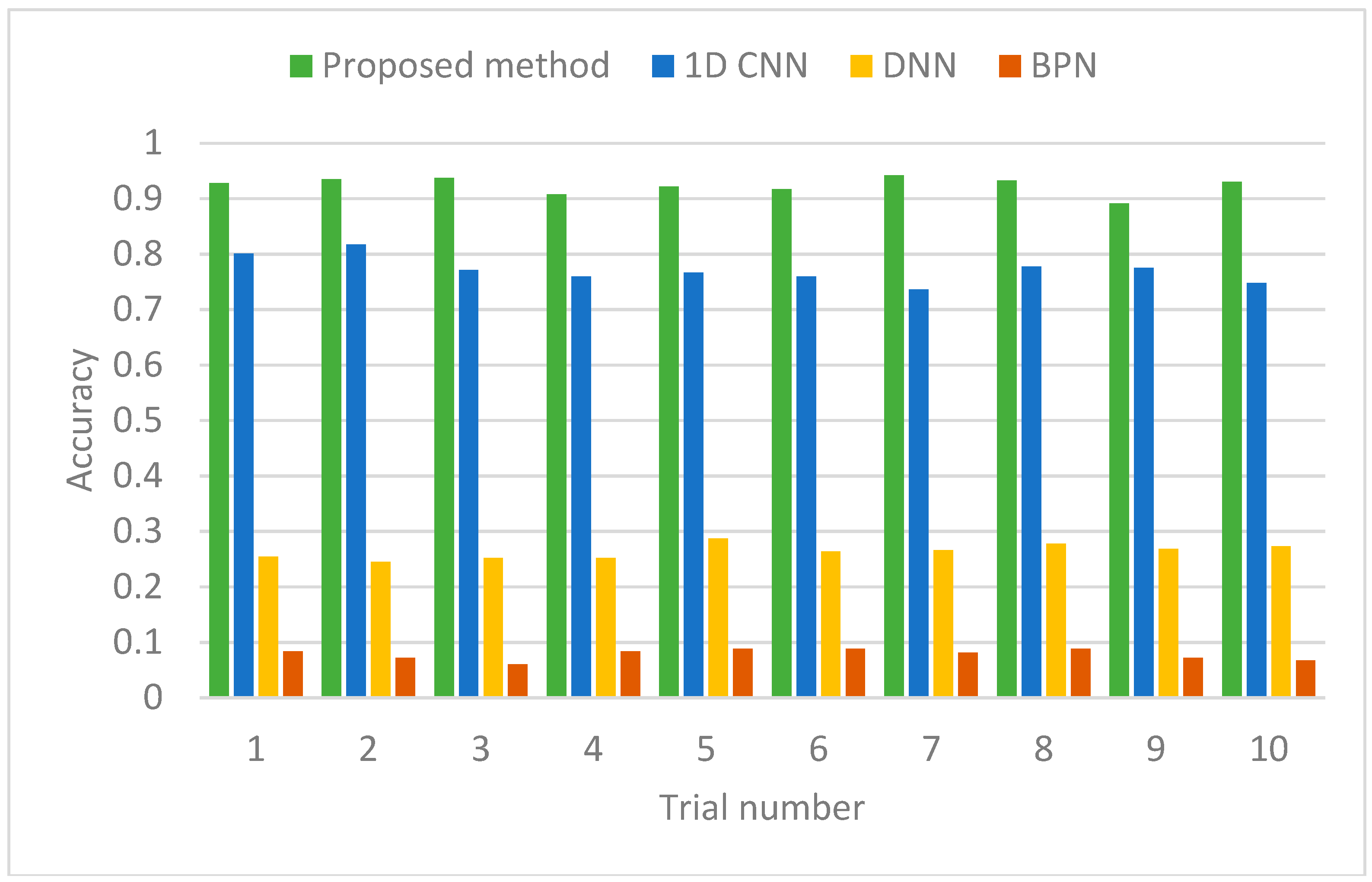
5.1.2. Parameter Optimization and Identification Accuracy Comparison
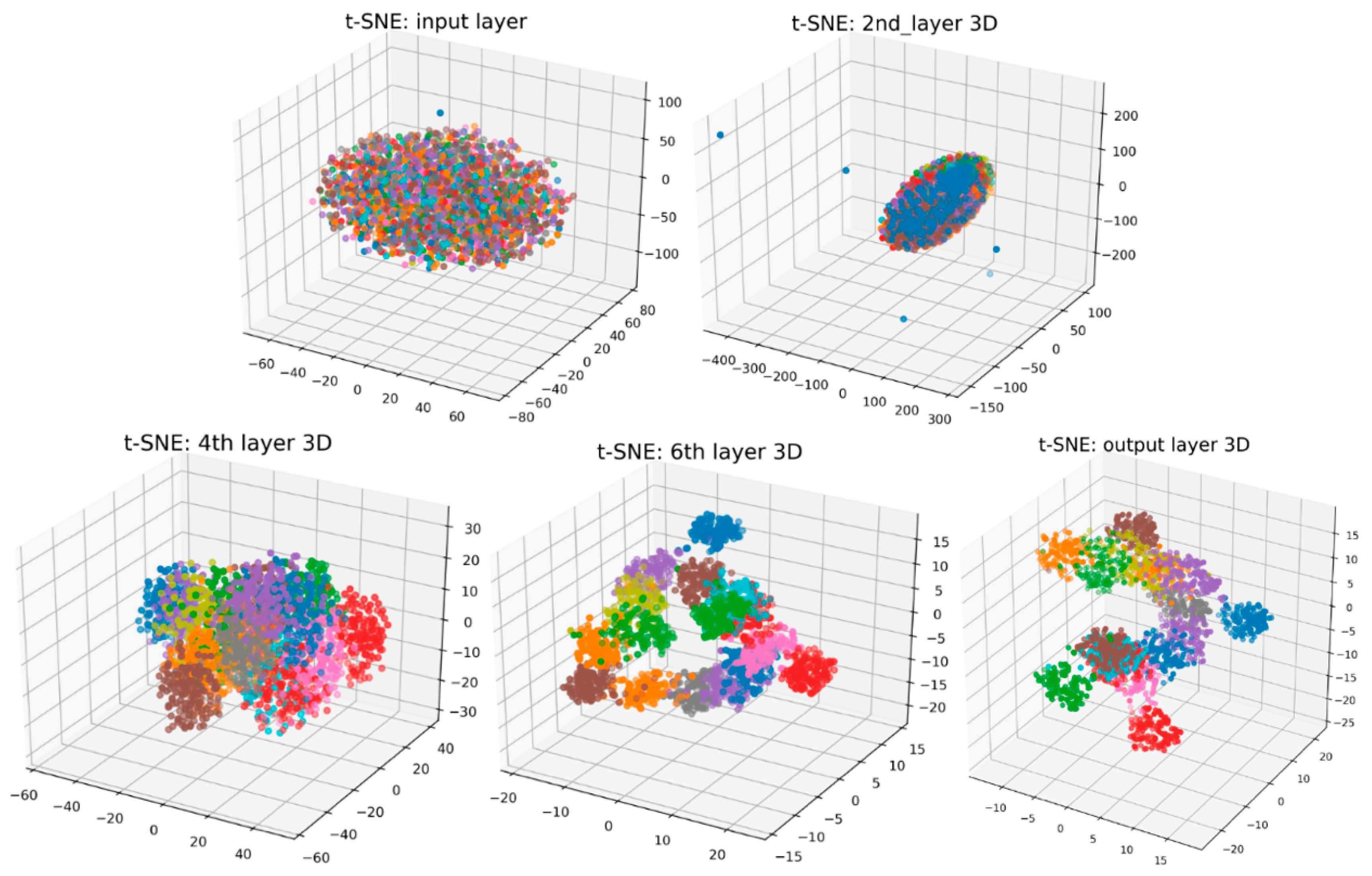
5.1.3. Visualization of the Learning Process
5.2. Stall Detection and Alerting
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- NASA. Fly-By-Feel Systems Represent The Next Revolution In Aircraft Controls; NASA: Washington, DC, USA, 2011.
- Kopsaftopoulos, F.; Nardari, R.; Li, Y.H.; Chang, F.K. A stochastic global identification framework for aerospace structures operating under varying flight states. Mech. Syst. Signal Process. 2018, 98, 425–447. [Google Scholar] [CrossRef]
- Kopsaftopoulos, F.; Nardari, R.; Li, Y.H.; Wang, P.; Ye, B.; Chang, F.K. Experimental identification of structural dynamics and aeroelastic properties of a self-sensing smart composite wing. In Proceedings of the 10th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 1–3 September 2015. [Google Scholar]
- Brenner, M.J. Controller Performance Evaluation of Fluy-by-feel (FBF) Technology; NASA: Washington, DC, USA, 2012.
- Mangalam, A.S.; Brenner, M.J. Fly-by-Feel Sensing and Control: Aeroservoelasticity. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Suh, P.; Chin, A.; Mavris, D. Virtual Deformation Control of the X-56A Model with Simulated Fiber Optic Sensors. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Suh, P.M.; Chin, A.; Mavris, D.N. Robust Modal Filtering and Control of the X-56A Model with Simulated Fiber Optic Sensor Failures. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Lanzara, G.; Feng, J.; Chang, F.-K. Design of Micro-Scaled Highly Expandable Networks of Polymer Based Substrates for Macro-Scale Applications. Smart Mater. Struct. 2010, 19, 45013. [Google Scholar] [CrossRef]
- Salowitz, N.; Guo, Z.; Li, Y.H.; Kim, K.; Lanzara, G.; Chang, F.K. Bio-inspired stretchable network-based intelligent composites. J. Compos. Mater. 2013, 47, 97–105. [Google Scholar] [CrossRef]
- Salowitz, N.; Guo, Z.; Roy, S.; Nardari, R.; Li, Y.H.; Kim, S.J.; Kopsaftopoulos, F.; Chang, F.K. Recent advancements and vision toward stretchable bio-inspired networks for intelligent structures. Struct. Heal. Monit. 2014, 13, 609–620. [Google Scholar] [CrossRef]
- Guo, Z.; Aboudi, U.; Peumans, P.; Howe, R.T.; Chang, F.K. A Super Stretchable Organic Thin-Film Diodes Network That Can Be Embedded into Carbon Fiber Composite Materials for Sensor Network Applications. J. Microelectromec. Syst. 2016, 25, 524–532. [Google Scholar] [CrossRef]
- Roy, S.; Lonkar, K.; Janapati, V.; Chang, F.-K. A novel physics-based temperature compensation model for structural health monitoring using ultrasonic guided waves. Struct. Heal. Monit. Int. J. 2014, 13, 321–342. [Google Scholar] [CrossRef]
- Kopsaftopoulos, F.P.; Fassois, S.D. Vector-dependent functionally pooled ARX models for the identification of systems under multiple operating conditions. IFAC Proc. Vol. 2012, 16, 310–315. [Google Scholar] [CrossRef]
- Kopsaftopoulos, F.; Nardari, R.; Li, Y.-H.; Wang, P.; Chang, F.-K. Stochastic global identification of a bio-inspired self-sensing composite UAV wing via wind tunnel experiments. Health Monit. Struct. Biol. Syst. 2016, 9805. [Google Scholar] [CrossRef]
- Guyon, I. Feature Extraction Foundations and Applications; Springer: Berlin, Germany, 2006; Volume 207, ISBN 9783540354871. [Google Scholar]
- Samanta, B. Gear fault detection using artificial neural networks and support vector machines with genetic algorithms. Mech. Syst. Signal Process. 2004, 18, 625–644. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, X.; Zhang, X.; He, Z. A novel intelligent gear fault diagnosis model based on EMD and multi-class TSVM. Measurement 2012, 45, 30–40. [Google Scholar] [CrossRef]
- Xi, Y.L.; Xi, Z.H.; Xi, Y.Z. Fault Diagnosis of Rotating Machinery Based on Multiple ANFIS Combination with Gas Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAs. Mech. Syst. Signal Process. 2007, 21, 2280–2294. [Google Scholar] [CrossRef]
- Chen, X.; Kopsaftopoulos, F.; Wu, Q.; Ren, H.; Chang, F.K. Flight state identification of a self-sensingwing via an improved feature selection method and machine learning approaches. Sensors 2018, 18, 1379. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Gehring, J.; Miao, Y.; Metze, F.; Waibel, A. Extracting deep bottleneck features using stacked auto-encoders. In Proceedings of the ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Yu, D.; Deng, L. Deep Learning and Its Applications to Signal and Information Processing. IEEE Signal Process. Mag. 2011, 28, 145–150. [Google Scholar] [CrossRef]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Walle, R.; Van Hoecke, S. Convolutional Neural Network Based Fault Detection for Rotating Machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Madić, M.; Marković, D.; Radovanović, M. Comparison of meta-heuristic algorithms for solving machining optimization problems. Mech. Eng. 2013, 11, 29–44. [Google Scholar]
- Shao, H.; Jiang, H.; Zhao, H.; Wang, F. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis. Mech. Syst. Signal Process. 2017, 95, 187–204. [Google Scholar] [CrossRef]
- Fuan, W.; Hongkai, J.; Haidong, S.; Wenjing, D.; Shuaipeng, W. An adaptive deep convolutional neural network for rolling bearing fault diagnosis. Meas. Sci. Technol. 2017, 28. [Google Scholar] [CrossRef]
- Shao, H.; Jiang, H.; Zhang, X.; Niu, M. Rolling bearing fault diagnosis using an optimization deep belief network. Meas. Sci. Technol. 2015, 26. [Google Scholar] [CrossRef]
- Rasdi Rere, L.M.; Fanany, M.I.; Arymurthy, A.M. Metaheuristic Algorithms for Convolution Neural Network. Comput. Intell. Neurosci. 2016, 2016. [Google Scholar] [CrossRef]
- Nawi, N.M.; Khan, A.; Rehman, M.Z.; Herawan, T.; Deris, M.M. Comparing Performances of Cuckoo Search Based Neural Networks; Springer: Cham, Switzerland, 2014; Volume 287, ISBN 9783319076911. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 620, 267–284. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 1–9. [Google Scholar] [CrossRef]
- Abdel-Hamid, O.; Mohamed, A.; Jiang, H.; Deng, L.; Penn, G.; Yu, D. Convolutional Neural Networks for Speech Recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1533–1545. [Google Scholar] [CrossRef]
- Bayram, I.; Selesnick, I.W. On the dual-tree complex wavelet packet and M-band transforms. IEEE Trans. Signal Process. 2008, 56, 2298–2310. [Google Scholar] [CrossRef]
- Wang, Y.; He, Z.; Zi, Y. Enhancement of signal denoising and multiple fault signatures detecting in rotating machinery using dual-tree complex wavelet transform. Mech. Syst. Signal Process. 2010, 24, 119–137. [Google Scholar] [CrossRef]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning—ICML’06, Pittsburgh, PA, USA, 25–29 June 2006. [Google Scholar]
- Powers, D.M.W. Evaluation: From Precision, Recall and F-Measure To Roc, Informedness, Markedness and Correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
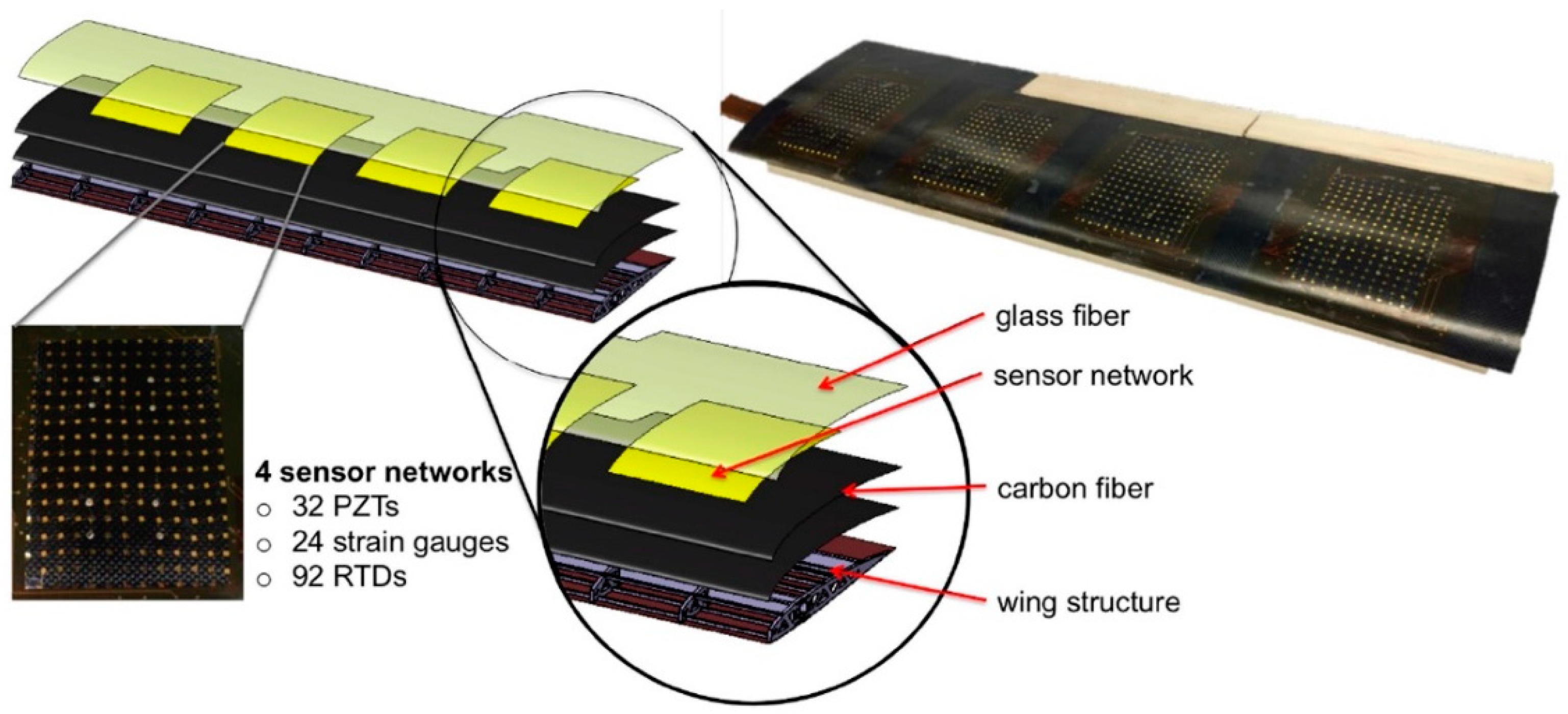
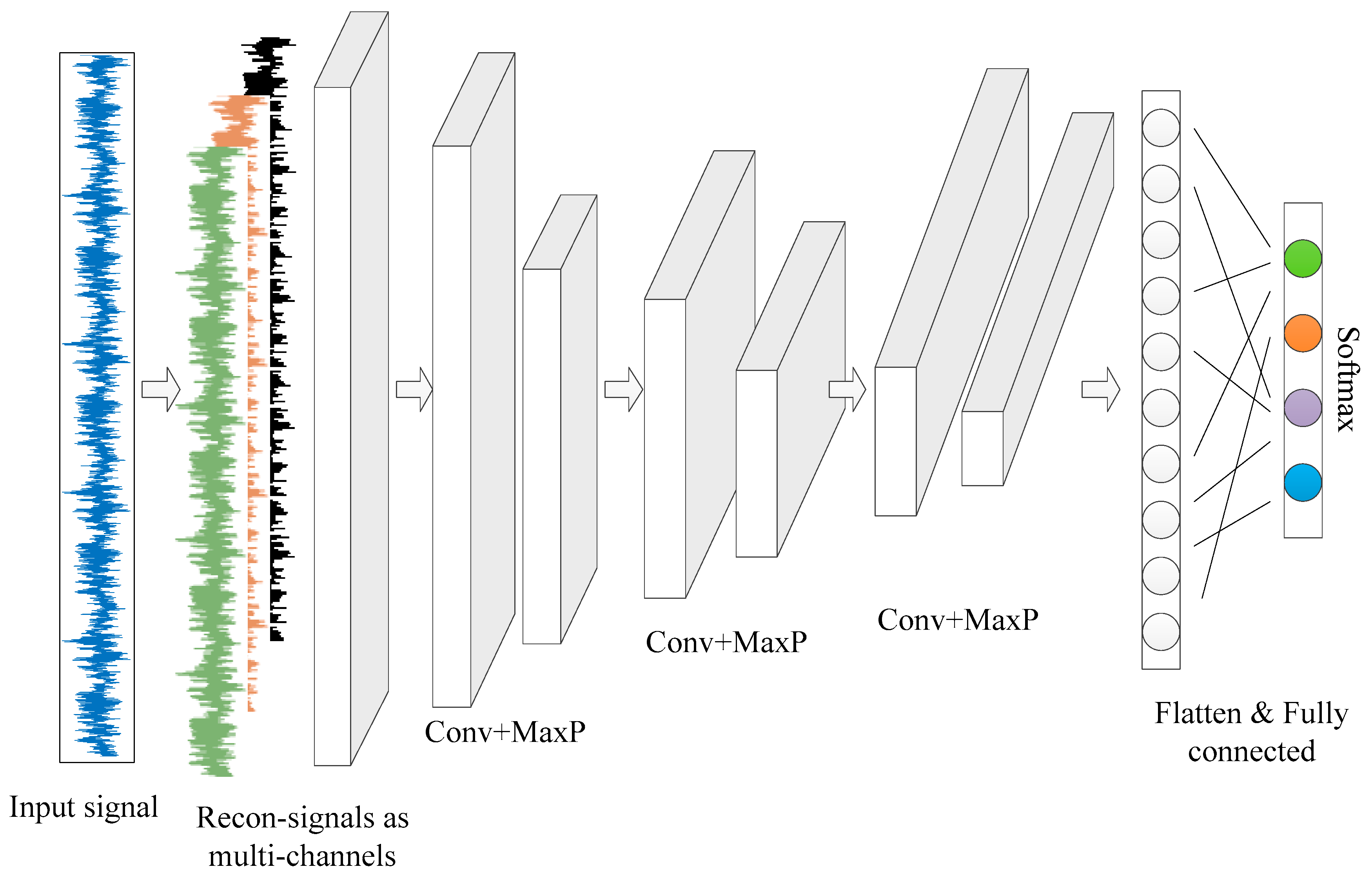



| Parameter Description | Value after GWO | Value Before (Used in Normal CNN in the Following Comparison) |
|---|---|---|
| Population of GWO | 20 | - |
| Iteration number | 20 | - |
| Dimensionality of particles | 3 | - |
| Kernel size in C2 and C3 layers | 5 | 10 |
| Learning rate | 0.0012 | 0.001 |
| Dropout rate | 0.4 | 0.5 |
| Methods | Input Dimension | Size of Training/Testing Sample | Average Testing Accuracy | Standard Deviation | Total Parameters |
|---|---|---|---|---|---|
| Proposed method | 500 | 2304/576 | 85.15% | 2.07% | 260,432 |
| 1D CNN | 500 | 2304/576 | 77.53% | 2.20% | 500,816 |
| DNN | 500 | 2304/576 | 15.45% | 1.22% | 214,100 |
| BPN | 500 | 2304/576 | 1.37% | 0.27% | 129,000 |
| Parameter Description | Value after GWO | Value before (Used in Normal CNN in the Following Comparison) |
|---|---|---|
| Population of GWO | 20 | - |
| Iteration number | 20 | - |
| Dimensionality of particles | 3 | - |
| Kernel size in C2 and C3 layers | 3 | 10 |
| Learning rate | 0.0011 | 0.001 |
| Dropout rate | 0.4 | 0.5 |
| Methods | Input Dimension | Size of Training/Testing Sample | Average Testing Accuracy | Standard Deviation | Total Parameters |
|---|---|---|---|---|---|
| Proposed method | 500 | 1728/432 | 92.43% | 1.48% | 160,588 |
| 1D CNN | 500 | 1728/432 | 77.11% | 2.27% | 498,764 |
| DNN | 500 | 1728/432 | 26.41% | 1.24% | 213,700 |
| BPN | 500 | 1728/432 | 7.82% | 0.94% | 128,000 |
| States ID | AoA deg | Speed m/s | Precision | Recall | F1 Score | |
|---|---|---|---|---|---|---|
| Safe | 1 | 11 | 10 | 0.97 | 0.94 | 0.96 |
| 2 | 11 | 11 | 0.90 | 0.97 | 0.93 | |
| 3 | 11 | 12 | 0.94 | 0.94 | 0.94 | |
| 4 | 11 | 13 | 0.82 | 0.89 | 0.85 | |
| Alert | 5 | 12 | 10 | 1.00 | 0.97 | 0.99 |
| 6 | 12 | 11 | 0.95 | 0.97 | 0.96 | |
| 7 | 12 | 12 | 1.00 | 0.92 | 0.96 | |
| 8 | 12 | 13 | 0.78 | 0.81 | 0.79 | |
| Stall | 9 | 13 | 10 | 0.94 | 0.94 | 0.94 |
| 10 | 13 | 11 | 0.94 | 0.92 | 0.93 | |
| 11 | 13 | 12 | 0.97 | 0.97 | 0.97 | |
| 12 | 13 | 13 | 1.00 | 0.94 | 0.97 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Kopsaftopoulos, F.; Wu, Q.; Ren, H.; Chang, F.-K. A Self-Adaptive 1D Convolutional Neural Network for Flight-State Identification. Sensors 2019, 19, 275. https://doi.org/10.3390/s19020275
Chen X, Kopsaftopoulos F, Wu Q, Ren H, Chang F-K. A Self-Adaptive 1D Convolutional Neural Network for Flight-State Identification. Sensors. 2019; 19(2):275. https://doi.org/10.3390/s19020275
Chicago/Turabian StyleChen, Xi, Fotis Kopsaftopoulos, Qi Wu, He Ren, and Fu-Kuo Chang. 2019. "A Self-Adaptive 1D Convolutional Neural Network for Flight-State Identification" Sensors 19, no. 2: 275. https://doi.org/10.3390/s19020275
APA StyleChen, X., Kopsaftopoulos, F., Wu, Q., Ren, H., & Chang, F.-K. (2019). A Self-Adaptive 1D Convolutional Neural Network for Flight-State Identification. Sensors, 19(2), 275. https://doi.org/10.3390/s19020275







