Gradient-Based Multi-Objective Feature Selection for Gait Mode Recognition of Transfemoral Amputees
Abstract
:1. Introduction
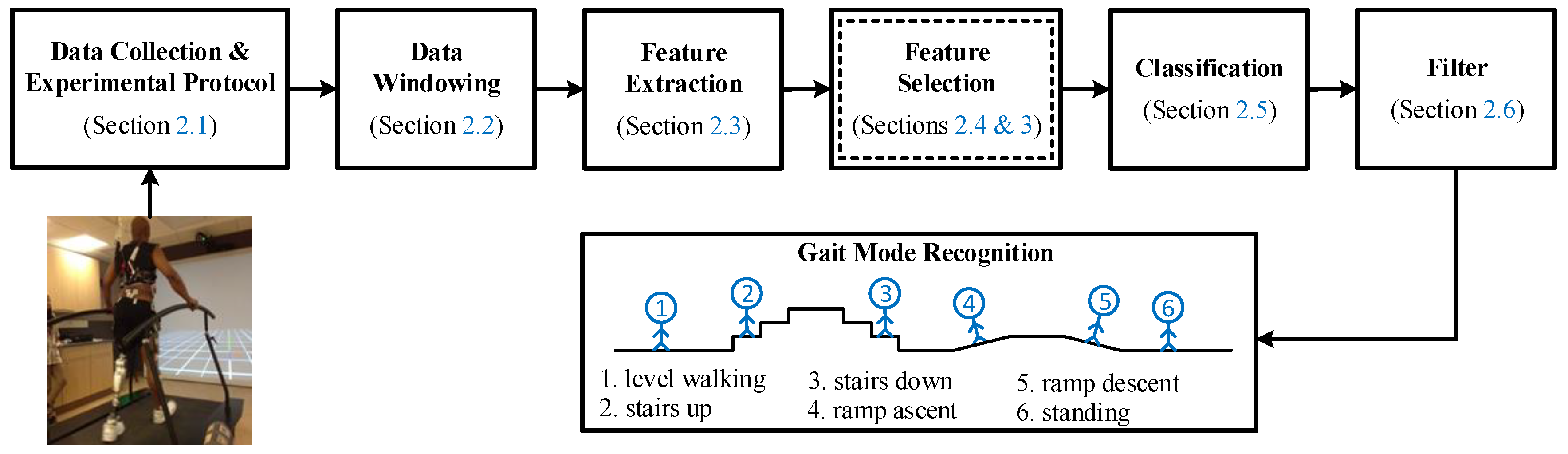
2. Materials and Methods
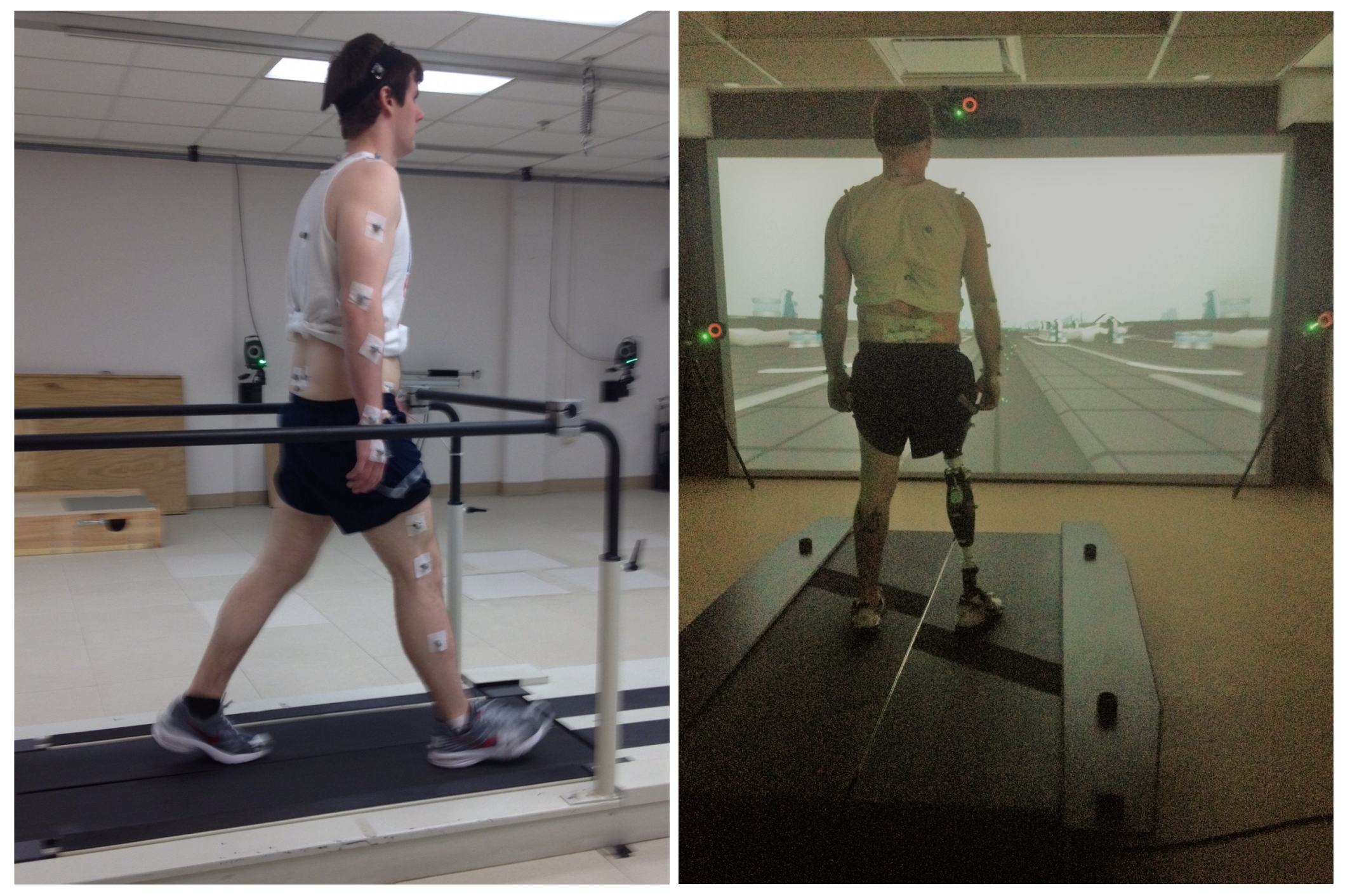
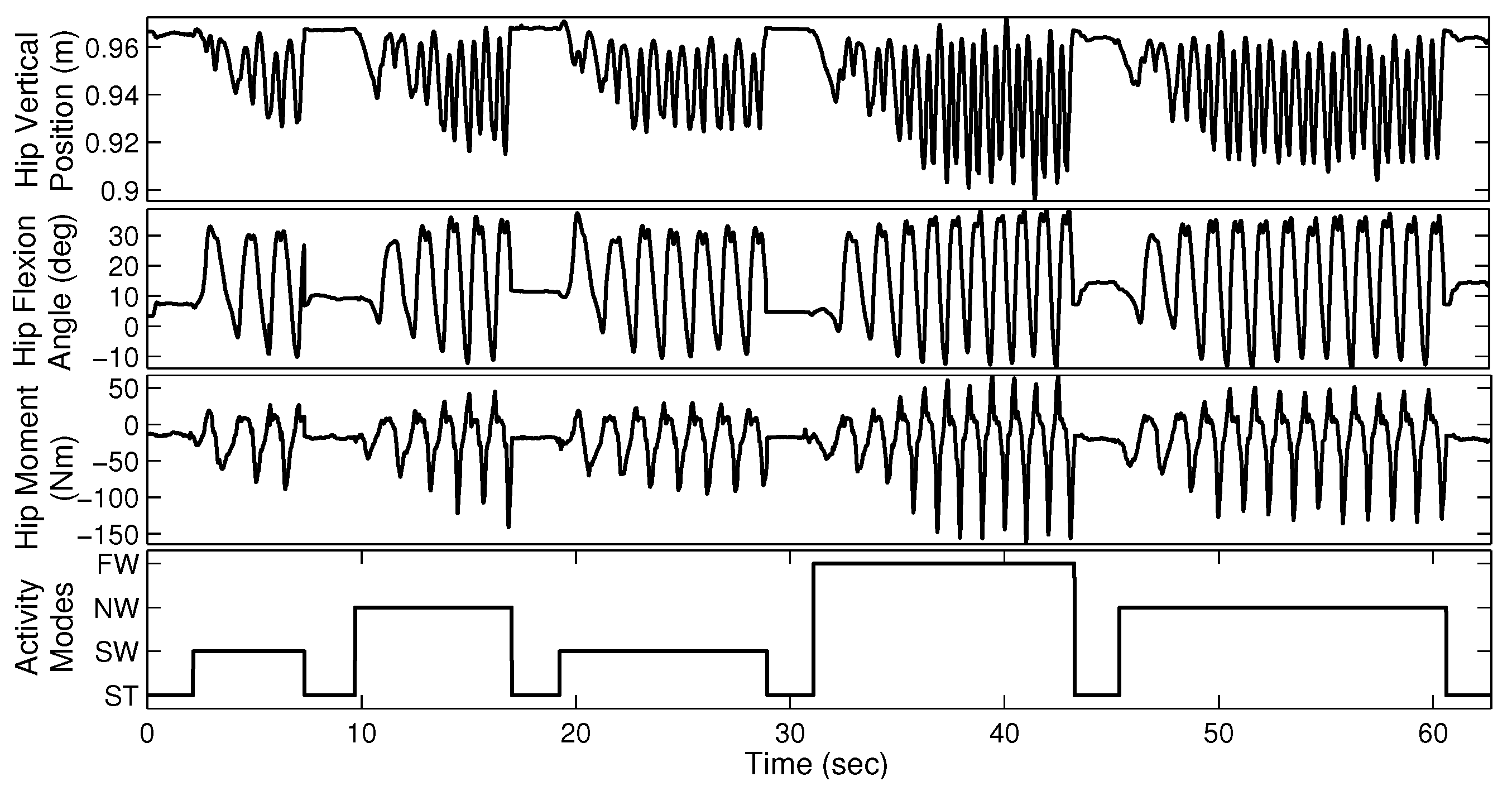
2.1. Data Collection and Experimental Protocol
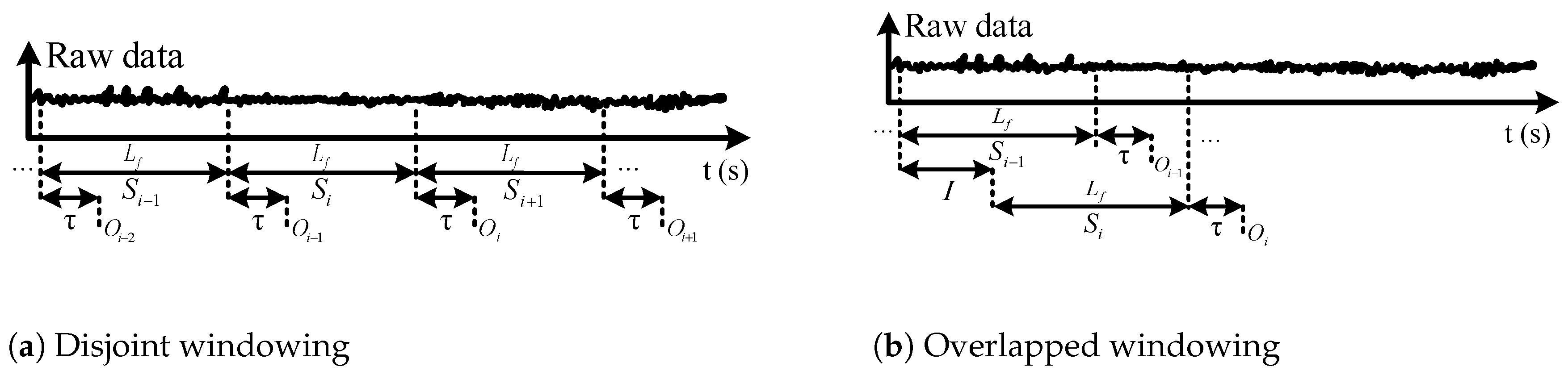
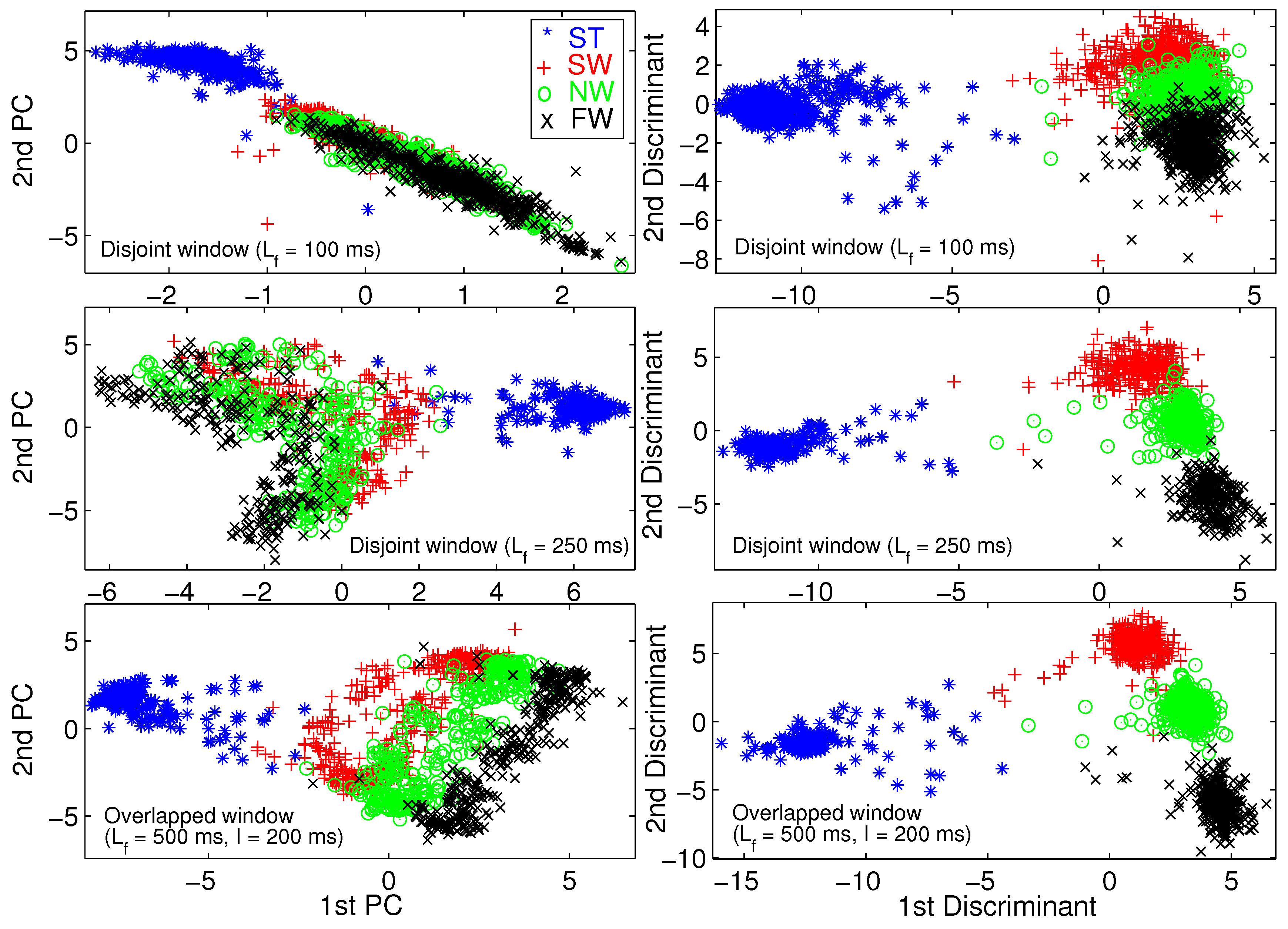
2.2. Data Windowing
2.3. Feature Extraction
2.4. Feature Selection
2.5. Classification
2.6. Filter
3. Feature Selection Algorithm Development
3.1. Biogeography-Based Multi-Objective Optimization
3.2. Gradient-Based Multi-Objective Feature Selection
| Algorithm 1: The outline of gradient-based multi-objective feature selection (GMOFS), where is the i-th feature in the training set X, and Y is the corresponding set of output classes. |
| Initialization:, Population = ∅, While Step 1: Use the training data to train the constrained MLP network in Equation (4) by solving Equation (5) Step 2: Sort the input weights in descending order Use Equation (7) to select subset where size() ≤ size(X) Step 3: Population ← Population Next Step 4: For each subset in Population Use cross-validation to train and test a classifier with dataset Calculate objective functions and using Equation (3) Next subset Step 5: Find the Pareto set using Equation (8) |
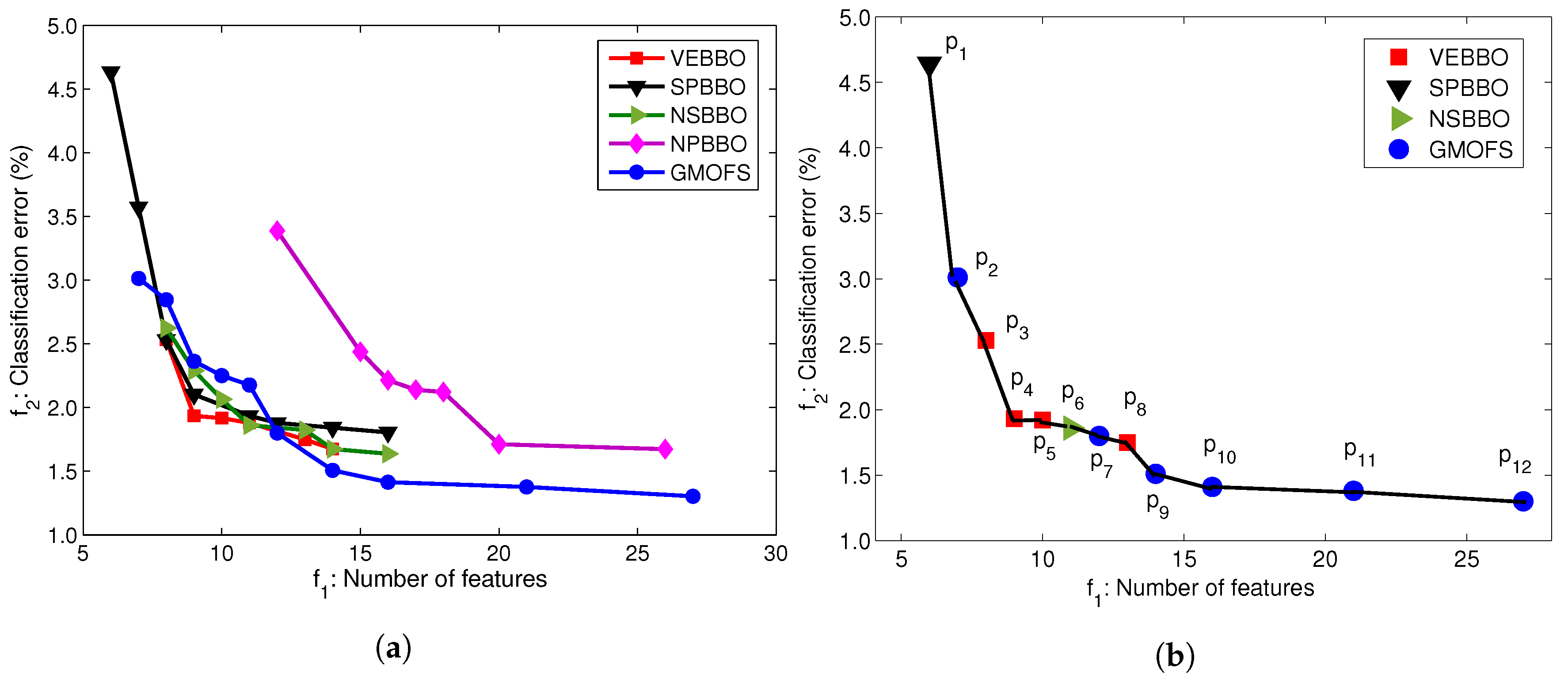
3.3. Evaluation of Multi-Objective Optimization Pareto Fronts
4. Results and Discussion
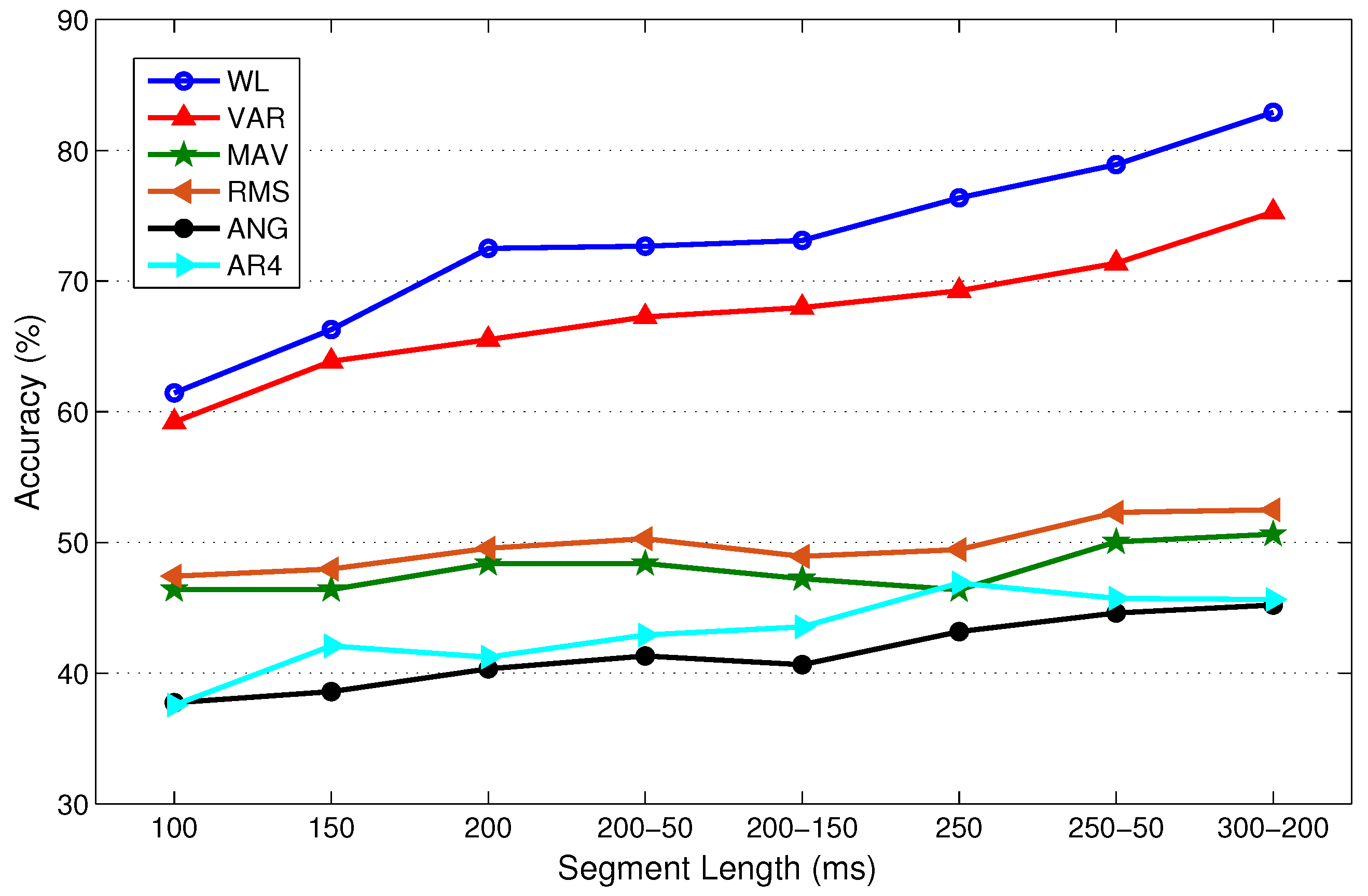
4.1. Effect of Frame Length on Classification Performance
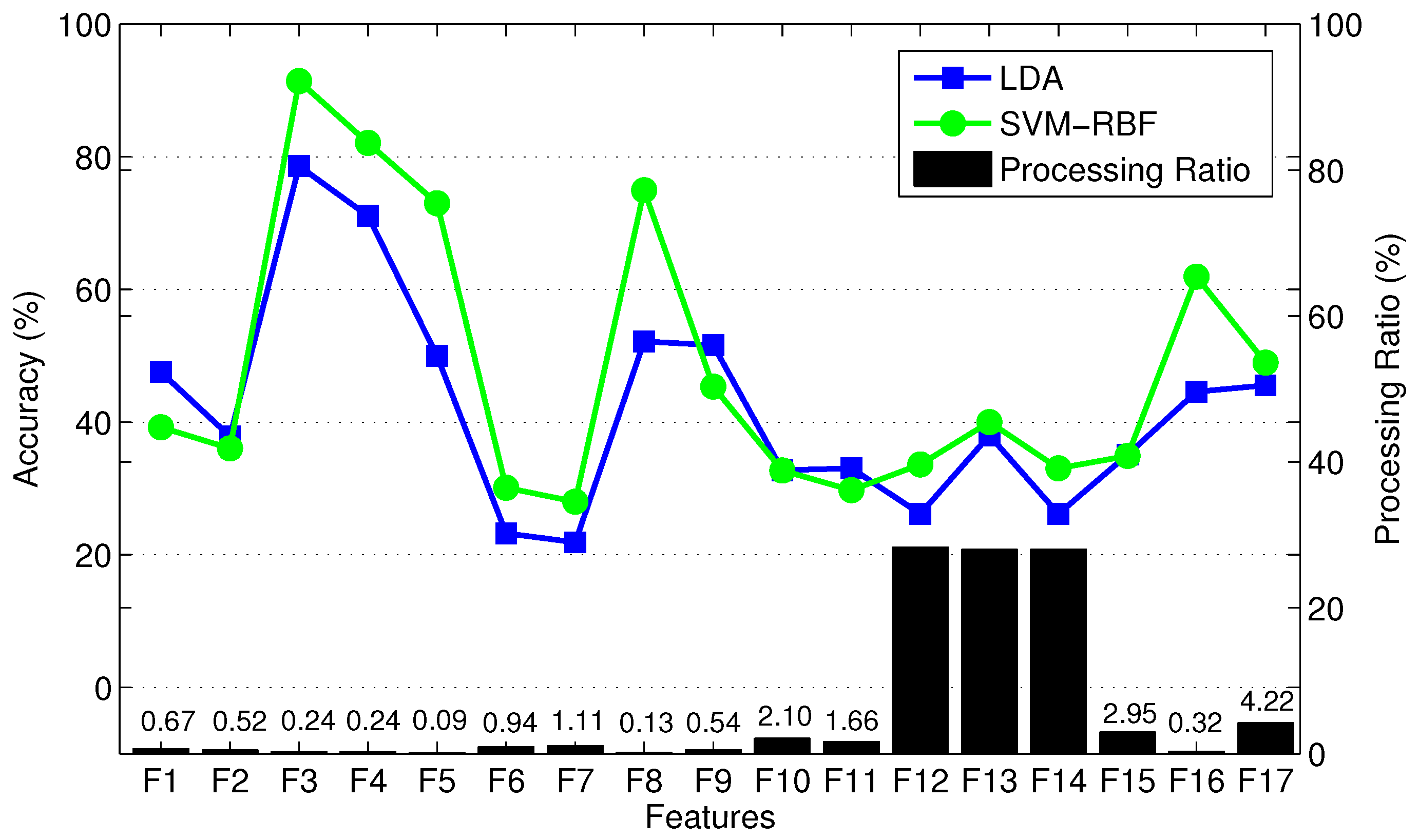
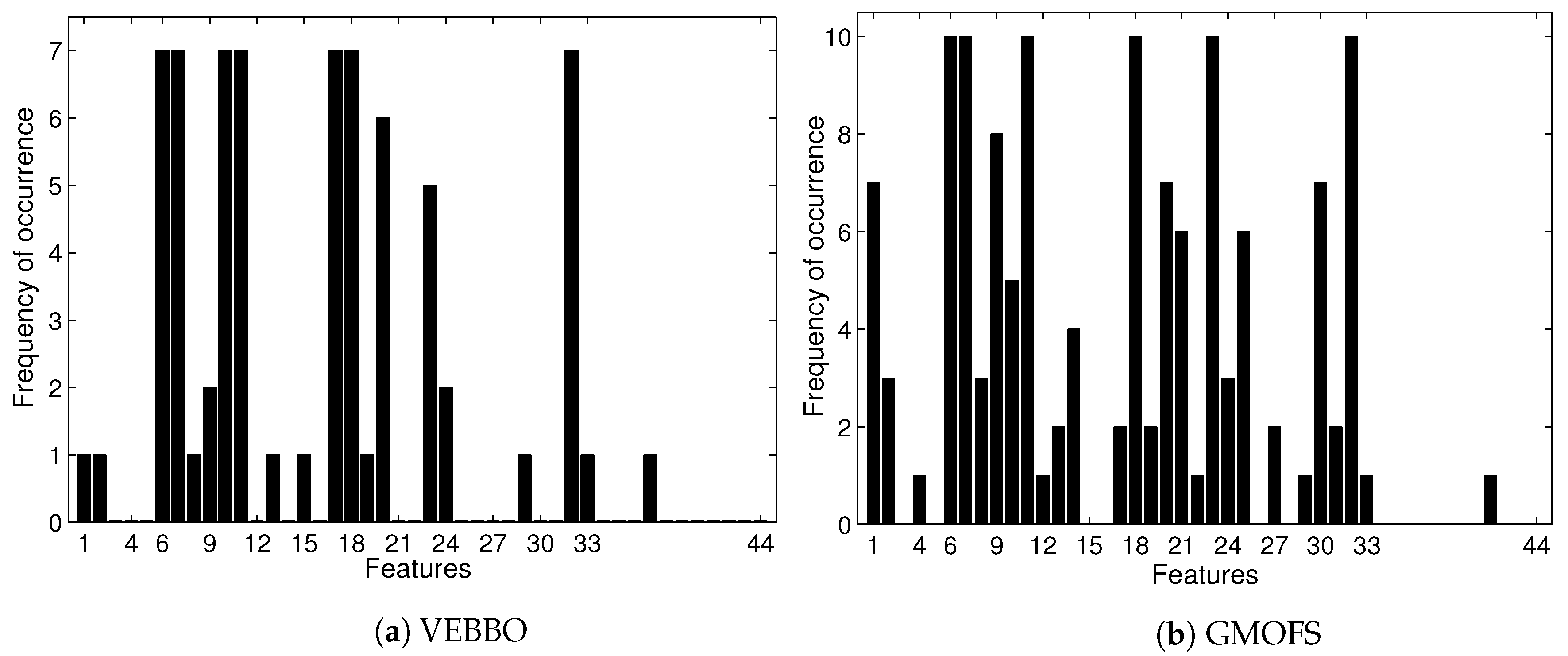
4.2. Multi-Objective Feature Selection
4.3. Comparison Results of Classification Algorithms
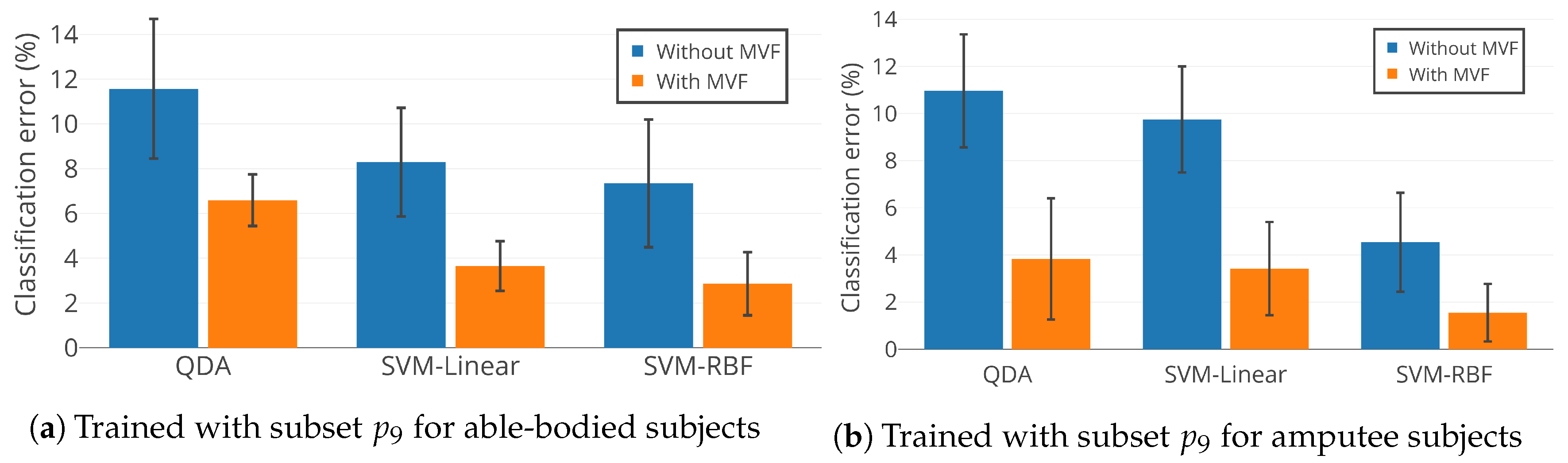
4.4. Performance Assessment of Selected Subset
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| List of acronyms in order of appearance | |||
| Acronym | Definition | Acronym | Definition |
| UIR | User intent recognition | ZC | Zero crossing |
| MOO | Multi-objective optimization | WL | Waveform length |
| GMOFS | Gradient-based multi-objective feature selection | VAR | Variance |
| MOBBO | Multi-objective biogeography-based optimization | MAV | Mean absolute value |
| SVM | Support vector machine | RMS | Root mean square |
| RBF | Radial basis function | WAMP | Willison amplitude |
| MVF | Majority voting filter | SK | Skewness |
| sEMG | Surface electromyography | KU | Kurtosis |
| LDA | Linear discriminant analysis | COR | Correlation |
| QDA | Quadratic discriminant analysis | ANG | Angle |
| GMM | Gaussian mixture model | PSD | Periodogram spectrum density |
| ANN | Artificial neural network | MNF | Mean frequency |
| BBO | Biogeography-based optimization | MDF | Median frequency |
| VEBBO | Vector evaluated BBO | MAXF | Maximum frequency |
| NSBBO | Non-dominated sorting BBO | AR | Auto-regressive model |
| NPBBO | Niched Pareto BBO | CV | Cross validation |
| SPBBO | Strength Pareto BBO | AB01 | Able-bodied subject 01 |
| EA | Evolutionary algorithm | AM01 | Amputee subject 01 |
| MLP | Multilayer perceptron | PS | Preferred speed |
| TD | Time domain | ST | Standing |
| FD | Frequency domain | NW | Normal walking |
| FLDA | Fisher’s linear discriminant analysis | SW | Slow walking |
| PCA | Principal component analysis | FW | Fast walking |
| DT | Decision tree | ||
| SSC | Slope sign change | ||
References
- Lawson, B.E.; Varol, H.A.; Huff, A.; Erdemir, E.; Goldfarb, M. Control of stair ascent and descent with a powered transfemoral prosthesis. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 21, 466–473. [Google Scholar] [CrossRef] [PubMed]
- Khademi, G.; Richter, H.; Simon, D. Multi-objective optimization of tracking/impedance control for a prosthetic leg with energy regeneration. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 5322–5327. [Google Scholar]
- Sup, F.; Varol, H.A.; Mitchell, J.; Withrow, T.J.; Goldfarb, M. Preliminary evaluations of a self-contained anthropomorphic transfemoral prosthesis. IEEE/ASME Trans. Mechatron. 2009, 14, 667–676. [Google Scholar] [CrossRef] [PubMed]
- Tucker, M.R.; Olivier, J.; Pagel, A.; Bleuler, H.; Bouri, M.; Lambercy, O.; del R Millán, J.; Riener, R.; Vallery, H.; Gassert, R. Control strategies for active lower extremity prosthetics and orthotics: A review. J. Neuroeng. Rehabil. 2015, 12, 1. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Kuiken, T.A.; Lipschutz, R.D. A strategy for identifying locomotion modes using surface electromyography. IEEE Trans. Biomed. Eng. 2009, 56, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Huang, H. Real-time recognition of user intent for neural control of artificial legs. In Proceedings of the 2011 MyoElectric Controls/Powered Prosthetics Symposium Fredericton, Fredericton, NB, Canada, 14–19 August 2011. [Google Scholar]
- Stolyarov, R.; Burnett, G.; Herr, H. Translational motion tracking of leg joints for enhanced prediction of walking tasks. IEEE Trans. Biomed. Eng. 2018, 65, 763–769. [Google Scholar] [CrossRef] [PubMed]
- Hargrove, L.; Englehart, K.; Hudgins, B. The effect of electrode displacements on pattern recognition based myoelectric control. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 2203–2206. [Google Scholar]
- Winkel, J.; Jorgensen, K. Significance of skin temperature changes in surface electromyography. Eur. J. Appl. Physiol. Occup. Physiol. 1991, 63, 345–348. [Google Scholar] [CrossRef] [PubMed]
- Zachariah, S.G.; Saxena, R.; Fergason, J.R.; Sanders, J.E. Shape and volume change in the transtibial residuum over the short term: Preliminary investigation of six subjects. J. Rehabil. Res. Dev. 2004, 41, 683. [Google Scholar] [CrossRef] [PubMed]
- Varol, H.A.; Sup, F.; Goldfarb, M. Multiclass real-time intent recognition of a powered lower limb prosthesis. IEEE Trans. Biomed. Eng. 2010, 57, 542–551. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wang, D.; Huang, H.H. Development of an environment-aware locomotion mode recognition system for powered lower limb prostheses. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 434–443. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, Q.; Zheng, E.; Wei, K.; Wang, L. A wearable plantar pressure measurement system: Design specifications and first experiments with an amputee. Intell. Autom. Syst. 2013, 194, 273–281. [Google Scholar]
- Huang, H.; Zhang, F.; Hargrove, L.J.; Dou, Z.; Rogers, D.R.; Englehart, K.B. Continuous locomotion-mode identification for prosthetic legs based on neuromuscular–mechanical fusion. IEEE Trans. Biomed. Eng. 2011, 58, 2867–2875. [Google Scholar] [CrossRef] [PubMed]
- Young, A.J.; Simon, A.M.; Fey, N.P.; Hargrove, L.J. Classifying the intent of novel users during human locomotion using powered lower limb prostheses. In Proceedings of the IEEE International Conference on Neural Engineering, San Diego, CA, USA, 6–8 November 2013; pp. 311–314. [Google Scholar]
- Ha, K.H.; Varol, H.A.; Goldfarb, M. Volitional control of a prosthetic knee using surface electromyography. IEEE Trans. Biomed. Eng. 2011, 58, 144–151. [Google Scholar] [CrossRef]
- Young, A.J.; Hargrove, L.J. A Classification Method for User-Independent Intent Recognition for Transfemoral Amputees Using Powered Lower Limb Prostheses. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Young, A.; Kuiken, T.; Hargrove, L. Analysis of using EMG and mechanical sensors to enhance intent recognition in powered lower limb prostheses. J. Neural Eng. 2014, 11, 056021. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Zheng, E.; Wang, Q.; Wang, L. A new strategy for parameter optimization to improve phase-dependent locomotion mode recognition. Neurocomputing 2015, 149, 585–593. [Google Scholar] [CrossRef]
- Simon, D.; Omran, M.G.; Clerc, M. Linearized biogeography-based optimization with re-initialization and local search. Inf. Sci. 2014, 267, 140–157. [Google Scholar] [CrossRef] [Green Version]
- Simon, D. Evolutionary Optimization Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Xue, B.; Zhang, M.; Browne, W.N. Particle swarm optimization for feature selection in classification: A multi-objective approach. IEEE Trans. Cybern. 2013, 43, 1656–1671. [Google Scholar] [CrossRef]
- Ghaemi, M.; Feizi-Derakhshi, M.R. Feature selection using forest optimization algorithm. Pattern Recognit. 2016, 60, 121–129. [Google Scholar] [CrossRef]
- Hall, M.A.; Smith, L.A. Feature Selection for Machine Learning: Comparing a Correlation-Based Filter Approach to the Wrapper. In FLAIRS Conference; AAAI: Menlo Park, CA, USA, 1999; pp. 235–239. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef] [Green Version]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef] [Green Version]
- Ma, S.; Huang, J. Penalized feature selection and classification in bioinformatics. Brief. Bioinform. 2008, 9, 392–403. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Van den Bogert, A.J.; Geijtenbeek, T.; Even-Zohar, O.; Steenbrink, F.; Hardin, E.C. A real-time system for biomechanical analysis of human movement and muscle function. Med. Biol. Eng. Comput. 2013, 51, 1069–1077. [Google Scholar] [CrossRef] [Green Version]
- Healthcare Inspection Prosthetic Limb Care in VA Facilities; Technical Report; Department of Veterans Affairs Office of Inspector General: Washington, DC, USA, 2011.
- Lara, O.D.; Labrador, M.A. A survey on human activity recognition using wearable sensors. IEEE Commun. Surv. Tutor. 2013, 15, 1192–1209. [Google Scholar] [CrossRef]
- Oskoei, M.A.; Hu, H. Support vector machine-based classification scheme for myoelectric control applied to upper limb. IEEE Trans. Biomed. Eng. 2008, 55, 1956–1965. [Google Scholar] [CrossRef]
- Hudgins, B.; Parker, P.; Scott, R.N. A new strategy for multifunction myoelectric control. IEEE Trans. Biomed. Eng. 1993, 40, 82–94. [Google Scholar] [CrossRef]
- Valls-Solé, J.; Rothwell, J.C.; Goulart, F.; Cossu, G.; Munoz, E. Patterned ballistic movements triggered by a startle in healthy humans. J. Physiol. 1999, 516, 931–938. [Google Scholar] [CrossRef] [Green Version]
- Stark, L. Neurological Control Systems: Studies in Bioengineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Phinyomark, A.; Limsakul, C.; Phukpattaranont, P. A novel feature extraction for robust EMG pattern recognition. arXiv, 2009; arXiv:0912.3973. [Google Scholar]
- Oskoei, M.A.; Hu, H. Myoelectric control systems—A survey. Biomed. Signal Process. Control 2007, 2, 275–294. [Google Scholar] [CrossRef]
- Englehart, K.; Hudgins, B. A robust, real-time control scheme for multifunction myoelectric control. IEEE Trans. Biomed. Eng. 2003, 50, 848–854. [Google Scholar] [CrossRef] [PubMed]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Oskoei, M.A.; Hu, H. GA-based feature subset selection for myoelectric classification. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 1465–1470. [Google Scholar]
- Xue, B.; Zhang, M.; Browne, W.N.; Yao, X. A survey on evolutionary computation approaches to feature selection. IEEE Trans. Evol. Comput. 2016, 20, 606–626. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Moore, B. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
| Gender | Age | Weight | Height | Walking Speed (m/s) | |||
|---|---|---|---|---|---|---|---|
| (years) | (kg) | (cm) | SW | PS | FW | ||
| AB01 | Male | 37 | 79.5 | 188 | 0.98 | 1.30 | 1.63 |
| AB02 | Male | 20 | 73.9 | 172 | 0.86 | 1.15 | 1.44 |
| AB03 | Male | 28 | 80.9 | 179 | 0.75 | 1.00 | 1.25 |
| AM01 | Male | 32 | 79.1 | 174 | 0.60 | 1.00 | - |
| AM02 | Male | 64 | 99.2 | 177 | 0.56 | 0.94 | - |
| AM03 | Male | 35 | 81.7 | 176 | 0.60 | 0.90 | - |
| Frame Length (ms) | 150 | 200 | 200–50 | 200–150 | 250 | 250–50 | 300–200 | |
|---|---|---|---|---|---|---|---|---|
| 100 | vs. | W (+) | W (+) | W (+) | W (+) | W (+) | W (+) | W (+) |
| 150 | vs. | − | W (+) | W (+) | W (+) | W (+) | W (+) | W (+) |
| 200 | vs. | * | − | W (+) | T (≈) | W (+) | W (+) | W (+) |
| 200–50 | vs. | * | * | − | T (≈) | T (≈) | W (+) | W (+) |
| 200–150 | vs. | * | * | * | − | W (+) | W (+) | W (+) |
| 250 | vs. | * | * | * | * | − | W (+) | W (+) |
| 250–50 | vs. | * | * | * | * | * | − | T (≈) |
| Symbol | Value | |
|---|---|---|
| MOBBO | ||
| Mutation rate | 0.04 | |
| Number of elites | E | 2 |
| Population size | N | 100 |
| Number of generations | 1000 | |
| Problem dimension | d | 44 |
| Migration model | sinusoidal | |
| GMOFS | ||
| Number of hidden nodes | p | 5 |
| Elastic net parameter | 0 | |
| Bound for shrinkage parameter | [] | [0, 150] |
| Bound for neuron weights | 5 | |
| Increment of shrinkage parameter | 1 if ; and 10 if | |
| Trust region reflective | ||
| Maximum allowable iterations | MaxIter | 100 |
| Termination tolerance on the independent variable | TolX | 0.001 |
| Termination tolerance on the cost function | TolFun | 0.001 |
| Typical values for the independent variable | TypicalX | 0.1 |
| Finite difference method | FinDiffType | central |
| VEBBO | SPBBO | NSBBO | NPBBO | GMOFS | |
|---|---|---|---|---|---|
| VEBBO | − | 62.5 | 75.0 | 85.7 | 40.0 |
| SPBBO | 0.0 | − | 25.0 | 71.4 | 40.0 |
| NSBBO | 14.3 | 50.0 | − | 100.0 | 40.0 |
| NPBBO | 0.0 | 0.0 | 0.0 | − | 0.0 |
| GMOFS | 14.3 | 50.0 | 50.0 | 100.0 | − |
| Mean RC | 7.2 | 40.4 | 37.5 | 89.3 | 30.0 |
| Normalized Hypervolume | ||
|---|---|---|
| VEBBO | 7 | 0.5026 |
| SPBBO | 8 | 0.5814 |
| NSBBO | 8 | 0.5676 |
| NPBBO | 7 | 0.8013 |
| GMOFS | 10 | 0.5332 |
| Pareto Point | NF | LDA | QDA | SVM-Linear | SVM-RBF | MLP | DT | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACC | STD | ACC | STD | ACC | STD | ACC | STD | ACC | STD | ACC | STD | ||
| 6 | 93.56 | 0.740 | 94.33 | 0.852 | 95.37 | 1.218 | 98.33 | 0.421 | 97.34 | 0.698 | 96.15 | 1.16 | |
| 7 | 95.31 | 0.829 | 96.06 | 0.711 | 96.99 | 0.775 | 98.88 | 0.216 | 98.29 | 0.539 | 96.35 | 1.00 | |
| 8 | 96.69 | 0.835 | 96.82 | 0.410 | 97.47 | 0.694 | 98.86 | 0.378 | 98.20 | 0.411 | 96.67 | 1.18 | |
| 9 | 96.86 | 0.684 | 96.95 | 0.484 | 98.07 | 0.576 | 99.31 | 0.234 | 98.34 | 0.459 | 96.73 | 1.25 | |
| 10 | 97.04 | 0.657 | 96.99 | 0.427 | 98.08 | 0.430 | 98.90 | 0.406 | 98.47 | 0.645 | 96.56 | 1.22 | |
| 11 | 96.84 | 0.536 | 97.15 | 0.654 | 98.14 | 0.692 | 98.94 | 0.293 | 98.62 | 0.578 | 96.32 | 1.28 | |
| 12 | 96.93 | 0.656 | 97.36 | 0.372 | 98.20 | 0.497 | 99.05 | 0.356 | 98.87 | 0.406 | 97.21 | 1.00 | |
| 13 | 96.61 | 0.384 | 97.62 | 0.554 | 98.25 | 0.534 | 99.14 | 0.305 | 95.76 | 9.180 | 96.86 | 1.36 | |
| 14 | 96.76 | 0.485 | 97.79 | 0.311 | 98.49 | 0.500 | 98.88 | 0.290 | 98.90 | 0.355 | 97.15 | 0.78 | |
| 16 | 96.95 | 0.525 | 97.84 | 0.578 | 98.59 | 0.467 | 98.38 | 0.449 | 98.66 | 0.371 | 96.99 | 0.72 | |
| 21 | 97.13 | 0.501 | 97.93 | 0.716 | 98.62 | 0.564 | 98.40 | 0.392 | 99.00 | 0.432 | 97.30 | 0.54 | |
| 27 | 97.41 | 0.568 | 97.77 | 0.861 | 98.70 | 0.422 | 97.58 | 0.663 | 99.07 | 0.373 | 96.91 | 0.64 | |
| DT | SVM-RBF | SVM-linear | QDA | LDA | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| p-Value | W.T. | p-Value | W.T. | p-Value | W.T. | p-Value | W.T. | p-Value | W.T. | ||
| MLP | vs. | 2.44 × 10 | B | 7.32 × 10 | T | 8.50 × 10 | B | 5.02 × 10 | B | 2.44 × 10 | B |
| DT | vs. | − | 1.23 × 10 | W | 8.20 × 10 | W | 1.33 × 10 | T | 1.70 × 10 | T | |
| SVM-RBF | vs. | * | − | 6.70 × 10 | B | 2.44 × 10 | B | 1.22 × 10 | B | ||
| SVM-linear | vs. | * | * | − | 1.15 × 10 | B | 1.25 × 10 | B | |||
| QDA | vs. | * | * | * | − | 2.44 × 10 | B | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khademi, G.; Mohammadi, H.; Simon, D. Gradient-Based Multi-Objective Feature Selection for Gait Mode Recognition of Transfemoral Amputees. Sensors 2019, 19, 253. https://doi.org/10.3390/s19020253
Khademi G, Mohammadi H, Simon D. Gradient-Based Multi-Objective Feature Selection for Gait Mode Recognition of Transfemoral Amputees. Sensors. 2019; 19(2):253. https://doi.org/10.3390/s19020253
Chicago/Turabian StyleKhademi, Gholamreza, Hanieh Mohammadi, and Dan Simon. 2019. "Gradient-Based Multi-Objective Feature Selection for Gait Mode Recognition of Transfemoral Amputees" Sensors 19, no. 2: 253. https://doi.org/10.3390/s19020253
APA StyleKhademi, G., Mohammadi, H., & Simon, D. (2019). Gradient-Based Multi-Objective Feature Selection for Gait Mode Recognition of Transfemoral Amputees. Sensors, 19(2), 253. https://doi.org/10.3390/s19020253





