Minimum Cost Deployment of Bistatic Radar Sensor for Perimeter Barrier Coverage
Abstract
:1. Introduction
- Firstly, we investigate the Cassini oval sensing models and discuss a variety of barrier coverage cases. We discover and prove the optimized BR placement patterns and sequence on a circular ring. Then the unit costs of the BR sensor are taken into accounts to derive the minimum cost placement sequence, which is then used to design an algorithm for any minimum cost placement in circle-based barrier construction.
- Secondly, we further study the optimal BR placement on an circular barrier with a predefined breadth. We propose two division strategies, circular equipartition strategy and an adaptive segmentation strategy, to segment an annulus ring to several adjacent sub-ring with appropriate width so as to ensure the minimum cost annulus BR barrier coverage with required detection threshold.
- Finally, we propose approximate optimization placement algorithms for minimum cost placement of BR sensor for annulus barrier coverage with required width and detection threshold. We validate the effectiveness of the proposed algorithms through extensive simulation experiments.
2. Related Work
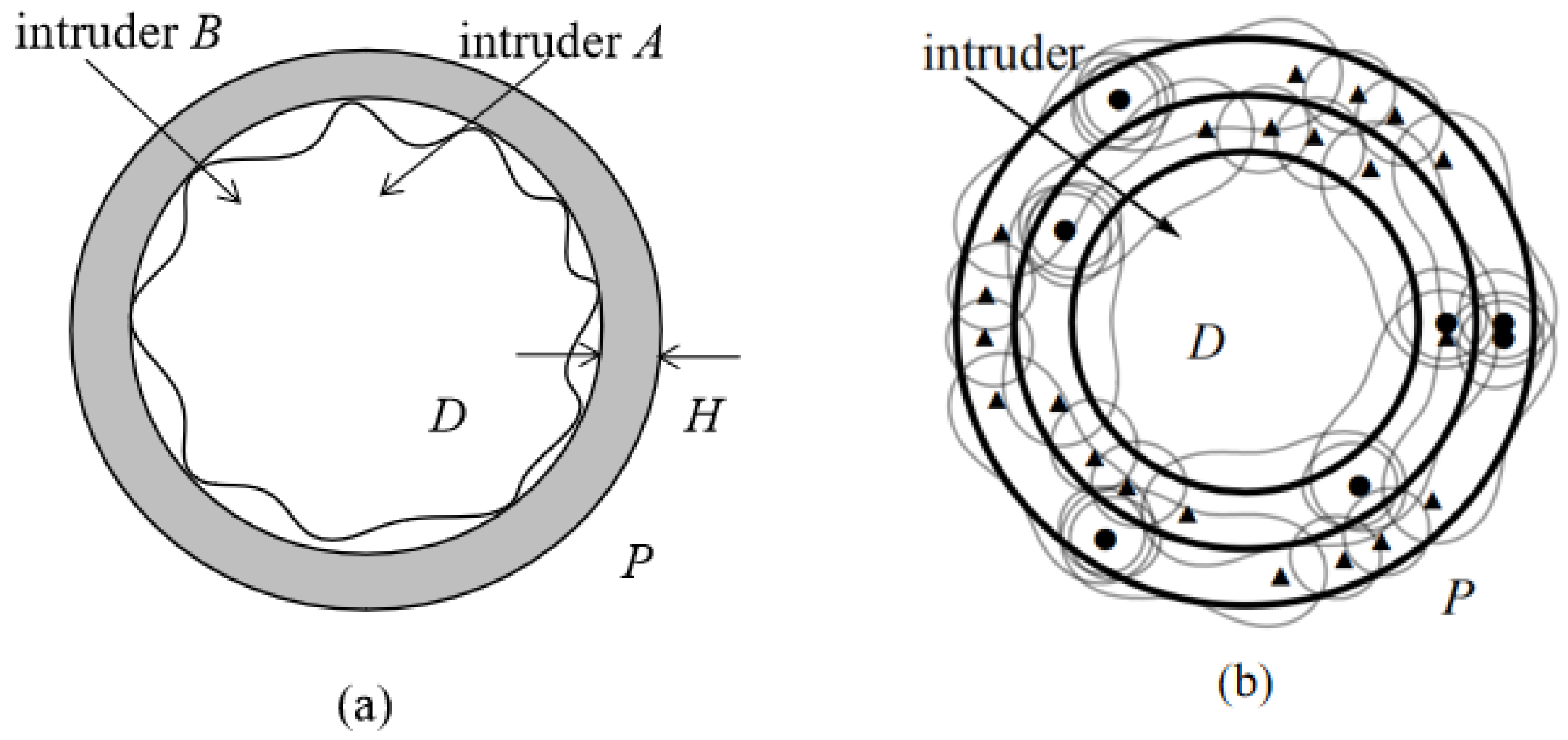
3. Sensor Model and Problem Description
3.1. Sensor Model
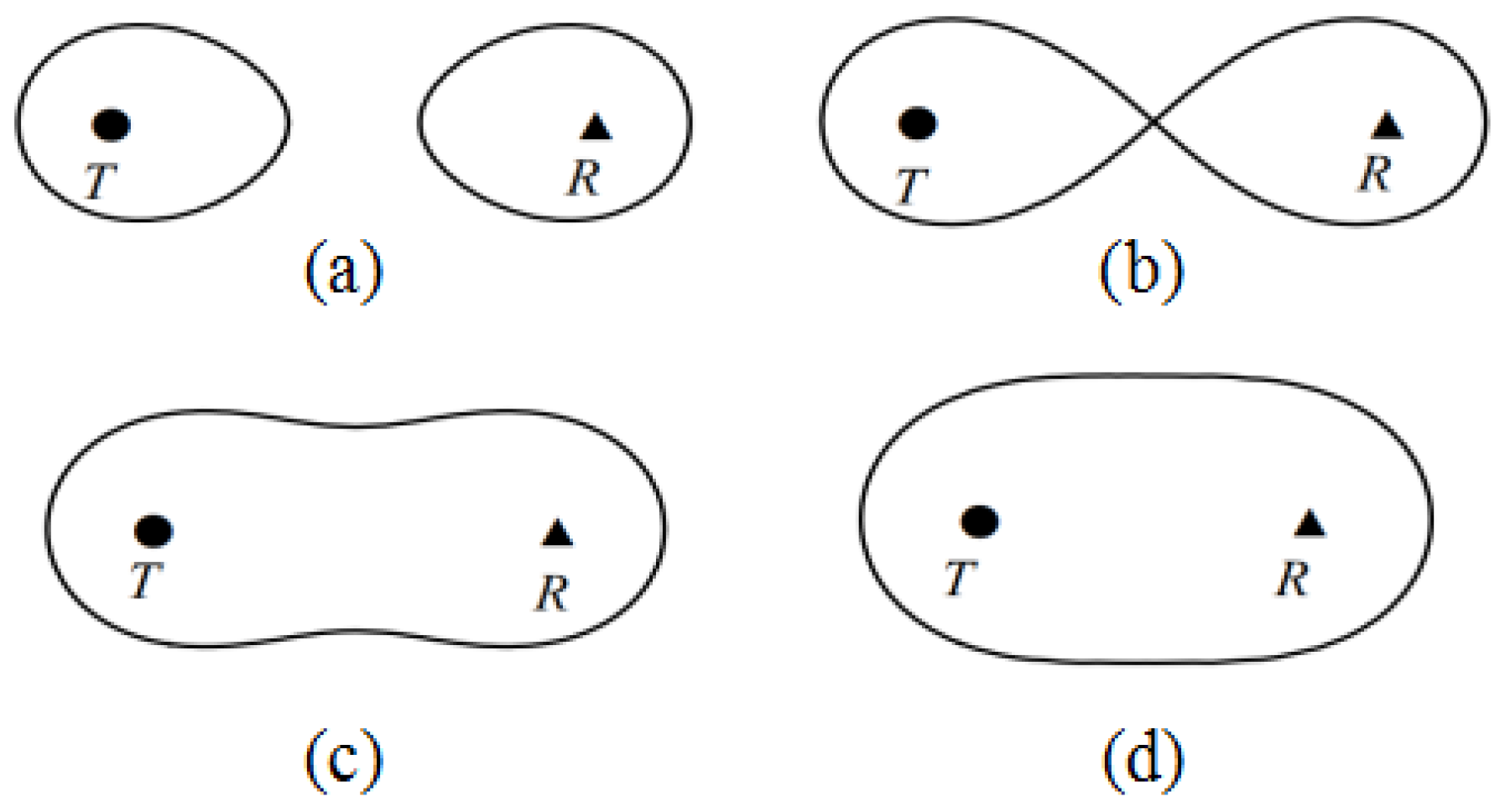
- (a)
- , the coverage area is two disjointed parts;
- (b)
- , the coverage area is surrounded by the Bernoulli double new line;
- (c)
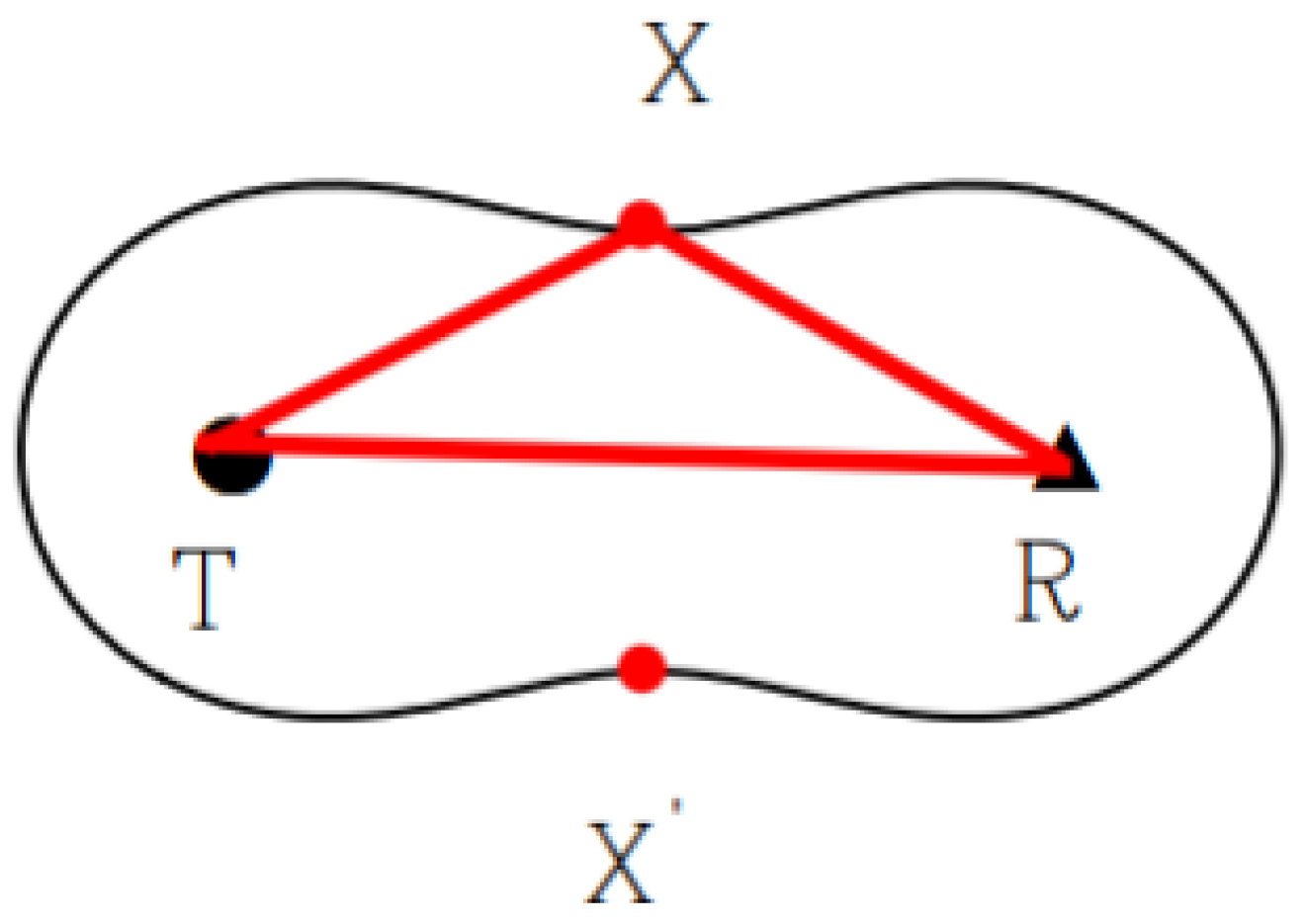
- , the coverage area is surrounded by the waist closed curve;
- (d)
- , the coverage area is surrounded by the elliptical curve,where represents the distance between the transmitter and the receiver.
3.2. Problem Definition
3.3. Basic Deployment Pattern
4. Solution for Single Circle with Width h
4.1. Coverage Model
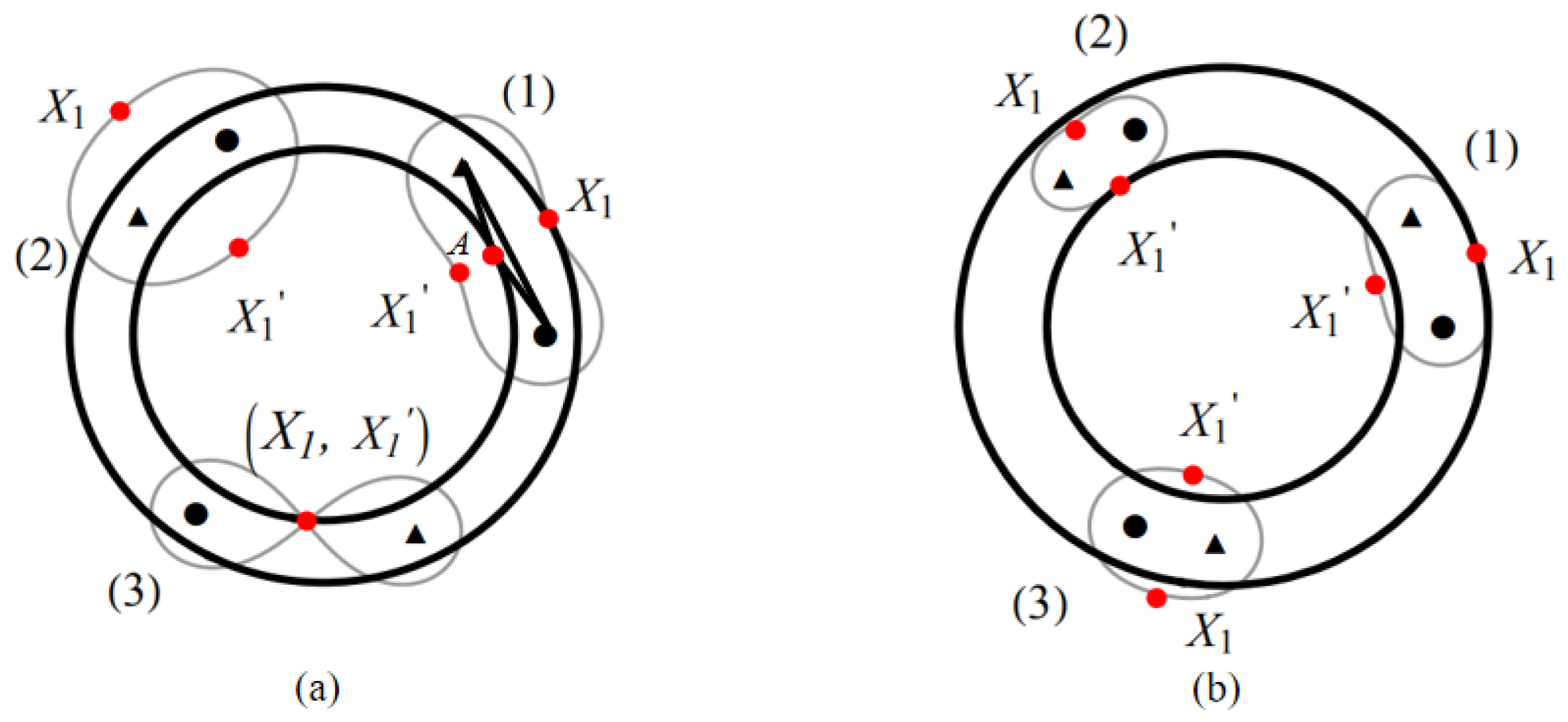
4.1.1. Case of Waist
- 1.1
- Suppose that there is only one point between and at the inner and outer boundaries of the annulus, and we find that point at the outer boundary is better than point at the inner boundary, as shown in Figure 4a(1). Since point is on the inner boundary, cannot meet the coverage requirement, one of the cases is shown in Figure 4a(3).
- 1.2
- Suppose that the two points and are not inside and outside the boundary of the annulus. To meet the coverage requirements, must be outside of the outer boundary and must be inside of the inner boundary, as shown in Figure 4a(2). However, it draws closer to the distance between , compared to the first case, the length of the cover is smaller.
- 1.3
- Suppose that the two points and are in the inner and outer boundaries of the annulus separately, as shown in Figure 4a(1). In this case, is on the location of point A, but cannot be on the outer boundary of the annulus, hence it is not feasible.
4.1.2. Case of Ellipse
- 2.1
- Suppose that there is only one point between and inside and outside the boundary of the annulus. We find that when point on the outer boundary of the annulus, the covering area is tangent to the outer boundary of the annulus at point . It is obvious that it does not meet the coverage requirements, as shown in Figure 4b(1), and the same conclusion can be drawn when point is on the inner boundary, as shown in Figure 4b(2).
- 2.2
- Assuming that the two points and are not inside and outside the boundary of the annulus, it is possible to satisfy the coverage condition at this point, but the coverage length is shorter than that of the waist model, as shown in Figure 4b(3).
- 2.3
- Suppose that both points and are inside and outside the boundary of the annulus, similar to the case of the waist coverage. This case is not feasible.
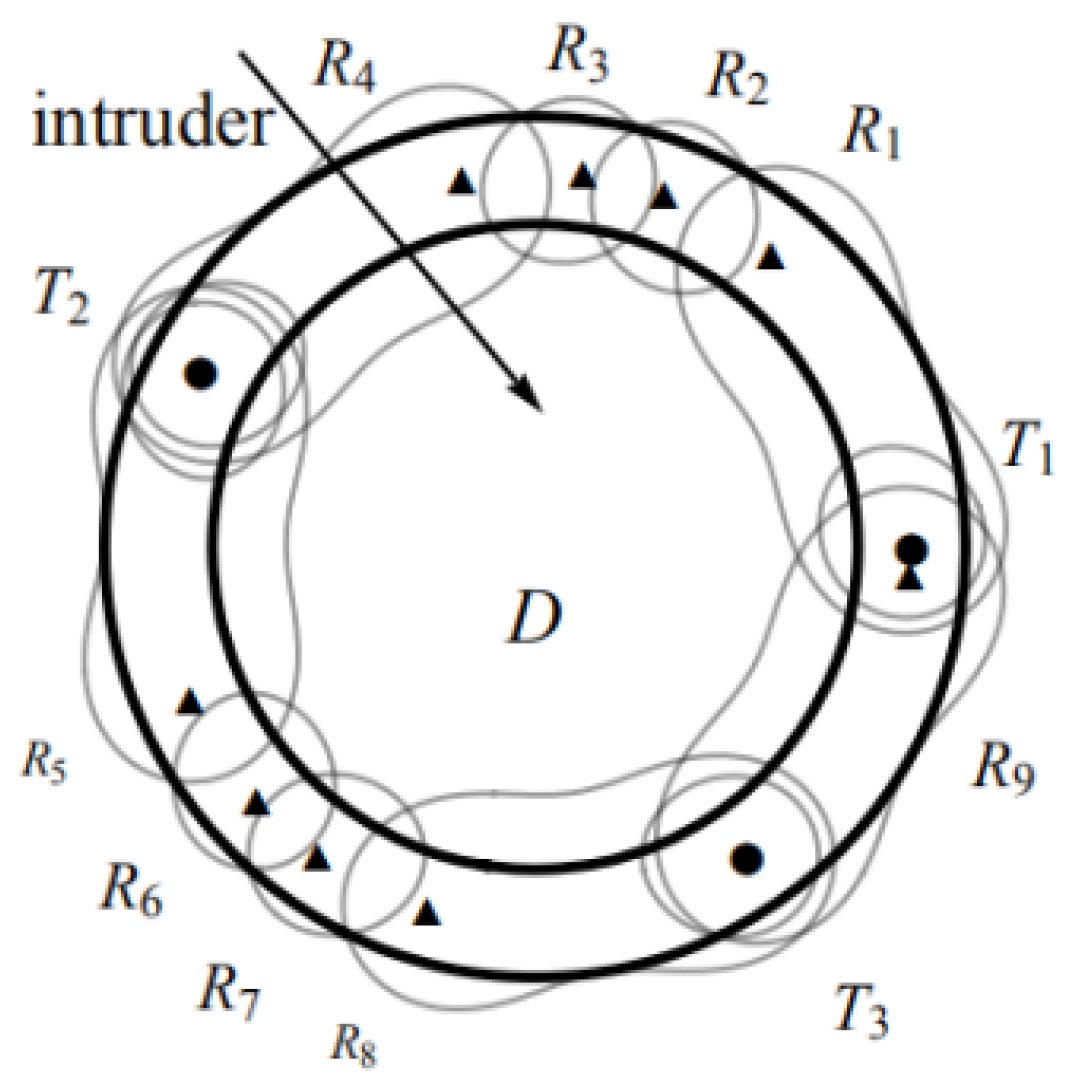
4.2. Placement Pattern of
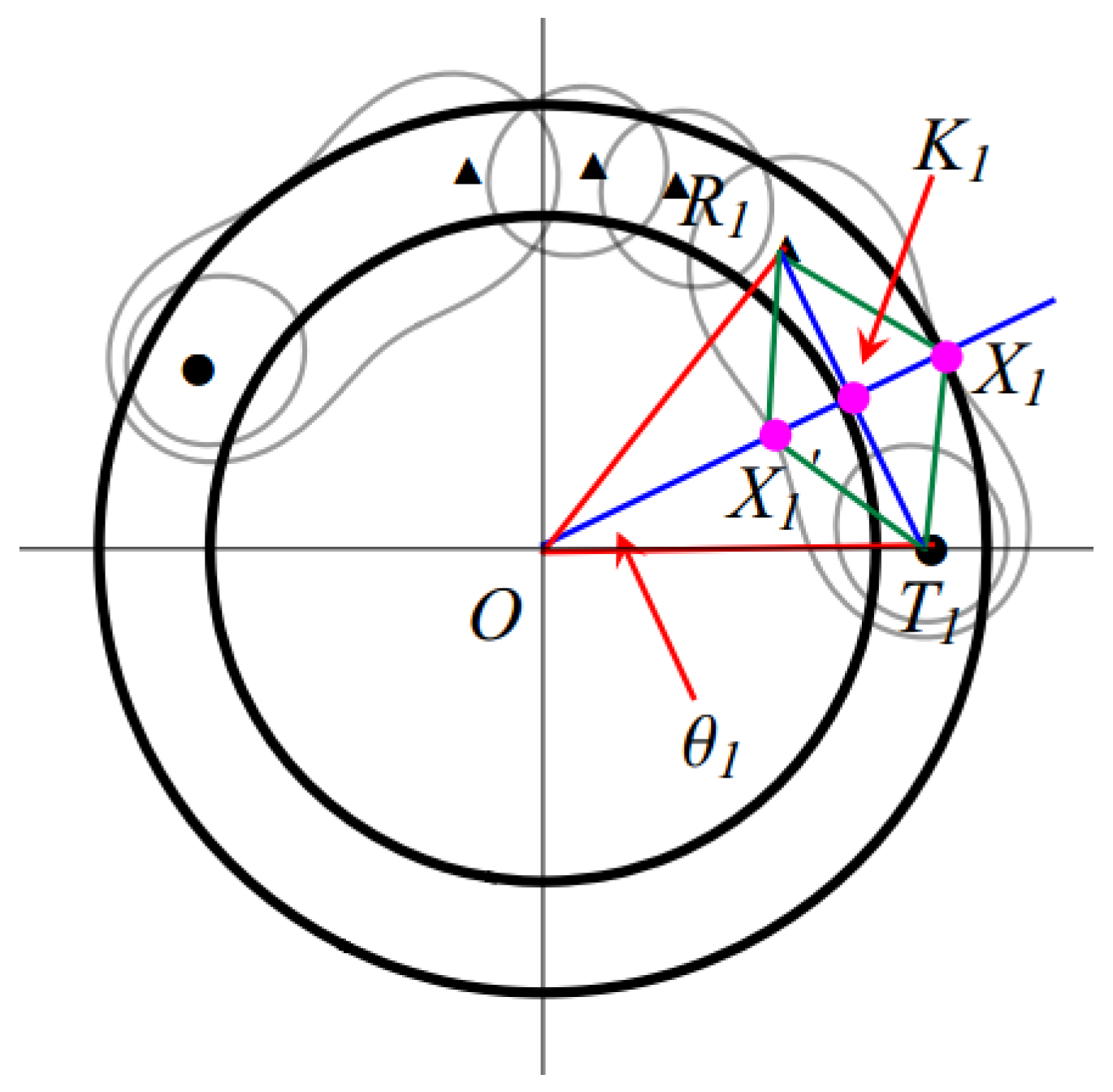
4.2.1. Determining Sensor Locations
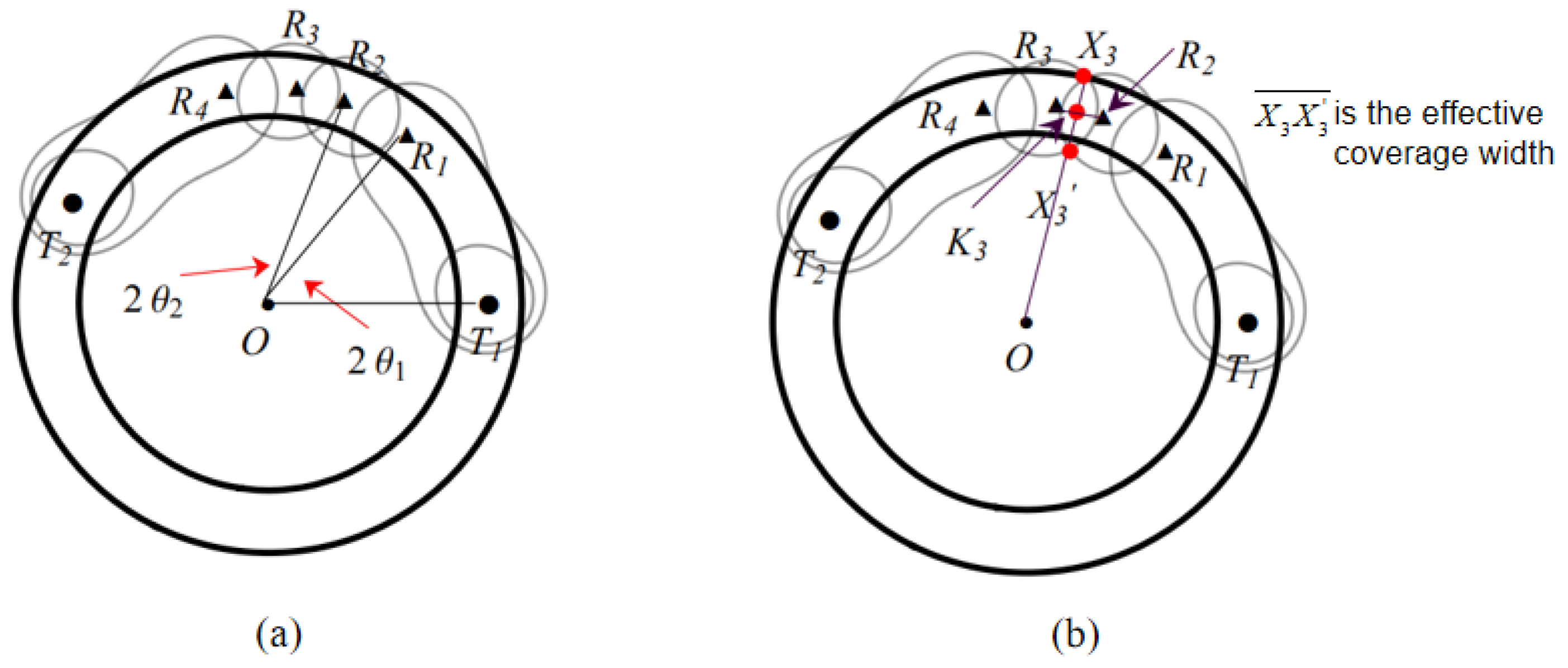
4.2.2. Effective Coverage Width of and Coverage Quality
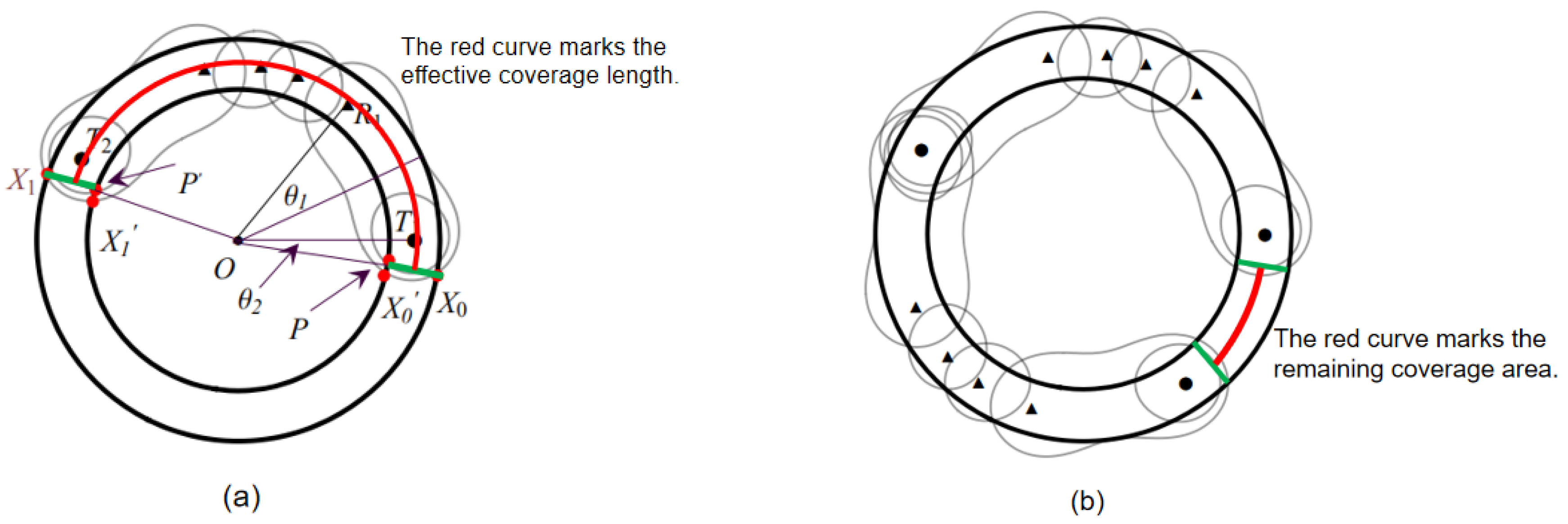
4.2.3. Effective Coverage Length of
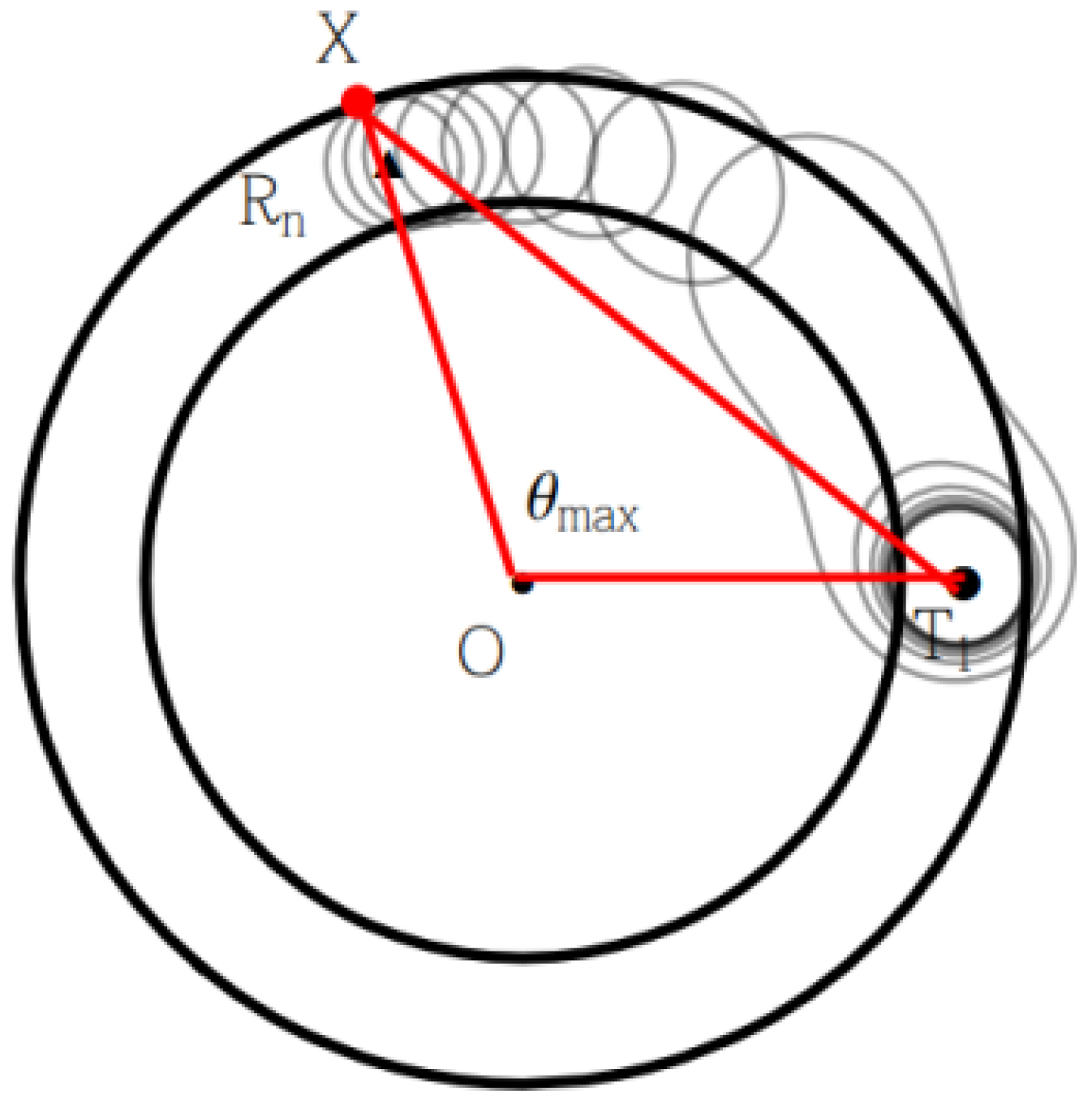
4.3. Optimal Placement Sequence on Single Circle with Width h
4.4. Overlay Boundary Problem on Single Circle with Width h
5. Solution of Minimum Coverage Cost on the Whole Circular Barrier with Width H
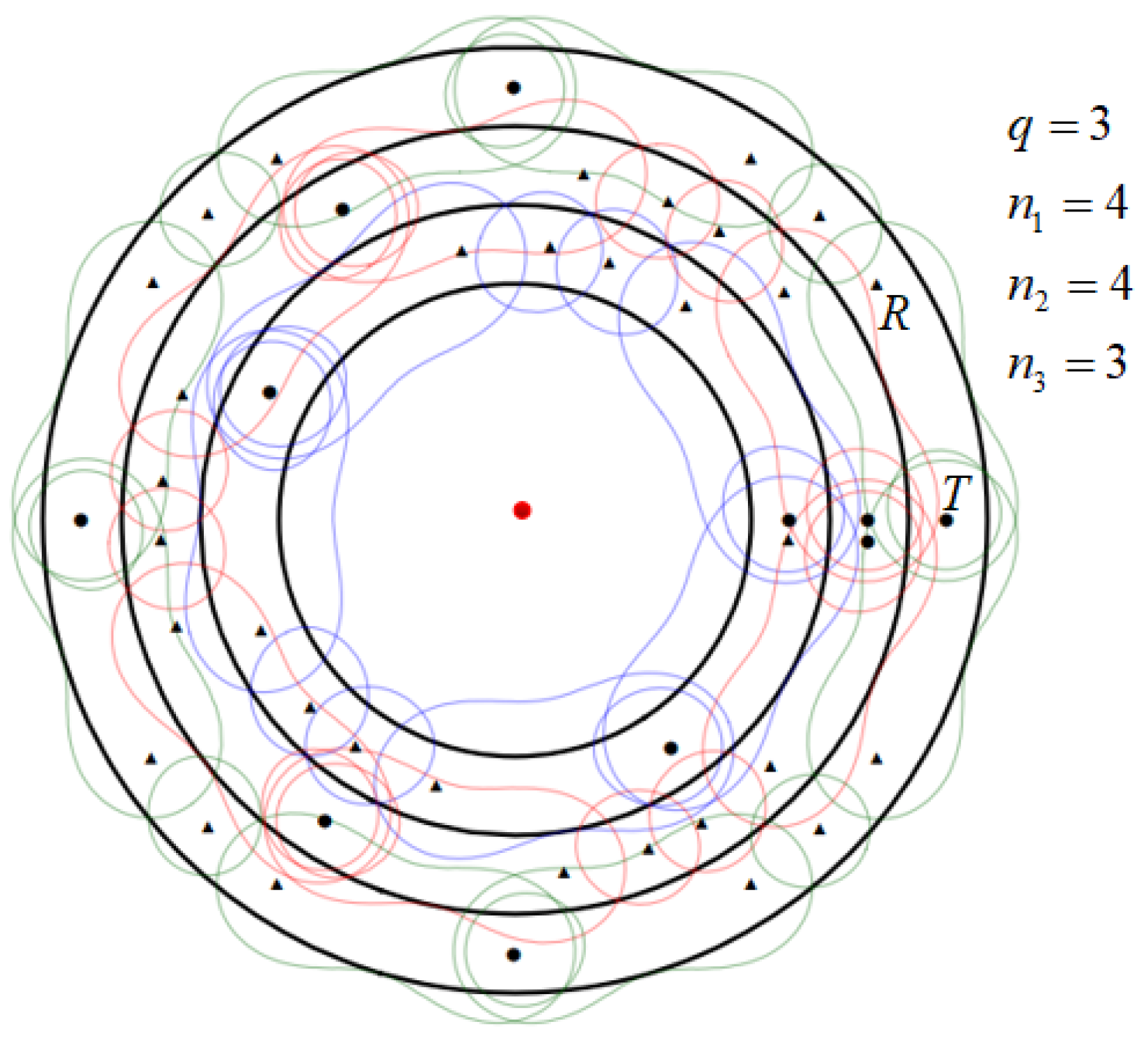
5.1. Equal Circle width Division Strategy and BR Sensors Placement Algorithm
5.1.1. Equal width Circle Division and Optimal Placement Algorithm
| Algorithm 1 Find and When |
| 1: Initialization: , , , 2: for do 3: for do 4: for do 5: 6: 7: 8: end for 9: 10: 11: end for 12: 13: 14: 15: end for 16: 17: 18: |
| Algorithm 2 Compute Cost When n and h are determined |
| 1: 2: for do 3: 4: if then 5: Compute M and N, Compute RT and RR 6: , 7: break 8: end if 9: end for 10: 11: return |
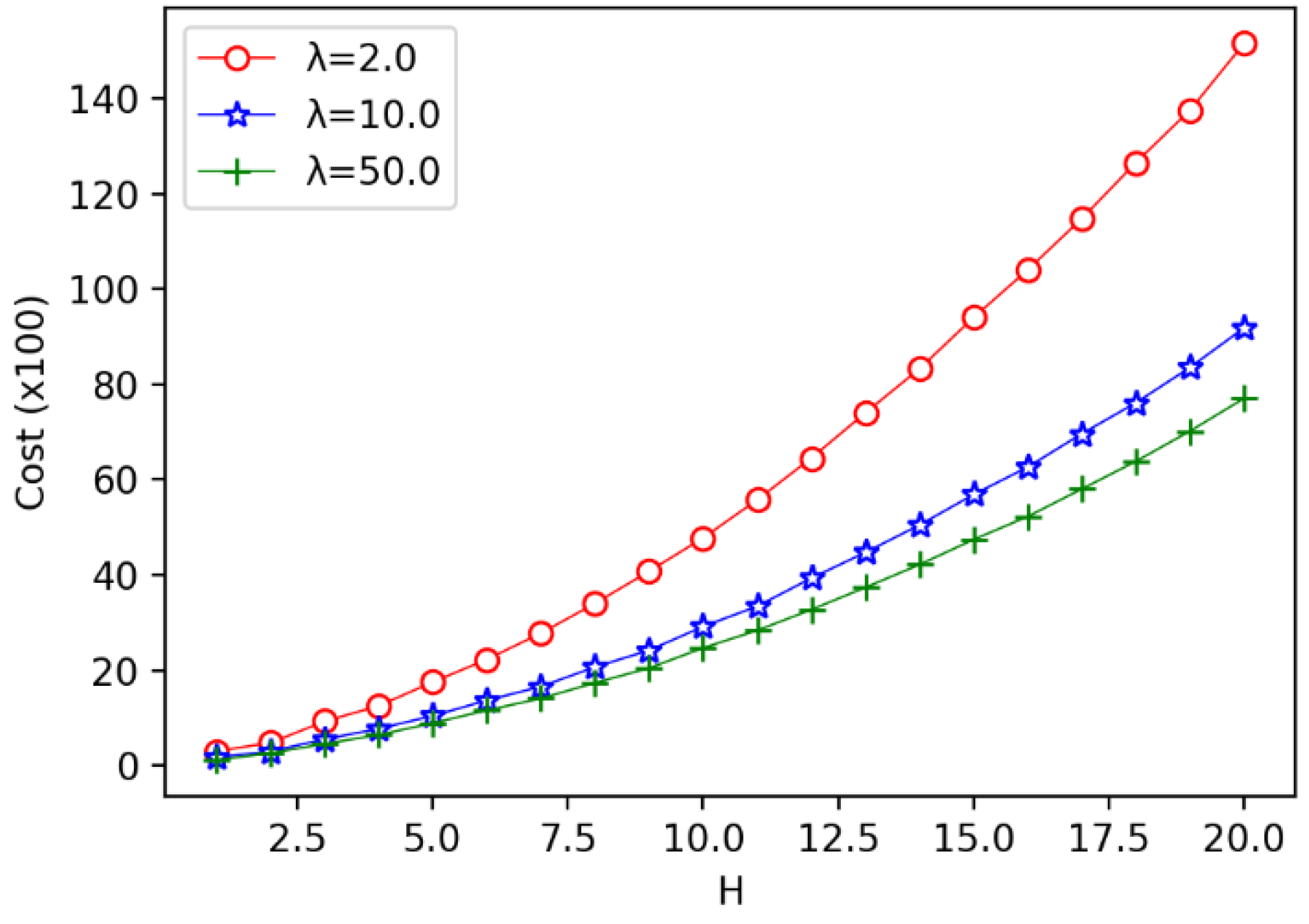
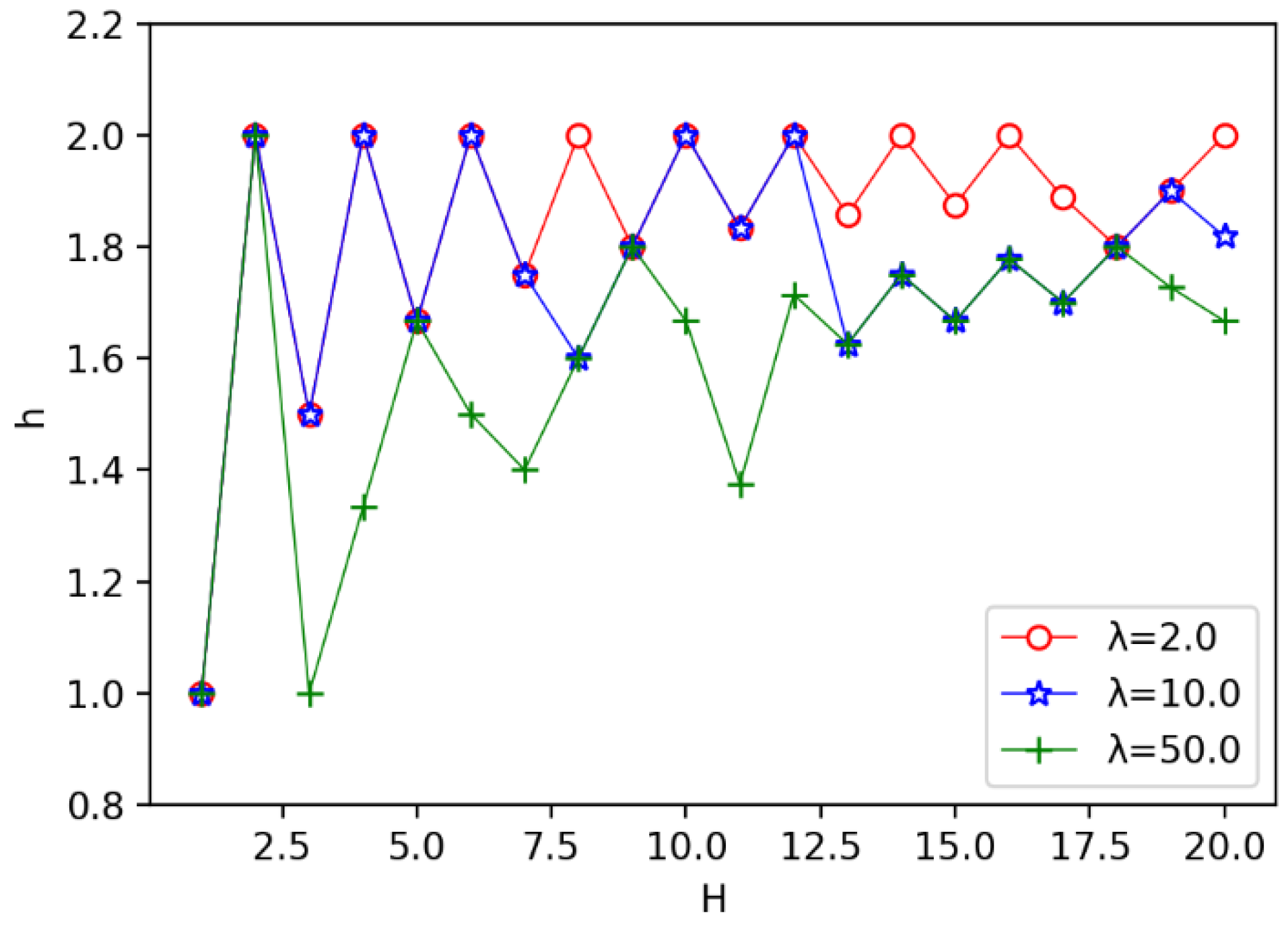
5.1.2. Experimental Result of the Equal Circle Width Division Strategy
5.1.3. Algorithm Analysis of the Equal Circle Width Division Strategy
5.2. Adaptive Circle Width Division Strategy and BR Sensors Placement Algorithm
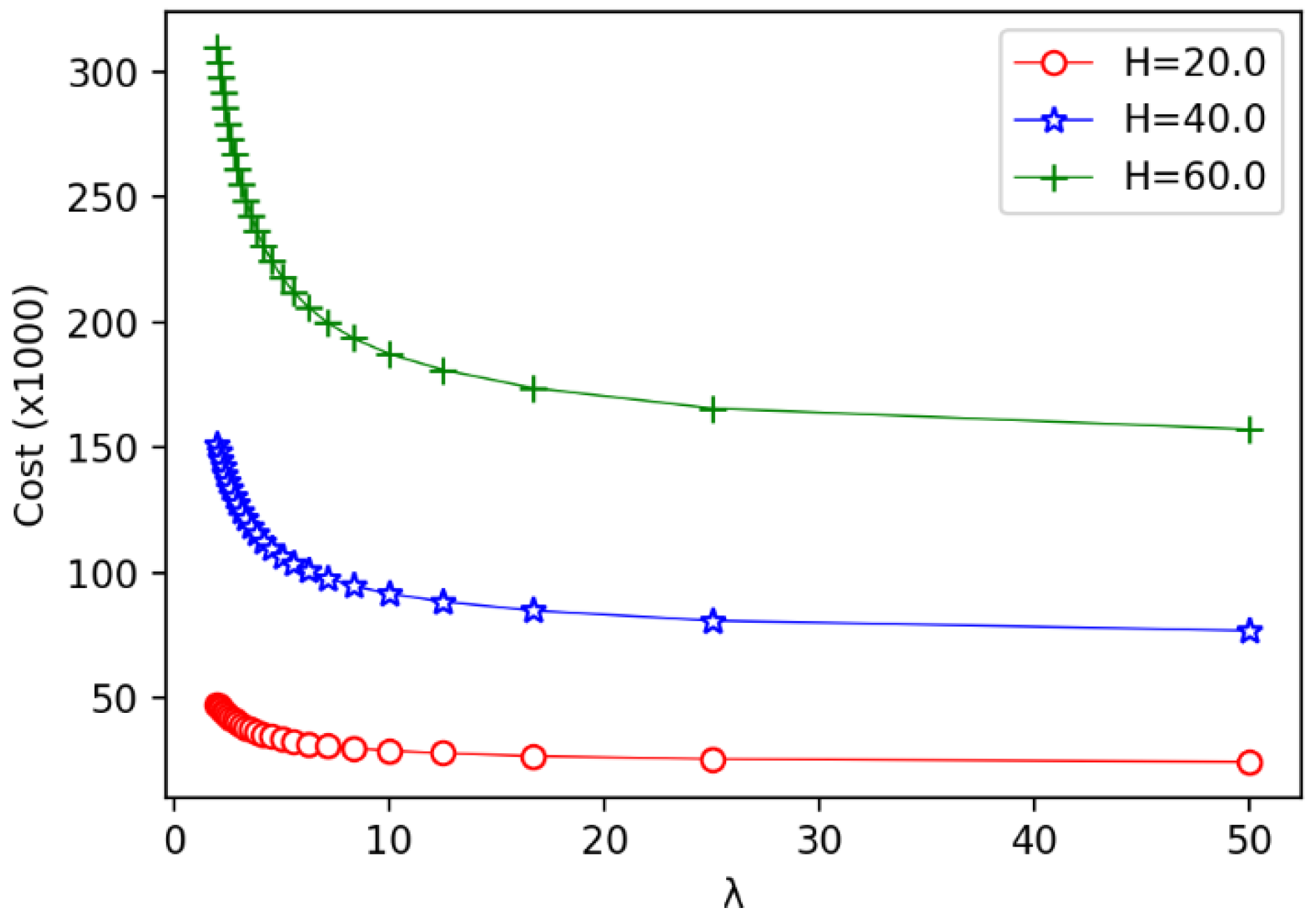
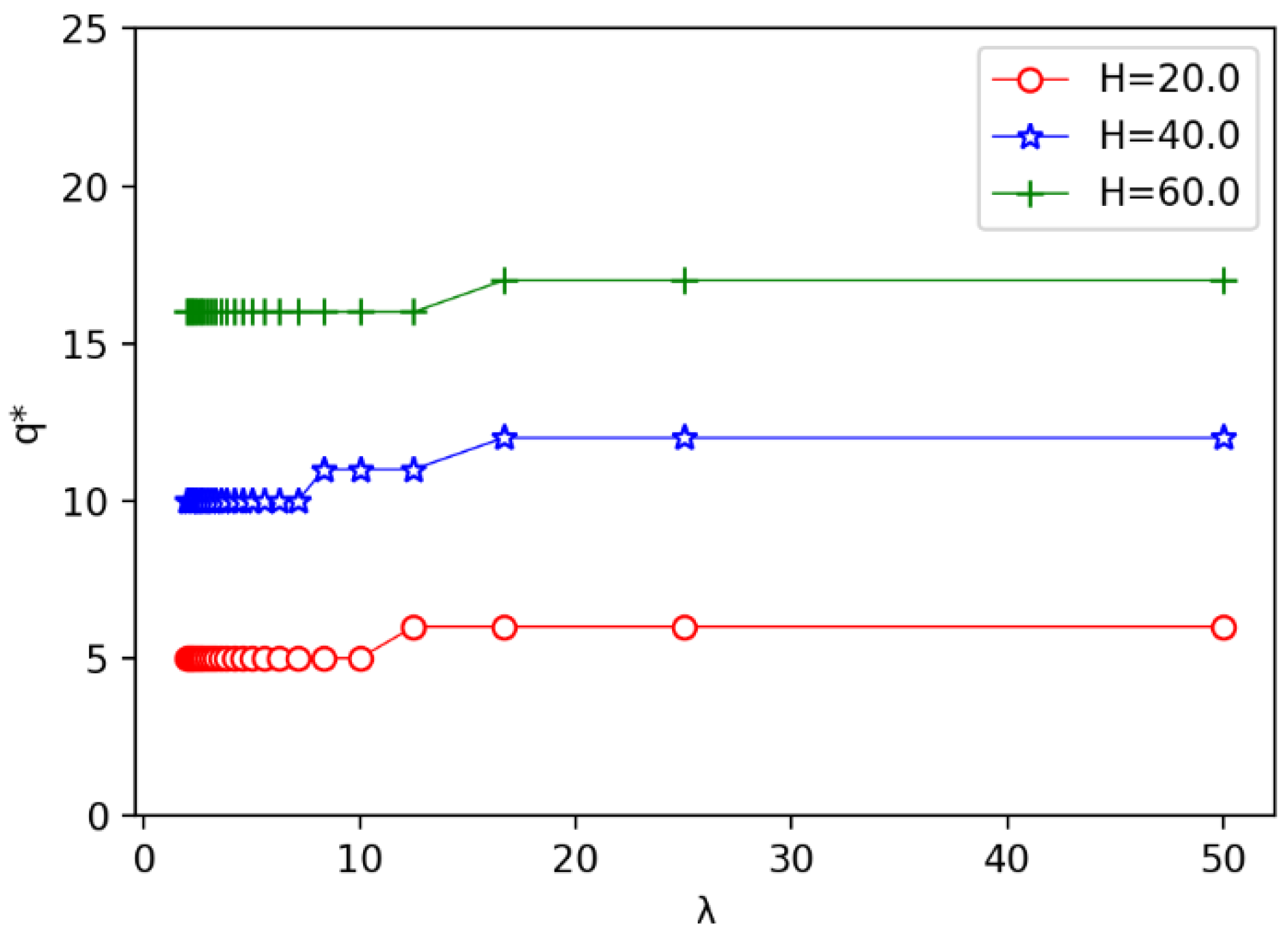
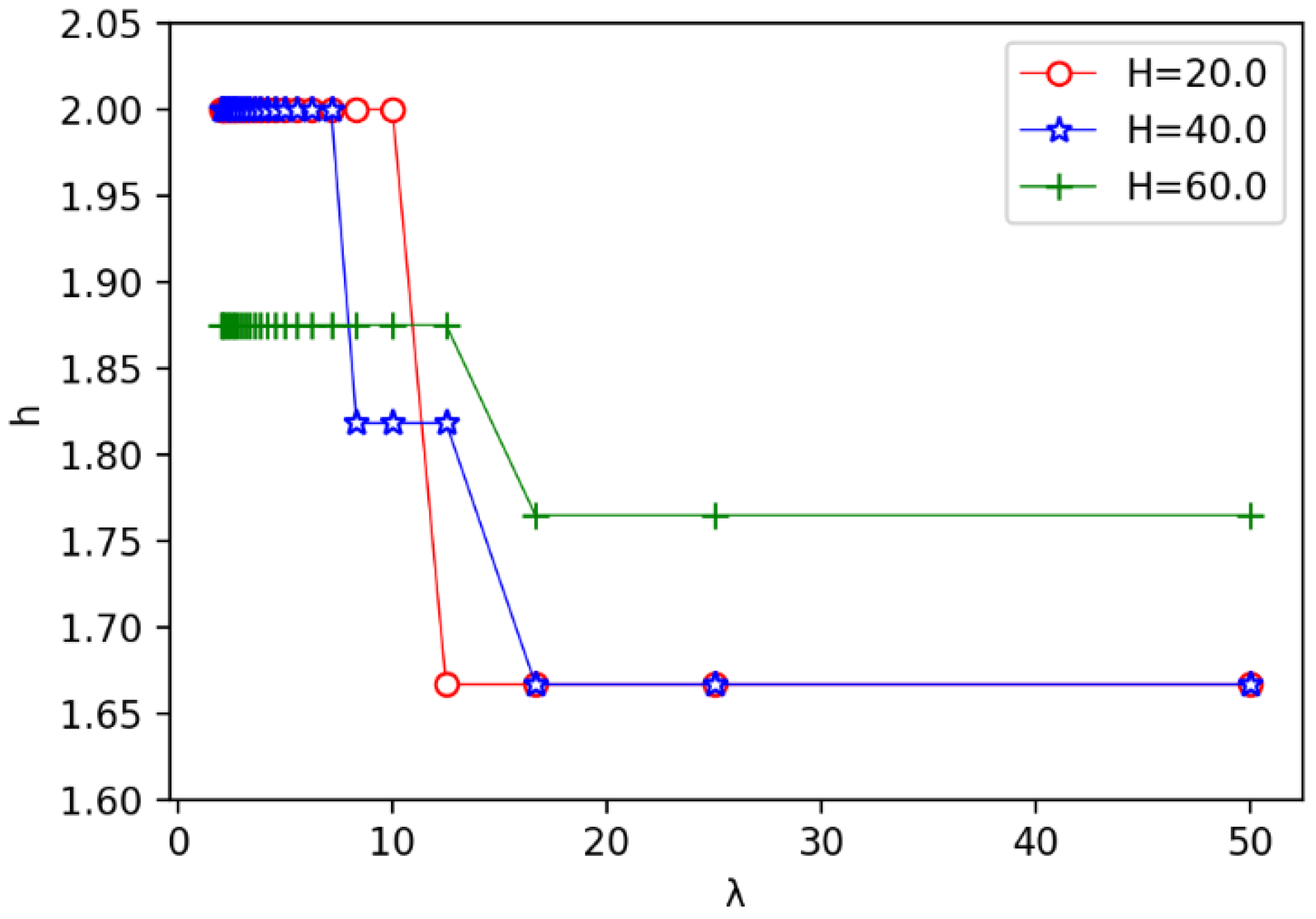
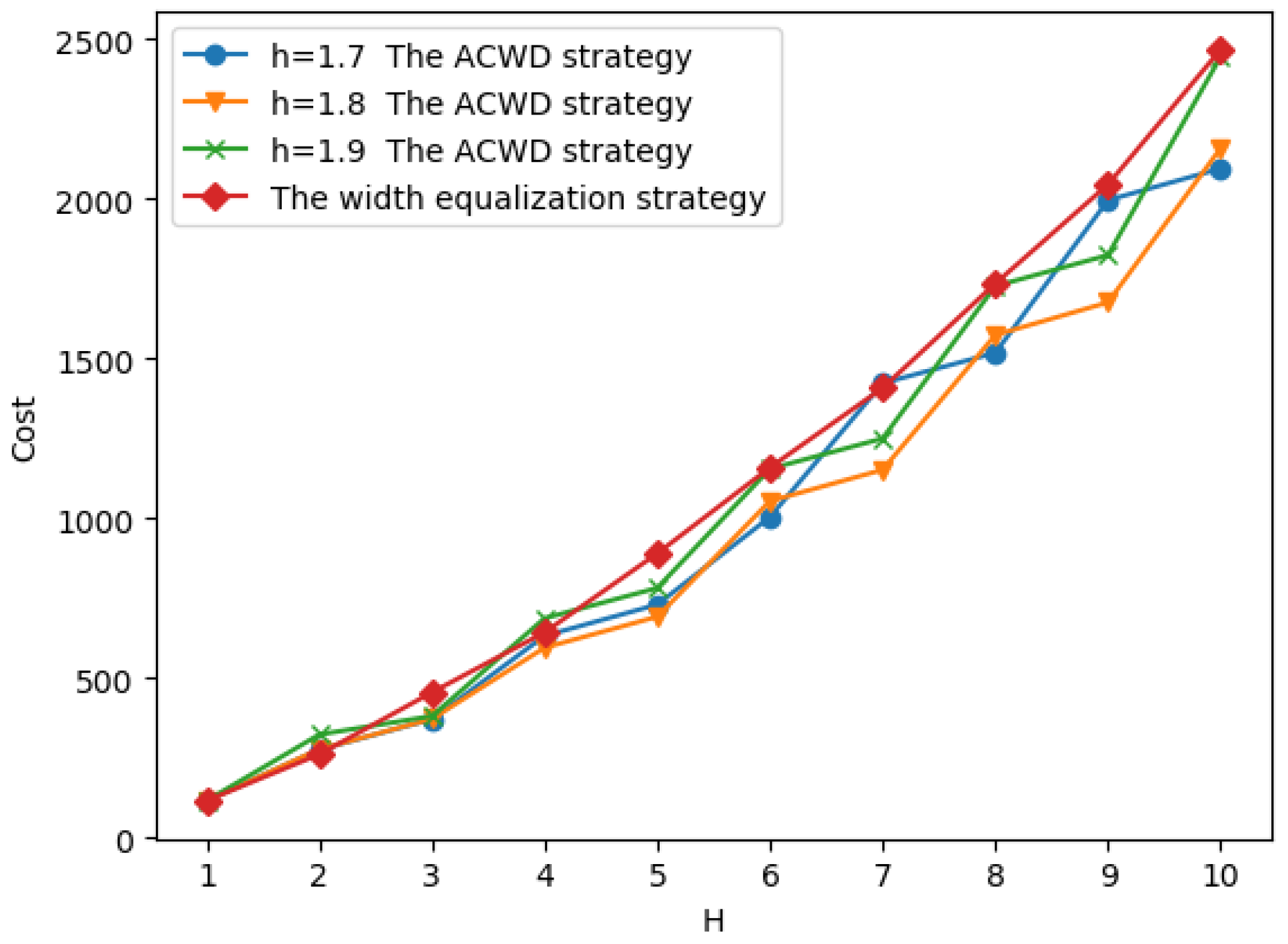
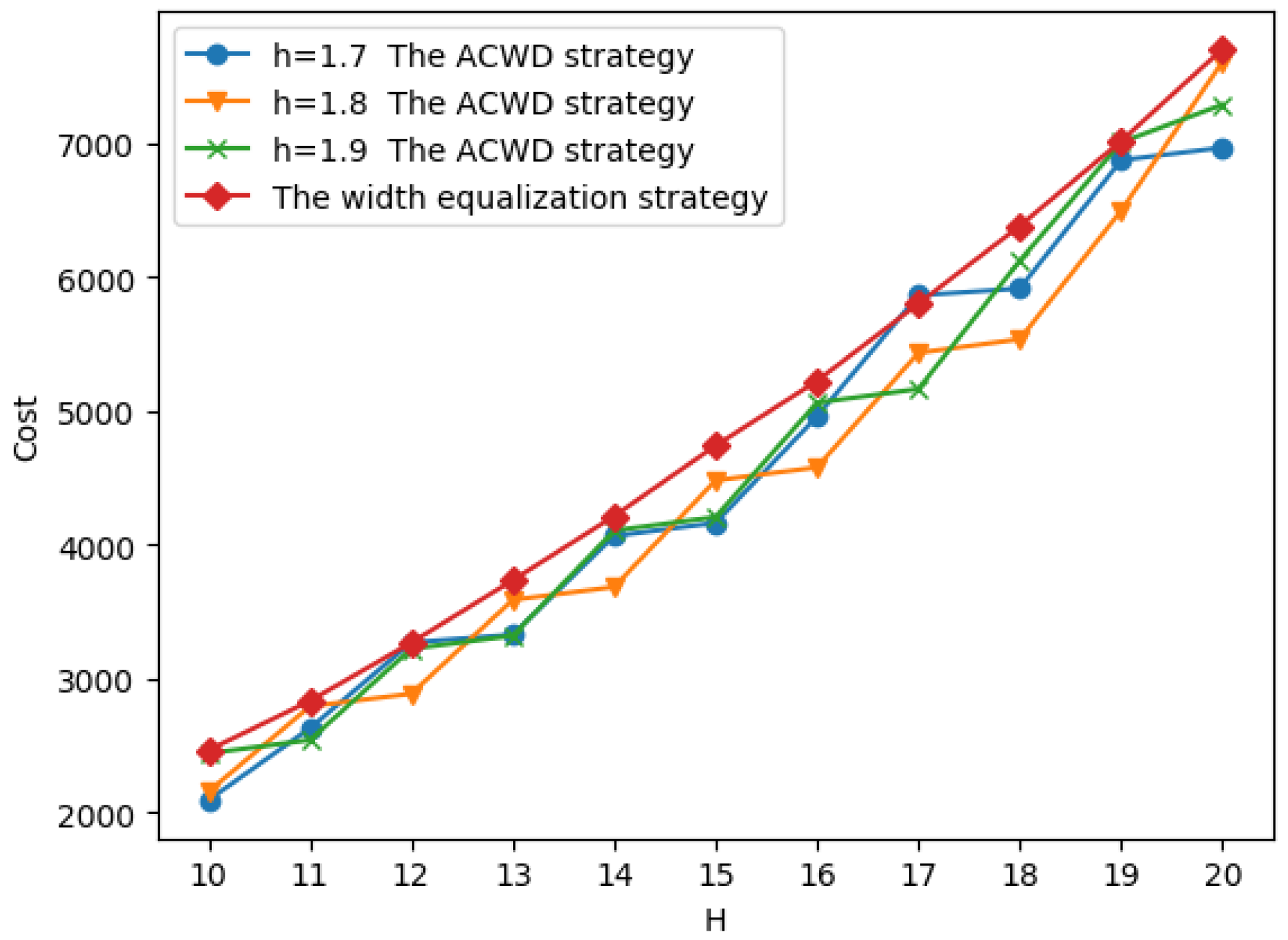
5.3. Experiment Result Comparison of Equal Division vs. Adaptive Division Strategy
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A




- (1)
- When , is odd, is even, we can get:At this point, .
- (2)
- When , may be odd or even, so we continue to categorize.a. If is odd, is even, then we can getAnd then we compare and :Because , so we get the second step, at the same time, , so, we get the last step. We see that in the last step, it contains A, B, C, D, four parts, only need to compare the size of the four parts can judge the size of and . We get , . Therefore, the A and B contain the same number of angles. At the same time, Theorem 2 gets the value of the angle , and we can find that decreases with i increase. Compared to the first angle of A and B, we get , that is . Compared to the last angle of A and B, we get , so . We can also get , so . In summary, .b. When is even, is odd, then we getWe also compare and :Similarly, because of , we get the second step, at the same time, because of , we get the fourth step. Also because of , so A and B contain the same number of angles. Because of , , so . Also because of , so . In summary, .
References
- Liu, B.; Dousse, O.; Wang, J.; Saipulla, A. Strong barrier coverage of wireless sensor networks. In Proceedings of the ACM Interational Symposium on Mobile Ad Hoc NETWORKING and Computing, MOBIHOC 2008, Hong Kong, China, 26–30 May 2008; pp. 411–420. [Google Scholar]
- Yildiz, E.; Akkaya, K.; Sisikoglu, E.; Sir, M.Y. Optimal Camera Placement for Providing Angular Coverage in Wireless Video Sensor Networks. IEEE Trans. Comput. 2014, 63, 1812–1825. [Google Scholar] [CrossRef]
- Ammari, H.M.; Das, S.K. Centralized and Clustered k-Coverage Protocols for Wireless Sensor Networks. IEEE Trans. Comput. 2011, 61, 118–133. [Google Scholar] [CrossRef]
- Wang, B.; Xu, H.; Liu, W.; Liang, H. A Novel Node Placement for Long Belt Coverage in Wireless Networks. IEEE Trans. Comput. 2013, 62, 2341–2353. [Google Scholar] [CrossRef]
- Saipulla, A.; Westphal, C.; Liu, B.; Wang, J. Barrier coverage with line-based deployed mobile sensors. Ad Hoc Netw. 2013, 11, 1381–1391. [Google Scholar] [CrossRef]
- Chen, J.; Wang, B.; Liu, W. Constructing Perimeter Barrier Coverage With Bistatic Radar Sensors. J. Network Comput. Appl. 2015, 57, 129–141. [Google Scholar] [CrossRef]
- Wang, B.; Chen, J.; Liu, W.; Yang, L.T. Minimum Cost Placement of Bistatic Radar Sensors for Belt Barrier Coverage. IEEE Trans. Comput. 2016, 65, 577–588. [Google Scholar] [CrossRef]
- Chang, H.Y.; Kao, L.; Chang, K.P.; Chen, C. Fault-Tolerance and Minimum Cost Placement of Bistatic Radar Sensors for Belt Barrier Coverage. In Proceedings of the International Conference on Network and Information Systems for Computers, Barcelona, Spain, 20–22 December 2017; pp. 1–7. [Google Scholar]
- Ammari, H.M. A Unified Framework for K-Coverage and Data Collection in Heterogeneous Wireless Sensor Networks. J. Parallel Distrib. Comput. 2016, 89, 37–49. [Google Scholar] [CrossRef]
- Rahman, M.O.; Razzaque, M.A.; Hong, C.S. Probabilistic Sensor Deployment in Wireless Sensor Network: A New Approach. In Proceedings of the International Conference on Advanced Communication Technology, Phoenix Park, Korea, 12–14 February 2007; pp. 1419–1422. [Google Scholar]
- Lu, Z.; Li, W.W.; Pan, M. Maximum Lifetime Scheduling for Target Coverage and Data Collection in Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2015, 64, 714–727. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Li, D.; Kwon, S.S.; Tokuta, A.O.; Cobb, J.A. Maximum lifetime dependable barrier-coverage in wireless sensor networks. Ad Hoc Netw. 2016, 36, 296–307. [Google Scholar] [CrossRef]
- Kumar, S.; Lai, T.H.; Arora, A. Barrier Coverage with Wireless Sensors; Springer Inc.: New York, NY, USA, 2007; pp. 817–834. [Google Scholar]
- Chen, A.; Kumar, S.; Lai, T.H. Local Barrier Coverage in Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2010, 9, 491–504. [Google Scholar] [CrossRef]
- Tao, D.; Tang, S.; Zhang, H.; Mao, X.; Ma, H. Strong barrier coverage in directional sensor networks. Comput. Commun. 2012, 35, 895–905. [Google Scholar] [CrossRef]
- Zorbas, D.; Razafindralambo, T. Prolonging network lifetime under probabilistic target coverage in wireless mobile sensor networks. Comput. Commun. 2013, 36, 1039–1053. [Google Scholar] [CrossRef]
- Cheng, C.F.; Tsai, K.T. Distributed Barrier Coverage in Wireless Visual Sensor Networks With β-QoM. IEEE Sens. J. 2012, 12, 1726–1735. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, X.; Ma, H. Exposure-Path Prevention in Directional Sensor Networks Using Sector Model Based Percolation. In Proceedings of the IEEE International Conference on Communications, Dresden, Germany, 14–18 June 2009; pp. 1–5. [Google Scholar]
- Gong, X.; Zhang, J.; Cochran, D.; Xing, K. Barrier coverage in bistatic radar sensor networks: Cassini oval sensing and optimal placement. In Proceedings of the Fourteenth ACM International Symposium on Mobile Ad Hoc Networking and Computing, Bangalore, India, 29 July–1 August 2013; pp. 49–58. [Google Scholar]
- Tang, L.; Gong, X.; Wu, J.; Zhang, J. Target Detection in Bistatic Radar Networks: Node Placement and Repeated Security Game. IEEE Trans. Wirel. Commun. 2013, 12, 1279–1289. [Google Scholar] [CrossRef]
- Kim, H.; Ben-Othman, J. HeteRBar: Construction of Heterogeneous Reinforced Barrier in Wireless Sensor Networks. IEEE Commun. Lett. 2017, 21, 1859–1862. [Google Scholar] [CrossRef]
- Han, R.; Yang, W.; Zhang, L. Achieving Crossed Strong Barrier Coverage in Wireless Sensor Network. Sensors 2018, 18, 534. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Ben-Othman, J.; Cho, S.; Mokdad, L. On Virtual Emotion Barrier in Internet of Things. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar]
- Wang, G.; Cao, G.; La Porta, T. A Bidding Protocol for Deploying Mobile Sensors. In Proceedings of the IEEE International Conference on Network Protocols, Atlanta, GA, USA, 4–7 November 2003; pp. 315–324. [Google Scholar]
- Silvestri, S. MobiBar: Barrier Coverage with Mobile Sensors. In Proceedings of the Global Telecommunications Conference, Kathmandu, Nepal, 5–9 December 2011; pp. 1–6. [Google Scholar]
- Kong, L.; Liu, X.; Li, Z.; Wu, M.Y. Automatic Barrier Coverage Formation with Mobile Sensor Networks. In Proceedings of the IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010; pp. 1–5. [Google Scholar]
- Kim, H.; Oh, H.; Bellavista, P.; Ben-Othman, J. Constructing Event-driven Partial Barriers with Resilience in Wireless Mobile Sensor Networks. J. Netw. Comput. Appl. 2017, 82, 77–92. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, H.; Cao, Q.; Qi, H.; Wang, Z.; Wang, Q. Achieving location error tolerant barrier coverage for wireless sensor networks. Comput. Netw. Int. J. Comput. Telecommun. Netw. 2017, 112, 314–328. [Google Scholar] [CrossRef]
- Willis, N.J.; Griffiths, H.D. Advances in bistatic radar (Willis, N.J. and Griffiths, H.D., Eds.; 2007) [Book Review]. IEEE Aerosp. Electron. Syst. Mag. 2008, 23, 46. [Google Scholar] [CrossRef]
- Liang, J.; Liang, Q. Orthogonal Waveform Design and Performance Analysis in Radar Sensor Networks. In Proceedings of the Military Communications Conference, MILCOM, Washington, DC, USA, 23–25 October 2006; pp. 1–6. [Google Scholar]
- Ly, H.D.; Liang, Q. Collaborative Multi-Target Detection in Radar Sensor Networks. In Proceedings of the IEEE Military Communications Conference, MILCOM 2007, Orlando, FL, USA, 29–31 October 2007; pp. 1–7. [Google Scholar]
- Yang, Q.; He, S.; Chen, J. Energy-efficient area coverage in bistatic radar sensor networks. In Proceedings of the IEEE Global Communications Conference, London, UK, 8–12 June 2015; pp. 280–285. [Google Scholar]

| Symbols | Descriptions |
|---|---|
| The ith BR transmitter (jth receiver) | |
| H | The width of circular barrier coverage |
| The detection threshold of SNR | |
| The detectability of A | |
| The maximum threshold | |
| The distance between T and R | |
| The unit price of BR transmitter(receiver) | |
| The number of BR transmitter(receiver) | |
| q | The number of circles |
| S | The deployment sequence of BR sensors |
| The optimal deployment sequence of BRs | |
| h | The width of circle |
| The inner radius of circle | |
| The outer radius of circle | |
| r | |
| The center angle of a circle | |
| The maximum angle which the sequence can cover | |
| The effective coverage width of | |
| The effective coverage length of | |
| The upper bound of the number of circles |
| Parameter | Value |
|---|---|
| 3 | |
| h | (0, 2.4) |
| q | [, ] |
| 3 | |
| H | [1, 20] |
| 50 | |
| 1, 5, 25 | |
| [1, 50] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Zhao, C.; Ye, T.; Gu, T. Minimum Cost Deployment of Bistatic Radar Sensor for Perimeter Barrier Coverage. Sensors 2019, 19, 225. https://doi.org/10.3390/s19020225
Xu X, Zhao C, Ye T, Gu T. Minimum Cost Deployment of Bistatic Radar Sensor for Perimeter Barrier Coverage. Sensors. 2019; 19(2):225. https://doi.org/10.3390/s19020225
Chicago/Turabian StyleXu, Xianghua, Chengwei Zhao, Tingcong Ye, and Tao Gu. 2019. "Minimum Cost Deployment of Bistatic Radar Sensor for Perimeter Barrier Coverage" Sensors 19, no. 2: 225. https://doi.org/10.3390/s19020225
APA StyleXu, X., Zhao, C., Ye, T., & Gu, T. (2019). Minimum Cost Deployment of Bistatic Radar Sensor for Perimeter Barrier Coverage. Sensors, 19(2), 225. https://doi.org/10.3390/s19020225





