Automated Recognition of Epileptic EEG States Using a Combination of Symlet Wavelet Processing, Gradient Boosting Machine, and Grid Search Optimizer
Abstract
1. Introduction
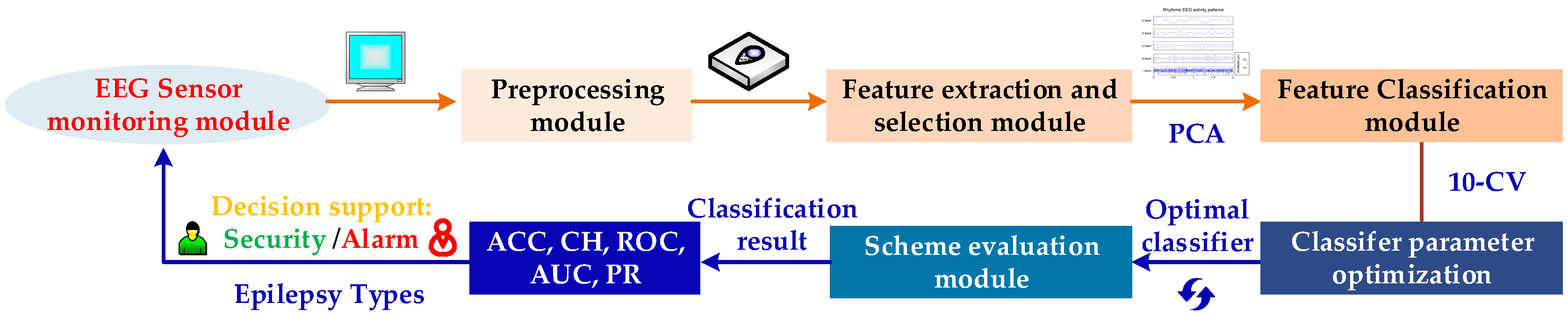
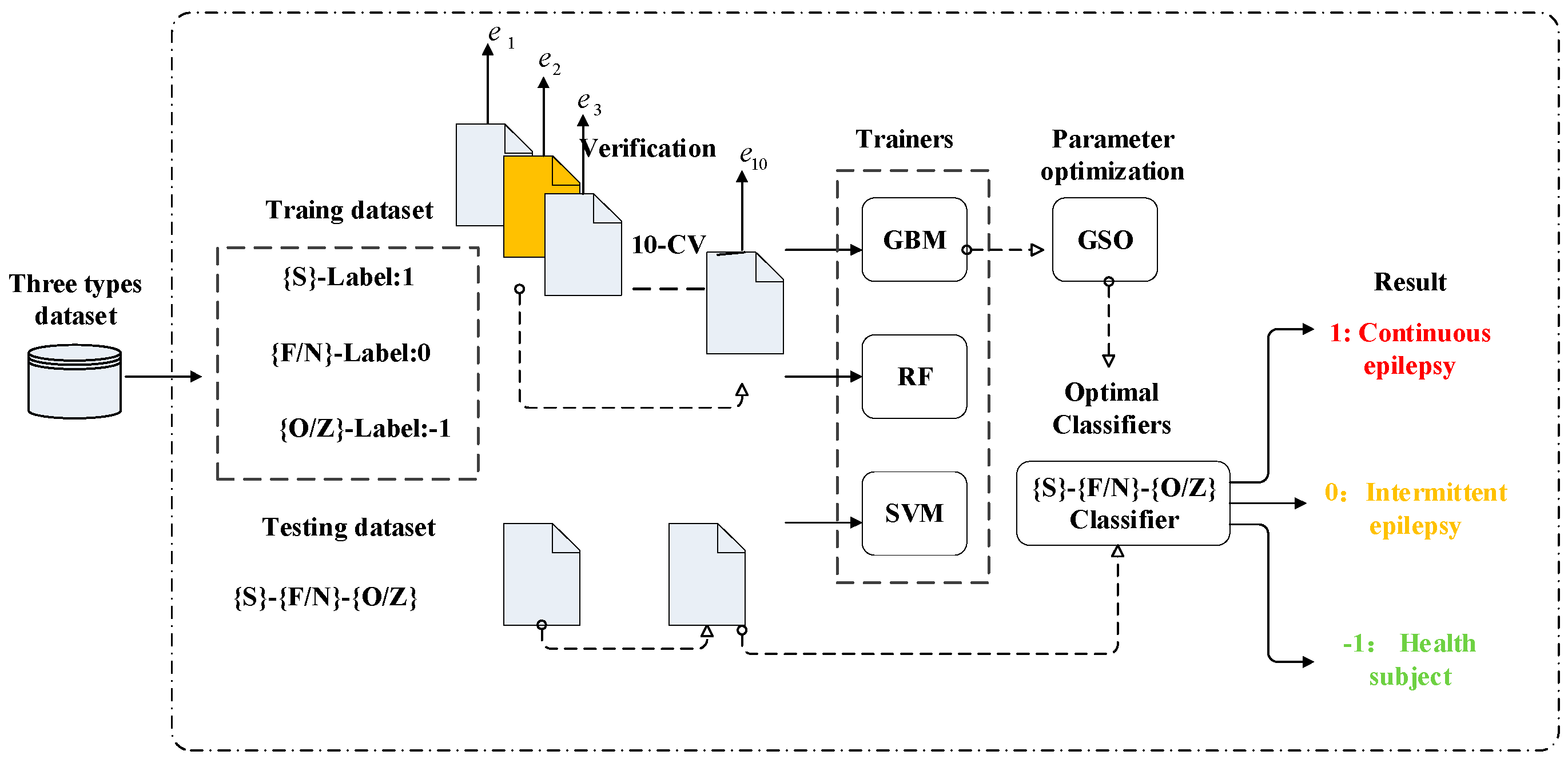
2. Proposed Scheme for Seizure EEG Detection
3. Scheme Implementation
3.1. Real Epilepsy EEG Dataset
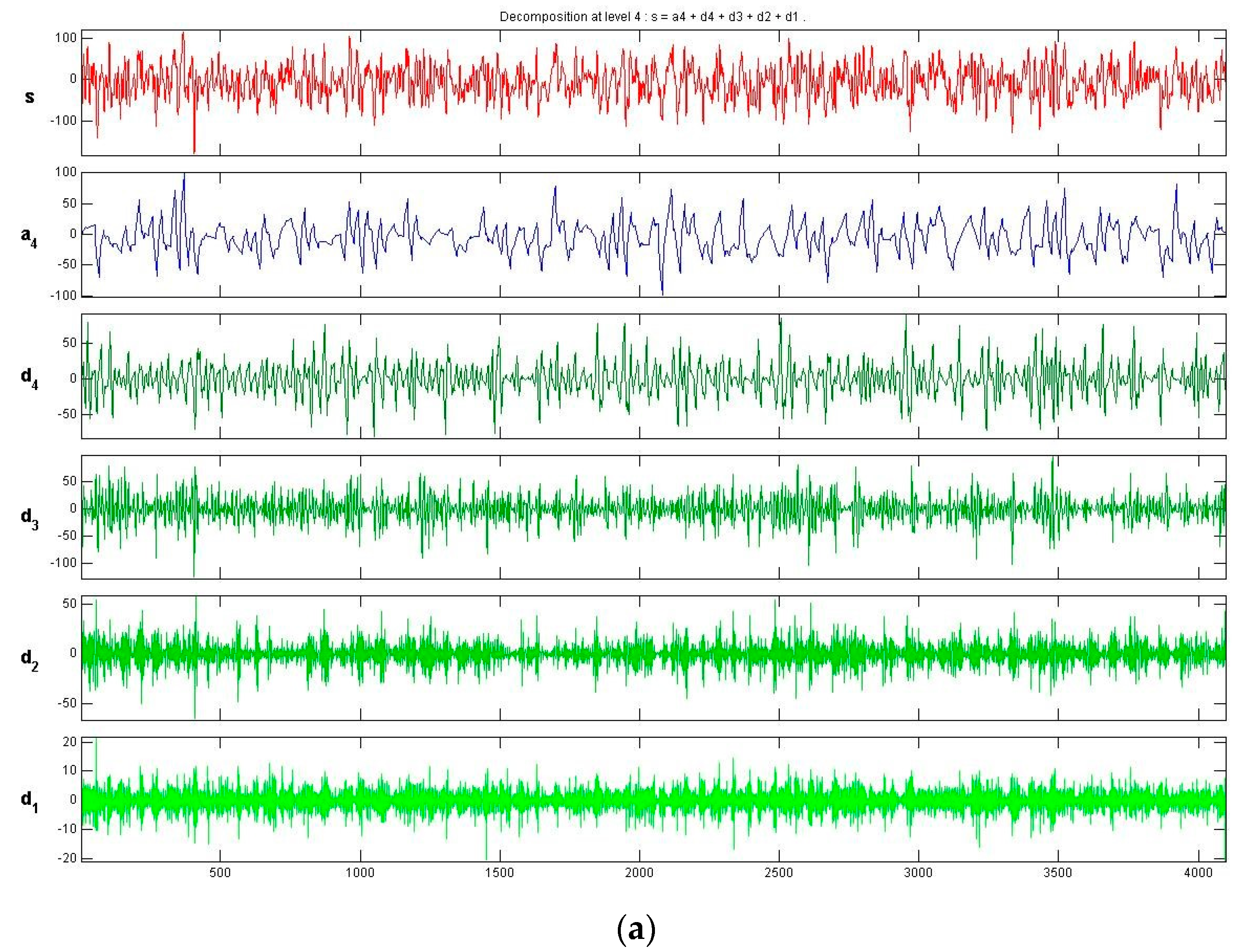
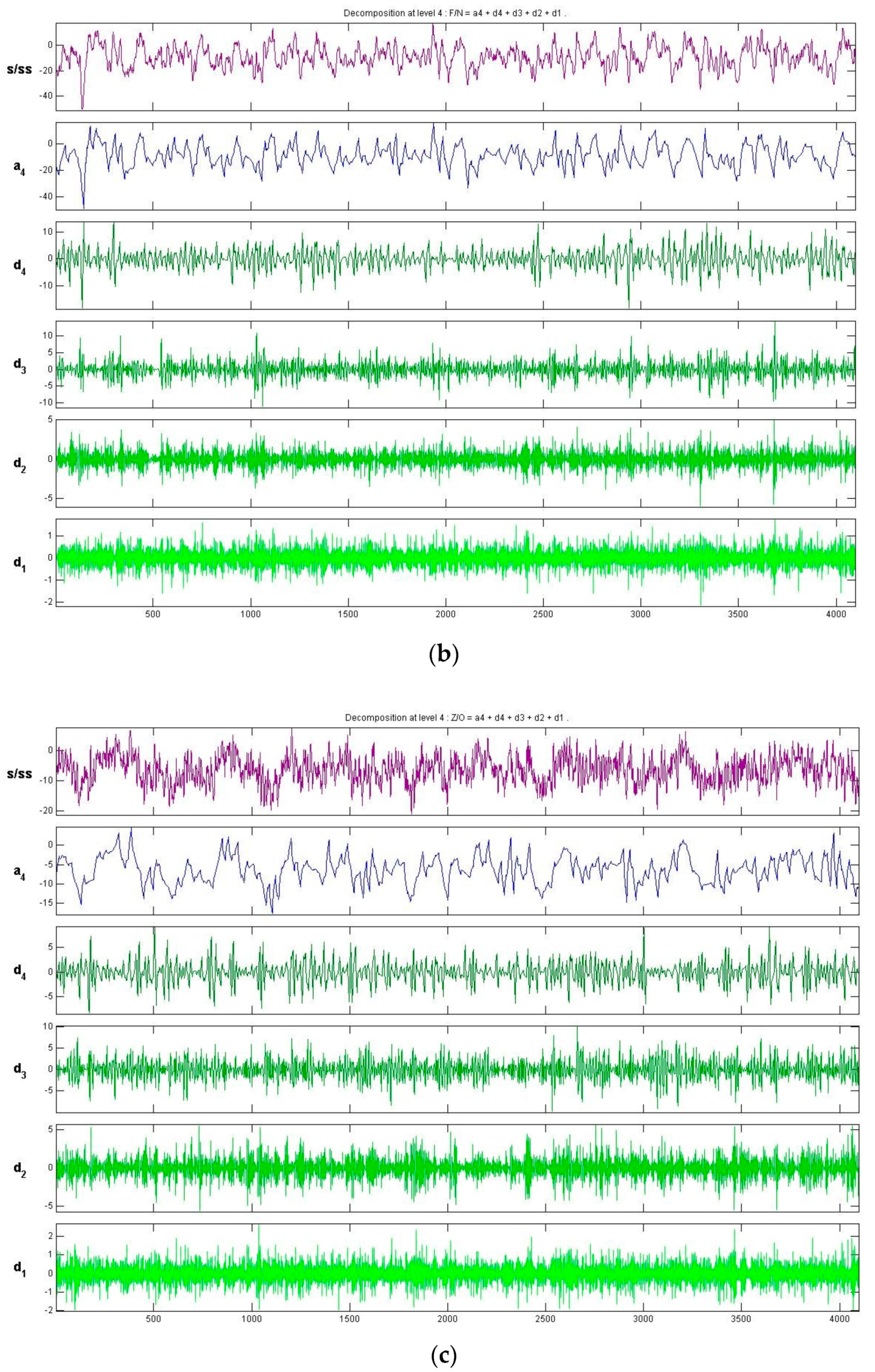
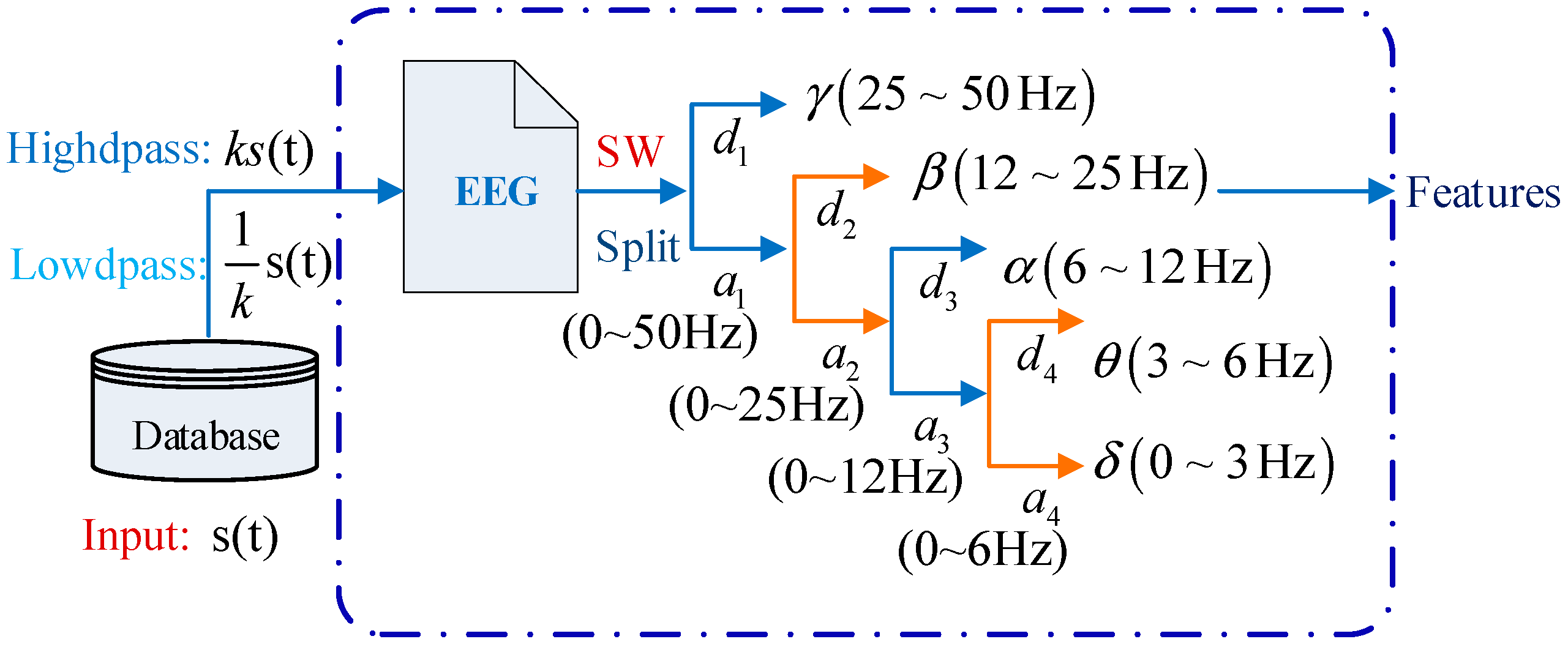
3.2. Feature Extraction Using the Symlet Wavelet
3.3. Classifier Implementation
3.3.1. Gradient Boosting Machine
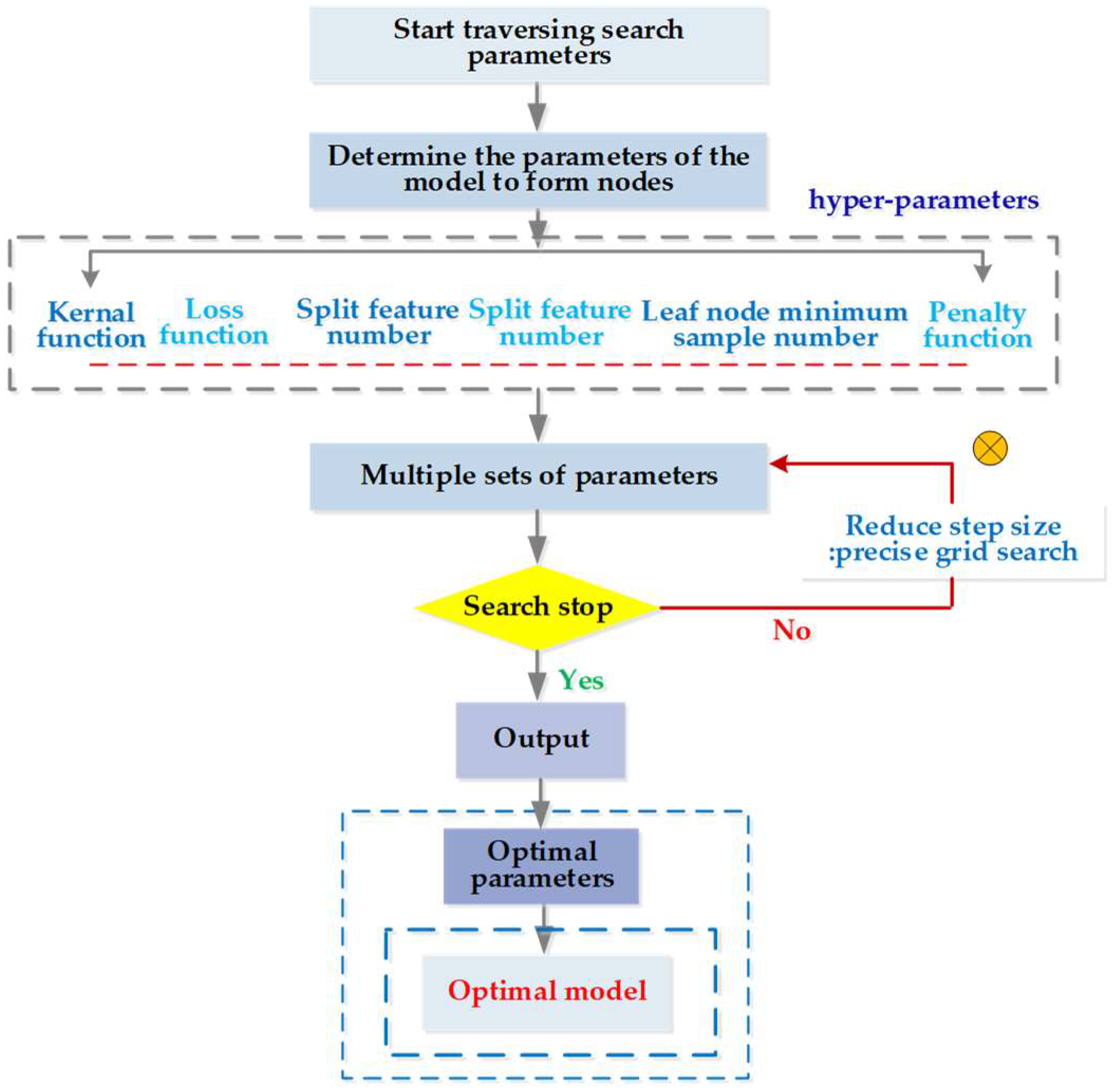
3.3.2. Parameter Optimization and CV
4. Experimental Results and Discussion
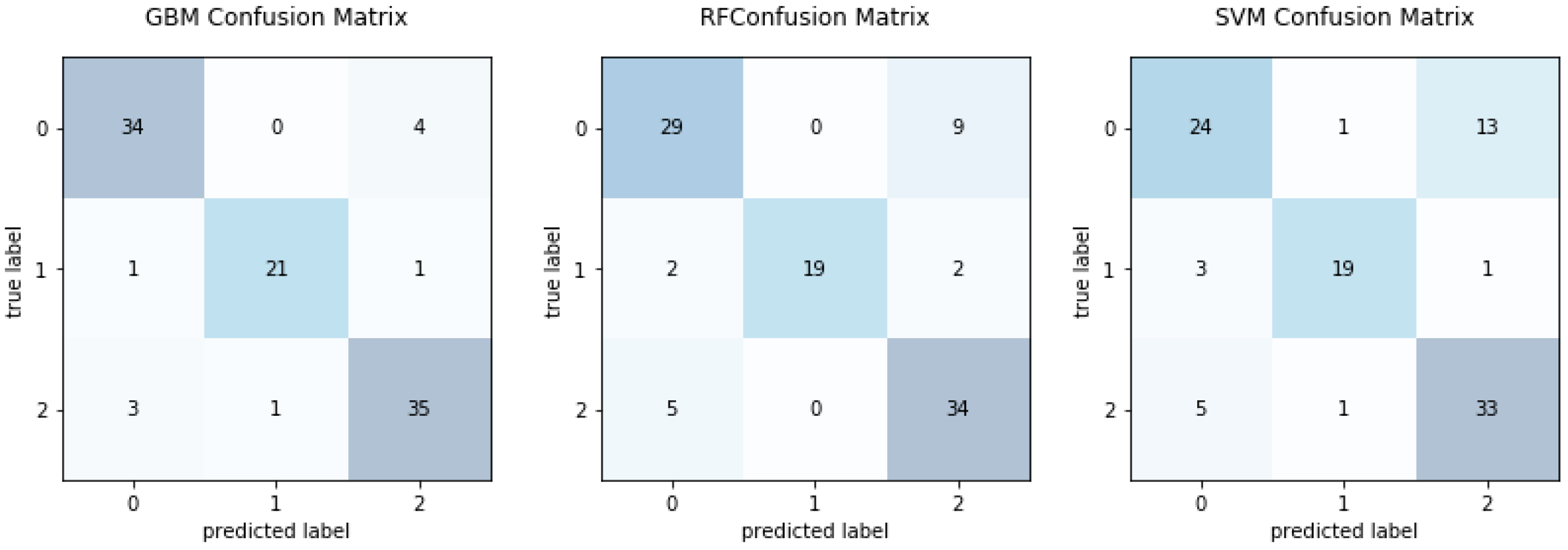
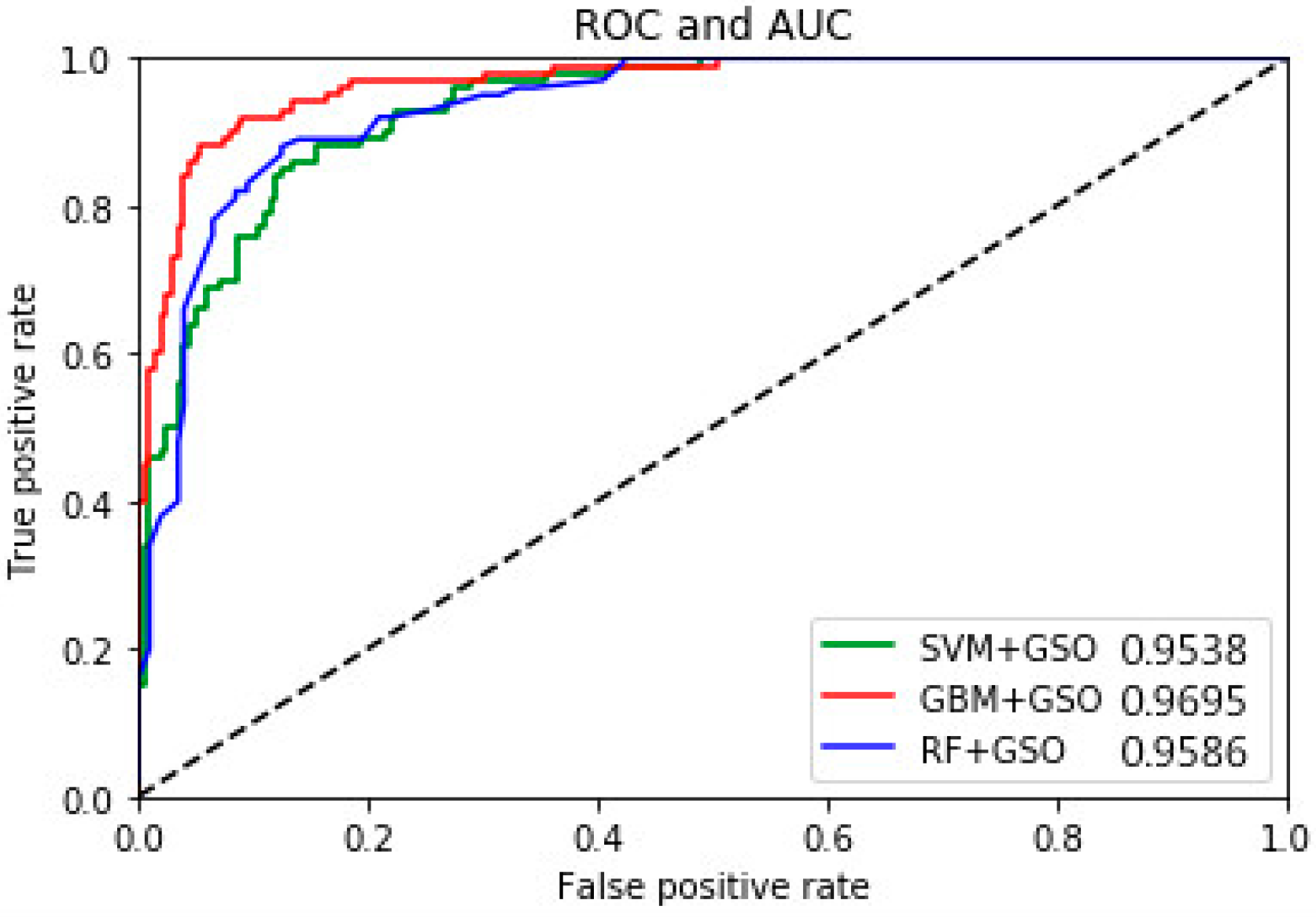
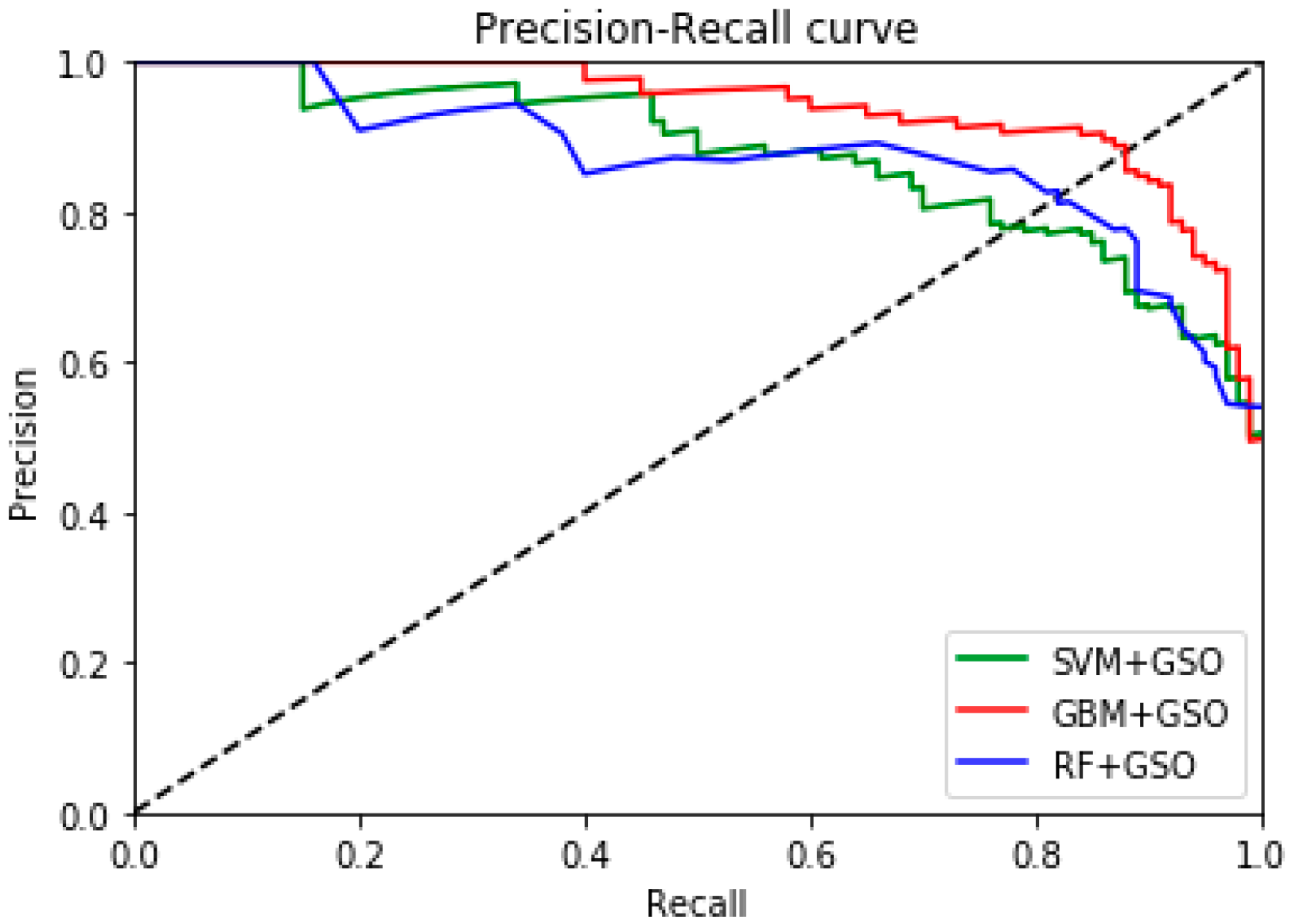
4.1. Multiple Performance Evaluation and Results Comparison
4.2. Comparative Analysis of Classifiers
4.3. Contribution and Advantages of the Proposed System
- (a)
- It not only enables representation of the core time–frequency information of EEGs through wavelet transforms, but also extracts key statistical information. The statistical information of time–frequency features are used as recognition features, and these features reflect the overall characteristics of the data. Simultaneously, a PCA is adopted to reduce the dimensionality of the data. Thus, the proposed method reduces the amount of hardware calculation under the premise of guaranteeing the accuracy of the classifier.
- (b)
- The proposed GBM recognition system was highly parallelized to improve operational efficiency. Another advantage is that it can process large-scale data. However, the recognition system generates many parameters in the course of the training process, and it can be difficult to determine the optimal parameters by manual tuning. This paper proposes a GSO to optimize these parameters and determine the best recognition system filtering parameters by repeatedly varying the step size. To prevent over-fitting in the GBM training process, we adopted a 10-fold CV strategy, which ensures that the optimized system is more robust.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Moshé, S.L.; Perucca, E.; Ryvlin, P.; Tomson, T. Epilepsy: New advances. Lancet 2015, 385, 884–898. [Google Scholar] [CrossRef]
- Leijten, F. Multimodal seizure detection: A review. Epilepsia 2018, 59, 42–47. [Google Scholar] [CrossRef] [PubMed]
- Sukumaran, D.; Enyi, Y.; Sun, S.; Basu, A.; Zhao, D.; Dauwels, J. A low-power, reconfigurable smart sensor system for EEG acquisition and classification. In Proceedings of the 2012 IEEE Asia Pacific Conference on Circuits and Systems, Kaohsiung, Taiwan, 2–5 December 2012; pp. 9–12. [Google Scholar]
- Nijsen, T.M.E.; Aarts, R.M.; Cluitmans, P.J.M.; Griep, P.A.M. Time-Frequency Analysis of Accelerometry Data for Detection of Myoclonic Seizures. IEEE Trans. Inf. Technol. Biomed. 2010, 14, 1197–1203. [Google Scholar] [CrossRef] [PubMed]
- Milosevic, M.; Van de Vel, A.; Bonroy, B.; Ceulemans, B.; Lagae, L.; Vanrumste, B.; Van, H.S. Automated Detection of Tonic-Clonic Seizures using 3D Accelerometry and Surface Electromyography in Pediatric Patients. IEEE J. Biomed. Health Inf. 2016, 20, 1333–1341. [Google Scholar] [CrossRef]
- Chen, H.; Xue, M.; Mei, Z.; Oetomo, S.B.; Chen, W. A Review of Wearable Sensor Systems for Monitoring Body Movements of Neonates. Sensors 2016, 16, 2134. [Google Scholar] [CrossRef] [PubMed]
- Coosemans, J.; Hermans, B.; Puers, R. Integrating wireless ECG monitoring in textiles. In Proceedings of the International Conference on Solid-State Sensors, Actuators and Microsystems, Seoul, Korea, 5–9 June 2005; Digest of Technical Papers, Transducers. Volume 221, pp. 228–232. [Google Scholar]
- Yang, B.; Yu, C.; Dong, Y. Capacitively Coupled Electrocardiogram Measuring System and Noise Reduction by Singular Spectrum Analysis. IEEE Sens. J. 2016, 16, 3802–3810. [Google Scholar] [CrossRef]
- Jung, H.C.; Moon, J.H.; Baek, D.H.; Lee, J.H.; Choi, Y.Y.; Hong, J.S.; Lee, S.H. CNT/PDMS composite flexible dry electrodes for long-term ECG monitoring. IEEE Trans. Biomed. Eng. 2012, 59, 1472–1479. [Google Scholar] [CrossRef]
- Yokus, M.A.; Jur, J.S. Fabric-Based Wearable Dry Electrodes for Body Surface Biopotential Recording. IEEE Trans. Bio-Med. Eng. 2016, 63, 423–430. [Google Scholar] [CrossRef]
- Lei, R.; Jiang, Q.; Chen, K.; Chen, Z.; Pan, C.; Jiang, L. Fabrication of a Micro-Needle Array Electrode by Thermal Drawing for Bio-Signals Monitoring. Sensors 2016, 16, 908. [Google Scholar]
- Spencer, S.S. MRI, SPECT, and PET imaging in epilepsy: Their relative contributions. Epilepsia 1994, 35, S72–S89. [Google Scholar] [CrossRef]
- Szabó, C.Á.; Morgan, L.C.; Karkar, K.M.; Leary, L.D.; Lie, O.V.; Girouard, M.; Cavazos, J.E. Electromyography-based seizure detector: Preliminary results comparing a generalized tonic–clonic seizure detection algorithm to video-EEG recordings. Epilepsia 2015, 56, 1432–1437. [Google Scholar] [CrossRef] [PubMed]
- Gu, Y.; Cleeren, E.; Dan, J.; Claes, K.; Paesschen, W.V.; Huffel, S.V.; Hunyadi, B. Comparison between Scalp EEG and Behind-the-Ear EEG for Development of a Wearable Seizure Detection System for Patients with Focal Epilepsy. Sensors 2018, 18, 29. [Google Scholar] [CrossRef] [PubMed]
- Gotman, J.; Gloor, P. Automatic recognition and quantification of interictal epileptic activity in the human scalp EEG. Electroencephalogr. Clin. Neurophysiol. 1976, 41, 513–529. [Google Scholar] [CrossRef]
- Tzallas, A.T.; Tsipouras, M.G.; Fotiadis, D.I. Epileptic seizure detection in EEGs using time-frequency analysis. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 703–710. [Google Scholar] [CrossRef] [PubMed]
- Whitmer, D.; Worrell, G.; Stead, M.; Lee, I.K.; Makeig, S. Utility of Independent Component Analysis for Interpretation of Intracranial EEG. Front. Hum. Neurosci. 2010, 4, 184. [Google Scholar] [CrossRef] [PubMed]
- Subasi, A.; Ismail Gursoy, M. EEG signal classification using PCA, ICA, LDA and support vector machines. Expert Syst. Appl. 2010, 37, 8659–8666. [Google Scholar] [CrossRef]
- Bajaj, V.; Pachori, R.B. Classification of seizure and non-seizure EEG signals using empirical mode decomposition. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 1135–1142. [Google Scholar] [CrossRef]
- Kovacs, P.; Samiee, K.; Gabbouj, M. On application of rational Discrete Short Time Fourier Transform in epileptic seizure classification. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 5839–5843. [Google Scholar]
- Wang, X.; Gong, G.; Li, N. Multimodal fusion of EEG and fMRI for epilepsy detection. Int. J. Model. Simul. Sci. Comput. 2018, 9, 1850010. [Google Scholar] [CrossRef]
- Boashash, B.; Boubchir, L.; Azemi, G. Time-frequency signal and image processing of non-stationary signals with application to the classification of newborn EEG abnormalities. In Proceedings of the IEEE International Symposium on Signal Processing and Information Technology, Bilbao, Spain, 14–17 December 2011; pp. 120–129. [Google Scholar]
- Boashash, B.; Ouelha, S. Automatic signal abnormality detection using time-frequency features and machine learning. Knowl.-Based. Syst. 2016, 106, 38–50. [Google Scholar] [CrossRef]
- Adeli, H.; Zhou, Z.N. Analysis of EEG records in an epileptic patient using wavelet transform. J. Neurosci. Methods 2003, 123, 69–87. [Google Scholar] [CrossRef]
- Song, J.; Park, I.C. Pipelined Discrete Wavelet Transform Architecture Scanning Dual Lines. IEEE Trans. Circuits Syst. Express Briefs 2009, 56, 916–920. [Google Scholar] [CrossRef]
- Qinghua, H.E.; Peng, C.; Baoming, W.U.; Wang, H.E.; Zhu, L. Vep Signal Extraction Using Wavelet in Brain-Computer Interface Research. Wavelet Anal. Appl. 2003, 2, 937–942. [Google Scholar]
- Li, D.; Xie, Q.; Jin, Q.; Hirasawa, K. A sequential method using multiplicative extreme learning machine for epileptic seizure detection. Neurocomputing 2016, 214, 692–707. [Google Scholar] [CrossRef]
- Swami, P.; Gandhi, T.K.; Panigrahi, B.K.; Bhatia, M.; Santhosh, J.; Anand, S. A comparative account of modelling seizure detection system using wavelet techniques. Int. J. Syst. Sci. Oper. Logist. 2016, 4, 41–52. [Google Scholar] [CrossRef]
- Sharma, M.; Pachori, R.B.; Acharya, U.R. A new approach to characterize epileptic seizures using analytic time-frequency flexible wavelet transform and fractal dimension. Pattern Recognit. Lett. 2017, 94, 172–179. [Google Scholar] [CrossRef]
- He, Q.; Wu, B.; Wang, H.; Zhu, L. VEP Feature Extraction and Classification for Brain-Computer Interface. In Proceedings of the 8th International Conference on Signal Processing, Guilin, China, 16–20 November 2006. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A Training Algorithm for Optimal Margin Classiiers. In Proceedings of the Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Fu, K.; Qu, J.; Chai, Y.; Zou, T. Hilbert marginal spectrum analysis for automatic seizure detection in EEG signals. Biomed. Signal Process. Control 2015, 18, 179–185. [Google Scholar] [CrossRef]
- Brabanter, K.D.; Karsmakers, P.; Ojeda, F.; Alzate, C.; Brabanter, J.D.; Pelckmans, K.; Moor, B.D.; Vandewalle, J.; Suykens, J.A.K. LS-SVMlab Toolbox User’s Guide: Version 1.7; Ku Leuven Leuven: Leuven, Belgium, 2010. [Google Scholar]
- Liu, Y.C.; Lin, C.C.K.; Jing-Jane, T.; Sun, Y.N. Model-Based Spike Detection of Epileptic EEG Data. Sensors 2013, 13, 12536–12547. [Google Scholar] [CrossRef]
- Isa, R.M.; Pasya, I.; Taib, M.N.; Jahidin, A.H.; Omar, W.R.W.; Fuad, N.; Norhazman, H. EEG brainwave behaviour due to RF Exposure using kNN classification. In Proceedings of the IEEE International Conference on System Engineering and Technology, Shah Alam, Malaysia, 19–20 August 2013; pp. 385–388. [Google Scholar]
- Chai, R.; Tran, Y.; Naik, G.R.; Nguyen, T.N.; Ling, S.H.; Craig, A.; Nguyen, H.T.; Chai, R.; Tran, Y.; Naik, G.R. Classification of EEG based-mental fatigue using principal component analysis and Bayesian neural network. In Proceedings of the Engineering in Medicine and Biology Society, Orlando, FL, USA, 16–20 August 2016; p. 4654. [Google Scholar]
- Wang, Y.; Li, Z.; Feng, L.; Bai, H.; Wang, C. Hardware design of multiclass SVM classification for epilepsy and epileptic seizure detection. IET Circuits Devices Syst. 2018, 12, 108–115. [Google Scholar] [CrossRef]
- Jouny, C.C.; Franaszczuk, P.J.; Bergey, G.K. Signal complexity and synchrony of epileptic seizures: Is there an identifiable preictal period? Clin. Neurophysiol. 2005, 116, 552–558. [Google Scholar] [CrossRef]
- Brinkmann, B.H.; Patterson, E.E.; Vite, C.; Vasoli, V.M.; Crepeau, D.; Stead, M.; Howbert, J.J.; Cherkassky, V.; Wagenaar, J.B.; Litt, B.; et al. Forecasting Seizures Using Intracranial EEG Measures and SVM in Naturally Occurring Canine Epilepsy. PLoS ONE 2015, 10, e0133900. [Google Scholar] [CrossRef]
- Brinkmann, B.H.; Joost, W.; Drew, A.; Phillip, A.; Bosshard, S.C.; Chen, M.; Tieng, Q.M.; He, J.; Muñoz-Almaraz, F.J.; Paloma, B.R. Crowdsourcing reproducible seizure forecasting in human and canine epilepsy. Brain 2016, 139, 1713–1722. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, R.G.; Lehnertz, K.; Mormann, F.; Rieke, C.; David, P.; Elger, C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E 2001, 64, 061907. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, R.G.; Widman, G.; Lehnertz, K.; Rieke, C.; David, P.; Elger, C.E. The epileptic process as nonlinear deterministic dynamics in a stochastic environment: An evaluation on mesial temporal lobe epilepsy. Epilepsy Res. 2001, 44, 129–140. [Google Scholar] [CrossRef]
- Tang, Y.; Durand, D. A tunable support vector machine assembly classifier for epileptic seizure detection. Expert Syst. Appl. 2012, 39, 3925–3938. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Jiang, T.; Shen, A.; Li, W.; Wang, X.; Hu, J. A background elimination method based on wavelet transform for Raman spectra. Chemom. Intell. Lab. Syst. 2007, 85, 94–101. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Zabihi, M.; Ince, D. Automated patient-specific classification of long-term Electroencephalography. J. Biomed. Inform. 2014, 49, 16–31. [Google Scholar] [CrossRef] [PubMed]
- Hefron, R.; Borghetti, B.; Schubert, C.K.; Christensen, J.; Estepp, J. Cross-Participant EEG-Based Assessment of Cognitive Workload Using Multi-Path Convolutional Recurrent Neural Networks. Sensors 2018, 18, 1339. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Hoffmann, U.; Garcia, G.; Vesin, J.; Diserens, K.; Ebrahimi, T. A Boosting Approach to P300 Detection with Application to Brain-Computer Interfaces. In Proceedings of the IEEE EMBS Conference on Neural Engineering, Arlington, VA, USA, 16–19 March 2005. [Google Scholar]
- Yan, A.; Zhou, W.; Yuan, Q.; Yuan, S.; Wu, Q.; Zhao, X.; Wang, J. Automatic seizure detection using Stockwell transform and boosting algorithm for long-term EEG. Epilepsy Behav. 2015, 45, 8–14. [Google Scholar] [CrossRef]
- Guo, L.; Rivero, D.; Dorado, J.; Rabuñal, J.R.; Pazos, A. Automatic epileptic seizure detection in EEGs based on line length feature and artificial neural networks. J. Neurosci. Methods 2010, 191, 101–109. [Google Scholar] [CrossRef]
- Nicolaou, N.; Georgiou, J. Detection of epileptic electroencephalogram based on Permutation Entropy and Support Vector Machines. Expert Syst. Appl. 2012, 39, 202–209. [Google Scholar] [CrossRef]
- Samiee, K.; Kovács, P.; Gabbouj, M. Epileptic Seizure Classification of EEG Time-Series Using Rational Discrete Short-Time Fourier Transform. IEEE Trans. Biomed. Eng. 2015, 62, 541–552. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, T.; Panigrahi, B.K.; Anand, S. A Comparative Study of Wavelet Families for Eeg Signal Classification. Neurocomputing 2011, 74, 3051–3057. [Google Scholar] [CrossRef]
- Swami, P.; Gandhi, T.K.; Panigrahi, B.K.; Tripathi, M.; Anand, S. A novel robust diagnostic model to detect seizures in electroencephalography. Expert Syst. Appl. 2016, 56, 116–130. [Google Scholar] [CrossRef]
- Li, P.; Li, K.; Liu, C.; Zheng, D.; Li, Z.M.; Liu, C. Detection of Coupling in Short Physiological Series by a Joint Distribution Entropy Method. IEEE Trans. Bio-Med. Eng. 2016, 63, 2231–2242. [Google Scholar] [CrossRef] [PubMed]
- Alam, S.M.; Bhuiyan, M.I. Detection of seizure and epilepsy using higher order statistics in the EMD domain. IEEE J. Biomed. Health Inf. 2013, 17, 312–318. [Google Scholar] [CrossRef] [PubMed]
- Plöchl, M.; Ossandón, J.P.; König, P. Combining EEG and eye tracking: Identification, characterization, and correction of eye movement artifacts in electroencephalographic data. Front. Hum. Neurosci. 2012, 6, 278. [Google Scholar] [CrossRef] [PubMed]
- Saini, R.; Kaur, B.; Singh, P.; Kumar, P.; Roy, P.P.; Raman, B.; Singh, D. Don’t Just Sign Use Brain Too: A Novel Multimodal Approach for User Identification and Verification. Inf. Sci. 2017, 430, 163–178. [Google Scholar] [CrossRef]
- Liu, N.H.; Chiang, C.Y.; Chu, H.C. Recognizing the degree of human attention using EEG signals from mobile sensors. Sensors 2013, 13, 10273–10286. [Google Scholar] [CrossRef]
- Archer, K.J.; Kimes, R.V. Empirical characterization of random forest variable importance measures. Comput. Stat. Data Anal. 2008, 52, 2249–2260. [Google Scholar] [CrossRef]
- Li, G.; Chung, W.Y. Estimation of Eye Closure Degree Using EEG Sensors and Its Application in Driver Drowsiness Detection. Sensors 2014, 14, 17491–17515. [Google Scholar] [CrossRef] [PubMed]
- Chiang, J.; Ward, R.K. Energy-Efficient Data Reduction Techniques for Wireless Seizure Detection Systems. Sensors 2014, 14, 2036–2051. [Google Scholar] [CrossRef] [PubMed]
| Data Sources | Parameter Description | Dataset Category | Subject Condition | Epileptogenic Foci | Electrode Collection Area | Number of Samples |
|---|---|---|---|---|---|---|
| Bonn University | 5 groups 173.6 Hz. 23.6 s. 4096 data points. | {OZ} | Healthy volunteers | Scalp surface | All brain areas | 200 |
| {FN} | Intermittent epilepsy | Intracranial site | Lesion outside inside area | 200 | ||
| {S} | Continuous ictal epilepsy | Intracranial site | Intra-lesional area | 100 |
| Datasets | {FN} | {OZ} | {S} |
|---|---|---|---|
| Mean | −5.94 | −6.31 | −4.74 |
| Number of cases | 4097 | 4097 | 4097 |
| Standard deviation | 13.10 | 4.56 | 38.55 |
| ALGORITHM: Gradient Boosting Machine (GBM) |
| Data: observed data features {T-F features, statistical features } |
| Process: Calculate loss function and base-learner classifier to number of iterations M. |
|
| end for; |
| return; |
| Test/Real Type | {OZ} | {FN} | {S} | Sensitivity (SEN) | Specificity (SPE) | Accuracy (ACC) |
|---|---|---|---|---|---|---|
| {OZ} | ||||||
| {FN} | ||||||
| {S} |
| Authors | Techniques | 10-Fold CV | Dataset | ACC (%) | AUC | CM/PRC |
|---|---|---|---|---|---|---|
| Guo et al. (2010) [55] | DWT and line length, ANN | No | {Z}-{S} {FNOZ}-{S} | 100 97.7 | No | No |
| Gandhi et al. (2011) [53] | DWT, energy and std, SVM, NN | Yes | {FNOZ}-{S} | 95.4 | No | No |
| Nicolaou et al. (2012) [51] | Permutation entropy, SVM | No | {Z}-{S} {O}-{S} {N}-{S} {F}-{S} {FNOZ}-{S} | 93.5 82.8 88.0 79.94 86.1 | No | No |
| Shafiul Alam and Bhuiyan et al. (2013) [56] | EMD, higher order moments, ANN | No | {O}-{S} {F}-{S} {FN}-{OZ}-{S} | 100 100 80 | No | No |
| Samiee et al. (2015) [52] | STFT Spectral coefficients with their statistical, values, Bayes, LR, SVM, KNN, and ANN | No | {Z}-{S} {O}-{S} {N}-{S} {F}-{S} {FNOZ}-{S} | 99.8 99.3 98.5 94.9 98.1 | No | No |
| Swami et al. (2016) [53] | DTCWT, energy and std, Shannon entropy features, RNN | Yes | {Z}-{S} {O}-{S} {N}-{S} {F}-{S} {OZ}-{S} {NF}-{S} {FNOZ}-{S} | 100 98.89 98.72 93.3 99.1 95.1 95.2 | No | No |
| Li et al. (2016) [54] | Distribution entropy and sample entropy Statistical analysis | No | for sample entropy distribution entropy for short length data | mean | Yes 2-class classification 0.93–0.97 0.66–0.87 | No |
| Manish et al. (2017) [29] | ATFFWT and FD, LS-SVM | Yes | {Z}-{S} {O}-{S} {N}-{S} {F}-{S} {OZ}-{S} {NF}-{S} {OZ}-{NF} {FNOZ}-{S} | 100 100 99 98.5 100 98.6 92.5 99.2 | No | No |
| Wang et al. (2017) [37] | DWT, SVM | No | {FN}-{OZ}-{S} | 93.9 | No | No |
| This work | Symlets wavelets, statistical mean energy std and PCA, GBM-GSO, RF, SVM | Yes | {Z}-{S} {O}-{S} {N}-{S} {F}-{S} {OZ}-{S} {NF}-{S} {OZ}-{NF} {FNOZ}-{S} {FN}-{OZ}-{S} | 100 100 98.4 98.1 100 98.1 93.2 98.4 96.5 | Yes 3-class classification GBM –GSO 0.9695 RF –GSO 0.9586 SVM –GSO 0.9538 | Yes |
| GBM | SVM | RF | |
|---|---|---|---|
| Multi-class classification ability | ★★★ | ★ | ★★★ |
| Sensitivity of parameter selection | ★ | ★★ | ★★ |
| Generalization ability | ★★★ | ★★ | ★★ |
| Strong: ★★★ Moderate: ★★ Weak: ★ | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Gong, G.; Li, N. Automated Recognition of Epileptic EEG States Using a Combination of Symlet Wavelet Processing, Gradient Boosting Machine, and Grid Search Optimizer. Sensors 2019, 19, 219. https://doi.org/10.3390/s19020219
Wang X, Gong G, Li N. Automated Recognition of Epileptic EEG States Using a Combination of Symlet Wavelet Processing, Gradient Boosting Machine, and Grid Search Optimizer. Sensors. 2019; 19(2):219. https://doi.org/10.3390/s19020219
Chicago/Turabian StyleWang, Xiashuang, Guanghong Gong, and Ni Li. 2019. "Automated Recognition of Epileptic EEG States Using a Combination of Symlet Wavelet Processing, Gradient Boosting Machine, and Grid Search Optimizer" Sensors 19, no. 2: 219. https://doi.org/10.3390/s19020219
APA StyleWang, X., Gong, G., & Li, N. (2019). Automated Recognition of Epileptic EEG States Using a Combination of Symlet Wavelet Processing, Gradient Boosting Machine, and Grid Search Optimizer. Sensors, 19(2), 219. https://doi.org/10.3390/s19020219





