Performance Analysis of Positioning Solution Using Low-Cost Single-Frequency U-Blox Receiver Based on Baseline Length Constraint
Abstract
:1. Introduction
2. Methods
3. Results
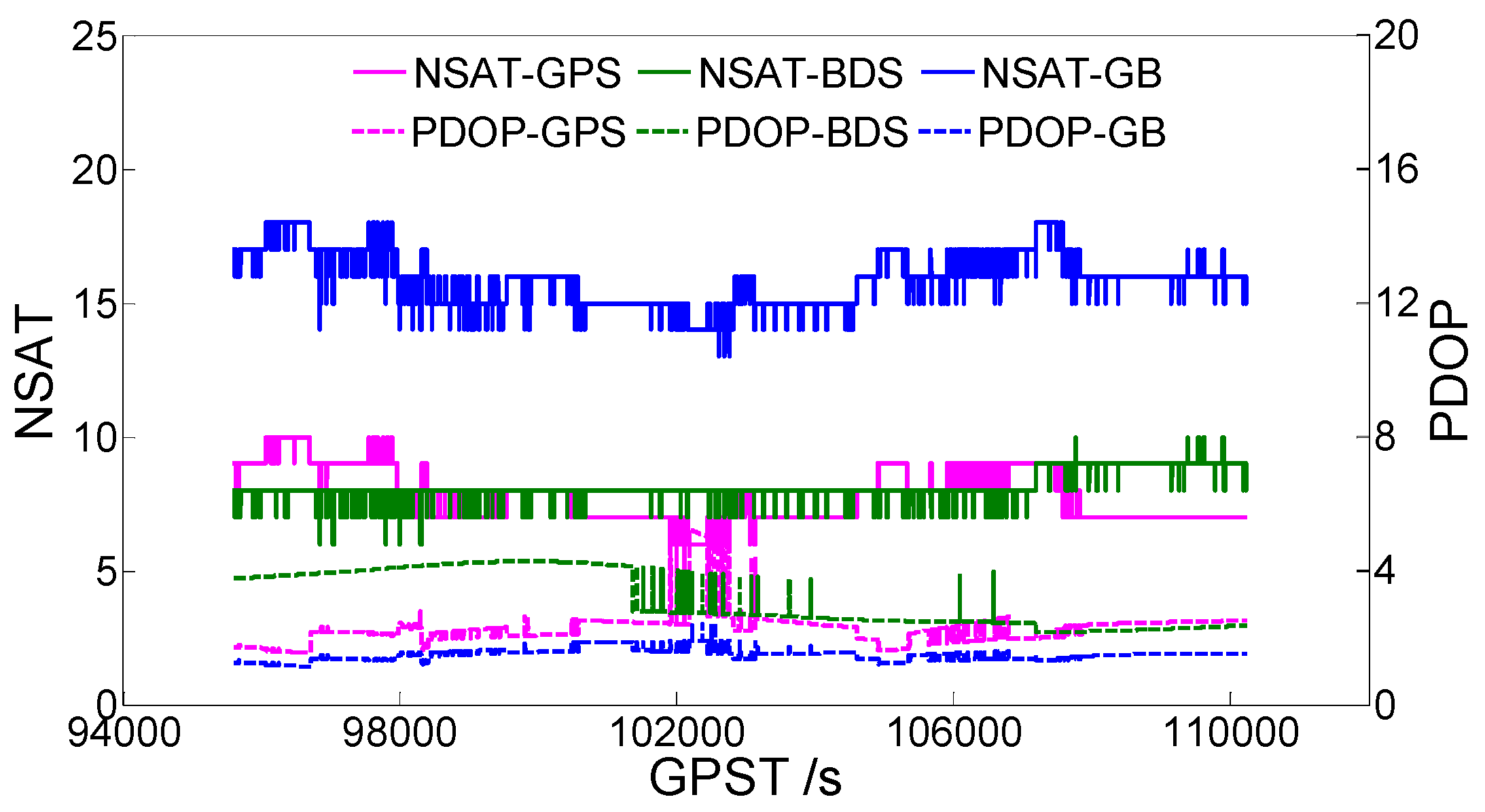
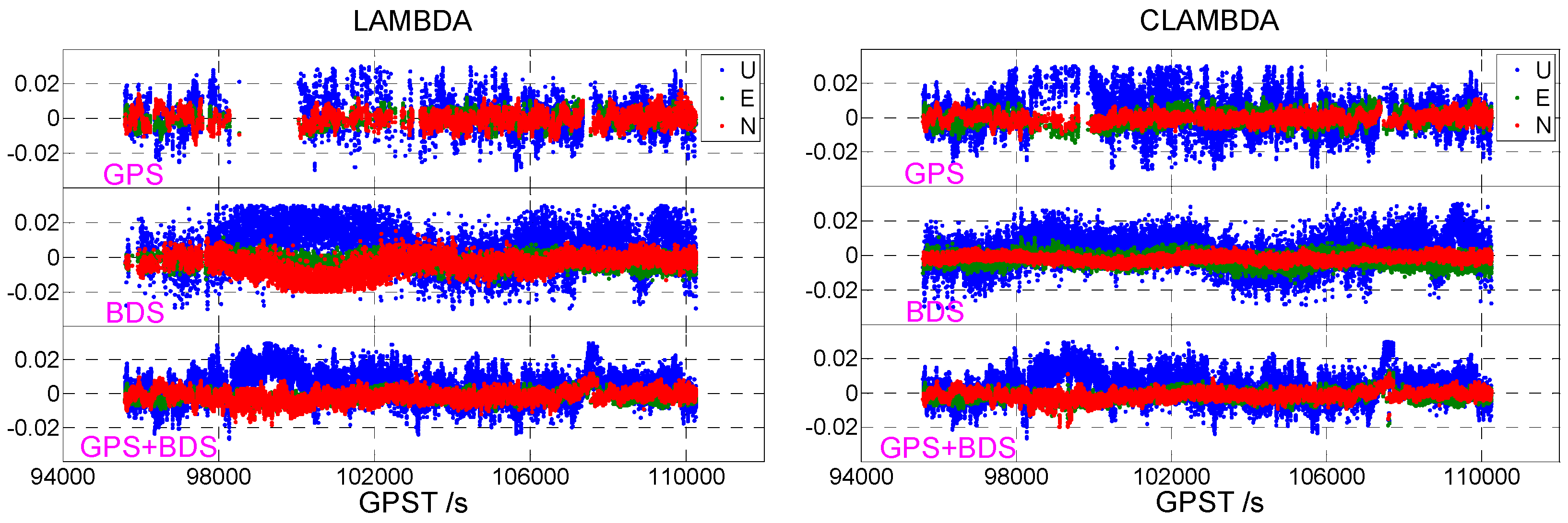
3.1. Static Data 1
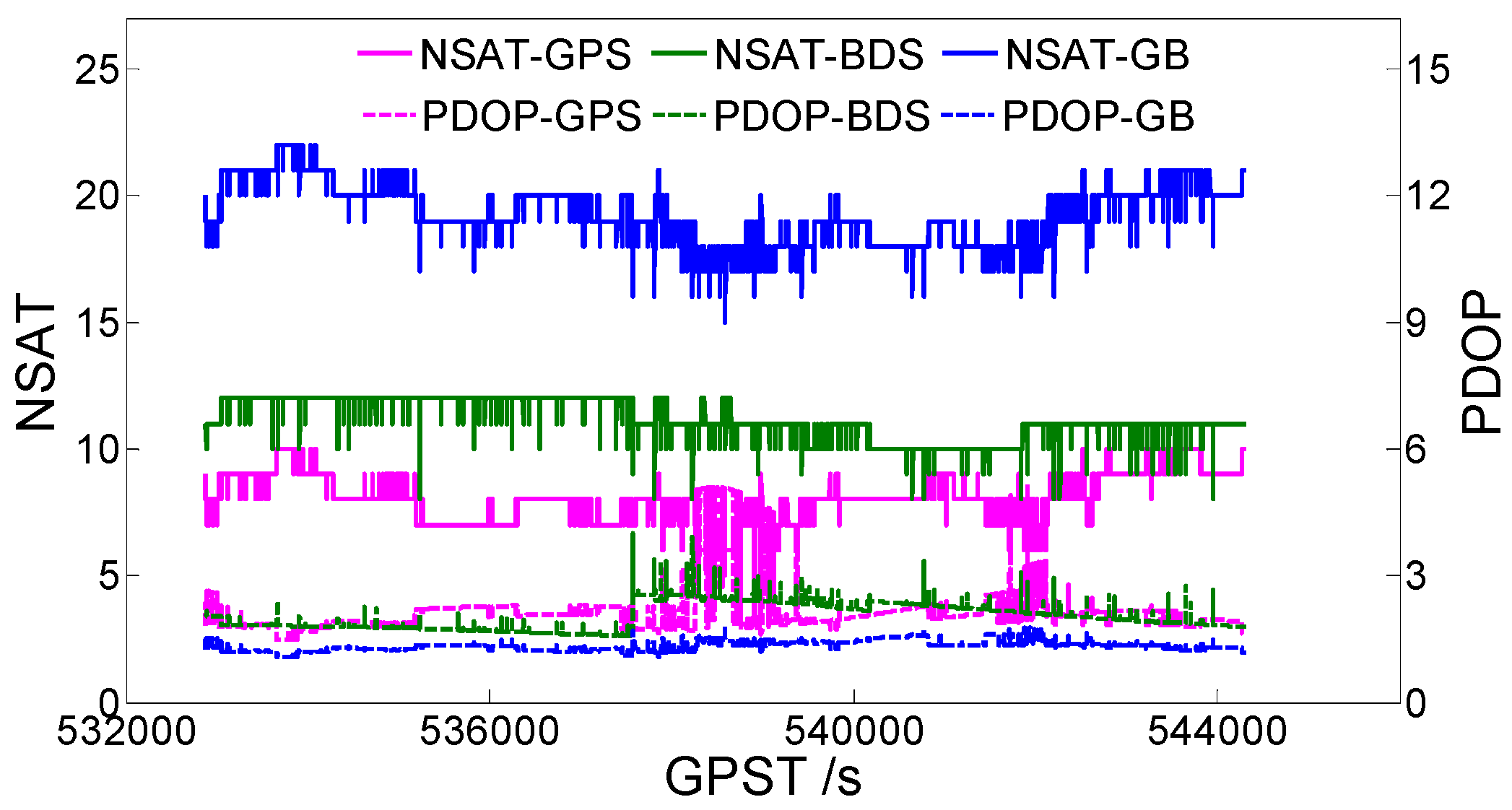
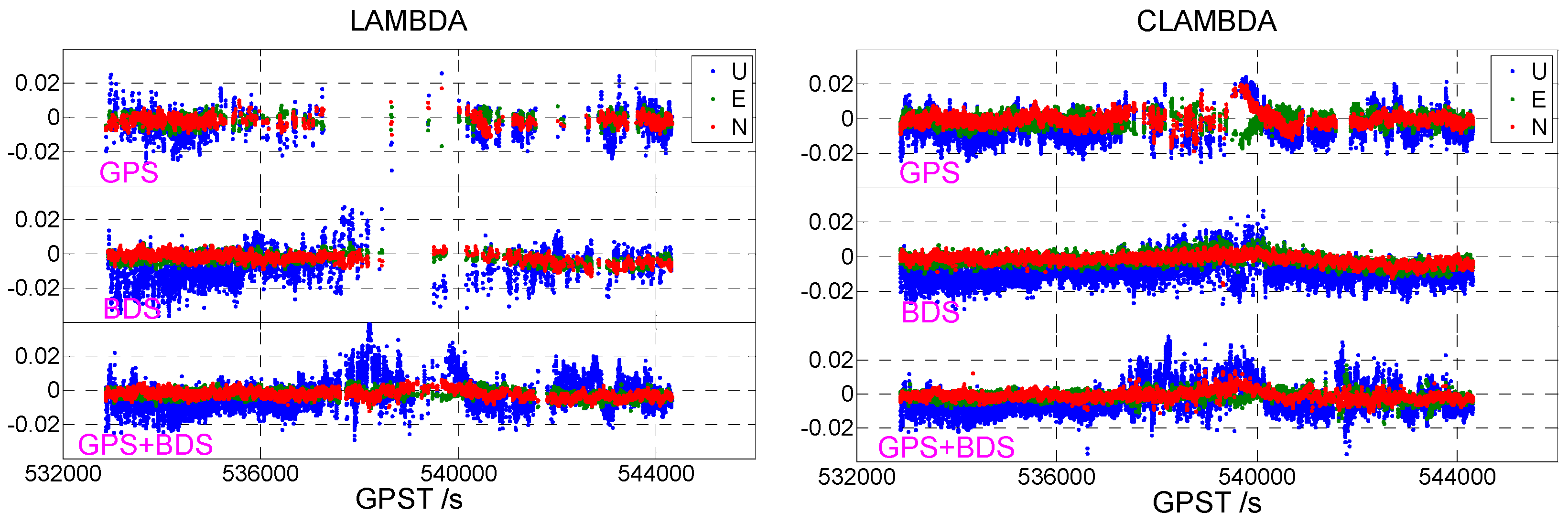
3.2. Static Data 2
3.3. Vehicle Data
4. Conclusions
- (1)
- Without baseline length constraints, BDS single-frequency data can obtain a higher ambiguity fixed success rate than GPS single-frequency data. GPS+BDS dual-system single-frequency data can significantly improve the accuracy of the ambiguity resolution.
- (2)
- Under a baseline length constraint, the CLAMBDA method can greatly improve the fixed success rate of ambiguity for single-frequency single-system data (for instance, the single GPS and BDS increased by 41.15% and 29.47% in static data 1, respectively, and the dynamic single GPS and BDS increased by 19.39% and 19.96%, respectively). Considering the single-frequency dual-system data, the CLAMBDA method has a relatively greater accuracy due to the high fixed success rate of the LAMBDA method itself.
- (3)
- Given that the ambiguity is fixed correctly, CLAMBDA and LAMBDA have the same positioning accuracy and both can reach the centimeter level. Under a static observation environment, the positioning accuracy can reach 0.5 cm in the horizontal direction and 1 cm in the vertical direction, while in the dynamic case, the positioning accuracy can reach 1 cm in the horizontal level and 2 cm in the vertical direction.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, T.X.; Li, B.F. Single-frequency BDS/GPS RTK with low-cost u-blox receivers. In Proceedings of the CPGPS 2017 Forum on Cooperative Positioning and Service, Harbin, China, 19–21 May 2017; pp. 232–238. [Google Scholar]
- Du, C.H.; Gao, X.W.; Ma, Y.; Yang, S.X.; Chen, J.H.; Yang, K.Y. Performance analysis of RTK positioning for single-frequency combination of BDS and GPS. In Proceedings of the China Satellite Navigation Conference, Harbin, China, 23–25 May 2018. [Google Scholar]
- Wang, D.; Park, S.; Fesenmaier, D.R. The Role of Smartphones in Mediating the Touristic Experience. J. Travel Res. 2012, 51, 371–387. [Google Scholar] [CrossRef]
- Saeedi, S.; Moussa, A.; El-Sheimy, N. Context-Aware Personal Navigation Using Embedded Sensor Fusion in Smartphones. Sensors 2014, 14, 5742–5767. [Google Scholar] [CrossRef] [PubMed]
- Specht, C.; Dabrowski, P.S.; Pawelski, J.; Specht, M.; Szot, T. Comparative analysis of positioning accuracy of GNSS receivers of Samsung Galaxy smartphones in marine dynamic measurements. Adv. Space Res. 2019, 63, 3018–3028. [Google Scholar] [CrossRef]
- Engelbrecht, J.; Booysen, M.J.; Bruwer, F.J.; Van Rooyen, G.J. Survey of smartphone-based sensing in vehicles for intelligent transportation system applications. IET Intell. Transp. Syst. 2015, 9, 924–935. [Google Scholar] [CrossRef]
- Chen, B.; Gao, C.; Liu, Y.; Sun, P. Real-Time Precise Point Positioning with a Xiaomi MI 8 Android Smartphone. Sensors 2019, 19, 2835. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.K.; Shi, X.; Zhu, F.; Tao, X.; Wang, F.H. Quality Analysis of Multi-GNSS Raw Observations and a Velocity-Aided Positioning Approach Based on Smartphones. Adv. Space Res. 2019, 63, 2358–2377. [Google Scholar] [CrossRef]
- Paziewski, J.; Sieradzki, R.; Baryla, R. Signal Characterization and Assessment of Code GNSS Positioning with Low-Power Consumption Smartphones. GPS Solut. 2019, 23, 98. [Google Scholar] [CrossRef]
- Eugenio, R.; Stefano, C.; Lisa, P.; Daniele, S. Precise GNSS Positioning Using Smart Devices. Sensors 2017, 17, 2434. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.S.; Zhao, J.J.; Zhou, K.; Wang, Z.Y.; Yuan, H. Smart Device-Supported BDS/GNSS Real-Time Kinematic Positioning for Sub-Meter-Level Accuracy in Urban Location-Based Services. Sensors 2016, 16, 2201. [Google Scholar] [CrossRef]
- Mongredien, C.; Doyen, J.P.; Strom, M.; Ammann, D. Centimeter-level positioning for UAVs and other mass-market applications. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 1441–1454. [Google Scholar]
- Tsakiri, M.; Sioulis, A.; Piniotis, G. The use of low-cost, single-frequency GNSS receivers in mapping surveys. Surv. Rev. 2016, 50, 46–56. [Google Scholar] [CrossRef]
- Caldera, S.; Realini, E.; Barzaghi, R.; Reguzzoni, M. Experimental Study on Low-Cost Satellite-Based Geodetic Monitoring over Short Baselines. J. Surv. Eng. 2016, 142, 04015016. [Google Scholar] [CrossRef]
- Biagi, L.; Grec, F.; Negretti, M. Low-Cost GNSS Receivers for Local Monitoring: Experimental Simulation, and Analysis of Displacements. Sensors 2016, 16, 2140. [Google Scholar] [CrossRef]
- Stempfhuber, W. 3D-RTk capability of single GNSS receivers. ISPRS-International Archives of the Photogrammetry. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2013, 40, 379–384. [Google Scholar] [CrossRef]
- Rapiński, J.; Tomaszewski, D.; Mateusz, K. Analysis of the code and carrier phase measurements performed with LEA-6T GPS receiver. In Proceedings of the 9th Conference “Environmental Engineering”, Vilnius, Lithuania, 22–23 May 2014. [Google Scholar]
- Odolinski, R.; Teunissen, P.J.G. Single-frequency, dual-GNSS versus dual-frequency, single-GNSS: a low-cost and high-grade receivers GPS-BDS RTK analysis. J. Geod. 2016, 90, 1255–1278. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G. Low cost, high-precision, single-frequency GPS-BDS RTK positioning. GPS Solut. 2017, 21, 1315–1330. [Google Scholar] [CrossRef]
- Odolinski, R.; Teunissen, P.J.G. Low-cost, 4-system, precise GNSS positioning: a GPS, Galileo, BDS and QZSS ionosphere-weighted RTK analysis. Meas. Sci. Technol. 2017, 28, 125801. [Google Scholar] [CrossRef] [Green Version]
- Odolinski, R.; Teunissen, P.J.G. An assessment of smartphone and low-cost multi-GNSS single-frequency RTK positioning for low, medium and high ionospheric disturbance periods. J. Geod. 2018, 93, 701–722. [Google Scholar] [CrossRef] [Green Version]
- Zuo, X.; Chen, Y.J.; Li, C.G.; Pan, G.F.; Shi, X.Y. Single frequency GPS/BDS precise positioning algorithm for low-cost receivers. In Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 152–158. [Google Scholar]
- Li, B.F.; Shen, Y.Z. Fast GPS ambiguity resolution constraint to available conditions. Geomat. Inf. Sci. Wuhan Univ. 2009, 34, 117–121. [Google Scholar] [CrossRef]
- Li, Z.H.; Liu, W.K.; Lou, Y.D.; Zhou, Z.B. Heading determination algorithm with single epoch dual-frequency GPS data. Geomat. Inf. Sci. Wuhan Univ. 2007, 32, 753–756. [Google Scholar] [CrossRef]
- Tang, W.M.; Li, D.; Chi, F.M. Research on single epoch orientation algorithm of BDS navigation satellite system. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 1014–1017. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The LAMBDA method for the GNSS compass. Artif. Satell. 2006, 41, 89–103. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Integer least-squares theory for the GNSS compass. J. Geod. 2010, 84, 433–447. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P.J.G.; Giorgi, G.; Buist, P.J. Testing of a New Single-Frequency GNSS Carrier Phase Attitude Determination Method: Land, Ship and Aircraft Experiments. GPS Solut. 2011, 15, 15–28. [Google Scholar] [CrossRef]
- Wang, B.; Sui, L.F.; Zhang, Q.H.; Gan, Y. Research on attitude determination algorithms using GPS. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 1392–1395. [Google Scholar] [CrossRef]


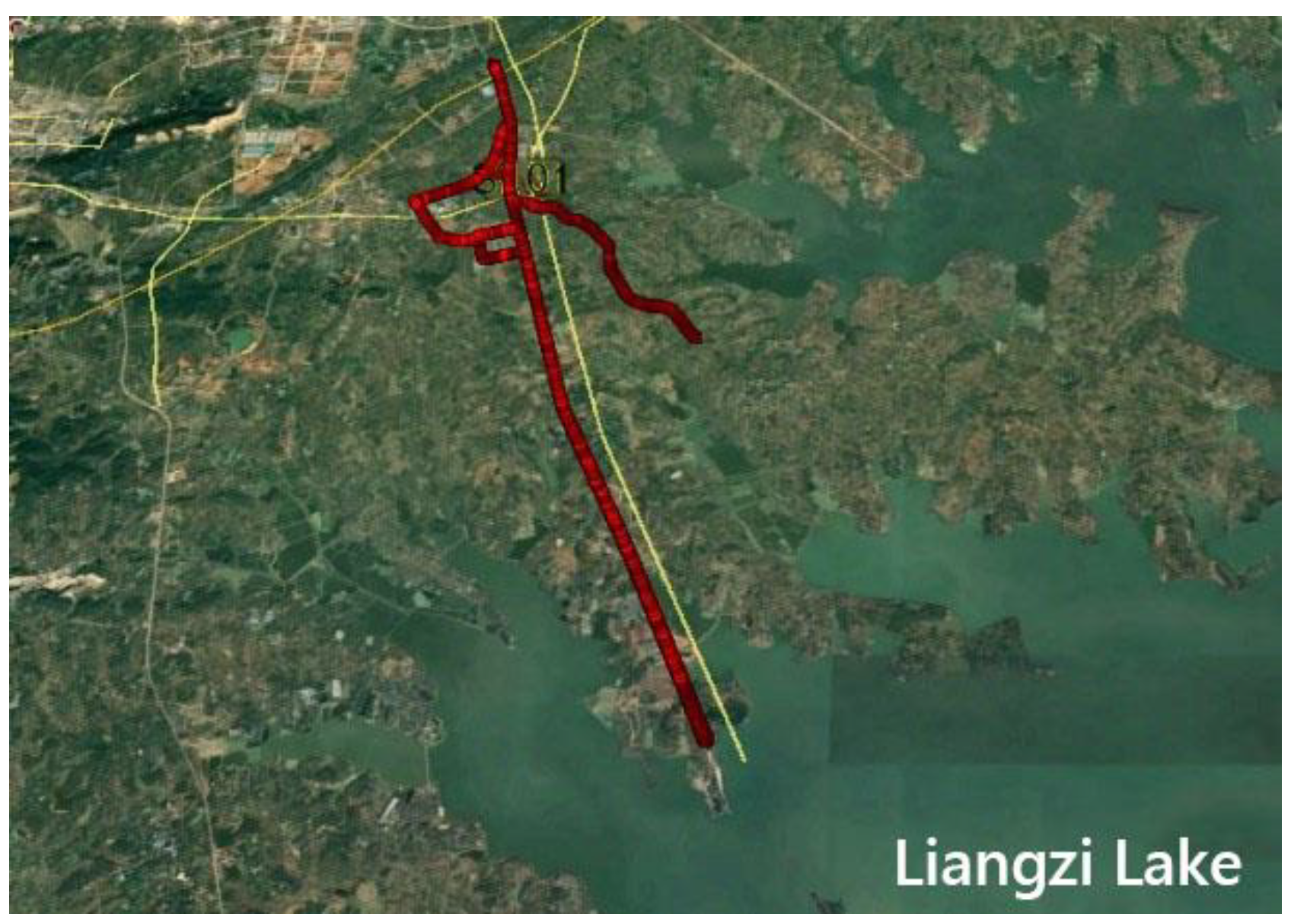
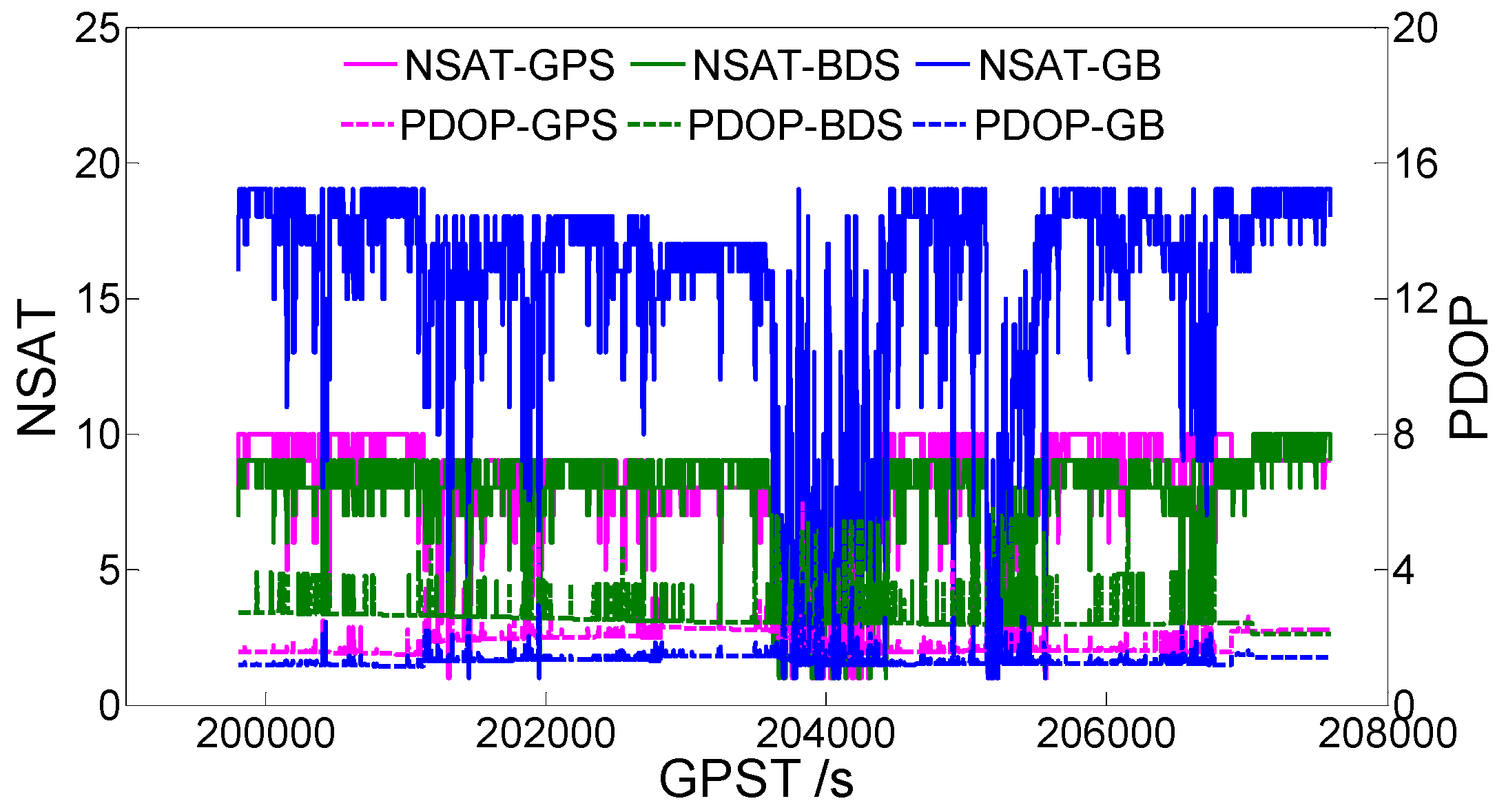
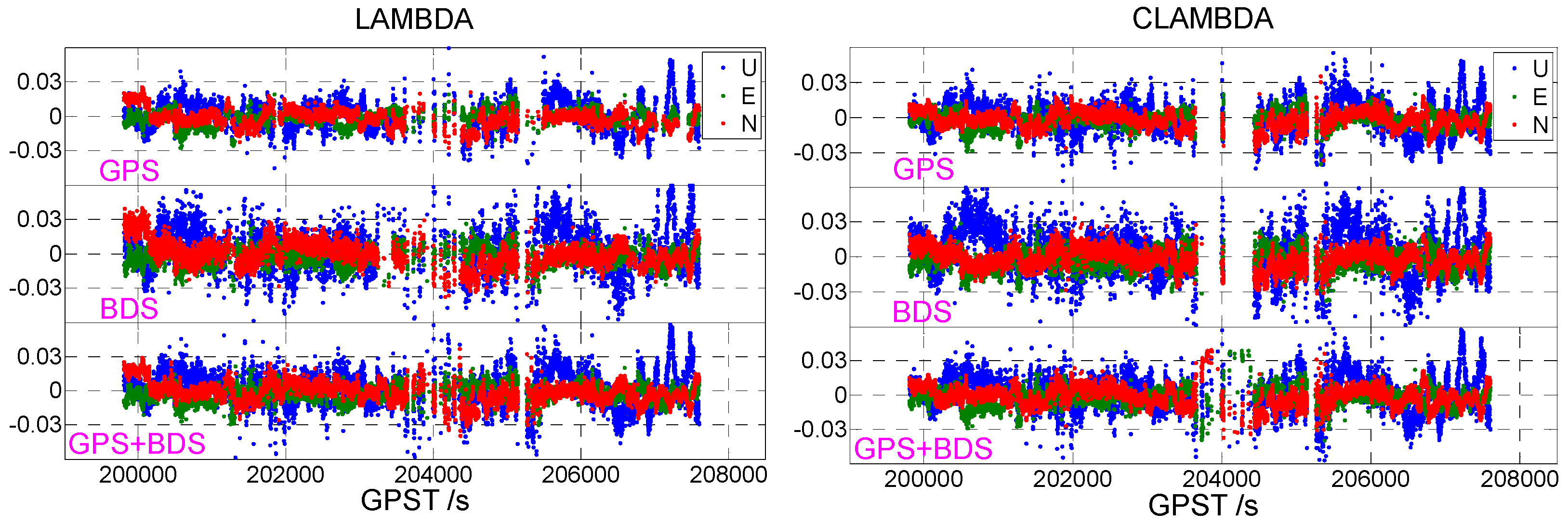
| Data | Scene | Time Span | Receiver | Antenna | Baseline Length |
|---|---|---|---|---|---|
| 1 | Static | 4 h | U-blox-M8P | Trimble Zephyr Model 2 | 3.28 m |
| 2 | Static | 3:10 h | U-blox-M8P | UniStrong UA91 3D/Trimble Zephyr Model 2 | 1637.41 m |
| 3 | Vehicle | 2:10 h | U-blox-M8P | Trimble Zephyr Model 2 | 1.13 m |
| System and Frequency | GPS (L1) and BDS (B1) |
| Process Model | Single-epoch RTK |
| Ambiguity Resolution | LAMBDA/CLAMBDA |
| Sampling Interval | 1 s |
| Cut-off Angle | 10° |
| Ionosphere Model | Klobuchar |
| Troposphere Model | Saastamoinen |
| Weight of Code and Phase | 1:100 |
| Method | Satellite System | RMS-E/m | RMS-N/m | RMS-U/m | Fixed Success Rate |
|---|---|---|---|---|---|
| LAMBDA | GPS | 0.0036 | 0.0044 | 0.0094 | 39.56% |
| BDS | 0.0040 | 0.0066 | 0.0127 | 69.75% | |
| GPS + BDS | 0.0031 | 0.0039 | 0.0093 | 97.46% | |
| CLAMBDA | GPS | 0.0038 | 0.0029 | 0.0101 | 80.71% |
| BDS | 0.0040 | 0.0025 | 0.0092 | 99.22% | |
| GPS + BDS | 0.0032 | 0.0031 | 0.0089 | 98.66% |
| Method | Satellite System | RMS-E/m | RMS-N/m | RMS-U/m | Fixed Success Rate |
|---|---|---|---|---|---|
| LAMBDA | GPS | 0.0033 | 0.0034 | 0.0086 | 20.44% |
| BDS | 0.0035 | 0.0036 | 0.0121 | 31.71% | |
| GPS + BDS | 0.0030 | 0.0030 | 0.0088 | 77.69% | |
| CLAMBDA | GPS | 0.0032 | 0.0036 | 0.0085 | 70.66% |
| BDS | 0.0036 | 0.0028 | 0.0109 | 93.58% | |
| G + B | 0.0029 | 0.0028 | 0.0088 | 93.91% |
| Method | Satellite System | RMS-E/m | RMS-N/m | RMS-U/m | Fixed Success Rate |
|---|---|---|---|---|---|
| LAMBDA | GPS | 0.0062 | 0.0078 | 0.0127 | 72.59% |
| BDS | 0.0077 | 0.0107 | 0.0189 | 73.44% | |
| G + B | 0.0069 | 0.0087 | 0.0152 | 98.03% | |
| CLAMBDA | GPS | 0.0063 | 0.0071 | 0.0133 | 91.98% |
| BDS | 0.0085 | 0.0085 | 0.0200 | 93.40% | |
| G + B | 0.0076 | 0.0084 | 0.0152 | 98.06% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, L.; Ma, L.; Wu, T.; Chen, X. Performance Analysis of Positioning Solution Using Low-Cost Single-Frequency U-Blox Receiver Based on Baseline Length Constraint. Sensors 2019, 19, 4352. https://doi.org/10.3390/s19194352
Lu L, Ma L, Wu T, Chen X. Performance Analysis of Positioning Solution Using Low-Cost Single-Frequency U-Blox Receiver Based on Baseline Length Constraint. Sensors. 2019; 19(19):4352. https://doi.org/10.3390/s19194352
Chicago/Turabian StyleLu, Liguo, Liye Ma, Tangting Wu, and Xiaoyong Chen. 2019. "Performance Analysis of Positioning Solution Using Low-Cost Single-Frequency U-Blox Receiver Based on Baseline Length Constraint" Sensors 19, no. 19: 4352. https://doi.org/10.3390/s19194352
APA StyleLu, L., Ma, L., Wu, T., & Chen, X. (2019). Performance Analysis of Positioning Solution Using Low-Cost Single-Frequency U-Blox Receiver Based on Baseline Length Constraint. Sensors, 19(19), 4352. https://doi.org/10.3390/s19194352




