Spatial Distortion Assessments of a Low-Cost Laboratory and Field Hyperspectral Imaging System
Abstract
1. Introduction
2. Materials and Methods
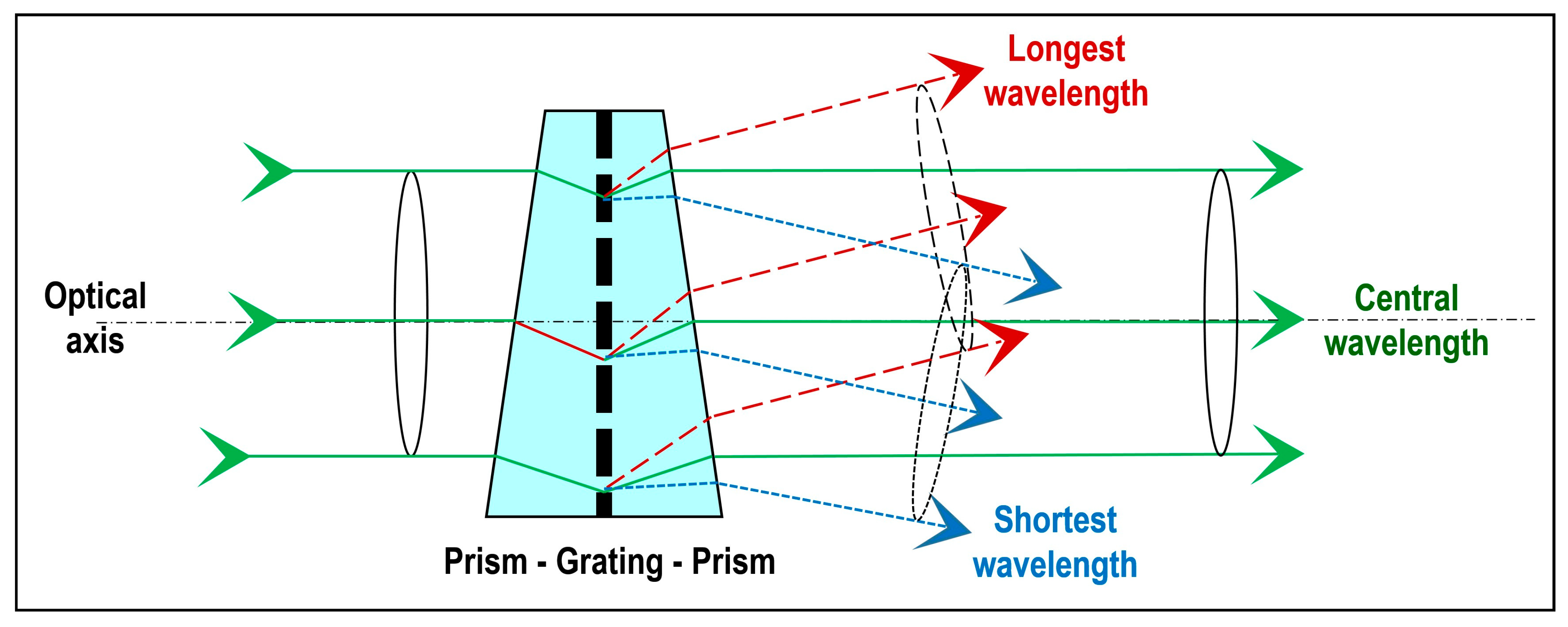
2.1. Hyperspectral Imaging System Design
2.2. Sensor Bracket and Control System
- Continual movement and collection of spectral samples at a given speed to the given position.
- Movement at the given speed by sections of the route, stopping at positions where spectral samples are collected.
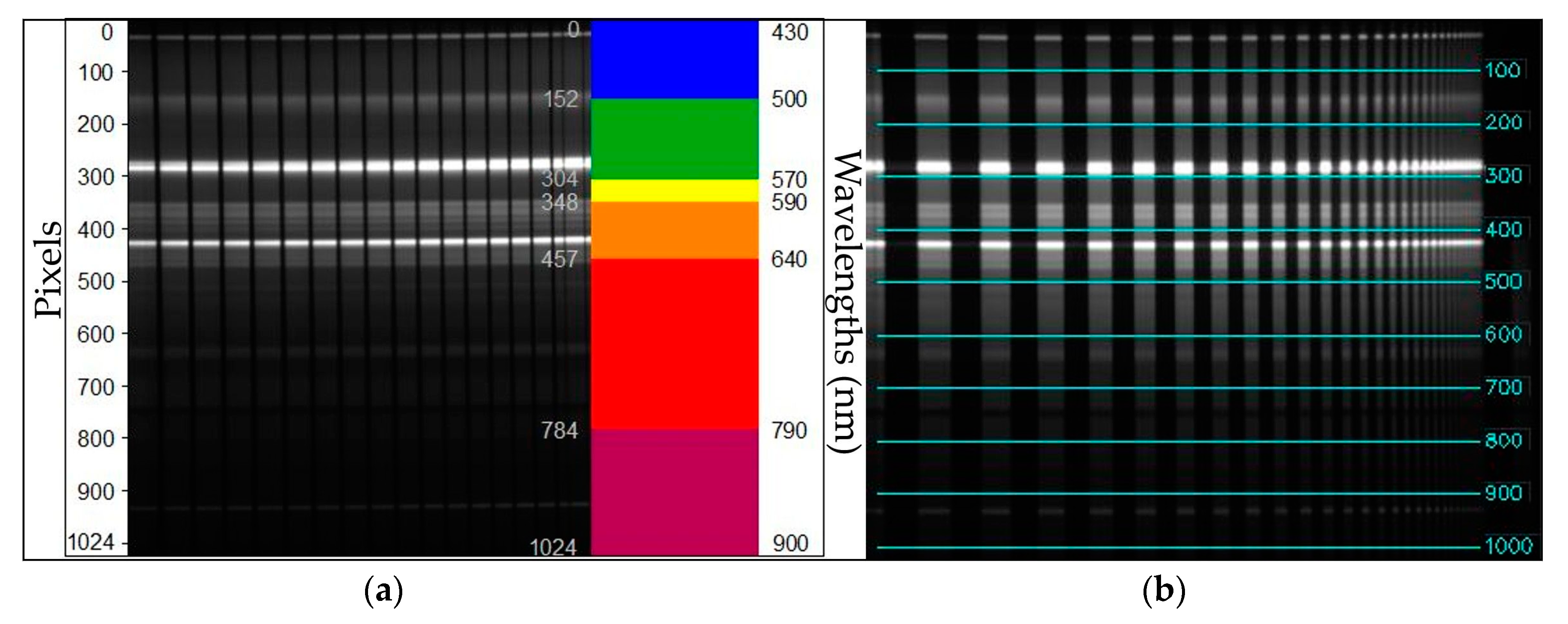
2.3. Spatial Calibration and Modulation Transfer Function
- is the image coordinate of the measured point.
- is the position of the principal point of autocollimation in the image coordinate system.
- c is the sensor’s principal distance.
- are the object’s reference coordinates for the measured point.
- α is the angle of the sensor’s optical axis in the reference coordinate system, and
- are the radial distortion coefficients of the 3th, 5th, and 7th orders.
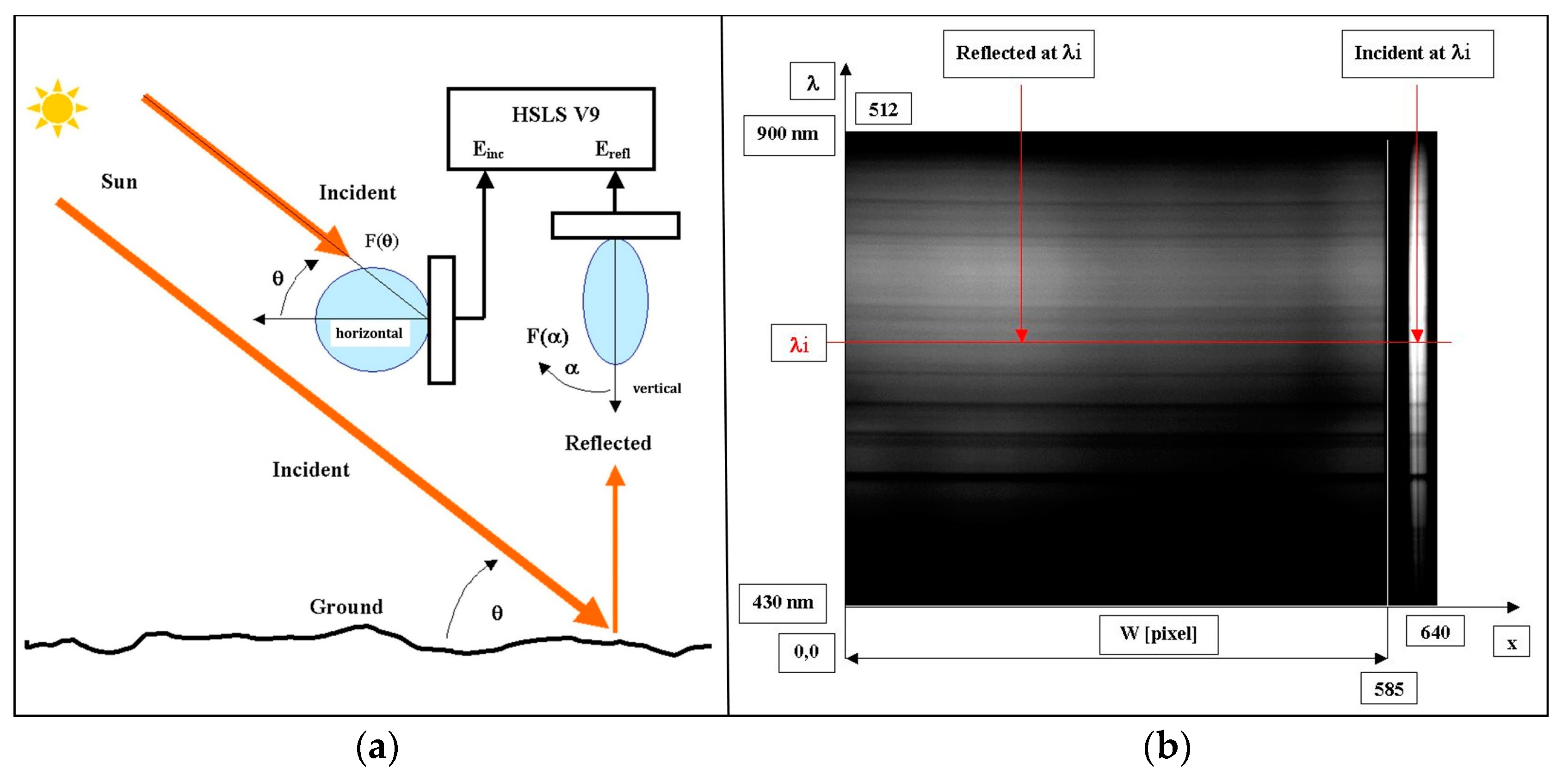
2.4. Creating a Hyperspectral Cube
- S is the speed of the HSLS V9 (m/s).
- GSD is the Ground Sampling Distance across the line scanner (m).
- fi is the imaging scan period (s).
- Exporting raw data (linear images) and transforming them into TIF format in Recorder program.
- Creating mean data on insolation collected with the diffuse collector, along each line.
- Calculating the reflectivity coefficient.
- Correcting the spectral responses with dark current data (dark image subtraction).
- Stacking spectral lines in the hyperspectral cube.
3. Results
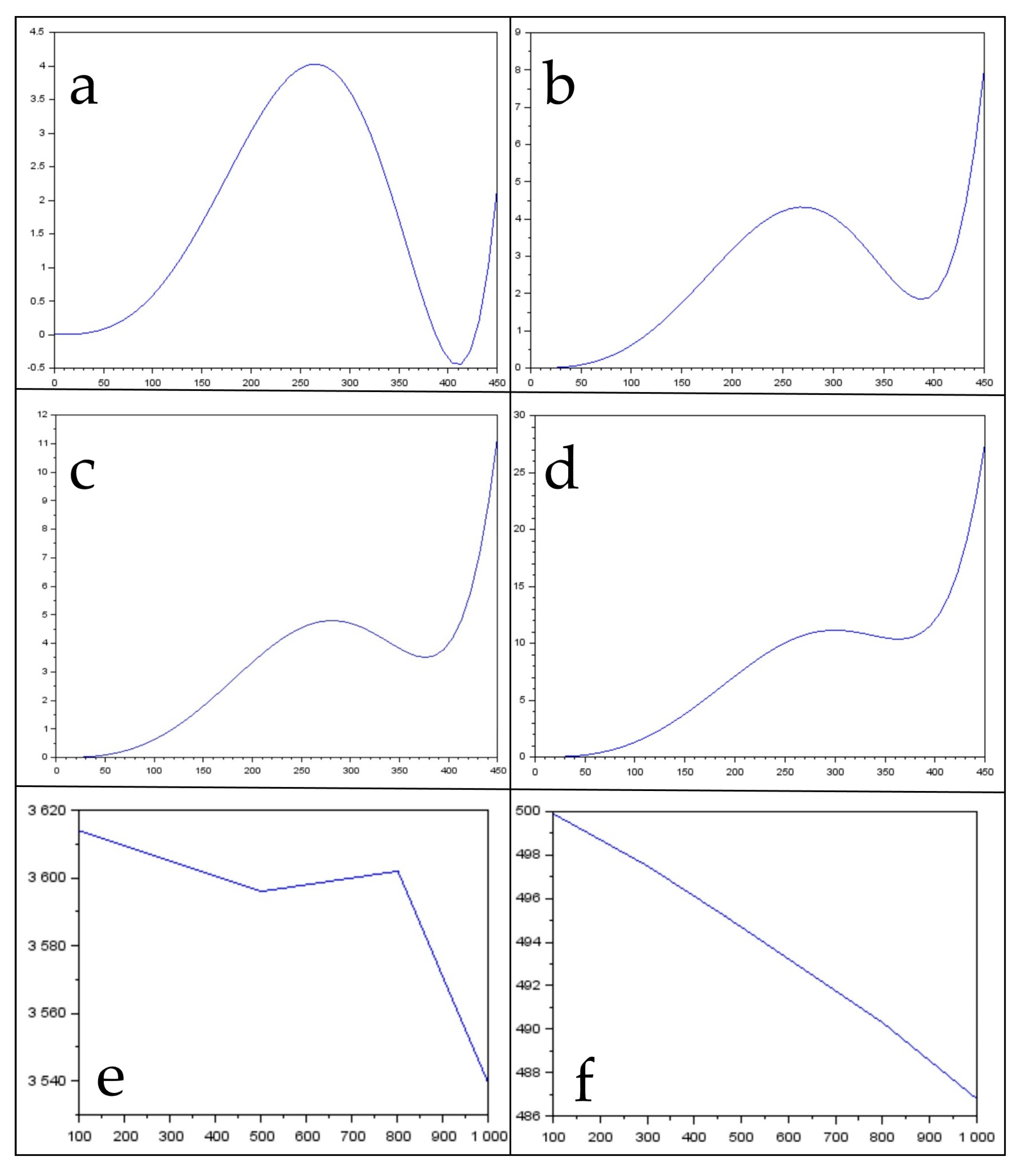
3.1. Spatial Calibration Results and Calculation of the Modulation Transfer Function
3.2. Field Hyperspectral Surveying of Vineyards
- Variant A: 50% ET—irrigation providing 50% of the calculated requirements of the vines for water (delivered by a single pipe with a diameter of 1 cm).
- Variant B: 75% ET—irrigation providing 75% of the calculated requirements of the vines for water (delivered by two pipes with diameters of 1 cm).
- Variant C: 100% ET—irrigation providing 100% of the calculated requirements of the vines for water (delivered by three pipes with diameters of 1 cm).
- Control variant: no irrigation.
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Herman, J.; Evans, R.; Cede, A.; Abuhassan, N.; Petropavlovskikh, I.; McConville, G. Comparison of ozone retrievals from the Pandora spectrometersystem and Dobson spectrophotometer in Boulder, Colorado. Atmos. Meas. Tech. 2015, 8, 3407–3418. [Google Scholar] [CrossRef]
- Czegan, D.A.C.; Hoover, D.K. UV−Visible Spectrometers: Versatile Instruments across the Chemistry Curriculum. J. Chem. Educ. 2012, 89, 304–309. [Google Scholar] [CrossRef]
- Onorato, P.; Malgieri, M.; Ambrosis, A.D. Measuring the hydrogen Balmer series and Rydberg’s constant with a homemade spectrophotometer. Eur. J. Phys. 2015, 36, 058001. [Google Scholar] [CrossRef][Green Version]
- Li, Q.; He, X.; Wang, Y.; Liu, H.; Xu, D.; Guo, F. Review of spectral imaging technology in biomedical engineering: Achievements and challenges. J. Biomed. Opt. 2013, 18, 100901. [Google Scholar] [CrossRef] [PubMed]
- Gowen, A.; O’Donnell, C.; Cullen, P.; Downey, G.; Frias, J. Hyperspectral imaging an emerging process analytical tool for food quality and safety control. Trends Food Sci. Technol. 2007, 18, 590–598. [Google Scholar] [CrossRef]
- Mishra, P.; Asaari, M.S.M.; Herrero-Langreo, A.; Lohumi, S.; Diezma, B.; Scheunders, P. Close range hyperspectral imaging of plants: A review. Biosyst. Eng. 2017, 164, 49–67. [Google Scholar] [CrossRef]
- Kurz, T.H.; Buckley, S.J.; Howell, J.A.; Schneider, D. Integration of panoramic hyperspectral imaging with terrestrial lidar data. Photogramm. Rec. 2011, 26, 212–228. [Google Scholar] [CrossRef]
- Schneider, D.; Maas, H.G. A geometric model for linear-array-based terrestrial panoramic cameras. Photogramm. Rec. 2006, 21, 198–210. [Google Scholar] [CrossRef]
- Hui, B.; Wen, G.; Zhao, Z.; Li, D. Line-scan camera calibration in close-range photogrammetry. Opt. Eng. 2012, 51, 053602. [Google Scholar] [CrossRef]
- Lawrence, K.C.; Park, B.; Windham, W.R.; Mao, C. Calibration of a pushbroom hyperspectral imaging system for agricultural inspection. Trans. ASAE 2003, 46, 513–521. [Google Scholar] [CrossRef]
- Kurz, T.H.; Buckley, S.J.; Howell, J.A. Close-range hyperspectral imaging for geological field studies: Workflow and methods. Int. J. Remote Sens. 2013, 34, 1798–1822. [Google Scholar] [CrossRef]
- Maggetti, M. Chemical analyses of ancient ceramics: What for? CHIMIA Int. J. Chem. 2001, 55, 923–930. [Google Scholar]
- Verhoeven, G.J. Providing an archaeological bird’s-eye view—An overall picture of ground-based means to execute low-altitude aerial photography (LAAP) in Archaeology. Archaeol. Prospect. 2009, 16, 233–249. [Google Scholar] [CrossRef]
- Tuniz, C.; Bernardini, F.; Cicuttin, A.; Crespo, M.L.; Dreossi, D.; Gianoncelli, A.; Mancini, L.; Mendoza Cuevas, A.; Sodini, N.; Tromba, G.; et al. The ICTP-Elettra X-ray laboratory for cultural heritage and archaeology. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2013, 711, 106–110. [Google Scholar] [CrossRef]
- Manoharan, C.; Sutharsan, P.; Venkatachalapathy, R.; Vasanthi, S.; Dhanapandian, S.; Veeramuthu, K. Spectroscopic and rock magnetic studies on some ancient Indian pottery samples. Egypt. J. Basic Appl. Sci. 2015, 2, 39–49. [Google Scholar] [CrossRef]
- Farjas, M.; Rejas, J.G.; Mostaza, T.; Zancajo, J. Deepening in the 3-D Modelling: Multisource Analysis of a Polychrome Ceramic Vessel Through the Integration of Thermal and Hyperspectral Information. In Revive the Past, Proceedings of the 39th Annual Conference of Computer Applications and Quantitative Methods in Archaeology (CAA), Beijing, China, 12–16 April 2011; Zhou, M., Romanowska, I., Wu, Z., Xu, P., Eds.; Pallas Publications: Amsterdam, The Netherlands, 2011; pp. 116–125. ISBN 9789085550662. [Google Scholar]
- Kubik, M.E. Preserving the Painted Image: The Art and Science of Conservation. JAIC J. Int. Colour Assoc. 2010, 5, 1–8. [Google Scholar]
- Hain, M.; Bartl, J.; Jacko, V. Multispectral Analysisof Cultural Heritage Artefacts. Meas. Sci. Rev. 2003, 3, 9–12. [Google Scholar]
- Carvalhal, J.A.; Linhares, J.M.M.; Nascimento, S.M.C.; Regalo, M.H.; Leite, M.C.V.P. Estimating the best illuminants for appreciation of art paintings. In AIC Colour, Proceedings of 10th Congress of the International Colour Association, Granada, Spain, 8–13 May 2005; Nieves, J.L., Hernández-Andrés, J., Eds.; Comité Español del Color: Granada, Spain, 2005; pp. 383–38684. ISBN1 84-609-5163-4. ISBN2 84-609-5164-2. [Google Scholar]
- Orych, A.; Walczykowski, P.; Jenerowicz, A.; Zdunek, Z. Impact of the cameras radiometric resolution on the accuracy of determining spectral reflectance coefficients. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 347–349. [Google Scholar] [CrossRef]
- Painter, T.H.; Berisford, D.F.; Boardman, J.W.; Bormann, K.J.; Deems, J.S.; Gehrke, F.; Mattmann, C. The Airborne Snow Observatory: Fusion of scanning lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo. Remote Sens. Environ. 2016, 184, 139–152. [Google Scholar] [CrossRef]
- Lemp, D.; Weidner, U. Improvements of Roof Surface Classification Using Hyperspectral and Laser Scanning Data, ISPRS Archives, XXXVI, Joint Symposia URBAN-URS; Karlsruhe Institute of Technology: Tempe, AZ, USA, 2005. [Google Scholar]
- Mewes, G.T. The Impact of the Spectral Dimension of Hyperspectral Datasets on Plant Disease Detection. Ph.D. Thesis, Rheinischen Friedrich-Wilhelms-Universitat, Bonn, Germany, 2010. [Google Scholar]
- Koukouvinos, G.; Τsialla, Z.; Petrou, P.; Misiakos, K.; Goustouridis, D.; Ucles Moreno, A.; Fernandez-Alba, A.; Raptis, I.; Kakabakos, S. Fast simultaneous detection of three pesticides by a White Light Reflectance Spectroscopy sensing platform. Sens. Actuators B Chem. 2017, 238, 1214–1223. [Google Scholar] [CrossRef]
- Nardella, F.; Beck, M.; Collart-Dutilleul, P.; Becker, G.; Boulanger, C.; Perello, L.; Ubeaud-Séquier, G. A UV–Raman spectrometry method for quality control of anticancer preparations: Results after 18 months of implementation in hospital pharmacy. Int. J. Pharm. 2016, 499, 343–350. [Google Scholar] [CrossRef] [PubMed]
- Banas, A.; Banas, K.; Kalaiselvi, S.M.P.; Pawlicki, B.; Kwiatek, W.M.; Breese, M.B.H. Is it possible to find presence of lactose in pharmaceuticals? Preliminary studies by ATR-FTIR spectroscopy and chemometrics. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2017, 171, 280–286. [Google Scholar] [CrossRef] [PubMed]
- Minet, O.; Scheibe, P.; Beuthan, J.; Zabarylo, U. Correction of motion artefacts and pseudo colour visualization of multispectral light scattering images for optical diagnosis of rheumatoid arthritis. In Saratov Fall Meeting 2009: International School for Junior Scientists and Students on Optics, Laser Physics, and Biophotonics; International Society for Optics and Photonics: Saratov, Russia, 2009; p. 75470B. [Google Scholar]
- Nouri, D.; Lucas, Y.; Treuillet, S. Calibration and test of a hyperspectral imaging prototype for intra-operative surgical assistance Calibration and test of a hyperspectral imaging prototype for intra-operative surgical assistance. In Medical Imaging 2013: Digital Pathology; SPIE Medical Imaging; International Society for Optics and Photonics: Orlando, FL, USA, 2013; p. 86760P. [Google Scholar]
- Barreira, E.; Almeida, R.; Delgado, J. Infrared thermography for assessing moisture related phenomena in building components. Constr. Build. Mater. 2016, 110, 251–269. [Google Scholar] [CrossRef]
- Hyvarinen, T.; Herrala, E.; Dall’Ava, A. Direct sight imaging spectrograph: A unique add-on component brings spectral imaging to industrial applications. Presented at 1998 IS&T/SPIE’s Symposium on Electronic Imaging: Science and Technology (EI98). In Conference 3302: Digital Solid State Cameras: Design and Applications, Paper 3302-21, 25–30 January 1998; San Jose Convention Center: San Jose, CA, USA, 1998. [Google Scholar]
- Mao, C. Hyperspectral imaging systems with digital CCD cameras for both airborne and laboratory application. In Proceedings of 17th Biennial Workshop on Videography and Color Photography in Resource Assessment; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 1999; pp. 31–40. [Google Scholar]
- Inoue, Y.; Peñuelas, J. An AOTF-based hyperspectral imaging system for field use in ecophysiological and agricultural applications, International. J. Remote Sens. 2001, 22, 3883–3888. [Google Scholar] [CrossRef]
- Yang, C.; Everitt, J.H.; Davis, M.R.; Mao, C. A CCD Camera-based Hyperspectral Imaging System for Stationary and Airborne Applications. Geocarto Int. 2003, 18, 71–80. [Google Scholar] [CrossRef]
- Ye, X.; Sakai, K.; Okamoto, H.; Garciano, L.O. A ground-based hyperspectral imaging system for characterizing vegetation spectral features. Comput. Electron. Agric. 2008, 63, 13–21. [Google Scholar] [CrossRef]
- Gutiérrez-Gutiérrez, J.A.; Pardo, A.; Real, E.; López-Higuera, J.M.; Conde, O.M. Custom Scanning Hyperspectral Imaging System for Biomedical Applications: Modeling, Benchmarking, and Specifications. Sensors 2019, 19, 1692. [Google Scholar] [CrossRef]
- Farley, V.; Belzile, C.; Chamberland, M.; Legault, J.F.; Schwantes, K.R. Development and testing of a hyperspectral imaging instrument for field spectroscopy. In Imaging Spectrometry X; International Society for Optics and Photonics: Denver, CO, USA, 2004; Volume 5546, pp. 29–36. [Google Scholar] [CrossRef]
- Eisl, M.; Khalili, M. ARC—Airborne Minefield Area Reduction. In Proceedings of the International Conference Requirements and Technologies for the Detection, Removal and Neutralization of Landmines and UXO, Brussels, Belgium, 15–18 September 2003. [Google Scholar]
- Yvinec, Y. A validated method to help area reduction in mine action with remote sensing data. In Proceedings of the 4th International Symposium on Image and Signal Processing and Analysis (ISPA 2005), Zagreb, Croatia, 15–17 September 2005; p. 6. [Google Scholar] [CrossRef]
- Fiedler, T.; Bajić, M.; Gajski, D.; Gold, H.; Pavković, N.; Milošević, D.I. System for Multi-Sensor Airborne Reconnaissance and Surveillance in Crisis Situations and Environmental Protection (Final Report of Technology Project TP-006/0007-01 (Internal Document in Croatian for GF, CTRO, FTTS); Faculty of Geodesy University of Zagreb: Zagreb, Croatia, 2008. [Google Scholar]
- Yvinec, Y.; Baudoin, Y.; De Cubber, G.; Armada, M.; Marques, L.; Desaulniers, J.-M.; Bajić, M.; Cepolina, E.; Zoppi, M. TIRAMISU: FP7-Project for an integrated toolbox in Humanitarian Demining, focus on UGV, UAV and technical survey. In Proceedings of the 6th IARP Workshop on Risky Interventions and Environmental Surveillance (RISE), Warsaw, Poland, 11–15 September 2012; p. 17. [Google Scholar]
- Bajic, M.; Gold, H.; Pračić, Ž.; Vuletić, D. Airborne sampling of the reflectivity by the hyperspectral line scanner in a visible and near infrared wavelengths. In Proceedings of the 24th Symposium of the European Association of Remote Sensing Laboratories, Dubrovnik, Croatia, 25–27 May 2004; pp. 703–710. [Google Scholar]
- Šemanjski, S.; Gajski, D.; Bajić, M. Transformation of the Hyperspectral Line Scanner into a Strip Imaging System. In Proceedings of the First EARSeL Conference of Disaster Management and Emergency Response in the Mediterranean Region, Zadar, Croatia, 22–24 September 2008; pp. 369–376. [Google Scholar]
- Bajic, M.; Ivelja, T.; Brook, A. Developing a Hyperspectral Non-Technical Survey for Minefields via UAV and Helicopter. J. Conv. Weapons Destr. 2017, 21, 11. [Google Scholar]
- Behmann, J.; Mahlein, A.; Paulus, S.; Kuhlmann, H.; Oerke, E.; Plümer, L. Calibration of hyperspectral close-range pushbroom cameras for plant phenotyping. ISPRS J. Photogramm. Remote Sens. 2015, 106, 172–182. [Google Scholar] [CrossRef]
- Miljković, V. Spatial Calibration of Multispectral and Hyperspectral Sensors in Close-Range Photogrammetry. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, 12 April 2017. [Google Scholar]
- Miljković, V.; Gajski, D.; Vela, E. Spatial Calibration of the Hyperspectral Line Scanner by the Bundle Block Adjusting Method. Geodetski List 2017, 2, 127–142. [Google Scholar]
- Boreman, G.D. Modulation Transfer Function in Optical and Electro-Optical Systems; SPIE Press: Bellingham, WA, USA, 2001. [Google Scholar]
- Rossmann, K. Point Spread–Function, Line Spread–Function, and Modulation Transfer Function. Radiology 1969, 93, 257–272. [Google Scholar] [CrossRef] [PubMed]
- Petković, D.; Shamshirband, S.; Saboohi, H.; Ang, T.F.; Anuar, N.B.; Rahman, Z.A.; Pavlović, N.T. Evaluation of modulation transfer function of optical lens system by support vector regression methodologies, A comparative study. Infrared Phys. Technol. 2014, 65, 94–102. [Google Scholar] [CrossRef]
- Alaruri, S.D. Calculating the modulation transfer function of an optical imaging system incorporating a digital camera from slanted-edge images captured under variable illumination levels: Fourier transforms application using MATLAB. Optik-Int. J. Light Electron. Opt. 2016, 127, 5820–5824. [Google Scholar] [CrossRef]
- Spectral Imaging LTD. ImSpector Imaging Spectrograph User Manual, Version 2.21; Spectral Imaging LTD: Oulu, Finland, 2003. [Google Scholar]
- PCO Imaging. PixelFly High Performance Digital 12bit CCD Camera System. 2003. Available online: https://www.pco.de/fileadmin/user_upload/db/products/datasheet/pixelfly_20090505.pdf (accessed on 20 June 2019).
- PCO Imaging. PixelFly Operating Instructions; The COOKE Corporation: Eliot, ME, USA, 2002. [Google Scholar]
- Gajski, D.; Jakšić, J. The impact of Position and Attitude Offset Calibration on the Geocoding Accuracy of Hyperspectral Line Scanner ImSpector V9. Eng Power Bull. Croat. Acad. Eng. 2018, 13, 18–21. [Google Scholar]
- Miljković, V.; Gajski, D. Adaptation of Industrial Hyperspectral Line Scanner for Archaeological Applications. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, 5, 343–345. [Google Scholar] [CrossRef]
- Holst, G.C. CCD Arrays, Cameras and Displays; SPIE Optical Engineering Press: Bellingham, WA, USA, 1998. [Google Scholar]
- Kuittinen, R. Transportable Test-Bar Targets and Microdensitometer Measurements-A Method to control the Quality of Aerial Imagery. Int. Arch. Photogramm. Remote Sens. 1996, 31, 99–104. [Google Scholar]
- Schlaepfer, D. PARametric Geocoding, Orthorectification for Airborne Scanner Data, User Manual Version 2.3; ReSe Applications Schlaepfer and Remote Sensing Laboratories (RSL) of the University of Zurich: Zurich, Switzerland, 2006. [Google Scholar]
- Schläpfer, D.; Schaepman, E.M.; Itten, I.K. PARGE: Parametric Geocoding Based on GCP-Calibrated Auxiliary Data; Imaging Spectroscopy IV: San Diego, CA, USA, 1998; Volume 3438, pp. 334–344. [Google Scholar]
- Romić, D.; Romić, M.; Ondrašek, G.; Bakić, H.; Bubalo, M.; Zovko, M.; Matijević, L.; Husnjak, S.; Jungić, D.; Rubinić, V.; et al. Irrigation Pilot Project (Vine Grapes and Olives) on Established Plots within the Karst Area (Donje Polje JADRTOVAC, Šibensko-Kninska County, Project Report for 2015 (in Croatian)); University of Zagreb Faculty of Agriculture: Zagreb, Croatia, 2015. [Google Scholar]
- Luna, C.; Mazo, M.; Lázaro, J.; Vázquez, J. Calibration of Line–Scan Cameras. IEEE Trans. Instrum. Meas. 2010, 59, 2185–2190. [Google Scholar] [CrossRef]
- Zhao, Z. Line Scan Camera Calibration for Fabric Imaging. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2012. [Google Scholar]
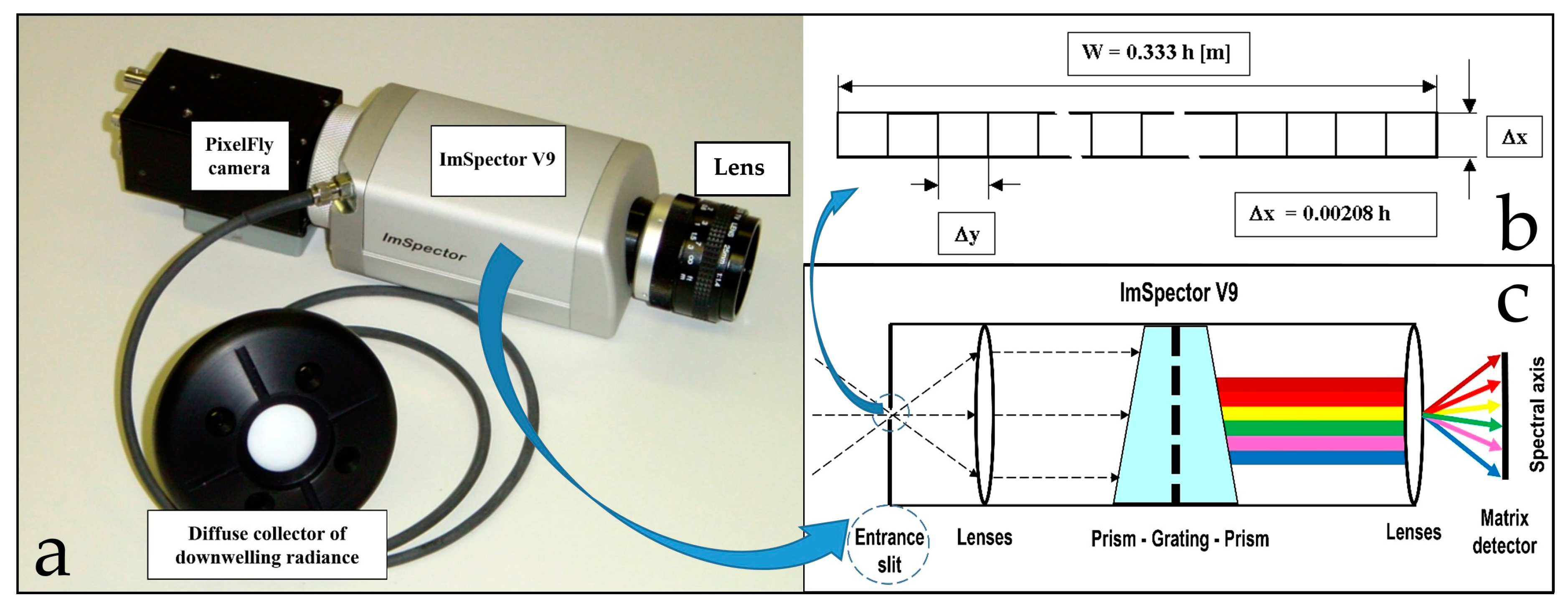





| ImSpector V9 Specifications | ||
| Spectral range | 430∓900 nm ± 5 nm | Designed for 6.6 mm detector; corresponding to shorter axis of 2/3” CCD |
| Spectral resolution | 4.4 nm | With 50 µm slit |
| Numerical aperture | 0.18 | F/2.8 |
| Slit width | 50 µm | |
| Effective slit length | 8.8 mm | |
| Image size | 6.6 mm × 8.8 mm | Corresponding to standard 2/3” CCD |
| Magnification of spectrograph optics | 1x | |
| PixelFly Basic Specifications | ||
| Image resolution | 1280 × 1024 pixels | |
| Pixel size | 6.7 µm × 6.7 µm | |
| Scan area | 6.9 mm × 8.6 mm | |
| Imaging frequency (frame rate) | 12.5 fps | At binning with factor 1 |
| 24 fps | At binning with factor 2 | |
| Pixel scan rate | 20 MHz | |
| Exposure time | 10 µs–10 s | |
| Binning horizontal: Binning vertical: | factor 1, factor 2 factor 1, factor 2 | |
| ζ0 (px) | c (px) | K1 | K2 | K3 | Positions of the Spectral Lines (px) |
|---|---|---|---|---|---|
| 499.9 ± 0.1 | 3614 ± 14 | 0.660 | −0.080 | 0.0024 | 100 |
| 497.5 ± 0.1 | 3605 ± 14 | 0.695 | −0.085 | 0.0027 | 300 |
| 494.7 ± 0.1 | 3569 ± 14 | 0.710 | −0.084 | 0.0027 | 500 |
| 486.8 ± 0.1 | 3539 ± 14 | 1.459 | −0.164 | 0.0053 | 1000 |
| Theoretical GSDh (mm) (Binning factor 1) | Determined (Actual) GSDh | |||
|---|---|---|---|---|
| 100 Pixels (mm) | 500 Pixels (mm) | 700 Pixels (mm) | 1000 Pixels (mm) | |
| 0.48 | 0.58 | 0.58 | 0.51 | 0.51 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krtalić, A.; Miljković, V.; Gajski, D.; Racetin, I. Spatial Distortion Assessments of a Low-Cost Laboratory and Field Hyperspectral Imaging System. Sensors 2019, 19, 4267. https://doi.org/10.3390/s19194267
Krtalić A, Miljković V, Gajski D, Racetin I. Spatial Distortion Assessments of a Low-Cost Laboratory and Field Hyperspectral Imaging System. Sensors. 2019; 19(19):4267. https://doi.org/10.3390/s19194267
Chicago/Turabian StyleKrtalić, Andrija, Vanja Miljković, Dubravko Gajski, and Ivan Racetin. 2019. "Spatial Distortion Assessments of a Low-Cost Laboratory and Field Hyperspectral Imaging System" Sensors 19, no. 19: 4267. https://doi.org/10.3390/s19194267
APA StyleKrtalić, A., Miljković, V., Gajski, D., & Racetin, I. (2019). Spatial Distortion Assessments of a Low-Cost Laboratory and Field Hyperspectral Imaging System. Sensors, 19(19), 4267. https://doi.org/10.3390/s19194267







