On-Chip Non-Dispersive Infrared CO2 Sensor Based on an Integrating Cylinder †
Abstract
:1. Introduction
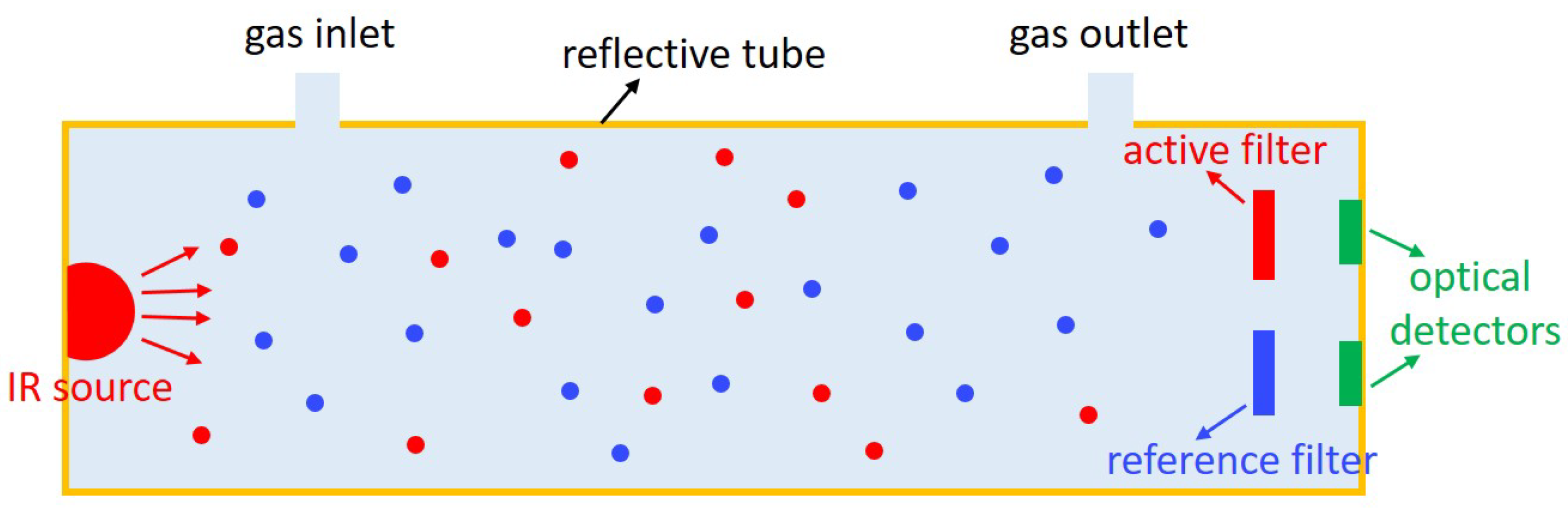
2. NDIR Working Principle
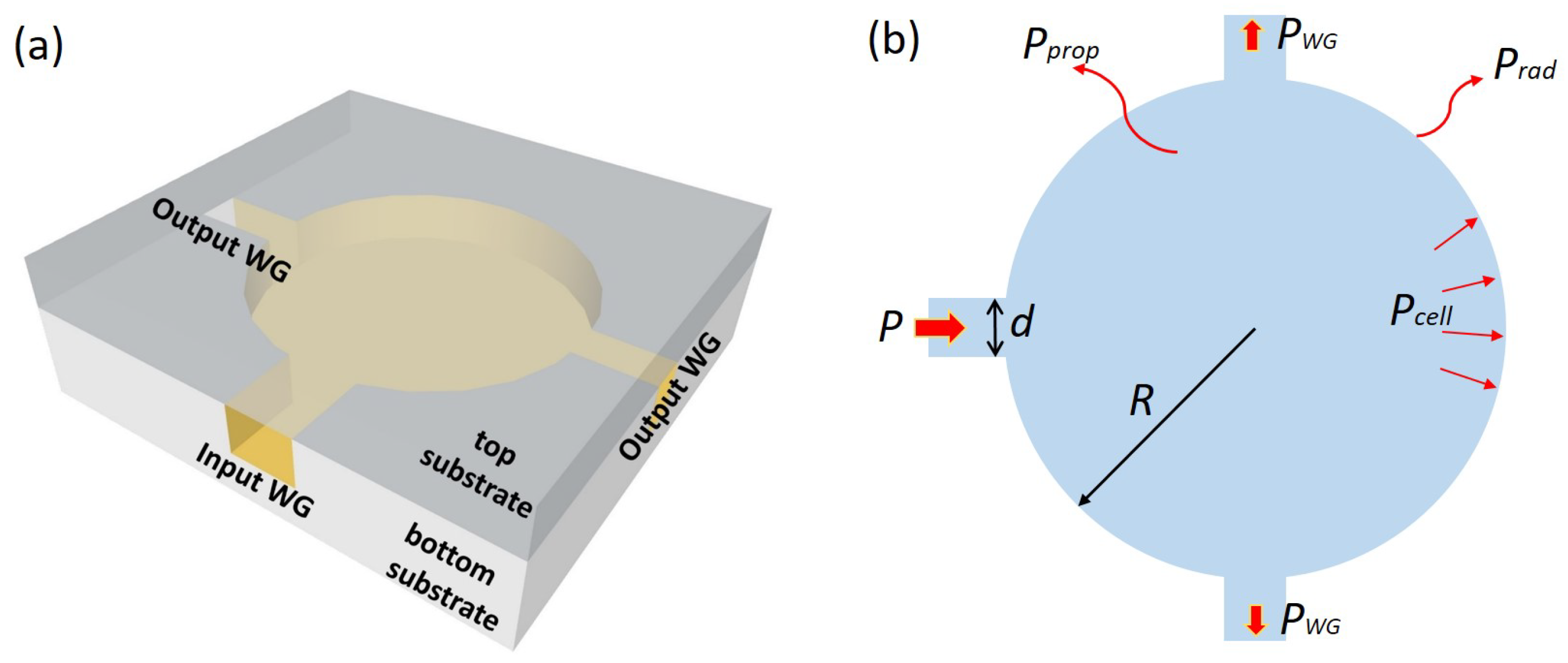
3. Sensor Design
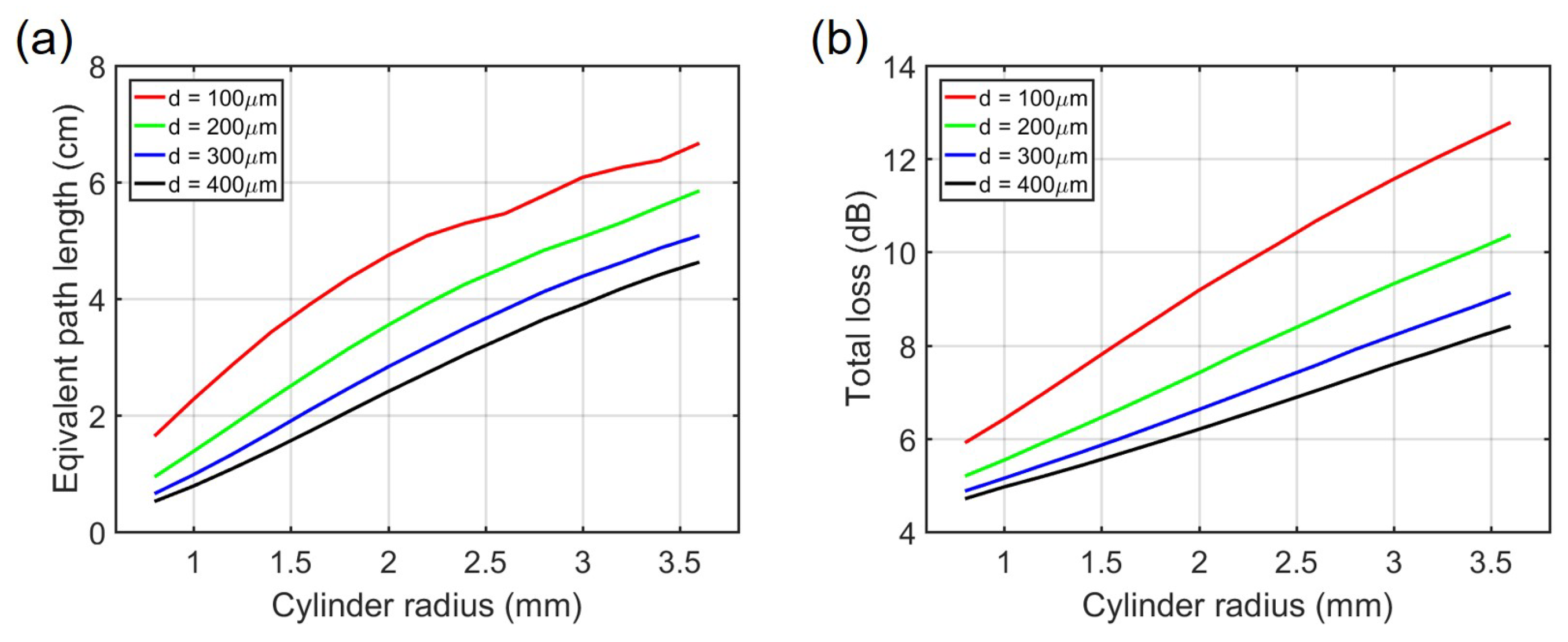
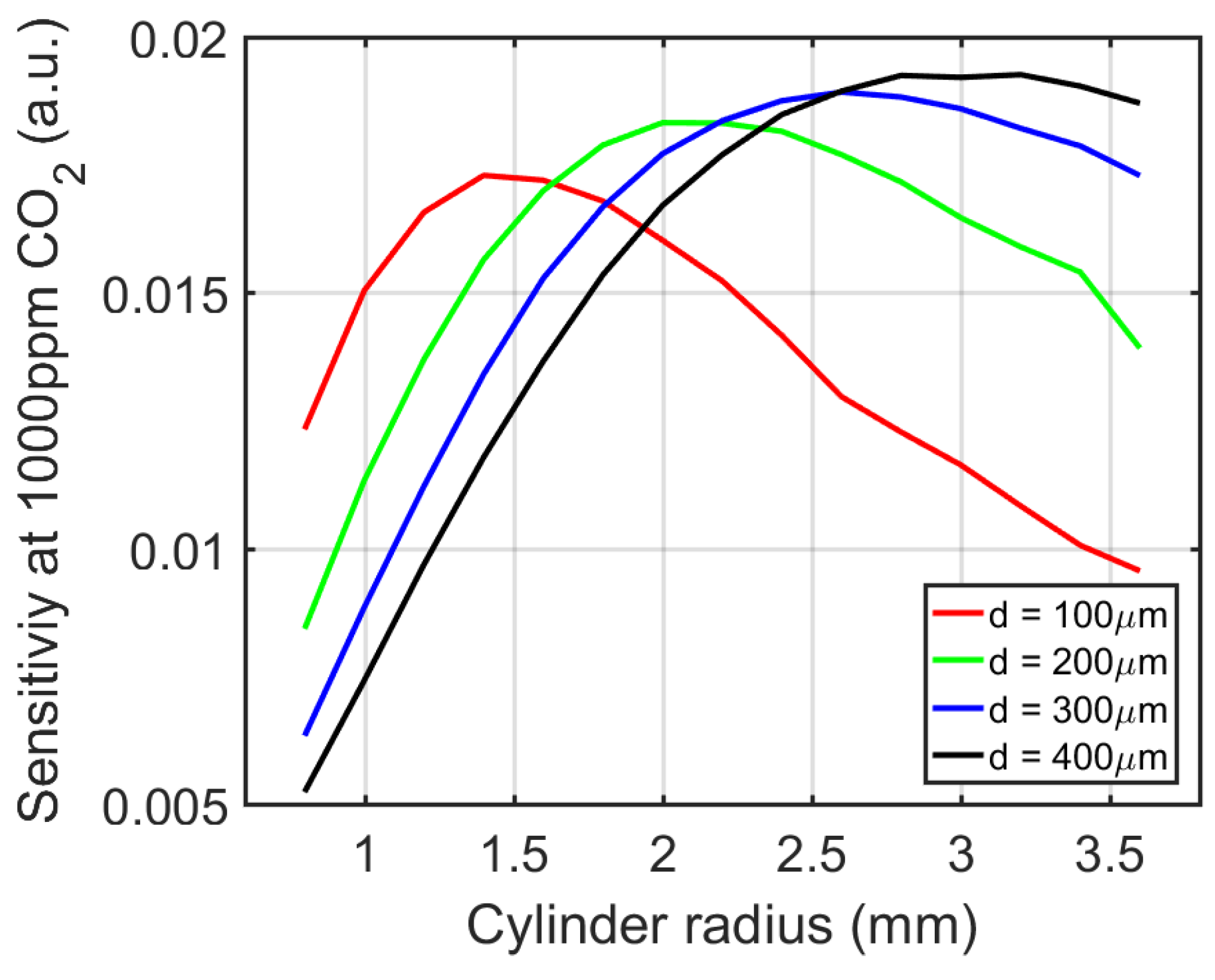
4. Simulations
5. Sensor Fabrication and Experimental Setup
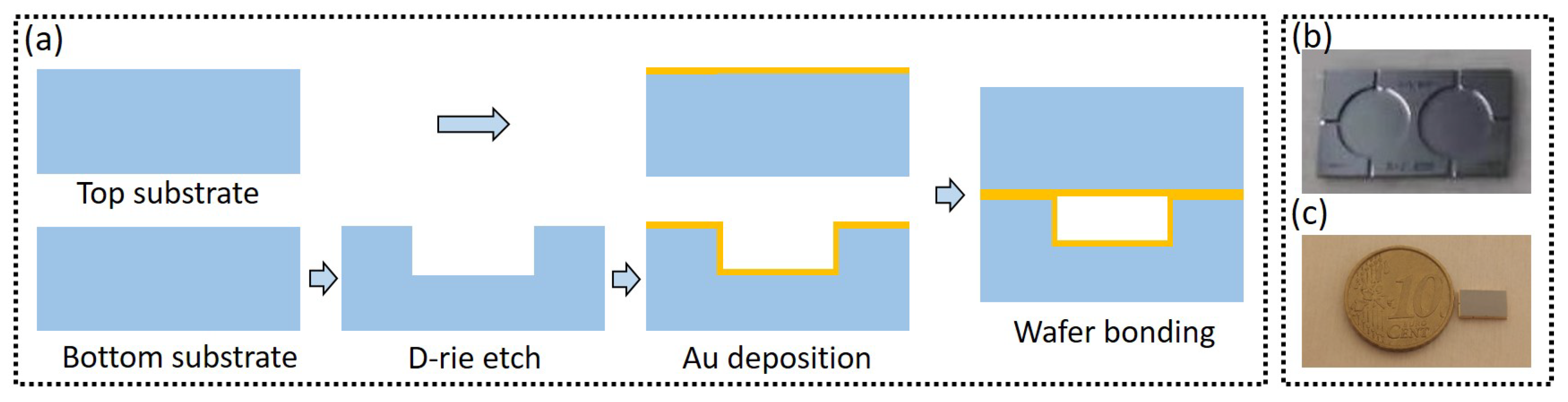
5.1. Sensor Fabrication
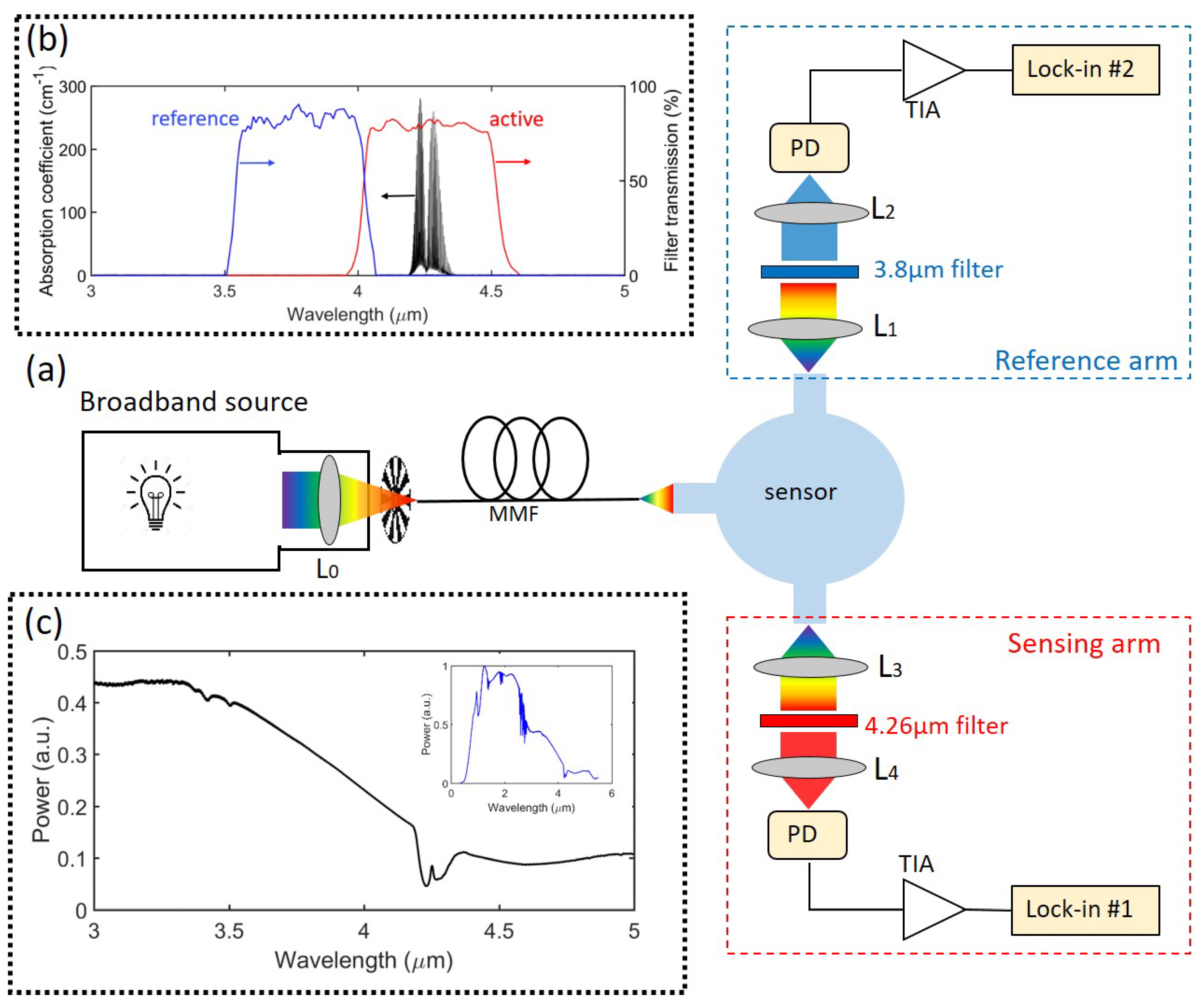
5.2. Measurement Setup
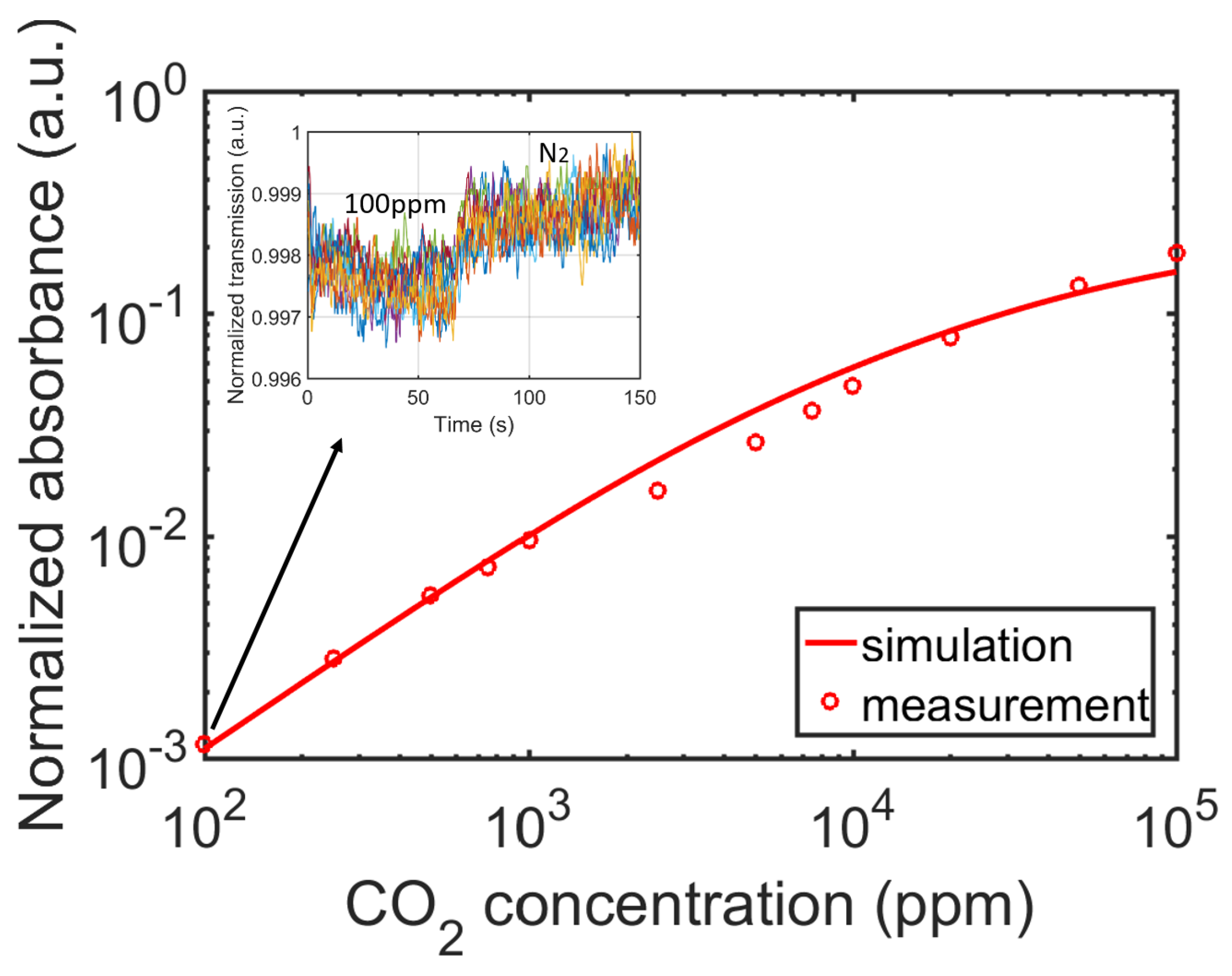
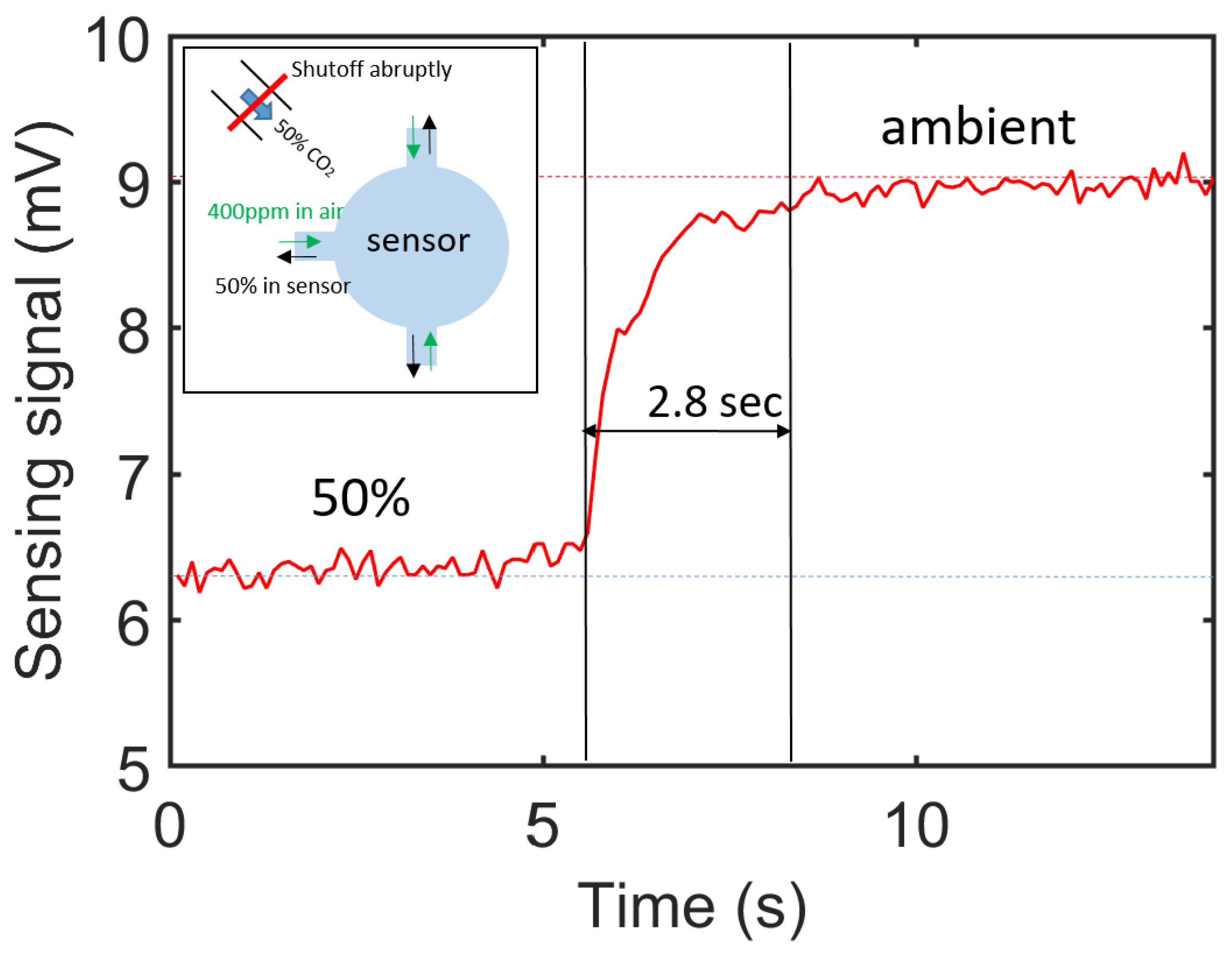
6. Experimental Results
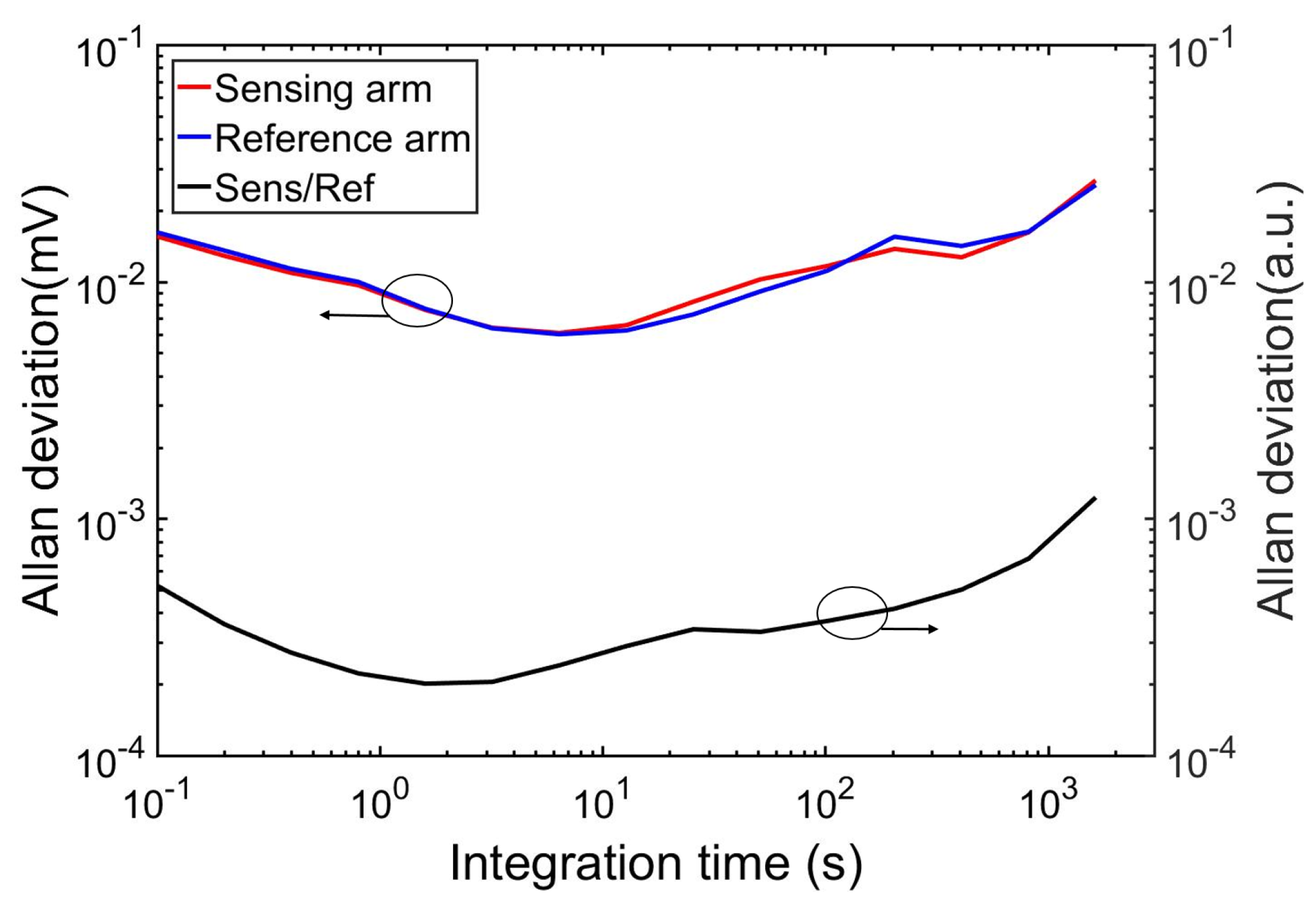
6.1. Allan Deviation Plot
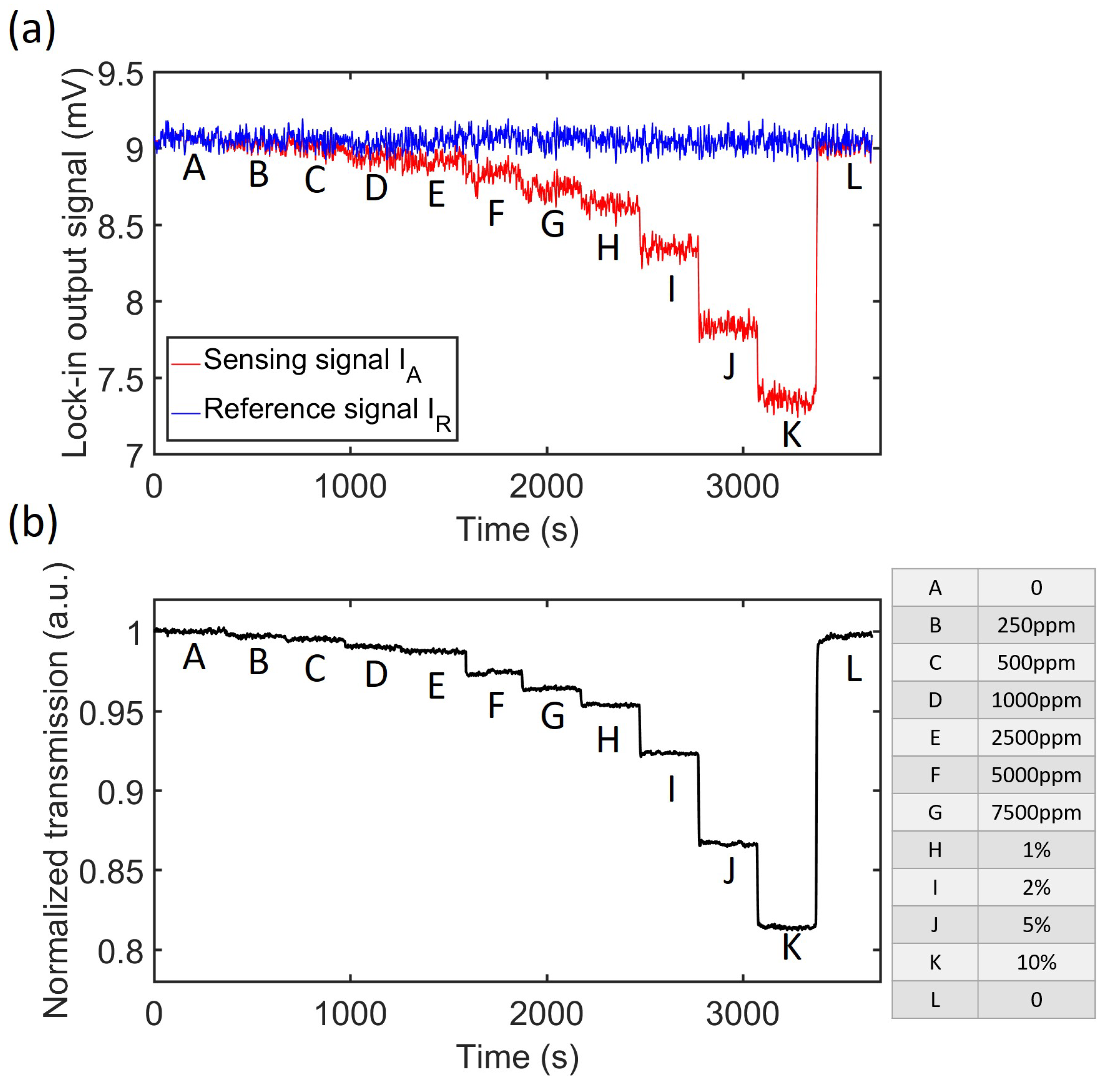
6.2. CO2 Response
6.3. Response Time
7. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ortiz Perez, A.; Bierer, B.; Scholz, L.; Wöllenstein, J.; Palzer, S. A Wireless Gas Sensor Network to Monitor Indoor Environmental Quality in Schools. Sensors 2018, 18, 4345. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zheng, L.; Niu, X.; Zheng, C.; Wang, Y.; Tittel, F.K. Mid-infrared absorption-spectroscopy-based carbon dioxide sensor network in greenhouse agriculture: Development and deployment. Appl. Opt. 2016, 55, 7029–7036. [Google Scholar] [CrossRef] [PubMed]
- Wells, S.L.; DeSimone, J. CO2 technology platform: An important tool for environmental problem solving. Angew. Chem. Int. Ed. 2001, 40, 518–527. [Google Scholar] [CrossRef]
- Europe Advanced CO2 Sensor Market Analysis—Global Forecast 2016 to 2022. Available online: https://www.marketresearchfuture.com/reports/europe-advanced-co2-sensor-market-2574 (accessed on 30 May 2019).
- Directive 2006/40/EC of the European Parliament and of the Council of 17 May 2006 Relating to Emissions from air-Conditioning Systems in Motor Vehicles and Amending Council Directive 70/156/EEC. Available online: https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2006:161:0012:0018:EN:PDF (accessed on 28 May 2019).
- Aprea, C.; Greco, A.; Maiorino, A. The substitution of R134a with R744: An exergetic analysis based on experimental data. Int. J. Refrig. 2013, 36, 2148–2159. [Google Scholar] [CrossRef]
- Malvicino, C.; Seccardini, R.; Markowitz, M.; Schuermanns, K.; Bergami, A.; Arnaud, C.; Haller, R.; Petitjean, C.; Strupp, C.; Lemke, N.; et al. B-Cool pRoject-Ford Ka and Fiat Panda r-744 Mac Systems; 2009-01-0967; SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Law, J.; Watkins, S.; Alexander, D. In-flight carbon dioxide exposures and related symptoms: Association, susceptibility, and operational implications. NASA Tech. Pap. 2010, 2010, 216126. [Google Scholar]
- Satish, U.; Mendell, M.J.; Shekhar, K.; Hotchi, T.; Sullivan, D.; Streufert, S.; Fisk, W.J. Is CO2 an indoor pollutant? Direct effects of low-to-moderate CO2 concentrations on human decision-making performance. Environ. Health Perspect. 2012, 120, 1671–1677. [Google Scholar] [CrossRef]
- Allen, J.G.; MacNaughton, P.; Satish, U.; Santanam, S.; Vallarino, J.; Spengler, J.D. Associations of cognitive function scores with carbon dioxide, ventilation, and volatile organic compound exposures in office workers: A controlled exposure study of green and conventional office environments. Environ. Health Perspect. 2015, 124, 805–812. [Google Scholar] [CrossRef] [PubMed]
- Willa, C.; Yuan, J.; Niederberger, M.; Koziej, D. When Nanoparticles Meet Poly(Ionic Liquid)s: Chemoresistive CO2 Sensing at Room Temperature. Adv. Funct. Mater. 2015, 25, 2537–2542. [Google Scholar]
- Kreno, L.E.; Leong, K.; Farha, O.K.; Allendorf, M.; Van Duyne, R.P.; Hupp, J.T. Metal—organic framework materials as chemical sensors. Chem. Rev. 2011, 112, 1105–1125. [Google Scholar] [CrossRef]
- Puligundla, P.; Jung, J.; Ko, S. Carbon dioxide sensors for intelligent food packaging applications. Food Control 2012, 25, 328–333. [Google Scholar] [CrossRef]
- Boudaden, J.; Klumpp, A.; Eisele, I.; Kutter, C. Smart capacitive CO2 sensor. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; pp. 1–3. [Google Scholar]
- Hodgkinson, J.; Tatam, R.P. Optical gas sensing: A review. Meas. Sci. Technol. 2012, 24, 012004. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, S.; Liu, H.; Hu, S.; Zhang, D.; Ning, H. A survey on gas sensing technology. Sensors 2012, 12, 9635–9665. [Google Scholar] [CrossRef] [PubMed]
- Neethirajan, S.; Jayas, D.; Sadistap, S. Carbon dioxide (CO2) sensors for the agri-food industry—A review. Food Bioprocess Technol. 2009, 2, 115–121. [Google Scholar] [CrossRef]
- Massie, C.; Stewart, G.; McGregor, G.; Gilchrist, J.R. Design of a portable optical sensor for methane gas detection. Sens. Actuators Chem. 2006, 113, 830–836. [Google Scholar] [CrossRef]
- Thurmond, K.; Loparo, Z.; Partridge, W.; Vasu, S.S. A light-emitting diode-(LED-) based absorption sensor for simultaneous detection of carbon monoxide and carbon dioxide. Appl. Spectrosc. 2016, 70, 962–971. [Google Scholar] [CrossRef] [PubMed]
- Tan, Q.; Tang, L.; Yang, M.; Xue, C.; Zhang, W.; Liu, J.; Xiong, J. Three-gas detection system with IR optical sensor based on NDIR technology. Opt. Lasers Eng. 2015, 74, 103–108. [Google Scholar] [CrossRef]
- Tan, Q.; Pei, X.; Zhu, S.; Sun, D.; Liu, J.; Xue, C.; Liang, T.; Zhang, W.; Xiong, J. Development of an optical gas leak sensor for detecting ethylene, dimethyl ether and methane. Sensors 2013, 13, 4157–4169. [Google Scholar] [CrossRef]
- Gibson, D.; MacGregor, C. A novel solid state non-dispersive infrared CO2 gas sensor compatible with wireless and portable deployment. Sensors 2013, 13, 7079–7103. [Google Scholar] [CrossRef]
- Hodgkinson, J.; Smith, R.; Ho, W.O.; Saffell, J.R.; Tatam, R.P. Non-dispersive infra-red (NDIR) measurement of carbon dioxide at 4.2 μm in a compact and optically efficient sensor. Sens. Actuators Chem. 2013, 186, 580–588. [Google Scholar] [CrossRef]
- Ayerden, N.P.; de Graaf, G.; Wolffenbuttel, R.F. Compact gas cell integrated with a linear variable optical filter. Opt. Express 2016, 24, 2981–3002. [Google Scholar] [CrossRef]
- Ayerden, N.P.; Ghaderi, M.; Enoksson, P.; de Graaf, G.; Wolffenbuttel, R.F. A miniaturized optical gas-composition sensor with integrated sample chamber. Sens. Actuators Chem. 2016, 236, 917–925. [Google Scholar] [CrossRef]
- Moumen, S.; Raible, I.; Krauß, A.; Wöllenstein, J. Infrared investigation of CO2 sorption by amine based materials for the development of a NDIR CO2 sensor. Sens. Actuators Chem. 2016, 236, 1083–1090. [Google Scholar] [CrossRef]
- Sklorz, A.; Schafer, A.; Lang, W. Merging ethylene NDIR gas sensors with preconcentrator-devices for sensitivity enhancement. Sens. Actuators Chem. 2012, 170, 21–27. [Google Scholar] [CrossRef]
- Jia, X.; Roelkens, G.; Baets, R.; Roels, J. A miniaturized non-dispersive infrared CO2 sensor based on a 2D integrating cylinder. In Proceedings of the Optical Sensors and Sensing Congress, San Jose, CA, USA, 25–27 June 2019. [Google Scholar]
- Rothman, L.S.; Gordon, I.E.; Babikov, Y.; Barbe, A.; Benner, D.C.; Bernath, P.F.; Birk, M.; Bizzocchi, L.; Boudon, V.; Brown, L.R.; et al. The HITRAN2012 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 4–50. [Google Scholar] [CrossRef]
- Circle Line Picking. Available online: http://mathworld.wolfram.com/CircleLinePicking.html (accessed on 30 May 2019).
- Fohrmann, L.S.; Sommer, G.; Pitruzzello, G.; Krauss, T.F.; Petrov, A.Y.; Eich, M. Integrating cell on chip—Novel waveguide platform employing ultra-long optical paths. APL Photonics 2017, 2, 096102. [Google Scholar] [CrossRef]
- Babar, S.; Weaver, J. Optical constants of Cu, Ag, and Au revisited. Appl. Opt. 2015, 54, 477–481. [Google Scholar] [CrossRef]
- Tholabs Inc. Available online: https://www.thorlabs.com/ (accessed on 30 May 2019).
| d [um] | R [mm] | TL [dB] | Leq [cm] |
|---|---|---|---|
| 100 | 1.4 | 7.5 | 3.4 |
| 200 | 2.0 | 7.4 | 3.5 |
| 300 | 2.6 | 7.6 | 3.8 |
| 400 | 3.0 | 7.6 | 3.9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.; Roels, J.; Baets, R.; Roelkens, G.
On-Chip Non-Dispersive Infrared CO2 Sensor Based on an Integrating Cylinder
Jia X, Roels J, Baets R, Roelkens G.
On-Chip Non-Dispersive Infrared CO2 Sensor Based on an Integrating Cylinder
Jia, Xiaoning, Joris Roels, Roel Baets, and Gunther Roelkens.
2019. "On-Chip Non-Dispersive Infrared CO2 Sensor Based on an Integrating Cylinder
Jia, X., Roels, J., Baets, R., & Roelkens, G.
(2019). On-Chip Non-Dispersive Infrared CO2 Sensor Based on an Integrating Cylinder






