Hysteresis Compensation in Force/Torque Sensors Using Time Series Information
Abstract
:1. Introduction
2. Basic Principles
2.1. Signals of a Strain Gauge-Type Force Sensor
2.2. Linear Regression
3. Proposed Method
3.1. Machine Learning Incorporating Time Series Information
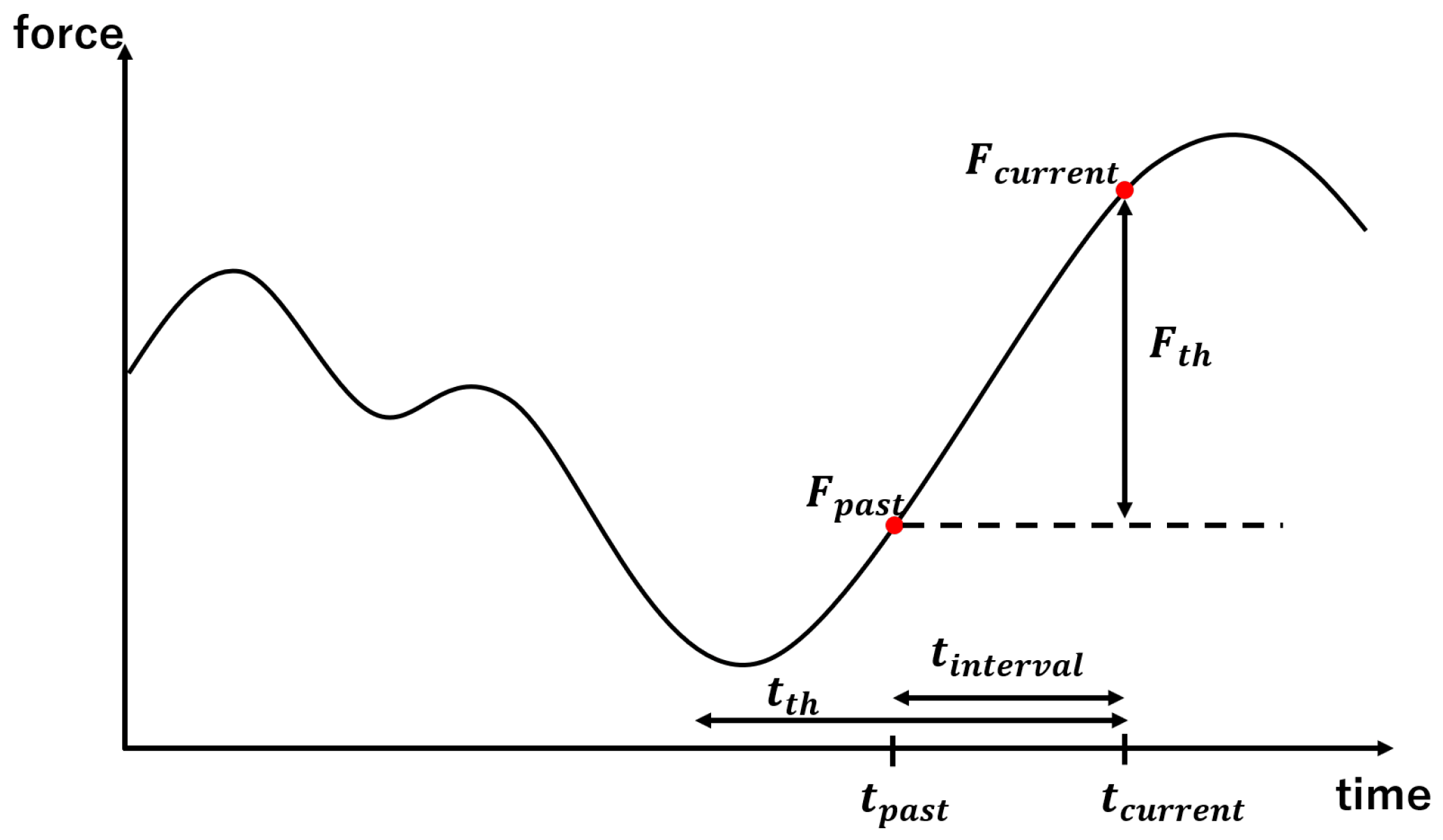
3.1.1. Acquiring Time Series Information
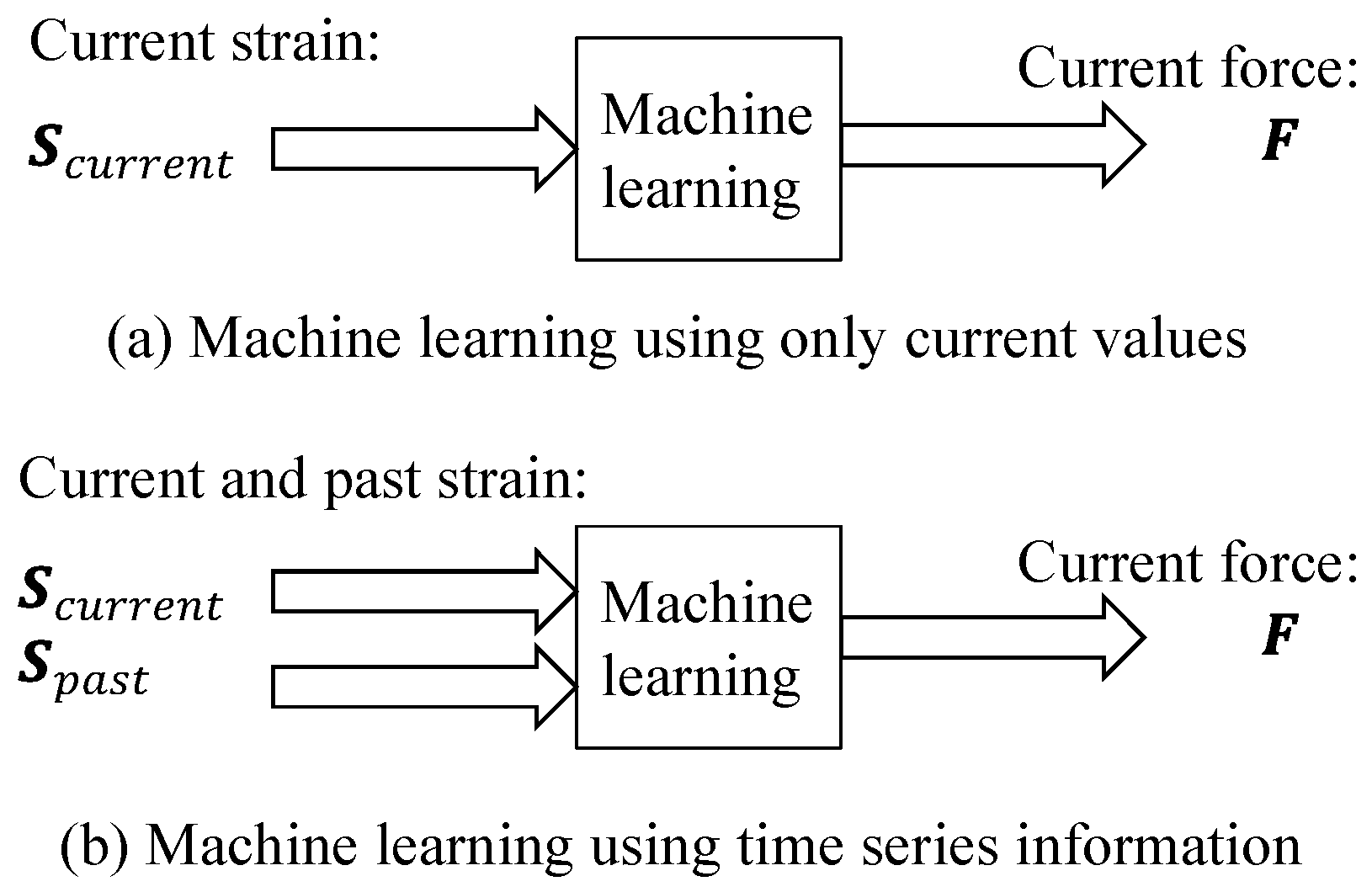
3.1.2. Utilization of Time Series Information for Machine Learning
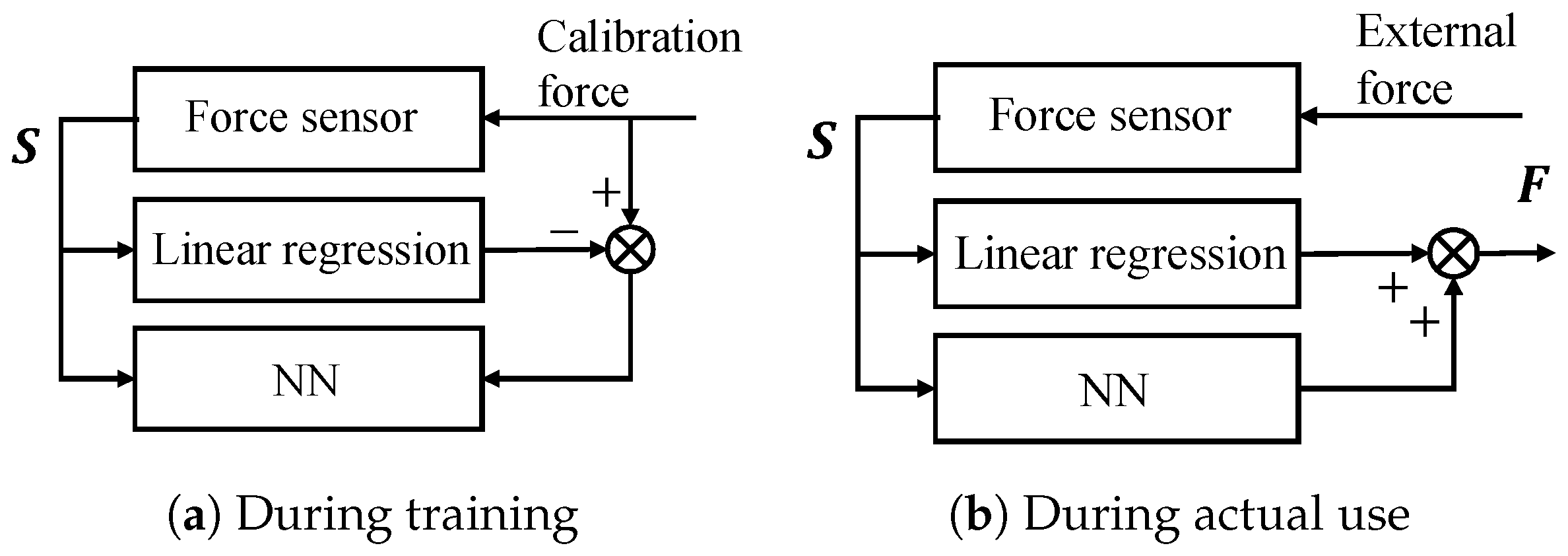
3.2. NN and Hybrid Model
4. Experiment
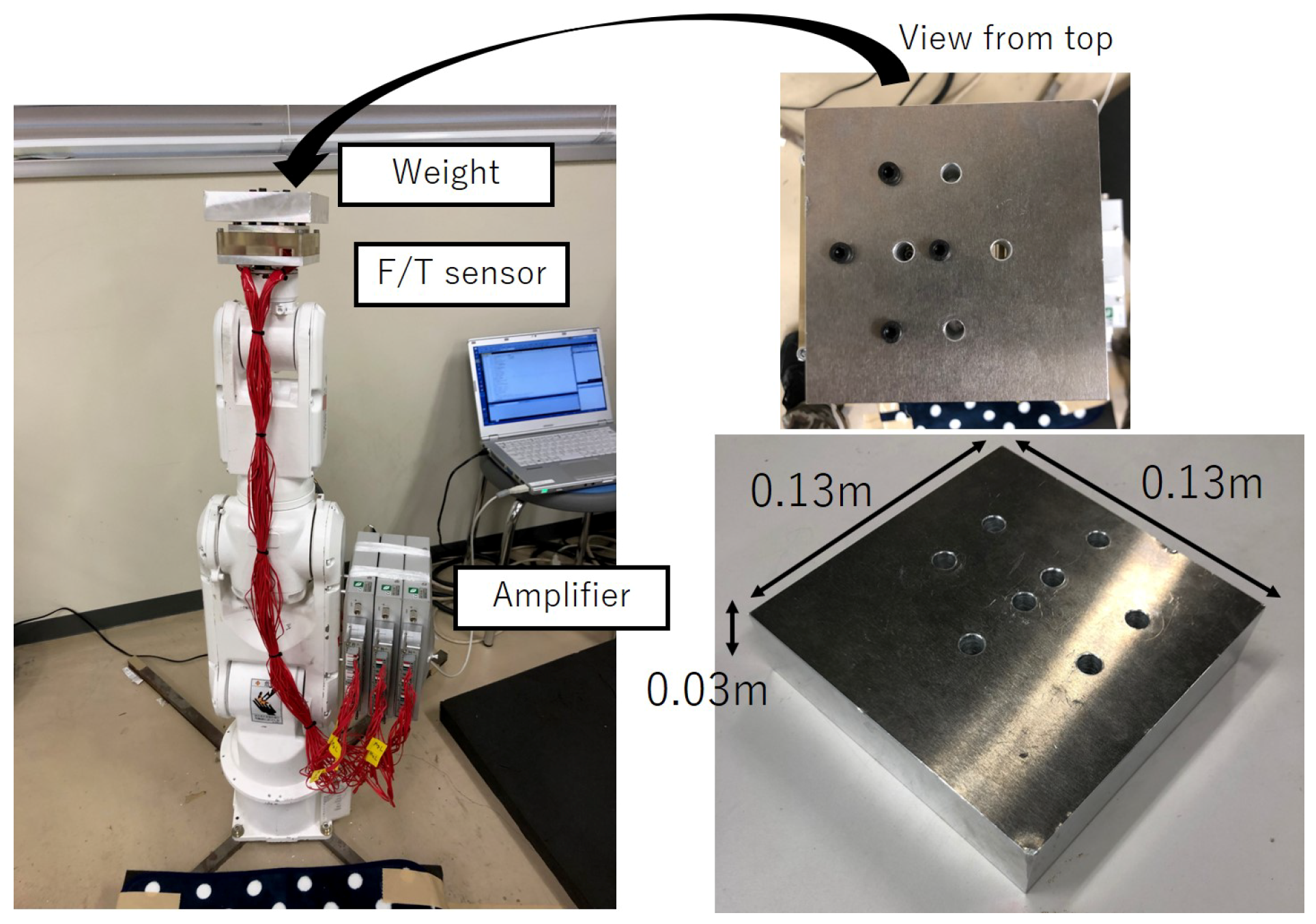
4.1. Experimental Equipment
4.1.1. Strain Gauge and Strain Measuring Device
4.1.2. Robot Arm-Based Force Application Device
4.2. Learning
4.2.1. NN Structure and the Hybrid Model
4.2.2. Training Patterns
- Pattern A
- (amount of training data: large)Six different paths are given in the experiments, so that most of the operating range is covered. The trajectories are all based on sinusoidal waves with random amplitude in each direction. The frequency of the sinusoidal wave was set to 0.05 Hz to avoid error owing to inertia force error. Five of these were used for training and the other was used for testing. Each path was examined with three trajectories with different velocities. Depending on the speed of each trajectory, the recorded time differs as 95 s, 135 s, and 175 s for fast, medium and slow speeds, respectively. We acquired five paths for each of these, recorded them at a rate of 20 samples/s and performed training with a total of 202,500 samples.
- Pattern B
- (amount of training data: small)The amount of data used for the training and testing of pattern A was reduced to 1/10th of the original size, simply by decimating the same trajectory. Through this operation, we created a state in which the amount of data was simply reduced and verified the precision of each technique. Depending on the speed of each trajectory, the time recorded differs as 95 s, 135 s and 175 s for fast, medium and slow speeds. We acquired five paths for each of these, recorded them at a rate of 2 samples/s and performed training with a total of 20,250 samples.
4.3. Results
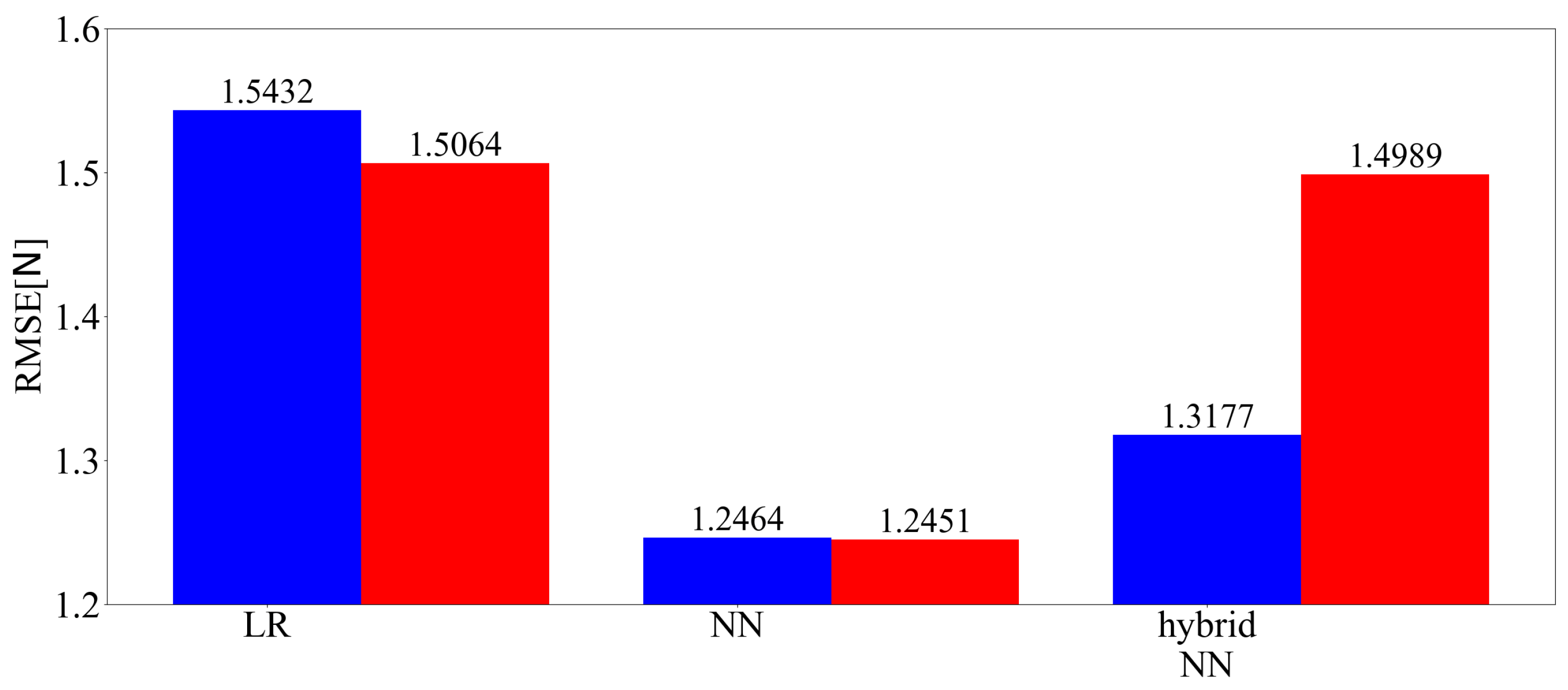
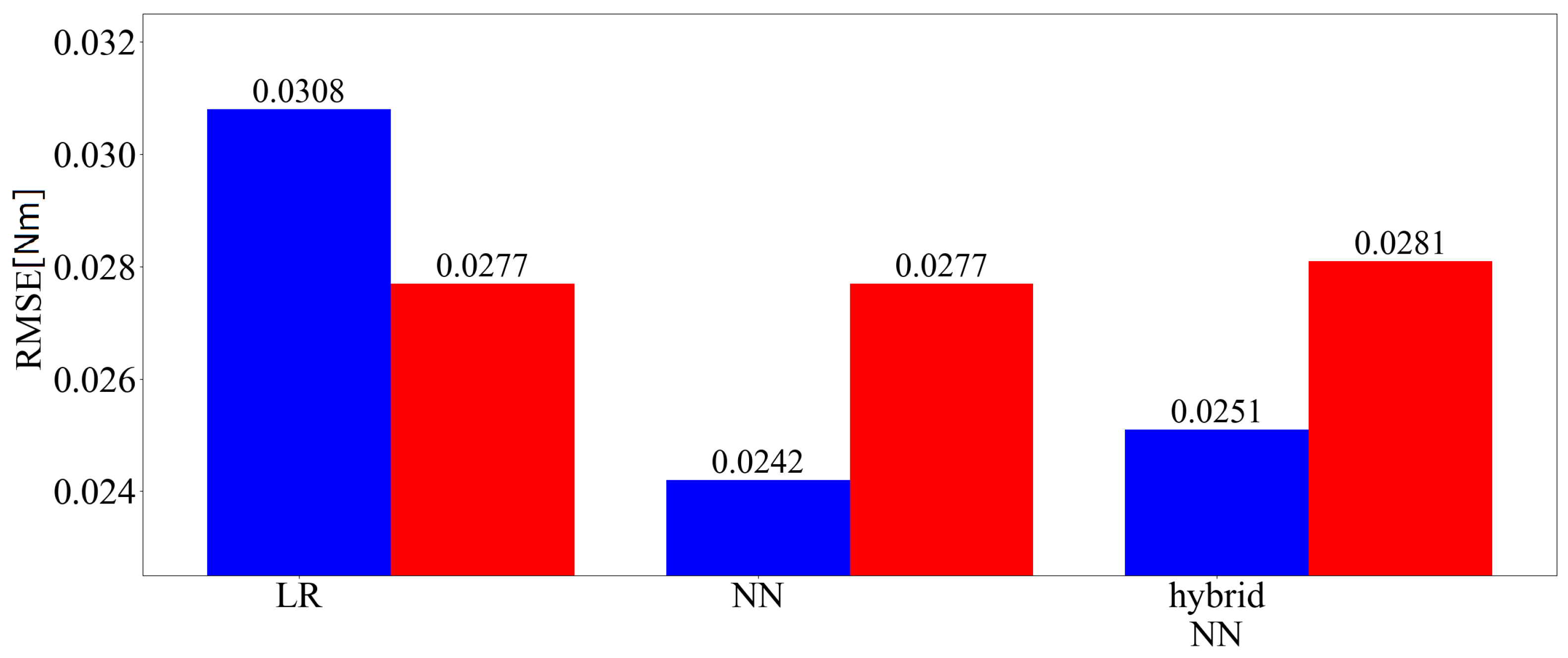
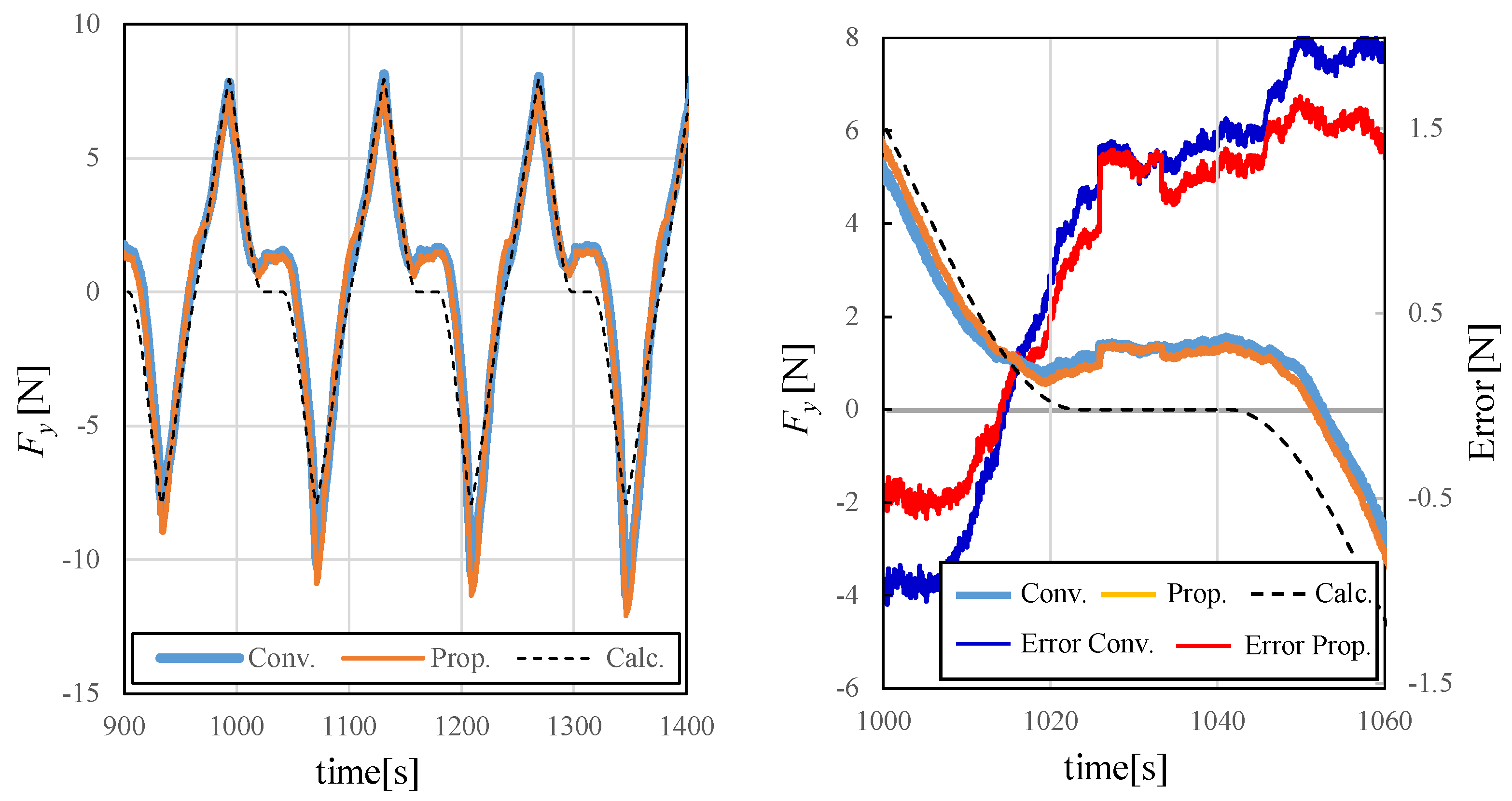
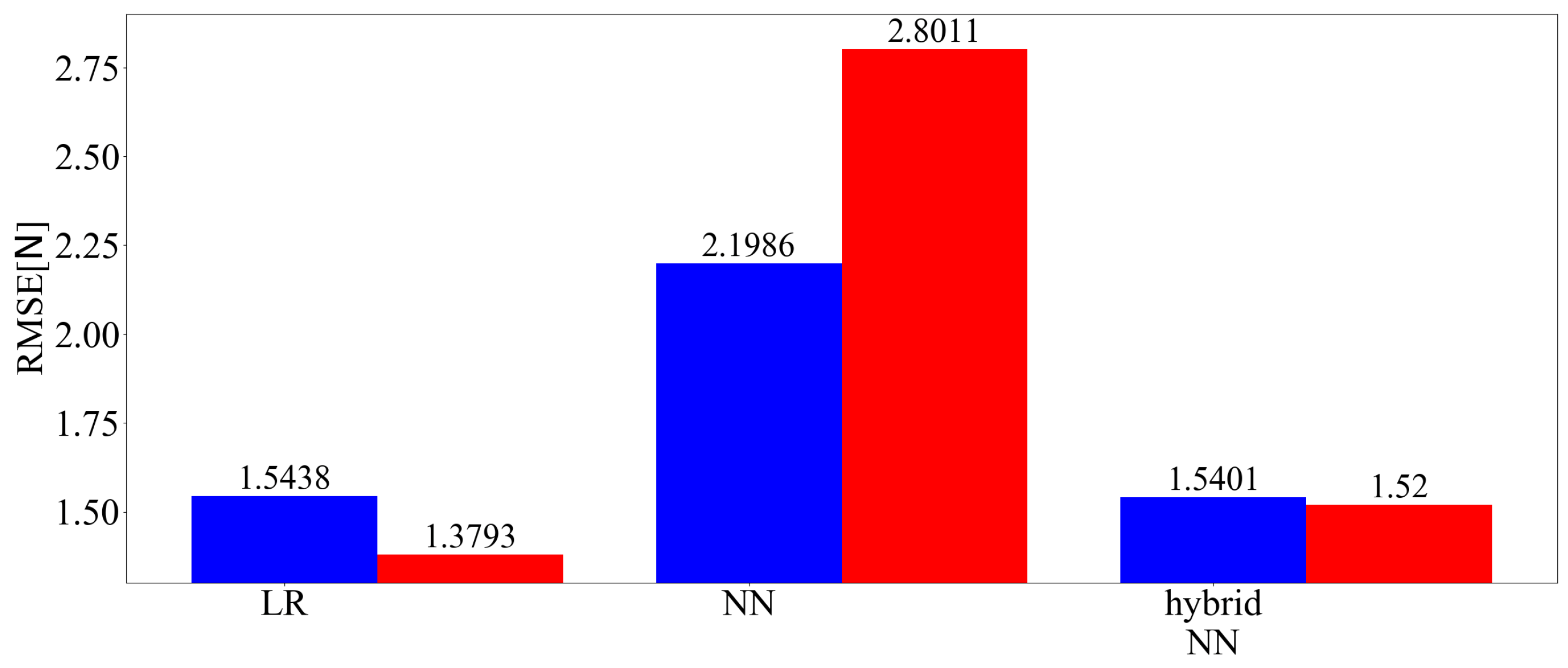
4.3.1. Pattern A (Amount of Training Data: Large)
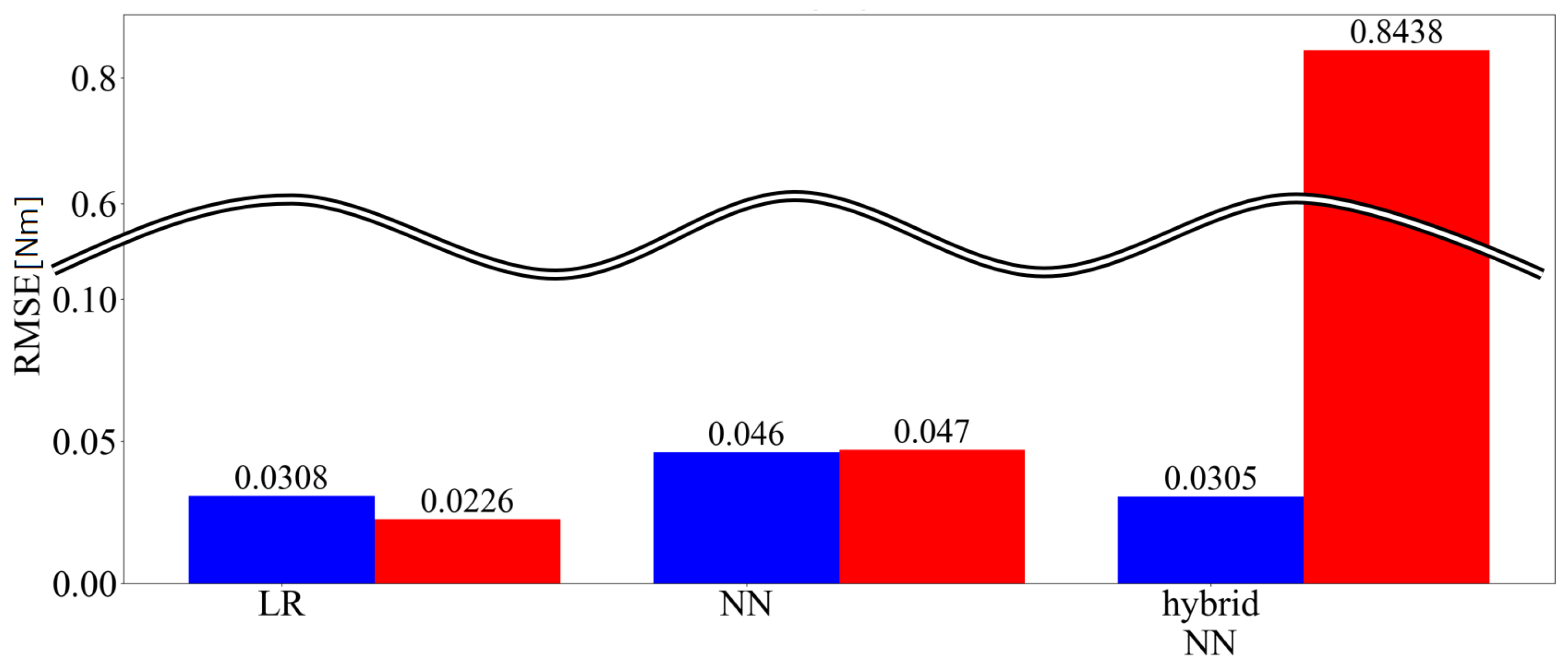
4.3.2. Pattern B (Amount of Training Data: Small)
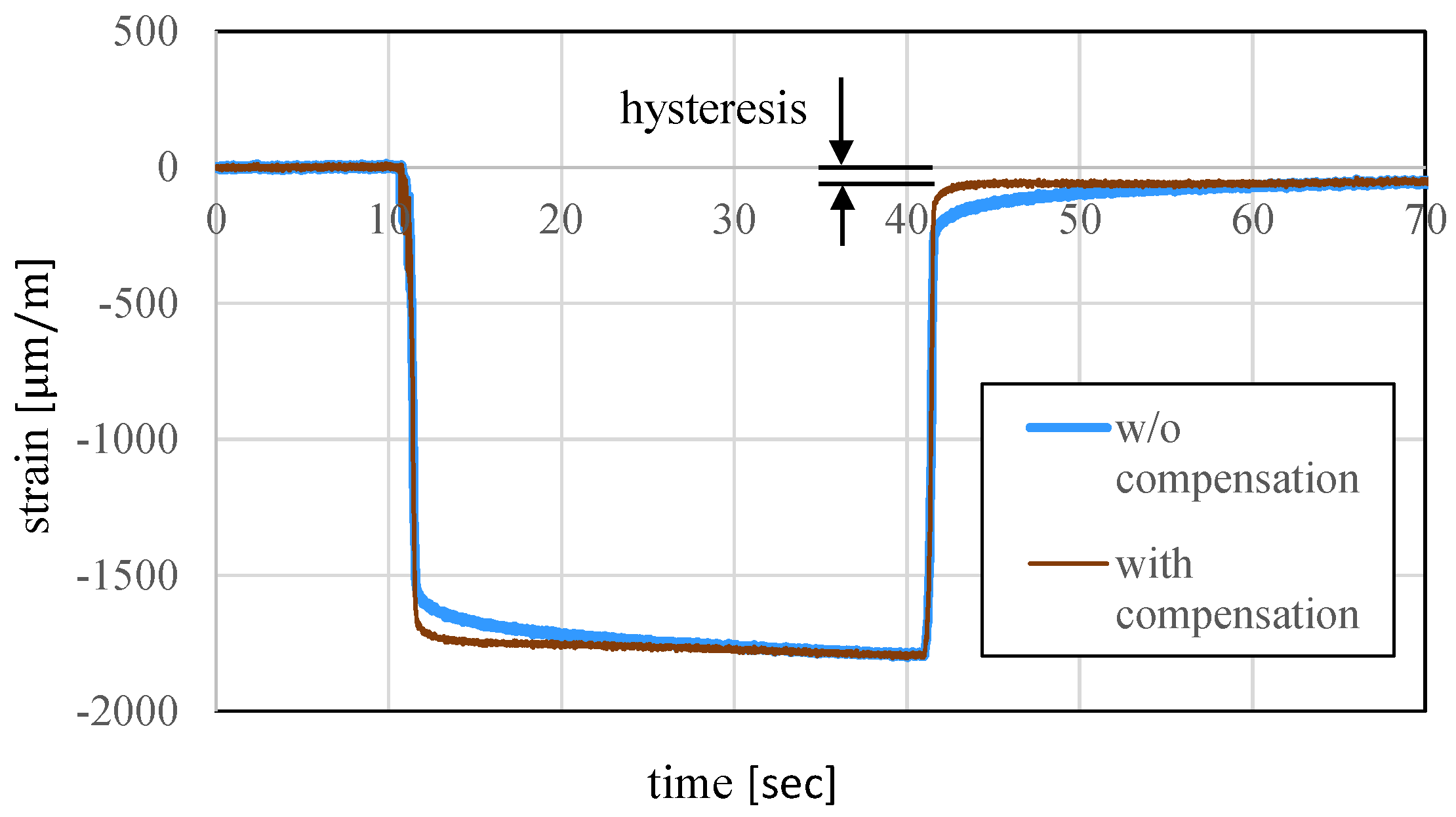
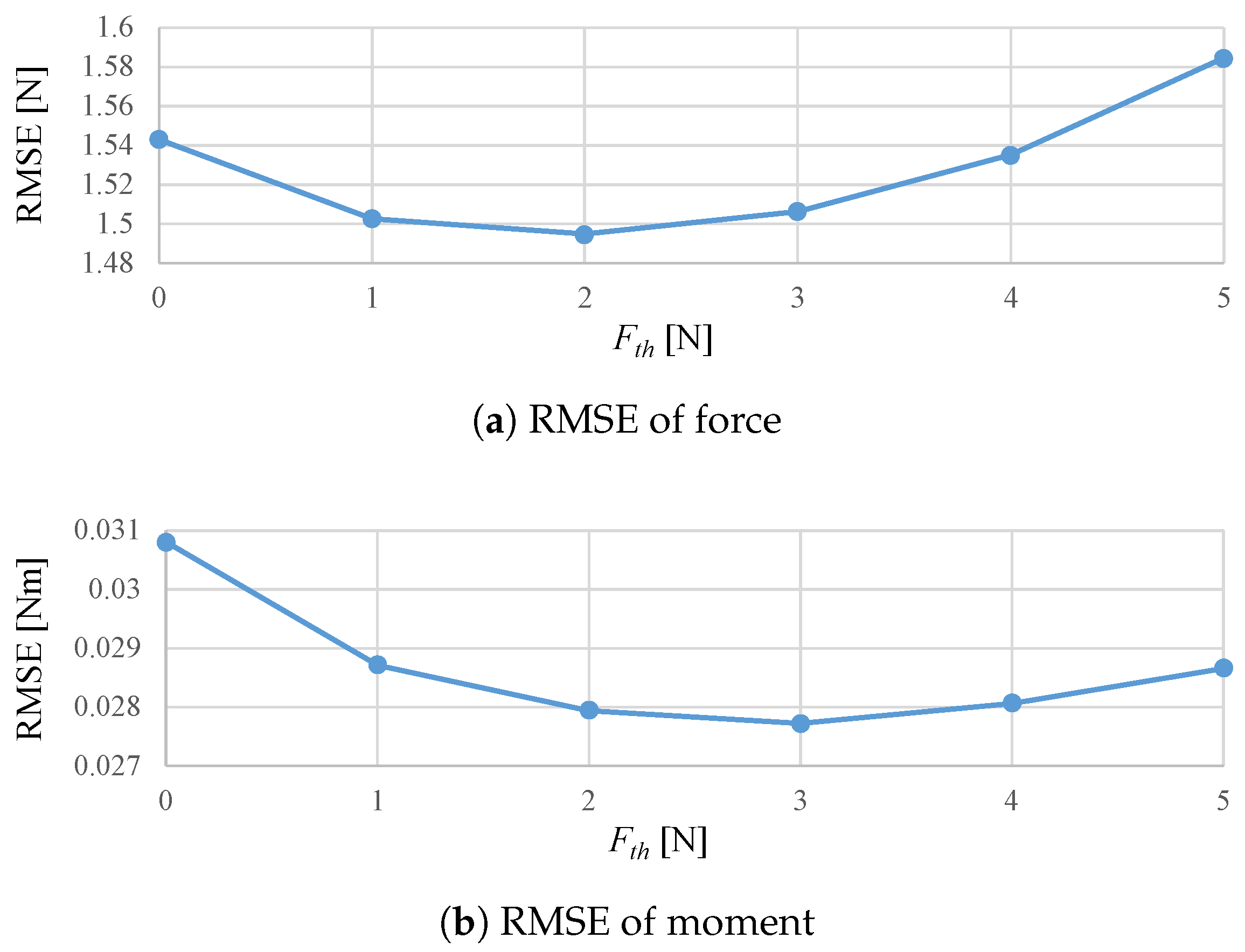
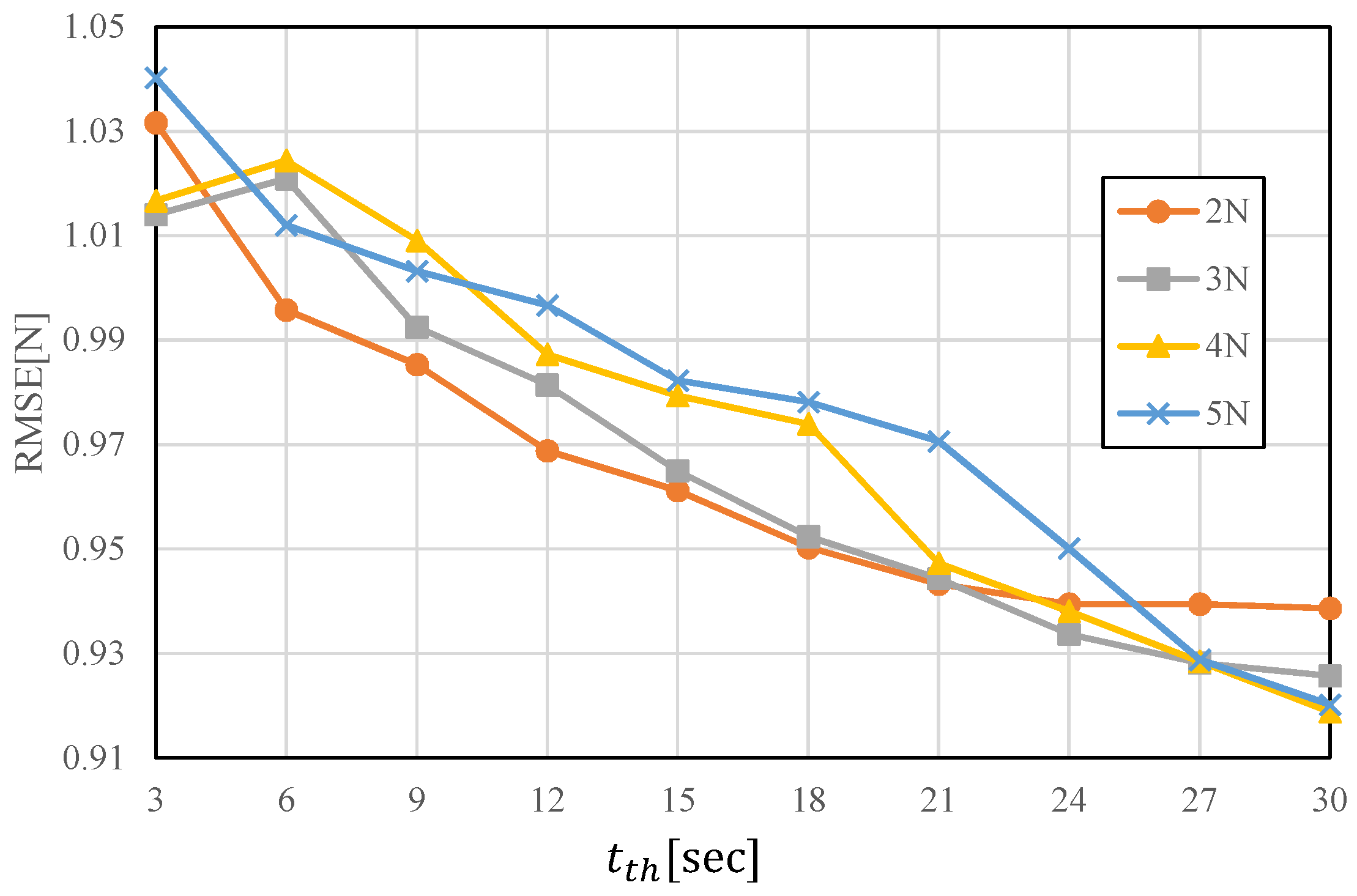
4.3.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Murakami, T.; Yu, F.; Ohnishi, K. Torque Sensorless Control in Multidegree-of-Freedom Manipulator. IEEE Trans. Ind. Electron. 1993, 40, 259–265. [Google Scholar] [CrossRef]
- Park, Y.; Paine, N.; Oh, S. Development of force observer in series elastic actuator for dynamic control. IEEE Trans. Ind. Electron. 2018, 65, 2398–2407. [Google Scholar] [CrossRef]
- Liang, Q.; Wu, W.; Coppola, G.; Zhang, D.; Sun, W.; Ge, Y.; Wang, Y. Calibration and decoupling of multi-axis robotic force/moment sensors. Robot. Comput. Integr. Manuf. 2018, 49, 301–308. [Google Scholar] [CrossRef]
- Yoshikawa, T.; Miyazaki, T. A Six-Axis Force Sensor with Three-Dimensional Cross-Shape Structure. In Proceedings of the IEEE 1989 International Conference on Robotics and Automation, Scottsdale, AZ, USA, 14–19 May 1989; pp. 249–255. [Google Scholar]
- Nishiwaki, K.; Murakami, Y.; Kagami, S.; Kuniyoshi, Y.; Inaba, M.; Inoue, H. A Six-Axis Force Sensor with Parallel Support Mechanism to Measure the Ground Reaction Force of Humanoid Robot. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 3, pp. 2277–2282. [Google Scholar]
- Beyeler, F.; Muntwyler, S.; Nelson, B.J. A six-axis mems force–torque sensor with micro-newton and nano-newtonmeter resolution. J. Microelectromech. Syst. 2009, 18, 433–441. [Google Scholar] [CrossRef]
- Dobrzynska, J.A.; Gijs, M. Polymer-based flexible capacitive sensor for three-axial force measurements. J. Micromech. Microeng. 2012, 23, 015009. [Google Scholar] [CrossRef]
- Pan, L.; Chortos, A.; Yu, G.; Wang, Y.; Isaacson, S.; Allen, R.; Shi, Y.; Dauskardt, R.; Bao, Z. An ultra-sensitive resistive pressure sensor based on hollow-sphere microstructure induced elasticity in conducting polymer film. Nat. Commun. 2014, 5, 3002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.-C.; Kim, K.-S.; Kim, S. Note: A compact three-axis optical force/torque sensor using photo-interrupters. Rev. Sci. Instrum. 2013, 84, 126109. [Google Scholar] [CrossRef] [PubMed]
- Su, H.; Fischer, G.S. A 3-Axis Optical Force/Torque Sensor for Prostate Needle Placement in Magnetic Resonance Imaging Environments. In Proceedings of the IEEE International Conference on Technologies for Practical Robot Applications, Woburn, MA, USA, 9–10 November 2009; pp. 5–9. [Google Scholar]
- Polygerinos, P.; Puangmali, P.; Schaeffter, T.; Razavi, R.; Seneviratne, L.D.; Althoefer, K. Novel Miniature Mri-Compatible Fiber-Optic Force Sensor for Cardiac Catheterization Procedures. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 2598–2603. [Google Scholar]
- Ma, Y.; Xie, S.; Zhang, X.; Luo, Y. Hybrid calibration method for six-component force/torque transducers of wind tunnel balance based on support vector machines. Chin. J. Aeronaut. 2013, 26, 554–562. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-J.; Wang, G.-C.; Yang, X.; Zhang, H.; Han, B.-B.; Zhang, Y.-L. Research on static decoupling algorithm for piezoelectric six axis force/torque sensor based on lssvr fusion algorithm. Mech. Syst. Signal Process. 2018, 110, 509–520. [Google Scholar] [CrossRef]
- Lu, T.-F.; Lin, G.C.; He, J.R. Neural-network-based 3d force/torque sensor calibration for robot applications. Eng. Appl. Artif. Intell. 1997, 10, 87–97. [Google Scholar] [CrossRef]
- Khan, S.A.; Shahani, D.; Agarwala, A. Sensor calibration and compensation using artificial neural network. ISA Trans. 2003, 42, 337–352. [Google Scholar] [CrossRef]
- De Maria, G.; Natale, C.; Pirozzi, S. Force/tactile sensor for robotic applications. Sens. Actuators A Phys. 2012, 175, 60–72. [Google Scholar] [CrossRef]
- Oh, H.S.; Kang, G.; Kim, U.; Seo, J.K.; You, W.S.; Choi, H.R. Force/Torque Sensor Calibration Method by Using Deep-Learning. In Proceedings of the IEEE 14th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, Korea, 28 June–1 July 2017; pp. 777–782. [Google Scholar]
- Sun, Y.; Liu, Y.; Liu, H. Analysis Calibration System Error of Six-Dimension Force/Torque Sensor for Space Robot. In Proceedings of the IEEE International Conference Mechatronics and Automation (ICMA), Tianjin, China, 3–6 August 2014; pp. 347–352. [Google Scholar]
- Tomo, T.P.; Somlor, S.; Schmitz, A.; Jamone, L.; Huang, W.; Kristanto, H.; Sugano, S. Design and characterization of a three-axis hall effect-based soft skin sensor. Sensors 2016, 16, 491. [Google Scholar] [CrossRef] [PubMed]
- Urban, S.; Ludersdorfer, M.; Van Der Smagt, P. Sensor calibration and hysteresis compensation with heteroscedastic gaussian processes. IEEE Sens. J. 2015, 15, 6498–6506. [Google Scholar] [CrossRef]
- Horii, T.; Nagai, Y.; Natale, L.; Giovannini, F.; Metta, G.; Asada, M. Compensation for Tactile Hysteresis Using Gaussian Process with sEnsory Markov Property. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; pp. 993–998. [Google Scholar]
- Okumura, D.; Sakaino, S.; Tsuji, T. Miniaturization of Multistage High Dynamic Range Six-Axis Force Sensor. In Proceedings of the IEEE 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4297–4302. [Google Scholar]
- Okumura, D.; Sakaino, S.; Tsuji, T. Development of a Multistage Six-Axis Force Sensor with a High Dynamic Range. In Proceedings of the IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 1386–1391. [Google Scholar]
- Koike, R.; Sakaino, S.; Tsuji, T. Hysteresis Compensation in Force/Torque Sensor Based on Machine Learning. In Proceedings of the 44th Annual Conference of the IEEE Industrial Electronics Society (IECON2018), Washington, DC, USA, 21–23 October 2018; pp. 2769–2774. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koike, R.; Sakaino, S.; Tsuji, T. Hysteresis Compensation in Force/Torque Sensors Using Time Series Information. Sensors 2019, 19, 4259. https://doi.org/10.3390/s19194259
Koike R, Sakaino S, Tsuji T. Hysteresis Compensation in Force/Torque Sensors Using Time Series Information. Sensors. 2019; 19(19):4259. https://doi.org/10.3390/s19194259
Chicago/Turabian StyleKoike, Ryuichiro, Sho Sakaino, and Toshiaki Tsuji. 2019. "Hysteresis Compensation in Force/Torque Sensors Using Time Series Information" Sensors 19, no. 19: 4259. https://doi.org/10.3390/s19194259




