Lower Limb Locomotion Activity Recognition of Healthy Individuals Using Semi-Markov Model and Single Wearable Inertial Sensor
Abstract
:1. Introduction
- Semi-Markov structure is embedded into the TMC model to make the hidden state transition closer to the realistic motion.
- GMM is adopted to overcome the weakness of non-parametric density, while still allowing to model non-Gaussian data.
- An EM-based on-line learning algorithm is adopted to SemiTMC-GMM for making the algorithm work on-line.
2. Related Works
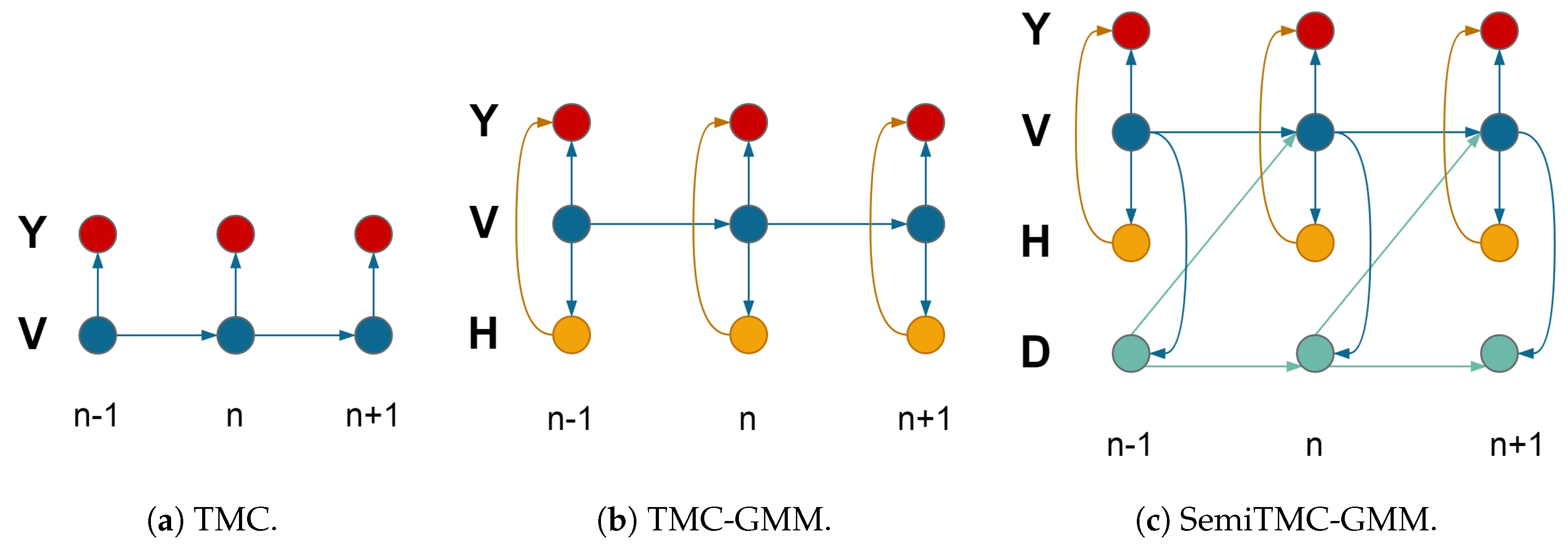
3. Model
3.1. Triplet Markov Chain
3.2. TMC Embedding a Gaussian Mixture Model
3.3. Semi TMC-GMM
- In Equation (9), when , the transition behaves the same as the state transition of TMC and TMC-GMM, which means that can be different from or same as , depending on the distribution of .
- is the probability of the minimal remaining sojourn time of , conditioned on and .
- and are same as the ones in TMC-GMM, shown in Equation (7a).
3.4. Application of SemiTMC-GMM
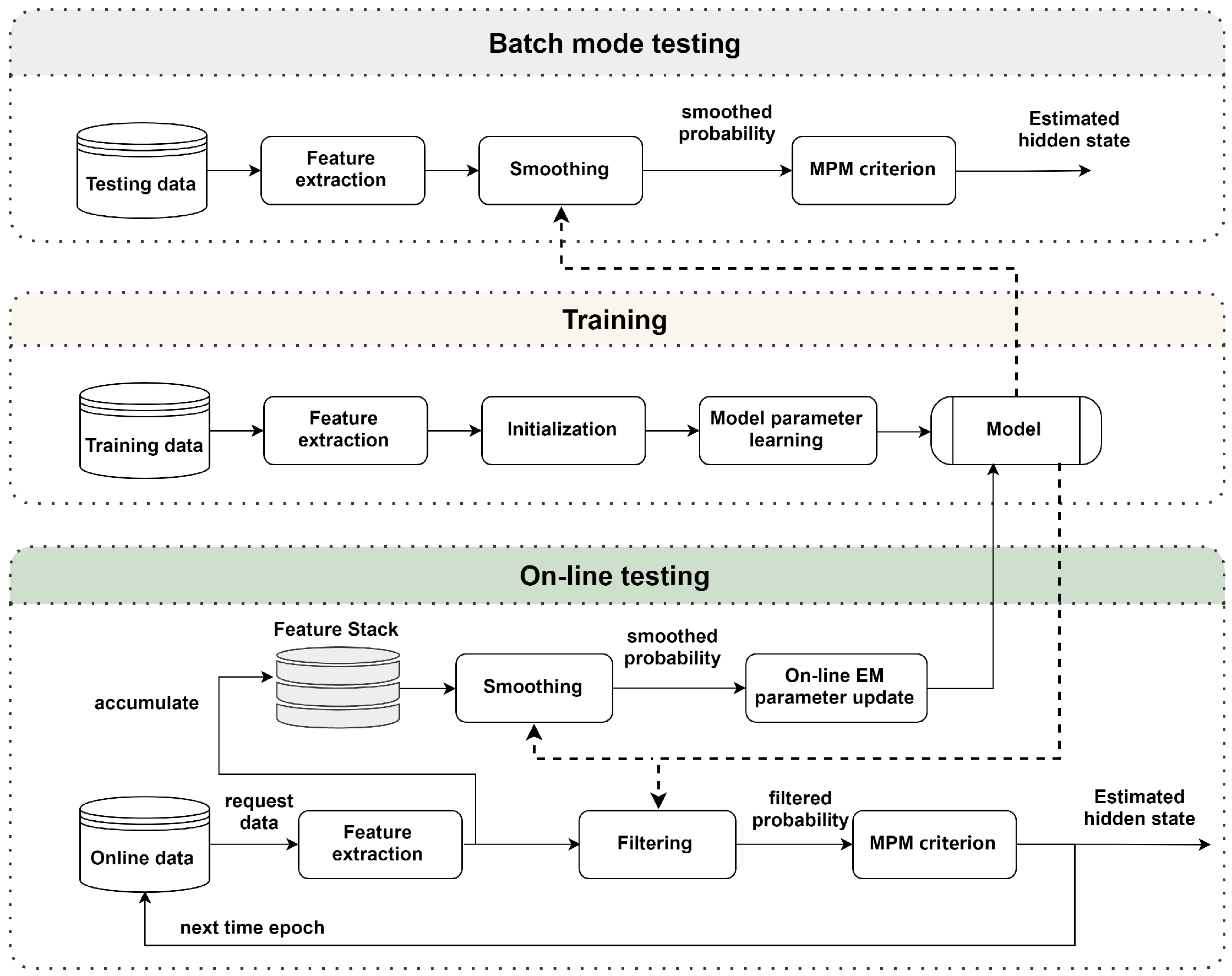
4. Parameter Estimation
4.1. Batch Mode EM Algorithm
4.2. Sufficient Data Statistics
4.3. On-Line Estimation
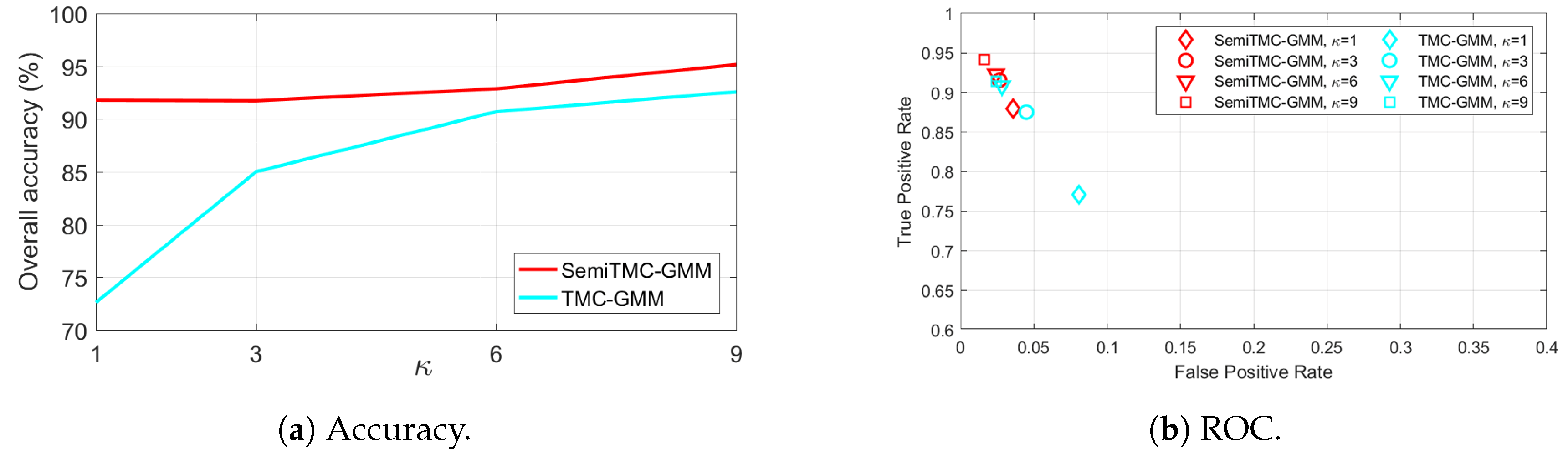
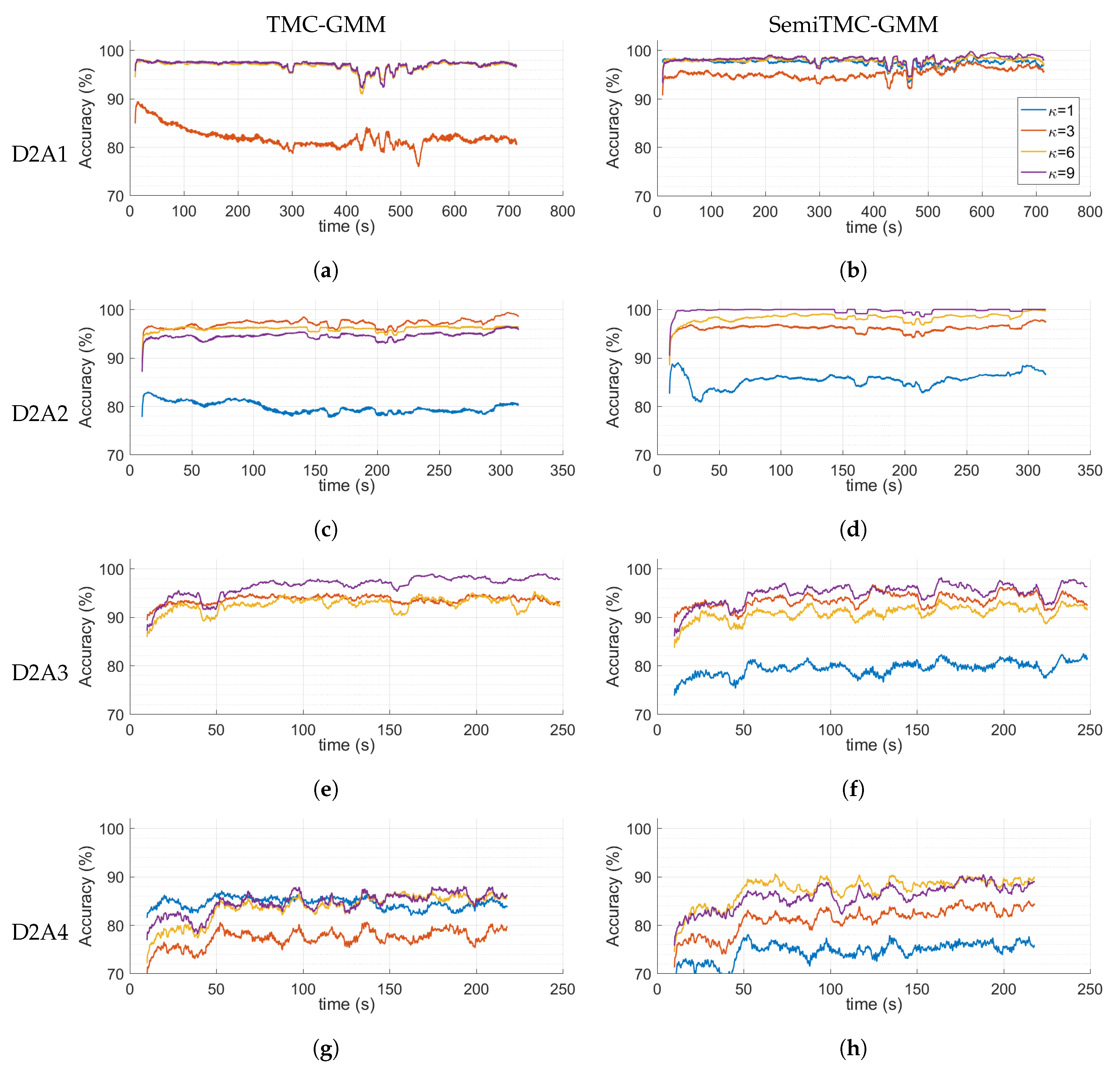
5. Experimental Results
5.1. SDA Dataset
5.2. LMFIMU Dataset
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhu, Z.; Lu, Y.; You, C.; Chiang, C. Deep learning for sensor-based rehabilitation exercise recognition and evaluation. Sensors 2019, 19, 887. [Google Scholar] [CrossRef] [PubMed]
- Susnea, I.; Dumitriu, L.; Talmaciu, M.; Pecheanu, E.; Munteanu, D. Unobtrusive monitoring the daily activity routine of elderly people living alone, with low-cost binary sensors. Sensors 2019, 19, 2264. [Google Scholar] [CrossRef] [PubMed]
- Elhoushi, M.; Georgy, J.; Noureldin, A.; Korenberg, M.J. A survey on approaches of motion mode recognition using sensors. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1662–1686. [Google Scholar] [CrossRef]
- Waheed, S.A.; Khader, P.S.A. A novel approach for smart and cost effective IoT based elderly fall detection system using Pi camera. In Proceedings of the IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Coimbatore, India, 14–16 December 2017; pp. 1–4. [Google Scholar]
- Hsu, Y.; Yang, S.; Chang, H.; Lai, H. Human daily and sport activity recognition using a wearable inertial sensor network. IEEE Access 2018, 6, 31715–31728. [Google Scholar] [CrossRef]
- Xie, L.; Tian, J.; Ding, G.; Zhao, Q. Human activity recognition method based on inertial sensor and barometer. In Proceedings of the IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Moltrasio, Italy, 26–29 March 2018; pp. 1–4. [Google Scholar]
- Li, H.; Derrode, S.; Pieczynski, W. An adaptive and on-line IMU-based locomotion activity classification method using a triplet Markov model. Neurocomputing 2019, 362, 94–105. [Google Scholar] [CrossRef]
- Gorynin, I.; Gangloff, H.; Monfrini, E.; Pieczynski, W. Assessing the segmentation performance of pairwise and triplet Markov models. Signal Process. 2018, 145, 183–192. [Google Scholar] [CrossRef]
- Pieczynski, W.; Hulard, C.; Veit, T. Triplet Markov chains in hidden signal restoration. In Image and Signal Processing for Remote Sensing VIII; International Society for Optics and Photonics: Crete, Greece, 2003; Volume 4885, pp. 58–68. [Google Scholar]
- Barshan, B.; Yüksek, M.C. Recognizing daily and sports activities in two open source machine learning environments using body-worn sensor units. Comput. J. 2014, 57, 1649–1667. [Google Scholar] [CrossRef]
- Parri, A.; Yuan, K.; Marconi, D.; Yan, T.; Crea, S.; Munih, M.; Lova, R.M.; Vitiello, N.; Wang, Q. Real-time hybrid locomotion mode recognition for lower limb wearable robots. IEEE/ASME Trans. Mechatron. 2017, 22, 2480–2491. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, Q.; Soh, Y.C.; Zhang, L. Robust human activity recognition using smartphone sensors via CT-PCA and online SVM. IEEE Trans. Ind. Inform. 2017, 13, 3070–3080. [Google Scholar] [CrossRef]
- Wannenburg, J.; Malekian, R. Physical activity recognition from smartphone accelerometer data for user context awareness sensing. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 3142–3149. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Z.; Qiu, S.; Wang, J.; Xu, F.; Wang, Z.; Shen, Y. Adaptive gait detection based on foot-mounted inertial sensors and multi-sensor fusion. Inf. Fusion 2019, 52, 157–166. [Google Scholar] [CrossRef]
- Van Kasteren, T.; Englebienne, G.; Kröse, B.J. Activity recognition using semi-Markov models on real world smart home datasets. J. Ambient Intell. Smart Environ. 2010, 2, 311–325. [Google Scholar] [Green Version]
- Sathyanarayana, A.; Joty, S.; Fernandez-Luque, L.; Ofli, F.; Srivastava, J.; Elmagarmid, A.; Taheri, S.; Arora, T. Impact of physical activity on sleep: A deep learning based exploration. arXiv 2016, arXiv:1607.07034. [Google Scholar]
- Mamoshina, P.; Vieira, A.; Putin, E.; Zhavoronkov, A. Applications of deep learning in biomedicine. Mol. Pharm. 2016, 13, 1445–1454. [Google Scholar] [CrossRef] [PubMed]
- Ordóñez, F.; Roggen, D. Deep convolutional and LSTM recurrent neural networks for multimodal wearable activity recognition. Sensors 2016, 16, 115. [Google Scholar] [CrossRef] [PubMed]
- Ramasamy Ramamurthy, S.; Roy, N. Recent trends in machine learning for human activity recognition—A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, 1254. [Google Scholar] [CrossRef]
- Bao, Y.; Chen, W. Automatic model construction for activity recognition using wearable devices. In Proceedings of the IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Athens, Greece, 19–23 March 2018; pp. 806–811. [Google Scholar]
- Rokni, S.A.; Ghasemzadeh, H. Autonomous training of activity recognition algorithms in mobile sensors: A transfer learning approach in context-invariant views. IEEE Trans. Mob. Comput. 2018, 17, 1764–1777. [Google Scholar] [CrossRef]
- Schneider, T.; Helwig, N.; Schütze, A. Automatic feature extraction and selection for condition monitoring and related datasets. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; pp. 1–6. [Google Scholar]
- Rezaie, H.; Ghassemian, M. An adaptive algorithm to improve energy efficiency in wearable activity recognition systems. IEEE Sens. J. 2017, 17, 5315–5323. [Google Scholar] [CrossRef]
- Dao, M.S.; Nguyen-Gia, T.A.; Mai, V.C. Daily human activities recognition using heterogeneous sensors from smartphones. Procedia Comput. Sci. 2017, 111, 323–328. [Google Scholar] [CrossRef]
- Martindale, C.F.; Sprager, S.; Eskofier, B.M. Hidden Markov model-based smart annotation for benchmark cyclic activity recognition database using wearables. Sensors 2019, 19, 1820. [Google Scholar] [CrossRef]
- Barbu, V.S.; Limnios, N. Semi-Markov Chains and Hidden Semi-Markov Models toward Applications: Their Use in Reliability and DNA Analysis; Springer Science & Business Media: New York, NY, USA, 2009; Volume 191. [Google Scholar]
- Yu, S.Z. Hidden Semi-Markov Models: Theory, Algorithms and Applications; Morgan Kaufmann: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Lapuyade-Lahorgue, J.; Pieczynski, W. Unsupervised segmentation of hidden semi-Markov non-stationary chains. Signal Process. 2012, 92, 29–42. [Google Scholar] [CrossRef] [Green Version]
- Shetty, N.; Bendall, S. Understanding the gait cycle, as it relates to the foot. Orthop. Trauma 2011, 25, 236–240. [Google Scholar] [CrossRef]
- Cappé, O. Online EM algorithm for hidden Markov models. J. Comput. Graph. Stat. 2011, 20, 728–749. [Google Scholar] [CrossRef]
- Yang, J.; Nguyen, M.N.; San, P.P.; Li, X.; Krishnaswamy, S. Deep convolutional neural networks on multichannel time series for human activity recognition. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Roggen, D.; Calatroni, A.; Rossi, M.; Holleczek, T.; Förster, K.; Tröster, G.; Lukowicz, P.; Bannach, D.; Pirkl, G.; Ferscha, A.; et al. Collecting complex activity datasets in highly rich networked sensor environments. In Proceedings of the 2010 Seventh International Conference on Networked Sensing Systems (INSS), Kassel, Germany, 15–18 June 2010; pp. 233–240. [Google Scholar]
- Ronao, C.A.; Cho, S. Human activity recognition with smartphone sensors using deep learning neural networks. Expert Syst. Appl. 2016, 59, 235–244. [Google Scholar] [CrossRef]
- Bhat, H.S.; Kumar, N. On the Derivation of the Bayesian Information Criterion; School of Natural Sciences, University of California: Berkeley, CA, USA, 2010. [Google Scholar]
- Arnold, T.W. Uninformative parameters and model selection using Akaike’s Information Criterion. J. Wildl. Manag. 2010, 74, 1175–1178. [Google Scholar] [CrossRef]
- Li, Z.; Ding, B.; Han, J.; Kays, R.; Nye, P. Mining periodic behaviors for moving objects. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010; pp. 1099–1108. [Google Scholar]
- He, Z.; Wang, X.S.; Lee, B.S.; Ling, A.C. Mining partial periodic correlations in time series. Knowl. Inf. Syst. 2008, 15, 31–54. [Google Scholar] [CrossRef]




| Activity | |||||||
|---|---|---|---|---|---|---|---|
| TMC-HIST | D1A1 | D1A2 | D1A3 | D1A4 | D1A5 | D1A6 | |
| Sensitivity | 0.4900 | 0.5463 | 0.6997 | 0.9017 | 0.7885 | 1.0000 | |
| Specificity | 0.9392 | 0.9883 | 0.9649 | 0.9839 | 0.9222 | 0.9939 | |
| F1 Score | 0.4687 | 0.6574 | 0.6837 | 0.8708 | 0.6057 | 0.9709 | |
| MCC | 0.4128 | 0.6461 | 0.6511 | 0.8587 | 0.5781 | 0.9684 | |
| D1A7 | D1A8 | D1A9 | D1A10 | D1A11 | Total | ||
| Sensitivity | 0.8308 | 0.7116 | 0.9489 | 0.9972 | 0.6618 | 0.7797 | |
| Specificity | 0.9911 | 0.9924 | 1.0000 | 1.0000 | 0.9813 | 0.9779 | |
| F1 Score | 0.8654 | 0.7966 | 0.9737 | 0.9986 | 0.7168 | 0.7826 | |
| MCC | 0.8535 | 0.7854 | 0.9715 | 0.9985 | 0.6936 | 0.7652 | |
| TMC-GMM | D1A1 | D1A2 | D1A3 | D1A4 | D1A5 | D1A6 | |
| Sensitivity | 0.6784 | 0.6797 | 0.5483 | 0.9146 | 0.8980 | 1.0000 | |
| Specificity | 0.9322 | 0.9993 | 0.9866 | 0.9689 | 0.9465 | 0.9995 | |
| F1 Score | 0.5777 | 0.8059 | 0.6525 | 0.8164 | 0.7305 | 0.9978 | |
| MCC | 0.5353 | 0.8067 | 0.6382 | 0.8025 | 0.7151 | 0.9975 | |
| D1A7 | D1A8 | D1A9 | D1A10 | D1A11 | Total | ||
| Sensitivity | 0.8843 | 0.8917 | 0.8602 | 0.9876 | 0.8784 | 0.8383 | |
| Specificity | 0.9961 | 0.9940 | 0.9987 | 0.9998 | 0.9999 | 0.9838 | |
| F1 Score | 0.9197 | 0.9140 | 0.9184 | 0.9930 | 0.9348 | 0.8419 | |
| MCC | 0.9129 | 0.9059 | 0.9132 | 0.9923 | 0.9309 | 0.8319 | |
| SemiTMC-GMM | D1A1 | D1A2 | D1A3 | D1A4 | D1A5 | D1A6 | |
| Sensitivity | 0.6672 | 0.7247 | 0.6182 | 0.9638 | 0.8767 | 0.9990 | |
| Specificity | 0.9457 | 0.9972 | 0.9860 | 0.9773 | 0.9563 | 0.9990 | |
| F1 Score | 0.6054 | 0.8273 | 0.7039 | 0.8752 | 0.7509 | 0.9944 | |
| MCC | 0.5644 | 0.8223 | 0.6862 | 0.8666 | 0.7327 | 0.9939 | |
| D1A7 | D1A8 | D1A9 | D1A10 | D1A11 | Total | ||
| Sensitivity | 0.9025 | 0.9410 | 0.8561 | 0.9956 | 0.9215 | 0.8606 | |
| Specificity | 0.9936 | 0.9922 | 0.9996 | 0.9994 | 1.0000 | 0.9860 | |
| F1 Score | 0.9175 | 0.9324 | 0.9208 | 0.9948 | 0.9590 | 0.8620 | |
| MCC | 0.9096 | 0.9255 | 0.9165 | 0.9943 | 0.9560 | 0.8516 | |
| Activity | ||||||
|---|---|---|---|---|---|---|
| D2A1 | D2A2 | D2A3 | D2A4 | Total | ||
| TMC-HIST | Sensitivity | 0.7007 | 0.9721 | 0.7705 | 0.9385 | 0.8454 |
| Specificity | 0.9858 | 0.8931 | 0.9174 | 0.9595 | 0.9389 | |
| F1 Score | 0.8169 | 0.8258 | 0.6885 | 0.8596 | 0.7977 | |
| MCC | 0.7194 | 0.7833 | 0.6317 | 0.8382 | 0.7431 | |
| TMC-GMM | Sensitivity | 0.9399 | 0.9475 | 0.9105 | 0.8590 | 0.9142 |
| Specificity | 0.9720 | 0.9996 | 0.9512 | 0.9787 | 0.9754 | |
| F1 Score | 0.9547 | 0.9723 | 0.8327 | 0.8641 | 0.9060 | |
| MCC | 0.9130 | 0.9654 | 0.8044 | 0.8419 | 0.8812 | |
| SemiTMC-GMM | Sensitivity | 0.9608 | 0.9829 | 0.9483 | 0.8749 | 0.9417 |
| Specificity | 0.9831 | 0.9987 | 0.9634 | 0.9910 | 0.9841 | |
| F1 Score | 0.9713 | 0.9891 | 0.8799 | 0.9071 | 0.9368 | |
| MCC | 0.9445 | 0.9861 | 0.8600 | 0.8932 | 0.9210 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Derrode, S.; Pieczynski, W. Lower Limb Locomotion Activity Recognition of Healthy Individuals Using Semi-Markov Model and Single Wearable Inertial Sensor. Sensors 2019, 19, 4242. https://doi.org/10.3390/s19194242
Li H, Derrode S, Pieczynski W. Lower Limb Locomotion Activity Recognition of Healthy Individuals Using Semi-Markov Model and Single Wearable Inertial Sensor. Sensors. 2019; 19(19):4242. https://doi.org/10.3390/s19194242
Chicago/Turabian StyleLi, Haoyu, Stéphane Derrode, and Wojciech Pieczynski. 2019. "Lower Limb Locomotion Activity Recognition of Healthy Individuals Using Semi-Markov Model and Single Wearable Inertial Sensor" Sensors 19, no. 19: 4242. https://doi.org/10.3390/s19194242
APA StyleLi, H., Derrode, S., & Pieczynski, W. (2019). Lower Limb Locomotion Activity Recognition of Healthy Individuals Using Semi-Markov Model and Single Wearable Inertial Sensor. Sensors, 19(19), 4242. https://doi.org/10.3390/s19194242





