Wearable Sensors for Estimation of Parkinsonian Tremor Severity during Free Body Movements
Abstract
:1. Introduction
2. Dataset
2.1. Data Collection
2.2. Data Preprocessing
3. Method
3.1. Segmentation and Feature Extraction
3.2. Tremor Estimation Methods
3.2.1. Gradient Tree Boosting
3.2.2. Deep Learning Model
4. Results
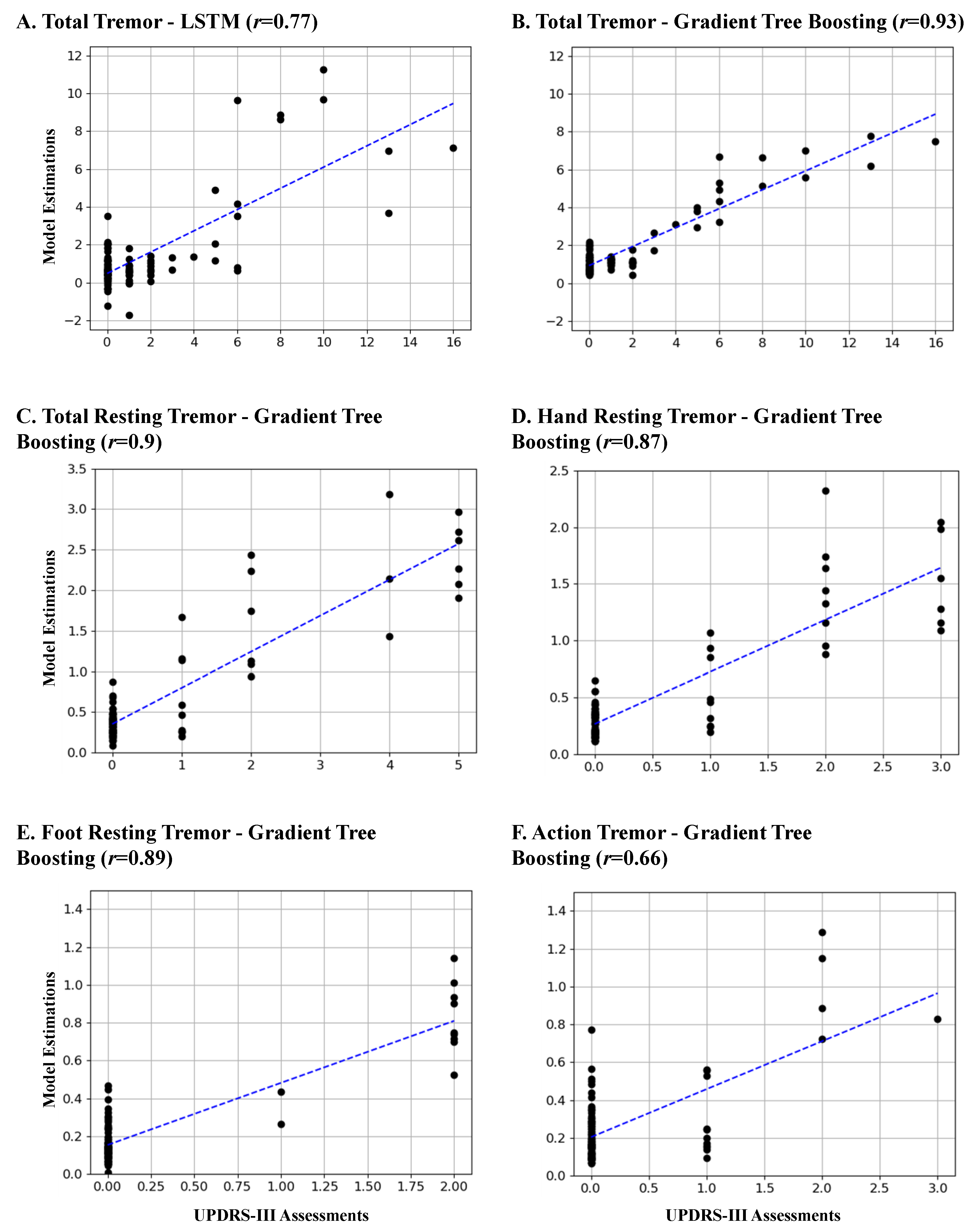
4.1. Total Tremor Subscore Estimation
4.2. Resting and Action Tremor Subscore Estimation
4.3. Feature Analysis
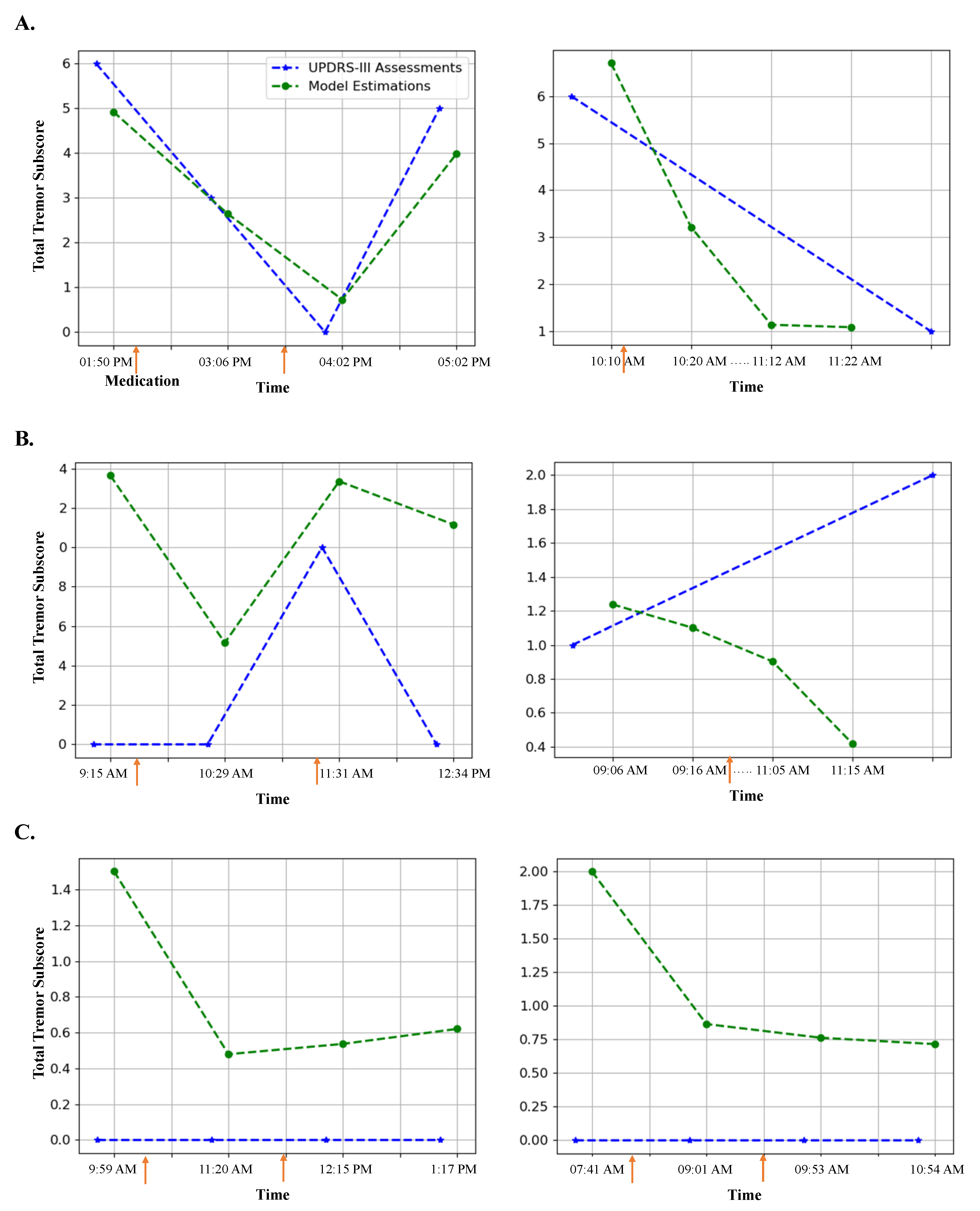
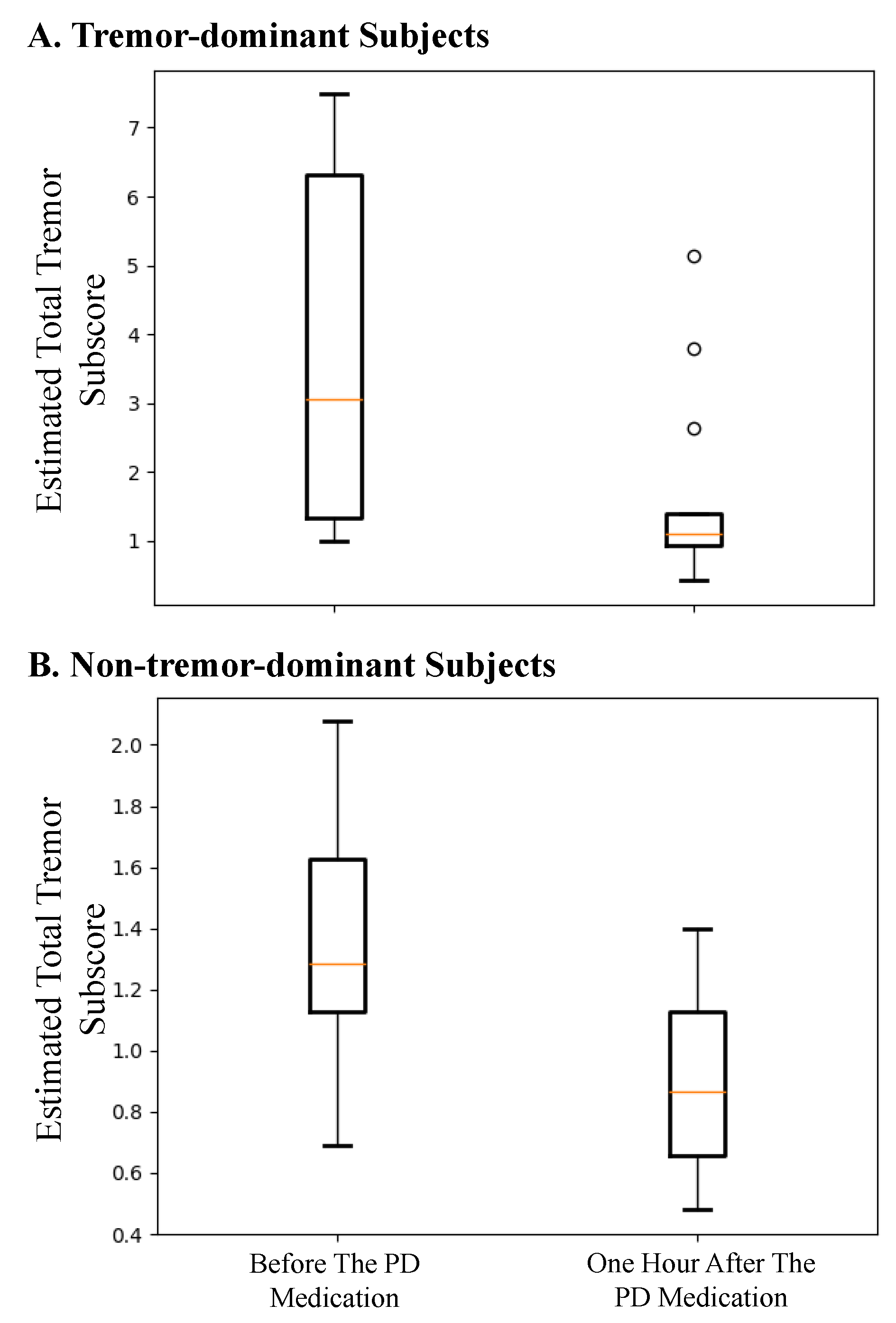
5. Discussion
5.1. Comparison to Other Studies
5.2. Study Limitations and Future Work
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bhidayasiri, R. Differential diagnosis of common tremor syndromes. Postgrad. Med. J. 2005, 81, 756–762. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goetz, C.G.; Tilley, B.C.; Shaftman, S.R.; Stebbins, G.T.; Fahn, S.; Martinez-Martin, P.; Poewe, W.; Sampaio, C.; Stern, M.B.; Dodel, R.; et al. Movement Disorder Society-sponsored revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS): Scale presentation and clinimetric testing results. Mov. Disord. Off. J. Mov. Disord. Soc. 2008, 23, 2129–2170. [Google Scholar] [CrossRef] [PubMed]
- Dorsey, E.R.; Venuto, C.; Venkataraman, V.; Harris, D.A.; Kieburtz, K. Novel methods and technologies for 21st-century clinical trials: A review. JAMA Neurol. 2015, 72, 582–588. [Google Scholar] [CrossRef] [PubMed]
- Salarian, A.; Russmann, H.; Wider, C.; Burkhard, P.R.; Vingerhoets, F.J.; Aminian, K. Quantification of tremor and bradykinesia in Parkinson’s disease using a novel ambulatory monitoring system. IEEE Trans. Biomed. Eng. 2007, 54, 313–322. [Google Scholar] [CrossRef] [PubMed]
- Giuffrida, J.P.; Riley, D.E.; Maddux, B.N.; Heldman, D.A. Clinically deployable Kinesia technology for automated tremor assessment. Mov. Disord. 2009, 24, 723–730. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Zhang, P.; Lueth, T.C. Quantitative assessment of Parkinsonian tremor based on an inertial measurement unit. Sensors 2015, 15, 25055–25071. [Google Scholar] [CrossRef]
- Pan, D.; Dhall, R.; Lieberman, A.; Petitti, D.B. A mobile cloud-based Parkinson’s disease assessment system for home-based monitoring. JMIR mHealth uHealth 2015, 3, e29. [Google Scholar] [CrossRef]
- Siddiqui, H.A.; Jimenez-Shahed, J.; Viswanathan, A.; Ince, N.F. A wireless sensor interface for the quantification of tremor using off the shelf components. In Proceedings of the 2016 32nd Southern Biomedical Engineering Conference (SBEC), Shreveport, LA, USA, 11–13 March 2016; pp. 177–178. [Google Scholar]
- Pulliam, C.L.; Heldman, D.A.; Brokaw, E.B.; Mera, T.O.; Mari, Z.K.; Burack, M.A. Continuous assessment of Levodopa response in Parkinson’s disease using wearable motion sensors. IEEE Trans. Biomed. Eng. 2018, 65, 159–164. [Google Scholar] [CrossRef]
- Delrobaei, M.; Memar, S.; Pieterman, M.; Stratton, T.W.; McIsaac, K.; Jog, M. Towards remote monitoring of Parkinson’s disease tremor using wearable motion capture systems. J. Neurol. Sci. 2018, 384, 38–45. [Google Scholar] [CrossRef]
- Sanchez-Perez, L.A.; Sanchez-Fernandez, L.P.; Shaout, A.; Martinez-Hernandez, J.M.; Alvarez-Noriega, M.J. Rest tremor quantification based on fuzzy inference systems and wearable sensors. Int. J. Med. Inform. 2018, 114, 6–17. [Google Scholar] [CrossRef]
- López-Blanco, R.; Velasco, M.A.; Méndez-Guerrero, A.; Romero, J.P.; del Castillo, M.D.; Serrano, J.I.; Rocon, E.; Benito-León, J. Smartwatch for the analysis of rest tremor in patients with Parkinson’s disease. J. Neurol. Sci. 2019, 401, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference On Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Wang, T.; Shoaran, M.; Emami, A. Towards Adaptive Deep Brain Stimulation in Parkinson’s Disease: Lfp-Based Feature Analysis and Classification. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2536–2540. [Google Scholar]
- Prasad, S.; Pandey, U.; Saini, J.; Ingalhalikar, M.; Pal, P.K. Atrophy of cerebellar peduncles in essential tremor: A machine learning–based volumetric analysis. Eur. Radiol. 2019, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Harar, P.; Galaz, Z.; Alonso-Hernandez, J.B.; Mekyska, J.; Burget, R.; Smekal, Z. Towards robust voice pathology detection. Neural Comput. Appl. 2018, 1–11. [Google Scholar] [CrossRef]
- Junior, S.B.; Costa, V.G.T.; Chen, S.H.; Guido, R.C. U-Healthcare System for Pre-Diagnosis of Parkinson’s Disease from Voice Signal. In Proceedings of the 2018 IEEE International Symposium on Multimedia (ISM), Taichung, Taiwan, 10–12 December 2018; pp. 271–274. [Google Scholar]
- Galaz, Z.; Mekyska, J.; Zvoncak, V.; Mucha, J.; Kiska, T.; Smekal, Z.; Eliasova, I.; Mrackova, M.; Kostalova, M.; Rektorova, I.; et al. Changes in Phonation and Their Relations with Progress of Parkinson’s Disease. Appl. Sci. 2018, 8, 2339. [Google Scholar] [CrossRef]
- Hammerla, N.; Andras, P.; Rochester, L.; Ploetz, T. PD disease state assessment in naturalistic environments using deep learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 1742–1748. [Google Scholar]
- Hssayeni, M.D.; Adams, J.L.; Ghoraani, B. Deep Learning for Medication Assessment of Individuals with Parkinson’s Disease Using Wearable Sensors. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 1–4. [Google Scholar]
- Eskofier, B.M.; Lee, S.I.; Daneault, J.F.; Golabchi, F.N.; Ferreira-Carvalho, G.; Vergara-Diaz, G.; Sapienza, S.; Costante, G.; Klucken, J.; Kautz, T.; et al. Recent machine learning advancements in sensor-based mobility analysis: Deep learning for Parkinson’s disease assessment. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 655–658. [Google Scholar]
- Zhao, A.; Qi, L.; Li, J.; Dong, J.; Yu, H. A hybrid spatio-temporal model for detection and severity rating of Parkinson’s Disease from gait data. Neurocomputing 2018, 315, 1–8. [Google Scholar] [CrossRef]
- Hssayeni, M.D.; Jimenez-Shahed, J.; Burack, M.A.; Ghoraani, B. Symptom-based, Dual-channel LSTM Network for The Estimation of Unified Parkinson’s Disease Rating Scale III. In Proceedings of the 2019 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), Chicago, IL, USA, 19–22 May 2019. [Google Scholar]
- Del Din, S.; Godfrey, A.; Mazzà, C.; Lord, S.; Rochester, L. Free-living monitoring of Parkinson’s disease: Lessons from the field. Mov. Disord. 2016, 31, 1293–1313. [Google Scholar] [CrossRef] [PubMed]
- Heldman, D.A.; Harris, D.A.; Felong, T.; Andrzejewski, K.L.; Dorsey, E.R.; Giuffrida, J.P.; Goldberg, B.; Burack, M.A. Telehealth management of Parkinson’s disease using wearable sensors: An exploratory study. Digit. Biomark. 2017, 1, 43–51. [Google Scholar] [CrossRef]
- Cova, I.; Priori, A. Diagnostic biomarkers for Parkinson’s disease at a glance: Where are we? J. Neural Transm. 2018, 125, 1417–1432. [Google Scholar] [CrossRef]
- Mera, T.O.; Burack, M.A.; Giuffrida, J.P. Objective motion sensor assessment highly correlated with scores of global Levodopa-induced dyskinesia in Parkinson’s disease. J. Park. Dis. 2013, 3, 399. [Google Scholar]
- Pulliam, C.L.; Burack, M.A.; Heldman, D.A.; Giuffrida, J.P.; Mera, T.O. Motion sensor dyskinesia assessment during activities of daily living. J. Park. Dis. 2014, 4, 609–615. [Google Scholar]
- Hssayeni, M.D.; Burack, M.A.; Jimenez-Shahed, J.; Ghoraani, B. Assessment of response to medication in individuals with Parkinson’s disease. Med. Eng. Phys. 2019, 67, 33–43. [Google Scholar] [CrossRef] [PubMed]
- Salarian, A. Ambulatory Monitoring of Motor Functions in Patients with Parkinson’s Disease Using Kinematic Sensors. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2006. [Google Scholar]
- Patel, S.; Lorincz, K.; Hughes, R.; Huggins, N.; Growdon, J.; Standaert, D.; Akay, M.; Dy, J.; Welsh, M.; Bonato, P. Monitoring motor fluctuations in patients with Parkinson’s disease using wearable sensors. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 864–873. [Google Scholar] [CrossRef] [PubMed]
- Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent neural network regularization. arXiv 2014, arXiv:1409.2329. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, G.S.A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org/ (accessed on 1 October 2018).
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Richards, M.; Marder, K.; Cote, L.; Mayeux, R. Interrater reliability of the Unified Parkinson’s Disease Rating Scale motor examination. Mov. Disord. 1994, 9, 89–91. [Google Scholar] [CrossRef] [PubMed]
- Post, B.; Merkus, M.P.; de Bie, R.M.; de Haan, R.J.; Speelman, J.D. Unified Parkinson’s disease rating scale motor examination: are ratings of nurses, residents in neurology, and movement disorders specialists interchangeable? Mov. Disord. 2005, 20, 1577–1584. [Google Scholar] [CrossRef]
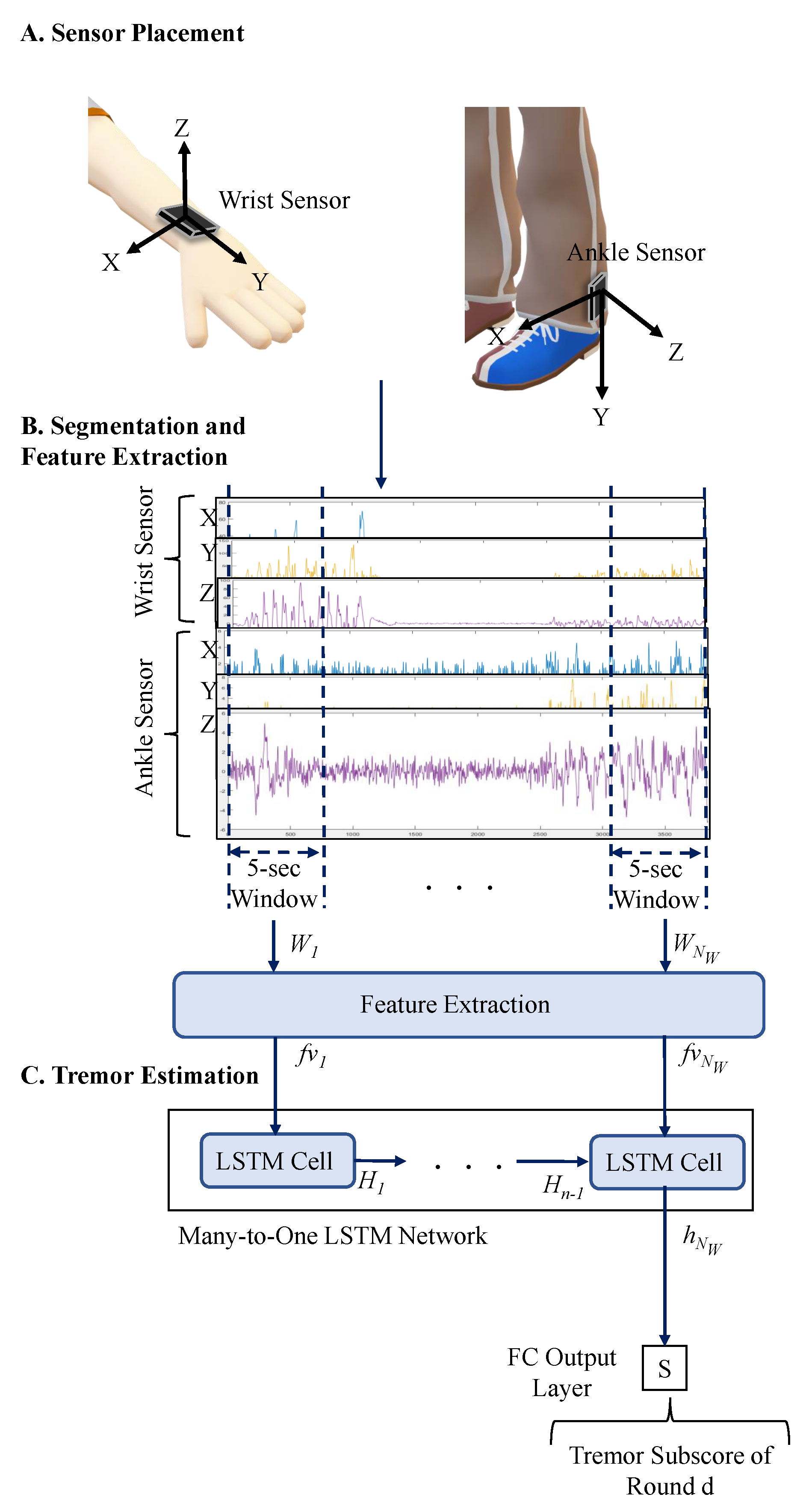
| Subject # | Number of Rounds | Total Duration (min) | Subject # | Number of Rounds | Total Duration (min) |
|---|---|---|---|---|---|
| 1 | 4 | 12.20 | 13 | 4 | 14.28 |
| 2 | 4 | 13.42 | 14 | 4 | 15.97 |
| 3 | 4 | 14.38 | 15 | 4 | 10.61 |
| 4 | 4 | 13.86 | 16 | 4 | 40.00 |
| 5 | 4 | 14.95 | 17 | 4 | 37.92 |
| 6 | 4 | 13.26 | 18 | 4 | 40.00 |
| 7 | 3 | 10.33 | 19 | 3 | 26.60 |
| 8 | 3 | 10.69 | 20 | 4 | 40.00 |
| 9 | 4 | 14.30 | 21 | 4 | 40.00 |
| 10 | 4 | 13.68 | 22 | 4 | 40.00 |
| 11 | 4 | 15.62 | 23 | 2 | 20.00 |
| 12 | 4 | 13.86 | 24 | 4 | 40.00 |
| Feature Name | Used Signals | # of Features |
|---|---|---|
| 1—4–6 Hz signal power | X, Y, Z—wrist and ankle | 6 |
| 2—0.5–15 Hz signal power | X, Y, Z—wrist and ankle | 6 |
| 3—Percentage power of frequencies >4 Hz | X, Y, Z—wrist and ankle | 6 |
| 4—Number of autocorrelation peaks | X, Y, Z—wrist and ankle | 6 |
| 5—Sum of autocorrelation peaks | X, Y, Z—wrist and ankle | 6 |
| 6—Amplitude of the first autocorrelation peak | X, Y, Z—wrist and ankle | 6 |
| 7—Lag of the first autocorrelation peak | X, Y, Z—wrist and ankle | 6 |
| 8—Spectral entropy | X, Y, Z—wrist and ankle | 6 |
| 9—First dominant frequency | X, Y, Z—wrist and ankle | 6 |
| 10—Power of first dominant frequency | X, Y, Z—wrist and ankle | 6 |
| 11—Second dominant frequency | X, Y, Z—wrist and ankle | 6 |
| 12—Power of second dominant frequency | X, Y, Z—wrist and ankle | 6 |
| 13—Cross-correlation | X and Y—wrist and ankle | 2 |
| 14—Cross-correlation | X and Z—wrist and ankle | 2 |
| 15—Cross-correlation | Y and Z—wrist and ankle | 2 |
| Total Number of Features | 78 | |
| Tremor Type | Sensor Used | Method Used (Specifications) | Held-Out Testing | Leave-One-Out Testing | ||
|---|---|---|---|---|---|---|
| MAE | r (p) | MAE | r (p) | |||
| Total rest and action tremor | Wrist and ankle | LSTM | 1.33 | 0.84 (<) | 1.32 | 0.77 (<) |
| Total rest and action tremor | Wrist and ankle | Gradient tree boosting | 1.56 | 0.96 (<) | 1.18 | 0.93 (<) |
| Total rest tremor | Wrist and ankle | Gradient tree boosting | 1.20 | 0.94 (<) | 0.58 | 0.90 (<) |
| Hand rest tremor | Wrist | Gradient tree boosting | 0.76 | 0.91 (<) | 0.41 | 0.87 (<) |
| Foot rest tremor | Ankle | Gradient tree boosting | 0.46 | 0.92 (<) | 0.27 | 0.89 (<) |
| Action tremor | Wrist | Gradient tree boosting | 0.41 | 0.75 (<) | 0.33 | 0.66 (<) |
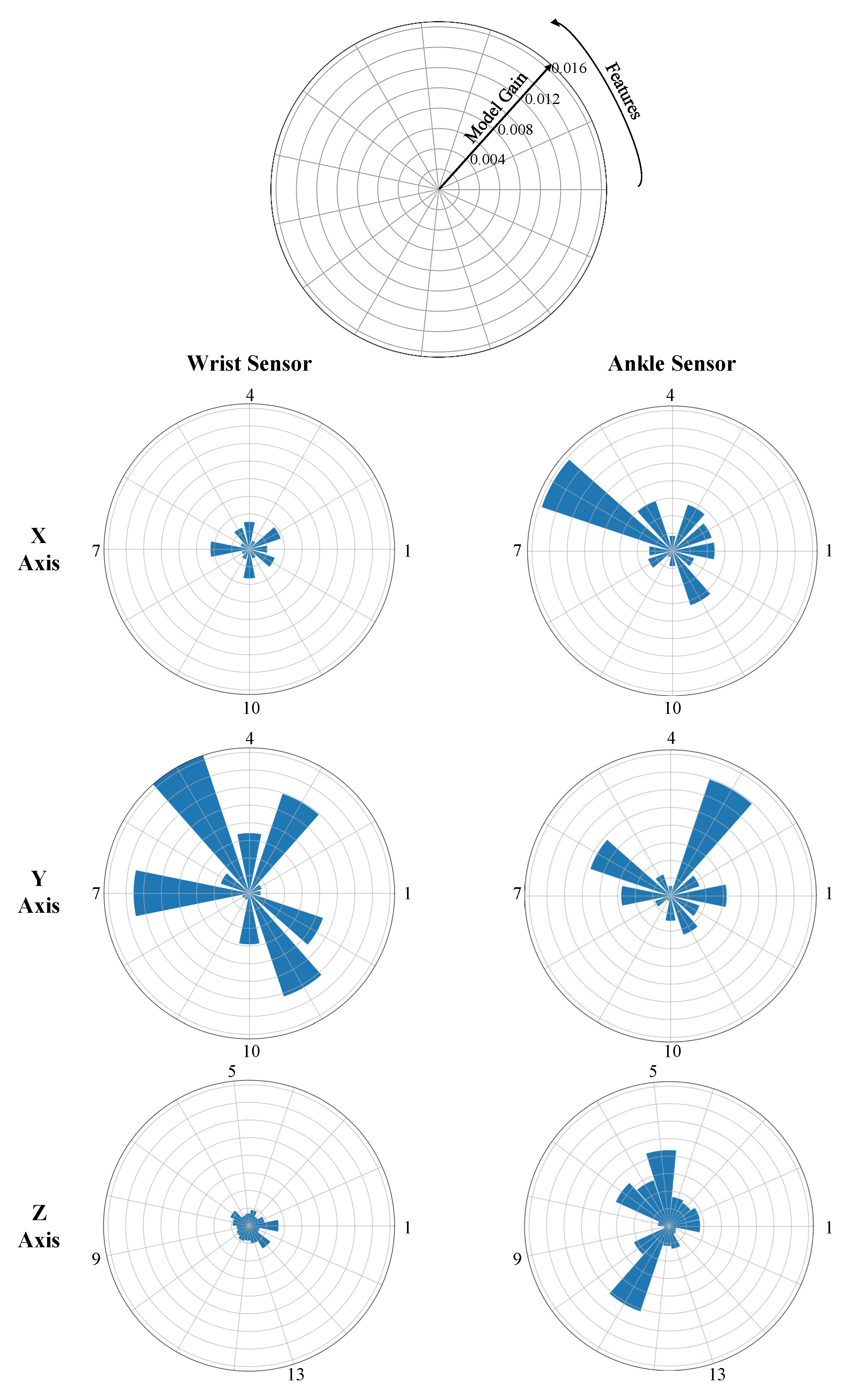
| Wrist Sensor | Ankle Sensor | ||
|---|---|---|---|
| Important Features | Axis | Important Features | Axis |
| Feature #5: sum of autocorrelation peaks | Y | Feature #6: amplitude of the first autocorrelation peak | X, Y and Z |
| Feature #7: lag of the first autocorrelation peak | Y | Feature #3: percentage power of frequencies > 4 Hz | X and Z |
| Feature #11: second dominant frequency | Y | Feature #11: second dominant frequency | X and Z |
| Feature #3: percentage power of frequencies > 4 Hz | Y | Feature #5: sum of autocorrelation peaks | X and Y |
| Feature #12: power of second dominant frequency | Y | Feature #7: lag of the first autocorrelation peak | Y |
| Feature #4: number of autocorrelation peaks | Y | Feature #1: 4–6 Hz signal power | Y |
| Feature #10: Power of first dominant frequency | Y | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hssayeni, M.D.; Jimenez-Shahed, J.; Burack, M.A.; Ghoraani, B. Wearable Sensors for Estimation of Parkinsonian Tremor Severity during Free Body Movements. Sensors 2019, 19, 4215. https://doi.org/10.3390/s19194215
Hssayeni MD, Jimenez-Shahed J, Burack MA, Ghoraani B. Wearable Sensors for Estimation of Parkinsonian Tremor Severity during Free Body Movements. Sensors. 2019; 19(19):4215. https://doi.org/10.3390/s19194215
Chicago/Turabian StyleHssayeni, Murtadha D., Joohi Jimenez-Shahed, Michelle A. Burack, and Behnaz Ghoraani. 2019. "Wearable Sensors for Estimation of Parkinsonian Tremor Severity during Free Body Movements" Sensors 19, no. 19: 4215. https://doi.org/10.3390/s19194215
APA StyleHssayeni, M. D., Jimenez-Shahed, J., Burack, M. A., & Ghoraani, B. (2019). Wearable Sensors for Estimation of Parkinsonian Tremor Severity during Free Body Movements. Sensors, 19(19), 4215. https://doi.org/10.3390/s19194215





