An Improved Locally Weighted PLS Based on Particle Swarm Optimization for Industrial Soft Sensor Modeling
Abstract
:1. Introduction
2. Preliminaries
2.1. Locally Weighted PLS
| Algorithm 1: LWPLS |
| 1: Set R and h. |
| 2: Calculate the weight matrix Ω |
| 3: Calculate X0, Y0, and Xq0; |
| 4: Set Xr= X0, Yr= Y0, Xq r= Xq0, |
| 5: for r = 1, to R do |
| 6: Derive the rth latent variables of X, Y, and Xq; |
| 7: Derive the rth loading vector of X and the rth regression coefficient of Y; |
| 8: Update |
| 9: if r = R |
| 10: Output the predicted value |
| 11: else |
| 12: Calculate Xr+1, Yr+1, and Xq r+1. |
| 13: end if |
| 14: end for |
2.2. PSO Algorithm
3. The Proposed PSO–LWPLS Method
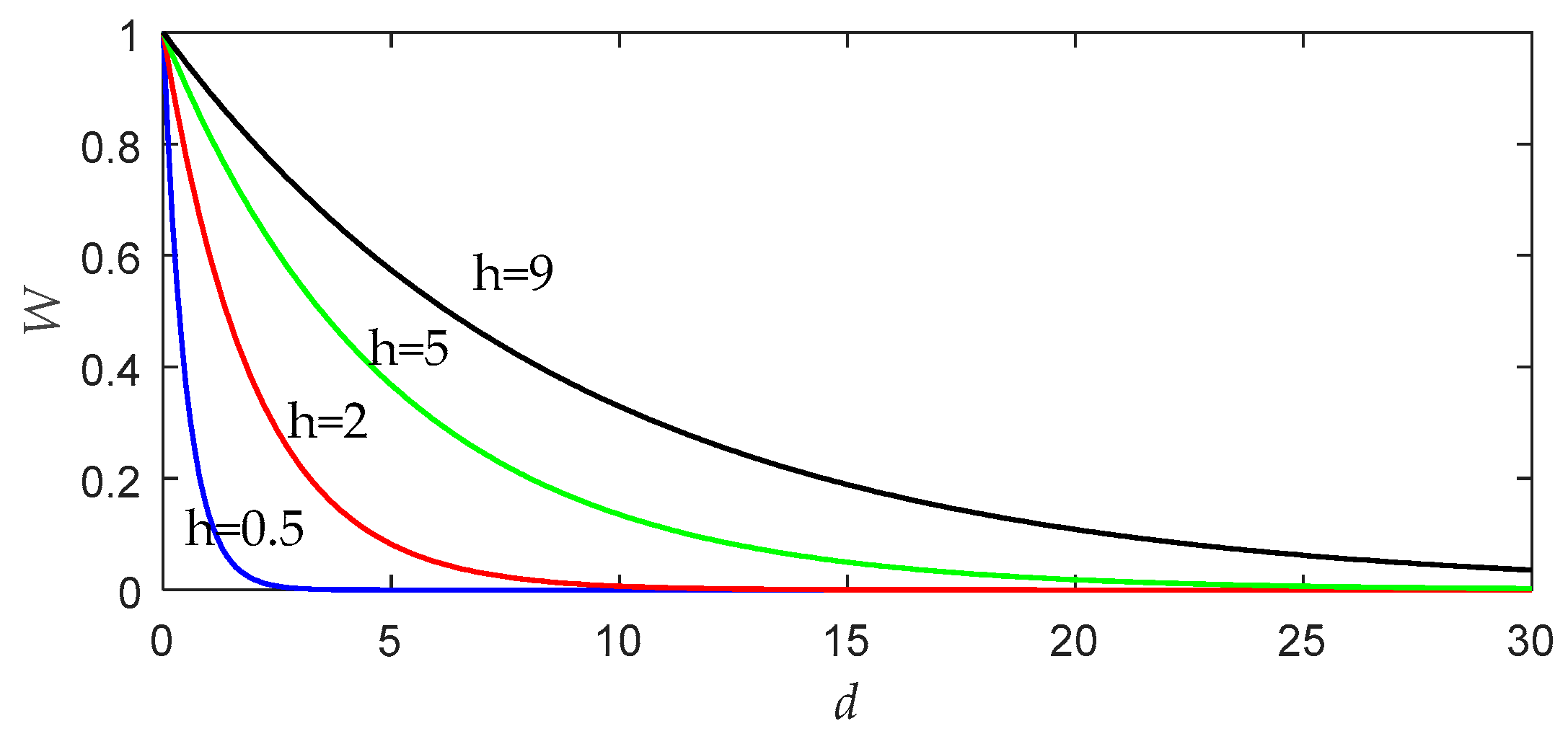
3.1. Bandwidth Tuning Problem in LWPLS
3.2. Why Use PSO?
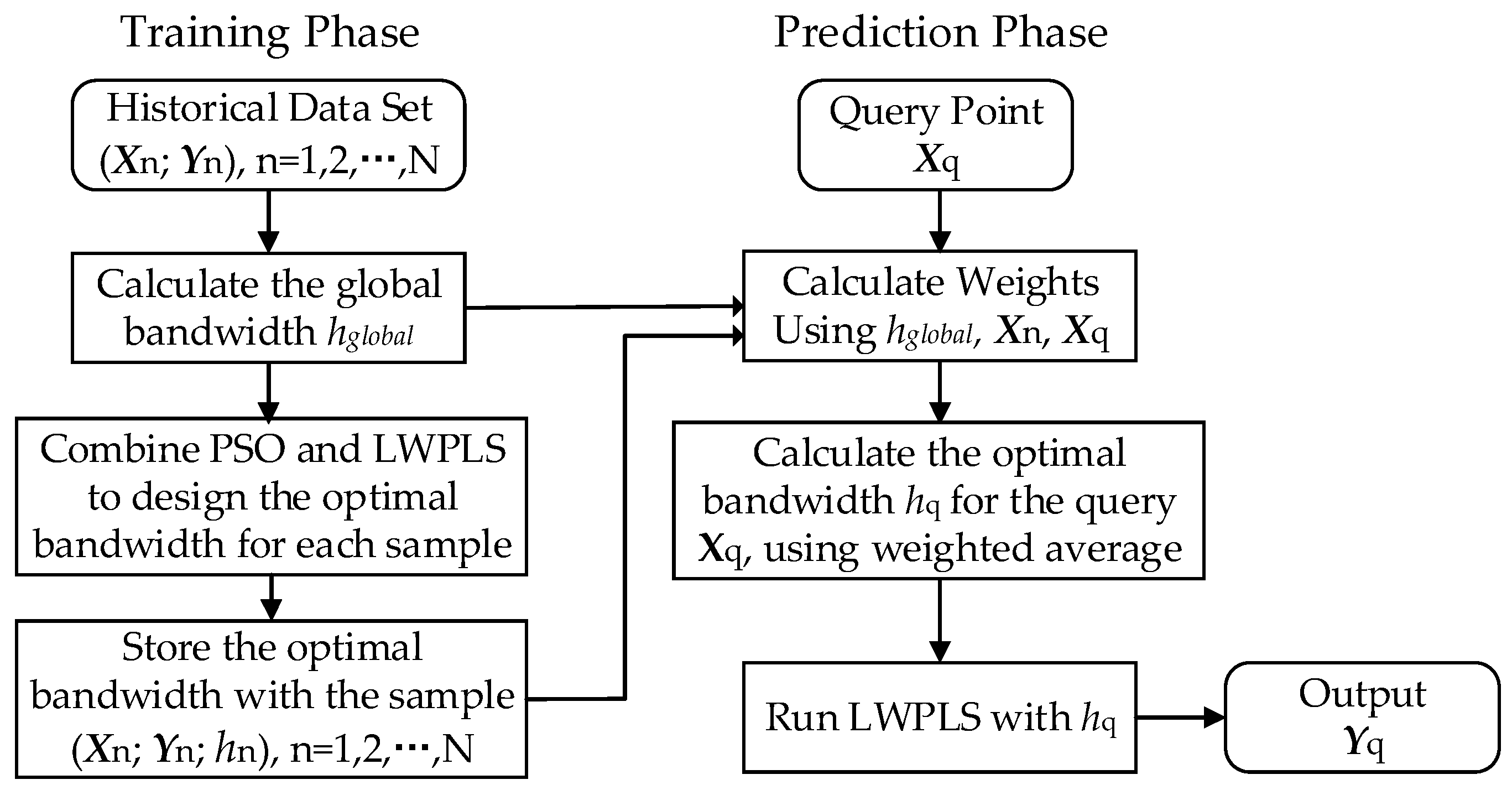
3.3. Optimal Bandwidth Selection Using PSO
3.3.1. Training Phase
3.3.2. Prediction Phase
4. Case Studies
4.1. Numerical Example
4.1.1. Problem Settings
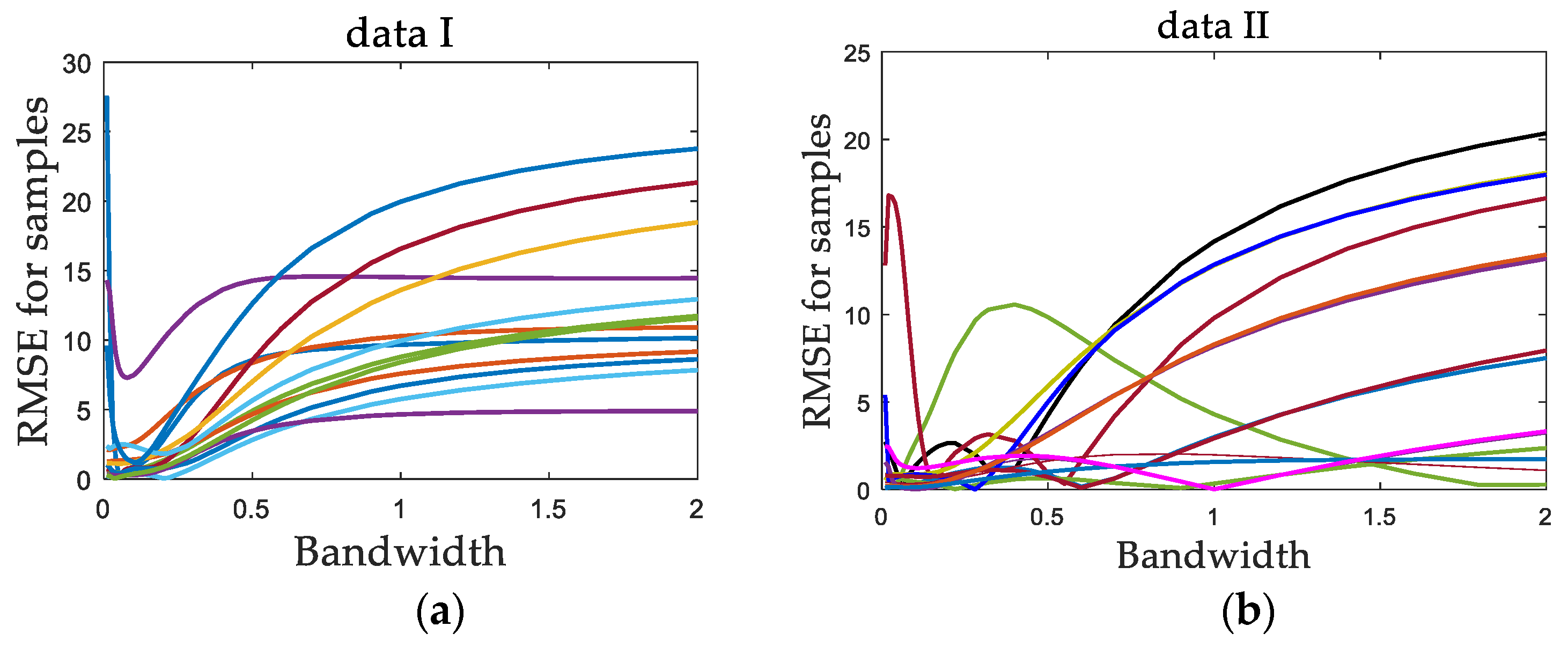
4.1.2. Results and Discussion
4.2. Application in the Production of Gray Cast Iron
4.2.1. Problem Statement
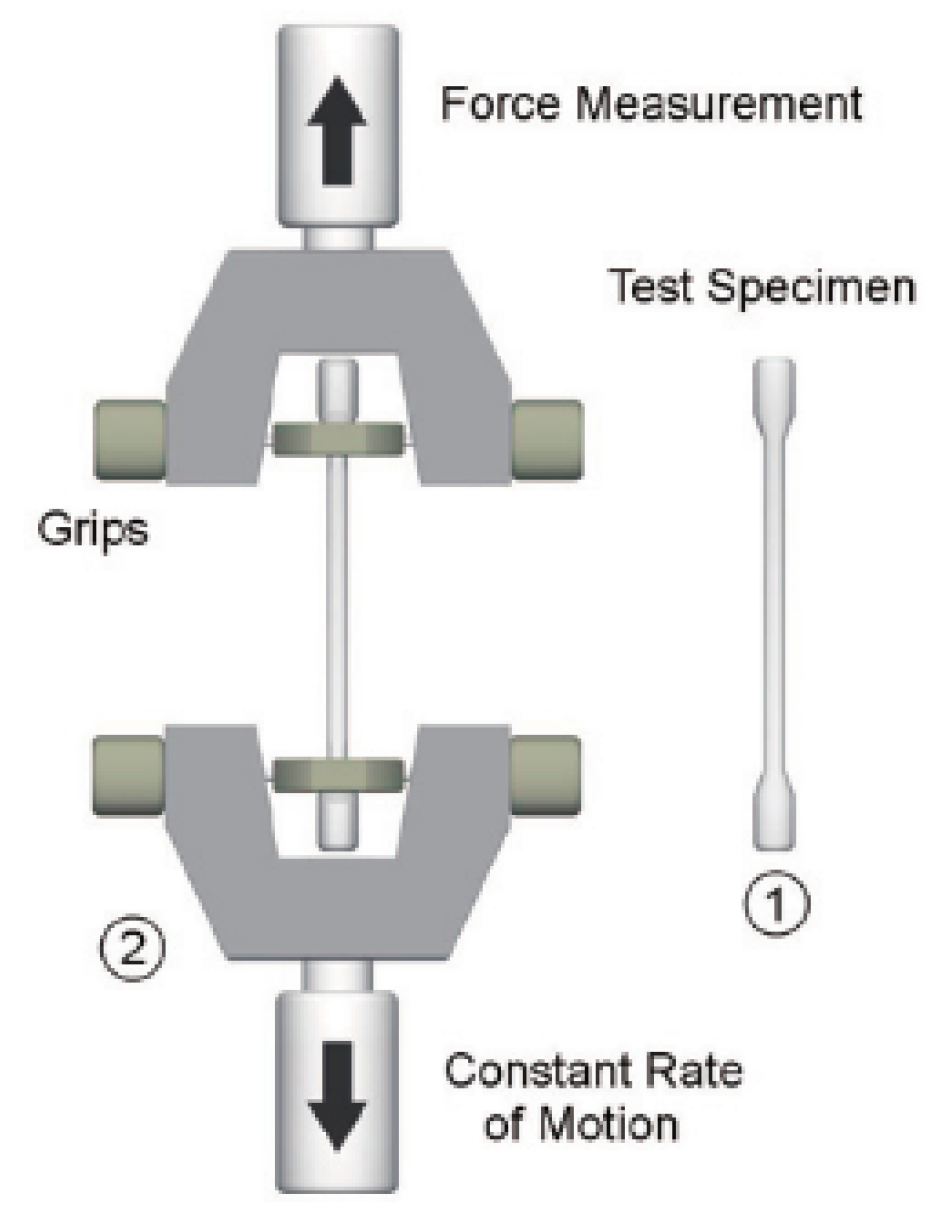
4.2.2. Data Acquisition
4.2.3. Multicollinearity Analysis
4.2.4. Results and Discussion
4.3. Computation Time Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fortuna, L.; Graziani, S.; Rizzo, A.; Xibilia, M.G. Soft Sensors for Monitoring and Control of Industrial Processes; Springer: London, UK, 2007. [Google Scholar]
- Kadlec, P.; Gabrys, B.; Strandt, S. Data-driven Soft Sensors in the process industry. Comput. Chem. Eng. 2009, 33, 795–814. [Google Scholar] [CrossRef] [Green Version]
- Kano, M.; Ogawa, M. The state of the art in chemical process control in Japan: Good practice and questionnaire survey. J. Process Control 2010, 20, 969–982. [Google Scholar] [CrossRef]
- Rani, A.; Singh, V.; Gupta, J.R. Development of soft sensor for neural network based control of distillation column. ISA Trans. 2013, 52, 438–449. [Google Scholar] [CrossRef] [PubMed]
- Gonzaga, J.C.B.; Meleiro, L.A.C.; Kiang, C.; Maciel, R. ANN-based soft-sensor for real-time process monitoring and control of an industrial polymerization process. Comput. Chem. Eng. 2009, 33, 43–49. [Google Scholar] [CrossRef]
- KanekoKimito, H.; Funatsu, F. Application of online support vector regression for soft sensors. AlChE J. 2014, 60, 600–612. [Google Scholar]
- Cai, X.Y.; Meng, Q.J.; Luan, W.L. Soft Sensor of Vertical Mill Material Layer Based on LS-SVM. Int. Conf. Meas. 2013, 1, 22–25. [Google Scholar]
- Zhang, X.; Huang, W.; Zhu, Y.; Zhu, Y.; Chen, S. A novel soft sensor modelling method based on kernel PLS. In Proceedings of the IEEE International Conference on Intelligent Computing & Intelligent Systems, Xiamen, China, 29–31 October 2010. [Google Scholar]
- Grbic, R.; Sliskovic, D.; Kadlec, P. Adaptive Soft Sensor for Online Prediction Based on Moving Window Gaussian Process Regression. In Proceedings of the 11th International Conference on Machine Learning and Applications (Icmla 2012), Boca Raton, FL, USA, 12–15 December 2012; Volume 2, pp. 428–433. [Google Scholar] [CrossRef]
- Ahmed, F.; Nazir, S.; Yeo, Y.K. A recursive PLS-based soft sensor for prediction of the melt index during grade change operations in HDPE plant. Korean J. Chem. Eng. 2009, 26, 14–20. [Google Scholar] [CrossRef]
- Poerio, D.V.; Brown, S.D. Highly-overlapped, recursive partial least squares soft sensor with state partitioning via local variable selection. Chemom. Intell. Lab. Syst. 2018, 175, 104–115. [Google Scholar] [CrossRef]
- Hazama, K.; Kano, M. Covariance-based locally weighted partial least squares for high-performance adaptive modelling. Chemom. Intell. Lab. Syst. 2015, 146, 55–62. [Google Scholar] [CrossRef]
- Yuan, X.F.; Ge, Z.Q.; Huang, B.; Song, Z.H.; Wang, Y.L. Semisupervised JITL Framework for Nonlinear Industrial Soft Sensing Based on Locally Semisupervised Weighted PCR. IEEE Trans. Ind. Inf. 2017, 13, 532–541. [Google Scholar] [CrossRef]
- Cheng, C.; Chiu, M.S. A new data-based methodology for nonlinear process modelling. Chem. Eng. Sci. 2004, 59, 2801–2810. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z. Online monitoring of nonlinear multiple mode processes based on adaptive local model approach. Control Eng. Pract. 2008, 16, 1427–1437. [Google Scholar] [CrossRef]
- Fujiwara, K.; Kano, M.; Hasebe, S.; Takinami, A. Soft-Sensor Development Using Correlation-Based Just-in-Time Modelling. AlChE J. 2009, 55, 1754–1765. [Google Scholar] [CrossRef]
- Kim, S.; Okajima, R.; Kano, M.; Hasebe, S. Development of soft-sensor using locally weighted PLS with adaptive similarity measure. Chemom. Intell. Lab. Syst. 2013, 124, 43–49. [Google Scholar] [CrossRef] [Green Version]
- Ge, Z.Q.; Song, Z.H. A comparative study of just-in-time-learning based methods for online soft sensor modelling. Chemom. Intell. Lab. Syst. 2010, 104, 306–317. [Google Scholar] [CrossRef]
- Kim, S.; Kano, M.; Hasebe, S.; Takinami, A.; Seki, T. Long-Term Industrial Applications of Inferential Control Based on Just-In-Time Soft-Sensors: Economical Impact and Challenges. Ind. Eng. Chem. Res. 2013, 52, 12346–12356. [Google Scholar] [CrossRef]
- Atkeson, C.G.; Moore, A.W.; Schaal, S. Locally weighted learning. Artif. Intell. Rev. 1997, 11, 11–73. [Google Scholar] [CrossRef]
- Leung, H.H.; Huang, Y.S.; Cao, C.X. Locally weighted regression for desulphurisation intelligent decision system modelling. Simul. Model. Pract. Theory 2004, 12, 413–423. [Google Scholar] [CrossRef]
- Pan, T.H.; Li, S.; Li, N. Optimal Bandwidth Design for Lazy Learning via Particle Swarm Optimization. Intell. Autom. Soft Comput. 2009, 15, 1–11. [Google Scholar] [CrossRef]
- Wang, H.Q.; Liao, X.F.; Cao, C.X. An Intelligent Model of LWA using Distributed Kernel. In Proceedings of the 7th World Congress on Intelligent Control and Automation, Chongqing, China, 25–27 June 2008. [Google Scholar] [CrossRef]
- Bai, W.; Ren, J.; Li, T. Modified genetic optimization-based locally weighted learning identification modelling of ship maneuvering with full scale trial. Future Gener. Comput. Syst. 2019, 93, 1036–1045. [Google Scholar] [CrossRef]
- Kamata, K.; Fujiwara, K.; Kinoshita, T.; Kano, M. Missing RRI Interpolation Algorithm based on Locally Weighted Partial Least Squares for Precise Heart Rate Variability Analysis. Sensors 2018, 18, 3870. [Google Scholar] [CrossRef] [PubMed]
- Hirai, T.; Kano, M. Adaptive Virtual Metrology Design for Semiconductor Dry Etching Process Through Locally Weighted Partial Least Squares. IEEE Trans. Semicond. Manuf. 2015, 28, 137–144. [Google Scholar] [CrossRef] [Green Version]
- Schaal, S.; Atkeson, C.G.; Vijayakumar, S. Scalable Techniques from Nonparametric Statistics for Real Time Robot Learning. Appl. Intell. 2002, 17, 49–60. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference, Perth, Australia, 27 November−1 December 1995; pp. 1942–1948. [Google Scholar]
- Xu, S.H.; Liu, J.P.; Zhang, F.H.; Wang, L.; Sun, L.J. A Combination of Genetic Algorithm and Particle Swarm Optimization for Vehicle Routing Problem with Time Windows. Sensors 2015, 15, 21033–21053. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shi, Y.; Eberhart, R.C. Parameter Selection in Particle Swarm Optimization; Springer: Berlin/Heidelberg, Germany, 1998; pp. 591–600. [Google Scholar]
- Sharma, S. Data Driven Soft Sensor Design: Just-in-Time and Adaptive Models; University of Alberta: Edmonton, AL, Canada, 2015. [Google Scholar]
- Santos, I.; Nieves, J.; Penya, Y.K.; Bringas, P.G. Machine-learning-based mechanical properties prediction in foundry production. In Proceedings of the ICROS-SICE International Joint Conference, ICCAS-SICE, Fukuoka, Japan, 18–21 August 2009; pp. 4536–4541. [Google Scholar]
- Shturmakov, A.J.; Loper, C.R. Predictive analysis of mechanical properties in commercial gray iron. Trans. Am. Foundry Soc. 1999, 107, 609–615. [Google Scholar]
- Bates, C.E.; Tucker, J.R.; Starrett, H.S. Composition, Section Size and Microstructural Effects on Tensile Properties of Pearlitic Gray Cast Iron; AFS Research Report; American Foundrymen’s Society: Schaumburg, IL, USA, 1991; Volume 5. [Google Scholar]
- Calcaterra, S.; Campana, G.; Tomesani, L. Prediction of mechanical properties in spheroidal cast iron by neural networks. J. Mater. Process. Technol. 2000, 104, 74–80. [Google Scholar] [CrossRef]
- Schroeder, M.A.; Lander, J.; Levine-Silverman, S. Diagnosing and Dealing with Multicollinearity. West. J. Nurs. Res. 1990, 12, 175–187. [Google Scholar] [CrossRef]
- Alin, A. Multicollinearity. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 370–374. [Google Scholar] [CrossRef]


| Case | Method | RMSE | MAE | MAX |
|---|---|---|---|---|
| 1 | PLS | 21.09 | 15.70 | 89.94 |
| LWPLS | 4.20 | 2.59 | 15.47 | |
| GSSM–LWPLS | 4.09 | 2.52 | 15.20 | |
| PSO–LWPLS | 4.07 | 2.49 | 15.15 | |
| 2 | PLS | 31.18 | 24.08 | 92.86 |
| LWPLS | 7.58 | 5.77 | 31.28 | |
| GSSM–LWPLS | 6.74 | 4.91 | 25.63 | |
| PSO–LWPLS | 4.02 | 2.81 | 15.66 |
| Correlation Coefficients | C | Si | Mn | P | S | TS |
|---|---|---|---|---|---|---|
| C | 1.000 | 0.611 | –0.125 | 0.372 | 0.199 | –0.738 |
| Si | 1.000 | –0.156 | 0.298 | 0.302 | –0.559 | |
| Mn | 1.000 | 0.033 | 0.151 | 0.252 | ||
| P | 1.000 | 0.523 | –0.351 | |||
| S | 1.000 | –0.516 | ||||
| TS | 1.000 |
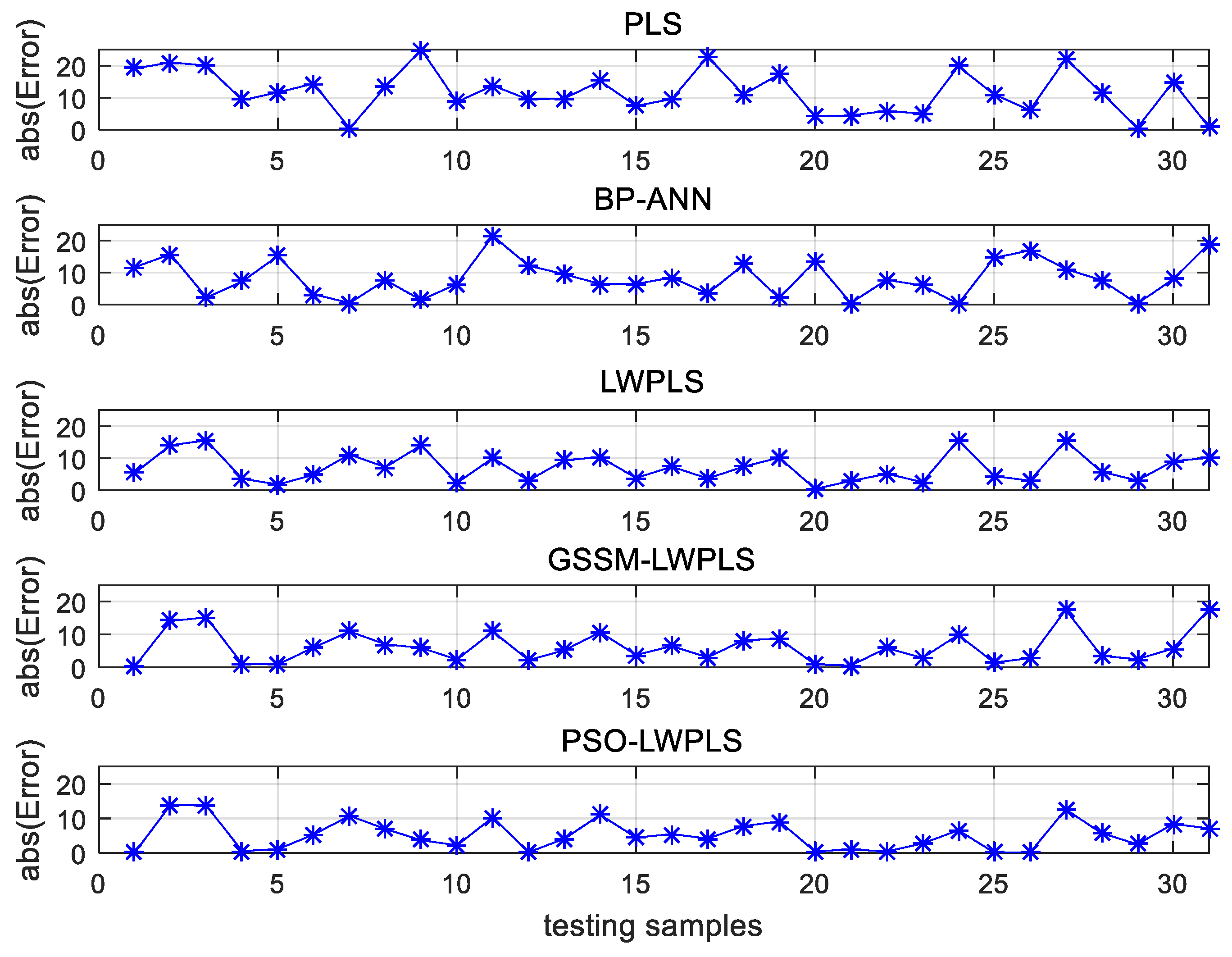
| Method | RMSE | RE (%) | MAE | MAX |
|---|---|---|---|---|
| PLS | 13.6 | 5.63 | 11.8 | 25.0 |
| BP-ANN | 10.8 | 4.38 | 8.9 | 22.5 |
| LWPLS | 8.5 | 3.44 | 7.2 | 15.7 |
| GSSM–LWPLS | 8.0 | 3.27 | 6.3 | 17.7 |
| PSO–LWPLS | 6.8 | 2.84 | 5.3 | 13.9 |
| Method | Training Time (s) | Prediction Time (s) |
|---|---|---|
| PLS | 3.8 | <1 |
| BP-ANN | 9.8 | <1 |
| LWPLS | 3.7 | |
| GSSM–LWPLS | 5.1 | 3.9 |
| PSO–LWPLS | 100.7 | 3.9 |
| Time (s) | Number of Training Samples | ||||||
|---|---|---|---|---|---|---|---|
| 100 | 200 | 300 | 400 | 600 | 800 | 1000 | |
| Training time | 33.6 | 98.4 | 212.6 | 498.1 | 1248.0 | 3749.2 | 10,046.7 |
| Prediction time | <1 | <1 | 1.0 | 1.0 | 1.1 | 1.2 | 1.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, M.; Song, Y.; Chu, W. An Improved Locally Weighted PLS Based on Particle Swarm Optimization for Industrial Soft Sensor Modeling. Sensors 2019, 19, 4099. https://doi.org/10.3390/s19194099
Ren M, Song Y, Chu W. An Improved Locally Weighted PLS Based on Particle Swarm Optimization for Industrial Soft Sensor Modeling. Sensors. 2019; 19(19):4099. https://doi.org/10.3390/s19194099
Chicago/Turabian StyleRen, Minglun, Yueli Song, and Wei Chu. 2019. "An Improved Locally Weighted PLS Based on Particle Swarm Optimization for Industrial Soft Sensor Modeling" Sensors 19, no. 19: 4099. https://doi.org/10.3390/s19194099
APA StyleRen, M., Song, Y., & Chu, W. (2019). An Improved Locally Weighted PLS Based on Particle Swarm Optimization for Industrial Soft Sensor Modeling. Sensors, 19(19), 4099. https://doi.org/10.3390/s19194099





