High-Accuracy Correction of a Microlens Array for Plenoptic Imaging Sensors
Abstract
1. Introduction
2. Correlated MLA Error Model
3. Correction Method
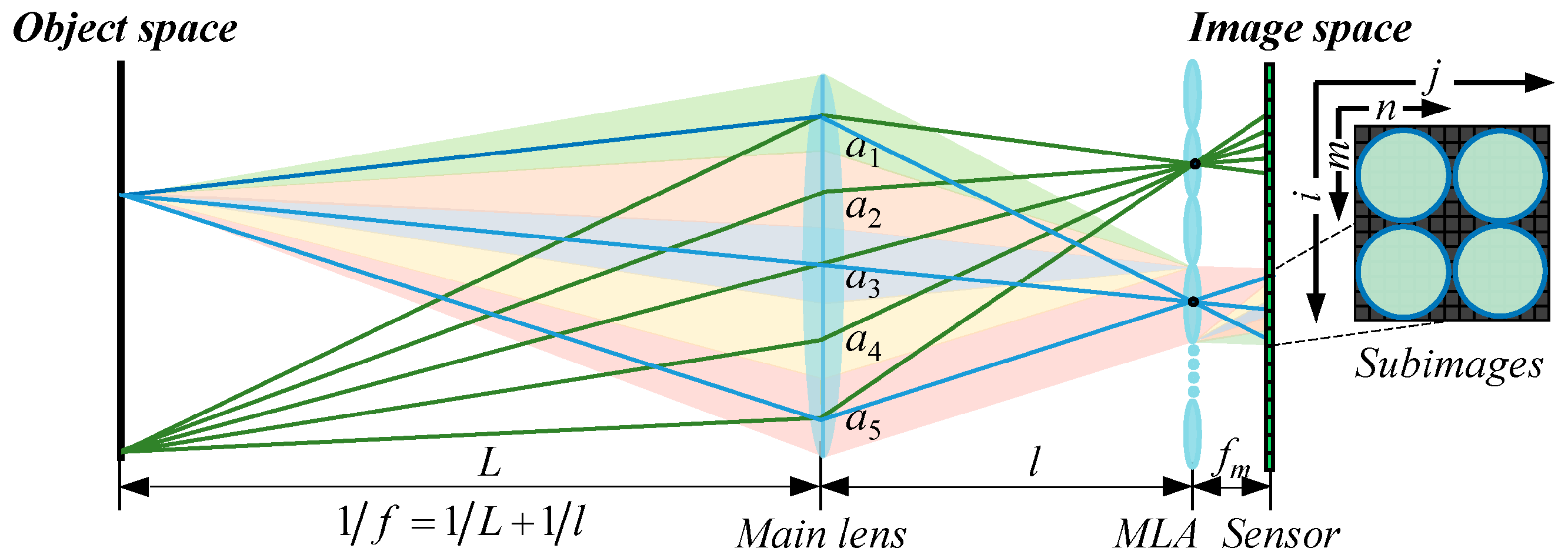
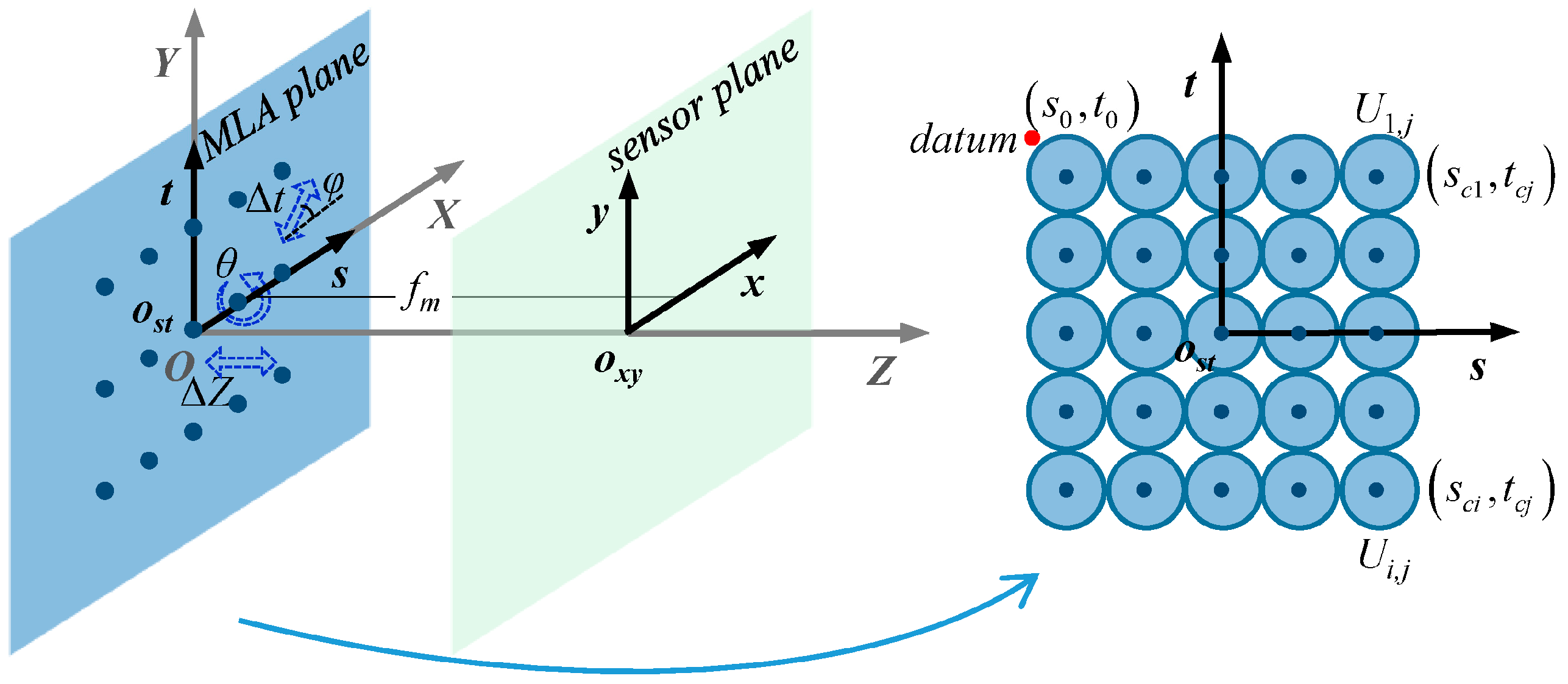
3.1. Principle
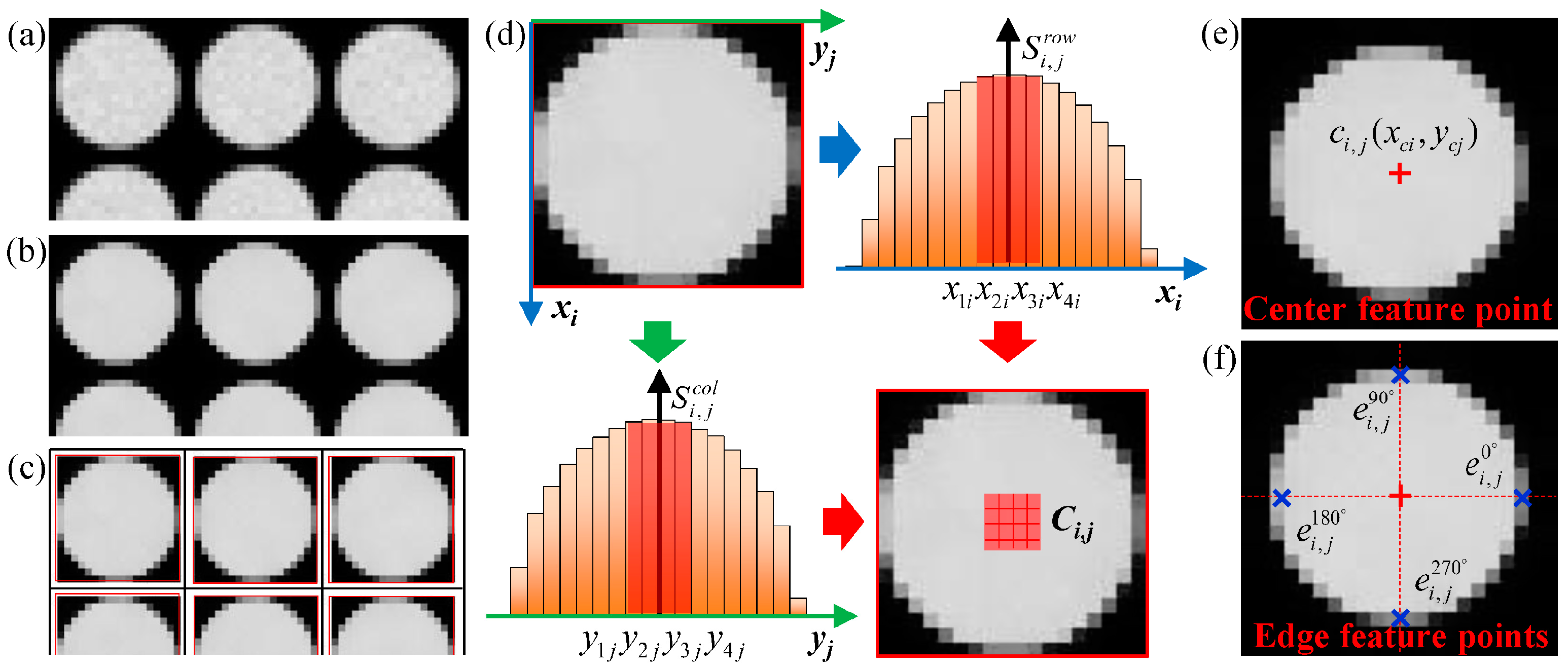
3.2. Subpixel Feature-Point Extraction
| Algorithm 1 Feature-Point Extraction Procedures | |
| Capture a white light-field raw image | |
| Bilateral filtering | |
| Segment microlens subimage regions by the threshold method | |
| 1: Procedure Center-Point Estimation | |
| Compute the overall intensity of the pixels within each row and column of the subimage region | Equation (10) |
| Determine coarse center regions | Equation (11) |
| Subdivided center regions by bilinear interpolation | Equation (12) |
| Estimate the coordinates of the center point at a subpixel level based on a center-of-gravity algorithm | Equation (13) |
| 2: Procedure Edge-Point Estimation | |
| Detect edge pixels using Sobel operator and polynomial interpolation | Equations (14)–(16) |
| Fit defined parabolic functions and to edge pixels and adjacent pixels | Equation (17) |
| Estimate the coordinates of the edge point at a subpixel level | Equation (18) |
3.3. Geometric and Grayscale Correction
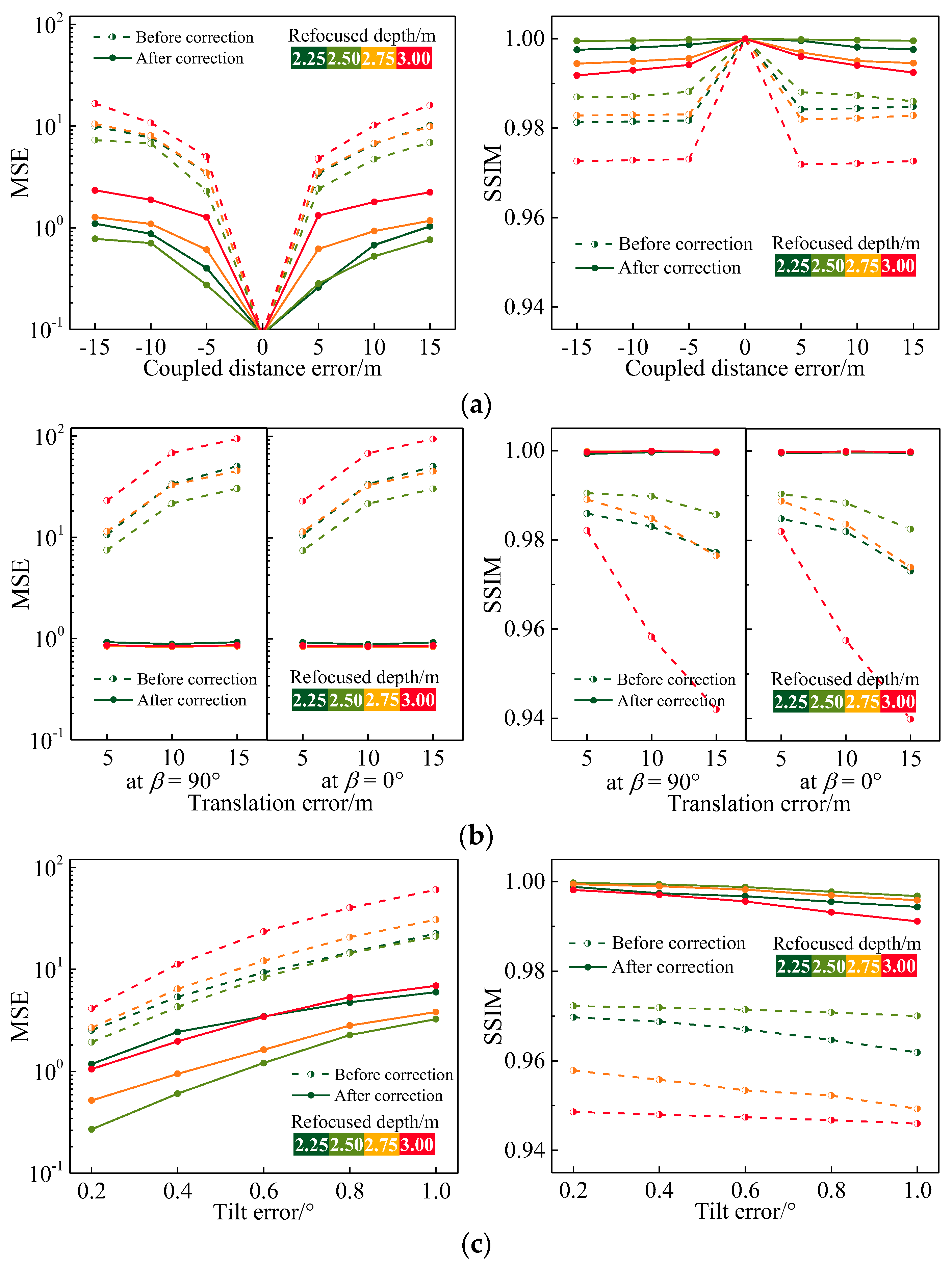
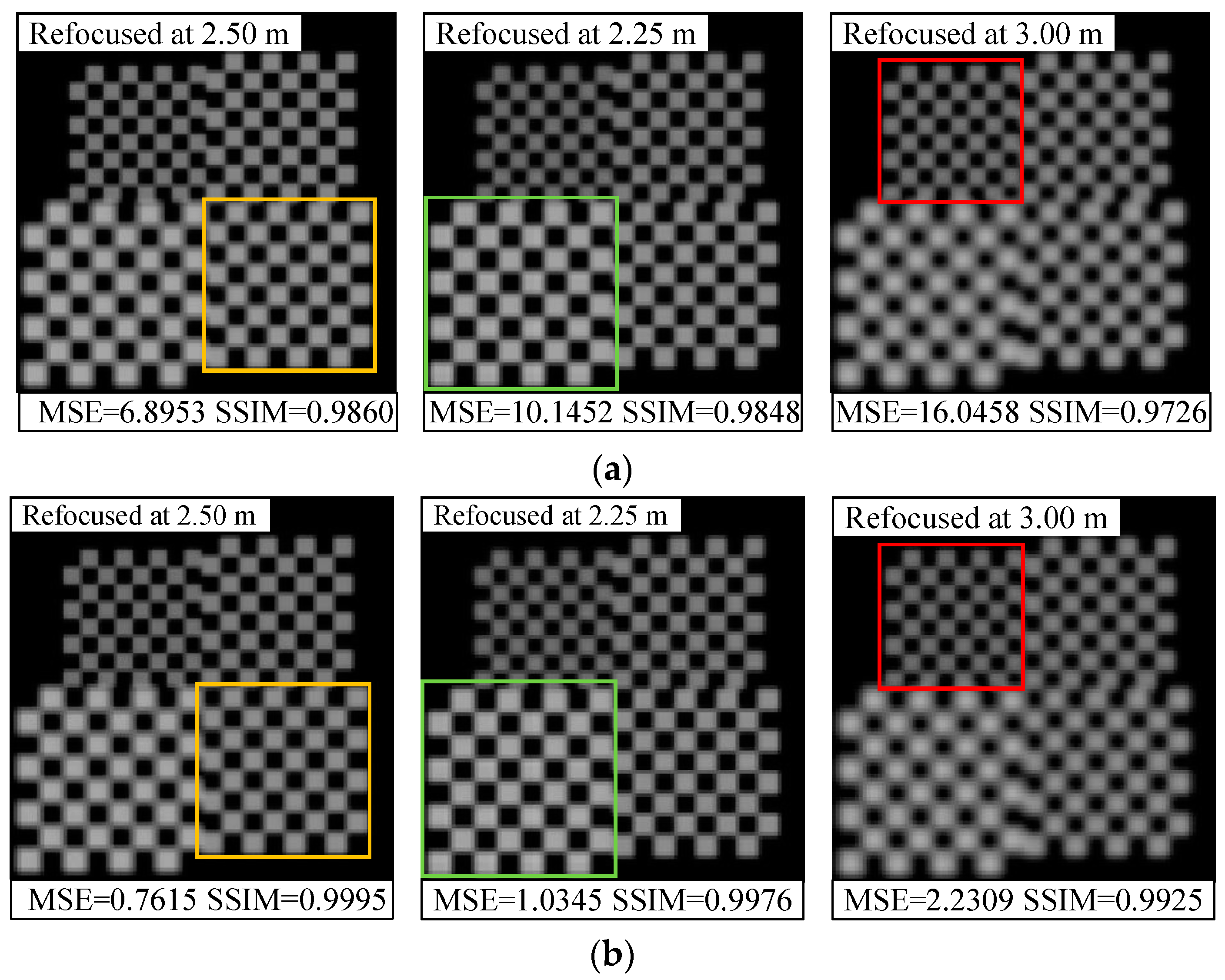
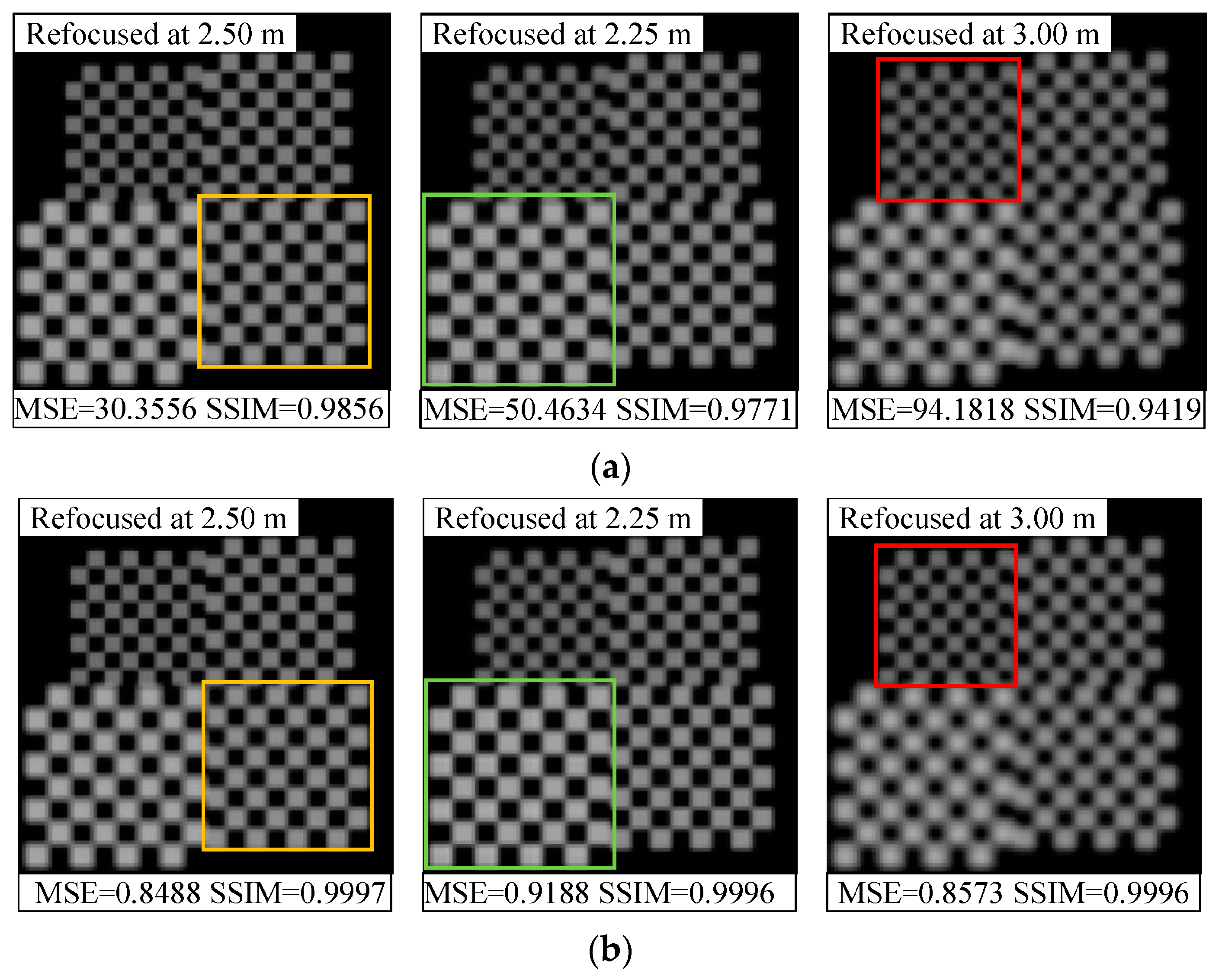
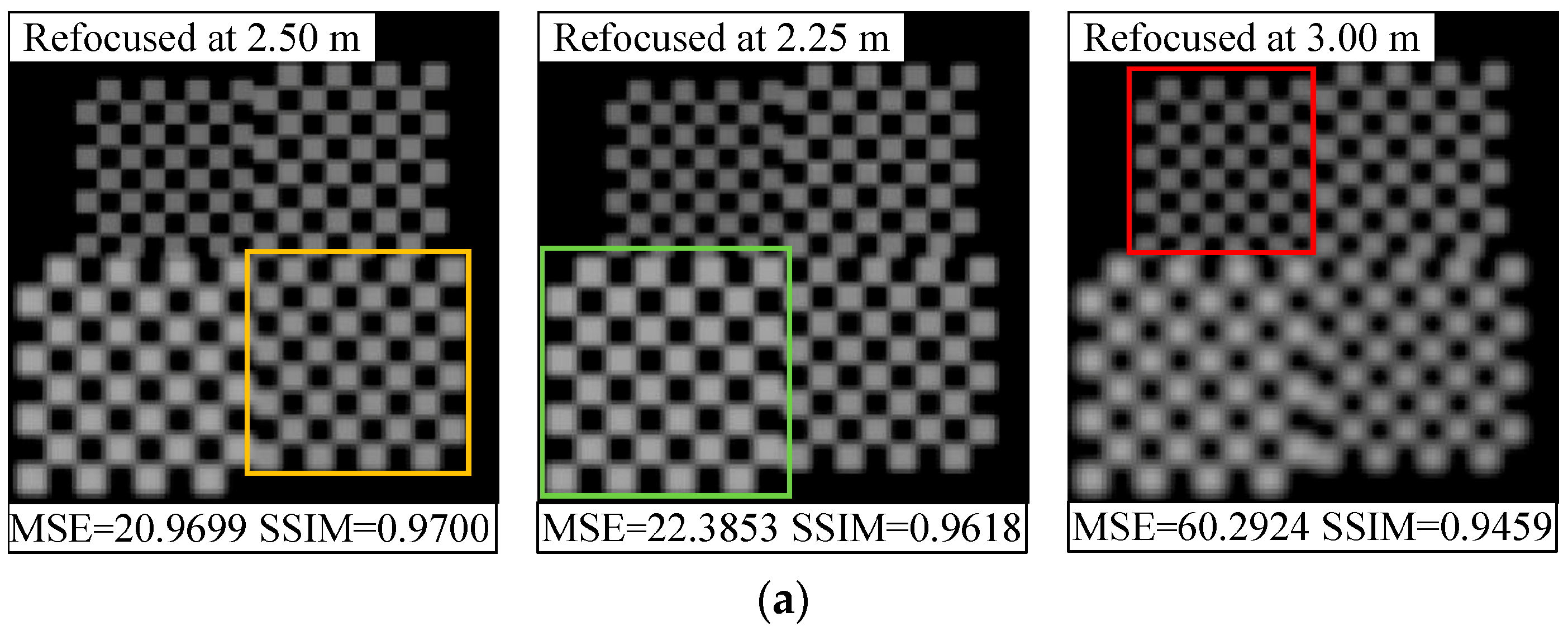
4. Results and Discussion
4.1. Improved Method Validation
4.2. Orientation Error Correction Effect
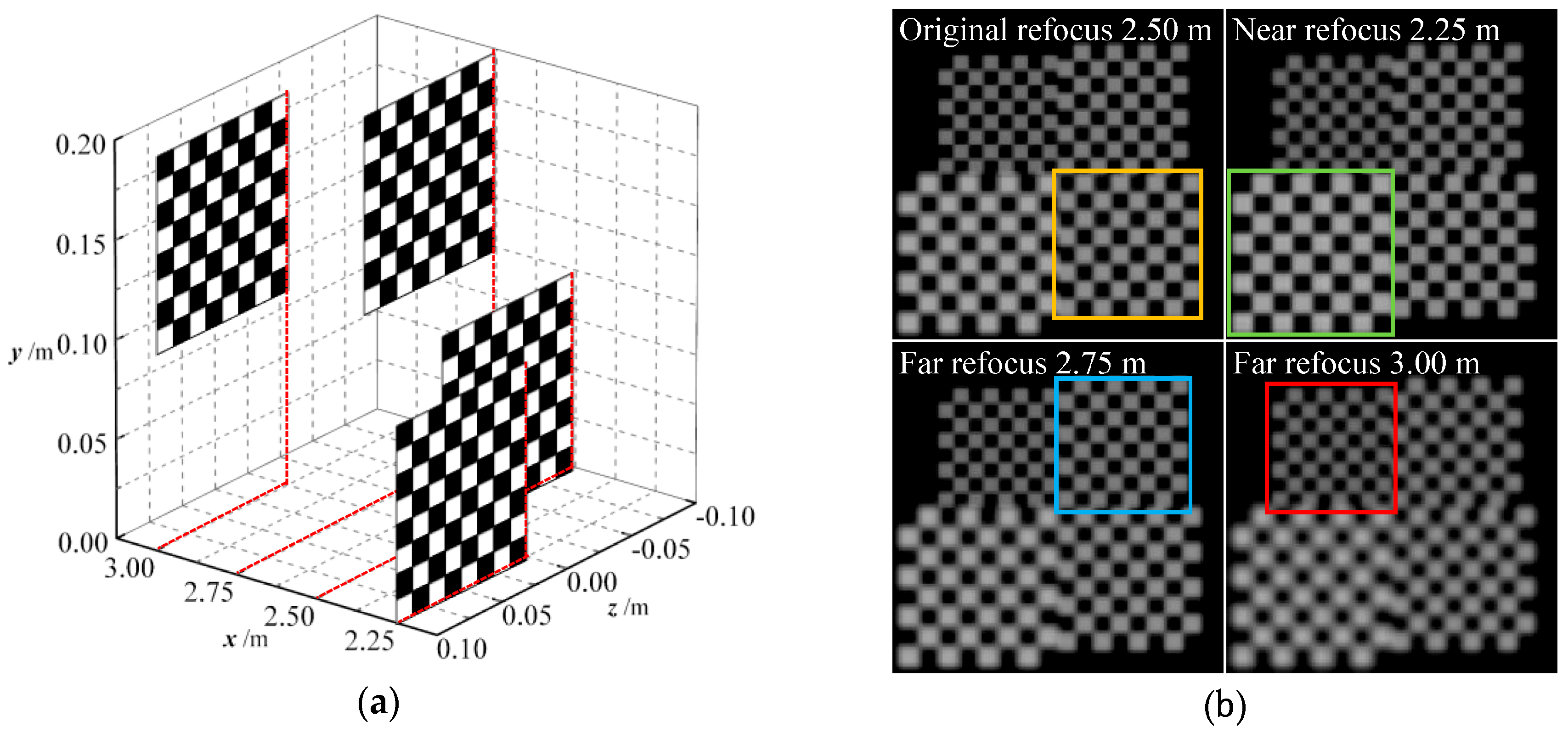
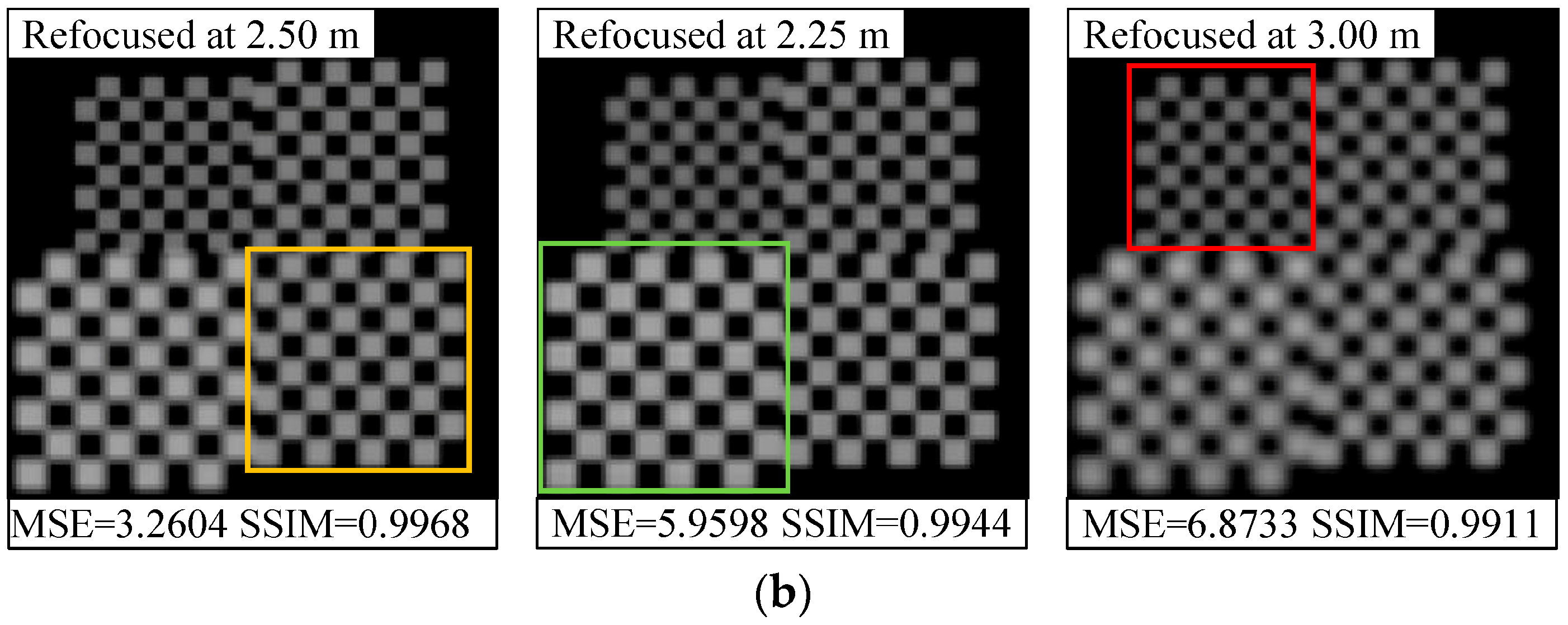
4.3. Evaluation of Light-Field Correction Performance for Real Scene
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ng, R.; Levoy, M.; Brédif, M.; Duval, G.; Horowitz, M.; Hanrahan, P. Light field photography with a hand-held plenoptic camera. Stanford Tech. Rep. CTSR 2005, 2, 1–11. [Google Scholar]
- Palmieri, L.; Scrofani, G.; Incardona, N.; Saavedra, G.; Martínez-Corral, M.; Koch, R. Robust depth estimation for light field microscopy. Sensors 2019, 19, 500. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Liu, X.; Tang, Q.; Peng, X.; Gao, B.Z. Light field 3D measurement using unfocused plenoptic cameras. Opt. Lett. 2018, 43, 3746–3749. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Zhou, W.; Qian, T.; Cai, X. A depth estimation algorithm of plenoptic camera for the measurement of particles. In Proceedings of the IEEE International Conference on Imaging Systems and Techniques, Beihang University, Beijing, China, 18–20 October 2017; pp. 1–5. [Google Scholar]
- Bae, D.H.; Kim, J.W.; Heo, J.P. Content-aware focal plane selection and proposals for object tracking on plenoptic image sequences. Sensors 2019, 19, 48. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Zhao, W.; Hu, J.; Zhang, B.; Wang, S. Liquid lens-based optical sectioning tomography for three-dimensional flame temperature measurement. Fuel 2017, 196, 550–556. [Google Scholar] [CrossRef]
- Li, T.; Li, S.; Yuan, Y.; Wang, F.; Tan, H. Light field imaging analysis of flame radiative properties based on Monte Carlo method. Int. J. Heat Mass Tran. 2018, 119, 303–311. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, B.; Hossain, M.M.; Wang, S.; Qi, H.; Tan, H. Three-dimensional temperature field measurement of flame using a single light field camera. Opt. Express 2016, 24, 1118–1232. [Google Scholar]
- Cao, L.; Zhang, B.; Li, J.; Song, X.; Tang, Z.; Xu, C. Characteristics of tomographic reconstruction of light-field Tomo-PIV. Opt. Commun. 2019, 442, 132–147. [Google Scholar] [CrossRef]
- Wu, C.; Ko, J.; Davis, C.C. Imaging through strong turbulence with a light field approach. Opt. Express 2016, 24, 11975–11986. [Google Scholar] [CrossRef]
- Chen, H.; Woodward, M.A.; Burke, D.T.; Jeganathan, V.S.E.; Demirci, H.; Sick, V. Human iris three-dimensional imaging at micron resolution by a micro-plenoptic camera. Biomed. Opt. Express 2017, 8, 4514–4522. [Google Scholar] [CrossRef]
- Song, Y.M.; Xie, Y.; Malyarchuk, V.; Xiao, J.; Jung, I.; Choi, K.J.; Liu, Z.; Park, H.; Lu, C.; Kim, R.H.; et al. Digital cameras with designs inspired by the arthropod eye. Nature 2013, 497, 95. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Xiao, J. Mechanics and optics of stretchable elastomeric microlens array for artificial compound eye camera. J. Appl. Phys. 2015, 117, 014904. [Google Scholar] [CrossRef]
- Zhou, P.; Cai, W.; Yu, Y.; Zhang, Y.; Zhou, G. A two-step calibration method of lenslet-based light field cameras. Opt. Lasers Eng. 2018, 115, 190–196. [Google Scholar] [CrossRef]
- Li, S.; Zhang, H.; Yuan, Y.; Liu, B.; Tan, H. Microlens assembly error analysis for light field camera based on Monte Carlo method. Opt. Commun. 2016, 372, 22–36. [Google Scholar] [CrossRef]
- Li, S.; Yuan, Y.; Shen, S.; Tan, H. Identification and correction of microlens array rotation error in plenoptic imaging systems. Opt. Lasers Eng. 2019, 121, 156–168. [Google Scholar] [CrossRef]
- Li, S.; Yuan, Y.; Liu, B.; Wang, F.; Tan, H. Influence of microlens array manufacturing errors on light-field imaging. Opt. Commun. 2018, 410, 40–52. [Google Scholar] [CrossRef]
- Li, S.; Yuan, Y.; Liu, B.; Wang, F.; Tan, H. Local error and its identification for microlens array in plenoptic camera. Opt. Lasers Eng. 2018, 108, 41–53. [Google Scholar] [CrossRef]
- Shih, K.; Hsu, C.; Yang, C.; Chen, H.H. Analysis of the effect of calibration error on light field super-resolution rendering. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Florence, Italy, 4–9 May 2014; pp. 534–538. [Google Scholar]
- Shi, S.; Ding, J.; New, T.H.; Liu, Y.; Zhang, H. Volumetric calibration enhancements for single-camera light-field PIV. Exp. Fluids 2019, 60, 21. [Google Scholar] [CrossRef]
- Kong, X.; Chen, Q.; Wang, J.; Gu, G.; Wang, P.; Qian, W.; Ren, K.; Miao, X. Inclinometer assembly error calibration and horizontal image correction in photoelectric measurement systems. Sensors 2018, 18, 248. [Google Scholar] [CrossRef] [PubMed]
- Hall, M.E.; Guildenbecher, R.D.; Thurow, S.B. Uncertainty characterization of particle location from refocused plenoptic images. Opt. Express 2017, 25, 21801–21814. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Wang, Q.; Cai, W. Assessment of plenoptic imaging for reconstruction of 3D discrete and continuous luminous fields. J. Opt. Soc. Am. A 2019, 36, 149–158. [Google Scholar] [CrossRef]
- Suliga, P.; Wrona, T. Microlens array calibration method for a light field camera. In Proceedings of the 19th International Carpathian Control Conference, Szilvasvarad, Hungary, 28–31 May 2018; pp. 19–22. [Google Scholar]
- Su, L.; Yan, Q.; Cao, J.; Yuan, Y. Calibrating the orientation between a microlens array and a sensor based on projective geometry. Opt. Lasers Eng. 2016, 82, 22–27. [Google Scholar] [CrossRef]
- Bok, Y.; Jeon, H.; Kweon, I.S. Geometric calibration of micro-lens-based light field cameras using line features. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 287–300. [Google Scholar] [CrossRef]
- Cho, D.; Lee, M.; Kim, S.; Tai, Y.W. Modeling the calibration pipeline of the lytro camera for high quality light-field image reconstruction. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 3280–3287. [Google Scholar]
- Jin, J.; Cai, W.; Cao, Y.; Zheng, W.; Zhou, P. An effective rectification method for lenselet-based plenoptic cameras. In Proceedings of the Optoelectronic Imaging and Multimedia Technology IV, Beijing, China, 12–14 October 2016. [Google Scholar]
- Li, S.; Zhu, Y.; Zhang, C.; Yuan, Y.; Tan, H. Rectification of images distorted by microlens array errors in plenoptic cameras. Sensors 2018, 18, 2019. [Google Scholar] [CrossRef]
- Liu, B.; Yuan, Y.; Li, S.; Shuai, Y.; Tan, H. Simulation of light-field camera imaging based on ray splitting Monte Carlo method. Opt. Commun. 2015, 355, 15–26. [Google Scholar] [CrossRef]
- Kim, H.M.; Kim, M.S.; Lee, G.J.; Yoo, Y.J.; Song, Y.M. Large area fabrication of engineered microlens array with low sag height for light-field imaging. Opt. Express 2019, 27, 4435–4444. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.; Fang, F.; Liu, S. Identification and compensation of main machining errors on surface form accuracy in ultra-precision diamond turning. Int. J. Mach. Tool Manu. 2016, 105, 45–57. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, C.; Ling, J.; Wang, Q.; Yu, J. A generic multi-projection-center model and calibration method for light field cameras. IEEE Trans. Pattern Anal. Mach. Intell. 2018. [Google Scholar] [CrossRef]
- Wang, Z. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE T. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]

| Errors | Center Coordinates | Surface Description Equations |
|---|---|---|
| Pitch error Δp | ||
| Radius-of-curvature error Δr | ||
| Decenter error δ | ||
| Errors | Distorted Image | Previous [22] | Proposed | |||
|---|---|---|---|---|---|---|
| Geometric Correction | Grayscale Correction | Geometric Correction | Grayscale Correction | |||
| Pitch error Δp/μm | 0.2 | 15.2614 | 27.3087 | 27.3401 | 29.7926 | 29.7975 |
| 0.4 | 11.3084 | 26.5720 | 26.6383 | 29.6418 | 29.6524 | |
| 0.6 | 9.5670 | 27.7079 | 27.8181 | 29.6799 | 29.6992 | |
| 0.8 | 8.5864 | 28.1185 | 28.2683 | 29.6587 | 29.6842 | |
| 1.0 | 7.9800 | 27.2738 | 27.4589 | 29.6771 | 29.7143 | |
| Radius-of-curvature error εr/% | −10 | 21.6809 | 22.5709 | 25.4931 | 26.5234 | 26.8382 |
| −5 | 27.3614 | 28.2296 | 28.9152 | 30.3768 | 30.5047 | |
| −1 | 32.2685 | 32.3726 | 32.7820 | 32.9302 | 32.9569 | |
| 5 | 32.0104 | 32.0559 | 32.1552 | 32.0739 | 32.0916 | |
| 10 | 28.2675 | 29.4416 | 29.8102 | 30.1497 | 30.1912 | |
| Decenter error δ/μm | 2.0 | 27.8829 | 29.3994 | 29.4021 | 30.6986 | 30.6988 |
| 4.0 | 22.4982 | 26.5645 | 26.5748 | 28.9067 | 28.9081 | |
| 6.0 | 19.3433 | 25.7290 | 25.7774 | 28.9735 | 28.9756 | |
| 8.0 | 17.1759 | 27.2166 | 27.2793 | 30.4878 | 30.4928 | |
| 10.0 | 15.5782 | 27.5018 | 27.5799 | 31.9829 | 31.9908 | |
| Errors | Without Correction | Geometric Correction | Grayscale Correction | |
|---|---|---|---|---|
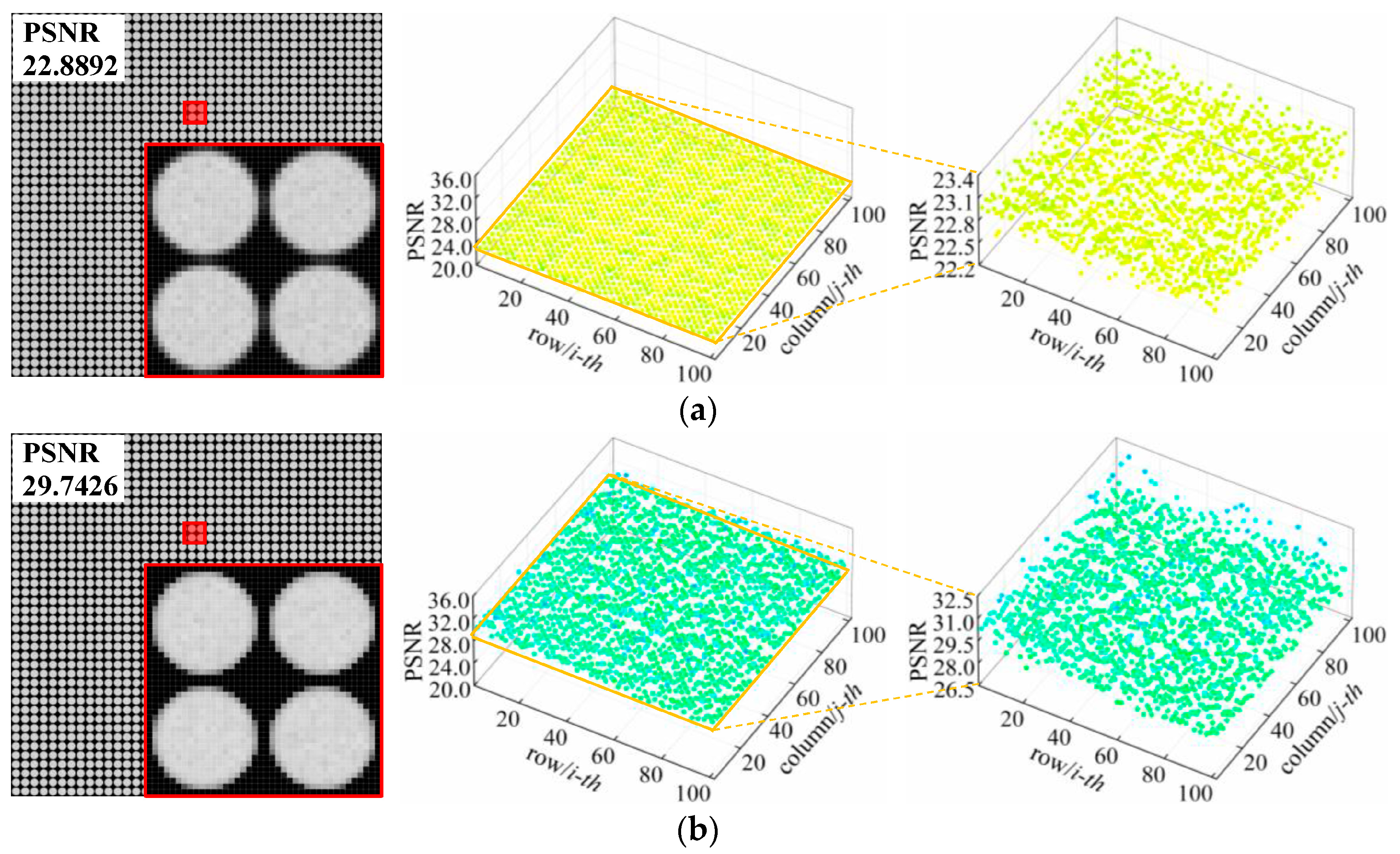
| Coupled distance error Δz/μm | −15 | 22.8892 | 29.7112 | 29.7426 |
| −10 | 25.9022 | 31.6473 | 31.6594 | |
| −5 | 31.0463 | 34.2698 | 34.2597 | |
| 5 | 30.7221 | 34.1088 | 34.1179 | |
| 10 | 25.1907 | 31.9324 | 31.9624 | |
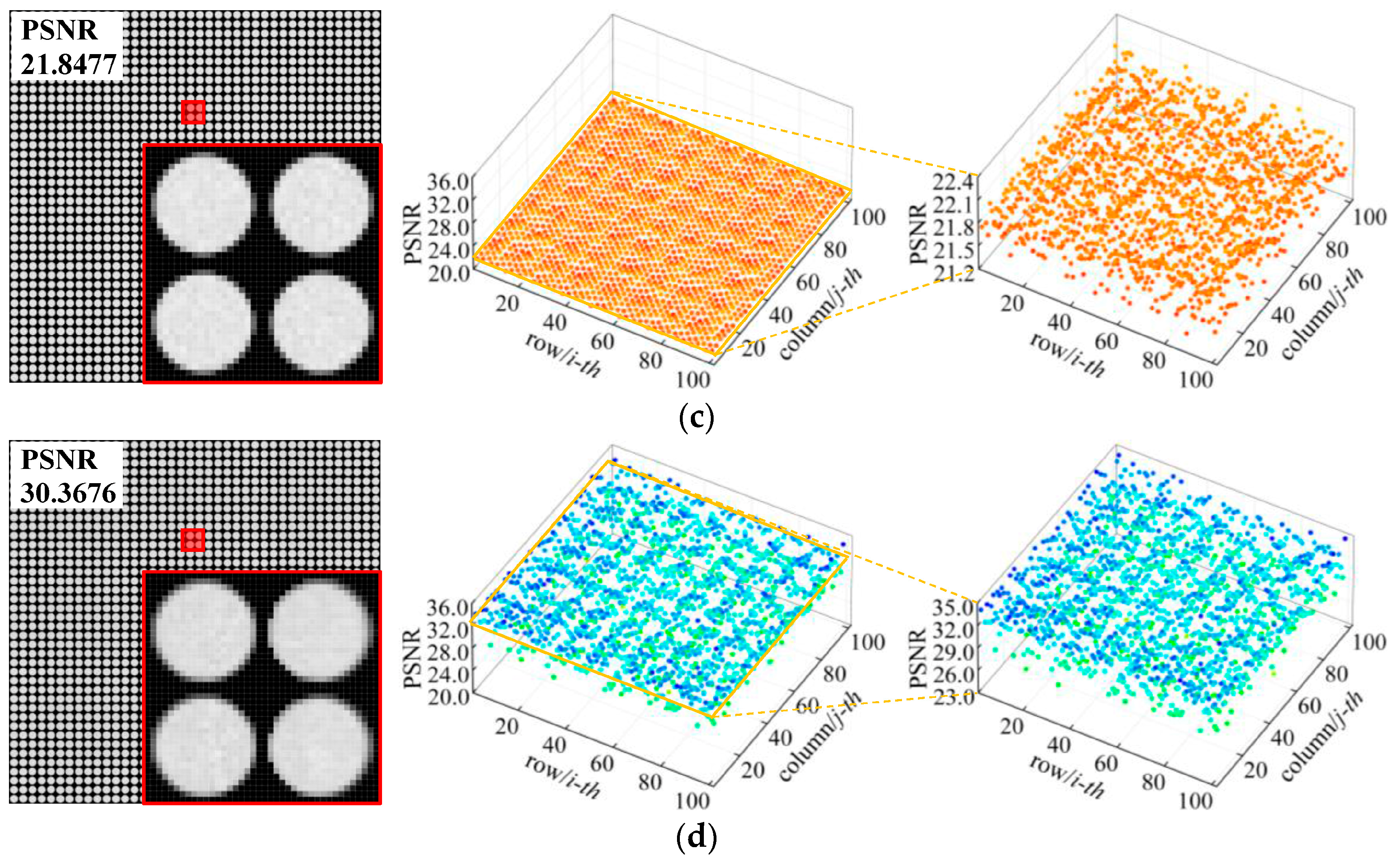
| 15 | 21.8477 | 30.3313 | 30.3676 | |
| Translation error Δtx/μm | 5 | 15.7850 | 31.3175 | 31.3192 |
| 10 | 11.3673 | 31.1689 | 31.1711 | |
| 15 | 9.2537 | 31.0213 | 31.0235 | |
| Δty/μm | 5 | 15.7861 | 31.3819 | 31.3837 |
| 10 | 11.3678 | 31.0084 | 31.0105 | |
| 15 | 9.2537 | 31.0483 | 31.0503 | |
| Tilt error θ/° | 0.2 | 25.6067 | 32.7456 | 32.7587 |
| 0.4 | 20.3286 | 31.1000 | 31.1177 | |
| 0.6 | 17.5186 | 29.1576 | 29.1997 | |
| 0.8 | 15.8102 | 26.8395 | 26.9160 | |
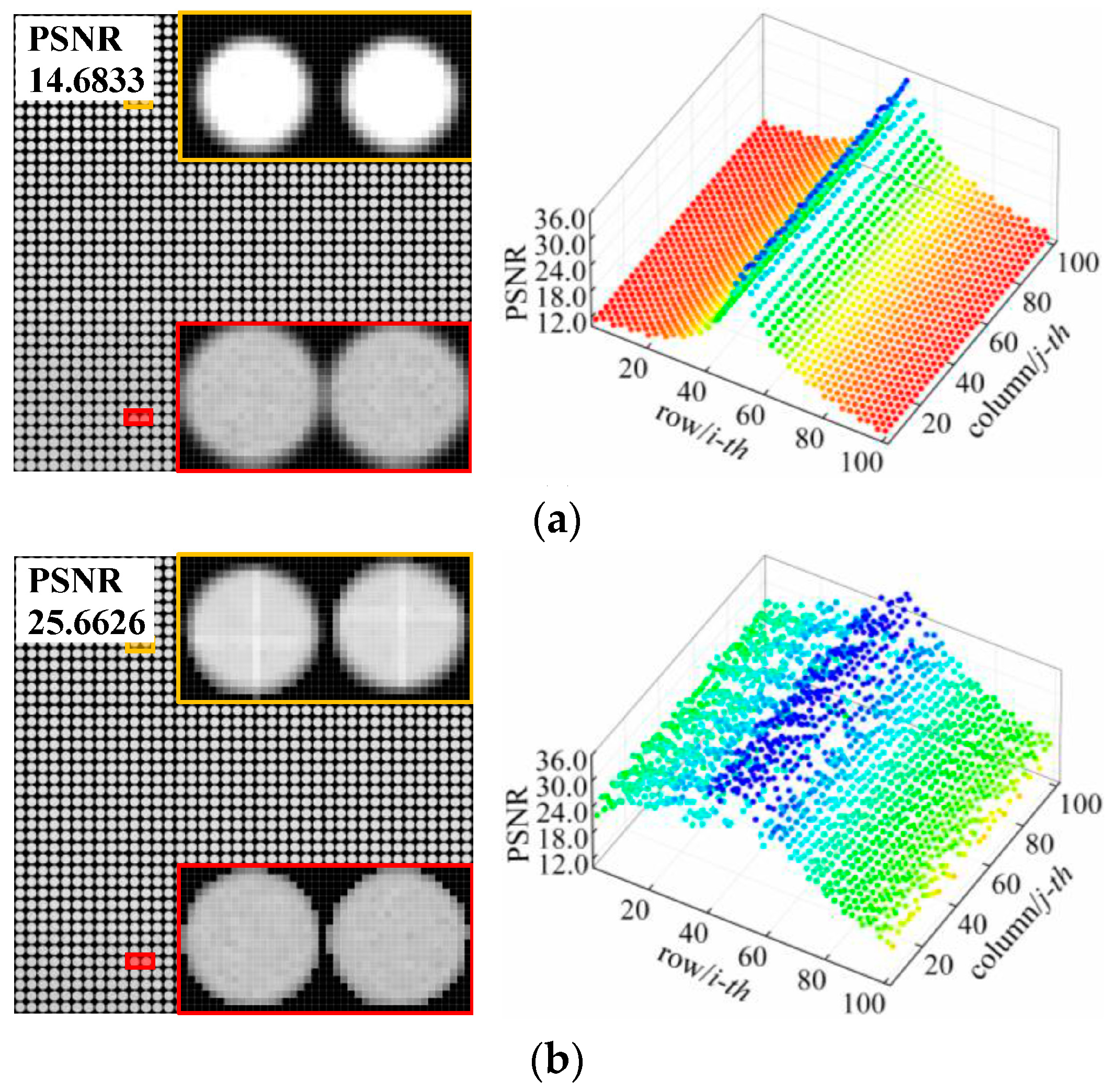
| 1.0 | 14.6833 | 25.4762 | 25.6626 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Yuan, Y.; Gao, Z.; Tan, H. High-Accuracy Correction of a Microlens Array for Plenoptic Imaging Sensors. Sensors 2019, 19, 3922. https://doi.org/10.3390/s19183922
Li S, Yuan Y, Gao Z, Tan H. High-Accuracy Correction of a Microlens Array for Plenoptic Imaging Sensors. Sensors. 2019; 19(18):3922. https://doi.org/10.3390/s19183922
Chicago/Turabian StyleLi, Suning, Yuan Yuan, Ziyi Gao, and Heping Tan. 2019. "High-Accuracy Correction of a Microlens Array for Plenoptic Imaging Sensors" Sensors 19, no. 18: 3922. https://doi.org/10.3390/s19183922
APA StyleLi, S., Yuan, Y., Gao, Z., & Tan, H. (2019). High-Accuracy Correction of a Microlens Array for Plenoptic Imaging Sensors. Sensors, 19(18), 3922. https://doi.org/10.3390/s19183922





