Quantitative and Qualitative Analysis of Multicomponent Gas Using Sensor Array
Abstract
:1. Introduction
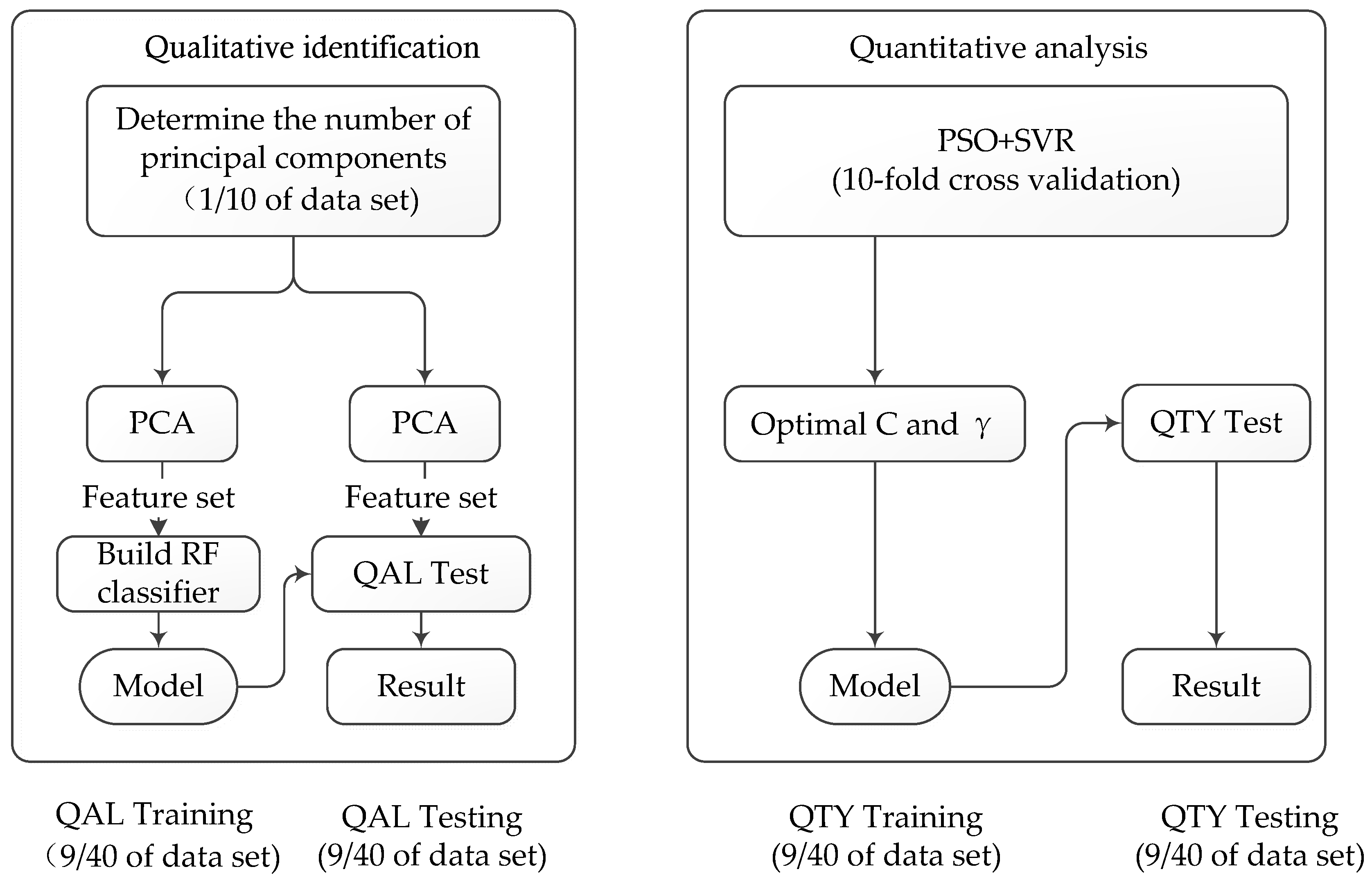
2. Gas Mixture Analysis Method
3. Qualitative Identification Method for Gas Mixture
3.1. Principal Component Analysis
3.2. Random Forest
| Algorithm 1. Decision Tree |
| Input: Training set |
| Attribute set |
Process: Function Tree Generate (D, A)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Output: A decision tree with root node |
4. Quantitative Analysis Method for Gas mixture
4.1. Support Vector Regression
4.2. PSO
- Step 1.
- Initialize a group of particles with the group size n, set their original velocity and location, and set the maximum number of iterations at the same time;
- Step 2.
- Define the fitness function to evaluate the fitness of each particle;
- Step 3.
- Find the optimal solution for each particle (individual extremum), from which a global value is found, which is called the global optimal solution;
- Step 4.
- Update the velocity and position of the particle by Equations (9) and (10), where Vid and Xid are the d dimensional velocity and position of particle i, Pid and Pgd are the d dimensional optimal position searched by particle i and the global optimal position of the whole group, is the inertia factor, C1 and C2 are the learning factor, and random(0, 1) is a random number between (0, 1):
- Step 5.
- The algorithm will be terminated when the number of iterations reaches the setting; otherwise, it will return to step 2 to continue execution.
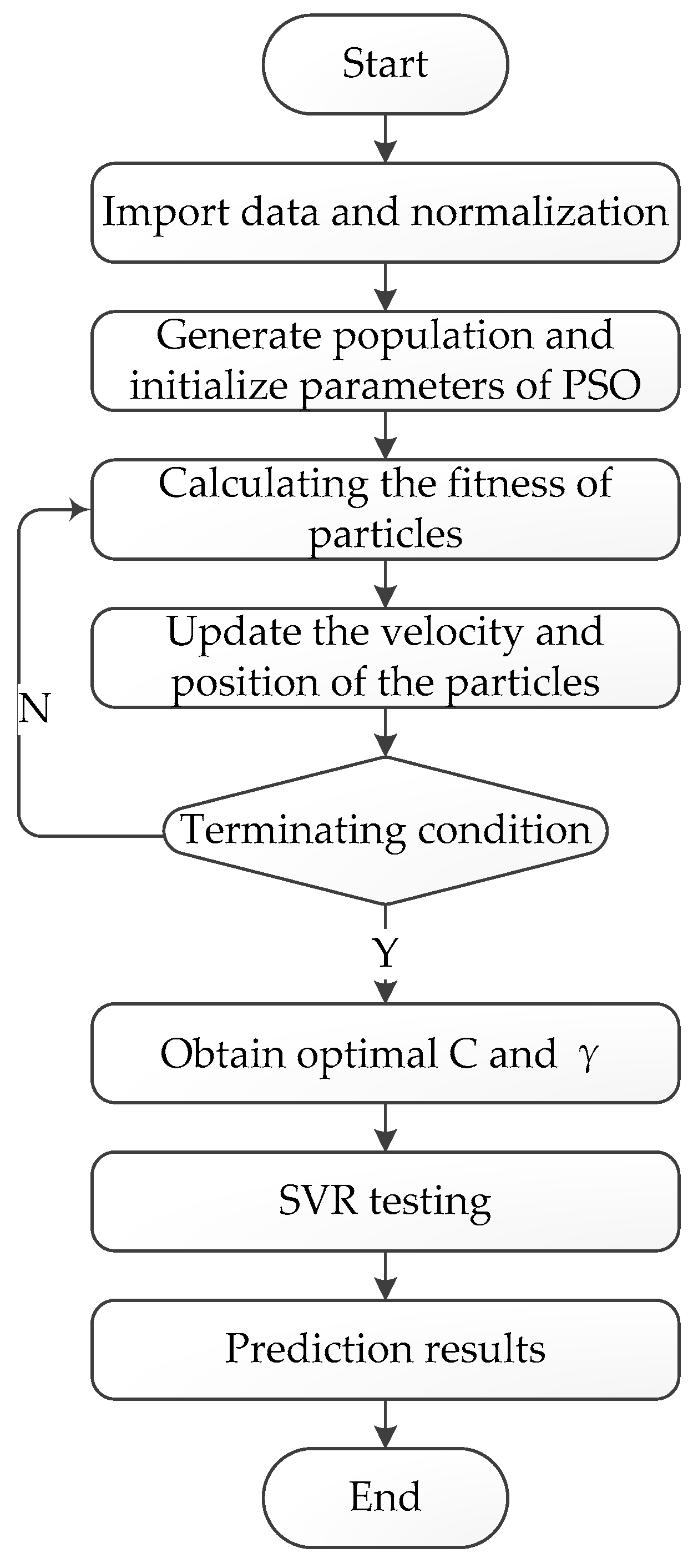
4.3. SVR Optimized by the PSO Algorithm
- Step 1.
- Import the original data, divide it into training data and test data, and normalize these;
- Step 2.
- Initialize the parameters of PSO, including population n, particle velocity v, and position x, and iteration number;
- Step 3.
- Calculate the fitness value of the particle. The current fitness value of the particle is compared with the fitness value of the historically optimal position. If it is better, it will be regarded as the current optimal position. Compared with the global optimal position fitness value of each particle, if it is better, it will be considered the current global optimal position;
- Step 4.
- Update the velocity and position of the particle by Equations (9) and (10);
- Step 5.
- Determine whether termination conditions are met. If they are satisfied, the optimal C value and value are output and assigned to SVR. Otherwise, return to step 3;
- Step 6.
- Test the optimal model of SVR and obtain the prediction results.
5. Experiments and Results
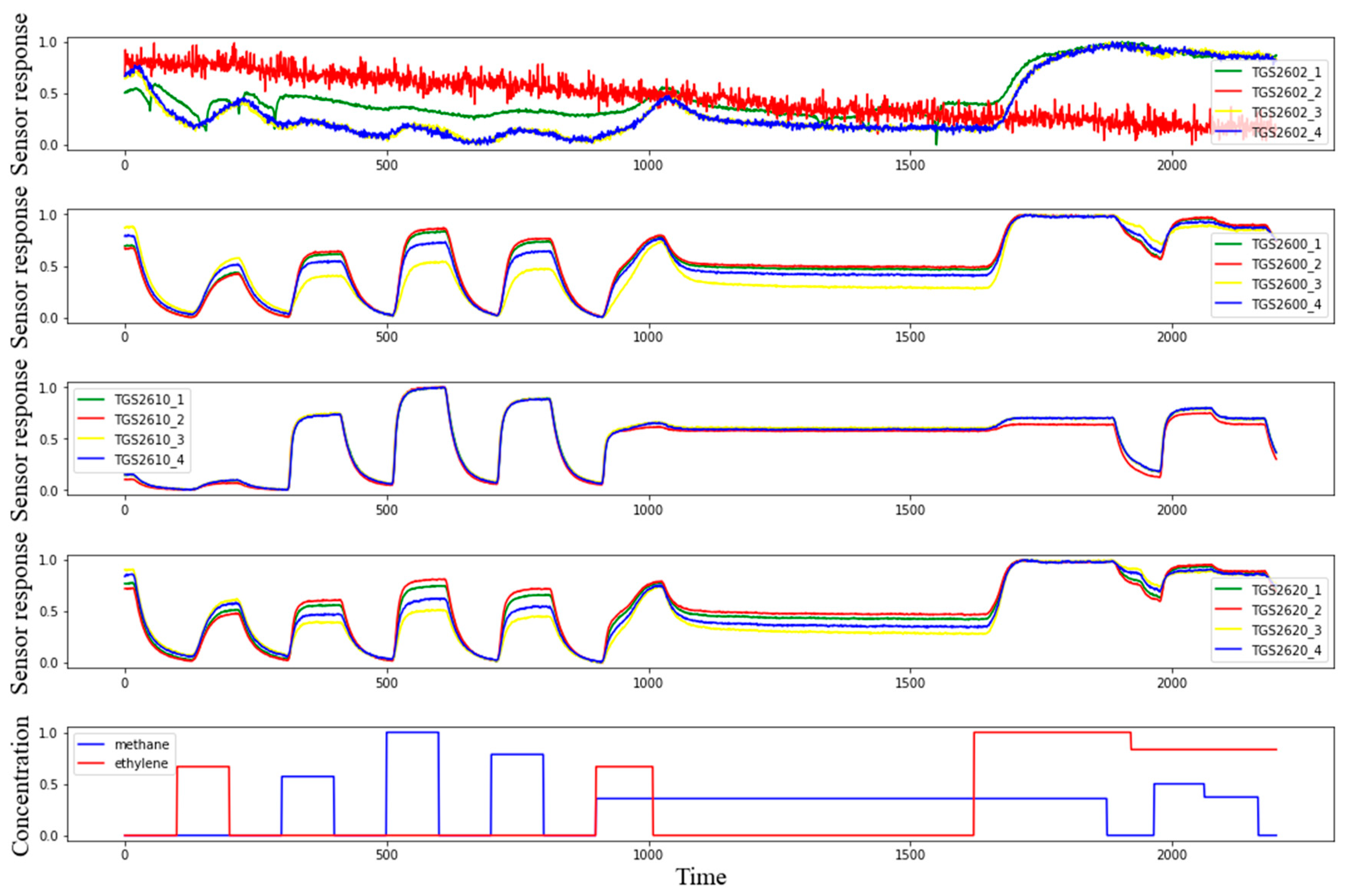
5.1. Dataset
5.2. PCA Feature Extraction
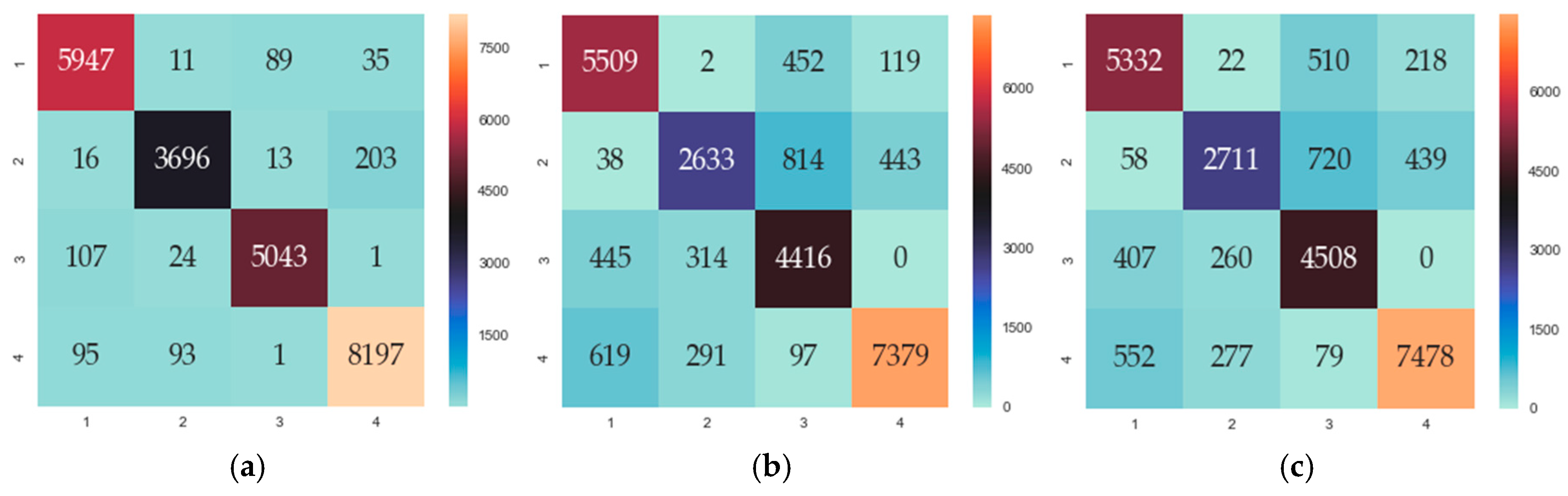
5.3. Qualitative Identification for Gas Mixture
- LR: penalty: ‘l2’, C: ‘1’, solver: ‘lbfgs’, multiclass: ‘multinomial’;
- SVM: ‘kernel: ‘linear’, decision_function_shape: ‘ovo’.
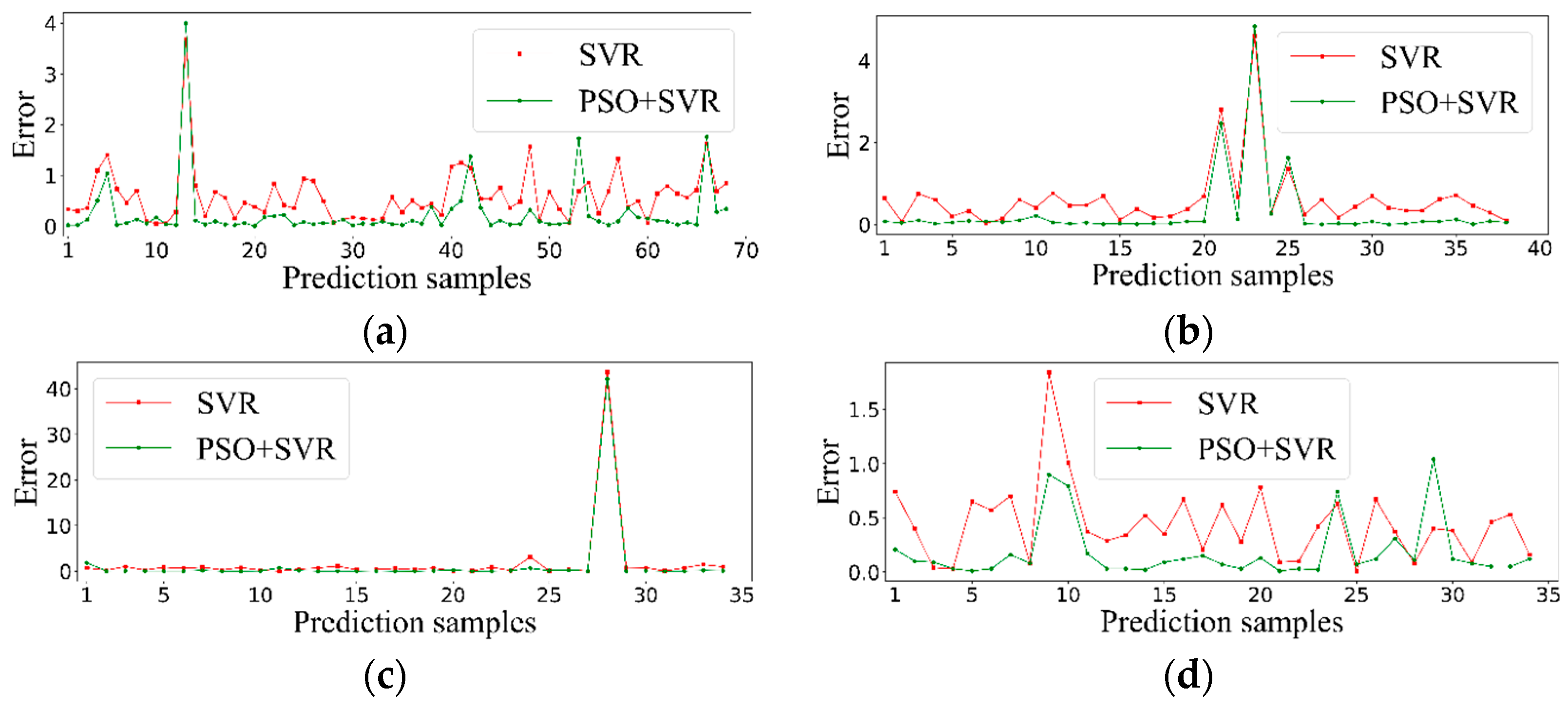
5.4. Quantitative Analysis for Gas Mixture
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Asal, M.; Nasirian, S. Acetone gas sensing features of zinc oxide/tin dioxide nanocomposite for diagnosis of diabetes. Mater. Res. Express 2019, 9, 095093. [Google Scholar] [CrossRef]
- Pagonas, N.; Vautz, W.; Seifert, L.; Slodzinski, R.; Jankowski, J.; Zidek, W.; Westhoff, T.H. Volatile organic compounds in uremia. PLoS ONE 2012, 9, e46258. [Google Scholar] [CrossRef] [PubMed]
- Gancarz, M.; Wawrzyniak, J.; Gawrysiak-Witulska, M.; Wiącek, D.; Nawrocka, A.; Rusinek, R. Electronic nose with polymer-composite sensors for monitoring fungal deterioration of stored rapeseed. Int. Agrophys. 2017, 3, 317–325. [Google Scholar] [CrossRef]
- Rusinek, R.; Gancarz, M.; Krekora, M.; Nawrocka, A. A novel method for generation of a fingerprint using electronic nose on the example of rapeseed spoilage. J. Food Sci. 2019, 1, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Zhang, M.; Bhandari, B.; Adhikari, B. Application of electronic tongue for fresh foods quality evaluation: A review. Food Rev. Int. 2018, 8, 746–769. [Google Scholar] [CrossRef]
- Qiu, S.; Wang, J. The prediction of food additives in the fruit juice based on electronic nose with chemometrics. Food Chem. 2017, 230, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Men, H.; Fu, S.; Yang, J.; Cheng, M.; Shi, Y.; Liu, J. Comparison of SVM, RF and ELM on an electronic nose for the intelligent evaluation of paraffin samples. Sensors 2018, 18, 285. [Google Scholar] [CrossRef] [PubMed]
- Gorji-Chakespari, A.; Nikbakht, A.M.; Sefidkon, F.; Ghasemi-Varnamkhasti, M.; Brezmes, J.; Llobet, E. Performance Comparison of Fuzzy ARTMAP and LDA in Qualitative Classification of Iranian Rosa damascena Essential Oils by an Electronic Nose. Sensors 2016, 16, 636. [Google Scholar] [CrossRef]
- Gu, Q.; R Michanowicz, D.; Jia, C. Developing a Modular Unmanned Aerial Vehicle (UAV) Platform for Air Pollution Profiling. Sensors 2018, 18, 4363. [Google Scholar] [CrossRef]
- Morawska, L.; Thai, P.K.; Liu, X.; Asumadu-Sakyi, A.; Ayoko, G.; Bartonova, A.; Bedini, A.; Chai, F.; Christensen, B.; Dunbabin, M.; et al. Applications of low-cost sensing technologies for air quality monitoring and exposure assessment: How far have they gone? Environ. Int. 2018, 286–299. [Google Scholar] [CrossRef]
- Rai, A.C.; Kumar, P.; Pilla, F.; Skouloudis, A.N.; di Sabatino, S.; Ratti, C.; Yasar, A.; Rickerby, D. End-user perspective of low-cost sensors for outdoor air pollution monitoring. Sci. Total Environ. 2017, 691–705. [Google Scholar] [CrossRef] [PubMed]
- Al Barakeh, Z.; Breuil, P.; Redon, N.; Pijolat, C.; Locoge, N.; Viricelle, J.P. Development of a normalized multi-sensors system for low cost on-line atmospheric pollution detection. Sens. Actuators B Chem. 2017, 1235–1243. [Google Scholar] [CrossRef]
- Escobar, J.M.; Suescun, J.P.S.; Correa, M.A.; Metaute, D.O. Forecasting concentrations of air pollutants using support vector regression improved with particle swarm optimization: Case study in Aburrá Valley, Colombia. Urban Clim. 2019. [Google Scholar] [CrossRef]
- Na, J.; Jeon, K.; Lee, W.B. Toxic gas release modeling for real-time analysis using variational autoencoder with convolutional neural networks. Chem. Eng. Sci. 2018, 68–78. [Google Scholar] [CrossRef]
- Li, X.B.; Wang, D.S.; Lu, Q.C.; Peng, Z.R.; Wang, Z.Y. Investigating vertical distribution patterns of lower tropospheric PM2.5 using unmanned aerial vehicle measurements. Atmos. Environ. 2018, 62–71. [Google Scholar] [CrossRef]
- Li, M.; Wang, W.L.; Wang, Z.Y.; Xue, Y. Prediction of PM 2.5 concentration based on the similarity in air quality monitoring network. Build. Environ. 2018, 11–17. [Google Scholar] [CrossRef]
- Liu, H.; Wu, H.; Lv, X.; Ren, Z.; Liu, M.; Li, Y.; Shi, H. An intelligent hybrid model for air pollutant concentrations forecasting: Case of Beijing in China. Sustain. Cities Soc. 2019. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Bian, X.; Huang, X.; Qi, L. A continuous gas leakage localization method based on an improved beamforming algorithm. Measurement 2017, 143–151. [Google Scholar] [CrossRef]
- Zeng, L.; Long, W.; Li, Y. A novel method for gas turbine condition monitoring based on KPCA and analysis of statistics T2 and SPE. Processes 2019, 7, 124. [Google Scholar] [CrossRef]
- Liu, L. Research on logistic regression algorithm of breast cancer diagnose data by machine learning. In Proceedings of the 2018 International Conference on Robots & Intelligent System (ICRIS), Changsha, China, 26–27 May 2018. [Google Scholar]
- Zhang, J.; Zheng, C.H.; Xia, Y.; Wang, B.; Chen, P. Optimization enhanced genetic algorithm-support vector regression for the prediction of compound retention indices in gas chromatography. Neurocomputing 2017, 183–190. [Google Scholar] [CrossRef]
- Fonollosa, J.; Sheik, S.; Huerta, R.; Marco, S. Reservoir computing compensates slow response of chemosensor arrays exposed to fast varying gas concentrations in continuous monitoring. Sens. Actuators B Chem. 2015, 618–629. [Google Scholar] [CrossRef]
- Gancarz, M.; Nawrocka, A.; Rusinek, R. Identification of volatile organic compounds and their concentrations using a novel method analysis of MOS sensors signal. J. Food Sci. 2019, 8, 2077–2085. [Google Scholar] [CrossRef] [PubMed]
- Lentka, Ł.; Smulko, J.M.; Ionescu, R.; Granqvist, C.G.; Kish, L.B. Determination of gas mixture components using fluctuation enhanced sensing and the LS-SVM regression algorithm. Metrol. Meas. Syst. 2015, 3, 341–350. [Google Scholar] [CrossRef]
- Roy, P.S.; Ryu, C.; Dong, S.K.; Park, C.S. Development of a natural gas Methane Number prediction model. Fuel 2019, 246, 204–211. [Google Scholar] [CrossRef]
- Murguia, J.S.; Vergara, A.; Vargas-Olmos, C.; Wong, T.J.; Fonollosa, J.; Huerta, R. Two-dimensional wavelet transform feature extraction for porous silicon chemical sensors. Anal. Chim. Acta 2013, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Chen, S.; Qiao, F.; Ukkusuri, S.V.; Tang, K. Estimation of real-driving emissions for buses fueled with liquefied natural gas based on gradient boosted regression trees. Sci. Total Environ. 2019, 741–750. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Song, S.; Li, S.; Ma, L.; Pan, S.; Han, L. Research on Gas concentration prediction models based on LSTM multidimensional time series. Energies 2019, 12, 161. [Google Scholar] [CrossRef]
- Wei, N.; Li, C.; Duan, J.; Liu, J.; Zeng, F. Daily Natural gas load forecasting based on a hybrid deep learning model. Energies 2019, 12, 218. [Google Scholar] [CrossRef]
- Liu, Y.; Nie, F.; Gao, Q.; Gao, X.; Han, J.; Shao, L. Flexible unsupervised feature extraction for image classification. Neural Netw. 2019, 65–71. [Google Scholar] [CrossRef]
- Fonollosa, J.; Rodríguez-Luján, I.; Trincavelli, M.; Vergara, A.; Huerta, R. Chemical discrimination in turbulent gas mixtures with MOX sensors validated by gas chromatography-mass spectrometry. Sensors 2014, 14, 19336–19353. [Google Scholar] [CrossRef]

| Methodology | Application |
|---|---|
| Two-dimensional wavelet transformation feature extraction + linear-SVM classifier [26] | QAL-ID for gas mixture |
| PCA and partial least squares (PLS) feature extraction + SVM, RF, extreme learning machine (ELM) [7] | QAL-ID for volatile gas of the paraffin |
| Fuzzy adaptive resonant theory map (ARTMAP) and linear discriminant analysis (LDA) [8] | QAL-ID for gas mixture of essential oils |
| Two-dimensional wavelet transformation feature extraction + PLS regression [26] | QTY-ANLS for gas mixture |
| Least-squares support vector machine-based (LSSVM-based) nonlinear regression [24] | QTY-ANLS for gas mixture |
| Reservoir computing [22] | QTY-ANLS for gas mixture |
| Gradient boosted regression tree [27] | QTY-ANLS for emissions of LNG bus |
| Long Short-Term Memory(LSTM) [28] | QTY-ANLS for gas in coal mine |
| SVM, RF, extreme learning machine (ELM), and partial least squares regression (PLSR) [6] | QTY-ANLS for food additives in the fruit juice |
| Genetic algorithm + SVR [21] | QTY-ANLS for gas chromatography |
| Neural network [12] | QTY-ANLS for air pollutants |
| Empirical wavelet transformation (EWT)-multi-agent evolutionary genetic algorithm (MAEGA)-nonlinear auto regressive models (NARX) [17] | QTY-ANLS for air pollutants |
| SVR [16] | QTY-ANLS for PM2.5 |
| Principal component correlation analysis (PCCA) and LSTM [29] | QTY-ANLS for natural gas |
| Multiple regression (MR) and SVR [25] | QTY-ANLS for methane |
| Sensors | Sensitivity (Rate of Change for RS) | Stability | Detection Range (ppm) |
|---|---|---|---|
| TGS2602 | 0.08~0.5 | Long-term stability | 0~10 |
| TGS2600 | 0.3~0.6 | Long-term stability | 0~10 |
| TGS2610 | 0.5~0.62 | Long-term stability | 500~10,000 |
| TGS2620 | 0.3~0.5 | Long-term stability | 50~5000 |
| Principal Components | Eigenvalues | Contribution Rate/% | Cumulative Contribution Rate/% |
|---|---|---|---|
| PC1 | 10.134 | 63.33 | 63.33 |
| PC2 | 4.204 | 26.27 | 89.61 |
| PC3 | 1.277 | 7.98 | 97.59 |
| PC4 | 0.336 | 2.10 | 99.69 |
| PC5 | 0.025 | 0.15 | 99.85 |
| PC6 | 0.016 | 0.10 | 99.95 |
| PC7 | 0.003 | 0.02 | 99.97 |
| PC8 | 0.002 | 0.01 | 99.98 |
| PC9 | 0.002 | 0.01 | 99.99 |
| … | … | … | … |
| PC16 | 0.000 | 0.00 | 100.00 |
| Categories | Single Gas | Mixed Gas | ||
|---|---|---|---|---|
| Components | Methane | Ethylene | Methane | Ethylene |
| C | 22,481 | 13,892 | 27,047 | 8546 |
| γ | 2.86 | 0.45 | 0.44 | 0.28 |
| R2 | 0.996 | 0.979 | 0.979 | 0.828 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, S.; Li, Z.; Xia, K.; Hao, D. Quantitative and Qualitative Analysis of Multicomponent Gas Using Sensor Array. Sensors 2019, 19, 3917. https://doi.org/10.3390/s19183917
Fan S, Li Z, Xia K, Hao D. Quantitative and Qualitative Analysis of Multicomponent Gas Using Sensor Array. Sensors. 2019; 19(18):3917. https://doi.org/10.3390/s19183917
Chicago/Turabian StyleFan, Shurui, Zirui Li, Kewen Xia, and Dongxia Hao. 2019. "Quantitative and Qualitative Analysis of Multicomponent Gas Using Sensor Array" Sensors 19, no. 18: 3917. https://doi.org/10.3390/s19183917
APA StyleFan, S., Li, Z., Xia, K., & Hao, D. (2019). Quantitative and Qualitative Analysis of Multicomponent Gas Using Sensor Array. Sensors, 19(18), 3917. https://doi.org/10.3390/s19183917






