Towards Evaluating Proactive and Reactive Approaches on Reorganizing Human Resources in IoT-Based Smart Hospitals
Abstract
1. Introduction
- (i)
- We devise Human Resources IoT-based Elasticity, for automatic management of human resources in healthcare environments, making use of elasticity for smart, IoT-enabled hospitals;
- (ii)
- A cost-benefit analysis of the use of reactive and predictive strategies (of elasticity in cloud computing) for human resources reorganization. The cost refers to the health staff allocation costs in each approach, and the benefit is the anticipation of problems, based on the reduction of waiting time for care.
- (iii)
- We introduce Human resources cost and Elastic number of human resources used metrics for evaluating human resources elasticity.
2. Related Work
2.1. Reactive and Proactive Systems
2.2. Human Resources in Healthcare Environments
2.3. Comparison and Research Opportunities
- In the best of our knowledge, there are no approaches that evaluate the use of reactive and predictive elasticity for human resource management;
- Although several models are capable of identifying current and future demand in a hospital environment, these models lack solutions to help to solve the problem of deficiency of hospital resources;
3. ElHealth Model
3.1. Design Decisions
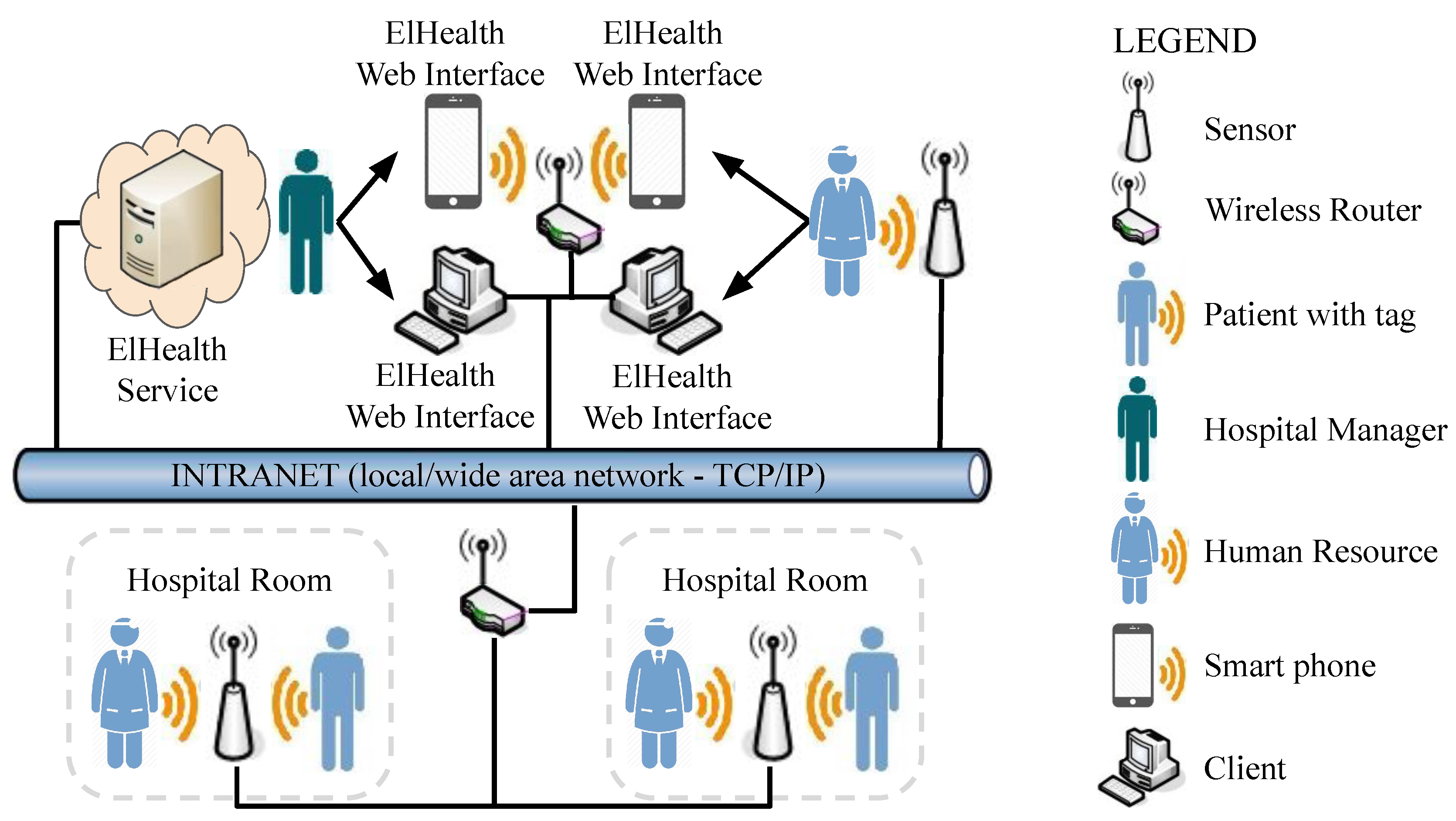
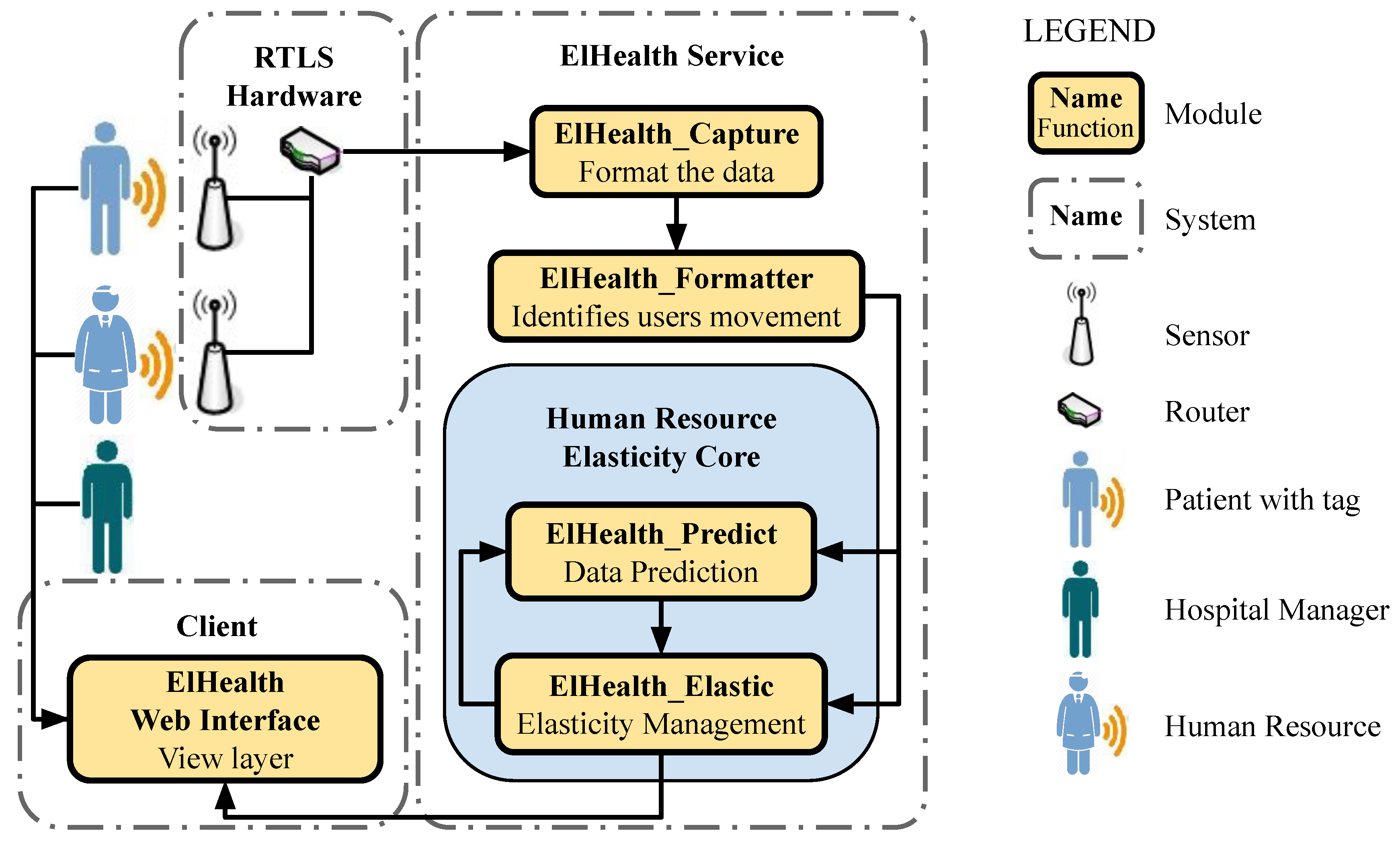
3.2. Architecture
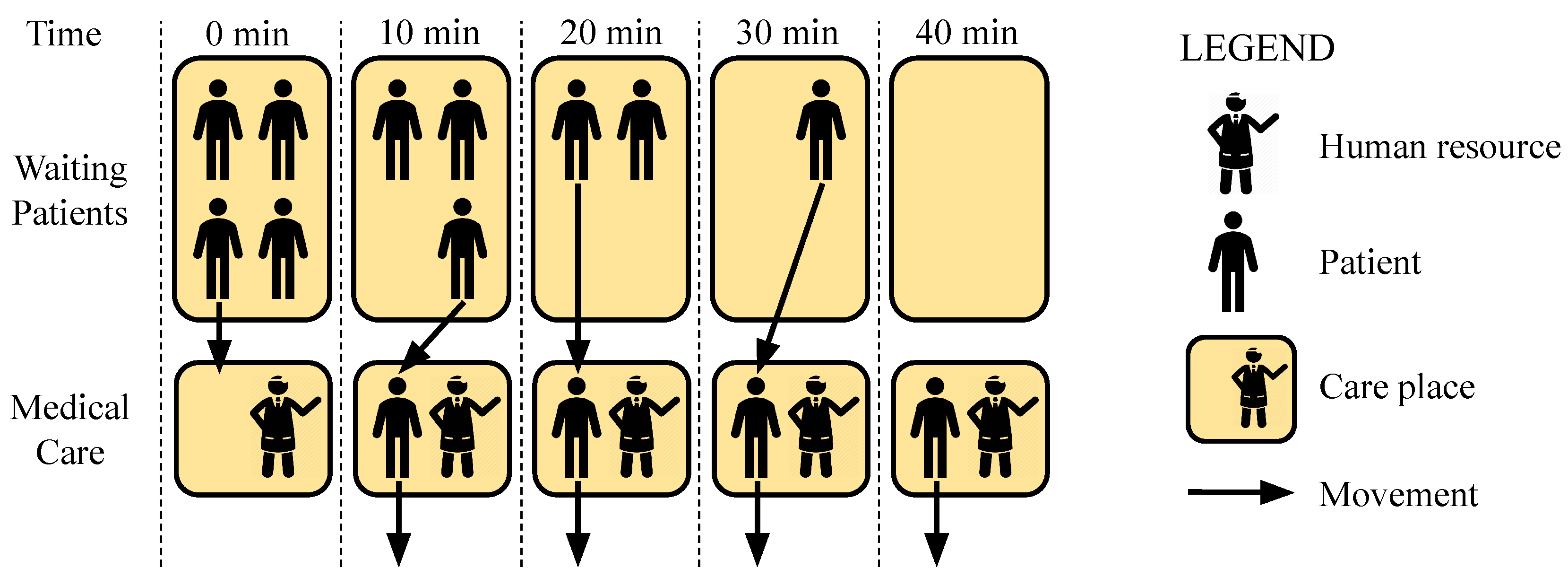
3.3. Human Resources Elasticity
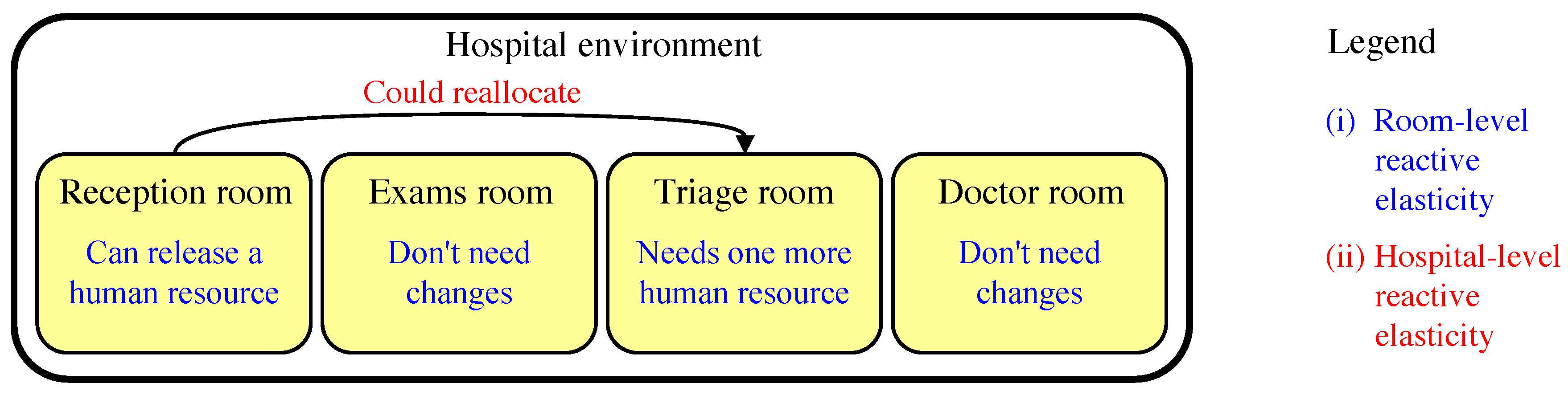
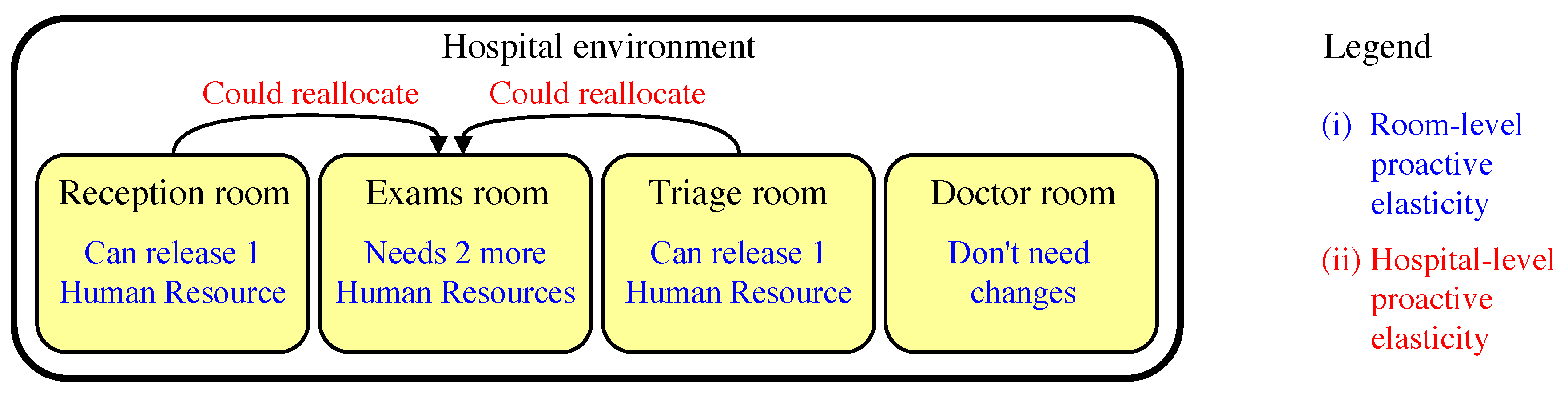
- Allocation, which denotes the capacity of the system to request health professionals who are not in the hospital to attend the current patients’ demand;
- Reallocation (or migration), which denotes the ability of the system to migrate professionals who are allocated to a particular hospital environment to some other environment where more professionals are needed;
- Deallocation which denotes the capacity of the system to release human resources no longer needed to attend the current patients’ demand.
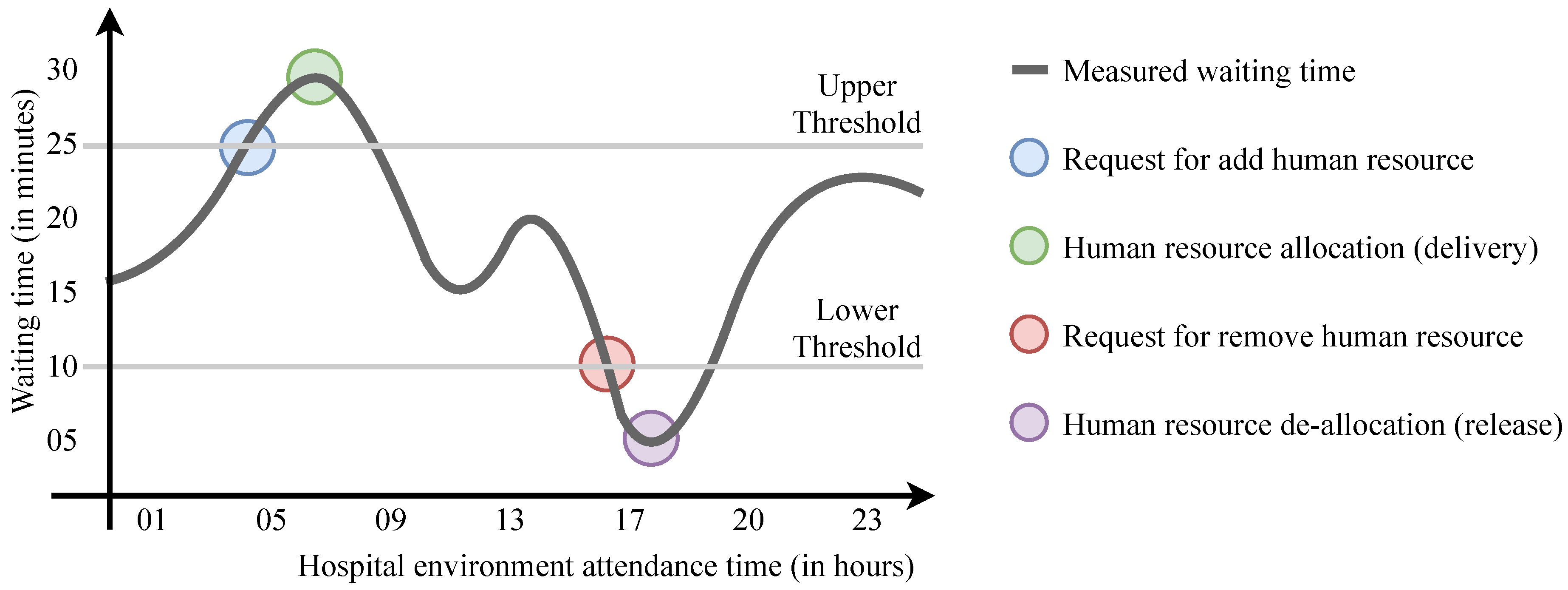
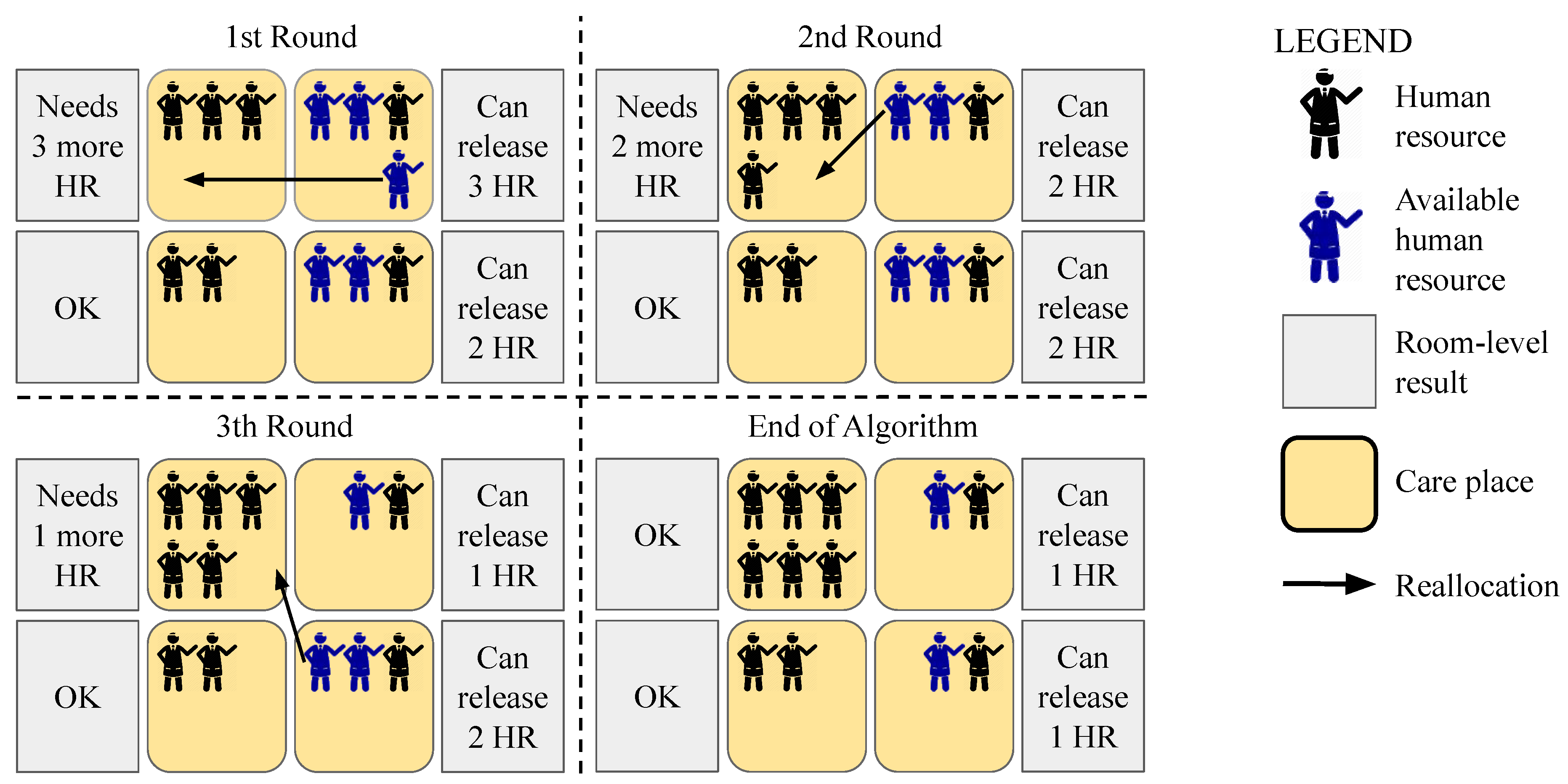
3.3.1. Reactive Elasticity
| Algorithm 1: Hospital-Level Reactive Elasticity. |
Data: Hospital room list h, vector v with all attendants of hospital Result: Updated hospital room list h 1 begin 2 a new vector of rooms and quantity of attendants to allocate or deallocate; 3 forall Room r on hospital room list h do 4 execute Room-level Reactive Elasticity Algorithm using r as Data; 5 ; 6 end 7 sort l, available attendants; 8 execute for Human Resources Deallocation Algorithm using l and allocated attendants of v as Data; 9 sort l, available attendants; 10 forall Room r on list l do 11 sort l, available attendants with room r specialty; 12 list of all human resources available for allocation with room r specialty; 13 execute Human Resources Reallocation Algorithm using r and as Data; 14 if r need more attendants then 15 Execute Human Resources Allocation Algorithm using r, and as Data; 16 end 17 end 18 rooms of l vector; 19 return h; 20 end |
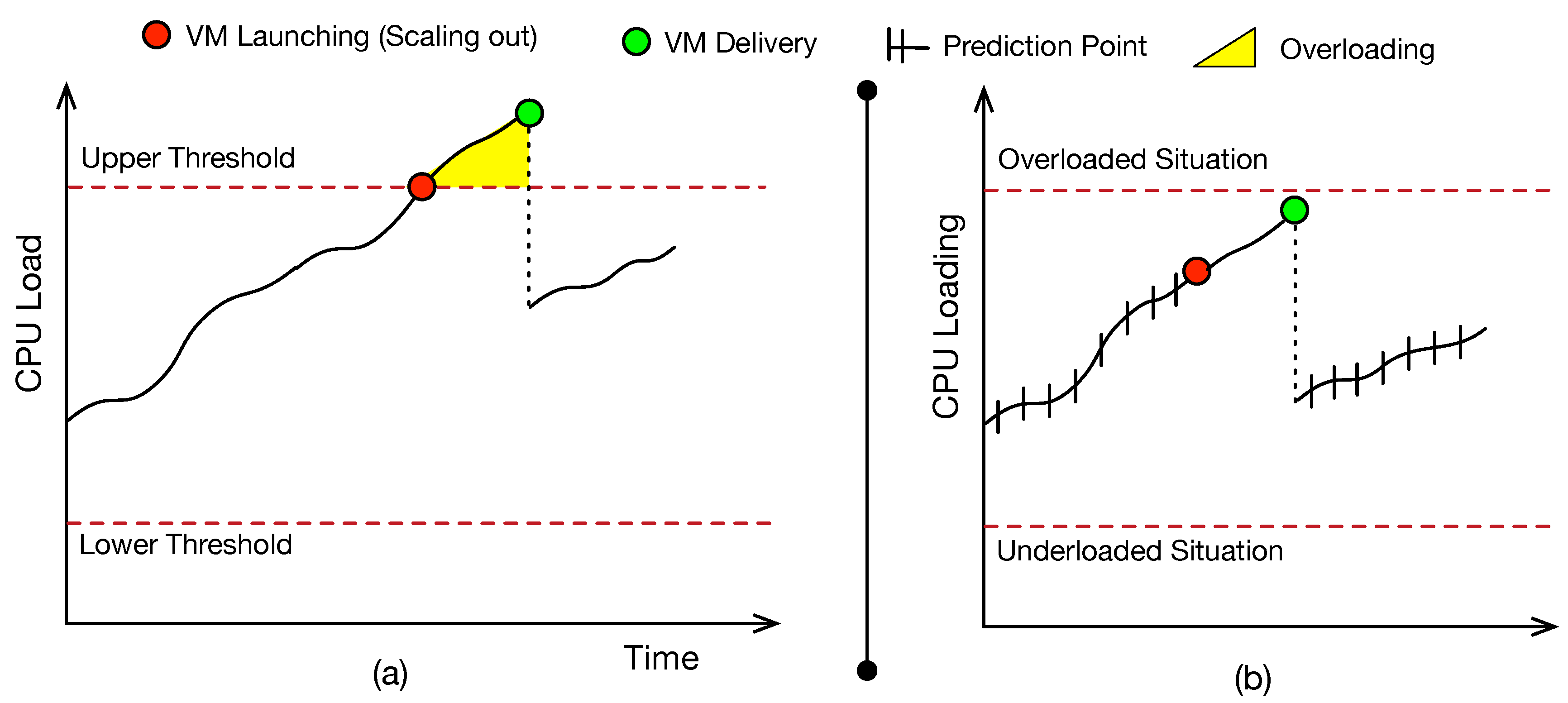
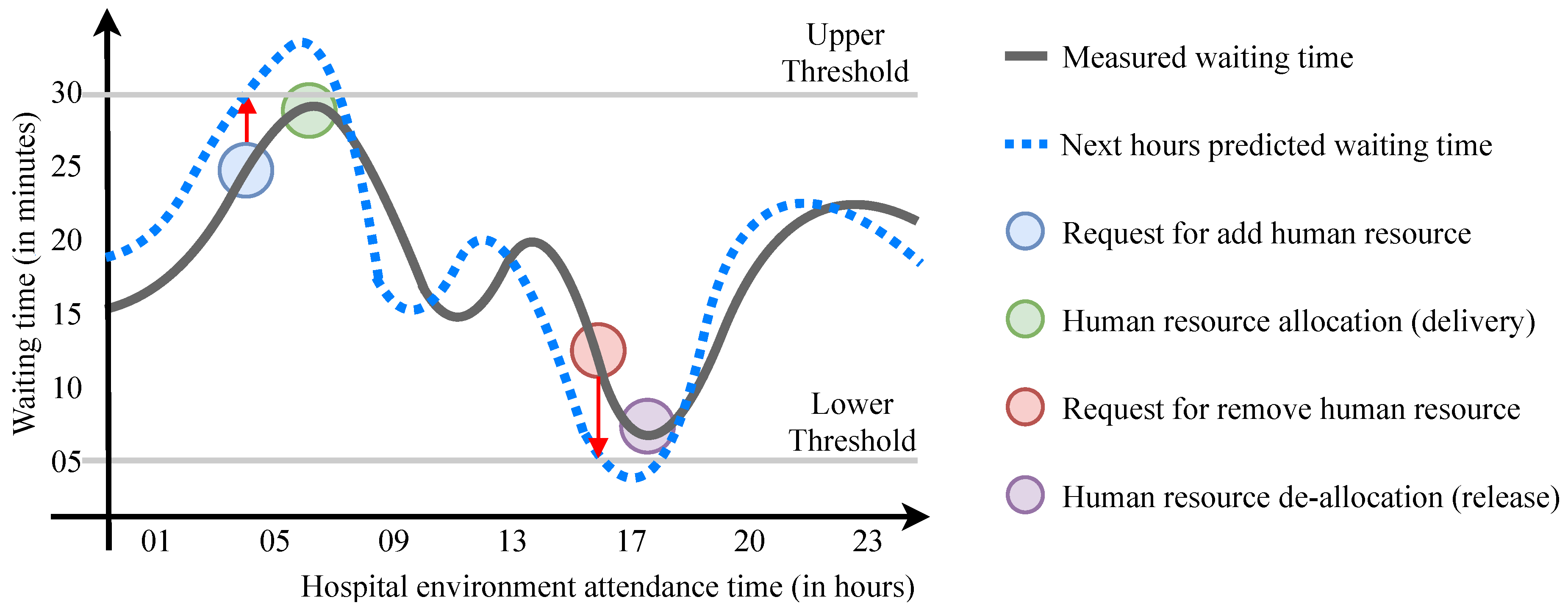
3.3.2. Proactive Elasticity
| Algorithm 2: Room-Level Predictive Elasticity. |
Data: Room r, a attendants, future initial time , future final time Result: Quantity of attendants to allocate or deallocate 1 begin 2 Upper Threshold of waiting time in r; 3 Lower Threshold of waiting time in r; 4 ; 5 ; 6 if then 7 while e do 8 ; 9 ; 10 end 11 else if then 12 while e do 13 ; 14 ; 15 end 16 end 17 return n; 18 end |
| Algorithm 3: Hospital-Level Predictive Elasticity. |
Data: Hospital room list h, vector v with all attendants of hospital, future initial time , future final time Result: Updated hospital room list h 1 begin 2 a new vector of rooms and quantity of attendants to allocate or deallocate; 3 forall Room r on hospital room list h do 4 number of attendants allocated in r; 5 run Algorithm 2 for Room-level Predictive Elasticity using r, a, and as Data; 6 ; 7 end; 8 sort l, quantity of available attendants; 9 execute Human Resources Deallocation Algorithm using l and allocated attendants of v as Data; 10 sort l, quantity of available attendants; 11 forall Room r on list l do 12 sort l, quantity of available attendants with room r specialty; 13 list of all human resources available for allocation with room r specialty; 14 execute Human Resources List Scheduling Algorithm using r and as Data; 15 if r need more attendants then 16 Execute Human Resources Allocation Algorithm using r, and as Data; 17 end 18 end 19 rooms of l vector; 20 return h; 21 end |
4. Evaluation Methodology
4.1. Considered Scenarios
- S1:
- Hospital without ElHealth: in order to have data for comparison, the first test scenario is based on the simulation of a non-elastic hospital
- S2:
- Smart hospital with ElHealth’s reactive elasticity: the second scenario focuses on the simulation of the hospital environment with the use of the allocation, reallocation, and deallocation of human resources proposed in the ElHealth model, using reactive elasticity approach.
- S3:
- Smart hospital with ElHealth’s proactive elasticity: the third scenario is similar to the second, based on the simulation of the hospital environment with ElHealth’s elasticity model, but unlike the previous scenario, using proactive elasticity approach.
4.2. Performance Evaluation Parameters
- Rule 1:
- The minimum rest period for a human resource to be available for allocation is eleven hours;
- Rule 2:
- An allocated employee cannot works outside of the regular work shift for a long time period. The largest possible work period allowed in Brazilian legislation is twelve hours. Thus, an allocated employee cannot work more than twelve hours;
- Rule 3:
- Allocated employees must be deallocated no later than 11 h before they next normal work shift; and
- Rule 4:
- Each employee must meet one of the 36 h rest periods within the same week in order to comply with a law determination that requires all workers to have a 24 h paid-rest period per week.
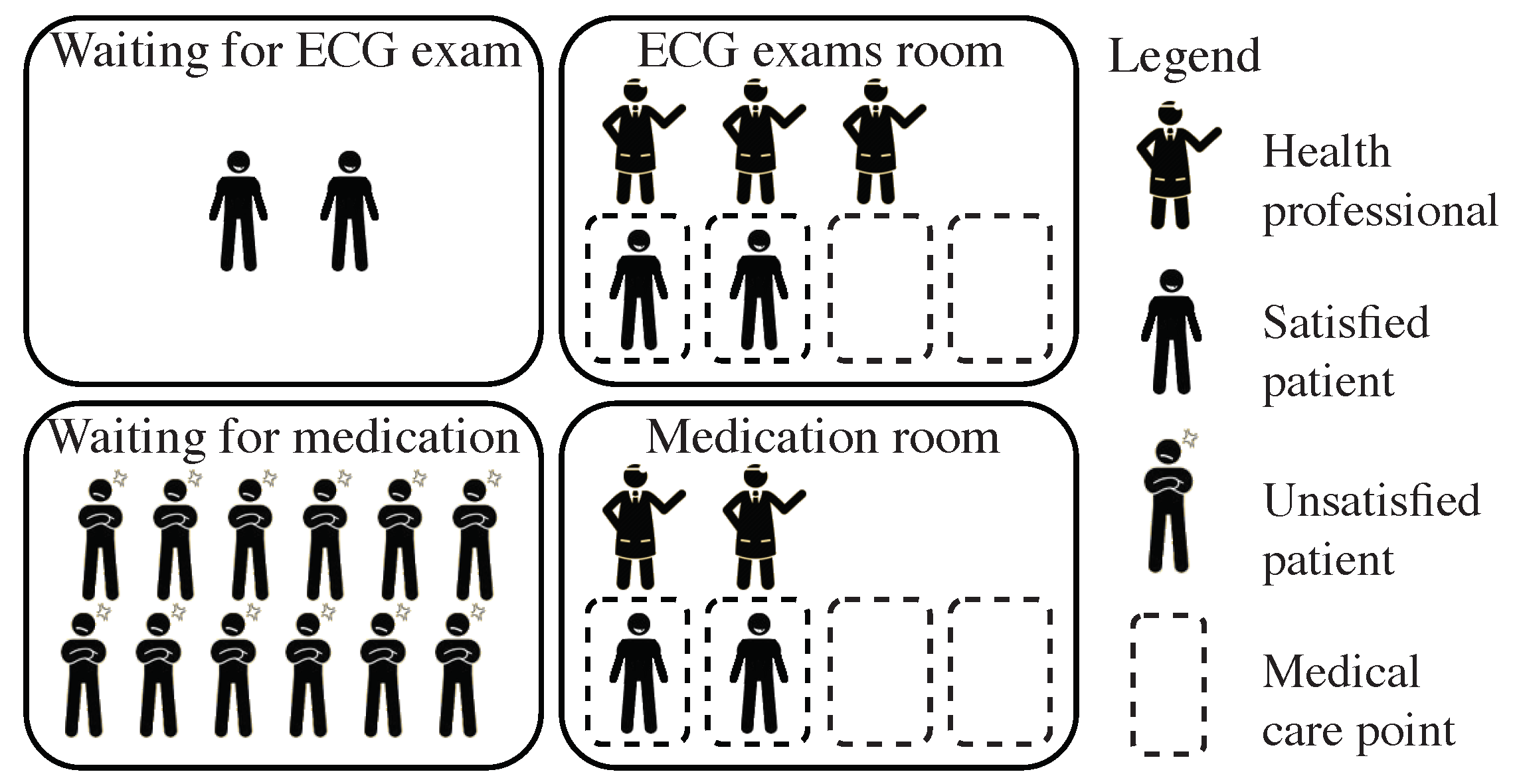
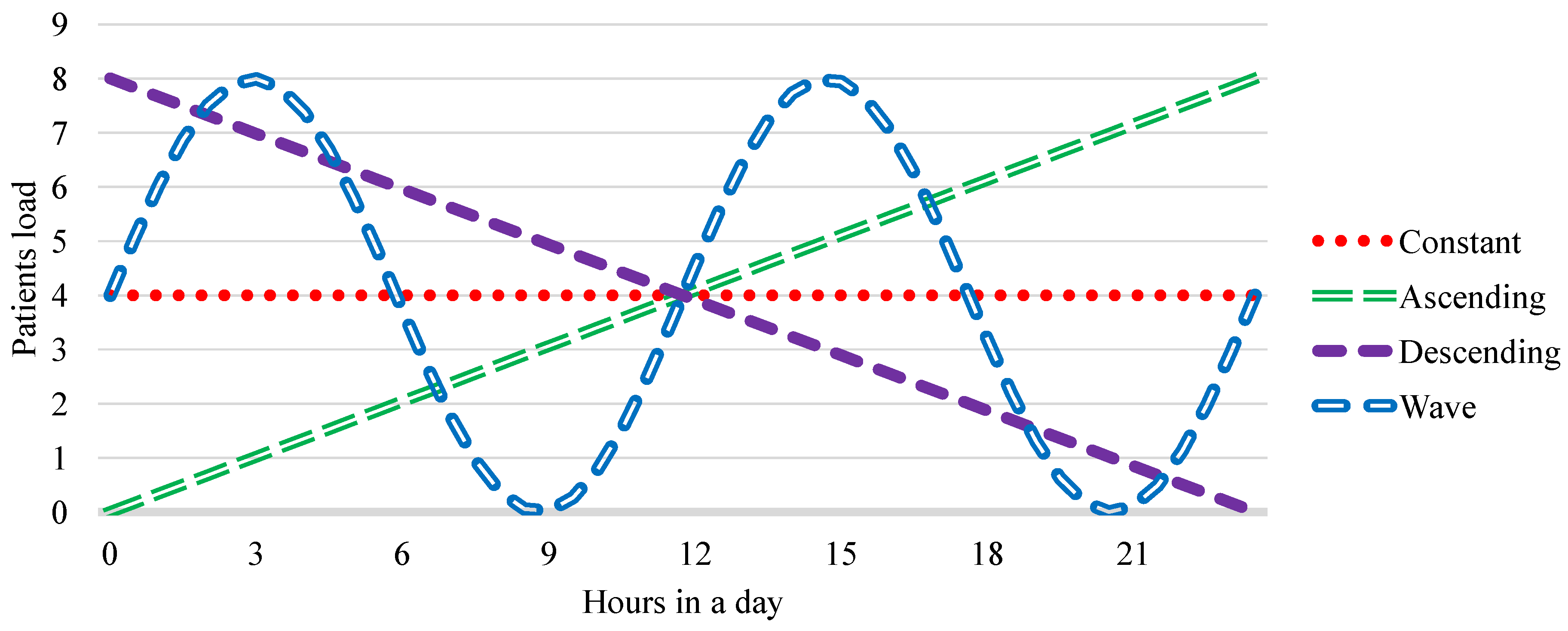
4.3. Workload
4.4. Performance Evaluation Metrics
- Maximum waiting time for care;
- Human resources cost;
- Elastic number of human resources used.
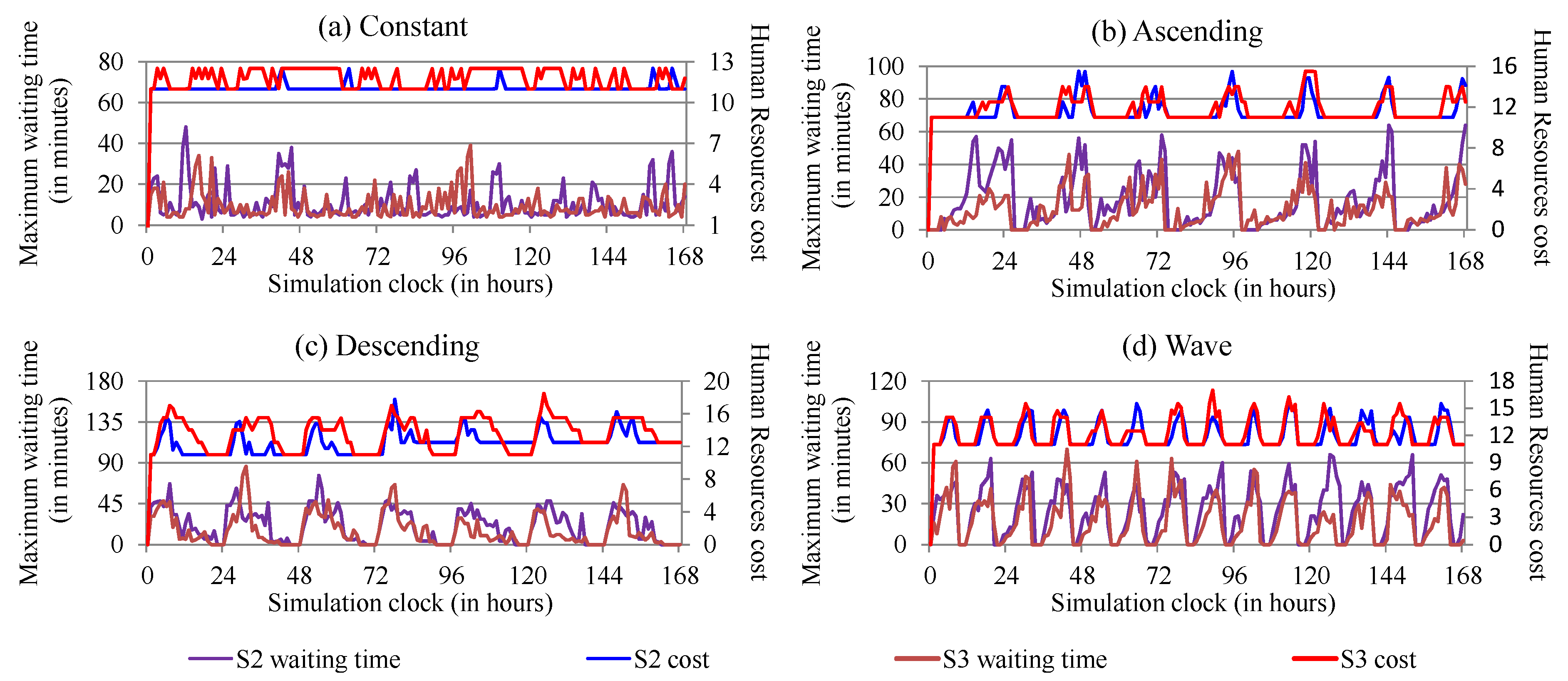
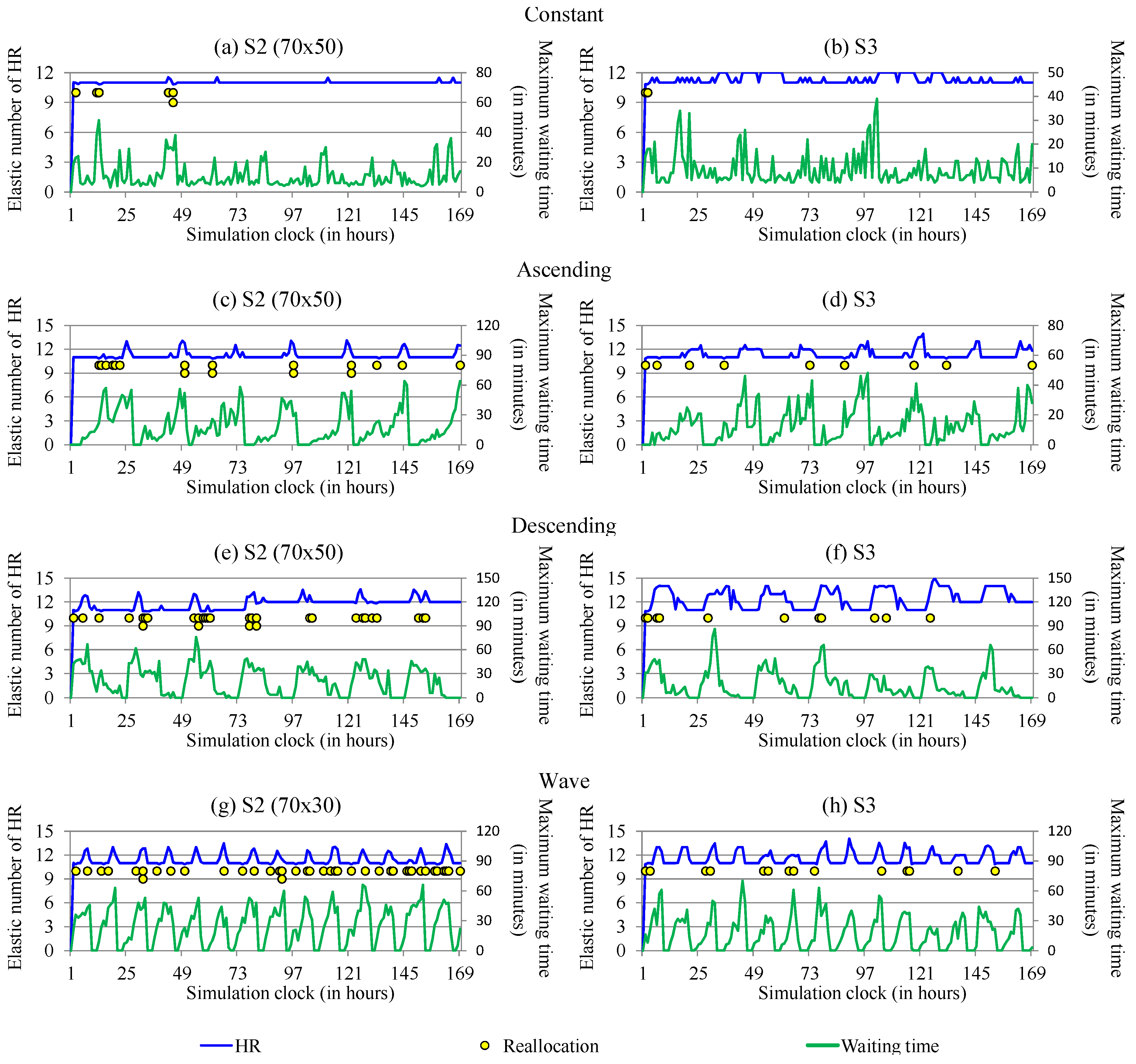
5. Performance Evaluation and Results Analysis
Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ElHealth | Elastic allocation of human resources in Healthcare environments |
| IoT | Internet of Things |
| ECG | Electrocardiogram |
| C-RAN | Cloud Radio Access Network |
| BBU | Baseband Unit |
| RAN | Radio Acess Network |
| ARMA | Autoregressive Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| EPCIS | Eletronic Product Code Information Services |
| SD | System Dynamics |
| GIS | Geographic Information Systems |
| RTLS | Real-Time Location System |
| WMA | Weighted Moving Average |
References
- Singh, K.J.; Kapoor, D.S. Create Your Own Internet of Things: A survey of IoT platforms. IEEE Consum. Electron. Mag. 2017, 6, 57–68. [Google Scholar] [CrossRef]
- Ruz, M.L.; Garrido, J.; Jiménez, J.; Virrankoski, R.; Vázquez, F. Simulation Tool for the Analysis of Cooperative Localization Algorithms for Wireless Sensor Networks. Sensors 2019, 19, 2866. [Google Scholar] [CrossRef] [PubMed]
- da Costa, C.A.; Pasluosta, C.F.; Eskofier, B.; da Silva, D.B.; da Rosa Righi, R. Internet of Health Things: Toward intelligent vital signs monitoring in hospital wards. Artif. Intell. Med. 2018, 89, 61–69. [Google Scholar] [CrossRef]
- Mavrogiorgou, A.; Kiourtis, A.; Perakis, K.; Pitsios, S.; Kyriazis, D. IoT in Healthcare: Achieving Interoperability of High-Quality Data Acquired by IoT Medical Devices. Sensors 2019, 19, 1978. [Google Scholar] [CrossRef] [PubMed]
- Sarhan, Q.I. Internet of things: a survey of challenges and issues. Int. J. Internet Things Cyber-Assur. 2018, 1, 40–75. [Google Scholar] [CrossRef]
- Darshan, K.R.; Anandakumar, K.R. A comprehensive review on usage of Internet of Things (IoT) in healthcare system. In Proceedings of the 2015 International Conference on Emerging Research in Electronics, Computer Science and Technology (ICERECT), Mandya, India, 17–19 December 2015; pp. 132–136. [Google Scholar]
- Butean, A.; David, A.; Buduleci, C.; Daian, A. Auxilum Medicine: A Cloud Based Platform for Real-Time Monitoring Medical Devices. In Proceedings of the 2015 20th International Conference on Control Systems and Computer Science; IEEE: Bucharest, Romania, 2015; pp. 874–879. [Google Scholar]
- Nierop-van Baalen, C.; Grypdonck, M.; van Hecke, A.; Verhaeghe, S. Health professionals’ dealing with hope in palliative patients with cancer, an explorative qualitative research. Eur. J. Cancer Care 2019, 28, e12889. [Google Scholar] [CrossRef] [PubMed]
- Da Rosa Righi, R.; Rodrigues, V.F.; De Nardin, I.F.; Da Costa, C.A.; Alves, M.A.Z.; Pillon, M.A. Towards providing middleware-level proactive resource reorganisation for elastic HPC applications in the cloud. Int. J. Grid Util. Comput. 2019, 10, 76–92. [Google Scholar] [CrossRef]
- Righi, R.D.R.; Rodrigues, V.F.; Rostirolla, G.; Costa, C.A.D.; Roloff, E.; Navaux, P.O.A. A lightweight plug-and-play elasticity service for self-organizing resource provisioning on parallel applications. Future Gener. Comput. Syst. 2018, 78, 176–190. [Google Scholar] [CrossRef]
- Xu, M.; Buyya, R. Brownout Approach for Adaptive Management of Resources and Applications in Cloud Computing Systems: A Taxonomy and Future Directions. ACM Comput. Surv. 2019, 52, 8. [Google Scholar] [CrossRef]
- Rostirolla, G.; da Rosa Righi, R.; Barbosa, J.L.V.; da Costa, C.A. ElCity: An Elastic Multilevel Energy Saving Model for Smart Cities. IEEE Trans. Sustain. Comput. 2018, 3, 30–43. [Google Scholar] [CrossRef]
- Al-Dhuraibi, Y.; Paraiso, F.; Djarallah, N.; Merle, P. Elasticity in Cloud Computing: State of the Art and Research Challenges. IEEE Trans. Serv. Comput. 2018, 11, 430–447. [Google Scholar] [CrossRef]
- Moreno-Vozmediano, R.; Montero, R.S.; Huedo, E.; Llorente, I.M. Efficient resource provisioning for elastic Cloud services based on machine learning techniques. J. Cloud Comput. 2019, 8, 5. [Google Scholar] [CrossRef]
- Rodrigues, V.F.; Righi, R.D.R.; Rostirolla, G.; Barbosa, J.L.V.; da Costa, C.A.; Alberti, A.M.; Chang, V. Towards Enabling Live Thresholding as Utility to Manage Elastic Master-Slave Applications in the Cloud. J. Grid Comput. 2017, 15, 535–556. [Google Scholar] [CrossRef]
- Wang, H.B.; Liu, X.; Song, P.; Tu, X.Y. Sensitive time series prediction using extreme learning machine. Int. J. Mach. Learn. Cybern. 2019, 1–16. [Google Scholar] [CrossRef]
- Netto, M.A.S.; Cardonha, C.; Cunha, R.L.F.; Assuncao, M.D. Evaluating Auto-scaling Strategies for Cloud Computing Environments. In Proceedings of the 2014 IEEE 22nd International Symposium on Modelling, Analysis Simulation of Computer and Telecommunication Systems, Paris, France, 9–11 September 2014; pp. 187–196. [Google Scholar]
- Al-Dhuraibi, Y.; Zalila, F.; Djarallah, N.; Merle, P. Model-Driven Elasticity Management with OCCI. IEEE Trans. Cloud Comput. 2019, 1. [Google Scholar] [CrossRef]
- da Rosa Righi, R.; Andrioli, L.; Rodrigues, V.F.; da Costa, C.A.; Alberti, A.M.; Singh, D. Elastic-RAN: An adaptable multi-level elasticity model for Cloud Radio Access Networks. Comput. Commun. 2019, 142, 34–47. [Google Scholar] [CrossRef]
- Hanafy, W.A.; Mohamed, A.E.; Salem, S.A. A New Infrastructure Elasticity Control Algorithm for Containerized Cloud. IEEE Access 2019, 7, 39731–39741. [Google Scholar] [CrossRef]
- da Rosa Righi, R.; Correa, E.; Gomes, M.M.; da Costa, C.A. Enhancing performance of IoT applications with load prediction and cloud elasticity. Future Gener. Comput. Syst. 2018. [Google Scholar] [CrossRef]
- Whittle, P. Hypothesis Testing in Time Series Analysis; Almqvist and Wicksell: Uppsala, Sweden, 1951. [Google Scholar]
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control; Holden-Day: San Fransisco, CA, USA, 1970. [Google Scholar]
- Winters, P.R. Forecasting Sales by Exponentially Weighted Moving Averages. Manage. Sci. 1960, 6, 324–342. [Google Scholar] [CrossRef]
- Capocci, N.R.; Nascimento, B.S.; Lopes, F.B.; Rodrigues, E.F.; Maiellaro, J.R. Simulation as a hospital management support tool. Indep. J. Manag. Prod. 2017, 8, 798–811. [Google Scholar] [CrossRef][Green Version]
- Vieira, D.; Hollmén, J. Resource Frequency Prediction in Healthcare: Machine Learning Approach. In Proceedings of the 2016 IEEE 29th International Symposium on Computer-Based Medical Systems (CBMS), Dublin, Ireland, 20–24 June 2016; pp. 88–93. [Google Scholar]
- Graham, B.; Bond, R.; Quinn, M.; Mulvenna, M. Using Data Mining to Predict Hospital Admissions From the Emergency Department. IEEE Access 2018, 6, 10458–10469. [Google Scholar] [CrossRef]
- Sundarapandian, V. Probability, Statistics and Queuing Theory; PHI Learning: New Delhi, India, 2009. [Google Scholar]
- Fix, E.; Hodges, J.L., Jr. Discriminatory Analysis—Nonparametric Discrimination: Consistency Properties; Technical Report; The University of California, Berkeley: Berkeley, CA, USA, 1951. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QB, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Cox, D.R. The Regression Analysis of Binary Sequences. J. R. Stat. Soc Ser. B Methodol. 1958, 20, 215–242. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Ishikawa, T.; Fujiwara, K.; Ohba, H.; Suzuki, T.; Ogasawara, K. Forecasting the regional distribution and sufficiency of physicians in Japan with a coupled system dynamics—geographic information system model. Hum. Resour. Health 2017, 15, 64. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.X.; Goryakin, Y.; Maeda, A.; Bruckner, T.; Scheffler, R. Global Health Workforce Labor Market Projections for 2030. Hum. Resour. Health 2017, 15, 11. [Google Scholar] [CrossRef] [PubMed]
- Al-Dhuraibi, Y.; Zalila, F.; Djarallah, N.B.; Merle, P. Coordinating Vertical Elasticity of both Containers and Virtual Machines. In Proceedings of the 8th International Conference on Cloud Computing and Services Science, Funchal, Madeira, Portugal, 19–21 March 2018. [Google Scholar]
- Shekhar, S.; Abdel-Aziz, H.; Bhattacharjee, A.; Gokhale, A.; Koutsoukos, X. Performance Interference-Aware Vertical Elasticity for Cloud-Hosted Latency-Sensitive Applications. In Proceedings of the 2018 IEEE 11th International Conference on Cloud Computing (CLOUD), San Francisco, CA, USA, 2–7 July 2018; pp. 82–89. [Google Scholar]
- Orimaye, S.O.; Leong, F.C.; Lee, C.H.; Ng, E.C.H. Predicting proximity with ambient mobile sensors for non-invasive health diagnostics. In Proceedings of the 2015 IEEE 12th Malaysia International Conference on Communications (MICC), Kuching, Malaysia, 23–25 November 2015; pp. 6–11. [Google Scholar]
- Zamanifar, A.; Nazemi, E.; Vahidi-Asl, M. DMP-IOT: A distributed movement prediction scheme for IOT health-care applications. Comput. Electric. Eng. 2017, 58, 310–326. [Google Scholar] [CrossRef]
- Boulos, M.N.K.; Berry, G. Real-time locating systems (RTLS) in healthcare: A condensed primer. Int. J. Health Geogr. 2012, 11, 1–8. [Google Scholar]
- Jachimczyk, B.; Dziak, D.; Kulesza, W.J. Customization of UWB 3D-RTLS Based on the New Uncertainty Model of the AoA Ranging Technique. Sensors 2017, 17, 227. [Google Scholar] [CrossRef]
- Berg, B.; Longley, G.; Dunitz, J. Improving Clinic Operational Efficiency and Utilization with RTLS. J. Med. Syst. 2019, 43, 56. [Google Scholar] [CrossRef]
- Nisha, K.G.; Sreekumar, K. A Review and Analysis of machine Learning and Statistical Approaches for Prediction. In Proceedings of the 2017 International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, 10–11 March 2017; pp. 135–139. [Google Scholar]
- Perez-Palacin, D.; Mirandola, R.; Scoppetta, M. Simulation of Techniques to Improve the Utilization of Cloud Elasticity in Workload-aware Adaptive Software. In Proceedings of the Companion Publication for ACM/SPEC on International Conference on Performance Engineering, Delft, The Netherlands, 12–16 March 2016; pp. 51–56. [Google Scholar]
- Kejariwal, A. Techniques for Optimizing Cloud Footprint. In Proceedings of the 2013 IEEE International Conference on Cloud Engineering (IC2E), Redwood City, CA, USA, 25–27 March 2013; pp. 258–268. [Google Scholar]
- Rosa Righi, R.; Costa, C.A.; Rodrigues, V.F.; Rostirolla, G. Joint-analysis of Performance and Energy Consumption when Enabling Cloud Elasticity for Synchronous HPC Applications. Concurr. Comput. Pract. Exp. 2016, 28, 1548–1571. [Google Scholar] [CrossRef]
- Righi, R.D.R.; Rodrigues, V.F.; Nardin, I.F.D.; Costa, C.A.D.; Alves, M.A.Z.; Pillon, M.A. Towards providing middleware-level proactive resource reorganisation for elastic HPC applications in the cloud. Int. J. Grid Util. Comput. 2019, 10, 76–92. [Google Scholar] [CrossRef]
- Wang, H.; Sinnen, O. List-Scheduling versus Cluster-Scheduling. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 1736–1749. [Google Scholar] [CrossRef]
- Islam, S.; Lee, K.; Fekete, A.; Liu, A. How a Consumer Can Measure Elasticity for Cloud Platforms. In Proceedings of the 3rd ACM/SPEC International Conference on Performance Engineering, Boston, MA, USA, 22–25 April 2012; pp. 85–96. [Google Scholar]
- Sedgewick, R.; Wayne, K. Class StdRandom. Available online: https://introcs.cs.princeton.edu/java/stdlib/javadoc/StdRandom.html (accessed on 12 January 2019).
- Roehrs, A.; da Costa, C.A.; da Rosa Righi, R.; de Oliveira, K.S.F. Personal Health Records: A Systematic Literature Review. J. Med. Internet Res. 2017, 19, e13. [Google Scholar] [CrossRef] [PubMed]
- Brazilian Government. Lei N° 13.467, de 13 de julho de 2017. Available online: https://legis.senado.leg.br/norma/17728053 (accessed on 1 September 2019). (In Portuguese)
- Brazilian Government. Decreto-Lei N° 5.452, de 1° de maio de 1943. Available online: http://www.planalto.gov.br/ccivil_03/decreto-lei/del5452.htm (accessed on 1 September 2019). (In Portuguese)
- Fabio, Z. Projeto de Lei da Câmara N° de 14 de junho de 2018. Available online: https://www25.senado.leg.br/web/atividade/materias/-/materia/132482 (accessed on 1 September 2019). (In Portuguese).
- Righi, R.R.; Rodrigues, V.F.; da Costa, C.A.; Galante, G.; de Bona, L.C.E.; Ferreto, T. AutoElastic: Automatic Resource Elasticity for High Performance Applications in the Cloud. IEEE Trans. Cloud Comput. 2016, 4, 6–19. [Google Scholar] [CrossRef]
- Al-Haidari, F.; Sqalli, M.; Salah, K. Impact of CPU Utilization Thresholds and Scaling Size on Autoscaling Cloud Resources. In Proceedings of the 2013 IEEE 5th International Conference on Cloud Computing Technology and Science, Bristol, UK, 2–5 December 2013; Volume 2, pp. 256–261. [Google Scholar]

| Work | Focus | Elasticity | Prediction Algorithm |
|---|---|---|---|
| Al-Dhuraibi et al. [18] | Cloud applications | Reactive | – |
| Elastic-RAN [19] | C-RANs | Reactive | – |
| ElCity [12] | City energy | Reactive | – |
| Hanafy et al. [20] | Cloud applications | Proactive | Time-series (ARMA) |
| Proliot [21] | IoT applications | Proactive | Time-series (ARIMA and WMA) |
| Work | Focus | Proposed Solution | Data Prediction Model | Human Resources Defi-Ciency |
|---|---|---|---|---|
| Capocci et al. [25] | Improve patient flow, decreasing the waiting time for care | Identify bottlenecks to propose human resources movement | Uses Queueing theory to estimate patient’s arrivals. | Proposes a nurse reallocation based on waiting time for screening process |
| Vieira and Hollmén [26] | Deficiency of resources to perform patients’ care | Identify the resources needed to ensure the patient’s care flow | Uses Nearest Neighbours and Random Forest to predict future resources usage | Only provides data to support decision- making |
| Ishikawa et al. [35] | Deficiency of doctors for current patients’ care demand in Japan (Hokkaido) | Identify health doctors distribution and suffi- ciency to propose ways for guarantee care for demand | Uses System Dynamics (SD) and Geographic Information System (GIS) to predict distribution and sufficiency of doctors | Proposes a plan for training physicians that considers geographic requirements |
| Liu et al. [36] | Deficiency of doctors for current patients’ care demand in global scale | Identify health doctors distribution and suffi- ciency until 2030 in order to compare with demand projections | Uses an economic model and a Generalized Li- near Model to predict distribution and sufficiency of health professionals, and patients’ demand | Only provides data to show the problem escalation, to support solutions proposal by the international community |
| Graham et al. [27] | Emergency depart- ments crowding and the negative conse- quences for patients | Use of data mining using machine learn- ing techniques to predict admissions in a hospital | Uses logistic regression, decision trees and Gradient Boosted Machines to predicts patients’ arrival in emergency | Only provides data to support decision- making of hospital managers |
| Nomenclature | Description |
|---|---|
| r | Hospital room |
| Initial time instant | |
| Future initial time instant | |
| a | Allocated attendants |
| Size of a x vector | |
| Average Care Time | |
| Average Number of Attendants | |
| Number of Incoming Patients | |
| Estimated Care Time | |
| Human Resources Elastic Speedup | |
| Specific n time instant | |
| Final time instant | |
| Future final time instant | |
| Care Vector | |
| Care Duration Time | |
| Number of Attendants | |
| Number of Waiting Patients | |
| Estimated Number of Patients | |
| Proactive Human Resources Elastic | |
| Speedup |
| Attendance | Attendance Time | ||
|---|---|---|---|
| Lower | Mode | Upper | |
| Reception room | |||
| PHR preparation | 2 min | 3 min | 5 min |
| X-Ray exams room | |||
| X-Ray exam | 10 min | 15 min | 23 min |
| Medication room | |||
| Intramuscular injection | 3 min | 3.5 min | 5 min |
| Intravenous and inhala- | 0.5 min | 1.5 min | 2.5 min |
| tion preparation | |||
| Intravenous medication | 40 min | 70 min | 120 min |
| Inhalation medication | 8 min | 10 min | 13 min |
| Triage room | |||
| Triage process | 5 min | 8 min | 10 min |
| Doctor treatment room | |||
| First care with doctor | 5 min | 11 min | 16 min |
| Return care with doctor | 4 min | 7 min | 10 min |
| Collection exams room | |||
| Laboratory exams | 6 min | 8 min | 13 min |
| Electrocardiogram exams room | |||
| ECG exam | 30 min | 45 min | 60 min |
| Scenario | Maximum Waiting Time | Human Resources Cost | Elastic Number of Human Resources Used |
|---|---|---|---|
| S1 | Current | Current | 11 by work shift |
| S2 (Expected) | Less than S1 | More than S1 | 11 or more by work shift |
| S3 (Expected) | Less than S2 | More than S2 | 11 or more by work shift |
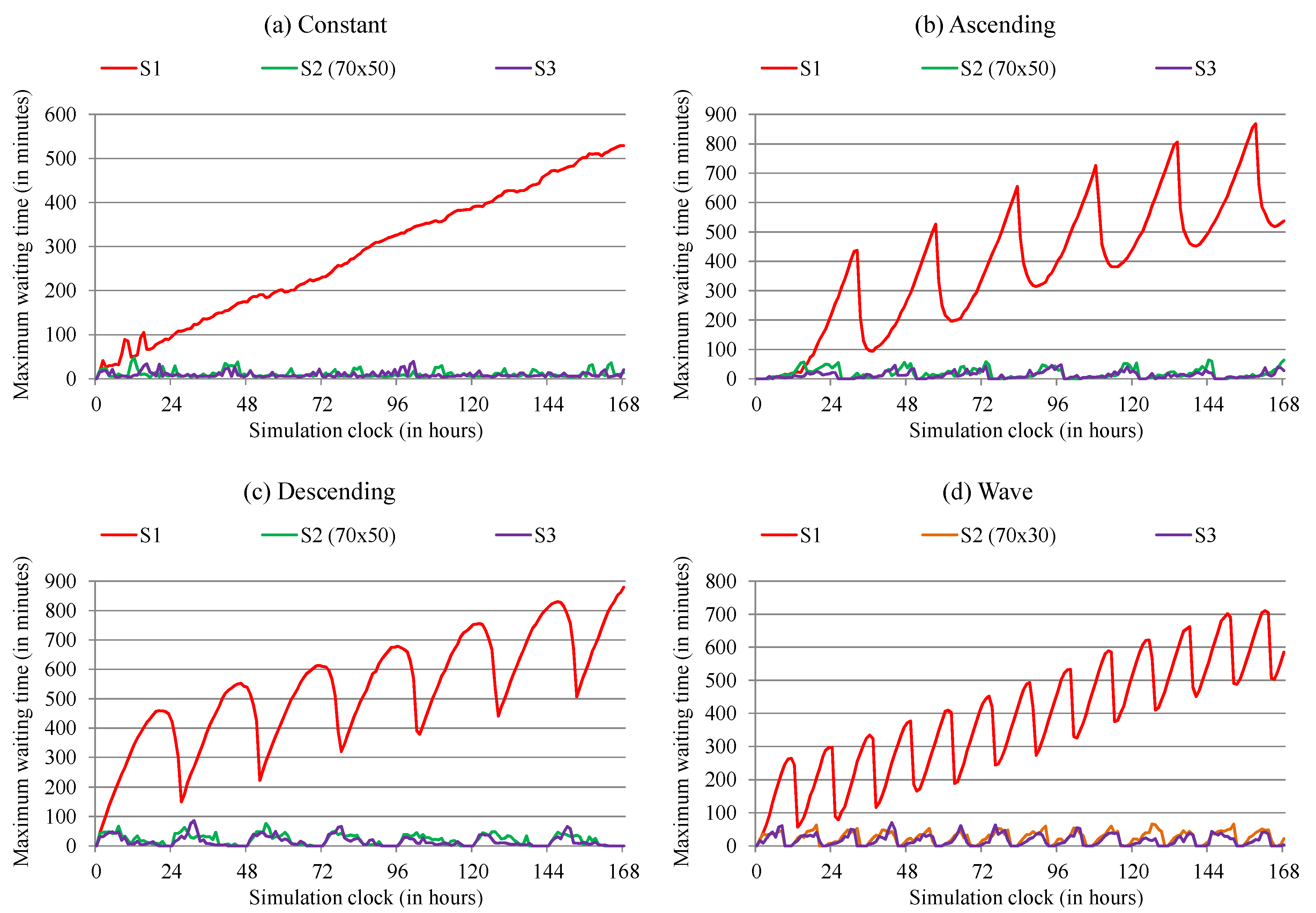
| Workload | Scenario | Thresholds | Maximum Waiting Time (in Minutes) | Human Resources Cost | Elastic Number of Human Resources | ||
|---|---|---|---|---|---|---|---|
| Upper | Lower | Average | Upper | ||||
| Constant | S1 | - | - | 282.32 (±147.7) | 529 | 11 | 11 |
| S2 | 90 | 50 | 21.71 (±15.8) | 58 | 11.04 | 11.01 | |
| 70 | 50 | 10.93 (± 8.6) | 48 | 11.07 | 11.02 | ||
| 90 | 30 | 19.67 (±14.8) | 57 | 11.01 | 10.99 | ||
| 70 | 30 | 15.22 (±11.1) | 64 | 11.07 | 10.99 | ||
| S3 | - | - | 9.42 (± 6.7) | 39 | 11.78 | 11.33 | |
| Ascending | S1 | - | - | 388.81 (±215.8) | 868 | 11 | 11 |
| S2 | 90 | 50 | 27.28 (±21.5) | 86 | 11.60 | 11.22 | |
| 70 | 50 | 18.39 (±17.3) | 64 | 11.55 | 11.19 | ||
| 90 | 30 | 28.82 (±19.8) | 66 | 11.70 | 11.23 | ||
| 70 | 30 | 20.14 (±19.1) | 88 | 11.57 | 11.19 | ||
| S3 | - | - | 12.70 (±11.7) | 48 | 11.81 | 11.36 | |
| Descending | S1 | - | - | 532.01 (±182.0) | 880 | 11 | 11 |
| S2 | 90 | 50 | 24.99 (±23.4) | 87 | 11.62 | 11.23 | |
| 70 | 50 | 21.01 (±18.2) | 76 | 12.46 | 11.75 | ||
| 90 | 30 | 28.23 (±25.0) | 97 | 11.68 | 11.25 | ||
| 70 | 30 | 23.05 (±23.0) | 83 | 11.86 | 11.34 | ||
| S3 | - | - | 15.65 (±17.6) | 86 | 13.51 | 12.42 | |
| Wave | S1 | - | - | 384.18 (±171.7) | 711 | 11 | 11 |
| S2 | 90 | 50 | 33.57 (±24.3) | 92 | 11.87 | 11.33 | |
| 70 | 50 | 28.99 (±22.6) | 95 | 12.08 | 11.42 | ||
| 90 | 30 | 34.68 (±22.5) | 75 | 11.89 | 11.33 | ||
| 70 | 30 | 25.37 (±19.1) | 66 | 12.02 | 11.38 | ||
| S3 | - | - | 12.88 (±12.4) | 70 | 11.36 | 11.59 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, G.S.; Righi, R.d.R.; Costa, C.A.d.; Galante, G.; Griebler, D. Towards Evaluating Proactive and Reactive Approaches on Reorganizing Human Resources in IoT-Based Smart Hospitals. Sensors 2019, 19, 3800. https://doi.org/10.3390/s19173800
Fischer GS, Righi RdR, Costa CAd, Galante G, Griebler D. Towards Evaluating Proactive and Reactive Approaches on Reorganizing Human Resources in IoT-Based Smart Hospitals. Sensors. 2019; 19(17):3800. https://doi.org/10.3390/s19173800
Chicago/Turabian StyleFischer, Gabriel Souto, Rodrigo da Rosa Righi, Cristiano André da Costa, Guilherme Galante, and Dalvan Griebler. 2019. "Towards Evaluating Proactive and Reactive Approaches on Reorganizing Human Resources in IoT-Based Smart Hospitals" Sensors 19, no. 17: 3800. https://doi.org/10.3390/s19173800
APA StyleFischer, G. S., Righi, R. d. R., Costa, C. A. d., Galante, G., & Griebler, D. (2019). Towards Evaluating Proactive and Reactive Approaches on Reorganizing Human Resources in IoT-Based Smart Hospitals. Sensors, 19(17), 3800. https://doi.org/10.3390/s19173800








