Sensor Configuration and Algorithms for Power-Line Interference Suppression in Low Field Nuclear Magnetic Resonance
Abstract
1. Introduction
2. Materials and Methods
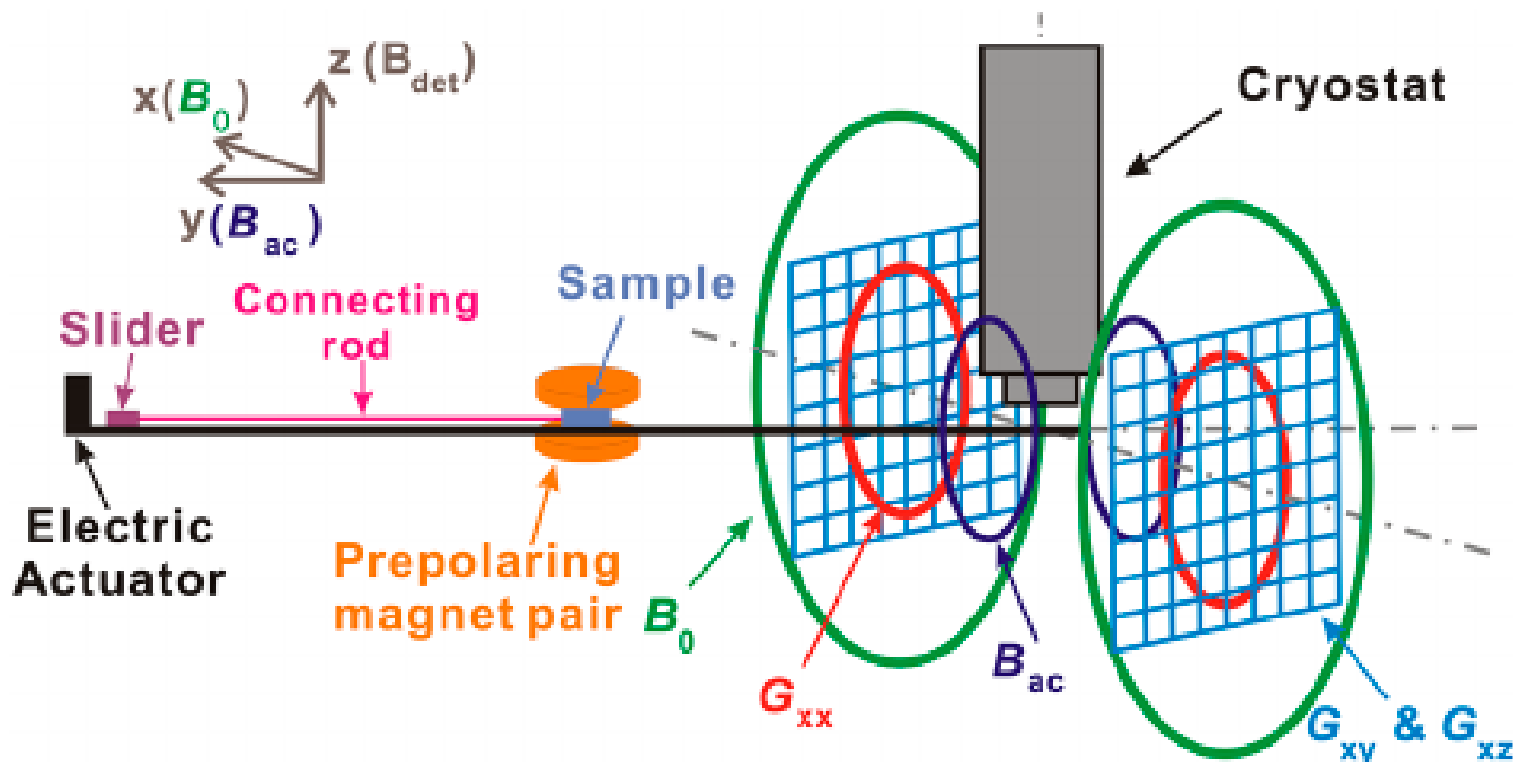
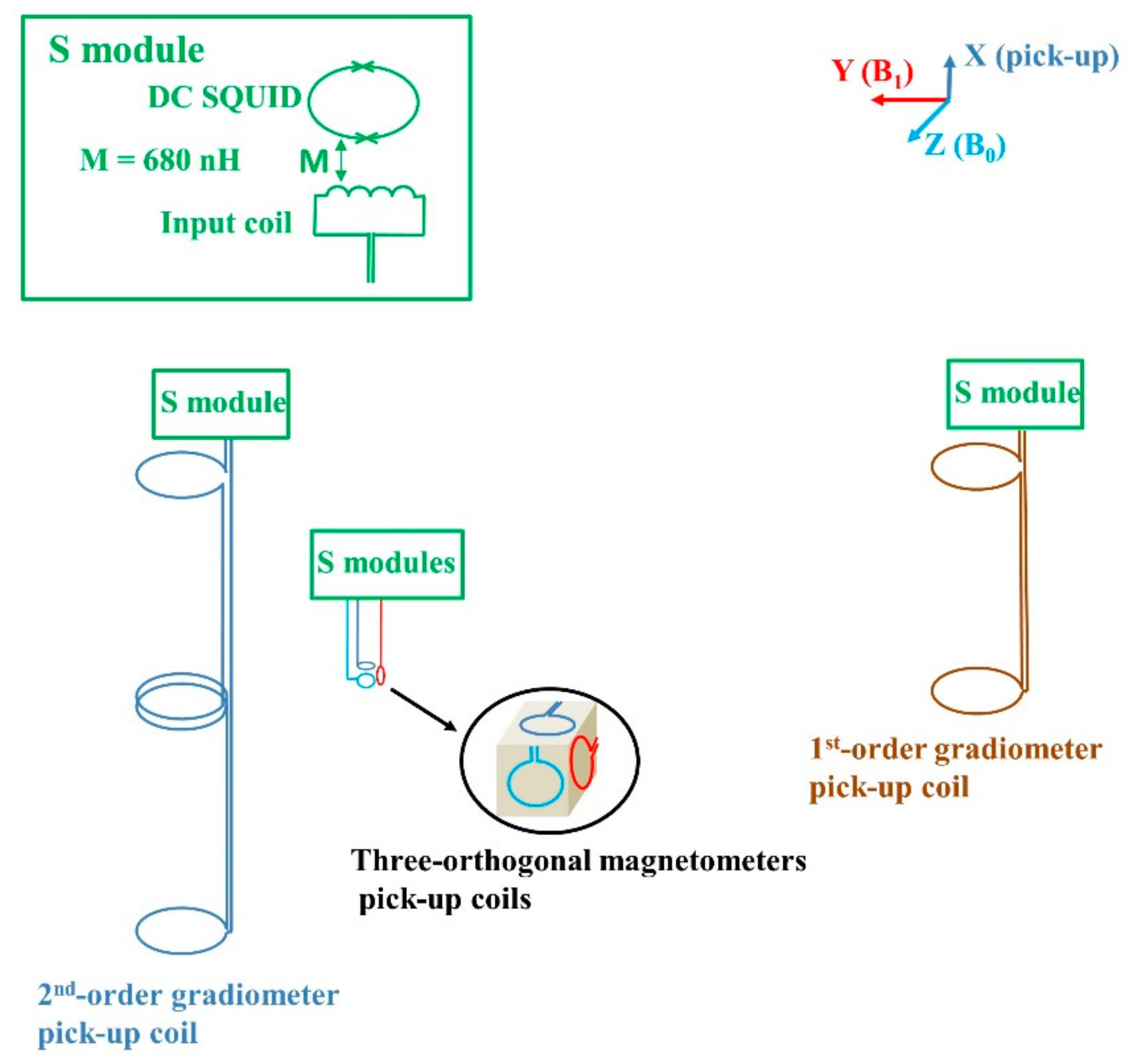
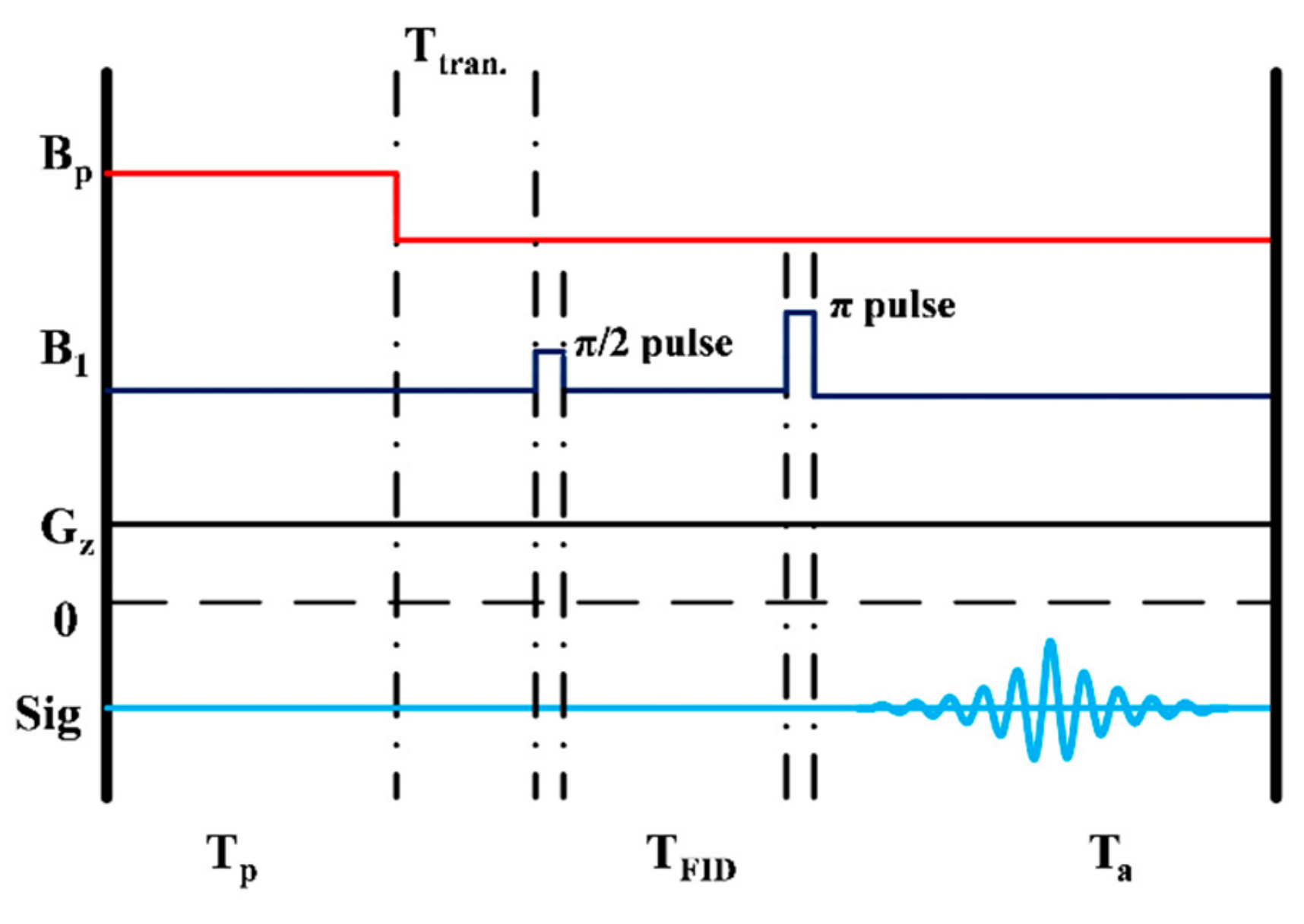
2.1. Sensor Configuration and Measurement Sequence
2.2. Interference Suppression Algorithms
2.2.1. Discrete Wavelet Analysis-Least Squares Method (DWA-LSM) Based De-Noising
2.2.2. Discrete Wavelet Analysis - Gradient Descending (DWA-GD) Based De-Noising
2.3. Numerical Simulation
3. Results and Discussion
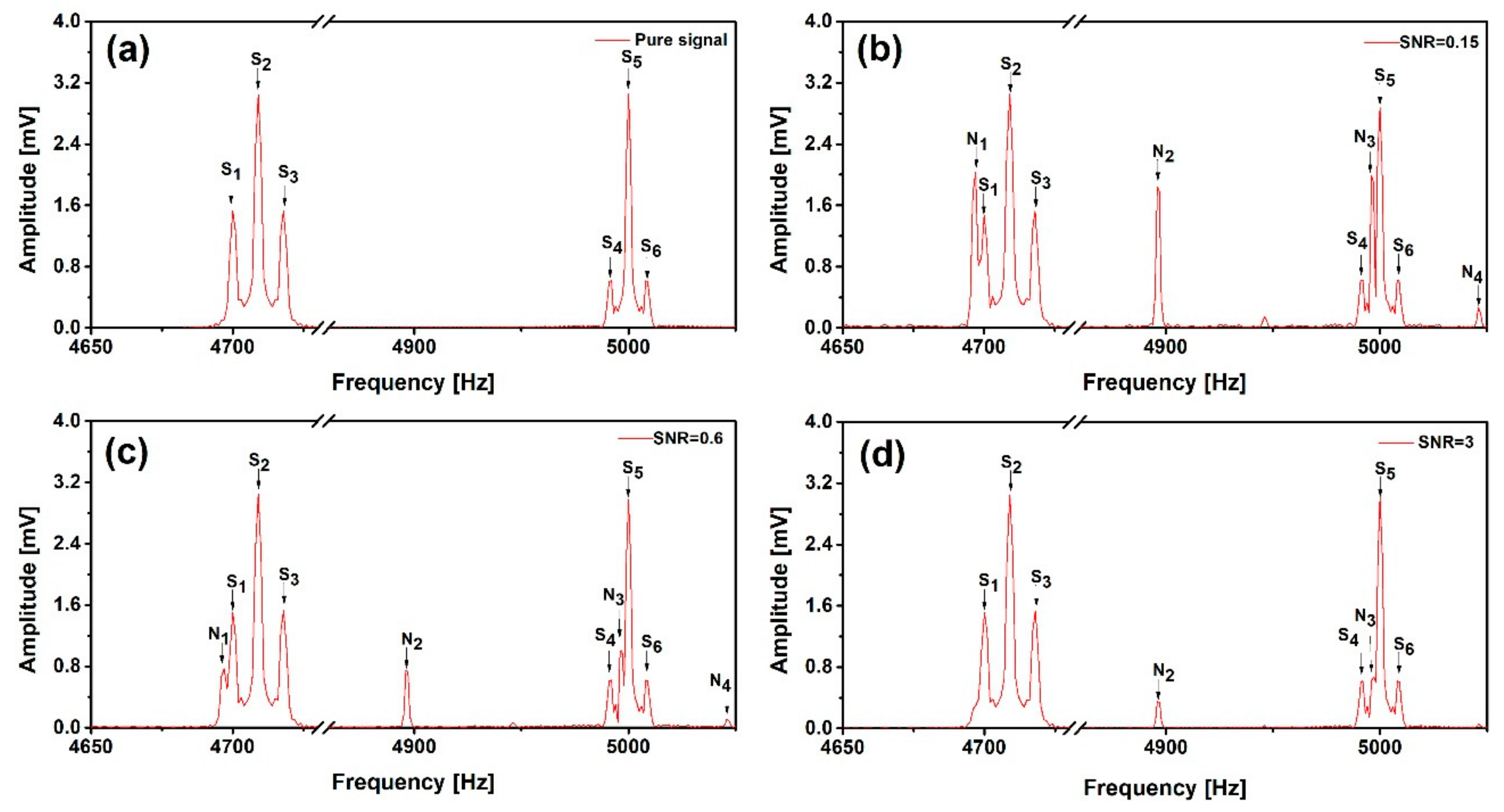
3.1. Spectral Correlation Coefficients
3.2. Interference Suppression Based on the DWA-LSM
3.3. Optimizing the Determination of the Suppression Coefficients
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Halse, M.; Coy, A.; Dykstra, R.; Eccles, C.; Hunter, M.; Ward, R.; Callaghan, P. A practical and flexible implementation of 3D MRI in the earth’s magnetic field. J. Magn. Reson. 2006, 182, 75–83. [Google Scholar] [CrossRef] [PubMed]
- Braginski, A.; Clarke, J. Applications of SQUIDs and SQUID systems. In The SQUID handbook; Wiley-VCH: Weinheim, Germen, 2006; pp. 269–390. [Google Scholar]
- Greenberg, Y. Application of superconducting quantum interference devices to nuclear magnetic resonance. Revi. Mode. Phys. 1998, 70, 175–222. [Google Scholar] [CrossRef]
- Ge, X.; Liu, J.; Fan, Y.; Xing, D.; Deng, S.; Cai, J. Laboratory investigation into the formation and dissociation process of gas hydrate by low-field NMR technique. J. Geophys. Res. Sol. Earth 2018, 123, 3339–3346. [Google Scholar] [CrossRef]
- Sutton, R.S.; Maei, H.R.; Precup, D.; Bhatnagar, S.; Silver, D.; Szepesvári, C.; Wiewiora, E. Fast gradient-descent methods for temporal-difference learning with linear function approximation. In Proceedings of the 26th Annual International Conference on Machine Learning, New York, NY, USA, 14–18 June 2009; pp. 993–1000. [Google Scholar]
- McDermott, R.; Trabesinger, A.H.; Mück, M.; Hahn, E.L.; Pines, A.; Clarke, J. Liquid-state NMR and scalar couplings in microtesla magnetic fields. Science 2002, 295, 2247–2249. [Google Scholar] [CrossRef] [PubMed]
- Burghoff, M.; Hartwig, S.; Trahms, L.; Bernarding, J. Nuclear magnetic resonance in the nanotesla range. Appl. Phys. Lett. 2005, 87, 054103. [Google Scholar] [CrossRef]
- Qiu, L.; Zhang, Y.; Krause, H.; Braginski, A.; Tanaka, S.; Offenhäusser, A. High-performance low-field NMR utilizing a high-Tc rf SQUID. IEEE Trans. Appl. Supercond. 2009, 19, 831–834. [Google Scholar] [CrossRef]
- Theis, T.; Blanchard, J.; Butler, M.; Ledbetter, M.; Budker, D.; Pines, A. Chemical analysis using J-coupling multiplets in zero-field NMR. Chem. Phys. Lett. 2013, 580, 160–165. [Google Scholar] [CrossRef]
- Elliott, D.; Schumacher, R. Proton resonance of fluorobenzene in the earth’s magnetic field. J. Chem. Phys. 1957, 26, 1350. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, L.; Krause, H.; Hartwig, S.; Burghoff, M.; Trahms, L. Liquid state nuclear magnetic resonance at low fields using anitrogen cooled superconducting quantum interference device. Appl. Phys. Lett. 2007, 90, 182503. [Google Scholar] [CrossRef]
- Espy, M.; Magnelind, P.; Matlashov, A.; Newman, S.; Sandin, H.; Schultz, L.; Sedillo, R.; Urbaitis, A.; Volegov, P. Progress toward a deployable SQUID-based ultra-low field MRI system for anatomical imaging. IEEE Trans. Appl. Supercond. 2015, 25, 1–5. [Google Scholar] [CrossRef]
- Dong, H.; Wang, Y.L.; Zhang, S.L.; Sun, Y.; Xie, X.M. Detection of proton NMR signal in the Earth’s magnetic field at an urban laboratory environment without shielding. Supercond. Sci. Technol. 2008, 21, 115009. [Google Scholar] [CrossRef]
- Mair, R.; Hrovat, M.; Patz, S.; Rosen, M.; Ruset, I.; Topulos, G.; Tsai, L.; Butler, J.; Hersman, F.; Walsworth, R. 3He lung imaging in an open access, very-low-field human magnetic resonance imaging system. Magn. Reson. Med. 2005, 53, 745–749. [Google Scholar] [CrossRef] [PubMed]
- Itagaki, H. Improvements of nuclear magnetic resonance image quality using iterations of adaptive nonlinear filtering. IEEE Trans. Med. Imag. 1993, 12, 322–327. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, O.; Fahmy, M. NMR signal enhancement via a new time-frequency transform. IEEE Trans. Med. Imag. 2001, 20, 1018–1025. [Google Scholar] [CrossRef] [PubMed]
- Zaroubi, S.; Goelman, G. Complex Denoising of MR data via wavelet analysis: application for functional MRI. Magn. Reson. Imag. 2000, 18, 59–68. [Google Scholar] [CrossRef]
- Lu, Y.H.; Joshi, S.; Morris, J. Noise Reduction for NMR FID signals via Gabor expansion. IEEE Trans. Biomed. Eng. 1997, 44, 512–528. [Google Scholar] [PubMed]
- Bouchouareb, R.; Benatia, D. Comparative Study between Wavelet Thresholding Techniques (Hard, Soft and Invariant-translation) in Ultrasound Images. Int. J. Bio-Sci. Bio-Tech. 2014, 6, 29–38. [Google Scholar]
- Ge, X.; Fan, Y.; Li, J.; Wang, Y.; Deng, S. Noise reduction of nuclear magnetic resonance (NMR) transversal data using improved wavelet transform and exponentially weighted moving average (EWMA). J. Magn. Reson. 2015, 251, 71–83. [Google Scholar] [CrossRef]
- Trabesinger, A.; McDermott, R.; Lee, S.; Mück, M.; Clarke, J.; Pines, A. SQUID-detected liquid state NMR in microtesla fields. J. Phys. Chem. A 2004, 108, 957–963. [Google Scholar] [CrossRef]
- Lane, J.E.; Martinez, E. DSP Filters; Butterworth-Heinemann: Oxford, UK, 2000; pp. 205–222. [Google Scholar]
- Widrow, B.; Glover, J.R.; McCool, J.M.; Kaunitz, J.; Williams, C.S.; Hearn, R.H.; Zeidler, J.R.; Dong, E.; Goodlin, R.C. Adaptive noise cancelling: Principles and applications. Proc. IEEE. 1975, 63, 1692–1716. [Google Scholar] [CrossRef]
- Jiruska, P.; Cmejla, R.; Powell, A.D.; Chang, W.C.; Vreugdenhil, M.; Jefferys, J.G. Reference noise method of removing powerline noise from recorded signals. J. Neurosci. Meth. 2009, 184, 110–114. [Google Scholar] [CrossRef] [PubMed]
- Legchenko, A.; Valla, P. Removal of power-line harmonics from proton magnetic resonance measurements. J. Appl. Geophys. 2003, 53, 103–120. [Google Scholar] [CrossRef]
- Huang, X.; Dong, H.; Qiu, Y.; Li, B.; Tao, Q.; Zhang, Y.; Krause, H.; Offenhäusser, A.; Xie, X. Adaptive suppression of power line interference in ultra-low field magnetic resonance imaging in an unshielded environment. J. Magn. Reson. 2018, 286, 52–59. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.; Qiu, L.; Shi, W.; Chang, B.; Qiu, Y.; Xu, L.; Liu, C.; Zhang, Y.; Krause, H.J.; Offenhäusser, A.; et al. Ultra-low field magnetic resonance imaging detection with gradient tensor compensation in urban unshielded environment. Appl. Phys. Lett. 2013, 102, 102602. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Noise Reduction in Speech Processing; Springer: Berlin, Heidelberg, 2009; pp. 37–40. [Google Scholar]
- Wu, Y.; Wang, S.; Wang, S. Research on wavelet threshold de-noising method of remainder detection for stand-alone electronic equipments in satellite. In Proceedings of the 2010 First International Conference on Pervasive Computing, Signal Processing and Applications, Harbin, China, 17–19 September 2010; pp. 1013–1017. [Google Scholar]
- Appelt, S.; Kühn, H.; Häsing, F.; Blümich, B. Chemical analysis by ultrahigh-resolution nuclear magnetic resonance in the Earth’s magnetic field. Nat. Phys. 2006, 2, 105–109. [Google Scholar] [CrossRef]
- Qiu, L.; Zhang, Y.; Krause, H.; Braginski, A. SQUID-detected NMR in Earth’s magnetic field. J. Phys. Conf. Ser. 2008, 97, 012026. [Google Scholar] [CrossRef]
- Zhanabaev, Z.Z.; Akhtanov, S.N.; Kozhagulov, E.T.; Karibayev, B.A. Determination of signal-to-noise ratio on the base of information-entropic analysis. arXiv 2016, arXiv:1609.09212. [Google Scholar]
- Graps, A. An introduction to wavelets. IEEE Comput. Sci. Eng. 1995, 2, 50–61. [Google Scholar] [CrossRef]
- Liu, Z.; Abbas, A.; Jing, B.; Gao, X. WaVPeak: picking NMR peaks through wavelet-based smoothing and volume-based filtering. Bioinformatics 2012, 28, 914–920. [Google Scholar] [CrossRef]
- Fan, G.; Wang, Z.; Kim, S.B.; Temiyasathit, C. Classification of high-resolution NMR spectra based on complex wavelet domain feature selection and kernel-induced random forest. Lect. Notes Comput. Sci. 2010, 6134. [Google Scholar] [CrossRef]
- Knuth, D.E. Big omicron and big omega and big theta. ACM Sigact News 1976, 8, 18–24. [Google Scholar] [CrossRef]
- Nesterov, Y. Introductory lectures on convex optimization: A basic course; Springer Science & Business Media: New York, NY, USA, 2014. [Google Scholar]
- Han, J.; Jian, P.; Michelin, K. Data Mining, Southeast Asia Edition, 2nd ed.; Elsevier: New York, NY, USA, 2006. [Google Scholar]
- Zhang, T. Solving large scale linear prediction problems using stochastic gradient descent algorithms. In Proceedings of the 21st Annual International Conference on Machine Learning, New York, NY, USA, 4–8 July 2004; p. 116. [Google Scholar]
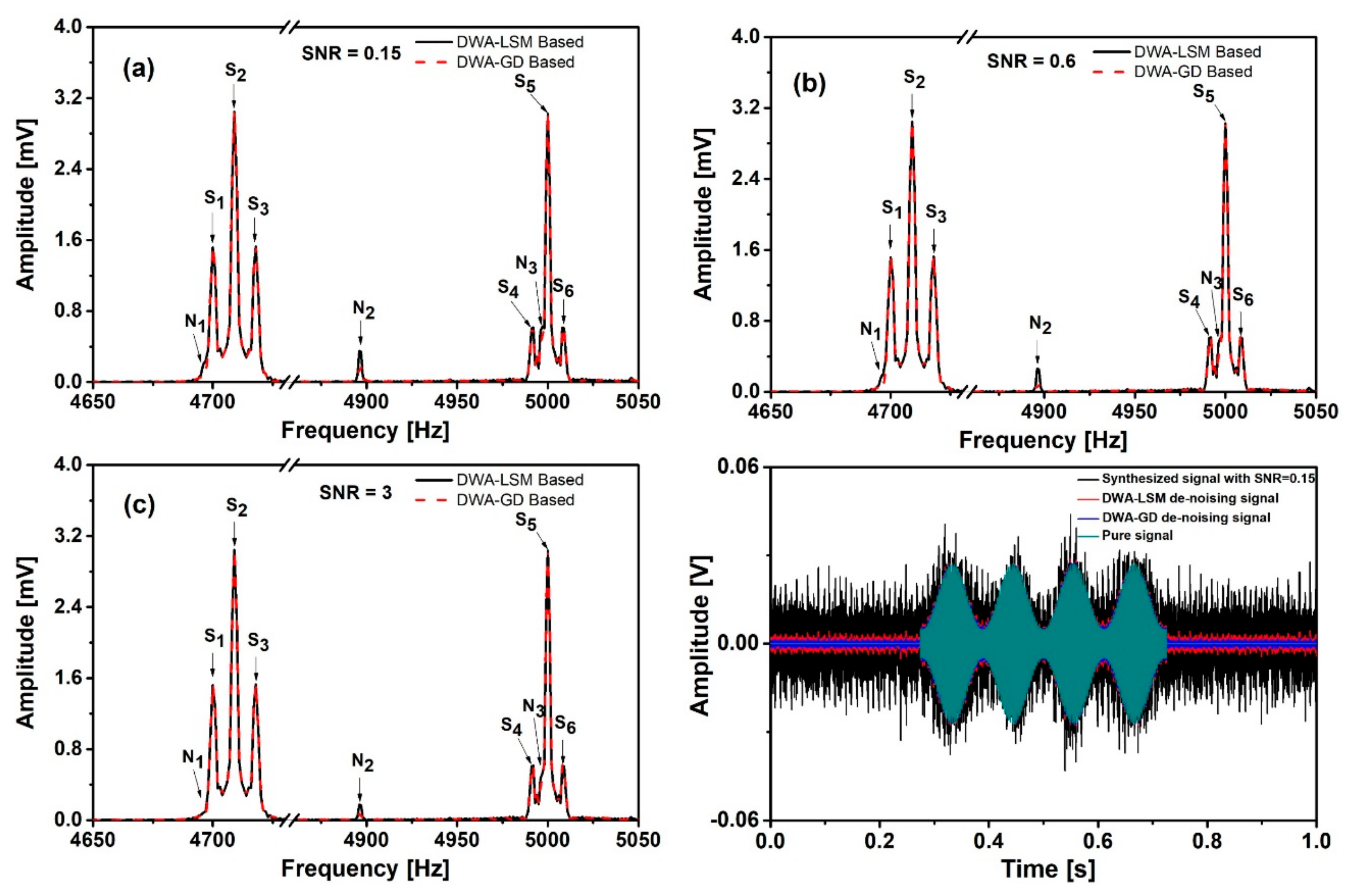
| SNR before De-Noising | 0.15 | 0.6 | 3 | ||
| SNR | After DWA-LSM | 2.9 | 5.3 | 11 | |
| After DWA-GD | 12.5 | 36 | 45 | ||
| The factors of SNR improvement | After DWA-LSM | 19.3 | 8.8 | 3.6 | |
| After DWA-GD | 83.3 | 60 | 15 | ||
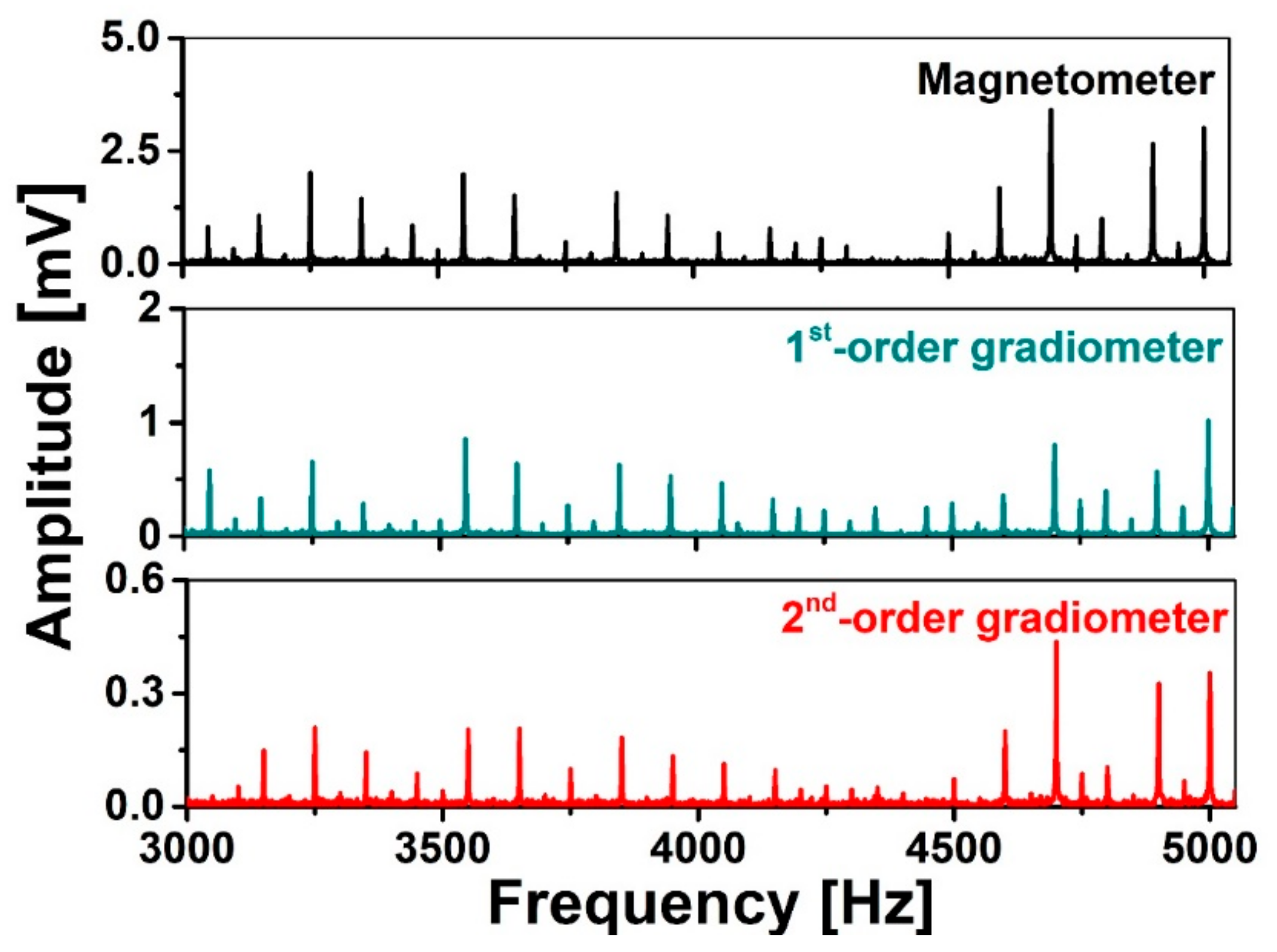
| PCC | Magnetometer | 1st-Order Gradiometer | 2nd-Order Gradiometer |
|---|---|---|---|
| Magnetometer | 1 | 0.91624 | 0.97076 |
| 1st-Order Gradiometer | 0.91624 | 1 | 0.89323 |
| 2nd-Order Gradiometer | 0.97076 | 0.89323 | 1 |
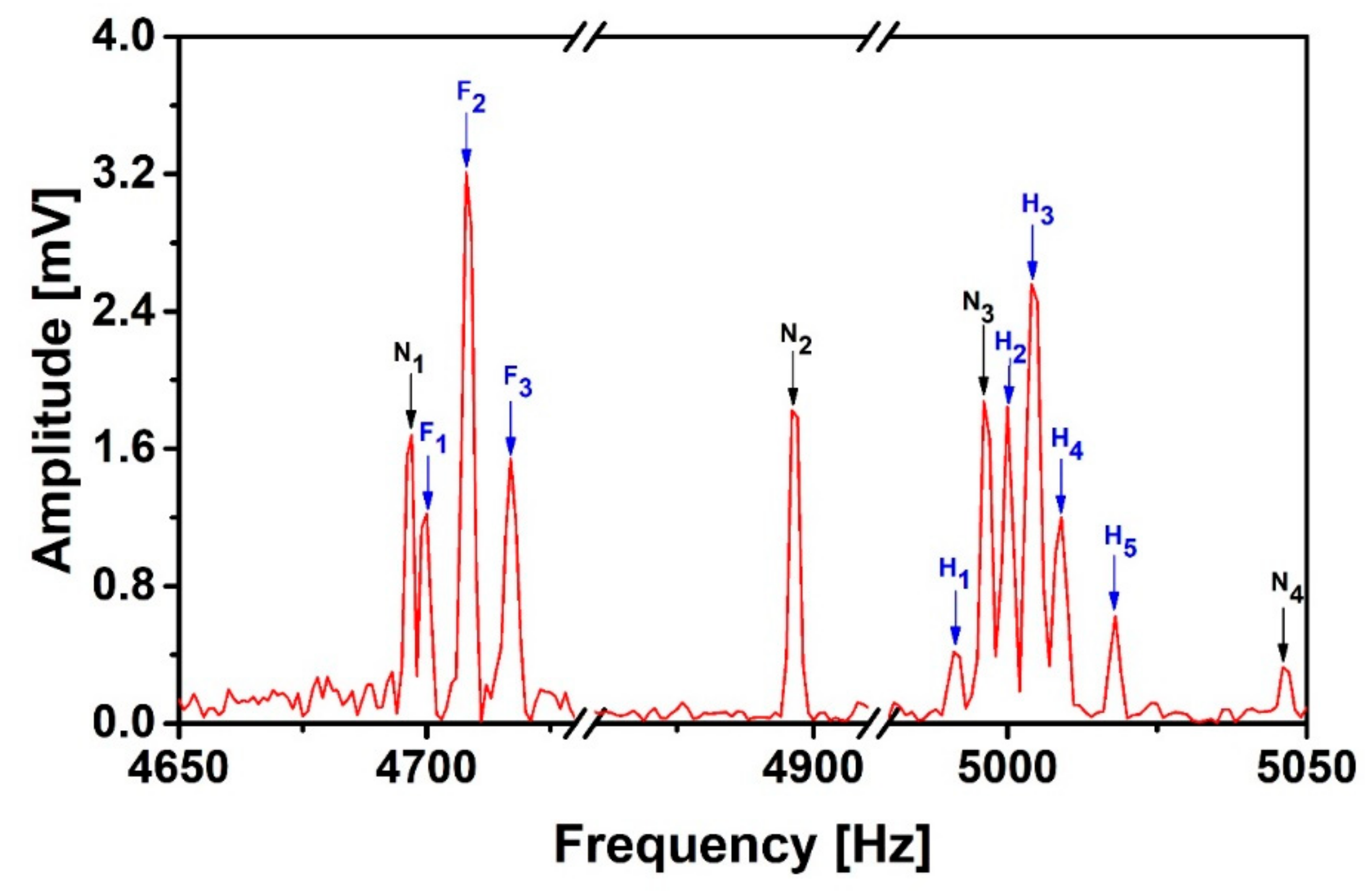
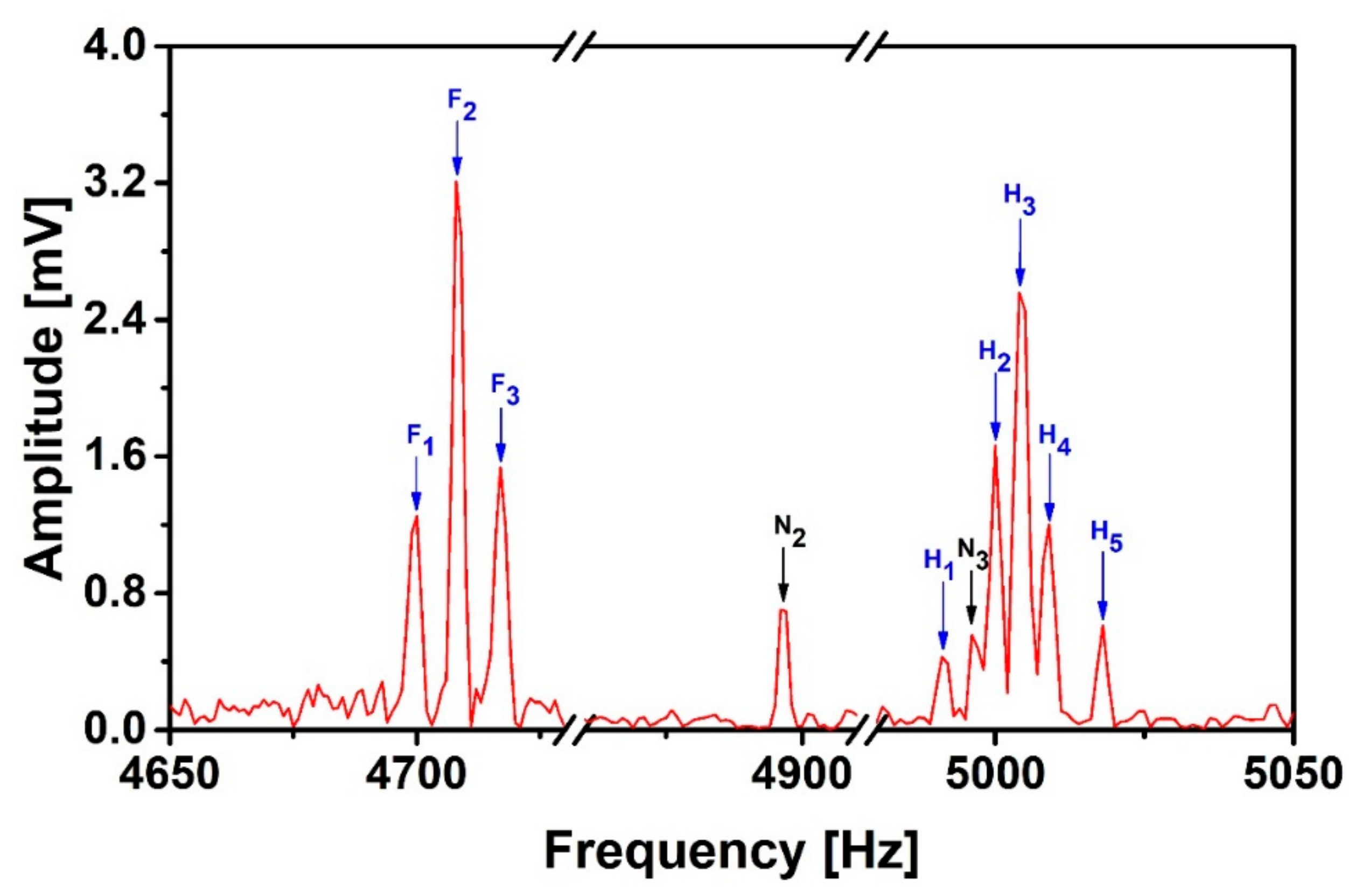
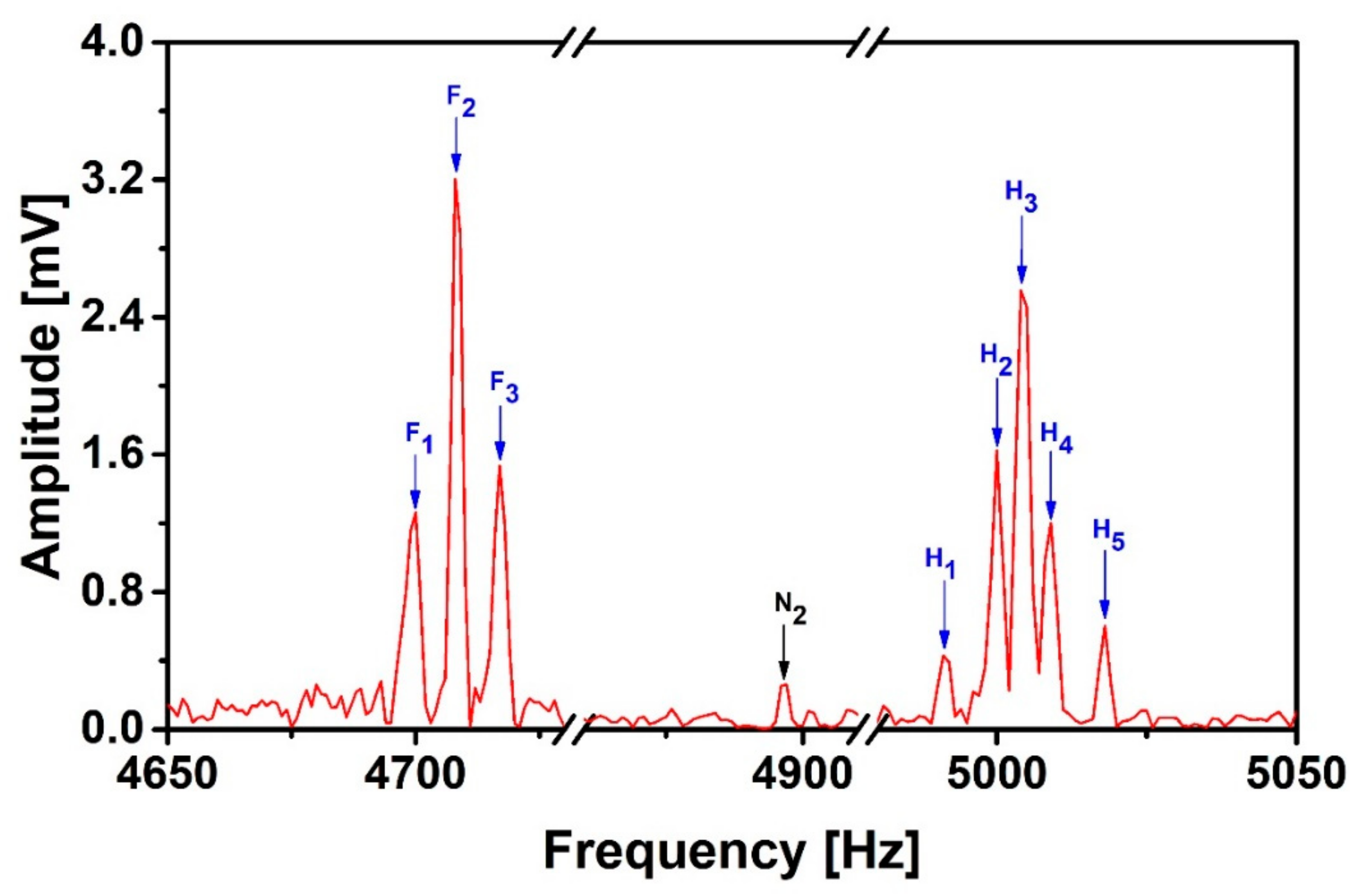
| Recorded Signal and Noise Peaks | F1 | F2 | F3 | H1 | H2 | H3 | H4 | H5 | N2 | ||
| Energy spectral density integral under peaks (10−6 J) * | Before de-noising | 3.3 | 22 | 5.56 | 0.38 | 5.11 | 15.3 | 3.09 | 0.6 | 6.62 | |
| After DWA-LSM | 3.52 | 22 | 5.53 | 0.39 | 4.8 | 15.3 | 3.08 | 0.58 | 1.02 | ||
| After DWA-GD | 3.62 | 22 | 5.53 | 0.4 | 4.5 | 15.3 | 3.08 | 0.57 | 0.14 | ||
| SNR | Before de-noising | 0.5 | 3.32 | 0.83 | 0.06 | 0.77 | 2.3 | 0.46 | 0.09 | / | |
| After DWA-LSM | 3.45 | 21.56 | 5.42 | 0.38 | 4.71 | 15 | 3.02 | 0.57 | |||
| After DWA-GD | 25.85 | 157.1 | 39.5 | 2.85 | 32.1 | 109.3 | 22 | 4.07 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Dong, H.; Tao, Q.; Yu, M.; Li, Y.; Rong, L.; Krause, H.-J.; Offenhäusser, A.; Xie, X. Sensor Configuration and Algorithms for Power-Line Interference Suppression in Low Field Nuclear Magnetic Resonance. Sensors 2019, 19, 3566. https://doi.org/10.3390/s19163566
Huang X, Dong H, Tao Q, Yu M, Li Y, Rong L, Krause H-J, Offenhäusser A, Xie X. Sensor Configuration and Algorithms for Power-Line Interference Suppression in Low Field Nuclear Magnetic Resonance. Sensors. 2019; 19(16):3566. https://doi.org/10.3390/s19163566
Chicago/Turabian StyleHuang, Xiaolei, Hui Dong, Quan Tao, Mengmeng Yu, Yongqiang Li, Liangliang Rong, Hans-Joachim Krause, Andreas Offenhäusser, and Xiaoming Xie. 2019. "Sensor Configuration and Algorithms for Power-Line Interference Suppression in Low Field Nuclear Magnetic Resonance" Sensors 19, no. 16: 3566. https://doi.org/10.3390/s19163566
APA StyleHuang, X., Dong, H., Tao, Q., Yu, M., Li, Y., Rong, L., Krause, H.-J., Offenhäusser, A., & Xie, X. (2019). Sensor Configuration and Algorithms for Power-Line Interference Suppression in Low Field Nuclear Magnetic Resonance. Sensors, 19(16), 3566. https://doi.org/10.3390/s19163566






