Logarithmic Strain Model for Nonlinear Load Cell
Abstract
1. Introduction
2. Logarithmic Strain Model
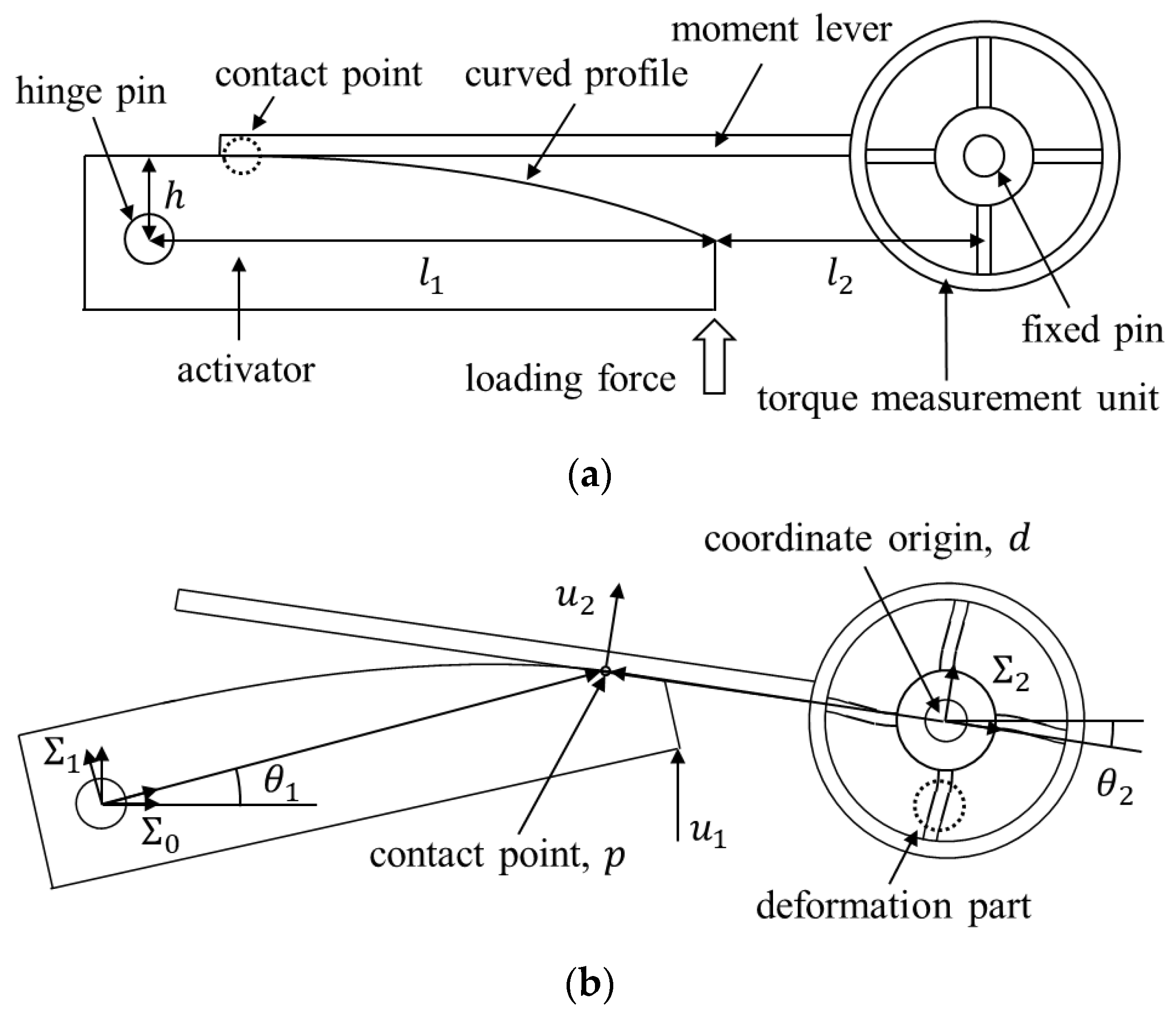
2.1. Logarithmic Map of Sensory System
2.2. Mechanism Design
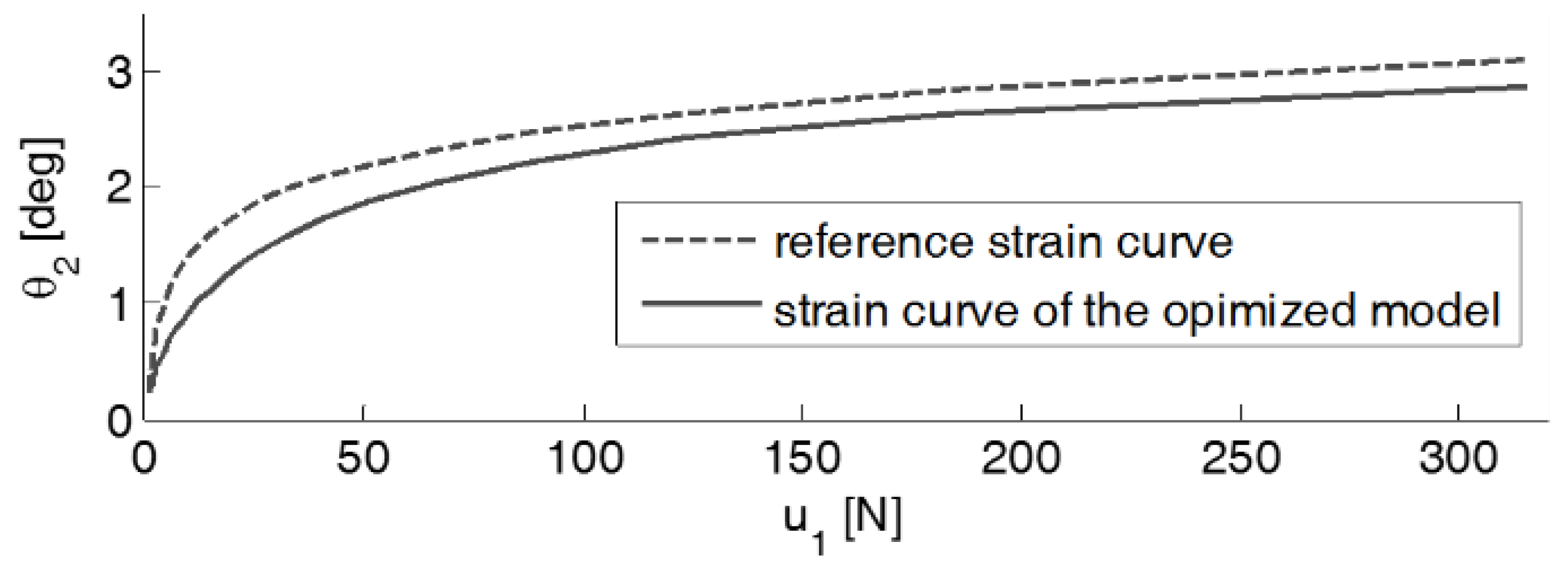
2.3. Optimization of Design Parameters
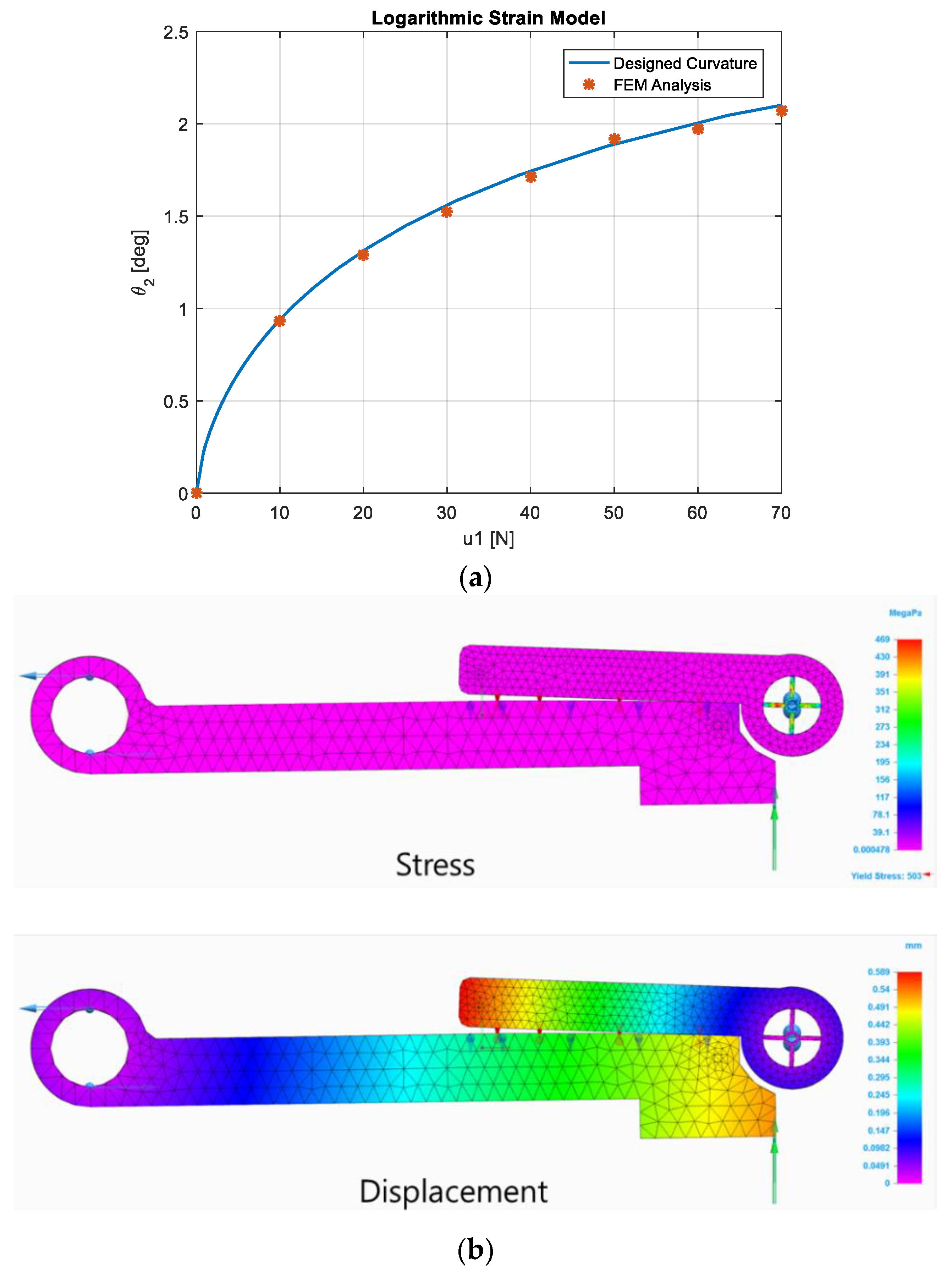
3. FEM Analysis
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kim, N.; Lee, B. Stack structured hybrid load cell for a high-stroke system. J. Adv. Mech. Des. Syst. Manuf. 2019, 13. [Google Scholar] [CrossRef]
- Muller, I.; de Brito, R.M.; Pereira, C.E.; Brusamarello, V. Load cells in force sensing analysis-theory and a novel application. IEEE Instrum. Meas. Mag. 2009, 13, 15–19. [Google Scholar] [CrossRef]
- Demetropoulos, C.K.; Morgan, C.R.; Sengupta, D.K.; Herkowitz, H.N. Development of a 4-axis load cell used for lumbar interbody load measurements. Med. Eng. Phys. 2009, 31, 846–851. [Google Scholar] [CrossRef] [PubMed]
- Adami, A.M.; Pavel, M.; Hayes, T.L.; Singer, C. Detection of movement in bed using unobtrusive load cell sensors. IEEE Trans. Inf. Technol. Biomed. 2009, 14, 481–490. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Yoon, H.; Han, C.; Joo, K.M.; Park, K.S. Physiological signal monitoring bed for infants based on load-cell sensors. Sensors 2016, 16, 409. [Google Scholar] [CrossRef] [PubMed]
- Balbinot, A.; Milani, C.; Nascimento, J. A new crank arm-based load cell for the 3D analysis of the force applied by a cyclist. Sensors 2014, 14, 22921–22939. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.-F.; Chu, C.-Y.; Xu, J.-Y.; Lan, C.-C. A humanoid robotic wrist with two-dimensional series elastic actuation for accurate force/torque interaction. IEEE/ASME Trans. Mechatron. 2016, 21, 1315–1325. [Google Scholar] [CrossRef]
- Schmitz, A.; Maggiali, M.; Natale, L.; Bonino, B.; Metta, G. A tactile sensor for the fingertips of the humanoid robot iCub. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 2212–2217. [Google Scholar]
- Park, H.; Lee, B.; Kim, D. Development of Anthropomorphic Robot Finger for Violin Fingering. ETRI J. 2016, 38, 1218–1228. [Google Scholar] [CrossRef]
- Park, I.-W.; Kim, J.-Y.; Lee, J.; Oh, J.-H. Mechanical design of the humanoid robot platform, HUBO. Adv. Robot. 2007, 21, 1305–1322. [Google Scholar] [CrossRef]
- Englsberger, J.; Werner, A.; Ott, C.; Henze, B.; Roa, M.A.; Garofalo, G.; Burger, R.; Beyer, A.; Eiberger, O.; Schmid, K.; et al. Overview of the torque-controlled humanoid robot TORO. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; pp. 916–923. [Google Scholar]
- Banala, S.K.; Kim, S.H.; Agrawal, S.K.; Scholz, J.P. Robot assisted gait training with active leg exoskeleton (ALEX). In Proceedings of the 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Scottsdale, AZ, USA, 19–22 October 2008; pp. 653–658. [Google Scholar]
- Mastinu, G.; Gobbi, M.; Previati, G. A new six-axis load cell. Part I: design. Exp. Mech. 2011, 51, 373–388. [Google Scholar] [CrossRef][Green Version]
- Gobbi, M.; Previati, G.; Guarneri, P.; Mastinu, G. A new six-axis load cell. Part II: Error analysis, construction and experimental assessment of performances. Exp. Mech. 2011, 51, 389–399. [Google Scholar] [CrossRef]
- Ballo, F.; Gobbi, M.; Previati, G.; Mastinu, G. Advances in force and moments measurements by an innovative six-axis load cell. Exp. Mech. 2014, 54, 571–592. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, Y.-D.; Lee, B. Logarithmic Strain Model for Nonlinear Load Cell. Sensors 2019, 19, 3486. https://doi.org/10.3390/s19163486
Hong Y-D, Lee B. Logarithmic Strain Model for Nonlinear Load Cell. Sensors. 2019; 19(16):3486. https://doi.org/10.3390/s19163486
Chicago/Turabian StyleHong, Young-Dae, and Bumjoo Lee. 2019. "Logarithmic Strain Model for Nonlinear Load Cell" Sensors 19, no. 16: 3486. https://doi.org/10.3390/s19163486
APA StyleHong, Y.-D., & Lee, B. (2019). Logarithmic Strain Model for Nonlinear Load Cell. Sensors, 19(16), 3486. https://doi.org/10.3390/s19163486




